Abstract
This paper presents an optimal watermark embedding method combining spread spectrum and quantization. In the method, the host signal vector is quantized to embed a multiple-bit watermark, and meanwhile, the quantized signal is made to locate in the detectable region defined in the context of spread spectrum watermarking. Under the two constraints, the optimal watermarked signal is derived in the sense of minimizing the embedding distortion. The proposed method is further implemented in wavelet transform domain, where the insensitive wavelet coefficients are selected according to the modified human visual model for watermark embedding. Simulations on real images by using the wavelet-based implementations demonstrate the proposed method performs very well in both watermark imperceptibility and robustness and is more robust to typical signal processes, e.g., additive noise, JPEG compression, etc., as compared with the state-of-the-art watermarking methods.
Similar content being viewed by others
1 Introduction
The notable benefits of digital multimedia, ease of manipulation and transmission, put more and more heavy pressure on the copyright protection. To solve the problem, the basic idea of digital watermarking is to embed auxiliary information into multimedia data, such as image, audio, video, and text [1].
Usually, robust watermarks are used for proof of ownership, while fragile watermarks are used to check the integrity and authenticity of digital contents [2, 3].
Most of existing watermarking schemes are designed for a single purpose by exploiting a single watermark. However, there has been recently increasing research interest in developing multiple watermark techniques to accomplish more than one purposes.
In [2], the problem of embedding multiple watermarks was first discussed, and several typical application situations were presented.
The specific methods on multiple watermarks were developed in [4] by introducing orthogonal watermarks into single watermarking algorithms. The corresponding optimization problem with respect to the crucial watermarking parameter was investigated in [5]. The drawback is that this type of watermarking is weak against collusion attack [6], and the closest encoded messages becomes inseparable as the watermark message length increases. Alternatively, multiple watermark embedding is performed by selecting different positions for the insertion of multiple watermarks. For example, in [7], multiple watermarks were independently inserted into the frequency and phase of an audio signal, and in [8], the robust and semifragile watermarks were respectively embedded into the approximation and residual components of an image, while in [9], the subsampling technique was applied to an host image for the insertion of both the invisible and visible watermarks. These watermarking schemes avoid the mutual effect of multiple watermarks to be hidden, but reduce the embedding capacity. In [10], multiple watermarks were sequentially embedded into an image based on elementary linear algebra against storage, transmission, and format conversion. The method significantly improves watermarking security. In [11], image Hash was generated and embedded into a host image based on multi-scale curvelet transform. The method realizes content authentication and copyright protection without considering embedding of two watermarks.
A novel dual watermarking method is presented in this paper. The main idea is that the host signal is quantized to embed a multi-bit message, and simultaneously, the quantized signal is made to be located in the detectable region defined according to spread spectrum (SS)-based watermarking paradigm [12, 13], while keeping the embedding distortion minimal. To the best of our knowledge, the combination of SS and quantization has not yet been attempted so far. The method is different from the existing dual watermark methods [4, 7–11], where no optimization is taken into account. In addition, the work related to ours is the optimization framework presented in [14]. The difference lies in that the theoretical framework is established only based on the method of projections onto convex sets.
The remainder of this paper is structured as follows. In Section 2, the basic dual watermarking model is developed by combining spread spectrum and quantization watermarking techniques. Next, Section 3 is devoted to the embedding optimization studies, and the expression of the embedding function is derived. A specific watermarking implementation is presented in Section 4 based on the new dual watermarking method. Then, the experimental results and performance comparisons are given in Section 5. Finally, Section 6 concludes.
2 Problem model
The proposed dual watermarking combines the currently popular two watermarking techniques, quantization, and SS watermarking. The scheme allows us to embed and extract a multi-bit watermark message and detect the existence of watermark even with a high error rate of information extraction. The basic watermarking model is described in detail as follows.
2.1 Models of quantization and SS watermarking
Let \(\boldsymbol {x} \in \mathbb {R}^{L}\) denote a host signal vector in which we wish to embed the watermark signal. The host signal could be a vector of pixel values, DCT coefficients, or any other transform domain coefficients from a host content. The extraction of the host signal affects the watermarking performance significantly, but it is not the main problem addressed in this paper. In the SS-based watermarking [12], a pseudo-random vector \(\boldsymbol {u}\in \mathbb {R}^{L}\) called the spreading vector is linearly combined with the host signal x to obtain the watermarked signal y s . Under the typical additive modulation, we can write
where α is the global gain factor to control the watermark strength. The elements of u are usually generated by uniformly taking values [−1,1]. The difference vector \(\boldsymbol {w}\mathop {=}\limits ^{\triangle }\boldsymbol {y}_{s}-\boldsymbol {x}\) is called the watermark signal.
At the detector side, a signal \(\boldsymbol {z}\in \mathbb {R}^{L}\), that might be a distorted version of y s , is received. The watermark detection is carried out on the received signal by using a standard detection statistic method
where ρ is the linear correlation (LC) between z and u. If the value of (2) is greater than a pre-determined threshold, then the watermark is said to be present. The threshold depends on the chosen false positive probability [15].
SS watermarking was shown to be efficient, robust, and cryptographically secured. But it does not cancel the host interference and thus causes the limited embedding capacity.
Different from SS-based watermarking, quantization-based watermarking works by quantizing a set of features extracted from the host content. An outstanding representative of this category is quantization index modulation (QIM) [13]. According to the basic implementation of QIM, called binary dither modulation (DM), the watermark message m is first represented by a vector b with L binary components, i.e., b j ∈{0,1},j=1,⋯,L. In this procedure, coding strategies, e.g., repetition coding, can be applied to offer a necessary performance gain.
Then, for each message bit b j , two one-dimensional uniform quantizers Q j,0(·) and Q j,1(·) are constructed, whose centroids are given by the lattices \(\Lambda _{j,0}=\Delta (\mathbb {Z}+d_{j})\) and \(\Lambda _{j,1}=\Delta \left (\mathbb {Z}+d_{j}+\frac {1}{2}\right)\) with Δ denoting the quantization step and d j being a key-dependent dither value. The watermarked vector y q is produced by quantizing each element of the host signal x with the quantizer indexed by the message bit to be hidden, i.e.,
where x j and y q,j are respectively the jth element of the vectors x and y q .
Last, a message \(\hat {\boldsymbol {b}}\) is extracted from the received signal z by using the minimal distance decoder
where z j and \(\hat {b}_{j}\) refers to the jth element of the vectors z and \(\hat {\boldsymbol {b}}\), respectively.
The quantization watermarking obtains null host signal interference and achieves a significant gain in terms of watermark capacity over SS watermarking. However, it suffers from serious disadvantages like extreme sensitivity to valumetric scaling [16] and fading operation [17].
2.2 Dual watermarking model
In the proposed watermarking model, the spreading watermark signal and a multi-bit watermark message can be inserted into the host signal simultaneously. A basic implementation of this model is developed based on the SS watermarking with LC-based detector and the quantization watermarking using binary DM.
For the sake of explanation, we introduce the definitions of the detectable region \(\mathcal {R}_{d}\) and a set of vectors \(\mathcal {V}_{m}\) associated with the embedded message m. The detection region is a set containing all the vectors from which the presence of the watermark can be verified. For the LC-based detector, considering the symmetry of LC, the detectable region is defined as \(\mathcal {R}_{d}=\{\boldsymbol {r}||\boldsymbol {r}^{T}\boldsymbol {u}|\geq \rho _{t},\boldsymbol {r} \in \mathbb {R}^{L}\}\), where ρ t ≥0 is the pre-determined threshold. Figure 1 illustrates a geometric interpretation for the detectable region. In Fig. 1, the detection region indicated by the shading is separated from the whole vector space by two hyperplanes perpendicular to the spreading vector u, and the distance from the origin to one hyperplane is determined by the detection threshold ρ t . The defined detection region is somehow different from the traditional one, which is just located on the right side of the right hyperplane in Fig. 1. The alteration expands the detection region and is thus favorable for inserting the multi-bit watermark message.
The introduced set \(\mathcal {V}_{m}\) contains all the vectors of length L, from each of which the embedded message m can be correctly extracted. With this meaning of \(\mathcal {V}_{m}\) and considering the minimal distance decoder (4), we define \(\mathcal {V}_{m}\) as \(\mathcal {V}_{m}=\left \{(v_{1},v_{2},\cdots,v_{L})^{T}|v_{j}\in \Lambda _{j,b_{j}},j=1,\cdots,L\right \}\) for binary DM. According to the definition, watermark embedding of binary DM can be rewritten as
where ∥·∥ stands for the Euclidean norm. A geometric interpretation for the embedding rule is given in Fig. 1. In this figure, quantization cells are represented by nested hexagonal lattices with the centroids marked by smaller solid points. The host vector x indicated by an open circle is quantized to the centroid of some nested hexagonal lattice, which belongs to the set \(\mathcal {V}_{m}\) and is nearest to x.
To achieve the goal of the dual watermarking, the watermarked signal should be selected from the set \(\mathcal {V}_{m}\) and made to be located in the detectable region \(\mathcal {R}_{d}\). Subject to the two constraints, the optimal watermarked signal \(\boldsymbol {y}_{o} \in \mathbb {R}^{L}\) is obtained by minimizing the embedding distortion in order to reduce the impact of watermark embedding. When the embedding distortion is measured by the squared Euclidean distance of the signals y o and x, i.e., ∥y o −x∥2, the dual embedding rule can be simply represented by
where ∩ is the intersection operator.
A geometric interpretation for the embedding rule is shown in Fig. 1. The watermark signal lies within the intersection of the points of the set \(\mathcal {V}_{m}\) and the detection region \(\mathcal {R}_{d}\) and is the nearest one to the host vector x. This will inevitably cause the extra embedding distortion comparing to the embedding rule (3). Our simulations showed that the quality loss may be neglected for practical applications.
The dual watermarking method allows us to achieve a high watermark payload. The advantage is offered by the adopted quantization scheme. The presence or absence of the watermark can be also verified as in SS watermarking. Their integration can fulfill multipurpose applications, such as ownership verification and content authentication.
According to the previous works [13, 15], a few observations are in order about the given method. The embedding capacity is closely related to the quantization step Δ, the signal size L, and the utilized coding technique. The watermark imperceptibility is mainly dependent on Δ and on the threshold ρ t . The watermark robustness in watermark extraction relies on Δ and the coding technique, while in watermark detection, the dominant effect arises from the choices of ρ t and L. Therefore, by choosing these embedding parameters and the coding technique, the proposed method can achieve high capacity-distortion-robustness trade-offs. The investigation of the theoretical performance of the method will be done in future. The goal of this paper is to solve (6) to give the explicit expressions for the watermark embedding.
3 Embedding function of dual watermarking
In this section, the watermark embedding function is achieved by solving the constrained optimization problem (6). For this purpose, we first present several properties that the optimal solution should satisfy. Based on them, the close-form expression of the optimal solution is then derived.
Let \(\boldsymbol {e}\mathop {=}\limits ^{\triangle }\boldsymbol {y}_{q}-\boldsymbol {x}\) denote the quantization error vector and define \(D_{0}\mathop {=}\limits ^{\triangle }\|\boldsymbol {e}\|^{2}\). With the definition of quantizers used in (3), we have ∥y a −x∥2≥D 0 for any vector \(\boldsymbol {y}_{a}\in \mathcal {V}_{m}\). As a result, if y q satisfies the constraint \(\boldsymbol {y}_{q}\in \mathcal {R}_{d}\), the solution of (6) is y q , i.e., y o =y q . However, in general, this case does not occur due to the fact that a relatively large ρ t is chosen for the real watermarking applications.
To deal with the general case, the vector \(\boldsymbol {y}_{a}\in \mathcal {V}_{m}\) is expressed as y a =y q +k Δ with \(\boldsymbol {k}\in \mathbb {Z}^{L}\). Letting \(\rho _{a}=|\boldsymbol {y}_{a}^{T}\boldsymbol {u}|\), we obtain \(\rho _{a}=|\boldsymbol {y}_{q}^{T}\boldsymbol {u}+\Delta \boldsymbol {k}^{T}\boldsymbol {u}|\). This expression shows that ρ a is a discrete variable with the step size Δ. Thus, the problem (6) can be solved by searching a sequence in the set \(\mathcal {V}_{m}\), \(\boldsymbol {y}_{i}\in \mathcal {V}_{m}, i=1,\cdots, N\), owing the following properties.
Property 1: the absolute inner products \(\rho _{0}=|\boldsymbol {y}_{q}^{T}\boldsymbol {u}|\) and \(\rho _{i}=|\boldsymbol {y}_{i}^{T}\boldsymbol {u}|,i=1,\cdots,N\) form an ascending series with the step size Δ, i.e., ρ i −ρ i−1=Δ.
Property 2: only for the last vector y N in the sequence, the absolute inner product ρ N is not lower than ρ t , that is, ρ N ≥ρ t but ρ N−1<ρ t .
Property 3: the resulting squared Euclidean distances D i ,i=1,⋯,N, with D i =∥y i −x∥2, satisfy D i >D i−1 and besides y q ,y 1,⋯,y i−1, the vector y i is the one nearest to x among all the other vectors of \(\mathcal {V}_{m}\), that is, \(\boldsymbol {y}_{i}=\text {arg}\min \limits _{\boldsymbol {y}\in \widetilde {\mathcal {V}}_{i-1}} \|\boldsymbol {y}-\boldsymbol {x}\|^{2}\), where the set \(\widetilde {\mathcal {V}}_{i}\) is defined as \(\widetilde {\mathcal {V}}_{i}=\{\boldsymbol {y}\in \mathcal {V}_{m}\mid \|\boldsymbol {y}-\boldsymbol {x}\|^{2}>D_{i}\}\).
Properties 1 and 3 guarantee that y i is the nearest vector to the host one x in \(\mathcal {V}_{m}\) having the absolute inner product ρ i =ρ 0+i Δ. Property 2 provides the necessary condition to stop searching. Obviously, to meet Property 2, N=⌈(ρ t −ρ 0)/Δ⌉ holds, where ⌈·⌉ refers to the ceil function.

Based on these properties, we can get the expressions of the vector sequence \(\boldsymbol {y}_{i}\in \mathcal {V}_{m}, i=1,\cdots, N\), which are shown in Lemmas 1 and 2.
Lemma 1.
Assuming n i ,i=1,⋯,L are the indices with which the elements of \(\text {sgn}(\boldsymbol {y}_{q}^{T}\boldsymbol {u})\boldsymbol {u}\cdot \boldsymbol {e}\) are sorted in ascending order, the vectors y i ,i=1,⋯,L can be constructed by y i =y i−1+k i Δ with y 0=y q and k i having the element
Lemma 2.
The vector y i with i>L can be constructed by
with λ=⌊i/L⌋ and p=i−λ×L, where ⌊·⌋ represents the floor function.
Proof.
See Appendix.
According to Lemmas 1 and 2, we present the procedure for solving the minimization problem (6), which is shown in Algorithm 1. In the algorithm, the vectors x, u, b, and d as well as parameters Δ and ρ t are regarded as the known variables to be input into the embedding function. From the 1st row to the 5th row, the vector in the set \(\mathcal {V}_{m}\) nearest to the host vector x is obtained, and is justified to be in the detection region \(\mathcal {R}_{d}\) or not. By the 6th row, the factor λ N and the index p N are initialized for the case of i=N in (8). The vector \(\boldsymbol {y}_{p_{N}}\) in (8) is calculated in the 7st row to the 12th row based on Lemma 1. Last, in the 13th row, the final watermarked vector y o is obtained according to Lemma 2.
4 Watermarking implementation for still images
In this section, we present a wavelet-domain dual watermarking implementation for still images. In this method, watermark embedding is achieved by modifying the insensitive wavelet coefficients of the host image with dual watermarking technology. The basic procedures of watermark embedding and detection are illustrated in Fig. 2 and described in detail as follows.
4.1 Watermark embedding
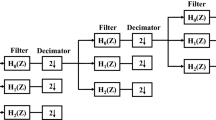
First, a four-level wavelet transform with HAAR filter is applied to the target image X, producing thirteen wavelet subbands, as shown in Fig. 3. The wavelet subband at resolution level l∈{0,1,2,3} and with orientation θ∈{0,1,2,3} is denoted by \(\boldsymbol {X}^{\theta }_{l}\) and the notation \(x^{\theta }_{l}(i,j)\) means the wavelet coefficient located at (i,j) of \(\boldsymbol {X}^{\theta }_{l}\). Wavelet transform is employed in the watermarking method, by considering the fact that in the transform domain, it is convenient to adapt the watermark signal to the local image characteristics and deal with some common attacks (e.g., lossy compression and filtering).
The local noise sensitivity \(\boldsymbol {S}^{1}_{2}\) of the wavelet subband \(\boldsymbol {X}^{1}_{2}\) is then computed by applying the modified human visual model (HVM) in [18]. To be specific, the noise sensitivity of each wavelet coefficient is determined by the weighted product of three terms
where the first two terms respectively reflect the effects of the orientation and the resolution level, and the local brightness on the noise sensitivity, which are defined as in [18]. The third term Ξ(l,i,j) in (9) gives a measure of texture activity in the neighborhood of the pixel. The definition of Ξ(l,i,j) is modified as
where Var(·) stands for the variance operator. The difference between (10) and the original expression of Ξ(l,i,j) in [18] is that the local mean square value of the subbands on the resolution level l is neglected in (10). By the alterations, it is guaranteed that the watermark embedding does not affect the host signal extraction for watermark detection.
Next, the wavelet coefficients of the subband \(\boldsymbol {X}^{1}_{2}\) are randomly grouped into L subsets, and in each subset, the wavelet coefficient with the largest local noise sensitivity, referred to as insensitive wavelet coefficient, is extracted to form the host vector x of length L. Meanwhile, the spreading vector u and the dither vector d are generated by using a pseudo-random number generator initialized with the secure key K. The detection threshold ρ t is chosen based on the resulting probability of false alarm (PFA), and by adjusting the quantization step Δ, the watermarking image is made to meet a given objective image quality index, e.g., peak signal-to-noise ratio (PSNR), the mean structural similarity index (MSSIM) [19]. The theoretical analysis for the effects of ρ t and Δ is beyond the scope of this paper and is a good direction for future research.
Last, the watermark message m and the spreading signal u are embedded into the extracted host vector x to produce the watermarked vector y o , by using Algorithm 1. The watermarked image Y is obtained by replacing the original wavelet coefficients in the subband \(\boldsymbol {X}^{1}_{2}\) with the corresponding watermarked ones and performing the inverse wavelet transform.
4.2 Watermark detection
The detection procedure consists of the following steps.
-
A four-level wavelet transform with HAAR filter is applied to the received image Z, and the resultant subband at resolution level l and with orientation θ is denoted by Z l θ.
-
The local noise sensitivity of the wavelet subband \(\boldsymbol {Z}^{1}_{2}\) is computed by applying the modified HVM in last subsection.
-
The vector z is extracted from the subband \(\boldsymbol {Z}^{1}_{2}\) by the local noise sensitivity as done in the watermark embedding procedure.
-
The dither vector d and the spreading vector u dependent on the key K are reproduced by using the pseudo-random number generator. With the step size Δ used in watermark embedding and the dither vector d, a message \(\hat {m}\) can be decoded by carrying out the the minimal distance decoder on z.
-
The LC ρ ′ between z and u is calculated as in (2) and compared with the detection threshold ρ t′ determined by the given PFA value to report whether or not the watermark exists in the received image.
The proposed scheme has the following advantages: (1) watermark embedding positions are determined according to the modified HVM, (2) watermark invisibility and robustness increase because the watermark is embedded in local insensitive wavelet coefficients, (3) a multi-bit message and the spreading watermark signal are simultaneously inserted into the target image by one-time embedding, and (4) the existence of the watermark can be verified even if a high error rate is present while extracting the hidden information.
5 Experimental results
In the experiments, we used a database of 1000 images from the Corel database, each of size 768×512. A host signal of length L=768 was extracted from each image in the wavelet transform domain. A binary message of length 192 bits was generated randomly and embedded into the extracted signal with the spreading watermark signal of length L=768. The watermarking performance is investigated in terms of imperceptibility and robustness.
5.1 Watermark imperceptibility
When fixing ρ t =16L (corresponding to PFA of 10−6), by adjusting the quantization step Δ, we obtained the watermarked images with the average PSNR of 42 dB, several examples of which are shown in Fig. 4. To assess the watermark imperceptibility, the MSSIM metric is adopted due to its compatibility with the human visual system. Impressively, for the given PSNR, the watermarked images shown in Fig. 4 (from top to bottom) have the MSSIM of 0.9953, 0.9972, 0.9960, and 0.9968, indicating that they are of high perceptual quality. As to the subjective visual quantity, these images look almost the same as the original ones and it is impossible to distinguish them by human eyes. Additionally, from the obtained difference images, shown in the 3rd column of Fig. 4, it is observed that the embedded watermarks are definitely reshaped into high activity regions and around edges. These observations reveal that the embedded watermarks are masked very well, and the pretty ideal imperceptibility is achieved.
Further, we examine the effect of the detection threshold on the watermark imperceptibility. For several typical values of the step size Δ, the obtained PSNR and MSSIM values averaged over all the tested images are plotted in Fig. 5 as a function of the redefined threshold \(\tilde {\rho }_{t}=\frac {1}{L}\rho _{t}\), where the range for \(\tilde {\rho }_{t}\) or ρ t covers the most interesting range for the watermark detection. As shown in Fig. 5 a, for the case of Δ=120, our method with \(\tilde {\rho }_{t}\geq 5\) presents the PSNR values near those of the original DM, corresponding to \(\tilde {\rho }_{t}=0\). Moreover, the PSNR degrades very slowly as the threshold ρ t increases. The effects become clearer for a large quantization step. That indicates that although we add the detection constraint on the basis of the DM watermarking as in (6), the watermark imperceptibility is slightly affected. Similar observations can be made from Fig. 5 b for MSSIM versus \(\tilde {\rho }_{t}\). Notably, the MSSIM is more slightly changed due to the increase of \(\tilde {\rho }_{t}\) and thus the perceptual quality loss caused by the addition of the detection constraint can be ignored in practical applications.
5.2 Watermark robustness
In what follows, the watermark robustness is tested on the image set with respect to several typical signal processes, including additive white Gaussian noise (AWGN), valumetric scaling, JPEG compression, and Gaussian low-pass filtering (GLPF).
In the test, the watermarked images are produced by our method with the same parameter setup as in Fig. 4. The decoding performance is assessed by bit error rate (BER). In Fig. 6, the resulting average BER results are shown under different types of attacks.
As a first experiment, the watermarked images undergo AWGN attacks. In Fig. 6 a, the obtained BER is plotted against the standard deviation σ n of AWGN. We observe that, BER approaches to zero in low-noise regimes, and after the noise deviation σ n exceeds 15, it obviously becomes larger as σ n increases. This reflects that the proposed method is very robust to this attack. Then, we put the watermarked images under valumetric scaling attacks (VSAs) with the gain factor β s from 0.1 to 2. Figure 6 b illustrates the robustness of our method to VSA. Clearly, within the interesting range [0.7,1.2] of β s , the BER is lower than 5 %, and it increases very fast only when β s movies beyond the range [0.6,1.3]. The results are very surprised, since as opposed to the case that quantization watermarking is largely vulnerable to VSA. Next, a classical nonlinear image processing operation, and JPEG compression is considered. Figure 6 c shows the effect of JPEG compression with the quality factor (QF) varying from 0 to 50. In this test, our method manifests satisfied robustness, and the BER of it remains to be approximately zero until a QF of 15 is reached. For the case of QF<8, the BER becomes larger than 30, but the caused quality loss is unacceptable in most applications. Last, the GLPF of window size 3×3 is applied to the watermarked images. The resultant BER is shown in Fig. 6 d as a function of the standard deviation σ f of GLPF. It can be seen that, in the considered range of σ f , the BER of our method is always lower than 3 %, which reflects that the GLPF attacks have a slight effect on the watermark robustness of our method. This can be explained by the fact that the introduced watermark is located into the low-frequency region where the wavelet coefficients are impaired less by low-pass filtering.
In the following, we examine the watermark robustness in the case of the detectable watermarking scenario. In the experiment, the watermarked images first undergo a certain attack and then the watermark detection is performed on the nonwatermarked images and the attacked images. The detection performance is measured by the receiver operating characteristics (ROC), which describes the relation between PFA and the probability of miss detection (PMD) under different values of the decision threshold [15]. In Fig. 7, the ROC curves of our method is shown, where the previous attacks are considered with typical parameter values.
Empirical ROC curves of our method with MSSIM=0.9939, ρ t =16, and a 192-bit embedded message being subject to a VSA with different values of scaling factor, b JPEG compression with different values of QF, c AWGN with different values of standard deviation, d GLPF with different values of standard deviation and window size
As shown in Fig. 7 a for AWGN attacks, the detection performance degrades with the increase of the standard deviation σ n . However, even for the high noise level σ n =32, the PMD lower than 0.9 % is reached with the PFA of 10−3, while the obtained BER is above 30 % (see Fig. 7 a). This reflects that although the attack causes the serious loss of the embedded multi-bit information, the presence of the watermark can be still verified with low PMD. The performance is achieved by taking advantage of SS watermarking technique. Similar observations can be made from Fig. 7 b for JPEG compression. Impressively, our method provides the PMD of 10−3 with the PFA of 4×10−3 for QF=8. Figure 7 c depicts the effect of VSA on the watermark detection. Clearly, the detection performance is less affected by this attack comparing with the previous ones. In the worse case of β s =0.6, our method gets the PMD of 10−3 with the PFA of 10−3. However, the slope of the ROC curve is very steep for PMD larger than 10−3. This is because the values of LC in (2) achieved by our method are approximately equal for each test image and they are scaled by the same factor under this attack. Additionally, according to (2), VSA with scaling factor over 1 should cause the detection performance improvement. Unfortunately, this does not happen in the case of β s =1.2, where our method performs worse than for β s =0.6. This is attributed to the fact that the luminance factor Λ(·) in (9) becomes smaller while the watermarked image undergoes this attack, giving rise to the negative effect on the signal extraction for watermark detection. Last, for GLPF attacks, Fig. 7 d shows the detection performance degrades as the standard deviation σ f increases, and it seems to be unrelated with the window size of the filter. In all the given situations, our method obtains satisfied detection performance.
5.3 Comparison with other watermarking methods
The proposed watermarking method is also compared with the state-of-the-art watermarking techniques including logarithmic QIM (LQIM) [20], Zareian’s method [16], and Wang’s method [21]. Method [21] is spread spectrum watermarking, and the other ones are quantization-based watermarking. To be fair, the watermarked images for all the tested methods should have the same perceptual quality and the hidden watermark message should be of the same length.
The average BER results of [16], [20], and our method with MSSIM=0.9939 and a 192-bit message embedded are obtained over the test image set and summarized in Table 1 under many typical attacks. It can be seen that, with respect to the VSA, both LQIM and Zareian’s method provide the BERs lower than 5 % and our method achieves the comparable performance. Notice that by applying valumetric scaling invariant quantization methods, the performance of our method can be further improved. For JPEG compression, the outstanding robustness is achieved by LQIM and the BER of it always remains lower than 1 % for the QF larger than 10. Our method gets a little larger BERs for the values of QF tested, but is much better than Zareian’s method. For GLPF with window size 3×3, AWGN with σ n =22, salt & pepper (S&P) noise with probability p s =2.5 %, and motion blur (Blu.) with the radius l=4 and the angle at 45°, the induced BER values for our method are respectively 1.1, 9.8, 8.4, and 5.0 %. These results are obviously better than those of Zareian’s method and LQIM, and Zareian’s method yields the BER values far greater than others. Last, for median filtering (Med.) with window size 5×5, histogram equalization (His.), and log transformation (Log.), LQIM is inferior to Zareian’s method and our method possesses the best performance.
Table 2 reports the BER results of Wang’s method [21], and the proposed method obtained on several typical images with PSNR=42 dB and a 256-bit message embedded, where the results of Wang’s method are directly quoted from [21]. As spread spectrum watermarking, Wang’s method is definitely robust to AWGN and salt & pepper noise. For the given noise strengths, it gets the BERs lower than 3 %. In the two cases, our method has a weak performance advantage. Wang’s method also exhibits good robustness against JPEG compression. However, it is fragile to median filtering. Our method performs much better than it under the last two attacks.
6 Conclusions
In this paper, an optimal watermark embedding method has been developed by combining spread spectrum and quantization techniques with the embedding distortion minimized. The watermarked signal was obtained in closed form, which was derived by solving the minimization problem with the constraints on watermark decoding and detection. Based on the method, a dual watermarking implementation was proposed in the DWT domain, where watermark embedding was carried out on the insensitive wavelet coefficients determined by the modified HVM. The watermarking method permits to insert a multi-bit message, and the spreading watermark signal simultaneously and reduces the mutual interference of them. Simulation results demonstrated that our method achieves good imperceptibility and is more robust against operations such as JPEG compression, additive noise, etc., in comparison with other watermarking methods. Notably, by the method, the existence of the watermark can be detected even if serious information loss happens to the hidden message.
Interestingly, the new embedding strategy we introduced can also be extended in many directions, including using other quantization modulation techniques, defining a different watermark detection region, selecting a different objective function for optimization, and proposing more practical implementations for applications, which are good directions for future work.
7 Appendix
7.1 A.1 Proof of Lemma 1
The proof of Lemma 1 begin with the derivation of y 1, which owes the properties 1–3 in Section 3.
First, we compute the absolute inner product ρ 1 and the squared Euclidean distance D 1. Because of \(\boldsymbol {y}_{1}\in \mathcal {V}_{m}\), we can write y 1=y q +k 1 Δ with \(\boldsymbol {k}_{1}\in \mathbb {Z}^{L}\). This results in
and
with k 1,i being the i-th element of k 1.
Then, we derive the vector k 1 by applying the constraints of ρ 1 and D 1 described in Properties 1 and 3. According to Property 1, ρ 1=ρ 0+Δ holds. Thus, from (11), it is obtained that
Under the constraints (13) and \(\boldsymbol {k}_{1}\in \mathbb {Z}^{L}\), from (12) and Property 3, it is easy to see that the vector k 1 has only one nonzero element. As a result, (13) simplifies to \(k_{1,n_{1}}=\text {sgn}\left (\boldsymbol {y}_{q}^{T}\boldsymbol {u}\cdot u_{n_{1}}\right)\cdot 1\), where the n 1-th element of k 1 is assumed to be nonzero. So, (12) becomes \(D_{1}=D_{0}+2\text {sgn}\left (\boldsymbol {y}_{q}^{T}\boldsymbol {u}\cdot u_{n_{1}}\right)e_{n_{1}}\Delta +\Delta ^{2}\). For the result, to minimize D 1, we have
The obtained y 1 is the solution of the minimization problem (6), if Property 2 is met, i.e., ρ 1>ρ t , otherwise, the vector y 2 needs to be derived. Due to \(\boldsymbol {y}_{1},\boldsymbol {y}_{2}\in \mathcal {V}_{m}\), we can write y 2=y 1+k 2 Δ with \(\boldsymbol {k}_{2}\in \mathbb {Z}^{L}\). With the similar considerations above about k 1, we readily understand the vector k 2 has only one nonzero element and the nonzero element of k 2 is \(k_{2,n_{2}}=\text {sgn}\left (\boldsymbol {y}_{1}^{T}\boldsymbol {u}\cdot u_{n_{2}}\right)\cdot 1\). Thus, \(\text {sgn}\left (\boldsymbol {y}_{1}^{T}\boldsymbol {u}\right)=\text {sgn}\left (\boldsymbol {y}_{q}^{T}\boldsymbol {u}\right)\) holds. Accordingly, D 2 becomes \(D_{2}=D_{1}+2\text {sgn}\left (\boldsymbol {y}_{q}^{T}\boldsymbol {u}\cdot u_{n_{2}}\right)\left (e_{n_{2}}+k_{1,n_{2}}\Delta \right)\Delta +\Delta ^{2}\). Similarly to (14), it is derived that the nonzero element of k 2 is located at
Recalling \(k_{1,n_{1}}=\text {sgn}\left (\boldsymbol {y}_{q}^{T}\boldsymbol {u}\cdot u_{n_{1}}\right)\cdot 1\) and due to \(|e_{i}|\leq \frac {\Delta }{2}\), we get \(\text {sgn}\left (\boldsymbol {y}_{q}^{T}\boldsymbol {u}\cdot u_{n_{1}}\right)e_{n_{1}}+\Delta \geq \text {sgn}\left (\boldsymbol {y}_{q}^{T}\boldsymbol {u}\cdot u_{i}\right)e_{i}\) for 1≤i≤L. Hence, (15) is simplified to
By repeatedly using the method to derive y 2, Lemma 1 is proved. □
7.2 A.2 Proof of Lemma 2
By Lemma 1, we can write
for i≤L and
In the case of i>L, the method to derive y 2 can be repeatedly used again to show that
References
JW Wang, SG Lian, On the hybrid multi-watermarking. Signal Process. 92(4), 893–904 (2012).
F Mintzer, GW Braudaway, in Proc. Int. Conf. Acoustics, Speech, Signal Processing. If one watermark is good, are more better? (Phoenix, AZ, 1999), pp. 2067–2070.
S Kiani, ME Moghaddam, A multi-purpose digital image watermarking using fractal block coding. J. Syst. Softw.84:, 1550–1562 (2011).
Z Xu, C Ao, B Huang, Channel capacity analysis of the multiple orthogonal sequence spread spectrum watermarking in audio signals. IEEE Signal Process. Lett.23(1), 20–24 (2015).
X Feng, H Zhang, H-C Wu, Y Wu, A new approach for optimal multiple watermarks injection. Signal Process. 18(10), 575–578 (2011).
H Feng, HF Ling, FH Zou, WQ Yan, ZD Lu, A collusion attack optimization strategy for digital fingerprinting. ACM Trans. Multimedia Comput. Commun. Appl.8:, 36–13620 (2012).
A Takahashi, R Nishimura, Y Suzuki, Multiple watermarks for stereo audio signals using phase-modulation techniques. IEEE Trans. Signal Process.53(2), 806–815 (2005).
Z-M Lu, D-G Xu, S-H Sun, Multipurpose image watermarking algorithm based on multistage vector quantization. IEEE Trans. Image Process.14(6), 822–831 (2005).
P-Y Lin, J-S Lee, C-C Chang, Dual digital watermarking for internet media based on hybrid strategies. IEEE Trans. Circuits Syst. Video Technol.19(8), 1169–1177 (2009).
G Boato, FGBD Natale, C Fontanari, Digital image tracing by sequential multiple watermarking. IEEE Trans. Multimedia. 9(4), 677–686 (2007).
C Zhang, LL Cheng, Z Qiu, LM Cheng, Multipurpose watermarking based on multiscale curvelet transform. IEEE Trans. Inform. Forensics Secur.3(4), 611–619 (2008).
H Sadreazami, MO Ahmad, MNS Swamy, Multiplicative watermark decoder in contourlet domain using the normal inverse gaussian distribution. IEEE Trans. Multimedia. 18(2), 196–207 (2016).
B Chen, GW Wornell, Quantization index modulation: a class of provably good methods for digital watermarking and information embedding. IEEE Trans. Inform. Theory. 47(4), 1423–1443 (2001).
HO Altun, A Orsdemir, G Sharma, MF Bocko, Optimal spread spectrum watermark embedding via a multistep feasibility formulation. IEEE Trans. Image Process.18(2), 371–387 (2009).
M Hamghalam, S Mirzakuchaki, MA Akhaee, Geometric modelling of the wavelet coefficients for image watermarking using optimum detector. IET Image Process.8(3), 162–172 (2014).
M Zareian, HR Tohidypour, A novel gain invariant quantization-based watermarking approach. IEEE Trans. Inform. Forensics Secur.9(11), 1804–1813 (2014).
SP Maity, S Maity, J Sil, Multicarrier spread spectrum watermarking for secure error concealment in fading channel. Telecommun. Syst.49(2), 219–229 (2012).
M Barni, F Bartolini, A Piva, Improved wavelet-based watermarking through pixel-wise masking. IEEE Trans. Image Process.10(5), 783–791 (2001).
Z Wang, AC Bovik, HR Sheikh, EP Simoncelli, Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process.13(4), 600–612 (2004).
NK Kalantari, SM Ahadi, A logarithmic quantization index modulation for perceptually better data hiding. IEEE Trans. Image Process.19(6), 1504–1517 (2010).
Y Wang, J Doherty, RV Dyck, A wavelet-based watermarking algorithm for ownership verification of digital images. IEEE Trans. Image Process.11(2), 77–88 (2002).
Acknowledgements
This study was supported by the National Natural Science Foundation of China (Grant No. 60803122, 61401303, 61573253, 61571324, and 51578189), by the National Program of International S&T Cooperation (Grant No. 2013DFA11040), by the Natural Science Foundation of Jiangsu Province (Grant No. BK2012683), and by the Natural Science Foundation of Tianjin (Grant No. 16JCZDJC30900). The authors would like to thank the anonymous reviewers for their detailed comments that improved both the editorial and technical quality of this article substantially.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhu, XS., Sun, Y., Meng, QH. et al. Optimal watermark embedding combining spread spectrum and quantization. EURASIP J. Adv. Signal Process. 2016, 74 (2016). https://doi.org/10.1186/s13634-016-0373-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13634-016-0373-8