Abstract
This paper proposes a novel technique of spatially coupled low-density parity-check (SC-LDPC) code-based soft forwarding relaying scheme for a two-way relay system. We introduce an array-based optimized SC-LDPC codes in relay channels. A more precise model is proposed to characterize the residual noise on the soft symbols, using a pre-calculated look-up table at the destination. This requires less signaling overhead compared to previous soft noise modeling techniques. We also introduce a variance correction factor to provide a rectification to the equivalent total noise variance at the destination. Finally, we propose an appropriate log likelihood ratio (LLR) former at the destination which is tailored to the proposed soft parity generation technique. Simulation results demonstrate that the proposed relay protocol yields an improved bit error rate (BER) performance compared to competing schemes proposed in the literature.
Similar content being viewed by others
1 Introduction
Cooperative communications in wireless networks provides improved transmit diversity and spectral efficiency [1]. Judiciously designed signal forwarding at the relay and an accurate detection at the destination can greatly enhance the system performance. Popular relay protocols are amplify-and-forward (AF) and decode-and-forward (DF) [2]. In the AF protocol, the relay transmits an amplified version of the received signal to the destination. In the AF, no noise suppression is performed; therefore, that protocol suffers from severe noise propagation and power inefficiency under poor channel conditions. By using a detector/decoder at the relay, the DF protocol allows for re-generating the transmitted signal, such that the noise propagation can be avoided. However, any decoding error in the regenerated signal can cause a performance degradation at the destination.
A promising relay protocol called soft information relaying (SIR) has recently gained significant attention [3–10]. In [3], the authors studied the implementation of SIR in conjunction with distributed turbo coding (DTC). A soft forwarding technique based on symbol-wise mutual information (SMI) was investigated in [4] using physical layer network coding (PLNC) in the two-way relay channel. Recently, a soft decode-compress-forward scheme was proposed in [5]; that work featured a new model, referred to as the soft scalar model, in order to facilitate the log likelihood ratio (LLR) computation at the destination. In [6], the authors suggested a “soft fading” model for the overall channel, experienced by a BPSK symbol, when transmitted from the source to relay to the destination. That idea was extended to soft two-step re-encoding together with per-scaling at the relay in [7]. In order to decode the SIR signals, the destination uses an independent Gaussian approximation, which models the residual noise in the estimated symbols as in [3, 5].
Error-correcting code is a pivotal ingredient of the DF cooperative relay system. The right choice of the code can greatly improve the performance. Low-density parity-check (LDPC) codes, which became extremely popular in point-to-point communications due to their excellent performance, are a natural candidate for use in such systems.
It was observed in [12] that the so-called “convolutional LDPC codes” outperform classical LDPC block codes. Recently, it has been shown that regular spatially coupled low-density parity-check (SC-LDPC) achieve capacity of the binary erasure channel (BEC) [13] and of general binary-input memoryless output-symmetric channel [14] under sliding-window message-passing decoding. Therefore, SC-LDPC codes can be viewed as excellent candidates for use in the relay schemes.
In [15], it was shown that bilayer SC-LDPC codes can achieve the Shannon limit of a DF relay system with orthogonal BEC links. As the SC-LDPC code ensembles are regular, the design complexity is low compared to the schemes based on irregular LDPC code ensembles. However, the idea of using the SC-LDPC codes in the relay systems over the additive white Gaussian noise (AWGN) and Rayleigh fading channels was not well exploited yet. In [16], protograph-based SC-LDPC codes were employed in three-terminal erasure relay channel. It was empirically observed that spatially coupled protograph-based MacKay-Neal LDPC codes approach the theoretical performance limits. In [17], SC-LDPC codes were used in a decode-and-forward scheme for a network consisting of two sources, one relay and one destination, connected by binary erasure channels. Network coding was used in the relay node. Analytical bounds on the achievable rate region were derived, and it was shown, in particular, by using density evolution, that the scheme based on the SC-LDPC codes achieves the theoretical performance limits. The theoretical results were further justified by the experimental observations.
In another related work [18], the author considers array-based SC-LDPC codes and studies the minimum distance of the corresponding spatially coupled codes, obtained by various “unwrapping” vectors. A number of bounds on the minimum distance of the corresponding codes for special selections of parameters are obtained by mathematical analysis.
In this paper, we propose a new framework for designing a SC-LDPC code-based soft SDF protocol over AWGN and Rayleigh/fading channels in the two-way relay channels. The paper proposes a more realistic soft noise approximation model using an estimated look-up table at the destination. The impacts of the different noise modelings are compared by the simulations. Also, a variance coefficient at the destination (referred to as a variance correction factor) is proposed to improve the accuracy of the Gaussian approximation made initially in the previous work in [5] on the equivalent noise modeling at the destination. In this paper, we also study the design of array-based SC-LDPC block codes for relay channels. The code construction is based on coupling of array-based LDPC block codes akin [18–20]. We experimentally compare the performance of the proposed system for different selections of the “unwrapping” vectors in the employed quasi-cycle low-density parity-check (QC-LDPC) matrix code, decoded by message-passing algorithm. The present work can be viewed as a set of simple but effective enhancements to the SIR scheme.
2 System model
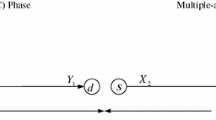
Two-way communication is a common scenario where two parties transmit information to each other via a common relay. We consider a two-way relay channel involving three nodes as shown in Fig. 1. In this paper, the letters A and B denote the users (sources), and the letter R denotes the relay. The subscript i∈{A, B} stands for a source, and \(\bar {i} \) is the opposite source of i. Vectors are denoted by bold letters, and the jth element of vector a is represented as a j. We use regular letters to denote scalars (including random variables). For a random variable x, we use \(\mathbb {E}(x)\) to denote the expected value of x. The “soft symbol” corresponding to symbol a is represented by \(\tilde {a}\). User A broadcasts its message x A to both user B and the relay in the first time slot. In the second time slot, user B transmits a message x B to both the relay and user A. In the third time slot, the relay broadcasts a “soft network-coded” signal \(\check {\boldsymbol {x}}_{R}\) to users A and B.
In the first time slot, user A encodes a bit vector u A of length K using an LDPC encoder of rate R=K/N to produce the codeword c A of length N; this LDPC code is defined by a (N−K)×N parity-check matrix H, i.e., we have \(\boldsymbol {H}\boldsymbol {c}_{A}^{T}=\boldsymbol {0}\). Here, 0 denotes the zero matrix, whose size is clear from the context. The bit vector c A is mapped to a BPSK symbol vector x A , via the mapping 0↦+1, 1↦−1, before the transmission takes place. We assume that all nodes have only one antenna working in a half-duplex mode. In the second time slot, the process at user B is similar to that at user A in the first time slot.
We denote by h iR , h iD , and \(h_{R\bar {i}}\) where i∈{A, B}, the channel coefficients between i and R, between i and D, and between R and \(\bar {i}\), respectively. The corresponding distances between nodes are denoted by d iR , \(d_{R\bar {i}}\), and \(d_{i\bar {i}}\), respectively. We assume that h iR , \(h_{R\bar {i}}\), and \(h_{i\bar {i}}\) are independent and identically Rayleigh distributed. The channel gains are related to the corresponding distances by the attenuation exponent ν, i.e., ζ iR =1/(d iR )ν, \(\zeta _{i\bar {i}}=1/(d_{i\bar {i}})^{\nu }\), and \(\zeta _{R\bar {i}}=1/(d_{R\bar {i}})^{\nu }\), respectively. We consider quasi-static fading channels, i.e., the channel coefficients are constant during one transmission phase (time slot) and change independently from one phase to another. The received signals at each of the nodes in the first and second time slots are
and
where n iR and \(\boldsymbol {n}_{i\bar {i}}\) are vectors having independent and identically distributed (i.i.d.) real Gaussian (noise) entries with zero mean and variance \( {\sigma}_{iR}^2 \) and \(\sigma _{i\bar {i}}^{2}\), respectively (both of which are here assumed to be equal to N 0/2, where N 0 denotes the channel noise power spectral density). Here, \(i,\,\bar {i}\,\in \{A,\, B\}\) with \(i\neq \bar {i}\). Also, P i is the transmit power constraint at node i, and h ik stands for the Rayleigh fading coefficient between nodes i and k where \(\,k\,\in \{\bar {i},\, R\}\). In the third time slot, the relay aids the destination by transmitting a network-coded message based on the signals received in the first and second time slots, i.e., c R =c A ⊕c B where ⊕ denotes the XOR operation. This is equivalent to the multiplication of the corresponding BPSK symbols, i.e., \({x_{R}^{\,j}}=\hat {x}_{A}^{\,j}\hat {x}_{B}^{\,j}\), where \(\hat {x}_{i}^{j}\) is the (BPSK symbol) hard decision corresponding to \({x_{i}^{\,j}}\) at the relay.
In the low signal-to-noise (SNR) regime, errors may occur in the decoding process at the relay and error propagation may be introduced. As a remedy, in the proposed scheme, the relay transmits a “soft” version of these network-coded parity symbols. This process will be elucidated in Section 4.
3 Code design
LDPC block codes were discovered in the sixtieth but were almost forgotten [11]. They became widely used in the practical applications in the last two decades due to their excellent performance at rates close to the theoretical limit, when decoded by the message-passing algorithms. LDPC codes possess a sparse parity-check matrix.
Convolutional LDPC codes, or QC-LDPC codes, outperform classical LDPC block codes, when decoded by using sliding-window message-passing algorithms. The use of sliding window allows for low latency, since the decoding can be successfully performed on a small part of a codeword, without waiting for the remaining part of the codeword. At the same time, for carefully chosen decoding window size, the error performance of the sliding-window decoder is similar to that of the standard message-passing decoder. Therefore, QC-LDPC codes with sliding-window decoders are an interesting alternative to classical block LDPC codes with message-passing decoders.
In this paper, we consider array-based QC-LDPC codes, as described below.
Definition 1 (see, for example, [19]).
Array-based (quasi-cyclic) code C γ,p is a regular LDPC code, defined by an γ p×p 2 parity-check matrix H γ,p , 1≤γ≤p, p is an odd prime, as follows
where I denotes the p×p identity matrix, and σ is the p×p permutation matrix of the form
In the sequel, we make use of the array-based SC-LDPC codes by using a special type of unwrapping procedure as described in [12, 20, 21]. This unwrapping procedure, which allows for obtaining the SC-LDPC block code, is as follows. First we “cut” the parity-check matrix into two γ p×p 2 matrices, H u and H l . The cutting pattern is defined by an integer vector δ=(δ 0,δ 1,δ 2,⋯,δ γ−1), where 0≤δ 0≤δ 1≤⋯≤δ γ−1≤p.
-
The row i+1 of the matrix H l contains δ i first entries as in the row i+1 of the matrix H γ,p , for all 0≤i≤γ−1. The remaining entries in H l are set to zeros.
-
The row i+1 of the matrix H u contains γ p−δ i last entries as in the row i+1 of the matrix H γ,p , for all 0≤i≤γ−1. The remaining entries in H u are set to zeros.
This procedure is illustrated by the following example.
Example 1.
Take p=5, γ=3, δ=(1,3,4). Then,

and so we have
and
It is possible to define the γ p×κ p submatrix H γ,p,κ of H γ,p , for general κ<p, by taking its first κ p columns. The corresponding code is LDPC, and the same unwrapping procedure can be applied to it.
Next, fix an integer L≥1, which denotes the desired coupling length. By using the matrices H u and H l , we construct an array-based SC-LDPC code, whose (L+1)γ p×L p 2 parity-check matrix is
It is worth mentioning that the matrix H(γ,p, L,δ) has the same row and column weights as the original matrix H γ,p (except for the row weights of the first p rows and the last p rows of H(γ,p, L,δ)).
The matrix H(γ,p, L,δ) might not have full rank. Its rank, in particular, depends on the decomposition of H γ,p and the internal structure of the terms in that decomposition. The optimal choice of δ is not obvious.
Next, we test different cutting vectors δ as in Table 1. By the empirical study of the bit error rate (BER) performance, we found that, for the selected parameters of γ, κ, p and L, the choice δ=(5,4,2) provides the best performance (among the tested alternatives) over the AWGN and Rayleigh fading channels. Note that the optimality of the vectors may vary for different underlying channels. We have tested other vectors δ, which do not appear in Table 1 as they have similar performance to the listed vectors.
3.1 Channel-network-coded cooperative scheme
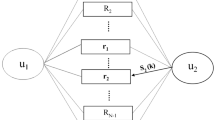
In each time slot, the destination (source i) receives a signal; one signal comes from the opposite source \( \bar {i} \) in the up-link transmission and another signal comes at the down-link transmission. In the case of error-free decoding at the relay, the forwarded packet by the relay is viewed as redundancy produced by the channel coding of the network-coded sequence. Hence, the channel-network-coded cooperative scheme can be considered as a network-coded distributed LDPC (NC-LDPC) coding scheme. Note that in contrast to the channel codes, the network code combines the information bits of A and B.
Distributed coding scheme relies on the assumption of error-free decoding at the relay. Therefore, if decoding errors occur at the relay, the forwarded relay codeword c R is an incorrect network-coded information sequence at the destination. If the relay-destination link is more reliable than the direct link which is given in most of the cases, it is highly probable that the overall decoding at the destination will be incorrect influenced by the incorrect relay codeword and consequently the decoding may fail; error propagation. In this work, we apply SIR in order to mitigate the error propagation effect due to the erroneous decoding at the relay. The principle of the network-coded SIR (NC-SIR) is depicted in Fig. 2. A joint network and channel decoding is established to increase the benefits of the two involved sources from the relay component codeword as common redundancy.
4 Soft information relaying scheme
In this section, we explain in detail how the relay performs the function of SIR. The first step required for SIR is the calculation of the a posteriori LLRs using the LDPC decoder
for each user i. This computation can be easily performed using an LDPC decoder based on the received signal frame y iR from each user i. Then, the relay computes the corresponding soft network-coded symbols. The network coding operation can be approximately implemented in the soft domain using the computed a posteriori LLR values as (see, e.g., [8])
where \( \left |\tilde {x}_{R}^{\,j}\right | \lesssim 1 \) as \( \left|{\overset{\sim }{x}}_{AR}^{\kern0.3em j}\right|,\left|{\overset{\sim }{x}}_{BR}^{\kern0.3em j}\right|\lesssim 1 \). When the SNR is large, the soft symbols are polarized around the areas close to −1 and +1. However, due to heavy fading and low SNR regime in the source-relay channel, the power of the soft symbols can be very small or negligible. Therefore, the network-coded symbols always satisfy \( \left|{\overset{\sim }{x}}_R^{\kern0.3em j}\right|< \min \left\{\left|\underset{AR}{\overset{\kern0.3em j}{\overset{\sim }{x}}}\right|,\left|\underset{BR}{\overset{\kern0.3em j}{\overset{\sim }{x}}}\right|\right\} \). This is susceptible to noise due to very small power. Therefore, we propose the following network coding form to improve the reliability of network-coded symbol \( \tilde {x}_{R}^{\,j} \), namely,
The intuition behind (9) is as follows. Since \(\tilde {x}_{R}^{\,j}\) is an estimate of \({x_{A}^{\,j}}{x_{B}^{\,j}}\) from \(\tilde {x}_{A}^{\,j}\) and \(\tilde {x}_{B}^{\,j}\), its sign should be equal to the sign of \(\tilde {x}_{A}^{\,j}\tilde {x}_{B}^{\,j}\). On the other hand, the magnitude of the signal does not change significantly.
Finally, the signal transmitted from the relay can be written as \( \check {\boldsymbol {x}}_{R}=\beta \tilde {\boldsymbol {x}}_{R},\label {eq:relay_transmission} \) where the factor β is chosen to satisfy the transmit power constraint at the relay, i.e., \(\mathbb {E}\left (\left (\check {x}_{R}^{\,j}\right)^{2}\right) = 1\). Thus, the received signal at source i in the third time slot can be written as
where n Ri is a vector having i.i.d. real Gaussian entries each having zero mean and variance \( {\sigma}_{Ri}^2={N}_0/2 \).
5 Calculation of LLR at the destination
In general, when LDPC coding is used in conjunction with relaying, the formation of the LLRs at the destination corresponding to the relay transmission is non-trivial. The source A receives two different signals via two independent fading routes in the second and third time slots, i.e., y BA and y RA . Similarly, the source B receives y AB and y RB in the first and third time slots, respectively. We use the following model for the relationship between the correct symbols \({x_{R}^{\,j}} = {x_{A}^{\,j}} {x_{B}^{\,j}}\) and the soft symbols \(\tilde {x}_{R}^{\,j}\) as first proposed in [5]:
where \(\tilde {n}^{j}\) is called the soft error variable and the constant η is called the soft scalar. We compute the value of η which minimizes the mean-square value of the soft error, i.e., \(\eta =\mathbb {E}(x_{R}\tilde {x}_{R})\) (c.f. [5]). In general, the soft scalar may be computed offline as \(\eta = \frac {1}{N}\sum _{i=1}^{N}[x_{R,i}\tilde {x}_{R,i}]\) for any desired source-relay SNR. We identified some properties of the parameter η as follows:
Property 1.
In general, the soft scalar has value −1≤η≤1. For the high values of source-relay SNR, \( \tilde {x}_{R}^{\,j} \approx 1 \), and this gives \( \tilde {x}_{R}^{\,j} \approx {x}_{R}^{\,j} \approx 1 \). In that case, η=1. In the event that \( \tilde {x}_{R}^{\,j} \) gives a hard decision error, \( \tilde {x}_{R}^{\,j} \approx {x}_{R}^{\,j} \approx -1 \). In that case, η=−1.
Property 2.
The relay does not forward when η=0. Note that the value of η=0 occurs in the very low SNR regime of the source-relay channel. In this regime, the a priori LLR will be very small in magnitude, and in turn, the generated soft symbols will have near-zero amplitude. This scenario is also similar to the case where the relay does not transmit any signal, i.e., the relay stays silent.
The effect of η is similar to that of a fading coefficient. We apply this model to the network-coded symbol and not to the “soft-modulated” symbols (an advantage of the current approach is that the soft symbol may have higher amplitudes when compared with the existing methods. This is one of the benefits from the network coding operation). The soft error variance may also be calculated as \(\sigma _{\tilde {n}}^{2}=(\sigma _{\tilde {x}_{R}}^{2}-\eta ^{2})\), where \(\sigma _{\tilde {x}_{R}}^{2}\) is the variance of \(\tilde {x}_{R}\). By the use of these statistics, soft error variance can be estimated as \( \beta = \sqrt {\frac {1}{\eta ^{2}+\sigma _{\tilde {n}}^{2}}} \;. \) By invoking symmetry of the channel, BPSK modulation, and LDPC decoding process, we also have \(\mathbb {E}(\tilde {x}_{R}) = 0\); it follows that \(\mathbb {E}(\tilde {n}) = 0\).
Assuming the model of (11), the received signal at each source i in the third time slot can be written as \( {\boldsymbol{y}}_{Ri}={\sqrt{P}}_R{h}_{Ri}\beta \eta {\mathbf{x}}_R+{\widehat{\boldsymbol{n}}}_{Ri} \), where \( {\widehat{\boldsymbol{n}}}_{Ri}={\boldsymbol{n}}_{Ri}+\sqrt{P_R}{h}_{Ri}\beta \overset{\sim }{\boldsymbol{n}} \), where \( {\widehat{\boldsymbol{n}}}_{Ri} \) is the total equivalent noise at the destination. In order to get the distribution of the total noise at the destination, the probability density function (PDFs) of the soft error and AWGN have to be convolved. As the exact distribution of our soft network-coded symbol not known, we can imagine the soft error with an impulse-like noise. As the convolution of a Gaussian distribution with an impulse gives rise to another Gaussian distribution, we conjecture that the total noise at the destination follows a Gaussian distribution. \( {\widehat{\boldsymbol{n}}}_{Ri} \) at the destination fits to an approximated Gaussian distribution with variance
The LLR corresponding to the third time slot transmission can be approximated by
Next, we describe the standard soft relay protocol as in [3]. The relationship between the correct symbols x R and the soft symbols \(\tilde {\boldsymbol {x}}_{R}\) is modeled in [3] by \(\tilde {x}_{R}^{\,j}={x_{2}^{\,j}}(1-\bar {n}^{\,j})\), where \(\bar {n}^{\,j}\) is a soft noise variable whose mean and variance can be measured offline as \(\mu _{\bar {n}}=\frac {1}{N}\left ({\displaystyle \Sigma _{l=1}^{N}} \tilde {x}_{R,l}-x_{R,l}\right)\) and \(\sigma _{\bar {n}}^{2}=\frac {1}{N}\left [\Sigma _{l=1}^{N}\left (1-\tilde {x}_{R,l}x_{R,l}-\mu _{\bar {n}}\right)^{2}\right ],\) respectively. Note that this model was used in [3] for soft BPSK but here we will apply it as a reference model for the soft network-coded symbols.
Using this model, the normalization factor β may be approximated from the soft noise statistics as \(\beta = \sqrt {\frac {1}{(1-\mu _{\bar {n}})^{2}+\sigma _{\bar {n}}^{2}}}\). Also, the received signal at the destination (source i) in the third time slot can be written as
where \(\bar {n}_{R{i}}^{\,j} = n_{R{i}}^{\,j} - \sqrt {P_{R}} h_{R{i}} \beta {x_{R}^{\,j}} (\bar {n}^{\,j}-\mu _{\bar {n}})\) is the equivalent (zero-mean) noise at the destination with variance \( {\bar{\sigma}}_{Ri}^2={\sigma}_{Ri}^2+{P}_R{h}_{Ri}^2{\beta}^2{\sigma}_{\bar{n}}^2 \) —this equivalent noise is modeled as having Gaussian distribution.
For soft BPSK, the corresponding LLR \( \lambda \kern0.3em \left({x}_R^{\kern0.3em j}\Big|{\boldsymbol{y}}_{Ri}\right) \) under this model is
Note that the a priori LLR at source i corresponding to the source \(\bar {i}\) is easily calculated as \(\lambda _{\bar {i}i}\!\left (x_{\,\bar {i}}^{\,j}|\boldsymbol {y}_{\,\bar {i}i}\right)=\frac {2\sqrt {P_{\bar {i}}}h_{\bar {i}i}}{\sigma _{\bar {i}i}^{2}}y_{\,\bar {i}i}^{\,j}. \) Next, the network decoded soft symbols at source i are computed via
At the destination, the received LLR’s from the relay and the source i will be added as they are referring to the same underline source ith transmission where i∈{A,B}.
5.1 Equivalent one-hop link model
In order to analyse the performance of the proposed scheme, we give a closed form expression of the virtual one-hop link to represent the two-hop links in the two-way relay channels in terms of equivalent SNR and other statistics [22]. We define the instantaneous SNR at links i to R and R to \(\bar {i} \) as: Γ iR and \( \Gamma _{R\bar {i}} \), respectively, where \( {\varGamma}_{iR}={\left|{h}_{iR}\right|}^2{P}_S/{\sigma}_{iR}^2 \), \( {\varGamma}_{R\bar{\i}}={\left|{h}_{\bar{\i}R}\right|}^2{P}_R/{\sigma}_{iR}^2 \), i∈{A,B}, and \( \bar {i} \in \{B,A\}\).
Note that for the BPSK modulation, the signal at \( \bar {i} \) in the equivalent model link is received in error only either when the i– R transmission is received correctly and R–\(\bar {i} \) transmission is received in error, or the i– R transmission is received in error and the R–\(\bar {i}\) transmission is received correctly. Now we have the following error probability \( {P_{R}^{\,e}} \) at the relay
The output SNR Γ eq,R at the relay in virtual equivalent one-hop link can be calculated as:
where the Q-function is formally defined as \( Q(x)= \frac {1}{\sqrt {2\pi }} \int _{x}^{\infty } \exp -\left (\frac {u^{2}}{2}\right)du\), Q −1(x) is the inverse function of Q(x), and Δ is a constant depending on the modulation scheme; for the BPSK scheme, Δ=2. This is an approximation of SNR of the two-way relay channel by the one-hop SNR link.
As per [22], we can now bound the output SNR Γ eq,R at the relay as
where Γ min,R =min{Γ AR ,Γ BR }. Intuitively, error occurred at the destination, i.e., \( \bar {i} \) cause by the information sent by R is in error and the transmission R-\(\bar {i}\) is correct or the information received by the relay R is correct and the transmission R-\(\bar {i}\) is in error. Now, we have the following error probability at the node \( \bar {i} \):
where \( {\varGamma}_{R\bar{\i}}=\frac{\left|{h}_{Ri}\beta \eta \right|{}^2{P}_R}{\sigma_{\tilde{n}}^2{P}_R\left|{h}_{Ri}\beta \eta \right|{}^2+{\sigma}_{R\tilde{\i}}^2} \). According to [22], we can bound the equivalent SNR Γ eq,R at the node \( \bar {i} \) as
where \( \Gamma _{\textup {min},\bar {i}} =\textup {min}\{\Gamma _{eq,R},\Gamma _{R\bar {i}}\}\). By combining (18) and (20), we obtain that Γ, the equivalent SNR of the source-relay-destination link, satisfies:
From (21), we can tightly approximate Γ in the high-SNR regime as
The parameter Δ depends on the modulation scheme. For QPSK, we have Δ=4, then, from (20) and (21) we can verify that (22) holds. Therefore, the analysis in this work can be extended to higher-order modulation schemes.
5.2 Estimation of model parameters
As we have seen, the values of β and equivalent noise variance \( {\widehat{\sigma}}_{Ri}^2 \) depend on the soft error variance \( \sigma _{\tilde {n}}^{2} \) and the soft scalar η. The exact computation of these parameters is non-trivial as the correct symbol \( {x_{R}^{\,j}} \) is not known at the relay or destination in online transmission. In order to offer a remedy for this issue, we propose to use look-up tables that store the average values of \(\sigma _{\tilde {n}}^{2} \). These estimated values are computed by using the linear piecewise interpolation. We denote by Γ in the received SNR at the relay, and using the inspiration of (22), we have the following relation at the relay:
where we assume power normalization P A =P B =P R =1. Here, we denote by Γ out the output SNR of the relay. Note that S N R iR and S N R R are the values of Γ in and Γ out, respectively, in decibels, where S N R iR indicates the SNR of node i and relay and S N R R is the output SNR at the relay. The output SNR of the relay can be presented as follows for our proposed soft scalar model
where \(P_{\tilde {n}}=\frac {1}{N_{1}}\sum _{j=1}^{N_{1}}|\tilde {n}^{j}|^{2}\). The relay can estimate Γ out from Γ in in the training phase and prepare a table of pairs (Γ in,Γ out) for the Rayleigh fading and AWGN channels. Then, it can approximate Γ out for general input Γ in by using the linear piecewise functions [23]. More specifically,
where the pairs {(a k ,b k )} k are estimated during the training phase and stored in the look-up table.
Figure 3 presents graphically the interpolation table of (Γ in,Γ out) and the Γ out obtain via (24). We can also apply the similar approach in order to estimate the average η. Figure 4 depicts the interpolation table of (Γ in,η), and the value of η is obtained by linear interpolation, which is similar to (24). As we can see in Figs. 3 and 4, as SNR increases, \( \tilde {x}_{R}^{\,j} \approx {x}_{R}^{\,j} \), η→1, and Γ out→∞.
Thus, we can readily compute \( \sigma _{\tilde {n}}^{2} = |\eta |^{2}/ \Gamma {}_{{\text {out}}}\) where η can be taken from the look-up table in Fig. 4, and \(\sigma _{\tilde {n}}^{2}=P_{\hat {n}} \) as \(\mathbb {E}(\tilde {n}) = 0\). Similarly, we can also compute β. In conventional SIR schemes in [3–5], statistical parameters \( \sigma _{\tilde {n}}^{2} \) and β (η in [5] as well) need to send from the relay to the destination for LLR computation. In our approach, the relay only has to send the received SNR to the destination, which decreases extra signaling overhead.
5.3 Variance correction factor
In the analysis of soft error and equivalent noise \( {\widehat{\boldsymbol{n}}}_{Ri} \), we found that the variance of the approximated Gaussian distribution \( {\widehat{\sigma}}_{Ri}^2 \) is not accurate as the exact distribution of \( \tilde {\boldsymbol {n}} \) is not known. This indicates that \( {\widehat{\sigma}}_{Ri}^2 \) is not exactly the variance of approximated Gaussian distribution of \( {\widehat{\boldsymbol{n}}}_{Ri}={\sigma}_{Ri}^2+{P}_R{h}_{Ri}^2{\beta}^2{\sigma}_{\tilde{n}}^2 \). This is mainly due to the fact that soft error variable \( \tilde {n} \) is not strongly following the Gaussian distribution. This is similar to the standard model presented in the literature [3]. Therefore, in order to correct this impreciseness present in the equivalent variance at the destination, we introduce a correction factor α, which eliminates the inaccuracy of the equivalent variance at the destination. Following this argument, we modify the equivalent noise variance term as follows:
where α is a scalar, which is used for correction of \( {\widehat{\sigma}}_{Ri}^2 \) at the destination. We call it a variance correction factor and compute its value via simulations. Finding an analytical form for α is not straightforward since the probability distribution of the soft symbols is not known. In fact, by using α, we obtain a correction criterion to \( {\widehat{\sigma}}_{Ri}^2 \), the variance of the received signal at the destination. From Fig. 7, we obtain that the decoder is sensitive to the variance when α≤2. In the next section, we present the simulation results to demonstrate the impact of the different values of α. We observe that α=2 yields very good performance (i.e., the free-propagation attenuation is considered). From this study, we observe that the soft noise varince \( \sigma _{\tilde {n}}^{2} \) is underestimated in the previous section when assuming that it is an approximated Gaussian distribution. Such an inaccurate variance can significantly degrade the system performance. To obtain a satisfactory BER performance, we have to increase its value by a factor of two.
6 Simulation results and discussion
In this section, the simulation results are provided to demonstrate the effectiveness of the proposed system. All channels are assumed to exhibit quasi-static fading, i.e., the channel coefficients h AD , h BD , h RD , h AR , and h BR are constant for each transmission phase and change independently from one phase to the next. First, we consider a symmetric relay setup where the two sources A and B have the same distance to the destination, and where the two sources, the relay, and the destination are aligned in the same horizontal line. The distances between the sources and the destination are normalized to unity, i.e. d AD =d BD =1. The attenuation exponent was chosen to be γ=2.
In the following simulations, we choose code parameters, which allow for convenient implementation. Thus, we take a SC-LDPC code with N=2425, K=1455, and the code rate \( \mathbb {R}=0.6 \). In the construction of the codes, we choose p=97, L=25, γ=3, and κ=5, and in the analysis as in Fig. 5, we found that the best decomposition (among the tested ones) is δ=(5,4,2) for point to point AWGN with Rayleigh fading and relay channels. The simulations assume BPSK and a power normalization of P A =P B =P R =1. We simulate the scenario where all links experience Rayleigh fading and AWGN. All simulations assume SNR AR =SNR BR .
BER performance of array-based spatially coupled LDPC codes using different cutting vectors together with regular array-based LDPC codes using Rayleigh fading and AWGN channel. We note that the cutting vector with δ=(5,4,2) shows improved performance. Legends in this figure incorporate with Table 1
Figure 5 demonstrates the BER performance of different array-based spatially coupled LDPC codes, i.e., different cutting vectors δ using Rayleigh fading AWGN channels. As we can see, δ=(5,4,2) shows good BER performance. In the following simulation setup, therefore, we use spatially coupled LDPC codes based on δ=(5,4,2). As a competing scheme, we also simulate block array-based LDPC code with parameters K 1=111, N 1=185, and rate \( \mathbb {R}=0.6 \) in the same figure. This LDPC code serves as the building block for the array-based SC-LDPC codes. It should be noted, that the latency of decoding block LDPC code using message-passing algorithm is comparable to the latency of decoding QC-LDPC codes constructed from that block LDPC code using sliding-window message-passing decoding, with appropriately selected size of the decoding window.
Figure 6 compares the BER performance of the spatially coupled LDPC-coded SIR scheme with the other existing relay schemes. The relay is fixed at SNR iR =1 dB to represent poor channel conditions. As a competing scheme, we simulate the standard SIR scheme in [3] by using spatially coupled LDPC codes. In the proposed SIR scheme, we have not assumed any re-encoding at the relay. As it is shown in Fig. 6, the previously proposed SIR scheme with spatially coupled LDPC codes achieved markedly better error rate performance than the SIR scheme in [3] over Rayleigh fading channels. Note that we have not assumed any soft re-encoding scheme here. By contrast, [3] has presented a soft re-encoding scheme. We also simulate hard DF scheme as a base line scheme using SC-LDPC codes.
When the source to relay channel is poor, there will be decoding errors at the destination. This creates a huge error propagation if hard decisions are forwarded from the relay to the destination. That is why we obtain relatively poor performance in hard DF. The proposed scheme does not make any premature decision at the relay and forwards the soft symbols to the destination. As the destination decoder also works in soft domain, its performance is improved. For completeness, we also simulate (AF) relaying. As expected, it shows degraded performance due to the noise amplification at the relay.
In the compress-and-forward (CF) strategy, the received signal vector sent via source-relay link is quantized and compressed at a relay before being forwarded to the destination [24]. The CF strategy is usually referred to as estimate-and-forward in the literature [25]. In fact, the received signals at the relay and the destination are correlated due to the nature of broadcasting. We simulated CF as well wih the simulation setup discussed in this paper.
As it can be observed in Fig. 6, the proposed look-up table method provides slightly better BER performance (0.4 dB at 10−3) as compared to the SIR scheme in [5] with SC-LDPC codes. In the case of [3] and [5], the relay has to forward all parameters required for LLR modeling to the destination. Additionally, the proposed scheme offers a reduced signaling overhead since the relay transmits Γ in only. By using the piecewise linear interpolation, the destination can create any combination of (γ in,γ out,η). The proposed SC-LDPC scheme together with the piecewise linear interpolation method and modified soft network coding outperforms the other schemes under comparison. The proposed modified soft network method improves on the amplitude of the soft network-coded symbol for the checked parameter settings. In the conventional approach, due to the product of two network-coded symbols, \( \tilde {x}_{R}^{\,j} \) could have a very small amplitude and is susceptible to channel noise. Then, it will deteriorate the joint error performance at the destination.
In the simulation in Fig. 7, we set SNR iR =1 dB and SNR iD =SNR Ri . The results show that the BER performance of the proposed SIR scheme verses various α values. In this scheme, we observe that the BER performance improves as α increases up to α=2. In the region of α>2, the BER performance remains almost invariant and does not contribute to the overall system performance. This observation suggests that the choice α=2 is close to the optimum. This also highlights that \( {\widehat{\sigma}}_{Ri}^2 \) actually underestimates the actual variance of \( {\widehat{\boldsymbol{n}}}_{Ri} \) when assuming that it is an approximated Gaussian distribution.
We next consider asymmetric scenario, where one source is closer to the relay than the other. Here d AR =0,7, d BR =0.3. Comparative performance results with various values of α are shown in Fig. 8, i.e. α=(0.5,1,1.5,2,2,5). From this figure, as we can see, our proposed scheme obtain optimal performance when the α≈2.
We also observe that the performance for α=2 is superior by around 0.8 dB when compared to α=1 in Figs. 7 and 8. It is natural to notice that as SNR Ri increases, the BER performance improves. Finding an analytical solution for α is involved as the complete PDF for \( \tilde {n} \) is not known, and therefore, our conclusions are based on the simulations only. Based on the simulations in Fig. 7 and by using the quantiles of the theoretical Gaussian distribution against the empirical data points of the total equivalent noise at the destination, we conclude that α=2 is close to optimal.
7 Conclusions
We have developed a novel optimized soft information relaying scheme based on cooperative network coding in a two-way relay system by means of spatially coupled LDPC codes. Instead of forwarding hard decisions, the proposed scheme forwards modified soft network-coded symbols. The error correction is achieved by using spatially coupled array-based LDPC codes. We also modify our previously proposed soft error model, such that the scaling factor and the soft error variance of the residual noise can be easily computed. It reduces the signaling overhead and achieves better performance. Finally, we introduce a correction factor parameter in order to model the soft error variance at the destination. We compare the proposed scheme with its counterparts. The proposed scheme shows significant performance improvement in terms of BER, when compared to the competing schemes.
References
JN Laneman, DNC Tse, GW Wornell, Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Trans. Inf. Theory. 50(12), 3062–3080 (2004).
G Kramer, M Gastpar, P Gupta, Cooperative strategies and capacity theorems for relay networks. IEEE Trans. Inf. Theory. 51(9), 3037–3063 (2005).
Y Li, B Vucetic, TF Wong, M Dohler, Distributed turbo coding with soft information relaying in multihop relay networks. IEEE J. Sel. Areas Comm. 24(11), 2040–2050 (2006).
J Li, MA Karim, J Yuan, Z Chen, Z Lin, B Vucetic, Novel soft information forwarding protocols in two-way relay channels. IEEE Veh. Technol. 62(5), 2374–2381 (2013).
DNK Jayakody, MF Flanagan, in Proc. 25th IEEE Symp. on Pers., Indoor and Mob. Radio Comm. Conf. (PIMRC 2013). A soft decode-compress-forward relaying scheme for cooperative wireless networks (IEEELondon, UK, 2013), pp. 205–209.
MH Azmi, J Li, J Yuan, R Malaney, in Proc. IEEE Int. Symp. Inf. Theory (ISIT 2011). Soft decode-and-forward using LDPC coding in half-duplex relay channels (IEEESt. Petersburg, Russia, 2011), pp. 1479–1483.
DNK Jayakody, MF Flanagan, in Proc. IEEE Wireless Comm. and Netw. Conf. (WCNC 2013). LDPC coding with soft information relaying in cooperative wireless networks (IEEEShanghai, China, 2013), pp. 4317–4322.
S Zhang, Y Zhu, S Liew, Soft network coding in wireless two-way relay channels. J. Commun. Networks. 10(4) (2008). doi:10.1109/JCN.2008.6389853.
DNK Jayakody, J Li, MF Flanagan, Novel multilevel soft quantization based scheme for multiple access relay network in cooperative wireless networks. IEEE Trans. Veh. Technol (2015). doi:10.1109/TVT.2015.2443253.
DNK Jayakody, J Li, in Proc. 81st IEEE Veh. Tech. Conference, (VTC2015-Spring). Optimum power allocation for LDPC coded soft forwarding scheme in wireless networks (Glasgow, UK, 2015), pp. 11–14.
RG Gallager, Low-Density Parity-Check Codes (MIT Press, Cambridge, MA, 1963).
AJ Felström, KS Zigangirov, Time-varying periodic convolutional codes with low-density parity-check matrix. IEEE Trans. Inf. Theory. 45(6), 2181–2191 (1991).
S Kudekar, TJ Richardson, RL Urbanke, Threshold saturation via spatial coupling: why convolutional LDPC ensembles perform so well over the BEC. IEEE Trans. Inf. Theory. 57(2), 803–834 (2011).
S Kudekar, T Richardson, RL Urbanke, Spatially coupled ensembles universally achieve under belief propagation. IEEE Trans. Inf. Theory. 59(12), 7761–7813 (2013).
Z Si, R Thobaben, M Skoglund, in Proc.IEEE Int. Symp. Inf. Theory (ISIT 2011). Bilayer LDPC convolutional codes for half-duplex relay channels (IEEESaint-Petersburg, Russia, 2011), pp. 1464–1468.
H Uchikawa, K Kasai, K Sakaniwa, in Proc. IEEE Int. Symp. Inf. Theory (ISIT 2011). Spatially coupled LDPC codes for decode-and-forward in erasure relay channel (IEEESt. Petersburg, Russia, 2011), pp. 1474–1478.
S Schwandter, A Graell i Amat, G Matz, Spatially-coupled LDPC codes for decode-and-forward relaying of two correlated sources over the BEC. IEEE Trans. Commun. 62(4), 1324–1337 (2014).
E Rosnes, in Proc. IEEE Int. Symp. Inf. Theory (ISIT 2015). On the minimum distance of array-based spatially-coupled low-density parity-check codes (IEEEHong, Kong, 2015).
JL Fan, in Proc. 2nd Int. Symp. Turbo Codes. Array codes as low-density parity-check codes (Brest, France, 2000), pp. 543–546.
DGM Mitchell, L Dolecek, DJ Costello Jr, in Proc.IEEE Int. Symp. Inf. Theory. Absorbing set characterization of array-based spatially coupled LDPC codes (IEEEHonolulu, HI, USA, 2014), pp. 886–890.
AE Pusane, R Smarandache, PO Vontobel, DJ Costello Jr, Deriving good LDPC convolutional codes from LDPC block codes. IEEE Trans. Info. Theory. 57(2), 835–857 (2011).
T Wang, A Cano, GB Giannakis, JN Laneman, High performance cooperative demodulation with decode-and-forward relays. IEEE Tans. Commun. 55(7), 1427–1438 (2007).
A Papoulis, SU Pillai, Probability, Random Variables and Stochastic Processes, 4th edn. (McGraw-Hill, New York, 2002).
S Simoens, J Vidal, O Munoz, in Proceedings of the IEEE 7th Workshop on Signal Processing Advances in Wireless Communications. Compress-and-forward cooperative relaying in MIMO-OFDM systems (IEEECannes, France, 2006), pp. 1–5.
R Dabora, S Servetto, Estimate-and-forward relaying for the Gaussian relay channel with coded modulation, in Proceedings of the IEEE International Symposium on Information Theory (IEEENice, France, 2007), pp. 1046–1050.
Acknowledgment
The authors wish to thank Eirik Rosnes, University of Bergen, Norway, and Michael Lentmaier, Lund University, Sweden, for the helpful discussions. This work is supported (in part) by the Norwegian-Estonian Research Cooperation Programme through the grant EMP133, by the Estonian Research Council through the research grants PUT405 and IUT2-1, and by the European Regional Development Fund through the Estonian Center of Excellence in Computer Science, EXCS.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Jayakody, D., Skachek, V. & Chen, B. Spatially coupled LDPC coding in cooperative wireless networks. EURASIP J. Adv. Signal Process. 2016, 20 (2016). https://doi.org/10.1186/s13634-016-0311-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13634-016-0311-9