Abstract
Background
In ICU patients with normal serum creatinine (SCr), a state of increased renal drug excretion has been described (creatinine clearance ≥130 ml/min/1.73 m2), and named augmented renal clearance (ARC). In ICU patients, the accuracy of GFR estimates is insufficient. However, in clinical practice, the physician has not at one’s disposal patient measured creatinine clearance (CrCl) when prescribing. The primary objective of this study was to assess the accuracy of 4 formulas to estimate GFR (Cockcroft-Gault (CG), Robert, sMDRD, and CKD-EPI formulas) with other covariates to detect ARC in ICU patients.
Methods
We enroled 360 consecutive ICU patients with normal SCr in this prospective observational study conducted in a primary teaching hospital. Comparisons between CrCl values and 4 estimated GFR (eGFR) formulas were estimated.
Results
In these 360 patients, ARC was observed in 33 % of patients most of them trauma. Individual predictive values of equations were poor and the phenomenon increased in ARC subgroup. CG and CKD-EPI were more accurate to detect an ARC. Multivariable analysis showed that the best-fitting model included 3 factors independently correlated to ARC: trauma patients, cut-off values of age ≤58 years, and CKD-EPI more than 108 ml/min/1.73 m2.
Conclusions
In ICU patients with normal SCr, eGFR formulas are imprecise in assessing CrCl. If measured CrCl must be ideally used to detect modifications of the renal function, in clinical practice, age, reason for admission, and CKD-EPI could be used as screening tool to identify ARC.
Similar content being viewed by others
Background
The glomerular filtration rate (GFR) can affect the pharmacokinetic/pharmacodynamic profile of drugs eliminated by the kidney. The dosages and schedules for the administration of these drugs are traditionally adjusted in patients with a diminished GFR in order to achieve effective plasma levels and to limit drug-induced toxicity. Direct measurement of the GFR with exogenous substances such as inulin is the gold standard for the assessment of renal function, but is not routinely performed in the intensive care units for practical reasons. Instead, one could measure the CrCl from a 24 or 8-h urine collection. However, in clinical practice, the GFR is most commonly estimated (eGFR) from the serum creatinine (SCr), using various formulas including Cockcroft-Gault, Roberts, Modification of Diet in Renal Disease (MDRD), and the 2011 Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) [1–6].
While critically ill patients can have a decreased GFR with impaired elimination of renally excreted drugs, a state of increased renal drug excretion has also been described and named “augmented renal clearance” (ARC). This state characterized by a creatinine clearance >130 ml/min/1.73 m2 has a reported incidence of 30–85 %, depending on the population studied and the cut-off values used for its definition [7–9]. Even though ARC is common in critically ill patients, a dose escalation for those patients is infrequently reported in clinical practice [1, 10–14]. This is probably because a normal SCr in critically ill patients which is not a sensitive indicator of renal dysfunction may induce an underestimation of the actual GFR, meaning that some ICU patients do not achieve adequate plasma levels of their antimicrobial drugs [15–21].
The primary objective of this study was to assess the accuracy of 4 commonly used formulas to estimate GFR with other covariates, to detect “augmented renal clearance” in ICU patients with normal serum creatinine concentrations.
Methods
Patients
This observational study was conducted in the ICU at Rangueil Hospital, a primary teaching hospital of the University of Toulouse (France) according to the declaration of Helsinki (approval by Ethical Research Committee of University Toulouse Hospital). Since the CrCl in our ICU is measured routinely at least once a week, the need for informed consent was waived.
All consecutive critically ill patients, older than 16 years, hemodynamically stable, with an arterial catheter, a urinary bladder catheter, and a stable SCr (in the normal range of 40–120 μmol/l; with less than 25 % variation between the 4th and the 10th day after admission) were included. Patients were divided into two groups, according to the diagnosis on admission: polytrauma (PT) and non-polytrauma (NPT) with the latter divided into surgical (SURG) and medical (MED) patients.
Patients were excluded from the study if they were hemodynamically unstable and needed a high dose of catecholamines (norepinephrine >1 mg/h); were recovering from or developing acute kidney injury (AKI); received histamine-2-receptor antagonist due to its interference with tubular creatinine secretion or if they had a medical history of diabetes, chronic liver disease, cirrhosis, or ongoing liver dysfunction with hepatitis [22, 23]. We excluded patients with the history of diabetes and liver disease, because glucose, ketoacids, and bilirubin are common interfering agents which lead to the overestimation of serum creatinine by Jaffe methods [24]. Patients treated with diuretics were also excluded.
Baseline characteristics for patients were recorded at enrolment in the study, and the SAPS II and SOFA scores were taken from the time of ICU admission.
Data collection
Clinical and biological data were collected between the 4th and the 10th day after admission, as soon as the patient met the inclusion criteria. Urines were sampled over 24 h for measuring urinary creatinine concentration, and SCr was measured during that same period (modified kinetic Jaffe colorimetric reaction). Measured CrCl was then calculated using the standard formula: CrCl = (UCr × V)/SCr, where UCr (urine creatinine concentration) and SCr were expressed in µmol/l and V corresponded to the urinary flow rate (diuresis) in ml/min. At the same time, the CrCl was calculated using different formulas, i.e., the Cockcroft formula \({\text{CrCl}}\; = \;\frac{{(140\; - \;{\text{age}})\; \times \;{\text{weight}}}}{{0.8\; \times \;{\text{SCr}}}}\) for men, with age in years and weight in kg [2]. A correcting factor of 0.85 was used for women. We adjusted the Cockcroft formula on body surface area (BSA) of 1.73 m2. The BSA was calculated as BSA (m2) = [weight (kg) × height (cm)/3600]1/2 [25]. We used weight at inclusion to calculate the Cockcroft formula and BSA. The formula proposed by Robert et al. uses the ideal body weight and serum creatinine concentration corrected to 85 µmol/l when the actual value is lower than 85 µmol/l [3]. Ideal body weight was determined as 50 kg for men and 45.5 kg for women, plus 2.3 kg for each inch >5 feet [26].
As per convention, CrCl values were normalized to a body surface area (BSA).
The following simplified Modification of Diet in Renal Disease equation (sMDRD) was used: sMDRD = 186.3 × SCr−1.154 × Age−0.203 × [1.212 if black], where SCr was expressed in mg/dl [5]. At the same time, we also calculated CrCl according to the CKD-EPI equation, taking into account SCr, gender and ethnicity as follows [6]:
Female
Male
A CrCl ≥ 130 ml/min/1.73 m2 was used to define ARC [10, 14].
Statistical analysis
Data are presented as mean ± standard deviation or ratio. Differences between groups were calculated using parametric and non-parametric tests as appropriate.
The agreement between the individual eGFRs by the CG, Robert, sMDRD, and CKD-EPI formulas and the measured CrCl was analyzed by residual plots according to the method of Bland and Altman [27].
The bias and the precision of the different formulas compared with the measured CrCl were evaluated according to Sheiner et Beal by the following equations [28]:
The results are expressed as a percentage of the mean measured CrCl.
The diagnostic accuracy of the 4 used formulas to estimate GFR and other significant variables in predicting ARC was assessed by measuring the area under the receiver operating characteristic (ROC) curves. Each measure was treated as an independent event. The areas under the ROC curves of the eGFRs were compared by the Wilcoxon rank test. The best threshold with their corresponding likelihood ratios (negative and positive) was defined by Youden’s index.
For each significant variable, the “gray zone” was determined using a two-step procedure as described by Cannesson [29]. The first step consisted of the determination of the best threshold for each parameter. The second step was conducted to determine a range of values for which formal conclusions could not be obtained. We defined inconclusive responses for values presenting with either sensitivity lower than 90 % or specificity lower than 90 % (diagnosis tolerance of 10 %). The gray zone was then defined as the values of the parameters that did not allow having 10 % of diagnosis tolerance. Nevertheless, if the characteristics of the study population produce a 95 % CI of the best thresholds larger than the inconclusive zone, the values obtained during the first step were retained as gray zone.
A logistic regression was performed to determine if polytrauma or any continuous variable or their cut-off with a p value of less than 0.20 in the univariate analysis was independently able to predict the presence of ARC. The odds ratio (OR) and 95 % confidence intervals (CI) were calculated. Goodness of fit of the model was assessed using the Hosmer–Lemeshow test [30].
Statistical analysis was performed using Medcalc (MedCalc Software, Ostend, Belgium). A p value ≤0.05 was considered as statistically significant.
Results
Baselines characteristics of study subjects
Three hundred and sixty eligible patients completed the study (Fig. 1). The interval from ICU admission to inclusion was 9 ± 5 days; 270 (75 %) of the patients were mechanically ventilated. Demographic and laboratory data are shown in Table 1, including a mean SCr of 72 ± 22 µmol/l.
Estimated GFRs based on the various formulas and measured CrCl for patients without (A) and with ARC (B) are presented in Table 2.
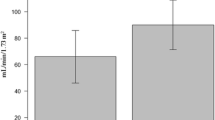
The incidence of ARC was 120 in the 360 patients (33 %), and the diagnosis of polytrauma was significantly more common among patient with ARC (89/120, 74 %) compared with the non-ARC group (100/240, 41 %, p < 0.0001). Patients with ARC were younger: 39 ± 16 years vs. 55 ± 19 years in non-ARC patients (p < 0.0001). Estimated GFRs were different between patients presenting ARC and the others. Glomerular hypofiltration (CrCl < 60 ml/min/1.73 m2) was observed in 21.4 % of the cases. 31 patients were classified as stage III CKD by CKD-EPI equation (eGFR between 30 and 59 ml/min/1.73 m2), but 5 of them presented CrCl ≥ 60 ml/min/1.73 m2. When stratifying patients based on CrCl > 130 ml/min/1.73 m2, CrCl between 60 and 130 ml/min/1.73 m2 and CrCl < 60 ml/min/1.73 m2, urine creatinine excretion decreases significantly with CrCl (1812.3 ± 757.6 mg/d/1.73 m2, 1116.7 ± 388.5 mg/d/1.73 m2, and 607.9 ± 229.6 mg/d/1.73 m2, respectively). The same occurred with urine output: 2878 ± 1353 ml/d in group with CrCl > 130 ml/min/1.73 m2, 2441 ± 1047 in group between 60 and 130 ml/min/1.73 m2, and 2216 ± 887 in group with CrCl < 60 ml/min/1.73 m2.
Formulas’ accuracy to estimate CrCl in ICU patients
Estimated GFRs by the 4 equations in patients with and without ARC were significantly different when compared to measured CrCl. Bland and Altman plots are presented in Fig. 2. The different formulas tended to overestimate the CrCl for low eGFR values and to underestimate the CrCl for normal and high eGFRs.
In ARC sub group, each formula underestimated CrCl (Table 2b). For all four formulas, a larger bias and a lower precision were observed in ARC group (Table 2).
Tools to screen ARC
Age, SAPS II, serum creatinine, and estimated GFRs based on the 4 formulas were different in patients with ARC. The area under the ROC curve of these covariates is presented in Table 3.
For the screening of ARC, the area under the ROC curve was 0.79 [95 % CI: 0.74–0.83] for the CG formula, 0.75 [95 % CI: 0.7–0.79] for the Robert formula, 0.73 [95 % CI: 0.69–.78] for the sMDRD equation, and 0.79 [95 % CI: 0.75–0.83] for the CKD-EPI equation (Table 3; Fig. 3).
As shown in Table 3, only CG and CKD-EPI formulas presented AUCs above 0.75 to detect an ARC with cut-off values of 107.5 for CG (sensitivity of 83 % and specificity of 63 %) and 108.11 ml/min/1.73 m2 for CKD-EPI (sensitivity of 75 % and specificity of 75 %). Considering the gray zones, the limits in which ARC classification could not be reliably predicted were 90–122.8 ml/min/1.73 m2 for CKD-EPI equation and 95.5–148.6 ml/min/1.73 m2 for CG formula.
Comparison of ROC curves of the 4 estimated formulas show no difference between CG and CKD-EPI AUCs (Fig. 3), but revealed a significant difference between AUC of serum creatinine and CKD-EPI, CG or sMDRD (p < 0.0001), and Robert formula (p = 0.0243).
We tested several logistic regression models with significant covariates, in particular, the cut-off values of ARC detection by CG and CKD-EPI (Table 4).
SCr was not significant and may be a confusing factor. SAPSII was not significant in multivariate analysis and was not included in the final model. The best fit model was obtained in the model including the cut-off value of ARC detection by CKD-EPI. Goodness of fit was 1 with the Hosmer–Lemeshow test and AUC equal to 0.825. In the model including ARC detection by CG equation, the adjustment was lower (goodness of fit equal to 0.86). Taking into account these data, the logistic regression analysis showed that an age less than or equal to 58 years, an admit diagnosis of polytrauma and an eGFR above 108.1 ml/min/m2 as calculated by CKD-EPI appeared the only independent predictors of ARC (Table 4).
Discussion
In ICU patients with normal serum creatinine, we found that none of the estimated GFR formulas allow accurate prediction of augmented renal clearance. However, multivariable analysis showed that 3 factors were independently correlated to ARC and useful to screen ARC: trauma patients, cut-off values of age ≤58 years, and CKD-EPI more than 108 ml/min/1.73 m².
ICU patients can exhibit important variations of their measured CrCl, despite a normal SCr with the CrCl being higher than 130 ml/min/1.73 m2 (ARC) in more than 33 % of the cases. In particular, younger severe trauma patients present most often with ARC compared to other groups (in our study 47 % vs. 18 %) [7]. In our sample of 360 ICU patients, the measured CrCl varied over a wide range and revealed unexpectedly low values (<60 ml/min/1.73 m2) in 21.4 % of the patients and very high values (>130 ml/min/1.73 m2) in 33.3 % of the cases. The prevalence of ARC among our patients is thus lower than in the cohort of 281 patients recently described by Udy who found an ARC in 65.1 % of cases (using the identical threshold of 130 ml/min/1.73 m2 to define ARC) [9]. This finding is mostly likely due to the fact that a somewhat different patient population was studied. Even though our incidence of ARC was lower, the data confirm again that in hemodynamically stable patient, a normal SCr is a poor predictor of changes in renal function [15, 31].
In 28 critically ill patients with normal SCr, Hoste demonstrated that the Cockcroft-Gault and MDRD formulas were not adequate in assessing renal function and we have previously shown similar findings in 36 burn patients [15, 31]. However, the populations of these studies were small. Our study, with 360 patients, allows a better evaluation of the large inter-individual variability presented by critically ill patients (high CrCl coefficient of variation of 51.2 %). Baptista demonstrated in 86 patients presenting ARC that both CG- and MDRD-derived values (the formula of Robert and CKD-EPI equations was not studied) significantly underestimate the measured CrCl and are insensitive in identifying ARC [16]. More recently, a study of 110 ICU patients (53 with ARC) evaluated the CKD-EPI equation and the authors showed a poor concordance with measured CrCl. It is clear that the bias and precision of these equations are significantly larger in patients with ARC [18].
In our 360 critically ill patients with normal SCr, the currently used formulas, including CKD-EPI equation, were found to be poor predictors of measured CrCl. The general increase in imprecision of estimated GFR methods at higher GFR values is well recognized [6]. Our findings, with respect to increased imprecision at measured higher creatinine clearance values, are consistent with data from the non-ICU setting. Taking into account the AUCs as well as the sensitivities and the specificities of these formulas, the CG and CKD-EPI formulas, with a cut-off, respectively, of 107.5 and 108.1 ml/min/1.73 m2, were found to be slightly more accurate than the other two formulas studied (Robert and sMDRD). The threshold of CG formula differs from these of Lautrette in his analysis of 32 patients admitted for acute infectious meningitis and presenting a high creatinine clearance in 47 % of the patients [1]. Our study extend on these prior works with an analysis of a large cohort of patients demonstrating again important variations of CrCl and a high prevalence of ARC that is difficult to predict based on the formulas which calculate the eGFR using the SCr.
The implications of this phenomenon primarily relate to the potential for sub-therapeutic drug levels, and treatment failures due to the correlation between CrCl and drug elimination [19]. Data provided by the Chronic Kidney Disease Epidemiology Collaboration have shown that mathematical estimates of GFR can result in up to about 20 % discordance in drug-dosing recommendations, depending on the formula used [32]. This discordance may be even higher in patients with ARC, since the population reported had significantly lower measured GFRs (75 ± 44 ml/min) compared to the patients in our study. Surprisingly, there are currently no guidelines for adjusting drug dosages for patients with an increased GFR, even though studies have clearly shown that in patients with ARC the plasma concentrations of various antibiotics (beta-lactams, vancomycin, and fluoroquinolones) were insufficient [10, 12, 14, 20, 31–37].
We acknowledge that our study has potential limitations. First, eGFRs depend on creatinine serum quantification, and the Jaffe method is prone to analytical interferences with non-creatinine compounds [24]. Our method of SCr measurement and calibration reduced these interferences [38]. Second, only direct measurement of the GFR with exogenous substances such as inulin is the gold standard for the assessment of renal function, but is not routinely performed in the intensive care units for practical reasons [39, 40]. Instead, one could measure the CrCl from a 24-h urine collection. CrCl can be affected by creatinine tubular secretion, but its impact is probably lower at higher GFRs, and we exclude patients receiving histamine-2-receptor antagonist due to its interference with tubular creatinine secretion [41]. Third, the 24-h CrCl requires steady state, and is not suited to detect rapid change in GFR [39]. Aware of these limits, we selected patients presenting SCr with less than 25 % variation between the 4th and the 10th day after admission, hemodynamically stable and without history of AKI. Furthermore, 24-h CrCl is considered imprecise in ICU practice. This method is the standard care in our unit for years, and nurse staff is well trained for 24-h urine collection. To limit bias, we mixed samples of urine bottles when diuresis was over 2 l. The quality of our 24-h urinary collection is supported by the 24-h creatinine urine excretion decreasing with CrCl [42].
A reliable way to predict the patient’s GFR is useful for the clinician and in non-ICU patients with normal GFR, a formula such as the CKD-EPI may perform reasonably well as we have recently shown to dose adjustment of vancomycin [43]. Identifying patients at risk for ARC is necessary. In our study, the multivariable analysis showed that the highest CrCls were observed more frequently in younger patients, in severe trauma patients and for cut-off values of CKD-EPI of 108.1 ml/min1/1.73 m2. However, the gray zone, the bias, and precision values of CKD-EPI showed the limits of these formulas, which is only a tool for screening patients with ARC. In such circumstance, the CrCl should be measured formally to accurately adjust dosage of drug eliminated by kidneys.
Conclusion
ARC appears to be common in ICU patients especially in severe trauma patients and or in patients <58 years. The bedside measured CrCl through urine collection remains the most reliable method to detect ARC in ICU patients with normal serum creatinine levels.
This study suggests that when taking into account age and reason for admission (polytrauma and non-polytrauma), the CKD-EPI equation could allow a first screening of patients with ARC.
Abbreviations
- AKI:
-
acute kidney injury
- ARC:
-
augmented renal clearance
- AUC:
-
area under the curve
- BMI:
-
body mass index
- BSA:
-
body surface area
- CI:
-
confidence interval
- CG:
-
cockcroft and gault
- CKD-EPI:
-
Chronic Kidney Disease Epidemiology Collaboration
- CrCl:
-
creatinine clearance
- GFR:
-
glomerular filtration rate
- IBW:
-
ideal body weight
- ICU:
-
intensive care unit
- ISS:
-
Injury Severity Score
- MED:
-
medical
- NKF K/DOQI:
-
National kidney foundation kidney/disease outcomes quality initiative
- NPT:
-
non-polytrauma
- OR:
-
odds ratio
- PT:
-
polytrauma
- SAPS II:
-
new simplified acute physiology score
- SCr:
-
serum creatinine
- SD:
-
standard deviation
- sMDRD:
-
simplified formula of the modification of diet in renal disease
- SOFA:
-
Sequential organ failure assessment
- SURG:
-
surgical
- UCr:
-
urinary creatinine
- V:
-
urinary flow rate
References
Lautrette A, Phan TN, Ouchchane L, Aithssain A, Tixier V, Heng AE, et al. High creatinine clearance in critically ill patients with community-acquired acute infectious meningitis. BMC Nephrol. 2012;13:124. doi:10.1186/1471-2369-13-124.
Cockcroft DW, Gault MH. Prediction of creatinine clearance from serum creatinine. Nephron. 1976;16(1):31–41.
Robert S, Zarowitz BJ, Peterson EL, Dumler F. Predictability of creatinine clearance estimates in critically ill patients. Crit Care Med. 1993;21(10):1487–95.
Levey AS, Bosch JP, Lewis JB, Greene T, Rogers N, Roth D. A more accurate method to estimate glomerular filtration rate from serum creatinine: a new prediction equation. Modification of Diet in Renal Disease Study Group. Ann Intern Med. 1999;130(6):461–70.
Levey AS, Greene T, Kusek JW, Beck GJ. A simplified equation to predict glomerular filtration rate from serum creatinine. J Am Soc Nephrol JASN. 2000;11:A155.
Levey AS, Stevens LA, Schmid CH, Zhang YL, Castro AF 3rd, Feldman HI, et al. A new equation to estimate glomerular filtration rate. Ann Intern Med. 2009;150(9):604–12.
Minville V, Asehnoune K, Ruiz S, Breden A, Georges B, Seguin T, et al. Increased creatinine clearance in polytrauma patients with normal serum creatinine: a retrospective observational study. Crit Care. 2011;15(1):R49. doi:10.1186/cc10013.
Udy A, Boots R, Senthuran S, Stuart J, Deans R, Lassig-Smith M, et al. Augmented creatinine clearance in traumatic brain injury. Anesth Analg. 2010;111(6):1505–10. doi:10.1213/ANE.0b013e3181f7107d.
Udy AA, Baptista JP, Lim NL, Joynt GM, Jarrett P, Wockner L, et al. Augmented renal clearance in the ICU: results of a multicenter observational study of renal function in critically ill patients with normal plasma creatinine concentrations*. Crit Care Med. 2014;42(3):520–7. doi:10.1097/CCM.0000000000000029.
Baptista JP, Sousa E, Martins PJ, Pimentel JM. Augmented renal clearance in septic patients and implications for vancomycin optimisation. Int J Antimicrob Agents. 2012;39(5):420–3. doi:10.1016/j.ijantimicag.2011.12.011.
Fuster-Lluch O, Geronimo-Pardo M, Peyro-Garcia R, Lizan-Garcia M. Glomerular hyperfiltration and albuminuria in critically ill patients. Anaesth Intensive Care. 2008;36(5):674–80.
Udy AA, Putt MT, Shanmugathasan S, Roberts JA, Lipman J. Augmented renal clearance in the Intensive Care Unit: an illustrative case series. Int J Antimicrob Agents. 2010;35(6):606–8. doi:10.1016/j.ijantimicag.2010.02.013.
Udy AA, Roberts JA, Boots RJ, Paterson DL, Lipman J. Augmented renal clearance: implications for antibacterial dosing in the critically ill. Clin Pharmacokinet. 2010;49(1):1–16. doi:10.2165/11318140-000000000-00000.
Udy AA, Varghese JM, Altukroni M, Briscoe S, McWhinney BC, Ungerer JP, et al. Subtherapeutic initial beta-lactam concentrations in select critically ill patients: association between augmented renal clearance and low trough drug concentrations. Chest. 2012;142(1):30–9. doi:10.1378/chest.11-1671.
Hoste EA, Damen J, Vanholder RC, Lameire NH, Delanghe JR, Van den Hauwe K, et al. Assessment of renal function in recently admitted critically ill patients with normal serum creatinine. Nephrol Dial Transpl Off Publ European Dial Transpl Assoc European Renal Assoc. 2005;20(4):747–53. doi:10.1093/ndt/gfh707.
Baptista JP, Udy AA, Sousa E, Pimentel J, Wang L, Roberts JA, et al. A comparison of estimates of glomerular filtration in critically ill patients with augmented renal clearance. Crit Care. 2011;15(3):R139. doi:10.1186/cc10262.
Pletz MW, Lipman J. Clinical measures for increased creatinine clearances and suboptimal antibiotic dosing. Intensive Care Med. 2013;39(7):1322–4. doi:10.1007/s00134-013-2918-8.
Udy AA, Morton FJ, Nguyen-Pham S, Jarrett P, Lassig-Smith M, Stuart J, et al. A comparison of CKD-EPI estimated glomerular filtration rate and measured creatinine clearance in recently admitted critically ill patients with normal plasma creatinine concentrations. BMC Nephrol. 2013;14:250. doi:10.1186/1471-2369-14-250.
Conil JM, Georges B, Mimoz O, Dieye E, Ruiz S, Cougot P, et al. Influence of renal function on trough serum concentrations of piperacillin in intensive care unit patients. Intensive Care Med. 2006;32(12):2063–6. doi:10.1007/s00134-006-0421-1.
Georges B, Conil JM, Ruiz S, Seguin T, Cougot P, Fourcade O, et al. Ceftazidime dosage regimen in intensive care unit patients: from a population pharmacokinetic approach to clinical practice via Monte Carlo simulations. Br J Clin Pharmacol. 2012;73(4):588–96. doi:10.1111/j.1365-2125.2011.04117.x.
Udy AA, Roberts JA, Lipman J. Implications of augmented renal clearance in critically ill patients. Nat Rev Nephrol. 2011;7(9):539–43. doi:10.1038/nrneph.2011.92.
Larsson R, Bodemar G, Kagedal B, Walan A. The effects of cimetidine (Tagamet) on renal function in patients with renal failure. Acta Med Scand. 1980;208(1–2):27–31.
Hull JH, Hak LJ, Koch GG, Wargin WA, Chi SL, Mattocks AM. Influence of range of renal function and liver disease on predictability of creatinine clearance. Clin Pharmacol Ther. 1981;29(4):516–21.
Miller WG, Myers GL, Ashwood ER, Killeen AA, Wang E, Thienpont LM, et al. Creatinine measurement: state of the art in accuracy and interlaboratory harmonization. Arch Pathol Lab Med. 2005;129(3):297–304. doi:10.1043/1543-2165(2005)129<297:CMSOTA>2.0.CO;2.
Mosteller RD. Simplified calculation of body-surface area. New Engl J Med. 1987;317(17):1098. doi:10.1056/NEJM198710223171717.
Devine BJ. Gentamicin therapy. Drug Intell Clin Pharm. 1974;8:650–5.
Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1(8476):307–10.
Sheiner LB, Beal SL. Some suggestions for measuring predictive performance. J Pharmacokinet Biopharm. 1981;9(4):503–12.
Cannesson M, Le Manach Y, Hofer CK, Goarin JP, Lehot JJ, Vallet B, et al. Assessing the diagnostic accuracy of pulse pressure variations for the prediction of fluid responsiveness: a “gray zone” approach. Anesthesiology. 2011;115(2):231–41. doi:10.1097/ALN.0b013e318225b80a.
Lemeshow S, Hosmer DW Jr. A review of goodness of fit statistics for use in the development of logistic regression models. Am J Epidemiol. 1982;115(1):92–106.
Conil JM, Georges B, Fourcade O, Seguin T, Lavit M, Samii K, et al. Assessment of renal function in clinical practice at the bedside of burn patients. Br J Clin Pharmacol. 2007;63(5):583–94. doi:10.1111/j.1365-2125.2006.02807.x.
Stevens LA, Nolin TD, Richardson MM, Feldman HI, Lewis JB, Rodby R, et al. Comparison of drug dosing recommendations based on measured GFR and kidney function estimating equations. Am J Kidney Dis Off J National Kidney Found. 2009;54(1):33–42. doi:10.1053/j.ajkd.2009.03.008.
Carlier M, Carrette S, Roberts JA, Stove V, Verstraete AG, Hoste E, et al. Meropenem and piperacillin/tazobactam prescribing in critically ill patients: does augmented renal clearance affect pharmacokinetic/pharmacodynamic target attainment when extended infusions are used? Crit Care. 2013;17(3):R84. doi:10.1186/cc12705.
Claus BO, Hoste EA, Colpaert K, Robays H, Decruyenaere J, De Waele JJ. Augmented renal clearance is a common finding with worse clinical outcome in critically ill patients receiving antimicrobial therapy. J Crit Care. 2013;. doi:10.1016/j.jcrc.2013.03.003.
Conil JM, Georges B, Lavit M, Seguin T, Tack I, Samii K, et al. Pharmacokinetics of ceftazidime and cefepime in burn patients: the importance of age and creatinine clearance. Int J Clin Pharmacol Ther. 2007;45(10):529–38.
Conil JM, Georges B, de Lussy A, Khachman D, Seguin T, Ruiz S, et al. Ciprofloxacin use in critically ill patients: pharmacokinetic and pharmacodynamic approaches. Int J Antimicrob Agents. 2008;32(6):505–10. doi:10.1016/j.ijantimicag.2008.05.019.
Goncalves-Pereira J, Povoa P. Antibiotics in critically ill patients: a systematic review of the pharmacokinetics of beta-lactams. Crit Care. 2011;15(5):R206. doi:10.1186/cc10441.
Myers GL, Miller WG, Coresh J, Fleming J, Greenberg N, Greene T, et al. Recommendations for improving serum creatinine measurement: a report from the Laboratory Working Group of the National Kidney Disease Education Program. Clin Chem. 2006;52(1):5–18. doi:10.1373/clinchem.2005.0525144.
Stevens LA, Coresh J, Greene T, Levey AS. Assessing kidney function–measured and estimated glomerular filtration rate. New Engl J Med. 2006;354(23):2473–83. doi:10.1056/NEJMra054415.
Bragadottir G, Redfors B, Ricksten SE. Assessing glomerular filtration rate (GFR) in critically ill patients with acute kidney injury–true GFR versus urinary creatinine clearance and estimating equations. Crit Care. 2013;17(3):R108. doi:10.1186/cc12777.
Kim KE, Onesti G, Swartz C. Creatinine clearance and glomerular filtration rate. Br Med J. 1972;1(5796):379–80.
Tynkevich E, Flamant M, Haymann JP, Metzger M, Thervet E, Boffa JJ, et al. Decrease in urinary creatinine excretion in early stage chronic kidney disease. PLoS One. 2014;9(11):e111949. doi:10.1371/journal.pone.0111949.
Conil JM, Georges B, Breden A, Ruiz S, Cougot P, Fourcade O, et al. Estimation of glomerular filtration rate to adjust vancomycin dosage in critically ill patients: superiority of the Chronic Kidney Disease Epidemiology Collaboration equation? Anaesth Intensive Care. 2014;42(2):178–84.
Authors’ contributions
SR, JMC, and MV collected data. KA, BG, and OF participated in the design of the study and helped to draft the manuscript. JMC, SR, and VM designed the study, performed the statistical analysis, and helped to draft the manuscript. All authors read and approved the final manuscript.
Acknowledgements
This work should be attributed to the Department of Anesthesia and Intensive Care. Support was provided solely from institutional and department sources. We acknowledge the support of the nursing and medical staff for achieving this study.
Competing interests
The authors declare that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ruiz, S., Minville, V., Asehnoune, K. et al. Screening of patients with augmented renal clearance in ICU: taking into account the CKD-EPI equation, the age, and the cause of admission. Ann. Intensive Care 5, 49 (2015). https://doi.org/10.1186/s13613-015-0090-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13613-015-0090-8