1 Introduction

The broadleaved tree species of temperate Europe include sessile oak (Quercus petraea (Matt.) Liebl.), which is likely to expand its range in the current context of climate change (Mette, Dolos et al. 2013; Stimm, Heym et al. 2021). This species is found throughout the continent of Europe, from Spain to Southern Sweden, Norway, and Russia (Camus 1938; Le Hardy de Beaulieu and Lamant 2006). In most central European countries, Q. petraea is a key economic and ecological resource (Hanewinkel, Cullmann et al. 2013; Eaton, Caudullo et al. 2016). Given current trends towards an expansion of the range of Q. petraea (Truffaut, Chancerel et al. 2017), concerns have been raised about meeting seed needs for plantations. Recent studies have shown that seed yields are increasing with climate change, potentially facilitating natural regeneration (Caignard, Kremer et al. 2017). Natural regeneration is currently advised for stand renewal, whenever sufficient seeds are available (Jarret 2004; Sardin 2008). If seed yields are insufficient or a new area is being forested, plantation approaches are used. According to French national statistics, more than 3.5 million sessile oak seedlings were produced in French nurseries in 2017 for field plantation, making Q. petraea the leading broadleaved species planted in the country (Anonymous 2017). Seed sourcing has, thus, become a matter of the utmost importance for ensuring afforestation success. The selection of appropriate seed sources is challenging when the future climate conditions of the plantation area are uncertain. In forestry, the traditional approach has been to use as much locally sourced seed as possible, particularly for species displaying local adaptation. However, there has been a move in recent years towards anticipating future climate change and selecting seeds from a current geographic origin with climate conditions matching the future climatic conditions predicted for the plantation area (assisted migration) (Saenz-Romero, OʼNeill et al. 2021). Provenance tests are a prerequisite for seed sourcing, as they provide invaluable clues to local adaptation and insights into the consequences of transferring seed sources. Provenance research in Quercus petraea has a long history (see Kleinschmit 1993 for a review). However, as the seed yield is irregular and acorns cannot be kept for more than one year, most provenance experiments comprise only a limited number of provenances of narrow geographic origin (Kleinschmit and Svolba 1994; Liesebach and Stephan 2000; Jensen and Hansen 2008; Burianek, Benedikova et al. 2011; Wilkinson, Eaton et al. 2017). Some provenance experiments have been performed at the juvenile stage, but such experiments provide limited information for seed sourcing (Liepe 1993; Deans and Harvey 1996; Alberto, Bouffier et al. 2011). Here, we made use of a comprehensive collection of provenances, assembling material over successive years due to irregular seed harvests, and including material originating from classified and non-classified seed stands. The whole experiment, which has now been running for about 26 years, was set up over a period of 4 years, at four sites. This experiment has already been used to achieve targeted objectives with a limited number of provenances (Ducousso, Guyon et al. 1996; Kremer, Petit et al. 1998; Ducousso, Louvet et al. 2005; Sinclair, Stone et al. 2015; Lobo, Torres-Ruiz et al. 2018; Pihain, Gerhold et al. 2019; Sáenz-Romero, Kremer et al. 2019; Torres-Ruiz, Kremer et al. 2019; Bert, Lebourgeois et al. 2020; Matyas 2021). This range-wide collection allowed us to address not only the ecological and historical drivers but also the human drivers that may have shaped the extant distribution of genetic variation. Indeed, the sampled populations are spread over wide ecological gradients and originate from different source populations. They are also part of forests that underwent longstanding contrasting silvicultural regimes. Finally, our ultimate aim was to provide practical recommendations for seed sourcing of Quercus petraea in France. We adopted a compromise strategy, with a balance between local sources (local adaptation) and transferred sources (assisted migration), by building clusters with multiple provenances, and recommending clusters for seed sourcing in France. The rationale underlying this strategy is the mixing of seeds of different provenances from a given cluster to ensure the maintenance of diversity and to enhance adaptability to future climatic conditions. Methodological efforts were thus mostly focused on the building of clusters of provenances based on traits of adaptive and economic value, through a combination of statistical and empirical approaches.

2 Materials and methods

2.1 Plant material

The study material was a collection of Quercus petraea provenances collected across Europe, from Spain to Scandinavia and from Ireland to Georgia (Kremer and Ducousso 2017; Ducousso, Ehrenmann et al. 2022). A collection unit corresponding to a provenance consisted of one or multiple forest compartments larger than 15 ha in which the species of interest was the only white oak present. Acorns were harvested from 50 spots evenly distributed throughout the collection unit and bulked into a single seed lot. The experiment focused mainly on Q. petraea, but a minor collection effort was devoted to Q. robur, which was included in the study for purely comparative purposes. Finally, collections were not restricted to seed stands or phenotypically outstanding stands. We also ensured the inclusion of provenances from the ecological and geographic margins of the distribution of the species, to obtain a representative sample of the genetic variation of the species. Seed yields are spatially and temporally heterogeneous in oaks, so acorn harvests were performed in four different years with sufficient seed crops (1986, 1987, 1989, and 1992) to ensure the construction of a range-wide collection. There were, therefore, four yearly sets of provenances. In this way, we were able to harvest the same provenance (i.e. from the same collection unit) in different years, thereby maintaining genetic connectivity across the different yearly sets. These provenances repeatedly collected over several years are referred to hereafter as “crossover” provenances. In a few forests, we also collected provenances from different collection units (within the same set, or in different sets), which we refer to as “twinned” provenances. In total, 127 provenances were harvested, including 74 French provenances (70 Q. petraea and 4 Q. robur), 27 “crossover populations” (common to several sets), and 20 “twinned” provenances (Additional file 1: Table S1a and Figure S1). The design also included four French Q. robur provenances. For the sake of clarity, a “provenance” is considered to be the geographic origin of a seed lot. The four yearly sets collected in 1986, 1987, 1989, and 1992 are referred to hereafter as sets 1, 2, 4, and 5 (Ducousso, Ehrenmann et al. 2022 Tables 3 and 4 therein). The 70 Q. petraea provenances comprised 60 seed stands from 17 provenance regions, with a total of 19 provenance regions in France (Colin, Ducousso et al. 2017; Additional file 1: Table S1a). In addition to the French collection, provenances from other countries of the natural distribution were included in the collection among which 38 are used in this study to analyse provenance-climate relationships (Additional file 1: Table S1b). The maternal lineage of all provenances was known, thanks to the prior genotyping of chloroplast haplotypes (Kremer, Kleinschmit et al. 2002; Petit, Csaikl et al. 2002). It was, therefore, possible to compare provenance trait values between haplotypic groups.

2.1.1 Plantation and experimental layout

Seed lots were heat-treated to prevent Ciboria batschiana contamination during seed storage. Seedlings were raised in the Guéméné-Penfao state nursery in North-West France (latitude: 47.631° N; longitude: 1.892° W), in an experimental layout with five randomized complete blocks. After 3 years in the nursery, the seedlings of each yearly set were planted in a common garden experiment replicated in four national forests located along a geographic gradient running from the west to the east of France (Additional file 1: Figure S1, Table 3 in Ducousso, Ehrenmann et al. 2022). The conditions at the sites of three of the forests (Petite Charnie, Vincence, Sillegny) were favourable for Q. petraea, whereas those in the fourth forest (Vierzon) were much harsher, due to the podzolic-like soil.

With very few exceptions, all the french provenances were established at all four sites (forests), in four yearly plantation sets corresponding to the four yearly collection sets. However, provenances from other countries were not systematically replicated in the four sites due to the limitation of material. Hence the overall analysis was restricted to the french material, while the climate-trait correlation analysis was limited to only one site (Sillegny) but for all provenances installed in Sillegny (Additional file 1: Tables S1a and b). The experiment thus comprised 16 tests (4 yearly sets replicated at four sites). The four yearly sets of seeds collected in 1986, 1987, 1989, and 1992 were used to generate saplings that were planted in the early months of 1990, 1991, 1993, and 1995, labelled sets 1, 2, 4, and 5 (Fig. 2 in Ducousso, Ehrenmann et al. 2022) for a full description of the experimental layout). In what follows, the sources of variation due to the year of seed collection, and to the year of plantation are thus confounded, and are designated in this study as effects due to the “yearly set”.

At each site, the four yearly sets were planted as four adjacent units. The full experimental layout is described in Figure 2 and Table 4 of Ducousso, Ehrenmann et al. (2022). Each test was subdivided into complete macroblocks, corresponding to homogeneous site conditions. The number of macroblocks ranged from 5 to 10, depending on the test. Each macroblock comprised several randomized incomplete microblocks, each consisting of eight plots of different provenances. Each plot consisted of 24 trees of the same provenance, distributed over four rows, with six trees per row. As rows were separated by 4 m, and there was 1.75 m between trees within a row, the plots were almost square (12 m * 10.5 m). Within a macroblock, an individual provenance was represented by at least two or three replicated plots. Within a test, each provenance was represented by 120 to 384 trees, on average. Given the complexity of the overall design, and to facilitate the construction of the statistical models for data analysis (Sections 2.2.1 to 2.2.3), Fig. 2 in Ducousso, Ehrenmann et al. (2022) helps to illustrate the different factorial and nested levels of variation considered in the experimental layout.

2.1.2 Phenotypic assessments and climatic data

Total height (HT) was assessed 4, 10, and 20 years after plantation, together with girth (CIRC) at breast height (1.3 m). Phenological observations were conducted during the spring of the third growing season. The developmental stage of the apical bud (DEB) was scored on a scale ranging from 0 to 5 (0 = dormant bud, 1 = swollen bud, 2 = bursting bud, 3 = leaf expansion, 4 = free leaf, 5 = elongating internodes). Phenological observations were conducted at a single time point in each test, usually when bud score variation was largest. Survival (SURV) was also recorded at each time point at which phenotypic observations were made. Stem shape (SHP) was assessed in years 10 and 20, with a scoring ranging from 0 to 10 (Additional file 1: Figure S2). The stem shape score took into account the straightness of the stem, the occurrence of forks, and the number and distribution of branches on the stem, as illustrated in Additional file 1: Figure S2. The experimental layout and phenotypic assessments are described in more detail in the companion data paper (Ducousso, Ehrenmann et al. 2022).

Climatic data for each provenance were extracted from the WorldClim database (Hijmans, Cameron et al., 2005), which were downscaled at 1-km spatial resolution and used in a previous range-wide investigation (Saenz-Romero, Lamy et al. 2017). We considered mean values of climatic data over the period 1950–2000 to gauge the climate at the provenance origin. Physiological meaningful climate variables were selected to account for the seasonal and annual balance of thermal energy and moisture (Saenz-Romero, Lamy et al. 2017 Supplemental Table S3 therein).

2.2 Statistical analysis

We implemented several linear mixed models, at different scales, to disentangle provenance effects from the other sources of variation. The ultimate goal was to generate a provenance classification that could be used for the selection of optimal seed sources. The mixed models were generated with R software (Munoz and Sanchez 2018), and are described in Sections 2.2.1 to 2.2.3. In all models, we considered provenance and quantitative covariables as fixed effects, and the components of the experimental layout (from yearly set to plot) as random effects. In all the models, the β, γ, and θ terms (see model [1] to [4]) are model parameters and ε denotes the residuals. We present the full models here. In some instances, they were simplified by removing some of the random effects, if the inclusion of these effects did not significantly decrease the AIC (Akaike information criterion) (Akaike 1973).

2.2.1 Models for traits with a continuous distribution

The use of linear models assumes the independence of residual terms. In the context of forest trees, this requires checking that there are no spatial and competition effects, particularly between neighbouring trees. We used the “breedR” package (Munoz and Sanchez 2018), which is particularly suitable for the analysis of forest genetic tests conducted in common gardens, to account for spatial and competition effects.

Within each test (Fig. 2 in Ducousso, Ehrenmann et al. 2022) and for each trait of interest for a given tree (Yijklm), we implemented the following linear model accounting for the different sources of variation:

$$ {Y}_{ijk lm}={\beta}_0+{\beta}_1{P}_i+{\beta}_2{B}_j+{\beta}_3{Pl}_{ijk}+\sum \limits_u{X}_{ijk lm}^{(u)}+{Spline}_l+{\varepsilon}_{ijk lm} $$
(1)

where P is the provenance, B is the microblock, Pl is the plot, X is the value of a trait (other than Y) used as an explanatory variable, ε is the residual effect, and Spline is the component of the residual due to the position of the tree.

The main objective of the model [1] was to estimate the value of Spline, which accounts for local spatial effects related to the position of the tree. In all subsequent calculations, Y values were corrected by removing the corresponding Spline estimate.

For potential competition effects, we used spatial statistics in BreedR to construct variograms to scale the variance of a trait according to the distance between trees (Additional file 1: Figure S3). Variograms displaying shifts over short distances indicate probable competition effects between neighbouring trees. In the case of HT4, HT10, and CIRC10, the variograms were rather flat for all tests, suggesting that there was no competition between the neighbouring trees in a plot (Additional file 1: Figure S3a). As a result, the following model was used to analyse the data:

$$ Y{\hbox{'}}_{ijklm n}={\gamma}_0+{\gamma}_1{P}_i+{\gamma}_2{Set}_j+{\gamma}_3{S}_k+{\gamma}_4{T}_{jk}+{\gamma}_5{B}_{jk l}+{\gamma}_6{Pl}_{ijklm}+{\in}_{ijklm n} $$
(2)

where Y’ is the phenotypic value (model [1]) for a tree corrected for the Spline effect, P is the provenance, Set is the yearly set, S is the site, T is the test, B is the microblock, and Pl is the plot.

We further restricted the analysis to the largest trees in each plot (in most cases, between 8 to 12 trees) to limit the bias due to the variation of survival among plots.

For CIRC20, local competition was detected based on the shape of the variogram (Additional file 1: Figure S3b). We accounted for competition effects, by amending the model [2] in two ways: we first restricted the analysis to yearly girth increments from years 10 to 20 (aCIRC10-20), rather than using CIRC20, and we then explicitly introduced additional variables accounting for competition with neighbouring trees into the model (Perot, Goreaud et al. 2010): with the two neighbours on the same row, the two neighbours in the same column, and with the four neighbours in adjacent rows and columns. Thus, model [2] becomes:

$$ Y{\hbox{'}}_{ijklmn}=W+{\gamma}_8{Cr}_{ijklmn}+{\gamma}_9{Cl}_{ijklmn}+{\gamma}_{10}{ Cr l}_{ijklmn}+{\varepsilon}_{ijklmn} $$
(3)

where W is the first six terms of model [2] and Cr is the mean basal area of the two adjacent trees in the same row, Cl is the mean basal area of the two adjacent trees in the same column, and Crl is the mean basal area of the four trees located in adjacent rows and columns. Y’ is the annual increase in girth between years 10 and 20 (aCIRC10-20). Adjustment for the competition effect in this way flattened the variogram of aCIRC10-20 (data not shown).

2.2.2 Models for traits with discrete distributions

Traits following binomial and polynomial distributions could not be adjusted with the spatial correction derived from the splines function of BreedR. We did not, therefore, use model [1] to account for spatial effects for traits with discrete distributions. Instead, spatial effects were mostly accounted for by microblock effects.

Survival

Survival at 10 years was modelled with a binomial logistic model similar to [2] but with Y replaced by logit(pr(Y = 1)), and the logit function of the probability that Yijklmn, the survival at 10 years of treeijklmn, is equal to 1 (i.e. the tree is alive). This approach was possible because tree mortality was not correlated with competition between neighbouring trees, so survival was independent for neighbouring trees. All the trees in the plots were used for survival analysis with the logit function.

Stem shape

Stem shape is of the utmost importance in forestry. A preliminary analysis showed that tree dominance, assessed on the basis of height-girth covariation, had an effect on the shape of the stem. There was a clear trend towards better shape quality in dominant trees (Additional file 1: Figure S4). Stem shape, as recorded in this study, was a factorial ordered variable. We therefore used a polytomic ordinal model to analyse its variation. This model resembled model [2] but also included adjustment for HT and CIRC:

$$ \mathit{\log} it\left( pr\left({Y}_{ijklm n}\le q\right)\right)={\uptheta}_q+{\uptheta}_1{P}_i+{\uptheta}_2{Set}_j+{\uptheta}_3{S}_k+{\uptheta}_4{T}_{jk}+{\uptheta}_5{B}_{jk l}+{\uptheta}_6{Pl}_{ijklm}+{\uptheta}_8{HT}_{ijklm n}+{\uptheta}_9{CIRC}_{ijklm n}+{\varepsilon}_{ijklm n} $$
(4)

where logit(pr(Yijklmn ≤ q)) is the logit of the probability that Yijklmn (stem shape score at 10 or 20 years after plantation (SHP10, SHP20) of treeijklmn) is equal to or lower than score q. Higher logit(pr(Yijklmn ≤ q)) values were considered to indicate a better tree shape. θq is the threshold parameter of the score q. All the other terms are the same as in the model [2].

All trees with recorded girth and height values were used for the analysis of SHP10. As stem shape at 20 years was recorded only at the Sillegny test site, for all sets, the analysis of SHP20 was restricted to this test site. Finally, as extreme stem shape scores (0 or 10) were extremely rare, their frequencies were bulked with the nearest scores.

Bud burst

Bud burst date is an important adaptive trait in oaks, as it may be correlated with various components of fitness, such as flowering, or the length of the growing season. Bud burst score three years after plantation (DEB3) was also analysed as a factorial ordered variable. We therefore used the same model as in [4] (where Yijklmn was the DEB3 value for treeijklmn). We did not include the effects of height and girth in the model, and all trees were used for the analysis. Thus, in this model, higher logit(pr(Yijklmn ≤ q)) values indicated an earlier bud burst.

2.2.3 Implementation of the models

Models [1] to [4] were implemented at two different levels of the whole analysis and according to the distribution of the trait analysed (Table 1).

Table 1 Trait definition and mixed models used to estimate provenance effects
Full size table

The first level of analysis was an analysis of spatial effects (model [1]). This analysis was conducted separately for each of the 16 tests (Fig. 2 in Ducousso, Ehrenmann et al. 2022). For continuous variables, this made it possible to correct the raw data for spatial effects.

The second level of analysis was a global analysis including all the terms of models [2, 3], and [4]. This global analysis extracted provenance effects (γ1 and θ1 values), which were subsequently used for provenance classification.

For the sake of completeness, the provenance * test, provenance * site, provenance * yearly set interaction terms were also considered in models [2, 3], and [4].

2.2.4 Multivariate analysis and provenance classification

Provenance effects (γ1 and θ1 values) corresponding to the different traits were integrated into a principal component analysis (PCA) to investigate multidimensional variation within the total data set. The objective of the PCA was to extract composite variables (PC, principal components) accounting for the largest proportion of multitrait variation between provenances, and to prevent the overexpression of particular traits in the next classification step. PCA was, thus, used to screen variables for their contribution to the overall variation between provenances. The selected variables were used to calculate Euclidean distances between all pairs of provenances. The matrix of these Euclidean distances was then used for hierarchical cluster analysis (HCA). HCA was performed with the agglomerative clustering algorithm, which assembles provenances in a stepwise manner to form clusters on the basis of similarity, until all provenances form a single cluster. The clustering generated by HCA was optimized by K means analysis (Kassambara, 2017). This involved assigning K clusters of provenances and reallocating provenances to clusters such that the sum of distances of the provenances to the centroid of the cluster reached a minimum value.

3 Results

3.1 Mixed models and estimation of provenance values

The spatial analysis (model [1]) for continuous traits showed that the Spline effects absorbed most of the spatial variation. Hence, the microblock became a negligible factor in models [2] and [3] and was discarded in the analysis of provenance effects (Table 2). Given the competition effects (Additional file 1: Figure S3) and the influence of tree size on tree shape (Additional file 1: Figure S4), corrections were made for aCIRC10-20, SHP10 and SHP20, according to models [3] and [4]. The mixed models also made it possible to account for random effects of the different sources of variation due to the experimental layout (Table 2). For dimensional continuous traits (HT and CIRC), the main sources of variation were test and plot, in addition to the residuals (mostly within-plot effects). For bud burst (DEB3), the dominant sources of variation were test and microblock, whereas for stem shape (SHP10), the dominant sources of variation were site and test. Large effects of yearly sets on survival were detected, suggesting a possible impact of yearly differences of stress events after plantation. Finally, the effects of interactions between provenance and experimental sources of variation (test, site, or set) were limited, and these effects were therefore discarded from the models for most discrete traits (Table 2).

Table 2 Variances due to random effects in the mixed models. Variances are expressed relative to the total variance of all random terms
Full size table

For all traits, we implemented all the linear models ([2] to [4]) both with and without the introduction of provenance as a fixed effect. We compared the Akaike information criterion (AIC) values between the two implementations of each model. The inclusion of provenance effects systematically decreased the AIC (by more than 2 AIC units), whether considering Q. petraea and Q. robur provenances together or separately. In addition, an analysis of variance showed that provenance effects were highly significant for all traits (F test, p < 0.001). The variation between provenances is illustrated in Additional file 1: Table S2. Height growth (HT10) ranged from 458 cm (provenance Parc Saint Quentin) to 369 cm (provenance Vouillé). Earlier-flushing provenances were located in the South of France (Grésigne and Vachères) and late-flushing provenances were found in the North East of France (provenance Sturzelbronn, Saint Jean, and Haguenau1). Pedunculate oak provenances (Fontainebleau2, Compiègne1 and Mees) also flushed later. The ranking of provenances for stem shape varied slightly from years 10 to 20. The provenances for which stem shape was best at age 20 were Blois2, and La Haie Rénaut. Finally, SURV10 varied little between provenances, as survival exceeded 90% for all provenances.

3.2 Correlation of provenance mean values and climatic variables

To account for the ecological drivers of provenance differentiation we computed Pearson correlations between provenance trait values and climatic data, using the data of the Sillegny site, that comprised the largest number of provenances, and where HT20 was recorded as well. Using the data of Sillegny allowed also to compute trait-climate correlations over the whole set of provenances including origins from other countries than France (Additional file 1: Table S1b), thus encompassing a larger range of climate variation. Calculations were done with two samples: the overall sample of provenances, and a restricted sample discarding provenances of Georgia and Ireland that distorted the range of climatic variables and traits (Table 3). We found significant clinal genetic variations between trait values and climatic data for growth and bud burst (Table 3); we illustrate some of the clines (Figs. 1, 2, and 3) for cases where correlations were significant for both samples. Growth traits (aCIRC10_20 and HT20) were positively correlated with temperature (Figs. 1 and 2) and, to a lesser extent, negatively with precipitation, resulting in higher growth for provenances originating from climates with stronger unbalance between heat and moisture (Table 3). The timing of apical bud burst (DEB3) was correlated with higher temperature (spring and annual temperature) and warmer growing season (SSD5, GSSD5), and with the mean diurnal range of temperature (MDR, Fig. 3): early flushing provenances originate from climates with large diurnal ranges. Survival and stem shape did not exhibit congruent correlation with climatic variables between the two samples, except for SURV10-MDR.

Table 3 Pearson correlation coefficients between provenance trait values and geographic and climatic variables (values indicated by superscript a are significant at p < 0.01); values indicated by superscript b are significant at p < 0.05)
Full size table
Fig. 1
figure 1

Linear regression between provenance mean annual girth increment between age 10 and 20 (aCIRC10-20, index, see Additional file 1: Table S2) at the site of Sillegny (whole sample of provenances) and mean annual temperature (MAT, in °C) at the origin of provenance. Legend: Vertical dashed line indicates MAT value at the site of Sillegny, black dots correspond to the French provenances. The blue line is the regression line (aCIRC10-20 = 1.84 + 0.03 MAT; p < 0.0004)

Full size image
Fig. 2
figure 2

Linear regression between provenance height at age 20 (HT20, in cm) at the site of Sillegny (whole sample of provenances) and the mean spring temperature (SPRMT, in Celsius degrees) at the origin of provenance. Legend: Vertical dashed line indicates SPRMT value at the site of Sillegny, black dots correspond to the French provenances. The blue line is the regression line (HT20 = 983 – 7.9 SPMRT; p < 0.03)

Full size image
Fig. 3
figure 3

Linear regression between provenance bud burst score (DEB3, index) at the site of Sillegny (whole sample of provenances) and the mean diurnal temperature range (MDR, in °C) at the origin of provenance. Legend: Vertical dashed line indicates MDR value at the site of Sillegny, black dots correspond to the French provenances. The blue line is the regression line (DEB3 = − 7.48 + 0.85 MDR; p < 10−8). Positive values of DEB3 correspond to early flushing provenances, and negative values to late flushing provenances

Full size image

3.3 Clustering of the provenances

Before performing a clustering analysis, we screened the variables to prevent highly correlated traits from making inflated contributions to the overall between-provenance variation. PCA based on the provenance effects shown in Additional file 1: Table S2 was performed to check for correlation between the eight traits. The first three principal components accounted for more than 75% of the total variation between provenances (Additional file 1: Figure S5). Component 1 (40% of the variation) was related mostly to growth traits (HT10, HT4, and CIR10), which were also highly correlated with each other. Component 2 (20% of the variation) was correlated with stem shape (SHP10 and SHP20), whereas component 3 was related to bud burst (DEB3) and girth increment (aCIRC10-20). Finally, MORT10 displayed little variation between provenances. The correlation circles shown in Additional file 1: Figure S5 were used to screen the traits for the subsequent clustering analysis, which was limited to the following five traits — HT10, aCIR10-20, SHP10, DEB3 and SHP20 — on the basis of the PCA analysis.

HCA assembled provenances into clusters according to their similarity based on the Euclidean distances calculated with the five selected traits. After several attempts with different numbers K of clusters, we set K to 13 for the K-means optimization procedure (clusters “a” to “m” in Additional file 1: Figure S6). An empirical examination of the 13 clusters was performed, in which cluster compositions were compared in terms of trait values. The HCA and K-means methods are based on Euclidean distance. We intended to “return” to the original trait values to provide biological support for the final clustering. A comparison of trait mean values and their confidence intervals within and between the 13 clusters (Additional file 1: Figure S7) and the assignments of provenance to the clusters by K-means optimization (Additional file 1: Figure S6) led to the merging of three of the original clusters (a, b and c) into one larger cluster (A). The provenance composition of the remaining clusters was conserved (d to m, converted into D to M). End-stacked branches (clusters) of the dendrogram were then grouped by minimizing the differences between the provenances belonging to the clusters (Fig. 4).

Fig. 4
figure 4

Provenance clustering according to the hierarchical classification and the K-means analyses. Legend: The colours of the provenance labels correspond to the final clusters after consolidation by the K-means method (see text). Letters are assigned to the clusters for their identification

Full size image

We facilitated biological interpretation of the clusters by plotting the provenance trait values nested within each cluster (Fig. 5). Between-cluster variation was greater for DEB3 and HT10 than for the other three traits. Using these violin diagrams, we focused our attention on clusters A, E, F, G, and H, which contained the provenances with the highest values of aCIR10-20, SHP10, and SHP20, which might be of primary importance for the choice of seed sources. The ranking of the clusters, for these three traits, decreased in a continuous manner from A to H, excluding D. However, there were noticeable differences for the other two traits (HT10 and DEB3): cluster E displayed greater height growth (HT10), G had a lower level of height growth, F flushed earlier, and H flushed later (DEB3). Clusters L and M consisted of provenances with the highest scores for shape at 10 years, but with poor growth (HT10 and aCIRC10-20). Clusters K and J had small circumference increments, late budburst and poor shapes, despite having above-average height growth. The provenances belonging to these clusters were Quercus robur provenances, with the exception of Parc Saint Quentin. Provenances of cluster I had lower levels of height growth and average values for the other traits. Cluster D consisted of a single provenance, Vachères, which was separated from all other provenances due to its extreme trait values (very early budburst, very low circumference increment and height, average shape).

Fig. 5
figure 5

Violin plot of the 11 clusters according to their provenance trait values. Legend: The density of the provenance distribution contributes to the violin form. The provenance trait values are expressed in standardized units

Full size image

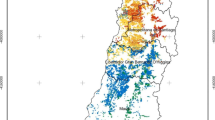
Finally, the various clusters did not correspond to clear-cut geographic groups (Fig. 6). Geographic proximities were observed for clusters A, F, and H, but the other clusters group together provenances with very diverse geographic origins (E, G, and L).

Fig. 6
figure 6

Geographic distribution of the provenances of the different clusters. Legend: Red dots correspond to provenances belonging to cluster A. Blue dots correspond to provenances belonging to cluster E, and black dots correspond to provenances belonging to any of the remaining clusters. Green area corresponds to the distribution of Quercus petraea according to Caudullo, Welk et al.(2017)

Full size image

3.4 Patterns of variation between provenances

We examined in more detail whether other sources of provenance variation should be accounted for in seed sourcing. Three sources of variation were examined:

  • Variation between provenances of the same forest

  • Variation within and between provenance regions

  • Variation within and between maternal lineages

Twinned provenances are collected from within the same forest, and are separated by no more than a few kilometres at maximum. Comparisons of twinned provenances can be used to explore the spatial extent of the provenance effect, which is of important practical value for seed collection. Among the eleven pairs of twinned provenances studied here, we found very low levels of phenotypic trait variation between twinned provenances in general, with only a few exceptions (Compiegne, Fontainebleau, and Bride) (Additional file 1: Figure S8). For Compiègne, one population came from a pedunculate oak stand, whereas the other came from a sessile oak stand. The reasons for the observed differences between twinned provenances at Fontainebleau and Bride remain unclear, as the ecological features of the different compartments in which the seeds were collected are very similar (substrate, soil depth, altitude, etc., data not shown). Some of the twinned provenances were probably planted and originated from different source materials (see Section 4).

The 70 Q. petraea provenances came from 17 different provenance regions (Additional file 1: Table S1a). We investigated whether there were significant differences between provenance regions. Significant differences were found only for growth (aCIR10_20), between provenance regions QPE104 and 106 (highest growth) and QPE204 and 212 (lowest growth) (Additional file 1: Table S3 and Figure S9). For two traits (SHP10 and DEB3), more variation was observed between provenances within the same provenance region than between provenance regions.

We also explored whether there were differences between provenances bearing different chloroplast haplotypes. This analysis was restricted to provenances in which all trees shared the same haplotype. Polymorphic haplotypic provenances were discarded from the analysis. Haplotypes of the three main maternal lineages (Atlantic, Balkan and Italian) were represented in the provenance sample, making it possible to compare haplotype groups. The mean trait values of provenances did not differ significantly between haplotype groups (Additional file 1: Figure S10 and Table S4).

4 Discussion

We performed a multitrait and multisite analysis of genetic variation between provenances of Q. petraea in France, with the main aim of providing recommendations for seed sourcing. Our investigations confirmed genetic differentiation for adaptive traits highlighting clear genetic clines triggered by climatic gradients across the distribution of the species. This was the case for the time of bud burst which follows a temperature cline confirming earlier reports along either latitudinal (Ducousso, Guyon et al. 1996) or altitudinal gradients (Vitasse, Delzon et al. 2009b). Our results are the first to report stronger genetic positive clines of growth with temperature than with precipitation in Quercus petraea (Table 3). Both phenology and growth clines are likely the result of directional diversifying selection along temperature gradients since the establishment of the populations. Our study was performed after a European wide investigation as part of the same experiment (but at multiple testing sites) concluded that the species displayed substantial resilience to environmental changes, thanks to the genetic and plastic responses of adaptive traits (Sáenz-Romero, Lamy et al. 2017; Sáenz-Romero, Kremer et al. 2019). For seed sourcing purposes, we concentrated on a narrower geographic range, but focused on traits of economic and ecological value considered important for plantation. The assessments were performed at a young age for such a long-lived species, but the selected traits are highly relevant from an ecological standpoint for management purposes. Growth (height and diameter) after 10 years provides a reliable evaluation of the capacity of trees to survive the critical juvenile stage in which they are exposed to competition from weeds and game damage. Stem shape at 20 years is of predictive value for subsequent stem quality and stiffness; large stocks of juvenile trees with a good shape ultimately resulting in tall, high-quality forest stands result in high forest stand of improved quality (Jarret, 2004). Finally, assessments of the date of bud burst, which displays strong genetic stability across ages (Vitasse, Delzon et al. 2009a), should help to prevent exposures to late frosts, spring drought or leaf pathogens, by making it possible to discard trees that flush extremely early or extremely late (Deans and Harvey 1996; Dantec, Ducasse et al. 2015). We found significant differences between provenances for all traits, and we grouped the provenances into 11 clusters of potential utility for seed sourcing, using multivariate approaches. Our results open up two important areas of discussion. We will first consider cluster composition with respect to other classifications of stands and silvicultural practices. We will then discuss targeted recommendations for seed sourcing that can be inferred from our results.

4.1 Provenance clustering

Our analysis of twinned provenances clarified the spatial envelope of a “provenance”. We found that there was less variation between seed lots collected from the same forest than between seed lots collected from different forests. However, this conclusion may be valid only for forests in which all the compartments were regenerated by natural means. The prior historical introduction of foreign material, which may not always be known, may affect this conclusion, due to genetic differentiation of the introduced material from the local population or genetic pollution resulting from interbreeding between introduced and local stands (Geburek and Myking 2018). This was probably the situation at Fontainebleau and Bride, for which we found differences between seed lots from the same forest. Such conclusions have important practical consequences for seed collection within a so-called “seed stand” within a given forest, as seed yields may be heterogeneous within a given forest. However, we draw attention to the temporal genetic differentiation between old and younger stands of sessile oak, due to the different selection pressures operating between the late Little Ice Age (before 1850) and Anthropocene warming (post-1850), suggesting to preferentially harvest seed in stands born after the Little Ice Age (Saleh, Chen et al. 2022). Twinned “temporal” provenances from the same forest were not sampled, a priori, during the collection of provenances, and it was not possible to investigate temporal differentiation in this study.

Overall, the cluster composition of provenances poorly matched the provenance regions identified on ecological grounds. Finally, the clusters (especially clusters A, F, and H) matched the geographic distribution to some extent (Fig. 6), despite some provenances from the same geographic area being assigned to different clusters. An illustration of this situation is provided by provenances from North East France (Bride1, Lembach, Westhoffen, Haslach, Haguenau1, Steinbach, Sturzelbronn). These seven provenances were assigned to seven different clusters, despite their geographic proximity (they are less than 80 km apart). One probable reason for their assignment to different clusters may be the more frequent use of plantation approaches to renew oak stands in North East France, due to more irregular seed yields in this region (Verger and Ducousso 2009). The German forestry administration implemented intensive oak afforestation, by direct seeding or plantation, in Alsace in the late nineteenth century, to repair the considerable damage to these forests incurred during the 30 years’ war (Dion 1970; Degron and Hussson 1999). However, the geographic origin of the material introduced during this period is unknown, and genetic marker analysis revealed no strong differentiation, suggesting probable transfers over short distances in the Rhine Valley (Neophytou, Gartner et al. 2015). For the clusters matching geographic distribution, climatic and ecological proximity may be the source of similarity. However, silvicultural practices may also have contributed to clustering, particularly for clusters A and E. Most of the provenances of clusters A and E are located in the Seine, Loire and Allier valleys (RénoValdieu, Bellème, Bercé, Blois, Fontainebleau, Montargis, Bertranges, Tronçais), where high-forest silvicultural treatment is a long-standing tradition (Ducousso, Louvet et al. 2004; Valadon, 2009), at least since Colbert’s royal “ordonnance” in 1669. We recently showed that high-forest practices generate genetic changes favouring faster-growing trees with straighter stems, even in a single generation (Alexandre, Truffaut et al. 2019; Alexandre, Truffaut et al. 2020). Conversely, forests in which silvicultural treatments have switched, at different times between coppicing under forest and high forest with standard trees may have been assigned to different clusters in our study.

4.2 Clustering for seed sourcing

Given the traits assessed, clusters A and E contain candidate provenances for seed sourcing in operational forestry. Provenances from these two clusters display high levels of juvenile growth and are, thus, better able to resist competition and to overcome game damage, and to achieve an acceptable stem shape. The main difference between the provenances of clusters A and E is the slightly earlier flushing and faster early growth of cluster E (Fig. 6).

Clusters A and E are part of the continuum of clusters A-E-F-G-H displaying only very small differences in growth (aCIR10_20) and shape (SHP10 and SHP20). However, these traits may vary considerably between extreme provenances within a cluster, even if these differences are not statistically significant. In addition, the provenances of clusters F-G-H differ from those of clusters A and E for other traits. The provenances of cluster F flush much earlier, potentially exposing them to more frequent damage due to biotic or abiotic agents. Conversely, the provenances of cluster H flush later and are more like Q. robur provenances, raising questions about possible genetic admixture in provenances belonging to this cluster. Provenances from the remaining clusters had extreme values for some traits, raising concerns about their use as seed sources. The provenances of cluster I have slow initial growth. The provenances of clusters L and M display poor growth after 10 years and provenances from cluster M flush very late.

Clusters J and K contain very few provenances, and most are Q. robur provenances. Finally, cluster D contains only one provenance (Vachères), located at the southern margin of the species distribution in France and with extreme trait values (very early flushing, poor growth, and poor stem shape). This analysis of the clusters obtained leads us to recommend the use of provenances from clusters A and E as potential seed sources. Provenances from clusters F, G, and H may be alternative candidates, provided that earlier or later flushing is not detrimental at the intended plantation site. The inclusion of multiples provenances within a cluster should also help to secure seed procurement regardless of heterogeneity in seed yields. Overall, our results confirm and reinforce earlier predictions based on juvenile traits in the same experimental plantations (Ducousso, Louvet et al. 2004).

Where could these recommendations be implemented? Our results were obtained at test sites within the central zone of sessile oak cultivation in France, between the Loire and Rhine rivers and encompassing areas of maritime to semi-continental climates. Each of the recommended clusters includes provenances with broad west-to-east (Saint Aubin du Cormier, Lembach), and north-to-south (Perseigne, Moulières) distributions. Previous genetic surveys conducted with protein markers (Zanetto and Kremer 1995; Le Corre, Roussel et al. 1998) or whole-genome sequences (Leroy, Louvet et al. 2020) showed that genetic differentiation within this rather large geographic unit is weak, providing additional genetic support for clusters A and E. In addition, our results also indicate that the effects of interactions between provenance and other experimental sources of variation (site, set, test) were weaker than provenance effects (Table 2). Based on this reasoning, we conclude that provenances from clusters A and E (or alternatively F, G, and H) are suitable for use throughout most of the territory of France, excluding the southern margins of the species distribution. We would also recommend the mixing of different sources from the same clusters for seedling procurement for plantations. The use of mixtures within clusters would improve the tolerance of ongoing climate change, by exposing trees of different origins to natural selection. Other currently proposed strategies are based on a climate-oriented approach for seed sourcing based on species distribution models, and thus recommend targeted assisted migration. Such reasoning, based exclusively on climatic data, ignores biotic interactions and may provide biased estimates of the niche of the species, ultimately leading to the misdirection of transfers (Boiffin, Badeau et al. 2017). The mixing of seeds from different provenances should be seen here as an alternative approach, enhancing adaptability to future climatic conditions and maintaining diversity.

5 Conclusion

We propose a collection of 34 provenances belonging to two clusters for seed sourcing, for the central part of the distribution range of Q. petraea in France, and we recommend the mixing of seeds from different provenances. We acknowledge that our conclusions are based on assessments performed in current climate conditions, but we anticipate their applicability during the next few decades, given the overall resilient response of sessile oak populations observed over a larger climatic range of provenance tests (Sáenz-Romero, Lamy et al. 2017; Sáenz-Romero, Kremer et al. 2019). Our recommendations should reinforce resilience and increase diversity, based on the provenance composition of the clusters. The future amendment of these recommendations based on ongoing assessments in established provenance tests remains possible.