Abstract
Key message
We present a new approach to calibrate timings of phenological events from satellite data (e.g., Sentinel-2 MSI data) with readily available surface temperature data. The new approach improves the estimation of growing season length in boreal forests.
Context
Satellite data is used to calibrate phenology models employed in land surface model components of climate models. However, realistic quantification of forest phenological transitions, such as the greenup and senescence, across large spatial scales remains challenging due to the lack of sufficient ground validation data representative of both forest tree canopy and forest understory species compositions.
Aims
The aim of this study was to develop a new approach to benchmark boreal forest land surface phenology obtained from Sentinel-2 (S2) against surface temperature data.
Methods
We computed S2 phenological transition dates and compared them to ground reference data on temperature from a network of meteorological stations across Finland (60–70N°).
Results
Our results showed that applying standard phenometrics directly to S2 data to estimate the growing season length in boreal forests may lead to clear biases in all species groups.
Conclusion
Our approach to use temperature data to calibrate boreal forest phenometrics allows flexible application across spatial scales (i.e., point or grid) and different satellite sensors. It can be combined with any vegetation land cover product to provide a link between surface temperature data and forest seasonal reflectance properties.
Similar content being viewed by others
1 Introduction
Vegetation phenology, the science of reoccurring vegetation lifecycles, is one of the key drivers of regional and global carbon and water cycles, and is identified as a critical variable required for the characterization of Earth’ s climate, e.g., in the UN’s Global Climate Observing System (GCOS, 2016). Plant phenology refers to specific growth or senescence events of individual plants, whereas satellite-based phenology, also called as land surface phenology (LSP), denotes aggregated phenology of all plants occupying an area viewed by a satellite sensor (Helman 2018; Berra and Gaulton 2021). LSP metrics (later in the paper referred to as phenometrics) refer to the detection of phenological events, such as the onset of greenness, greenup midpoint, maturity, peak greenness, senescence, greendown midpoint, and dormancy (Gray et al., 2019) based on remotely sensed greenness proxies, such as Normalized Difference vegetation Index (NDVI) or Enhanced Vegetation Index (EVI). Currently, satellites remain the only feasible tool for continuous monitoring of LSP at regional to global scales.
Land Surface Models (LSMs), terrestrial components of climate models, often employ remotely sensed maps of different Plant Functional Types (PFTs) to represent vegetation spatial distributions, and LSP is often used to derive models required for controlling vegetation phenology (Botta et al. 2000; Fisher and Koven, 2020; Fu et al. 2014; Piao et al. 2019). However, accurate quantification of vegetation phenological transitions, such as the greenup and the senescence, across large spatial scales remains challenging due to the lack of good quality satellite data time series and sufficient ground validation data representative of both forest tree canopy and forest understory species compositions. Differences between satellite and ground reference data are caused by, e.g., mismatches in temporal and spatial sampling, differences in terminology used to separate certain phenological transitions, the use of different view and observation angles, and varying wavelength regions of the bands of the sensors (Berra et al., 2019; Zeng et al. 2020). Although many budburst models have been developed for different species and research sites (e.g., Lappalainen et al. 2008; Linkosalo et al. 2006; Olsson and Jönsson 2014), they often perform poorly outside the geographical areas the models were developed for (Olsson and Jönsson 2014), and thus, they are not relevant for large area applications. While the majority of the published LSP studies have looked at temperate and boreal deciduous forests (e.g., Berra and Gaulton 2021; Hmimina et al. 2013), only a few studies have focused on boreal evergreen coniferous forest phenology (Helman 2018; Gill et al. 2015). In addition, only a few models exist for mapping and modeling autumn senescence, as the most studies have focused on greenup (Peaucelle et al. 2019).
The representation of vegetation phenological processes in LSMs have several shortcomings. For example, Richardson et al. (2012) found that, for temperate and boreal forests, almost all of the 14 vegetation models with different phenology parameterizations that they compared overestimated the length of the growing season and consequently the gross ecosystem photosynthesis. Accounting for evergreen coniferous phenology in LSMs may also significantly impact future projections of the carbon budget (Peaucelle et al. 2019). A recent paper by Piao et al. (2019) suggests that future studies should focus on scaling timings of phenological events and phenological phases from species to landscape-level. Noteworthy is that LSMs often predict the timings of greenup and senescence based on climatic derivatives, such as the growing degree day (GDD) sums (e.g., Botta et al. 2000; Fu et al. 2014; White et al. 1997; Richardson et al. 2012; CLM5, 2020), rather than greenness proxies obtained from satellite measured data. Although several LSMs may use so-called “satellite-based phenology” or “prescribed phenology,” these denote specifying for each site (or PFT) a single average seasonal change of leaf area index (LAI, m2/m2) based on satellite data (i.e., monthly mean LAI) (e.g., Levis and Bonan, 2004; Richardson et al. 2012; Sellers et al. 1996). The problem of the prescribed phenology approach is that using the monthly LAI does not depend on prevailing environmental conditions (Levis and Bonan, 2004; Richardson et al. 2012). Thus, there is a need for improved linking of temperature data and satellite-based greenness values. Regional and vegetation type-specific linking is a prerequisite for realistic prediction of future vegetation processes in LSMs.
The coarse spatial resolution of, e.g., Terra and Aqua combined Moderate Resolution Imaging Spectroradiometer (MODIS) and its products which are often temporal maximum value composites do not allow inspection of phenological differences between different tree species (or forest types) in fragmented landscapes or analyzing exact timings of the phenological transitions dates. For example, as results from Hmimina et al. (2013) demonstrated for evergreen forest areas, the 16-day max composite MODIS NDVI time series did not succeed in reproducing the general temporal phenological pattern, and significant discrepancies were observed with ground-based reference data due to weather conditions and spatial heterogeneity within the MODIS pixels. In addition, it has been shown that the frequency of high-quality satellite observations can have substantial impact on phenological detections during periods of phenological changes (White et al. 2014). Thus, there is a need for using finer spatial resolution daily data to better understand the seasonal changes in boreal forest reflectance of different forest types.
Obtaining landscape-level estimates of vegetation phenology from optical satellite data contains typically steps of cleaning and flagging the data, smoothing and reconstruction, and extraction of phenometrics from the reconstructed time series (e.g., Zeng et al. 2020). Although there is a myriad of methods for accomplishing the abovementioned tasks, different methods are known to perform well for different vegetation types and areas (e.g., de Beurs and Henebry, 2010; Zeng et al. 2020). Thus, it is often recommended to compare multiple fitting methods to evaluate the possible errors in predicted phenological transition dates (Helman 2018). The simplest and thus most often used approach to extract the phenological transition dates from reconstructed satellite-based time series data is to employ predefined greenness thresholds, the so-called phenometrics (e.g., Bolton et al. 2020; MCD12Q2v006 2020). This approach has been regionally used by the harmonized Landsat 8 and Sentinel-2 (S2) phenology product dataset (Bolton et al. 2020), which unfortunately currently only covers the North American continent. The European counterpart is currently being processed by COPERNICUS (2020) and should become available during 2021. Globally, the threshold method has been employed by the MODIS Land Cover Dynamics (MCD12Q2 v006) data product (a.k.a. informally called MODIS Global Vegetation Phenology product). MCD12Q2 has notably coarser spatial resolution (pixel size of 500 m) than S2 (10–60 m, respectively) (MCD12Q2v006 2020). In practice, the threshold method is fast and easy to apply, but the downside is that the biophysical meaning of the threshold selected may not be clear, and any single threshold value may not be assumed representative for different species mixtures and different geographical regions (Tan et al. 2010; White et al. 1997). Thus, for regional application of the threshold method, the biome-specific thresholds need to be benchmarked with ground data.
Challenges in optical remote sensing of boreal forests are caused by frequent cloudiness (i.e., data quantity and quality problems), low seasonal variation in evergreen conifer canopy leaf area (i.e., thresholding problem), and mixed signals from the ground floor vegetation and from deciduous trees (i.e., mixed signal problem) (e.g., Helman 2018). Due to these reasons, results regarding LSP of evergreen coniferous forests remain less interpretable and conclusive compared with results of ecosystems with deciduous trees (e.g., Bolton et al., 2020). In addition, even the user manual of MCD12Q2 (MCD12Q2v006, 2020) reports ongoing challenges in mapping LSP in the boreal region: “Greenup and Dormancy phenometrics are anomalously early/late in some high-latitude regions…”. Thus, there is an urgent demand to develop approaches for improving LSP mapping of evergreen conifers from optical satellite data, because such remotely sensed landcover/phenology products are used to calibrate phenology models incorporated into LSMs (Botta et al. 2000; Fu et al. 2014). In addition, there is a need to investigate possible biases that are introduced by using different phenometrics to define the beginning and end of the growing season. For example, currently the MODIS Technical guide (MCD12Q2v006 2020) recommends “…users are encouraged to use the more realistic and stable MidGreenup and MidGreendown metrics to capture season start/end in these regions (e.g., high-latitude evergreen forests)”. Thus, it is not clear how large biases in predicted surface fluxes may occur if these two phenometric-pairs are used interchangeably to define the growing season length (GSL). If clear biases occur in GSL estimates, regional benchmarking of the thresholds (i.e., phenometrics) is required to clarify the relation between satellite-based greenness and surface temperature data. While the majority of phenology research has targeted quantifying the spring greenup, notably fewer studies have focused on autumn senescence which is also needed to determine the GSL.
Vegetation phenology in the boreal region is driven by temperature and photoperiod (Gill et al. 2015; Olsson and Jönsson 2014; Piao et al. 2019). Thermal growing season (TGS) is defined to begin when the daily mean temperature rises above a selected threshold in spring and snow has melted from open areas, and in autumn, it terminates when daily mean temperature falls permanently below the same threshold (Ruosteenoja et al. 2016). The development of process-based phenology models is hindered by the lack of a mechanistic understanding regarding effects of, e.g., photoperiod, chilling, and dormancy on boreal forest phenology (Gill et al. 2015; Piao et al. 2019). Thus, at present, using temperature derived estimates of TGS remains the most feasible option for developing large area phenology models for areas dominated by boreal PFTs (e.g., Botta et al. 2000). The beginning and end dates of TGS are often approximated to occur, after the first 5-day period with average temperatures above a base temperature and after the first 5-day period with temperature below the same base temperature (Ruosteenoja et al. 2016). Typically, a base temperature threshold of 5°C is applied in boreal and temperate climate conditions (e.g., Kauppi et al. 2014; Skaugen and Tveito 2004) whereas in warmer climates higher thresholds, e.g., 10 °C, are used (Matzarakis et al. 2007). Meaningful links between landscape-level LSP greenness and temperature data is required by the LSMs which use gridded temperature data to predict vegetation responses to alternative future temperatures.
The goal of this study was to develop a new approach to benchmark satellite-based phenometrics against surface temperature data. Using the new approach, we computed phenological transition dates from S2 data and compared them to ground reference estimates based on temperature data from a network of meteorological stations across boreal Finland. Finally, using the new approach, we answer the following research question: How do estimates of growing season length (GSL) vary when obtained from S2 data or ground reference temperature data?
2 Material and methods
2.1 Data
We obtained daily mean temperature (°C) data from the Finnish Meteorological Institute’s (FMI) weather station network for 201 sites from the 1st of January 2017 to the 31st of December 2019. Both Sentinels 2A and 2B were operating during the growing seasons in 2017, 2018, and 2019. The data covers the whole of Finland. The data was ordered from FMI via Ilmastopalvelu web service (FMI 2020). In this study, we wanted to focus on pure forest pixels, and thus, in the case the meteorological station was not directly located in a forest, we made the assumption that the meteorological data represents sufficiently well also the forest pixels located in the closest forest from where the forest plot was selected. The forest plot locations were determined based on visual assessment of Google Earth Engine (Gorelick et al. 2017) map preview. Typically, the forest plot (used in our analyses) was ~270 m from the meteorological station. For each forest plot, a time-series of S2 data, corresponding to the daily temperature data period, was extracted from dataset “COPERNICUS/S2_SR” using Google Earth Engine. The COPERNICUS/S2_SR is a level-2A orthorectified atmospherically corrected surface reflectance product (SR) from the European Space Agency’s Copernicus program. S2 satellites have a global 5-day revisit frequency, and the S2 Multispectral Instrument (MSI) samples 13 spectral bands: at either 10-, 20-, or 60-m spatial resolution. The level-2A S2_SR data is only available for data periods when both S2 and 2B satellites were on the same orbit (S2_SR data available after March 28, 2017).
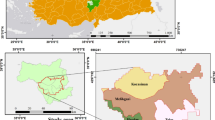
Finnish CORINE (2018a) landcover classification was used to extract the forest type information (i.e., whether the forest was conifer, broadleaved, or mixed forest) for the forest plot locations. The CORINE data has 20-m spatial resolution and is based on S2 satellite image mosaic compiled from 10×10 m spatial resolution data. The CORINE image mosaic interpretation employed the National Forest Inventory data (from Natural Resources Institute Finland), Biotope data (from Metsähallitus, a national organization managing state-owned land and water areas), and Digital Elevation Model and Soil Information from the Topographic Database (CORINE 2018b). Based on independent land use validation dataset, the percentage of correctly classified pixels in the CORINE is 95% for broadleaved forest, 98% for coniferous forest, and 97% for mixed forest (see Table 2 in CORINE 2018b). The number of plots used in our analyses was 103 from which 74 were dominated by coniferous, 14 by deciduous, and 15 by mixed species (Fig. 1, more details in section 2.3.1).
2.2 Processing of temperature data
The ground reference dates for the beginning and ending of the thermal growing season (TGSstart and TGSend, respectively) were calculated using the temperature deviation integral (TDI) method which has been in use in the operational climate service at the Finnish Meteorological Institute (FMI) since 2007 (Ruosteenoja et al. 2016) and thus is sufficient to provide a regional baseline to compare the satellite-based phenometrics with.
The TDI method is based on summing daily mean temperatures above the base temperature of 5°C starting from 1st of February. If temperature is above the base temperature on that day, then the first day when temperature falls below the base temperature is used. The 1st of June is used to constrain the search period to find the absolute minimum and maximum values (for all details see Ruosteenoja et al. 2016). In other words, in this study, TGSstart was determined to happen on the day the integral reaches the absolute minimum value not later than the 1st of June. TGSend was determined to happen on the day when the integral reaches the absolute maximum value starting integration on the 1st of June.
Following the TDI approach by Ruosteenoja et al. (2016), the Growing Degree Day (GDD, °C) sum, a measure of heat accumulation, was calculated for the time period between TGSstart and TGSend, by taking the total sum of daily mean temperatures above the base temperature. In addition, the period when daily mean temperatures were above-zero were searched using a base temperature of 0°C (referred to as “T>0” for spring and “T<0” for autumn) to indicate the potential photosynthesis period of evergreen conifers. All years (i.e., 2017, 2018 and 2019) had 365 days. An example of applying the TDI method for finding timings of TGSstart, TGSend, T>0, and T<0 is illustrated in Fig. 2.
An example application of the temperature deviation integral (TDI) method for finding timings of start and end of the thermal growing season (TGSstart, TGSend), and the timings of daily mean temperature (Tday) rising above-zero “T>0” and falling below-zero “T<0”. Tbase and T0 indicate the 5°C and the 0°C base temperatures, respectively. Tday-Tbase is plotted as cumulative temperature
2.3 Processing of Sentinel-2 (S2) data
2.3.1 Plot selection
Time-series of S2 surface reflectance (SR) data was extracted using a buffer of 30-m around plot center points. The 30-m buffer size was used as a compromise resolution between 10 and 60 m bands. In addition, pixel classification labels and quality flags were obtained.
The number of FMI’s meteorological stations suitable for this study was limited due to the following reasons: First, we excluded FMI sites for which the TGSstart and TGSend could not be determined (n=23), and sites located on treeless islets and locations for which no S2 data was available (n=9). Next, we removed plots which were not classified as forest by the CORINE (n=9), and plots which did not fall within 500-m from the FMI site center points (n=53). Finally, we excluded plots for which few good quality S2 observations (<10 during the 3-year period) were available (n=4). Thus, the number of plots retained in analyses was 103.
CORINE (2018a) was used to extract dominant forest type information and to reclassify the data into three phenological groups of coniferous, deciduous, and mixed species so that 1 = coniferous (i.e., CORINE class labels: 25, 26, and 27 denoting coniferous forest on mineral or on rocky soil or on peatland), 2 = deciduous (i.e., CORINE class label 23 meaning “Broad-leaved forest on mineral soil”), and 3 = mixed (i.e., CORINE class labels: 28, 29, 30, 34, and 36 referring to mixed forest on mineral or on rocky soil or on peatland, or transitional woodland/shrub with a canopy cover of 10–30% on mineral or on rocky soil). The number of plots classified as coniferous was 74, deciduous was 14 and mixed was 15 (Fig. 1).
2.3.2 Preprocessing S2 data
The S2 data was provided in atmospherically corrected format, but no Nadir BRDF-Adjusted Reflectance (NBAR) corrected S2 products were available at the time of this study. We removed duplicated observations of S2 overpasses (i.e., data from S2A was preferred over S2B), and selected pixels which were classified as good quality (later referred to as “GQ”; S2 QA60 flag had value 0).
Next, we compared two approaches to filter the S2 data, because this has direct effect on the number of S2 observations available data for the analyses. In the first approach, we selected observations which were identified as “vegetation” by the S2 Scene Classification Label (SCL, i.e., SCL value was four). This dataset will be later referred to as “GQ+SCL4”. In the second approach, we used three Vegetation Indices (VIs) to filter out anomalous data. Data obtained following this workflow will be later called as “GQ+VIs”. The three VIs were EVI, Normalized Difference Snow Index (NDSI), and Senescence Index (SI) defined as follows:
where B2 (490 nm, 10 m), B3 (560 nm, 10 m), B4 (665 nm, 10 m), B8A (865 nm, 20 m), B8 (842 nm, 10 m), and B11 (1610 nm, 20 m) are S2 band SR values (band center wavelength and their spatial resolution are given inside parenthesis, respectively).
To exclude abnormal data, EVI thresholds were set to 0.01 and 1 as we knew our plots contained vegetation. The NDSI thresholds were set to -0.1 and -1 as pixels with negative NDSI values are considered as cloud-free and snow-free (Sentinel-2 Technical guide 2020). For SI, the thresholds were 0.4 and 10, because SI values higher than 0.4 are considered as cloud-free vegetated pixels (Sentinel-2 Technical guide 2020).
2.3.3 Generation of daily time series of EVI
Monitoring and mapping LSP from satellite platforms relies on greenness proxies such as EVI. However, as good quality satellite data is not obtained at every satellite overpass (i.e., due to clouds, cloud shadows), there is need to fill-in the gaps in the data to construct a daily time-series that can be used to extract the phenological transition dates.
Plots which had a minimum of ten GQ-VIs observations during the three years period (2017–2019) were used in our analyses (i.e., 103 plots). Due to the sparsity of the annual S2 observations, a time-series of 3-year mean daily EVI was created to remove outlier observations from the annual EVI values in the following way. First, a time-series of daily 3-year mean EVI was predicted for each plot: This was accomplished by fitting a LOESS Local Regression with a span of 0.5 (i.e., parameter controlling the degree of smoothing, ranges between 0 and 1) to all good quality EVI observations from the years 2017–2019. Then, we excluded EVI values that fell outside two standard deviations (i.e., confidence limit of 95 %) from the mean EVI and refit the LOESS to predict the 3-year mean EVI. Finally, time-series of daily EVI values were obtained by using splines to interpolate (and extrapolate) over DOYs without EVI values. Noteworthy is that the daily time-series of the 3-year mean EVI was only used for outlier analysis (section 2.3.4), all results are based on annual EVI time-series.
Gap filling of the data was necessary as our study area was located between latitudes 60 and 70°N, where data gaps in optical satellite data availability cannot be avoided (i.e., data availability is limited by low Sun angles and polar night). The boreal zone has also typically one growth-cycle peaking around the mid-summer, which simplifies the approach. Given that our study area is mostly dominated by evergreen conifers (i.e., there is little seasonal changes in tree canopy leaf area), the evergreen conifer forest tree canopy may be assumed to remain green over the winter. However, reflectance properties of deciduous forest understory and tree canopy may vary between different seasons (Rautiainen et al. 2011).
Taking all these aspects into consideration allows the creation of simple rules to fill in the gaps in the daily EVI values: The max EVI was searched between the 15th of May and the 31st of August, and the peak EVI date was used to split the data into spring and autumn segments. For both segments, sub-zero EVI values were replaced with NA, and minimum EVI values and their DOYs were searched. Minimum spring (autumn) EVI was used to replace all EVI values occurring before (after) the occurrence of the minimum EVI.
2.3.4 Outlier detection of annual daily time-series of EVI
Due to the scarcity and often poor quality of S2 observations, we developed an objective measure to separate invalid and valid annual EVI time-series from each other. The time-series of annual daily EVI data was assumed valid if the relative shape value of the annual daily EVI curve (denoted as “x”) differed less than 30% from the relative shape value of the 3-year mean daily EVI-curve (denoted as X; i.e., abs(x) - abs(X) < 0.3). The relative shape values (x and X, respectively) of the EVI time-series curves were obtained by taking the difference between two consecutive daily EVI values (i.e., t2–t1 = d), and summing above- and below-zero values of d separately (“a”= sum(d > 0) and “b”= sum(d < 0)), and taking their ratio (x= a/b, and same for X, respectively).
The 30% threshold was arbitrary but sufficed to separate years for which interpolation (or extrapolation) clearly failed due to the sparsity of S2 data (i.e., years with 5 or more S2 observations were used to fit annual LOESS). Clearly, increasing the number of annual S2 observations would decrease the need for checks, but would also focus the analyses on regions with more cloudless days and a longer data acquisition period (i.e., it would introduce spatial bias). In addition, if the annual predicted plot-level EVI for the DOY corresponding TGSstart or TGSend was larger or equal to 0.8 or smaller or equal to 0.1, then the time-series of annual daily EVI data was assumed invalid. Thresholds of 0.8 and 0.1 EVI were arbitrarily chosen but sufficed to detect possible interpolation (or extrapolation) errors. The number of plots with valid daily time-series of EVI was 83 for coniferous, 26 for deciduous, and 15 for mixed species groups. To demonstrate the effect of preprocessing on S2 data availability, data from both approaches (i.e., GQ+SCL and GQ+VIs) were used to extract the DOYs for first, peak, and last S2 observations and their respective EVI values.
2.3.5 Identifying phenophase transition dates from S2
Phenometrics were used to identify phenophase transition dates from the daily EVI time-series. These transition dates were searched annually as our study area has one valid growth cycle per year. Start of the greenup, greenup midpoint, and maturity dates were obtained from the EVI data when the EVI time-series crossed 15%, 50%, and 90% of the spring segment EVI amplitude (Fig. 3). Correspondingly, start of the senescence, greendown midpoint, and dormancy were identified as the DOYs when EVI time-series crossed 90%, 50%, and 15% of the autumn segment EVI amplitude. These phenometrics were selected as they are well known (i.e., standard) and used by, e.g., MODIS Vegetation Phenology product (i.e., MCD12Q2 v006) (Gray et al., 2019) and the phenology product by Bolton et al. (2020).
Schematic of so-called standard phenometrics that are used to extract phenological transition dates from the Sentinel-2 data. Abbreviations: EVI= Enhanced Vegetation Index, DOY= day of year. The names and percentiles are similar to those used by MODIS Vegetation Phenology product (i.e., MCD12Q2 v006) and the phenology product by Bolton et al. (2020)
First, the max EVI peak was searched between May 15th and 31 of August, and then that date was used to split the year into two (i.e., spring and autumn) segments and minimum EVI values were searched separately for both segments (i.e., seasonal EVI amplitude was thus allowed to vary between spring and autumn). Finally, phenological transition dates were extracted from the time-series of daily EVI data using phenometrics.
2.3.6 Comparison of S2 and temperature-based transition dates
The S2-based phenological transition dates, obtained using standard phenometrics, were compared with phenometrics that were extracted from the S2 data corresponding to the daily mean temperature-based estimates of TGSstart and TGSend. In other words, for each plot, we obtained the phenometric that would correspond to the timing of TGSstart and TGSend. Selection of phenometrics to identify phenological transition dates has direct impact on growing season length (GSL), and thus, we also inspected temporal divergence of GSL estimates obtained using different phenometrics and temperature data.
3 Results
3.1 Effect of preprocessing on S2 data availability
Results showed that using the GQ+VIs approach extends the time period for which good quality data is available for vegetated pixels compared to the GQ+SCL4 approach that relied on the S2 pixel classification labels (Figs. 4 and 5). Using the GQ+SCL4 approach, data is available on average starting from DOYs 120, 131, and 115 for coniferous, deciduous, and mixed species groups, respectively. Whereas using the GQ+VIs approach, data are available clearly earlier - on average onwards from DOYs 77, 86, and 84. Respectively, using the GQ+SCL4 approach, the last observations for the plots were recorded on DOYs 271, 275, and 280 for coniferous, deciduous, and mixed species groups. Whereas using the GQ+VIs approach, the last observations were recorded clearly later (i.e., on average at DOYs 301, 318, and 312 for coniferous, deciduous, and mixed species groups). Given that the TGSstart may occur around DOY 100 and TGSend around DOY 320, using the GQ+VIs approach appears better than GQ+SCL4 for characterization of boreal forest phenology due to the longer time span S2 data is available. Thus, all following analyses were done using the GQ+VIs method.
Preprocessed Sentinel-2 (S2) data. “GQ+SCL4” denotes observations labeled as good quality (GQ) and vegetated (i.e., S2 Scene Classification Label (SCL) = four), and “GQ+VIs” observations labeled as good quality (GQ) and using Vegetation Indices (VIs) to exclude non-vegetated or anomalous observations. Boxplots’ lower and upper hinges correspond to the first and third quartiles, median is shown as the horizontal line, mean is marked using the star, and dots are the outlier points.
Time series plots demonstrating the effect of preprocessing on Sentinel-2 (S2) data availability in a–c coniferous, d–f deciduous, and h–j mixed forests. “GQ+SCL4” denotes observations labeled as good quality (GQ) and vegetated (i.e., S2 Scene Classification Label (SCL) = four), and “GQ+VIs” observations labeled as good quality (GQ) and using Vegetation Indices (VIs) to exclude non-vegetated or anomalous observations
3.2 Identification of phenophase transition dates
Results showed that there was more variation in EVI phenometrics during autumn than in spring, and the EVI boxplots appeared fairly symmetric for all species groups (Fig. 6). The overall trend was that the height of the boxplot describing the variation in EVI phenometrics increased towards the winter, and the smallest variation in EVI phenometrics was observed around the peak. In coniferous plots, the seasonal variation in peak EVI value rarely exceeded 0.5 EVI value, whereas in plots dominated by deciduous or mixed species the peak EVI did reach up to 0.7. In coniferous plots, the minimum EVI remained on average higher than in deciduous and mixed plots. In deciduous and mixed plots, the EVI values of the last phenometrics (i.e., the dormancy and the minimum EVI) were on average smaller than respective spring phenometrics (i.e., the minimum EVI and the greenup).
Variation in Enhanced Vegetation Index (EVI) values for the identified phenophase transitions for a Spring and b Autumn. Figure prepared from annual EVI time-series data. Boxplots’ lower and upper hinges correspond to the first and third quartiles, median is shown as the horizontal line, mean is marked using the star, and dots are the outlier points
3.3 Comparison of S2 and temperature-based estimates
There were clear differences between years in both S2 and temperature data (Fig. 7). The temporal pattern was that for years with the highest annual max EVI values the respective GDD sums were the smallest. For example, the year 2017 had the highest max annual EVI values and the smallest GDD sums for coniferous and deciduous species plots. Year 2018 was the warmest for coniferous and deciduous plots and had the smallest annual maximum EVI values, but for mixed species plots the smallest maximum EVI values and the highest GDD sums were observed for 2019.
Annual variations in a peak EVIs and b Growing Degree Day (GDD) sums for the plots. Figure was prepared from annual EVI time-series data, and as no valid annual EVI time-series were available for mixed forest plots for the year 2017 the respective GDD sum was excluded. Boxplots’ lower and upper hinges correspond to the first and third quartiles, median is shown as the horizontal line, mean is marked using the star, and dots are the outlier points
Results showed that during spring, the timing of the TGSstart corresponded to the greenup fairly well for all species groups (Fig. 8). TGSstart took place on average between DOYs 114 and 120 in different species groups, but the greenup started on average 1–2 weeks earlier (between DOYs 109 and 116). The midgreenup, on the other hand, took place on average 2–3 weeks later than the respective TGSstart. The above-zero temperatures began on average a month earlier than TGSstart, corresponding to the timing of the minimum EVI. During spring, the largest Root Mean Square Error (RMSE) between timings of the greenup and the TGSstart was observed for coniferous forests (Table 1).
Comparison of remotely sensed phenometrics with temperature-based estimates of the start and end of the thermal growing season (TGS). a Spring and b Autumn. Time period of temperature above-zero is indicated by “T>0” and “T<0”. Boxplots’ lower and upper hinges correspond to the first and third quartiles, median is shown as the horizontal line, mean is marked using the star, and dots are the outlier points
In autumn, all phenometrics had considerably more variation than in spring, and the timing of the TGSend occurred often between the midgreendown and the dormancy. TGSend took place on average between DOYs 276–292, and the midgreendown on average ~2–4 weeks earlier. The dormancy started 2–3 weeks after TGSend. Thus, while the timing of the TGSstart on average corresponded well with the greenup phenometric, neither the midgreendown nor the dormancy appeared to correspond with the timing of the TGSend. In autumn, the largest RMSE between the senescence and the TGSend was noted for deciduous forests (Table 1). The above-zero temperatures ended on average 6–7 weeks later than TGSend and approximately corresponded to the timing of the minimum EVI. During spring, there was little latitudinal connection between timings of the greenup and the TGSstart, but in autumn, a strong latitudinal trend was observed between timings of the senescence and the TGSend (Fig. 9).
Forests with deciduous broadleaved trees showed similar changes in EVI during spring while forests with coniferous species appeared more similar with each other during autumn. Based on valid annual time-series of S2 EVI data, the timing of TGSstart corresponded on average to EVI phenometric (i.e., relative threshold) of 28% (standard deviation: 27%) for coniferous, 15% (standard deviation: 15%) for deciduous, and 17% (standard deviation: 18%) for mixed species plots. Thus, while the 15% EVI amplitude for the greenup corresponds with the TGSstart of deciduous species (incl. mixed species), for areas with evergreen conifers higher EVI amplitude percentile should be used to identify the TGSstart due to a smaller EVI amplitude of coniferous species compared to that of deciduous species (Fig. 6). During autumn, the EVI amplitudes which corresponded to the timing of the TGSend were 45% (standard deviation: 44%) for coniferous, 33% (standard deviation: 20%) for deciduous, and 45% (standard deviation: 27%) for mixed species plots.
3.4 Comparison of growing season length estimates
In boreal forests, using the phenometrics for greenup-dormancy may be expected to result in a nearly month-long overestimation of the GSL, while using the midgreenup-midgreendown phenometrics may be expected to underestimate the GSL by nearly a month. Based on our results, applying the standard phenometrics directly to S2 data to estimate the GSL may lead to clear biases in all species groups (Fig. 10). The average GSL using the greenup-dormancy phenometrics is 189 days. Using the midgreenup-midgreendown phenometrics leads to an average GSL of 134 days. Both of these estimates are fairly far off from that estimated using ground reference temperature data (i.e., GSL of 161 days). The period of above-zero temperatures is shown to illustrate the potential period evergreen conifers are able to use for photosynthesis (i.e., soil not frozen), indicating that using the midgreenup-midgreendown phenometrics to constrain the GSL, as is currently suggested by the MODIS phenology product, leads to severe underestimation of GSL.
Comparison of growing season length (GSL) estimated using satellite-based phenometrics and temperature-based data. Figure prepared using annual EVI time-series data. Time period of temperature above-zero is indicated by “T>0”. Boxplots’ lower and upper hinges correspond to the first and third quartiles, median is shown as the horizontal line, mean is marked using the star, and dots are the outlier points
4 Discussion
Vegetation phenology has a central role in the functioning of the earth system as it acts as a driver of the energy, water, and carbon exchanges between the land surface and the atmosphere. In this paper, we introduced a benchmarking scheme for satellite-based phenometrics (i.e., relative greenness amplitudes) with daily mean temperature data to improve mapping of phenological transition dates at a regional scale. As phenology models used in LSMs are often based on optical satellite data, and as LSMs operate based on predicted future temperature data, regional linking between phenometrics and temperature data may help in developing more accurate phenology models for LSMs.
In the boreal region, vegetation phenology is controlled by temperature (and photoperiod which does not vary inter-annually) (Gill et al. 2015; Olsson and Jönsson 2014; Piao et al. 2019), and thus temperature-derived estimates of the TGS could be used to benchmark the remotely sensed phenometrics. Although TGS quantifies a theoretical growing period, not an actual growth period (Linderholm et al. 2008), the data is available at high frequency and allows retrieving sensible dates for different phenological stages. The TDI method was used in this study to obtain ground reference dates for the TGSstart and TGSend, because it accounts for the impacts of sudden cold and warm spells indicating the time period when vegetation growth conditions are favorable. Often TGSstart has been defined by requiring the base temperature to be exceeded on five (or more) consecutive days during spring (TGSend being derived analogously), but that may lead to inappropriate estimates if early spring is followed by an intense cold period (see example in Ruosteenoja et al. 2016). However, if the winter is too mild to unambiguously terminate the previous TGS before the start of the next season, then TDI cannot be used to determine TGS. Future studies should investigate if photoperiod thresholds would be needed to constrain the growth period during warm winters, but at present, such regional thresholds are not available. Earlier, the TDI approach has been used to investigate how future rising temperatures are reflected in the GSL and TGS in Europe (Ruosteenoja et al. 2016), and in this paper, this was used to benchmark phenometrics in a boreal forest based on S2 data. Noteworthy is that different baseline temperatures may be needed in different geographical regions with different vegetation types. Also, the uncertainties of the benchmarking approach should be evaluated at a regional level using near-surface data (e.g., networks of phenocameras, flux-towers, or observation stations).
Development of photosynthetic capacity of deciduous tree species in spring is linked to the easily observable growth of leaves, but for conifers, changes in the photosynthetic capacity are not readily detectable from the satellite sensor data (Suni et al. 2003; Yang et al. 2020). In conifer and mixed forests, the TGSend corresponded to an average EVI amplitude of 45%, which may be expected to reflect the senescence of deciduous vegetation (i.e., tree canopy and understory) rather than the phenology of evergreen conifers, which are able to continue photosynthesis until the soil freezes. The ending of the above-zero temperatures approximately corresponds to the timing of reaching autumn EVI minimum (Fig. 8), and thus possibly a very small EVI percentile (or photoperiod threshold) value could be used to approximate the ending of the conifer photosynthesis (i.e., conifer dormancy). Overall, the naming of the remotely sensed phenometrics using temperature-based terminology is ambiguous. To provide more descriptive names for the autumn phenometrics of boreal forests, perhaps the phenometric corresponding to the timing of TGSend could be called “senescence” and the phenometric corresponding to the timing of below zero temperatures called “dormancy.”
Some approaches exist for mapping evergreen conifer phenology and photosynthesis from optical satellite data (i.e., MODIS), but they are not directly applicable for higher resolution S2 data. For example, it is not yet known how the plant phenology index (PPI) proposed by Jin and Eklundh (2014) can be calculated based on S2 data as it was developed for the MODIS NBAR MCD43A4 dataset, and currently, S2 does not provide an NBAR product. However, the soon available (launch expected in 2021) COPERNICUS (2020) phenology products suite will contain PPI. Gamon et al. (2016) have suggested a chlorophyll/carotenoid index (CCI), which is expected to be sensitive to seasonally changing chlorophyll/carotenoid pigment ratios and thus able to track photosynthetic phenology in evergreen conifers. However, this index cannot be used for S2 data as one of the bands required by the ratio index (i.e., wavelength region of 526–536 nm) does not overlap with any of the S2 bands.
The optical satellite data may only observe changes in surface properties such as LAI, while the boreal forest vegetation phenology depends on surface temperature. Temperature data-based theoretical benchmarking has several advantages, over e.g., traditional phenological field observations, because daily temperature data is freely available from a myriad of stations that are scattered across the globe. The approach allows flexible application across spatial scales (i.e., point or grid) and different satellite sensors, and may be combined with any land cover mapping, and provides systematic linking between biome surface temperature data and its seasonal reflectance properties. Evergreen conifer forests have low annual variation in LAI and chlorophyll content but given that boreal evergreen conifer forests often have deciduous understory vegetation and minor deciduous mixed tree species, conifer forest LSP may be assumed detectable (Pisek et al. 2012) from S2 data (i.e., assuming that the understory responds to temperature induced changes exactly as the overstory despite being composed of different species and subject to different light levels). As in boreal conditions, the period of favorable growth conditions is constrained by the seasonal course of temperatures—that could be used to regionally benchmark annual greenness thresholds (i.e., greenness amplitude) that are used to indicate vegetation transition dates. Although the TDI method may not be as accurate as, e.g., data from flux towers to capture the start and end of the growing seasons, the TDI still provides a systematic means for theoretically analyzing growth stages of evergreen conifers. As evergreen conifer and deciduous broadleaf forests have clear differences in their seasonal greenness amplitudes, using the same relative thresholds (phenometrics) may be expected to lead to biased estimates of GLS for conifers.
Recently, high spatial resolution Harmonized Landsat/Sentinel-2 (HLS) LSP products have started to become available in phenological research (Bolton et al. 2020; Jönsson et al. 2018). Noteworthy is, that although the provisional global HLS data product (i.e., HLSS30 v015) has been available since summer 2020 from the Land Processes Distributed Active Archive Center (LP DAAC, 2020), the scientific quality of the product has not been yet validated, and thus, LP DAAC’s current recommendation is to avoid using the HLS product for scientific research or applications (LP DAAC, 2020). Although including Landsat data might increase the good quality data density, the technical differences in band spectral and radiometric properties might result in systematic level-differences between the two data sets, and thus, this remains an interesting option for future studies.
Our goal was to develop a simplified approach for regional benchmarking of satellite-based phenometrics with surface temperature data which would not require high computational power. Compared to the approach by Bolton et al. (2020), the northern location of our study area allowed us to employ a few simplifying rules. For example, instead of using 6-month buffers around each seasonal cycle as in Bolton et al. (2020), we had a naturally occurring gap in S2 data in the middle of the winter due to low sun angles. This also allowed us to look for the peak growing season to occur around June instead of screening for several annual peaks as was the case for Bolton et al. (2020). Previously, Jönsson et al. (2018) introduced a method for estimating LSP of evergreen conifers based on fused S2 and Landsat data. However, the method was tested in southern Sweden (i.e., 60°N), but not in higher latitudes with more challenging seasonal conditions. In addition, their approach requires long time series which is currently not yet available for S2.
Relying on satellite-based LSP estimates is based on the following assumptions (Helman 2018): (1) an LSP metric or VI is sensitive to changes in seasonal surface properties such as LAI and chlorophyll content (Huete 2012), (2) an LSP metric or VI is robust against atmospheric effects, (3) greenness dynamics are independent of both changes in surface brightness and wetness, and (4) land cover values stay constant. While it remains impossible to make sure all these assumptions are met in practice, suitable preprocessing may be used (and is necessary) to exclude anomalous observations. Yet, the benefit of optical remote sensing in LSP monitoring is that it provides holistic information regarding the ecosystem state (i.e., not limited to a single species, site, or growth stage). It also accounts for the phenology of forest floor understory species, which have large effect on forest reflectance especially in sparse (open canopy) forests (Rautiainen and Lukeš, 2015; Pisek et al. 2012). In boreal Finland, spectral phenology of the understory layer and the tree layer may develop at the same speed (Rautiainen et al. 2011), and thus, methods that focus on characterizing the seasonal amplitude of EVI can be used. However, if the seasonal course of forest understory reflectance differs much from that of the tree canopy, then applicability of amplitude-based methods remains unclear.
Although remote sensing data have been used in developing phenology models for different vegetation types used by the LSMs (Botta et al. 2000; Fu et al. 2014), for boreal evergreen conifers such approaches are rarely applied due to challenges in obtaining sufficiently good quality data. Phenology description of LSMs is currently based on empirical or ad hoc approaches (Dahlin et al. 2015; Taylor and White 2020). Empirically based approaches that are based on temperature data remain the preferred option to simulate phenological processes (Fu et al. 2014; Ruosteenoja et al. 2016), because the current understanding of mechanisms controlling budburst and dormancy are insufficient for mechanistic simulation of these processes in LSMs (Gill et al. 2015; Linkosalo et al. 2006; Piao et al. 2019). At present, only LSM ORCHIDEE contains an explicit parameterization of evergreen conifer budburst and senescence (Peaucelle et al. 2019), but as the approach is based on litterfall observations (i.e., data that is scarcely available for spatially limited plots only), it does not suffice for large area phenological mapping.
Simplified and alternating approaches for better representing the regional phenology are needed to allow development of modular approaches with different complexities for LSMs (Fisher and Koven 2020). Currently, one of the biggest problems in LSM development is the ever-increasing model intricacy which calls for process complexity management while allowing representation of land surface heterogeneity and understanding parameter dynamics (Fisher and Koven 2020). The approach presented in this paper can be applied for different satellite sensor systems, spatial resolutions, and different land cover classifications and with different temperature datasets (i.e., point or grid), thus providing a common framework for calibrating phenometrics. Calibrated phenometrics can then, in turn, to be used at regional scale to map variations in LSP across time and space to fit phenology models for LSMs which employ temperature data and its derivates such as GDD sums (Fu et al. 2014; Olsson and Jönsson, 2014).
Today’s LSMs may describe land surfaces either using prescribed monthly mean LAI climatologies (i.e., Community Land Surface Model) or use prognostic simulations involving environmental factors such as temperature to predict timings of phenological events of different vegetation types. Models with prescribed phenology will not be able to accurately predict the associated phenological responses to future climate change in prognostic studies (Richardson et al. 2012). However, if a prognostic phenology scheme is implemented into a model employing prescribed LAI, the coupling between biological processes on the land surface and feedback to the atmosphere can be restored (Levis and Bonan, 2004). Thus, improving the LSM phenology is critical as a multitude of climate system feedback are mediated by phenology.
5 Conclusion
We showed that selecting pixels classified as vegetation by the S2 scene classification labels constrains the number of valid S2 observations, and thus, in the boreal forest zone, alternative approaches such as vegetation indices should be preferred in preprocessing the S2 observations for phenological monitoring. We observed that the seasonal variations in EVI distributions of phenometrics were fairly symmetric between spring and autumn for all forest types. Based on our data, the spring greenup was well captured by the standard EVI phenometric of 15% in deciduous and mixed forests, but for evergreen conifer forests a higher (e.g., 28%), EVI amplitude value should be preferred. During autumn, the end of the thermal growing season was not well captured by the so-called standard phenometrics. We noted that the end of the thermal growing season was best captured by an EVI amplitude of 45% in conifer and mixed forests whereas in deciduous forests an amplitude of 33% could be used. In addition, we observed that using the standard phenometrics to estimate the growing season length may lead to clear biases in boreal forests. In our data, using the greenup-dormancy phenometrics resulted in on average a 1-month overestimation of the growing season length, while using the midgreenup-midgreendown phenometrics underestimated the growing season length on average by one month. A new approach to calibrate evergreen coniferous forest phenology was developed by linking ground reference temperature data and satellite-based greenness data.
Availability of data and materials
All data is publicly available (See reference list). The datasets generated during the current study are available from the corresponding author on reasonable request.
References
Berra EF, Gaulton R (2021) Remote sensing of temperate and boreal forest phenology: a review of progress, challenges and opportunities in the intercomparison of in-situ and satellite phenological metrics. For Ecol Manage 480:118663
Berra EF, Gaulton R, Barr S (2019) Assessing spring phenology of a temperate woodland: A multiscale comparison of ground, unmanned aerial vehicle andLandsat satellite observations. Remote Sens Environ 223:229-242
Bolton DK, Gray JM, Melaas EK, Moon M, Eklundh L, Friedl MA (2020) Continental-scale land surface phenology from harmonized Landsat 8 and Sentinel-2 imagery. Remote Sens Environ 240:111685
Botta A, Viovy N, Ciais P, Monfray FP (2000) A global prognostic scheme of leaf onset using satellite data. Glob Chang Biol 6:709–725
CLM5 Documentation (2020) https://www.cesm.ucar.edu/models/cesm2/land/. Accessed January 15th 2021
COPERNICUS, (2020) https://land.copernicus.eu/pan-european/biophysical-parameters/high-resolution-vegetation-phenology-and-productivity. Accessed November 15th 2020
CORINE, (2018a). https://ckan.ymparisto.fi/dataset/%7B0B4B2FAC-ADF1-43A1-A829-70F02BF0C0E5%7D Accessed November 23rd 2020 [Data obtained: May 3rd 2020]
CORINE, (2018b) Corine 2018 final report. https://www.syke.fi/en-US/Research__Development/Research_and_development_projects/Projects/Producing_land_cover_and_land_use_data_in_CORINE_Land_Cover_2018_project_in_Finland Accessed November 23rd 2021
Dahlin KM, Fisher RA, Lawrence PJ (2015) Environmental drivers of drought deciduous phenology in the Community Land Model. Biogeosci 12(16):5061–5074
de Beurs KM, Henebry GM (2010) Spatio-temporal statistical methods for modelling land surface phenology. In: Phenological research. Springer, Dordrecht, pp 177–208
Fisher RA, Koven CD (2020) Perspectives on the future of Land Surface Models and the challenges of representing complex terrestrial systems. J Adv Model Earth Syst s 12(4):e2018MS001453
FMI, (2020) Finnish Meteorological Institute ilmastopalvelu web service. https://www.ilmatieteenlaitos.fi/mennyt-saa-ja-ilmastotilastot Accessed November 20th 2020 [Data obtained: April 3rd 2020]
Fu Y, Zhang H, Dong W, Yuan W (2014) Comparison of phenology models for predicting the onset of growing season over the Northern Hemisphere. PloS ONE 9(10)
Gamon JA, Huemmrich KF, Wong CY, Ensminger I, Garrity S, Hollinger DY et al (2016) A remotely sensed pigment index reveals photosynthetic phenology in evergreen conifers. Proc Natl Acad Sci U S A 113(46):13087–13092
GCOS, (2016) The global observing system for climate: implementation needs. GCOS World Meteorological Organization (2016). https://library.wmo.int/doc_num.php?explnum_id=3417 Accessed November 20th 2020
Gill AL, Gallinat AS, Sanders-DeMott R, Rigden AJ, Short Gianotti DJ, Mantooth JA, Templer PH (2015) Changes in autumn senescence in northern hemisphere deciduous trees: a meta-analysis of autumn phenology studies. Ann Bot 116(6):875–888
Gorelick N, Hancher M, Dixon M, Ilyushchenko S, Thau D, Moore R (2017) Google Earth Engine: planetary-scale geospatial analysis for everyone. Remote Sens Environ https://earthengine.google.com/ Accessed November 20th 2020 [Data obtained April 29 2020]
Gray J, Sulla-Menashe D, Friedl M A (2019) User guide to collection 6 MODIS land cover dynamics (MCD12Q2) product. NASA EOSDIS Land Processes DAAC: Missoula, MT, USA. https://lpdaac.usgs.gov/documents/218/mcd12q2_v6_user_guide.pdf Accessed November 12th 2020
Helman D (2018) Land surface phenology: what do we really ‘see’ from space. Sci Total Environ 618:665–673
Hmimina G, Dufrêne E, Pontailler JY, Delpierre N, Aubinet M, Caquet B et al (2013) Evaluation of the potential of MODIS satellite data to predict vegetation phenology in different biomes: an investigation using ground-based NDVI measurements. Remote Sens Environ 132:145–158
Huete AR (2012) Vegetation indices, remote sensing and forest monitoring. Geography Compass 6(9):513–532
Jin H, Eklundh L (2014) A physically based vegetation index for improved monitoring of plant phenology. Remote Sens Environ 152:512–525
Jönsson P, Cai Z, Melaas E, Friedl MA, Eklundh L (2018) A method for robust estimation of vegetation seasonality from Landsat and Sentinel-2 time series data. Remote Sens 10(4):635
Kauppi PE, Posch M, Pirinen P (2014) Large impacts of climatic warming on growth of boreal forests since 1960. PLoS ONE 9(11):e111340
Lappalainen H, Linkosalo T, Venäläinen A (2008) Long-term trends in spring phenology in a boreal forest in central Finland. Boreal Environ Res 13:303–318
Levis S, Bonan GB (2004) Simulating springtime temperature patterns in the community atmosphere model coupled to the community land model using prognostic leaf area. J Clim 17(23):4531–4540
Linderholm HW, Walther A, Chen D (2008) Twentieth-century trends in the thermal growing season in the Greater Baltic Area. Clim Change 87(3-4):405–419
Linkosalo T, Häkkinen R, Hänninen H (2006) Models of the spring phenology of boreal and temperate trees: is there something missing? Tree phys 26(9):1165–1172
LP DAAC, (2020) Land processes distributed active archive center. https://lpdaac.usgs.gov/products/hlss30v015/ Accessed: November 17th 2020
Matzarakis A, Ivanova D, Balafoutis C, Makrogiannis T (2007) Climatology of growing degree days in Greece. Clim Res 34(3):233–240
MCD12Q2v006, (2020) https://lpdaac.usgs.gov/products/mcd12q2v006/Accessed January 14th 2021
Olsson C, Jönsson AM (2014) Process‐based models not always better than empirical models for simulating budburst of Norway spruce and birch in Europe. Glob Chang Biol 20(11):3492–3507
Peaucelle M, Ciais P, Maignan F, Nicolas M, Cecchini S, Viovy N (2019) Representing explicit budburst and senescence processes for evergreen conifers in global models. Agric For Meteorol 266:97–108
Piao S, Liu Q, Chen A, Janssens IA, Fu Y, Dai J et al (2019) Plant phenology and global climate change: current progresses and challenges. Glob Chang Biol 25(6):1922–1940
Pisek J, Rautiainen M, Heiskanen J, Mõttus M (2012) Retrieval of seasonal dynamics of forest understory reflectance in a Northern European boreal forest from MODIS BRDF data. Remote Sens Environ 117:464–468
R Core Team (2020) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria https://www.R-project.org/ Accessed November 17th 2020
Rautiainen M, Lukeš P (2015) Spectral contribution of understory to forest reflectance in a boreal site: an analysis of EO-1 Hyperion data. Remote Sens Environ 171:98–104
Rautiainen M, Mõttus M, Heiskanen J, Akujärvi A, Majasalmi T, Stenberg P (2011) Seasonal reflectance dynamics of common understory types in a northern European boreal forest. Remote Sens Environ 115:3020–3028
Richardson AD, Anderson RS, Arain MA, Barr AG, Bohrer G, Chen G et al (2012) Terrestrial biosphere models need better representation of vegetation phenology: results from the N orth A merican C arbon P rogram S ite S ynthesis. Glob Chang Biol 18(2):566–584
Ruosteenoja K, Räisänen J, Venäläinen A, Kämäräinen M (2016) Projections for the duration and degree days of the thermal growing season in Europe derived from CMIP5 model output. Int J Climatol 36(8):3039–3055
Sellers PJ, Randall DA, Collatz GJ, Berry JA, Field CB, Dazlich DA et al (1996) A revised land surface parameterization (SiB2) for atmospheric GCMs. Part I: Model formulation. J Clim 9(4):676–705
Sentinel-2 Technical guide, (2020) https://earth.esa.int/web/sentinel/technical-guides/sentinel-2-msi/level-2a/algorithm Accessed January 15th 2021
Skaugen TE, Tveito OE (2004) Growing-season and degree-day scenario in Norway for 2021-2050. Clim Res 26(3):221–232
Suni T, Berninger F, Vesala T, Markkanen T, Hari P, Mäkelä A et al (2003) Air temperature triggers the recovery of evergreen boreal forest photosynthesis in spring. Glob Chang Biol 9(10):1410–1426
Tan B, Morisette JT, Wolfe RE, Gao F, Ederer GA, Nightingale J, Pedelty JA (2010) An enhanced TIMESAT algorithm for estimating vegetation phenology metrics from MODIS data. IEEE J Sel Top Appl Earth Obs Remote Sens 4(2):361–371
Taylor SD, White EP (2020) Automated data‐intensive forecasting of plant phenology throughout the United States. Ecol Appl 30(1):e02025
White K, Pontius J, Schaberg P (2014) Remote sensing of spring phenology in northeastern forests: a comparison of methods, field metrics and sources of uncertainty. Remote Sens Environ 148:97–107
White MA, Thornton PE, Running SW (1997) A continental phenology model for monitoring vegetation responses to interannual climatic variability. Global biogeochem Cycles 11(2):217–234
Wickham H (2009) ggplot2: elegant graphics for data analysis. Springer, New York
Yang Q, Blanco NE, Hermida-Carrera C, Lehotai N, Hurry V, Strand Å (2020) Two dominant boreal conifers use contrasting mechanisms to reactivate photosynthesis in the spring. Nat Commun 11(1):1–12
Zeng L, Wardlow BD, Xiang D, Hu S, Li D (2020) A review of vegetation phenological metrics extraction using time-series, multispectral satellite data. Remote Sens Environ 237:111511
Acknowledgements
Analysis was conducted in R version 3.6.3 (R Core Team, 2020), and figures were produced using the package ggplot2 (Wickham, 2009). We thank Finnish Meteorological Institute Ilmastopalvelu web service (FMI, 2020) for providing the temperature data, and Google Earth Engine (Gorelick et al., 2017) for Sentinel-2 data access.
Code availability
Code is available from the author.
Funding
T. Majasalmi has received funding from Aalto ENG postdoctoral funds. M. Rautiainen has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 771049). The text reflects only the authors’ view, and the Agency is not responsible for any use that may be made of the information it contains.
Author information
Authors and Affiliations
Contributions
T. Majasalmi: Conceptualization, methodology, formal analysis, investigation, writing - original draft, writing—review & editing, and visualization. M. Rautiainen: Writing—review & editing. The authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable
Consent for publication
Both authors gave their informed consent to this publication and its content.
Disclaimer: The text reflects only the authors’ view, and the Agency is not responsible for any use that may be made of the information it contains.
Competing interests
The authors declare that they have no competing interests.
Additional information
Handling Editor: Barry A. Gardiner
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated in a credit line to the data.
About this article
Cite this article
Majasalmi, T., Rautiainen, M. Potential of using surface temperature data to benchmark Sentinel-2-based forest phenometrics in boreal Finland. Annals of Forest Science 79, 6 (2022). https://doi.org/10.1186/s13595-022-01130-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13595-022-01130-2