Abstract
Context
Understanding plant resilience and adaptation to drought is a major challenge in crop and forest sciences. Several methods have been developed to assess the vulnerability to xylem embolism. The in situ flow centrifuge (or cavitron) is the fastest technique allowing to characterise this trait for plants having vessel lengths shorter than the rotor size.
Aims
We present (i) a series of changes to the earlier cavitron design, aimed at improving the accuracy and speed of measurement through automated operations, and (ii) a new development through the design of a large diameter rotor expanding the range of species that can be measured.
Methods
Both hardware and software modifications to the original design have been developed. In order to avoid artefacts caused by cut open vessels, a centrifuge with a large rotor (1 m) has been developed, and vulnerability curves obtained with this new device were compared with those obtained using reference methods.
Results
The new set-up expands the range of conductance measurable with a cavitron and enables it to accurately determine the absolute value of conductivity even for species having very low hydraulic conductivity. The large rotor cavitron shows good agreement with the reference techniques for conifers and diffuse-porous species but also for ring-porous species having long vessels.
Conclusion
The set-up described in this manuscript provides a faster, safer and more accurate method to construct vulnerability curves, compared to the original cavitron design, and extends the measurement capabilities to new species that are difficult to measure to date.
Key message
Recent improvements to cavitron setup enable to measure xylem vulnerability curves for an expanded number of plant species, with longer vessels or lower hydraulic conductivity.
Similar content being viewed by others
1 Introduction
Xylem vulnerability to embolism has become one of the main traits in the studies of drought resistance in plants (Choat et al. 2012; Delzon and Cochard 2014; Anderegg et al. 2016). Several techniques have been proposed in the last few decades to establish vulnerability curves to embolism (VC) for which the loss of hydraulic conductivity or the amount of embolised vessel are measured for different levels of water stress and plotted against water column tension (Tyree and Dixon 1986). The most commonly used techniques to estimate VC are based on water mass movement measurement (Tyree and Dixon 1986; Cochard 2002), acoustic emission (Nolf et al. 2015) or direct observation with X-ray micro-computed tomography (Choat et al. 2016), transmitted light attenuation (Brodribb et al. 2017) or magnetic resonance imaging (Meixner et al. 2020). Among these techniques, the fastest is the flow centrifuge method (Melcher et al. 2012; Cochard et al. 2013).
It has been demonstrated several times that centrifugal force is an accurate and reliable way to impose a tension in the water column inside the xylem of a plant (Holbrook et al. 1995; Alder et al. 1997). A few years after this finding, the cavitron, an evolution of the “static” centrifuge method enabling measurement of the conductivity while the sample is spinning, has been proposed (Cochard 2002). The cavitron technique and some of its performances and limitations have been extensively described (Cochard et al. 2005; Li et al. 2008; Cochard et al. 2010; Beikircher et al. 2010; Cai et al. 2010; Wang et al. 2014b; Bouche et al. 2015; Pivovaroff et al. 2016). This technique is based on the measurement of hydraulic conductance of a xylem-bearing sample while the water column in the xylem is kept under tension by centrifugal force (P). The main advantage of the cavitron technique is that it simultaneously enables to (i) generate a controlled tension in the water column of the xylem (maximal in the central part of the sample) due to centrifugal forces and (ii) to measure the hydraulic conductivity with an optical method. Cavitron technique has been successfully used to obtain VC curves of branches (Delzon et al. 2010), trunk baguettes (Bouche et al. 2016), roots (Bouche et al. 2015, Schuldt et al. in press), long needles (Charra-Vaskou et al. 2012) and floral stems (Chacon Dória et al., 2019, Thonglim et al., 2021). In earlier cavitron set-ups, the operator was required to work very close to the centrifuge in order to (i) perform measurements with a binocular, (ii) add water in the reservoir for the measurements and (iii) change the centrifuge speed. This implied to work in a dark and noisy environment, often in an uncomfortable position, and close to a potentially dangerous fast spinning rotor. These operating conditions do not comply with modern health and safety rules and needed improvement. In addition, the size of the rotor of a standard cavitron, 27 cm, does not allow the measurement of long-vessel species such as the vast majority of tropical species and temperate ring-porous species. Indeed, it has been well established that centrifuge techniques do not allow to accurately determine the VC of samples having vessels longer than the rotor size (Choat et al. 2010, 2016; Cochard et al. 2010; Sperry et al. 2012; Martin-StPaul et al. 2014; Torres-Ruiz et al. 2014). VC being altered by the open vessel artefact (Martin-StPaul et al. 2014, Wang et al. 2014a), leading to substantial overestimations of xylem vulnerability (Torres-Ruiz et al. 2015).
We propose in this manuscript a new experimental set-up, enabling completely remote operation of the cavitron, by means of a camera-based image vision system and a software which controls all the parameters required for hydraulic conductivity measurement, logs data and computes variables of interest, in a safer and more user-friendly environment. A detailed assessment of the hydraulic conductivity measurement achieved resolution is also proposed for different sample sizes and measurement conditions. Finally, we hypothesise that these improvements, together with the development of a larger rotor, will allow us to extend the technique to long-vessel species. We therefore developed a new instrument specially designed to measure long-vessel species (called CAVI1000) and carried out a series of experiments to validate this set-up. This manuscript additionally presents general guidelines for selecting sample dimensions and establishing vulnerability curves with the cavitron technique.
2 Material and methods
2.1 Hydraulic conductivity measurement
Hydraulic conductance (kh) is defined as the amount of water flowing through a sample during a certain amount of time (water flow F in kg s−1) at a defined pressure difference between the sample ends (∆P in MPa).
In the cavitron, the pressure difference (∆P) is obtained by immersing the extremities of a sample in small transparent water-filled reservoirs, fitted with holes at different levels, while spinning. Water flow measurement is done by measuring the time taken by the air-water meniscus to cover a given distance. Distance and time are measured automatically with a camera (see Section 2.3) several times as the water flows from the upstream reservoir to the downstream reservoir (from 10 to 50 points depending on the water flow). Measurement frequency and duration are user-defined. Water delivery to the reservoir is provided through a 2-way normally closed PTFE solenoid valve (130 series, Biochem Valve) operated by a relay.
To compute the conductance in SI unit (kg MPa−1 s−1), without approximation, the analytical solution described in detail in Wang et al. (2014b) is used. In short, we use the result of the integral of Eq. 1 between two measurement points (Eq. 2), scaled by the cross-section of water in the reservoir (AH2O in m2), defined as the cross-section area of the reservoir minus the cross-section of the sample.
where x is the position of the meniscus at time t (m); x0 is the initial position of the meniscus (m); R is the distance between the centre of the rotor and upstream water-air meniscus (m); ω is the angular velocity (rad s−1); ρ is the density of water (998.30 kg m−3 at 20 °C) and AH2O cross-section of water in the reservoir (m2).
In practice, computation is made by plotting the meniscus position-dependent function y (defined in Eq. 3) against time.
We can extract the hydraulic conductance (kh) from the slope (m) of this curve according to Eq. 4:
Specific hydraulic conductivity (Ks) is computed in kg m−1 MPa−1 s−1 according to the following:
where L is the length of the sample (m), kh is the hydraulic conductance and Asw is the cross-section area of conductive sapwood (m2)
2.2 Instrumental set-up
An overview of the new experimental setup is presented in Fig. 1. A high-speed temperature-controlled centrifuge has been used to instal a custom cavitron rotor. In order to measure a wider range of sample lengths, we developed a series of four rotors that can be fitted in three configurations of centrifuges (see Table 1). Two of these centrifuges are modified from commercially available instruments (RC5 series, Sorvall, USA, or J6, Beckmann Coulter, USA) and one of them is a custom device (CAVI 1000) described in this manuscript. For all configurations, a similar methodology has been used, except for the control of rotation speed (see below).
All operations are controlled through a custom software (Cavisoft, Univ Bordeaux, France). A screenshot of the main window is presented in Fig. 2. Input/output (I/O) management, except images, is done through a multifunction data acquisition systems DAQ (USB 6008, National Instruments, USA) and a Digital I/O board (USB 6501, National Instruments, USA), both interfaced directly in .NET through a dedicated library (NI DAQmx v 9.4, National Instrument., USA). This software also logs metadata (sample name, diameter, organ type, sampling location, date, etc.) and relevant computed values (see Appendix Table 3 for a complete description of the data output).
Screenshot of Cavisoft v5.0 graphical user interface. The operator can see in one window the live image (central panel), along all measured variables (top left panel), parameters (bottom left panel), computed variables (bottom right panel) and resulting VC curve updated immediately after each measurement point (top right panel)
The computer used for data acquisition and control is located next to the centrifuge. It is remotely operated with a keyboard, video and mouse (KVM) extender (Link X50, Adder, UK). The receiver of the KVM is located in the room situated next to the centrifuge.
Rotation speed of the Sorvall centrifuge is set either by a potentiometer, encoding speed by adjusting resistance (model RC5B) or with 5-position encoders using Gray code to input speed set point value (model RC5C+). Our approach consists in bypassing these controls by providing a computer-controlled set point value to the Sorvall command internal bus. This is done by the digital I/O which controls a universal card 16 relays (K6714-16, Velleman, Belgium) providing either a variable resistance (model RC5B) or the actual Gray code required by the machine (model RC5C+). Start, stop and brake functionalities are also controlled with this relay card. Details on these operations are available upon request.
To spin a rotor at high speed, it is essential that they are well balanced in shape and mass. This is particularly a challenge for a cavitron system, because of the inherent dissymmetry due to the large groove in which the sample is positioned. To compensate for those irregularities, a series of reinforced aluminium honeycomb designed rotors has been developed, which can prevent excessive radial forces, and hence breakage. For the CAVI1000, a big dimension aluminium rotor with a diameter of 1060 mm and a 69-mm thickness has been designed. It contains a removable cylindrical sample holder fitted with specific polycarbonate reservoirs with an inner diameter of 25 mm. The rotor is mounted on an oil-cooled shaft associated with an AC asynchronous motor with a maximum rotation speed of 3000 rpm, controlled with a precision better than 5 rpm by a digital variator (Movidrive MDX60B, Sew Eurodrive, Germany). The set-up is enclosed in a sturdy shelter, and four proximity sensors are placed to detect safety faults, such as rotor imbalance and automatically stop the motor. This work has been done in collaboration with a precision mechanical workshop (DG Meca, Gradignan, France).
2.3 Image acquisition and processing
In order to read the air-water menisci positions computationally, a monochrome camera (Scout scA640-120gm, Basler, Germany) has been used and fitted with a C-mount lens (HF16 HA-1B, Fujinon, Japan) that enables to have an adjustable field of view of about 7 × 5 mm. This camera is interfaced with a Software Development Kit (Pylon 3.0 SDK, Basler, Germany) that outputs a buffer of vectors of 8 bits integer corresponding to grey levels of a 659 × 494 pixel matrix. From this matrix, images are reconstructed for display or analysis. In order to avoid delay in image analysis and display, only the last image of the buffer is read when the processor is available; the rest of the buffer is discarded. This image is time-coded with an independent counter with millisecond precision to process meniscus velocity and can be saved to disk with very limited and controlled time delay. This display approach is much faster than point-by-point bitmap reconstruction and enables safely-timed reconstructions of high quality, not compressed, images in about 20 ms (i.e. 50 image s−1), depending on the computer used for acquisition. This reconstruction time (comparable to the human eye retina persistence) enables access to both menisci in the same image, thanks to the stroboscopic effect.
Once the pixel matrix is acquired, we extract the intensities of one horizontal line of pixels into a vector to determine the distance between the 2 menisci. To increase the computation speed and to avoid light pollution problems, two small user-defined regions of interest (ROI) are defined close to each meniscus, typically 40 to 300 pixels in width. If the meniscus is well defined and stable (at least an intensity of 10 bit above baseline), this enables the use of a very simple and fast algorithm (e.g. simple comparison of maximum along the vector) for determination of the maximum intensity, corresponding to the position of the meniscus (Fig. 3). The whole process (from data acquisition to distance measurement) can therefore be performed directly, without post-processing, within 30–100 ms (depending on the computer).
Example of images acquired and corresponding pixel intensity plots along a segment in the middle of the image (yellow line). The green square represents the downstream ROI, and the blue square represents the upstream ROI. A Image with a slight light pollution, resulting in a wide meniscus and decreased precision. B Typical image, at high centrifugal speed, with sharp meniscus and a steady backline, ideal for easy meniscus detection. c Image at very high speed, with a very thick sample showing very little transmitted light. The camera still detects the meniscus when the human eye cannot
Meniscus height is typically less than 100 μm. There is no measurable difference between the upstream and the downstream meniscus height, so distances are similar across the width of the reservoir. Hence, the distance can be measured at any position within the frame of the camera. This also implies that using an average of several lines within the frame is not required.
In order to compute the conductance in SI unit, a calibration of the camera pixel size is necessary. This can be done by focusing the camera on a ruler placed at the reservoir level and measuring the number of pixels corresponding to a given distance. The ratio of these values gives a typical camera calibration of 14 to 30 μm pixel−1. This calibration is not very sensitive to slight optical focus modification (e.g. an extreme 3 mm focus modification leads to less than 0.02% of variation in conductance value).
Like in all image vision measurement systems, great care must be taken to avoid parasite light and to maximise the contrast of the measured element (in our case, the menisci). It requires a very focused and powerful light source (preferably > 10,000 lux) especially at high speed. Any light pollution from the side is prevented by the use of guides and/or panels intercepting unwanted light fitted around the guides. The light delivery near the rotor will also be exposed to water projection from the reservoir overflow and should therefore be waterproof (protection index at least equal to IP54 or NEMA3). Light is provided either by (i) a standard 150 W-equivalent cold light source (e.g. KL1500 LED, Schott, Germany) and guided at the proximity of the rotor side with a bundle of ca 25 cut-to-size fibre optics (each 1 mm in diameter) or (ii) a IP66 LED light source (e.g. TSPOT4, TPL VISION or SL164, Advanced illumination) enclosed in an aluminium case carefully fixed to the inner wall of the centrifuge and equipped with an adjustable slot. Both methods enable to regulate the amount of light reaching the rotor and enable a better control of image quality for each sample.
2.4 Resolution of measurement
To measure the conductance, the key measurement is the water flow in the sample. This flow is estimated by the speed of meniscus movement acquired by image vision in a 2-dimensional plane, which is not directly the amount of water surrounding the sample (see above). A thin sample will have more water around its extremities, and so the meniscus displacement speed will be slower (for a given conductance) than for a thicker sample. The resolution of cavitron measurement, for a given measurement time, is therefore highly dependent on (i) the sample diameter relative to the geometry of the reservoirs, (ii) camera and optics performance, (iii) rotation speed and (iv) sample (or rotor) length.
The resolution obtained with the cavitron has been assessed for different conditions of sample diameters, sample lengths and rotation speeds by a theoretical approach, based on the equations used to compute the conductance. A camera resolution of 14 μm pixel−1 has been used for sample lengths of 16, 27 and 40 cm. For the 100-cm sample length cavitron, camera resolution is set at 28 μm pixel−1.
2.5 Validation of the conductivity measurement and temperature effect
A comparison between the specific conductivity measured with the cavitron and with the gravimetric method has been performed for three species (Liquidambar styraciflua, Populus nigra and Pinus pinaster) following the protocol adapted from Li et al. (2007). In short, specific conductivity has been estimated alternatively by gravimetric and centrifuge methods on the same sample. For this, two to four branches from two adult trees of each species growing in southwestern France have been sampled in the morning during the spring of 2016. Once in the lab, samples of about 8 mm in diameter have been recut underwater to a size corresponding to each rotor dimensions (27 or 100 cm, respectively).
For the gravimetric method, measurements were performed at 3 heights (corresponding to 1, 2 and 3 kPa) to eliminate the effect of the background flow. The slope of the regression has been used to calculate specific conductivity (Torres-Ruiz et al. 2012). Once the samples were measured, they were inserted in the cavitron rotor, and specific conductivity was computed again at low speed (corresponding to − 0.8 MPa), following the protocol described in this manuscript. Samples were centrifuged for at least 120 s at each rotation speed before measurement. After this measurement, centrifuge speed was increased to a value known to induce embolism depending on each species, and conductivity was measured again with the cavitron and with the gravimetric method.
Similarly to every hydraulic measurement, the temperature of the water flowing in the sample has an impact on conductance, through the modification of the viscosity of water and modification of the membrane fluidity and permeability, mostly at higher temperature (Cochard et al. 2000). This issue is overcome by using a temperature-controlled centrifuge, with a temperature set point close to water source temperature (often at room temperature) and a correction factor. For that, an empirical equation based on water dynamic viscosity change with temperature (IAPWS report, Huber et al. 2009) is implemented for correcting any significant temperature change during a measurement (Eq. 6).
Wang et al. (2014b) present a detailed description of temperature effect and propose an elaborate method for correction, based on an evaluation of conductance at different temperature steps. They found that a 10 °C step change in air temperature leads to about 22% reduction of conductance in about 30 min. Therefore, if the increase in temperature is quite low and gradual (as it is usually the case for standard measurement), and air temperature can be used directly as a proxy of stem temperature, if the equilibration time is long enough. A rough estimate would be to allow 3 min for a change of 1 °C.
If more drastic changes in temperature are observed, a first-order rate reaction model using a 5-min running mean air temperature as the input can be used; for detail, see Wang et al. (2014b).
Air temperature inside the centrifuge tank is monitored with a class A PT100 (D00538, Correge, France) connected to a converter (LKM 104/1, LKM electronic, Germany). Data is logged through the Multifunction DAQ analogue input (USB 6008, National Instruments, USA).
2.6 Validation of vulnerability curves obtained with a large rotor
Here, we used a very large (100 cm) rotor developed on the basis of a cavitron called CAVI1000 (Lamarque et al. 2018) to obtain vulnerability curves which we then compared with those obtained with reference techniques (Burlett 2021). For three species, for which average conduit length is at least two times shorter than 30 cm, (Pinus pinaster, Populus nigra, Liriodendron tulipifera) the standard (27 cm rotor) cavitron method has been used as a reference. These species have reported a mean conduit length of below 0.1 cm for tracheid of Pinus pinaster, 10.13 (± 0.20) cm for Populus nigra and 16.7 (± 0.7) cm for Liriodendron tulipifera (Pan et al. 2015; Porte, personal communication). Branches of the same adult individuals, in close proximity, have been sampled in the early morning on the campus of the University of Bordeaux and recut at 1 m under water following the protocol of Torres-Ruiz (2017).
For species with longer vessels (Quercus ilex and Quercus robur) vulnerability curves obtained with X-ray microComputed tomography on intact plants were used as a reference, to avoid potential artefact due to cutting (Cochard et al., 2015a). These species have reported mean conduit length of 96.0 (± 7.0) cm for Quercus ilex and 83.0 (± 18.6) cm for Quercus robur (Martínez-Vilalta et al. 2002; Venturas et al. 2016). X-ray micro-CT-based VC measurements were performed at the PSICHE beamline of the SOLEIL synchrotron (Saclay, France) on intact 1.5 m tall saplings from the INRAE nursery. The main stems of those samples were scanned during a dehydration experiment using a high flux (3.1011 photons mm−1) 25-keV monochromatic X-ray beam while being rotated continuously from 0 to 360°. X-ray projections were collected with a 50-m exposure time during rotation and recorded with an Orca-flash sCMOS camera (Hamamatsu Photonics K.K., Nakaku, Japan) equipped with a 250-μm-thick LuAG scintillator. Each stem was scanned 20 cm above the base of the stem (around 1.2 cm in diameter) by positioning the plant in the hollow stage. All plants were 3 and 5 years old for Quercus robur and Quercus ilex, respectively, and were grown into 1.5-L pots. Water potential was measured on leaves just after scanning using a Scholander Pressure Chamber (DG Meca, Gradignan, France). Leaves were covered with plastic bags and aluminium foil for at least 30 min prior to each measurement of water potential. Tomographic reconstructions were conducted using the Paganin method (Paganin et al. 2002) in PyHST2 software (Mirone et al. 2014) and resulted in 2-bit volumic images with a 3.02-μm3 voxel resolution.
The theoretical hydraulic conductance (kh) used for the reference VC curve was calculated from a transverse cross-section of each micro-CT scans following the protocol described in Choat (2016) and Lamarque (2020). In short, the individual area and diameter of both air- and water-filled vessels were measured using the ImageJ software (Schneider et al., 2012) The maximum theoretical hydraulic conductance (kmax, m-4 MPa−1 s−1) was calculated as the sum of the conductance of each water-filled vessels conductance.
where D is the diameter of vessels (m), and η is the water viscosity (1.002 10−3 Pa s at 20 °C). The actual per cent loss of theoretical hydraulic conductance for each sample was then calculated as PLC = 100 × (1 − kh/kmax).
Vulnerability curves for both CAVI1000 and micro-CT measurements were fitted using the NLIN procedure in SAS 9.4 (SAS, Cary, NC, USA) based on the following equation (Pammenter and Willigen, 1998):
where P50 (MPa) is the xylem pressure inducing 50% loss of hydraulic conductivity, and S (% MPa-1) is the slope of the vulnerability curve at the inflexion point. The model was fitted on each vulnerability curve to obtain a P50 and slope value for each individual. Those values were then averaged for each method, and the curve reconstructed from these averaged values. Details of the sample size and number of replicates for each measurement can be found in Table 2.
2.7 Statistics
Computation and statistics have been performed using MS Excel, SAS 9.4 (SAS, Cary, NC, USA) or R (v 3.5). Differences in hydraulic traits (P50, slope) between the methods were performed with a generalised linear-mixed models with species as a random effect.
3 Results
3.1 Performance of the new system
Operations required to perform a vulnerability curve, while the centrifuge is spinning, are done completely remotely through a software, allowing safe and quiet working conditions for the operator. These working conditions are compliant with the “Convention concerning the protection of workers against occupational hazards in the working environment due to air pollution, noise and vibration” (ILO 1977) and its declination in national laws for protection of the workers.
Traditional floor model centrifuge manufacturers have been developing algorithms to regulate the speed of the rotor with great precision and stability, with virtually no overshoot. The measured precision for the rotation speed is better than 20 rpm (for Sorvall RC models or Beckman Coulter J6), which correspond to an error in the imposed pressure well below 0.01 MPa. This error is completely negligible compared to the other uncertainties (data not shown). We decided to build on that experience to construct cavitrons for short samples (< 50 cm). It is however impossible, with the tools these manufacturers provide, to control the speed remotely with a computer. Our approach enabled us to use two popular laboratory centrifuges (RC5B and RC5C+, Sorvall, Thermo, USA) to build a remotely speed controlled cavitron.
The limits of pressure imposed through centrifugation at the centre of the sample are dependent on the individual set-up of the centrifuges and rotors used. For the setups described in this manuscript, this pressure ranges from − 6 MPa (for 16 cm long samples) to − 22 MPa (for 27-cm-long samples). The maximum sample diameter that can be inserted into the reservoir ranges from 10 to 24 mm depending on the rotor design (see Table 1 for details).
Most of the cavitron rotors are designed to use commercially available reservoirs, either centrifugation tubes or spectroscopy cuvettes. While centrifugation tubes always state the maximum speed at which they can be spun, this information is not available for spectroscopy cuvettes. The cuvettes tested have a breaking point ranging from − 3 to − 22 MPa (corresponding to rotation speed from 6000 to 154,000 rpm for a 27-cm rotor) depending on their material. Polycarbonate cuvettes are recommended for high-speed rotation.
3.2 Resolution of measurement and detectability threshold
The relationship between resolutions achieved with different cavitron sizes and pressures is presented in Fig. 4, for a measurement time of 180 s. These values vary mainly with the rotor size and range from 0.0014 to 0.0032 kg m−1.MPa−1 s−1 at a pressure of − 0.8 MPa. Both minimum and maximum thresholds have exactly the same shape and are therefore presented in the same graph, with two different axes. Figure 5 shows the relationship between sample diameter and minimum conductivity measurable in 180 s at low speed (corresponding to a pressure of − 0.8 MPa). The values represent the conductivity corresponding to a meniscus displacement speed of 0.6 μm s−1 for each diameter. Below this threshold, the camera resolution is low, and the meniscus is often not stable, because of slight mechanical vibration (< 1 μm). In the same manner, the relationship between sample diameter and the higher conductivity measurable is shown in Fig. 6. The limit has been set for a measurement of 3 s at the standard speed used for the maximum conductance measurement (corresponding to a pressure of − 0.8 MPa). The points show the conductivity corresponding to a meniscus displacement speed of 1500 μm s−1 for each diameter. Above this threshold, the meniscus moves too fast to get enough measurement points for accurate real-time estimation of Ks. For both minimum and maximum, Ks is highly dependent of the sample diameter. For comparison with the gravimetric method, flow rate for different sample diameters are presented in Appendix Fig. 9.
Examples of detectability thresholds with different rotor sizes for samples, computed from equations presented in Section 2.1. For this analysis, we used a sample diameter corresponding to the maximum value possible for each rotor size. Both minimum and maximum thresholds have exactly the same shape and are therefore presented in the same graph, with two different axes. The left axis is for minimum conductivity, and the right axis is for maximum conductivity
3.3 Validation of the conductivity measurement and temperature effect
The comparison between the conductivity measured with the cavitron and with the gravimetric method shows that both methods provided equivalent Ks values, as shown by the linear regression in Fig. 7 (model p-value < 2.2e−16).
The slope was equal to 1.023 (± 0.030) and the offset of the linear model was not significantly different from zero (0.020 ± 0.032, p = 0.537). This relationship is consistent for all rotor sizes.
The equation used to model the temperature effect on viscosity of water (Eq. 6) provides a relative error below 0.12% within the range of 5 to 40 °C (see Appendix Fig. 10). The influence of temperature effect on conductance, as implemented in the Cavisoft software, is about 2.4%. C−1 within the temperature range of cavitron measurement (typically 20 to 30 °C, data not shown). If the centrifuge cannot control the temperature well enough (e.g. at very high speed, or if greater precision is needed), it is possible to correct for the systematic error induced by temperature change.
3.4 Vulnerability curve assessment
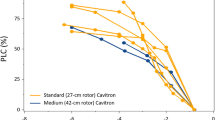
Figure 8 illustrates the similarity of the vulnerability curves obtained with the different techniques. Values of the P50 obtained with different techniques are reported in Table 2. For short-vessel species, the VCs obtained with the 100 cm rotor show no difference from those obtained with the standard rotor (27 cm). For the two long-vessel species, Fig. 8 also shows a good match between the two techniques (large cavitron and micro-CT), even if the mean vulnerability curves are not completely overlapping as was the case for the short-vessel species. On average, we did not detect any significant differences in P50 between methods (global model with all species, p = 0.8157).
Comparison of vulnerability curves showing PLC as a function of xylem pressure measured with different techniques for five species. Plain lines represent average curves obtained with a 100-cm rotor (n = 8). Dashed lines represent the average curves obtained with a reference method (n = 8 for cavitron and n = 3 for micro-CT). Insert graph show the P50 of each species estimated with the 100-cm rotor (P50 CAVI1000) versus P50 estimated with the reference techniques (P50 reference). Bands and error bars represent standard error
4 Discussion
4.1 Performance and ergonomic
Since the development of early versions of cavitron (Cochard 2002, Cochard et al., 2005), many improvements have been implemented resulting in a significant increase of the number of samples that can be processed in a given time, thanks to both ergonomic improvement allowing faster operations and working condition improvement, allowing better productivity.
The design of a more balanced rotor enabled to reach a higher rotation speed. For the 27-cm rotor, the maximum tension achieved is around − 22 MPa, which is very close to reported values of heterogeneous water cavitation (between − 20 and − 30 MPa) in physical systems or artificial trees (Vincent et al. 2012; Caupin et al. 2012). This implies that the cavitron can expose a sample to an extreme tension, close to the empirical threshold of water metastability, and thus to the maximum tension a plant can experience (Larter et al. 2015).
The new framework provides an easy way to keep traceability of the data and perform reproducible analysis. Handling of raw data, metadata and computed values for a complete set of experiments is done within one file, with an automatically generated unified format. Implementation in an automated processing pipeline is therefore possible with no data manipulation.
4.2 Resolution and precision
Within the plant kingdom, the reported range of specific conductivity (Ks) covers 4 orders of magnitude, from as low as 0.02 kg m−1 MPa−1 s−1 to more than 200 kg m−1 MPa−1 s−1 for tropical vine (Gartner et al. 1990).
Resolution achieved by the instrumental setup described here is typically well within this range, even though a camera with a relatively small pixel matrix is used. The required resolution is reached thanks to a good quality of optics and sensor providing steady and bright images. The main limitation of the system in terms of resolution appears when the sample diameter is very small compared to the cavitron reservoir. In this configuration, the amount of water surrounding the sample is big compared to the amount of water flowing in the sample, and the meniscus movement can become extremely slow. The model outputs (Figs. 6, 7, and 8), showing theoretical resolution and detectability thresholds for different conditions are presented as decision tools to select sample size (mostly diameter) according to the expected conductance of the sample.
4.3 Validation of the conductivity measurement
Although the cavitron has been widely used to produce vulnerability curves (hydraulic safety) rather than hydraulic conductance measurements, it seems extremely useful to also be able to estimate hydraulic efficiency with this increasingly popular device. The fact that the conductivity of a sample can be accurately measured in a SI unit with the flow-through centrifuge has already been shown by Li et al. (2008) for the standard rotor size. Our work confirmed their finding for three new species and different rotor sizes whatever the species used.
4.4 Validation of vulnerability curves obtained with a large rotor
Numerous studies have shown the inability of centrifuge techniques to unbiasedly assess resistance to xylem embolism in long-vesselled species (Choat et al. 2010; Cochard et al. 2010; Torres-Ruiz et al. 2014). The in situ flow centrifuge technique (Cavitron) has indeed been shown to overestimate vulnerability to cavitation when vessels are longer than the rotor diameter (Martin-StPaul et al., 2014; Wang et al., 2014a) due to open vessel artefact (Wheeler et al. 2013). Our challenge was therefore to develop and validate the use of a large rotor to increase the range of species that can be measured (e.g. oak, vitis). Firstly, our results showed that the large rotor provides similar results to the standard rotor for short vessel species, with no significant difference between rotor sizes. Secondly, we performed VC measurements on long-vessel species with this new device (large rotor and more precise resolution) and were able (i) to detect a change in xylem hydraulic conductance with decreasing xylem pressure and (ii) build an S-shaped vulnerability curve. Finally, we used the X-ray micro-CT method, which has proven to be a good method to directly visualise, at high resolution, the amount of embolised vessels and to estimate the loss of hydraulic conductance (Brodersen et al. 2013; Choat et al. 2016; Cochard et al., 2015b; Nolf et al. 2017) and the pattern of embolism spread in the vascular system (Torres-Ruiz et al., 2017) to validate the large rotor measurements. We found no or limited differences between the two techniques with P50 values of − 7.1 to − 7.6 MPa for Quercus ilex and − 4.7 and − 4.2 MPa for Quercus robur for the CAVI1000 and micro-CT techniques, respectively. The slight differences reported here can be explained by the plant material used: 1-m-long branches from mature trees for CAVI1000 and 1.5-m-long stems from saplings for micro-CT. Thanks to this new large rotor and the improved resolution of the hydraulic conductance measurements, it is now possible to measure with the in situ flow technique species that were very difficult to measure until now (long vessels or low conductivity). This will open up a new avenue for the characterisation of drought-induced cavitation in tropical forests or in viticulture for example.
5 Conclusion
The cavitron technique is mainly used for establishing VC curves based on a relative loss of hydraulic conductance (PLC), and therefore, absolute values of specific hydraulic conductivity are not required. We demonstrated in this study that it is also an accurate and reliable method to estimate specific hydraulic conductivity (Ks) in SI unit.
Software-based remote operation of the cavitron considerably increased productivity, by decreasing work hardness (noise, vibration, risk). Measurements are now performed in an environment compliant to modern health and safety rules, and with better ergonomics.
The use of a standard image vision system has also enabled to expand considerably the range of conductivity that can be measured with a centrifuge technique; plants with extremely low Ks or longer vessel length can now be characterised for their resistance to drought. Providing that the sample diameter and length is suitably selected, the new set-up of cavitron can now measure virtually any xylem bearing organs for which vessel length is shorter than the rotor, including herbaceous species (Chacon Dória et al. 2019) tropical or temperate long-vessel species (Lobo et al. 2018; Ziegler et al. 2019) or roots (Bouche et al. 2015).
Availability of data and materials
The datasets generated and/or analysed during the current study are available from the repository Dataverse INRAE (https://doi.org/10.15454/WRDBEW). The Cavisoft software is available at the Phenobois gitlab: https://forgemia.inra.fr/phenobois/cavisoft
References
Alder NN, Pockman WT, Sperry JS, Nuismer S (1997) Use of centrifugal force in the study of xylem cavitation. J Exp Bot 48(3):665–674. https://doi.org/10.1093/jxb/48.3.665
Anderegg WRL, Klein T, Bartlett M, Sack L, Pellegrini AFA, Choat B, Jansen S (2016) Meta-analysis reveals that hydraulic traits explain cross-species patterns of drought-induced tree mortality across the globe. Proc Natl Acad Sci U S A 113(18):5024–5029. https://doi.org/10.1073/pnas.1525678113
Beikircher B, Ameglio T, Cochard H, Mayr S (2010) Limitation of the Cavitron technique by conifer pit aspiration. J Exp Bot 61(12):3385–3393. https://doi.org/10.1093/jxb/erq159
Bouche PS, Delzon S, Choat B, Badel E, Brodribb TJ, Burlett R, Cochard H, Charra-Vaskou K, Lavigne B, Li S, Mayr S, Morris H, Torres-Ruiz JM, Zufferey V, Jansen S (2016) Are needles of Pinus pinaster more vulnerable to xylem embolism than branches? New insights from X-ray computed tomography. Plant Cell Environ 39(4):860–870. https://doi.org/10.1111/pce.12680
Bouche PS, Jansen S, Cochard H, Burlett R, Capdeville G, Delzon S (2015) Embolism resistance of conifer roots can be accurately measured with the flow-centrifuge method. J Plant Hydraul 2:e002. https://doi.org/10.20870/jph.2015.e002
Brodersen CR, Mcelrone AJ, Choat B et al (2013) In vivo visualizations of drought-induced embolism spread in Vitis vinifera. Plant Physiol 161(4):1820–1829. https://doi.org/10.1104/PP.112.212712
Brodribb TJ, Carriqui M, Delzon S, Lucani C (2017) Optical measurement of stem xylem vulnerability. Plant Physiol 174(4):2054–2061. https://doi.org/10.1104/PP.17.00552
Burlett R (2021) Dataset used in the paper “Measuring xylem hydraulic vulnerability for long-vessel species: an improved methodology with the flow centrifugation technique”, Data INRAE portal, V1. https://doi.org/10.15454/WRDBEW
Cai J, Hacke U, Zhang S, Tyree MT (2010) What happens when stems are embolized in a centrifuge? Testing the cavitron theory. Physiol Plant 140(4):311–320. https://doi.org/10.1111/j.1399-3054.2010.01402.x
Caupin F, Arvengas A, Davitt K, Azouzi MEM, Shmulovich KI, Ramboz C, Sessoms DA, Stroock AD (2012) Exploring water and other liquids at negative pressure. J Phys Condens Matter 24(28):284110. https://doi.org/10.1088/0953-8984/24/28/284110
Chacon Dória L, Meijs C, Podadera DS et al (2019) Embolism resistance in stems of herbaceous Brassicaceae and Asteraceae is linked to differences in woodiness and precipitation. Ann Bot 124(1):1–14. https://doi.org/10.1093/AOB/MCY233
Charra-Vaskou K, Badel E, Burlett R, Cochard H, Delzon S, Mayr S (2012) Hydraulic efficiency and safety of vascular and non-vascular components in Pinus pinaster leaves. Tree Physiol 32(9):1161–1170. https://doi.org/10.1093/treephys/tps071
Choat B, Badel E, Burlett R, Delzon S, Cochard H, Jansen S (2016) Noninvasive measurement of vulnerability to drought-induced embolism by X-Ray microtomography. Plant Physiol 170(1):273–282. https://doi.org/10.1104/pp.15.00732
Choat B, Drayton WM, Brodersen C et al (2010) Measurement of vulnerability to water stress-induced cavitation in grapevine: a comparison of four techniques applied to a long-vesseled species. Plant Cell Environ 33(9):1502–1512. https://doi.org/10.1111/j.1365-3040.2010.02160.x
Choat B, Jansen S, Brodribb TJ, Cochard H, Delzon S, Bhaskar R, Bucci SJ, Feild TS, Gleason SM, Hacke UG, Jacobsen AL, Lens F, Maherali H, Martínez-Vilalta J, Mayr S, Mencuccini M, Mitchell PJ, Nardini A, Pittermann J, Pratt RB, Sperry JS, Westoby M, Wright IJ, Zanne AE (2012) Global convergence in the vulnerability of forests to drought. Nature. 491(7426):752–755. https://doi.org/10.1038/nature11688
Cochard H (2002) A technique for measuring xylem hydraulic conductance under high negative pressures. Plant Cell Environ 25(6):815–819. https://doi.org/10.1046/j.1365-3040.2002.00863.x
Cochard H, Badel E, Herbette S, Delzon S, Choat B, Jansen S (2013) Methods for measuring plant vulnerability to cavitation: a critical review. J Exp Bot 64(15):4779–4791. https://doi.org/10.1093/jxb/ert193
Cochard H, Damour G, Bodet C, Tharwat I, Poirier M, Améglio T (2005) Evaluation of a new centrifuge technique for rapid generation of xylem vulnerability curves. Physiol Plant 124(4):410–418. https://doi.org/10.1111/j.1399-3054.2005.00526.x
Cochard H, Delzon S, Badel E (2015a) X-ray microtomography (micro-CT): a reference technology for high-resolution quantification of xylem embolism in trees. Plant Cell Environ 38(1):201–206. https://doi.org/10.1111/PCE.12391
Cochard H, Herbette S, Barigah T et al (2010) Does sample length influence the shape of xylem embolism vulnerability curves? A test with the Cavitron spinning technique. Plant Cell Environ 33(9):1543–1552. https://doi.org/10.1111/j.1365-3040.2010.02163.x
Cochard H, Martin R, Gross P, Bogeat-Triboulot MB (2000) Temperature effects on hydraulic conductance and water relations of Quercus robur L. J Exp Bot 51(348):1255–1259. https://doi.org/10.1093/jexbot/51.348.1255
Delzon S, Cochard H (2014) Recent advances in tree hydraulics highlight the ecological significance of the hydraulic safety margin. New Phytol 203(2):355–358. https://doi.org/10.1111/nph.12798
Delzon S, Douthe C, Sala A, Cochard H (2010) Mechanism of water-stress induced cavitation in conifers: bordered pit structure and function support the hypothesis of seal capillary-seeding. Plant Cell Environ 33(12):2101–2111. https://doi.org/10.1111/J.1365-3040.2010.02208.X
Gartner BL, Bullock SH, Mooney HA, Brown VB, Whitbeck JL (1990) Water transport properties of vine and tree stems in a tropical deciduous forest. Am J Bot 7(6):742–749. https://doi.org/10.1002/j.1537-2197.1990.tb14464.x
Holbrook NM, Burns MJ, Field CB (1995) Negative xylem pressures in plants: a test of the balancing pressure technique. Science (80- ) 270:1193–1194. https://doi.org/10.1126/science.270.5239.1193
Huber ML, Perkins RA, Laesecke A, Friend DG, Sengers JV, Assael MJ, Metaxa IN, Vogel E, Mareš R, Miyagawa K (2009) New international formulation for the viscosity of H2O. J Phys Chem Ref Data 38(2):101–125. https://doi.org/10.1063/1.3088050
ILO (1977) Convention C148 - convention concerning the protection of workers against occupational hazards in the working environment due to air pollution, noise and vibration
Lamarque LJ, Corso D, Torres-Ruiz JM et al (2018) An inconvenient truth about xylem resistance to embolism in the model species for refilling Laurus nobilis L. Ann For Sci 75:1–15. https://doi.org/10.1007/S13595-018-0768-9
Lamarque LJ, Delzon S, Toups H, Gravel AI, Corso D, Badel E, Burlett R, Charrier G, Cochard H, Jansen S, King A, Torres-Ruiz JM, Pouzoulet J, Cramer GR, Thompson AJ, Gambetta GA (2020) Over-accumulation of abscisic acid in transgenic tomato plants increases the risk of hydraulic failure. Plant Cell Environ 43(3):548–562. https://doi.org/10.1111/PCE.13703
Larter M, Brodribb TJ, Pfautsch S, Burlett R, Cochard H, Delzon S (2015) Extreme aridity pushes trees to their physical limits. Plant Physiol 168(3):804–807. https://doi.org/10.1104/pp.15.00223
Li Y, Sperry JS, Taneda H et al (2008) Evaluation of centrifugal methods for measuring xylem cavitation in conifers, diffuse- and ring-porous angiosperms. New Phytol 177(2):558–568. https://doi.org/10.1111/j.1469-8137.2007.02272.x
Lobo A, Torres-Ruiz JM, Burlett R, Lemaire C, Parise C, Francioni C, Truffaut L, Tomášková I, Hansen JK, Kjær ED, Kremer A, Delzon S (2018) Assessing inter- and intraspecific variability of xylem vulnerability to embolism in oaks. For Ecol Manag 424:53–61. https://doi.org/10.1016/j.foreco.2018.04.031
Martínez-Vilalta J, Prat E, Oliveras I, Piñol J (2002) Xylem hydraulic properties of roots and stems of nine Mediterranean woody species. Oecologia 133:19–29. https://doi.org/10.1007/S00442-002-1009-2
Martin-StPaul NK, Longepierre D, Huc R et al (2014) How reliable are methods to assess xylem vulnerability to cavitation? The issue of “open vessel” artifact in oaks. Tree Physiol 34(8):894–905. https://doi.org/10.1093/treephys/tpu059
Meixner M, Tomasella M, Foerst P, Windt CW (2020) A small-scale MRI scanner and complementary imaging method to visualize and quantify xylem embolism formation. New Phytol 226(5):1517–1529. https://doi.org/10.1111/NPH.16442
Melcher PJ, Michele Holbrook N, Burns MJ, Zwieniecki MA, Cobb AR, Brodribb TJ, Choat B, Sack L (2012) Measurements of stem xylem hydraulic conductivity in the laboratory and field. Methods Ecol Evol 3(4):685–694. https://doi.org/10.1111/j.2041-210X.2012.00204.x
Mirone A, Brun E, Gouillart E, Tafforeau P, Kieffer J (2014) The PyHST2 hybrid distributed code for high speed tomographic reconstruction with iterative reconstruction and a priori knowledge capabilities. Nucl Instrum Methods Phys Res Sect B Beam Interact Mater Atoms 324:41–48. https://doi.org/10.1016/J.NIMB.2013.09.030
Nolf M, Beikircher B, Rosner S, Nolf A, Mayr S (2015) Xylem cavitation resistance can be estimated based on time-dependent rate of acoustic emissions. New Phytol 208(2):625–632. https://doi.org/10.1111/NPH.13476
Nolf M, Lopez R, Peters JMR, Flavel RJ, Koloadin LS, Young IM, Choat B (2017) Visualization of xylem embolism by X-ray microtomography: a direct test against hydraulic measurements. New Phytol 214(2):890–898. https://doi.org/10.1111/NPH.14462
Paganin D, Mayo SC, Gureyev TE, Miller PR, Wilkins SW (2002) Simultaneous phase and amplitude extraction from a single defocused image of a homogeneous object. J Microsc 206(1):33–40. https://doi.org/10.1046/J.1365-2818.2002.01010.X
Pammenter NW, Willigen CV (1998) A mathematical and statistical analysis of the curves illustrating vulnerability of xylem to cavitation. Tree Physiol 18(8-9):589–593. https://doi.org/10.1093/treephys/18.8-9.589
Pan R, Geng J, Cai J, Tyree MT (2015) A comparison of two methods for measuring vessel length in woody plants. Plant Cell Environ 38(12):2519–2526. https://doi.org/10.1111/PCE.12566
Pivovaroff AL, Burlett R, Lavigne B, Cochard H, Santiago LS, Delzon S (2016) Testing the “microbubble effect” using the Cavitron technique to measure xylem water extraction curves. AoB Plants 8:plw011. https://doi.org/10.1093/aobpla/plw011
Schneider CA, Rasband WS, Eliceiri KW (2012) NIH Image to ImageJ: 25 years of image analysis. Nat Methods 9(7):671–675. https://doi.org/10.1038/nmeth.2089
Sperry JS, Christman MA, Torres-Ruiz JM et al (2012) Vulnerability curves by centrifugation: is there an open vessel artefact, and are “r” shaped curves necessarily invalid? Plant Cell Environ 35(3):601–610. https://doi.org/10.1111/j.1365-3040.2011.02439.x
Thonglim A, Delzon S, Larter M, Karami O, Rahimi A, Offringa R, Keurentjes JJB, Balazadeh S, Smets E, Lens F (2021) Intervessel pit membrane thickness best explains variation in embolism resistance amongst stems of Arabidopsis thaliana accessions. Ann Bot 128(2):171–182. https://doi.org/10.1093/AOB/MCAA196
Torres-Ruiz JM, Cochard H, Choat B, Jansen S, López R, Tomášková I, Padilla-Díaz CM, Badel E, Burlett R, King A, Lenoir N, Martin-StPaul NK, Delzon S (2017) Xylem resistance to embolism: presenting a simple diagnostic test for the open vessel artefact. New Phytol 215(1):489–499. https://doi.org/10.1111/NPH.14589
Torres-Ruiz JM, Cochard H, Mayr S, Beikircher B, Diaz-Espejo A, Rodriguez-Dominguez CM, Badel E, Fernández JE (2014) Vulnerability to cavitation in Olea europaea current-year shoots: further evidence of an open-vessel artifact associated with centrifuge and air-injection techniques. Physiol Plant 152(3):465–474. https://doi.org/10.1111/ppl.12185
Torres-Ruiz JM, Jansen S, Choat B, McElrone AJ, Cochard H, Brodribb TJ, Badel E, Burlett R, Bouche PS, Brodersen CR, Li S, Morris H, Delzon S (2015) Direct X-ray microtomography observation confirms the induction of embolism upon xylem cutting under tension. Plant Physiol 167(1):40–43. https://doi.org/10.1104/pp.114.249706
Torres-Ruiz JM, Sperry JS, Fernández JE (2012) Improving xylem hydraulic conductivity measurements by correcting the error caused by passive water uptake. Physiol Plant 146(2):129–135. https://doi.org/10.1111/j.1399-3054.2012.01619.x
Tyree MT, Dixon MA (1986) Water stress induced cavitation and embolism in some woody plants. Physiol Plant 66(3):397–405. https://doi.org/10.1111/j.1399-3054.1986.tb05941.x
Venturas MD, Rodriguez-Zaccaro FD, Percolla MI, Crous CJ, Jacobsen AL, Pratt RB (2016) Single vessel air injection estimates of xylem resistance to cavitation are affected by vessel network characteristics and sample length. Tree Physiol 36(10):1247–1259. https://doi.org/10.1093/TREEPHYS/TPW055
Vincent O, Marmottant P, Quinto-Su PA, Ohl C-D (2012) Birth and growth of cavitation bubbles within water under tension confined in a simple synthetic tree. Phys Rev Lett 108(18):184502. https://doi.org/10.1103/PhysRevLett.108.184502
Wang R, Zhang L, Zhang S et al (2014a) Water relations of Robinia pseudoacacia L.: do vessels cavitate and refill diurnally or are R-shaped curves invalid in Robinia? Plant Cell Environ 37(12):2667–2678. https://doi.org/10.1111/pce.12315
Wang Y, Burlett R, Feng F, Tyree MT (2014b) Improved precision of hydraulic conductance measurements using a Cochard rotor in two different centrifuges. J. Plant Hydraul. 1:007. https://doi.org/10.20870/jph.2014.e007
Wheeler JK, Huggett BA, Tofte AN, Rockwell FE, Holbrook NM (2013) Cutting xylem under tension or supersaturated with gas can generate PLC and the appearance of rapid recovery from embolism. Plant Cell Environ 36(11):1938–1949. https://doi.org/10.1111/PCE.12139/SUPPINFO
Ziegler C, Coste S, Stahl C et al (2019) Large hydraulic safety margins protect neotropical canopy rainforest tree species against hydraulic failure during drought. Ann For Sci 76:1–18. https://doi.org/10.1007/S13595-019-0905-0
Acknowledgements
All measurements have been performed at the PHENOBOIS platform, except Micro-Computed Tomography scans that have been performed at the PSICHE beamline (SOLEIL Synchrotron facility, project 20150954). The authors would like to thank Henri Inchauspe for his contribution to the camera module of the software; Anne-Isabelle Gravel, Cédric Lemaire and Melvin Tyree for many fruitful discussions about the cavitron technique; Stephane Ygorra and Luc Lasne for their advices on image vision; and Romain Souchal for the help in setting the rotation speed control on Sorvall centrifuge. A. Techene (SAM precis) and G. Dumercq (DG Meca) are also acknowledged for providing amazing rotors.
Funding
This work was supported by the programme ‘Investments for the Future’ (ANR-10-EQPX-16, XYLOFOREST) and the Cluster of Excellence COTE (ANR-10-LABX-45) from the French National Agency for Research and by the ERC project TREEPEACE (FP7-339728).
Author information
Authors and Affiliations
Contributions
RB and SD conceived and designed the research in collaboration with HC. RB wrote the Cavisoft software. GC, CP, LJL, AK, RB and SD acquired and processed the data. RB and SD performed the data analysis and statistics. RB and SD were involved in writing, revising, and editing the manuscript, with contributions from all the authors. The authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
All authors gave their informed consent to this publication and its content.
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Handling Editor: Maurizio Mencuccini
Appendix
Appendix
Relation between minimum measurable flow and diameter (mm) at a pressure of − 0.8 MPa for different rotor sizes. Note that this relationship is dependent on the geometry of the reservoir mainly. For comparison, typical minimal flow achieved with the gravimetric method by a 0.0001 g precision balance is plotted (discontinue line). The flow measured by the balance is not dependent on the diameter of the sample, but on the resolution of the balance
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated in a credit line to the data.
About this article
Cite this article
Burlett, R., Parise, C., Capdeville, G. et al. Measuring xylem hydraulic vulnerability for long-vessel species: an improved methodology with the flow centrifugation technique. Annals of Forest Science 79, 5 (2022). https://doi.org/10.1186/s13595-022-01124-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13595-022-01124-0