Introduction

Low-density lipoprotein cholesterol (LDL) is a well-known risk factor and therapeutic target for atherosclerotic disease [1, 2]. In patients at high cardiovascular risk due to dyslipidemia, low-density lipoprotein cholesterol (LDL) reduction is recommended as the primary treatment goal, with statins as first-line therapy in national and international clinical practice guidelines [3, 4]. LDL can be measured directly (LDLdirect) with several methods [5, 6]. The accepted gold-standard method for LDL measurement is labor-intensive, time-consuming, and expensive β-quantification after ultracentrifugation [7]. Instead, direct homogeneous assays for LDL measurement have been widely used and showed reasonable accuracy and precision compared with the reference method [5, 6]. Meanwhile, LDL is often calculated (LDLcal) from a lipid profile test that includes measurement of total cholesterol (TC), high-density lipoprotein cholesterol (HDL), and triglycerides (TG) [3, 8].

LDL is typically calculated using the Friedewald equation [LDLFriedewald = TC – HDL – (TG/5)], which was developed based on analysis of 448 patients in 1972 [9]. The Friedewald equation is inaccurate increasingly at TG concentrations from 200 to 400 mg/dL and is regarded as invalid when at TG level > 400 mg/dL [5, 10]. Although several LDL calculation equations have been suggested as alternatives for Friedewald, studies performed in populations using different analytical measurement methods for lipid quantification reported varying equation accuracy [3, 4, 8, 11,12,13,14,15,16,17,18,19,20,21]. For example, in the United States, Martin et al. suggested a new equation for LDL estimation (LDLMartin) using an adjustable factor for TG:very-low-density lipoprotein cholesterol (VLDL) ratio based on TG and non-HDL concentration (non-HDL = TC – HDL) stratification based on lipid profiles obtained from 1,350,908 subjects [4]. Martin et al. reported that the overall concordance in guideline risk classification with LDLdirect was 91.7% for LDLMartin and 85.4% for LDLFriedewald for patients with TG lower than 400 mg/dL, but the concordance was modest (from 57.8 to 69.8%) in patients with TG ≥ 400 mg/dL [4]. An indiVidual patient meta-analysis Of statin therapY in At risk Groups: Effects of Rosuvastatin, atorvastatin and simvastatin (VOYAGER) was conceived to compare the efficacy of three statins most commonly used in clinical practice (atorvastatin, rosuvastatin, and simvastatin) using patient meta-analysis to characterize the effect of individual statin agents on lipid levels using individual patient data from pooled clinical studies [22]. The VOYAGER database contains LDL concentrations using LDLFriedewald for patients with TG ≤ 400 mg/dL and LDLdirect using β-quantification for those with TG > 400 mg/dL [22]. However, a recent study from the VOYAGER meta-analysis database aimed to investigate the difference in LDLcal when using the LDLMartin and LDLFriedewald equations reported that LDLMartin might not be suitable for patients with TG ≥ 400 mg/dL and can result in overestimation of LDLdirect [13]. Considering that ethnically and ancestrally diverse populations having different allele frequencies of genetic determinants of blood lipids, for which transferable or non-transferable loci might affect lipids in gene-environment interactions [23], validation of accurate clinical applicability for all equations in various ethnic populations is needed [1, 3, 13, 20, 21].

In Korea, limited data are available on the accuracy of equations for LDLcal. Previous studies performed in Korea investigated the accuracy of limited numbers of equations for LDLcal [8, 14, 18]. In Korea, LDLFriedewald is most commonly used for LDLcal [8, 24]. Therefore, the aim of this study was to evaluate the performance of a new LDL equation (LDLChoi) along with previous LDL estimations using 11 equations for LDL calculation in comparison with directly measured LDL in Korean adults to improve understanding of LDL calculations when direct measurement is unavailable. To the best of our knowledge, this study includes the largest number of equations to be validated in a Korean population.

Materials and methods

Study subjects

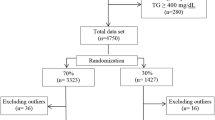
Clinical lipid profile test results (TC, HDL, TG, and LDLdirect) performed between July 4, 2017 and September 5, 2018 in Korean adults (> 19 years) from the Green Cross Laboratories information system were reviewed retrospectively. Green Cross Laboratories is a referral clinical laboratory in Korea that provides clinical specimen analysis services including lipid profile tests to clinics and hospitals nationwide. Data obtained between July 4, 2017, and September 5, 2018, were used to develop a new equation for LDL calculation (LDLChoi) in this study, and data obtained from September 6 to November 30, 2018, were used as a separate data set (population 2, the validation cohort 1) to validate the newly-developed LDLChoi equation. Data from the Korea National Health and Nutrition Examination Survey (KNHANES) 2017, a nationwide cross-sectional study regularly conducted by the Division of Chronic Disease Surveillance, Korea Centers for Disease Control and Prevention of the Ministry of Health and Welfare, was independently analyzed (population 3, the validation cohort 2) to evaluate generalizability of the 11 previously suggested equations and the LDLChoi equation developed in this study. All data were anonymized before analysis. The overall study design is shown in Fig. 1. The data that support the findings of this study are available from the corresponding authors upon reasonable request.

Fig. 1
figure 1

Study scheme

Full size image

Analytical procedures

Serum concentrations of TC, TG, HDL, and LDL were measured using enzymatic methods with an automatic analyzer (Cobas 8000 c702, Roche, Mannheim, Germany). LDL was measured using LDL-cholesterol plus 2nd generation reagent on samples between July 4, 2017, and February 4, 2018, and LDL-cholesterol Gen.3 (Roche, Mannheim, Germany) between February 5 and November 30, 2018. TC, TG, and HDL were measured using Cholesterol Gen.2, TRIGL, and HDL-Cholesterol plus 3rd generation, respectively. The accuracy of lipid measurements was assured through the Accuracy Based Lipid Survey proficiency testing program by the College of American Pathologists and by the Lipids Standardization Program by the Centers for Disease Control, USA [25].

For population 3 (validation cohort 2, KNHANES 2017), serum TC, TG, HDL, and LDL were measured using enzymatic methods with an automatic analyzer Hitachi 7600–210 (Hitachi, Tokyo, Japan) using PureautoS CHO-N, Pureauto S TG-N, Cholestest N HDL, and Cholestest LDL reagents (Sekisui Medical, Tokyo, Japan), respectively [24].

Selection of equations for calculated LDL

LDL was calculated using 11 previously published equations suggested by Friedewald et al. (LDLFriedwald) [9], DeLong et al. (LDLDeLong) [15], Rao et al. (LDLRao) [26], Hattori et al. (LDLHattori) [16], Anandaraja et al. (LDLAnandaraja) [17], Ahmadi et al. (LDLAhmadi) [27], Puavilai et al. (LDLPuavilai) [11], Chen and Zhang et al. (LDLChen and Zhang) [19], Vujovic et al. (LDLVujovic) [28], de Cordova et al. (LDLde Cordova) [29], and Martin et al. (LDLMartin) [4]. And a new equation (LDLChoi) using multiple linear regression analysis of TC, TG, HDL and LDLdirect values using the development cohort. All 12 of these equations were compared with LDLdirect measured using a homogenous enzymatic method for development and independent validation cohorts, which including populations of the KNHANES 2017 cohort.

Statistical analysis

The distribution of continuous variables is described as mean with standard deviation (for normally distributed variables) or as median with interquartile range (for skewed variables) and compared using an independent t-test and Wilcoxon rank sum test, respectively. Categorical variables are reported as observed number and percentage as calculated using the Chi-square test.

Agreement and accuracy of the 12 equations for estimating LDLcal were investigated using LDLdirect as the reference value. The intraclass correlation coefficient (ICC) was calculated to compare the degrees of agreement between the 12 equations and LDLdirect. The level of agreement was defined according to ICC value; good agreement was when ICC > 0.75, and moderate agreement was when 0.5 < ICC < 0.75 [18]. Bland–Altman plots were assessed to compare LDLdirect and multiple equations for LDLcal.

Subgroup analysis was performed to investigate whether discordant LDL quantification occurs when LDL cholesterol is measured or calculated with different assays, especially in patients with low LDL cholesterol or hypertriglyceridemia [1]. Data were classified into two groups (LDL < 70 mg/dL in LDL group 1 and LDL ≥ 70 mg/dL in LDL group 2) for subgroup analysis to investigate the performance of each equation based on LDL concentration. Data were classified into three groups according to serum TG concentration as follows: < 175, 175–400, and > 400 mg/dL [5, 10] for subgroup analysis to investigate the performance of each equation based on TG concentration.

Agreement according to category based on the National Cholesterol Education Program (NCEP) Adult Treatment Panel III (ATP III) between LDLcal estimated using the 12 equations and LDLdirect concentration was also assessed. Optimal LDL concentration for < 100 mg/dL, above optimal for 100–129 mg/dL, borderline high for 130–159 mg/dL, high for 160–189 mg/dL, and very high for ≥190 mg/dL were applied [30]. Equations for LDLcal and NCEP ATP III criteria for each LDLcal are provided as online Supplementary Material S1.

Statistical analysis was executed using MedCalc software for Windows, version 19.1.3 (MedCalc Software bv, Ostend, Belgium; https://www.medcalc.org; 2019). Statistical significance was defined as a P-value less than 0.05.

Results

A total of 5198 lipid profile test results from 4562 Korean adults was obtained between July 4, 2017, and September 5, 2018, and was used to develop a new equation for LDL calculation (LDLChoi). Using multiple linear regression analysis of the development cohort data with 5198 lipid profile test results, a new equation for estimated LDLcal was developed as follows: LDLChoi = TC – 0.87 x HDL – 0.13 x TG. Between September 6 and November 30, 2018, 2163 lipid profile test results from 2086 Korean adults were obtained in the same laboratory and used as a separate data set (population 2, validation cohort 1), with which LDLdirect was measured with a different reagent generation to validate the newly developed LDLChoi equation. For another independent validation cohort (population 3, validation cohort 2), a total of 889 lipid profile test results from 889 Korean adults was used. General characteristics and lipid profile test results in the three independent populations in this study are summarized in Table 1. In the KNHANES 2017 cohort (validation cohort 2, population 3), the proportion of male subjects was greater than that of female subjects, there were no subjects with TG < 175 mg/dL, and there were more patients with TG > 400 mg/dL compared to the other cohorts.

Table 1 Characteristics of study cohorts
Full size table

Including the newly developed equation (LDLChoi), 12 equations for LDLcal were analyzed. In populations 1 (development cohort) and 2 (validation cohort 1), the mean value of estimated LDLcal in total subjects (men and women) showed negative bias in comparison with LDLdirect except for LDLAhmadi (Supplementary Fig. S1 and Table S1). In population 3 (validation cohort 2, KNHANES 2017), estimated LDLAhmadi showed a mean value greater than two times that of LDLdirect. Because LDLRao, LDLAhmadi, and LDLde Cordova equations had several outliers with large differences between estimated LDL and LDLdirect, Bland–Altman plots for only nine of the equations are shown in Fig. 2.

Fig. 2
figure 2

Bland–Altman plots for nine equations with directly measured LDL concentration (excluding LDLRao, LDLAhmadi, and LDLde Cordova equations). X-axis represents directly measured LDL concentration (LDLdirect) and Y axis represents difference between calculated LDL and directly measured LDL (LDLdirect)

Full size image

Among the 12 equations for LDLcal, the newly developed LDLChoi equation showed the highest ICC in the development cohort (population 1) and in validation cohort 1 (population 2). However, LDLDeLong, LDLRao, LDLPuavilai, LDLChen and Zhang, LDLVujovic, and LDLMartin showed a higher ICC than did LDLChoi in validation cohort 2 (population 3, KNHANES 2017). All equations except LDLAhmadi showed good agreement with ICC > 0.75. LDLChoi showed the lowest mean systemic difference in populations 1 and 2, although other equations showed lower systemic differences than LDLChoi in validation cohort 2 (population 3, KNHANES 2017). The limits of agreement with LDLdirect and LDLcal from each equation are summarized in Supplementary Table S2. LDLChoi showed the lowest absolute percentage error for LDLdirect estimation in populations 1 and 2 but not in population 3.

In subgroup analysis according to LDLdirect concentration, the equations showed variable accuracy in comparison with LDLdirect (Supplementary Tables S3 to S4 and Supplementary Figs. S2). The top three equations that showed high ICC, low mean systemic differences, or low absolute percentage errors are presented in color. In LDL group 1 (LDLdirect < 70 mg/dL), no equation showed good agreement (ICC > 0.75) with LDLdirect except LDLChoi in women in population 2 (ICC = 0.81). Different equations ranked as top three among subgroups. In LDL group 1 (LDLdirect < 70 mg/dL), the newly developed LDLChoi equation was included frequently in the top three equations for ICC, mean systemic differences, and absolute percentage errors in populations 1 and 2 but not in population 3.

In subgroup analysis according to TG concentration (Supplementary Tables S5 and S6 and Supplementary Fig. S3), all equations except LDLde Cordova showed good agreement (ICC > 0.75) with LDLdirect in TG group 1 (TG < 175 mg/dL). In TG group 2 (TG 175–400 mg/dL), all equations showed good agreement with LDLdirect except LDLAhmadi in all three populations. In TG group 3 (TG > 400 mg/dL), the LDLDeLong, LDLVujovic, LDLChen and Zhang, LDLMartin, and LDLChoi equations showed good agreement with LDLdirect in all three populations.

Considering median and 95th percentile values of absolute percentage errors, no equations showed values ≤12.0% in all three populations. In subgroup analysis by LDLdirect concentration, only LDLChoi showed median absolute percentage error values ≤12.0% in populations 1 and 2 in LDL group 1 (LDL < 70 mg/dL). In subgroup analysis by TG concentration, no equation showed ≤12.0% error for 95th percentile values of absolute percentage error in TG group 2 (TG 175–400 mg/dL) or TG group 3 (TG > 400 mg/dL), while only LDLChoi showed ≤12.0% in TG group 1 (TG < 175 mg/dL) in populations 1 and 2.

Overall concordant categorization agreement according to the NCEP ATP III between LDLcal estimated using the 12 equations and LDLdirect concentration is summarized in Fig. 3. The concordance rate varied among equations for LDLcal. Categorization concordance according to the NCEP criteria in the other 11 equations was less than 80% in all three populations. However, LDLChoi showed the highest concordance with LDLdirect (86.8–88.0%) in populations 1 and 2, followed by LDLVujovic. In population 3, LDLChoi overestimated 38.8% of results, while the other equations except for LDLHattori showed higher concordance than LDLChoi.

Fig. 3
figure 3

Overall agreement of categorization according to the National Cholesterol Education Program Adult Treatment Panel III (NCEP ATP III) between calculated LDL and directly measured LDL. X-axis represents percentage of agreement. Red color represents underestimated, yellow color represents concordant, and green color represents overestimated patient categories according to NCEP ATP III in comparison with those categories assigned by directly measured LDL concentration

Full size image

Discussion

In this study, a new equation (LDLChoi) for LDL estimation is developed and validated in agreement and accuracy with LDLdirect as the reference value using two independent cohorts in comparison with 11 equations established in previous studies in a Korean population. Although several studies have been reported to validate several of the 11 equations in the Korean population, to the best of our knowledge, this study includes the largest number of concurrent equations for validation of estimating LDLcal.

The LDLChoi showed good agreement with LDLdirect in populations 1 and 2, which contained lipid profile data from different periods using different generations of reagents in the same laboratory. However, in population 3 data from KNHANES 2017, all other equations showed higher values for ICCs and lower values for systemic differences and absolute percentage errors. Different equations showed different performance among the three populations in this study. These findings might be due to various factors in measurement of LDLdirect, including analytical methods with use of different reagents and instruments as well as different ethnicities and populations with various health conditions [8]. These findings suggest that laboratory-specific equations would provide more accurate values of estimated LDLcal rather than use of LDLFriedwald.

In the era of personalized medicine, patient-specific risk estimation is important for health care [3]. In this study, categorization concordance according to the NCEP criteria in the previously developed 11 equations was less than 80% in all three populations. These findings suggest that LDLcal concentration was under- or over-estimated for more than 20% of patients. Previous studies regarding evaluation and validation of various equations for LDLcal estimation usually included specimen results with TG concentration < 400 mg/dL based on the limitation of accuracy for the LDLFriedewald equation [1]. In the present study, the accuracy of 12 equations of LDLcal was evaluated using 511 test results with > 400 TG mg/dL. Although the highest concordance rate according to NCEP ATP III criteria was observed as 81.3% in population 1 and 75.5% in population 2 for LDLChoi in TG subgroup 3 (TG > 400 mg/dL), the concordance according to NCEP ATP III criteria was 71.0% for LDLFriedwald, 55.7% for the newly developed LDLChoi equation, 77.1% for LDLVujovic and 76.3% for LDLPuavilai in population 3 for TG subgroup 3 (TG > 400 mg/dL). These findings confirmed the validation of equations for estimated LDLcal [1, 14, 18]. Considering that the NCEP ATP III criteria could affect the management plan, accurate assignment of patient categorization with accurate LDL estimation is needed [4].

According to NCEP criteria, the total error of LDL measurements should be within 12% of the true value [7]. In this study, although median values of absolute percentage errors were ≤ 12% in some equations, when considering both the median and 95th percentile values of absolute percentage errors ≤12%, no equations met these requirements. Only the LDLChoi equation met the median and 95th percentile values of absolute percentage errors ≤12% in specimens with LDL ≥ 70 mg/dL in the subgroup analysis for LDL concentration groups and in specimens with TG < 175 mg/dL in the subgroup analysis for TG concentration in populations 1 and 2. This finding confirmed that previous estimations of LDL might not be applicable in samples with low LDL or high TG concentration, and LDLdirect is needed for accurate assessment of LDL concentration [31, 32].

Comparisons with other equations

A recent randomized clinical trial (the Further Cardiovascular Outcomes Research with Proprotein convertase subtilisin/kexin type 9 (PCSK9) Inhibition in Subjects with Elevated Risk Trial) using data collected from 2013 to 2016, from 1242 centers in 49 countries including Korea, reported that the LDLMartin equation more closely approximated the gold-standard preparative ultracentrifugation values than did LDLFriedewald [3]. In the present study, LDLMartin showed good agreement with LDLdirect (ICC = 0.92), with mean systemic differences from − 11.1 to 5.7% (− 12.5 to 4.4 mg/dL) in the three populations. In the subgroup analysis, LDLMartin was in the top three equations for estimated LDL in both subgroups (LDLdirect < 70 mg/dL or ≥ 70 mg/dL, Supplementary Tables S3 and S4). In subgroups of TG, LDLMartin was in the top three equations for estimated LDL (TG group 2 with 175–400 mg/dL and TG group 3 with > 400 mg/dL), except for TG group 1 patients whose TG < 175 mg/dL. In patients with TG < 175 mg/dL, LDLChoi, LDLVujovic, and LDLdeLong frequently were listed in the top three equations (Supplementary Tables S5 and S6). Previous studies about LDLcal have been performed in various ethnic cohorts with different characteristics, such as range of lipid concentrations and measurement methods for LDLdirect (Table 2). All equations compared in this study varied in design factors, such as target population or specific characteristics, by developer. Because of this, equation comparisons should be interpreted carefully. In the present study, LDLcal using LDLHattori showed a very high result in population 3 (KNHANES 2017, Validation cohort 2). Meanwhile, as in Supplementary Tables S1 to S6 and Figs. 2 and 3, LDLAhmadi was different from the other equations. Each of the 12 equations for LDLcal reflected a different effect of TG in the population data used. Equations of LDLHattori and LDLAhmadi were designed using subjects with TG ≤ 400 mg/dL and TG < 100 mg/dL, respectively. While LDLVujovic was also from subjects with TG ≤ 400 mg/dL, it was based on LDLdirect values measured using an automated enzymatic method. Various measurement methods of lipids can vary in accuracy, convenience, and cost [15]. Considering that current clinical laboratories usually determine LDLdirect by automatic enzymatic methods and physicians manage patients with strategies based on these values from clinical laboratories, LDLcal obtained from LDLdirect calculated by automatic enzymatic methods might better classify patients at risk [28]. Future studies are needed to define the accuracy and clinical impacts of various equations in large numbers of populations.

Table 2 Characteristics of the 12 equations for calculated LDL
Full size table

Strengths and limitations

The strengths of this study are development of a new calculation equation (LDLChoi) using a relatively large number of Korean subjects and for which accuracy were compared with that of multiple other equations. Furthermore, calculators for the 12 equations are provided as an online supplementary material and can help physicians and researchers validate LDLcal in different ethnic populations. The limitations of this study are the retrospective design and the lack of clinical information including detailed history and physical examination and other laboratory and image studies associated with cardiovascular and other diseases, which is out of the scope of this study. The results of this study might not be generalizable to other populations as all data were from Korean adults. To enhance generalizability, future studies using different ethnic populations and ages are needed. Future studies on the clinical impact of the practice using large numbers of patients with various LDLcal and LDLdirect in various ethnicities are needed.

Conclusions

In conclusion, a new LDLChoi equation for estimated LDLcal was developed and validated in a Korean population and compared with 11 previous equations using LDLdirect as a reference method. The accuracy of LDLChoi was highest in laboratory-specific populations. Considering that the accuracy varied according to cohort (population), LDLdirect, and TG concentration, direct measurement of LDL is needed for accurate evaluation of LDL. This study can help to expand our knowledge about LDLcal in Korean populations and to improve test utilization.