Abstract
Background
Accurate exposure estimation in environmental epidemiological studies is crucial for health risk assessment. Failure to account for uncertainties in exposure estimation could lead to biased results in exposure-response analyses. Assessment of the effects of uncertainties in exposure estimation on risk estimates received a lot of attention in radiation epidemiology and in several studies of diet and air pollution. The objective of this narrative review is to examine the commonly used statistical approaches to account for exposure estimation errors in risk analyses and to suggest how each could be applied in environmental epidemiological studies.
Main text
We review two main error types in estimating exposures in epidemiological studies: shared and unshared errors and their subtypes. We describe the four main statistical approaches to adjust for exposure estimation uncertainties (regression calibration, simulation-extrapolation, Monte Carlo maximum likelihood and Bayesian model averaging) along with examples to give readers better understanding of their advantages and limitations. We also explain the advantages of using a 2-dimensional Monte-Carlo (2DMC) simulation method to quantify the effect of uncertainties in exposure estimates using full-likelihood methods. For exposures that are estimated independently between subjects and are more likely to introduce unshared errors, regression calibration and SIMEX methods are able to adequately account for exposure uncertainties in risk analyses. When an uncalibrated measuring device is used or estimation parameters with uncertain mean values are applied to a group of people, shared errors could potentially be large. In this case, Monte Carlo maximum likelihood and Bayesian model averaging methods based on estimates of exposure from the 2DMC simulations would work well. The majority of reviewed studies show relatively moderate changes (within 100%) in risk estimates after accounting for uncertainties in exposure estimates, except for the two studies which doubled/tripled naïve estimates.
Conclusions
In this paper, we demonstrate various statistical methods to account for uncertain exposure estimates in risk analyses. The differences in the results of various adjustment methods could be due to various error structures in datasets and whether or not a proper statistical method was applied. Epidemiological studies of environmental exposures should include exposure-response analyses accounting for uncertainties in exposure estimates.
Similar content being viewed by others
Background
Environmental epidemiological studies are designed to examine the impact of potentially toxic exposures on the health of occupationally exposed workers and members of the public [1]. These studies provide valuable information to public health authorities, especially with regard to health risks of hazardous environmental exposures [2]. The exposure estimate in such studies is usually a complex system which describes physical, chemical or biological characteristics of hazardous substances along with their transport mechanisms in the general environment or workplace over time and space. In addition, the role of individuals needs to be considered in exposure estimation to determine the mechanism of uptake as well as the amount of uptake of toxic substances by the human body. Such complex processes lead to formidable challenges in exposure estimation as well as make the issue of estimation error unavoidable.
In the past two years, about 2000 papers have been published which included some kind of risk analysis of the effects of environmental exposures. However, only 39 of these publications mentioned that ‘measurement error’ or ‘uncertainties’ may exist in exposure assessments. A smaller amount of these publications (15) have assessed the effect of measurement and/or estimation errors on risk estimates. Failure to account for uncertainties in exposure estimation may lead to biased results and undue confidence in their accuracy in the subsequent exposure-response analyses. As a result, inaccurate information about the risks of exposures may be distributed to other scientists, the public and to decision makers. The three main effects of performing an exposure-response analysis based on the error-prone exposure estimates are: (a) biased estimation of exposure-response parameters, (b) reduction of statistical power, and (c) hidden true exposure-response features (e.g., true exposure-response is distributed with a certain cyclic variation pattern such as sinusoidal trend, however, this feature may be masked if exposure is estimated with errors) [3].
Ionizing radiation is a known and well-studied carcinogen [4]. The effects of potential errors in exposure estimation on the radiation dose-response has been debated in radiation epidemiology for a number of years [5]. The process of estimation of radiation doses is usually subject to various sources of uncertainties [6, 7]. Little et al. (2015), Land et al. (2015) and others used a variety of statistical methods to examine the impact of uncertainties in individual dose estimates on risk estimates in different populations exposed to ionizing radiation [8, 9]. However, the topic of uncertainties in exposure estimation is not commonly considered for other exposure types in environmental epidemiological studies. The goal of this paper is to introduce and review various error types in exposure estimation as well as the statistical approaches to account for exposure estimation errors in risk analyses. The approaches reviewed are regression calibration, simulation-extrapolation, Monte Carlo maximum likelihood and Bayesian model averaging. We will summarize their advantages and limitations as well as provide suggestions for application of each method to other relevant scenarios in environmental epidemiological studies.
Main text
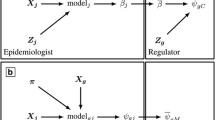
Exposure uncertainties could be evaluated based on investigator’s knowledge about distribution of each parameter required to estimate individual exposure values [10]. The various sources of exposure estimation errors may result in different types of errors which would require different approaches to minimize their effects on risk estimates. In this section, different error types in exposure estimation, statistical methods to account for exposure estimation errors and representative studies that applied these methods are reviewed. Figure 1 shows a diagram of various types of exposure estimation errors (adapted from [7]). Potential sources and relevant examples of each type of error are described in Table 1. Representative studies in radiation epidemiology and other environmental epidemiological fields are listed in Tables 2 and 3, respectively.
Error types
Uncertainty vs. variability
“Uncertainty” is sometimes defined as all possible sources that challenge the study’s validity (e.g., [11]). In such cases, variability is considered a special type of uncertainty. However, the U.S. Environmental Protection Agency (EPA) has suggested that researchers should follow the definitions of uncertainty and variability recommended by National Research Council (NRC), which distinguish the natures of these two error types ([12, 13]). According to the NRC (1994) definition, “uncertainty” is defined as a lack of precise knowledge that is presented during exposure assessment procedures and is due to absence of or imprecise measurements, observations or information pertinent to the assessment question. However, variability in exposure reflects the inherent heterogeneity of the exposure across individuals. Inter-individual variability of the unknown true exposure or dose will still exist due to randomness even if all other identified exposure characteristics (such as sex, age, life-style, location of residence, diet, job identifiers, etc.) are identical across a set of individuals [5, 7, 12].
Shared errors vs. unshared errors
Shared uncertainties are introduced when there is incomplete knowledge about model parameters that are used to estimate the exposure of a subgroup of individuals in a cohort. As a limit, uncertainties can be shared among parameters that apply to all members of the cohort (i.e., the subgroup can be equal to the entire cohort). The true values of these parameters are unknown but fixed (i.e., not varying on an individual-by-individual basis). The errors in these parameters lead to systematic errors in exposure estimates of all subgroup members [7]. In epidemiological studies, shared error (systematic error) refers to bias. Unshared errors, which usually refer to random errors, are the uncertainties that arise from parameters that vary independently between subjects. An unshared error could be random, which is usually classified into two types: classical error and Berkson error. It also could be non-random (e.g., errors in personal residence history records) because the true residence information is fixed to a specific individual [7].
Classical error vs. Berkson error
Both classical error and Berkson error are types of unshared random error. Classical error stems from an imprecise measuring device that is used to estimate individual exposure. It is also introduced by over-estimation of inter-individual random variability of true exposure. This error is most commonly defined as a situation when there are repeated measurements which vary around the unknown true value for each individual. Berkson errors are introduced when the same approximate exposure value (usually the arithmetic mean value for a group) is assigned to each member of a cohort sub-group who share similar exposure characteristics. The true exposure values for individuals in this group are unknown, but vary around the assigned value [14]. Examples of each error type are given in Table 1.
Suppose we are interested in an exposure D (e.g., radiation dose), and Dtr represents an unknown true value of the exposure, while Dest represents an estimated value of exposure D. In many studies, but especially when exposure refers to a radiation dose, the “measured” value is usually not directly used in the exposure-response analysis, and calibrations and calculations are applied to the “measured” value to obtain a final “estimated” exposure value. This “estimated” value will be used in the subsequent risk analyses. Thus, we prefer to use the term of “estimated exposure” rather than “measured exposure” in this paper in order to avoid misinterpretation. Using these notations, the classical error model is expressed as
where Uc is a classical error term with E(Uc| Dtr) = 0 and the estimated exposure Dest is an unbiased estimate of the true exposure, that is, E(Dest| Dtr) = Dtr. When the error term Uc has a constant variance, \( {\sigma}_u^2 \), Uc ∣ Dtr approximately follows a normal distribution [3], although other types of distributions may apply.
On the other hand, the Berkson error model could be expressed as
where E(Ub| Dest) = 0, and E(Dtr| Dest) = Dest.
For the studies with exposure measured independently between subjects, unshared errors are more likely to occur in exposure estimation. For example, when self-report values are used as individual exposures, almost all the uncertainties are from unshared components. In contrast, when a biased/uncalibrated measuring device is used or mathematical models to estimate exposure with uncertainty on mean values for the model parameters are applied for a group of people, shared errors are more likely to be introduced. For example, when a mathematical model is used to define the transport mechanism of a toxicant, shared uncertainties would be potentially large if this model is not well designed (i.e., it does not characterize the true transport features perfectly). Uncertainties introduced from this model will usually affect the entire cohort. In such cases, shared uncertainties could not be ignored in exposure estimates. Differentiation of classical error from Berkson error is relatively easy in practice. If the error-prone exposure is estimated uniquely to an individual, especially when some measurements during exposure estimation could be replicated, the errors should be considered classical. If a group of people are assigned the same value (usually the group average) of the error-prone exposure while the true exposure value is particular to an individual, errors are considered to be Berkson type [3, 15, 16].
Two types of error structure are usually considered in the analysis of exposure estimation error. They are described by a multiplicative error model or by an additive error model. The multiplicative error structure is considered when the spread of the true exposure given the estimated exposure increases proportionally to the estimated exposure values, while the additive error structure should be considered when the spread remains constant [17]. The true values of the exposure are unknown, but one can plot the average values of replicated exposure estimates per individual versus each of the replicated individual exposure estimates. When the plot (made on a linear scale) is in a “tube” shape, the error structure is most likely described by an additive error model, while a multiplicative model seems to be reasonable when the plot has a “trumpet” shape (Fig. 2) [17]. A “tube” shape of the plot displayed using a log scale indicates a multiplicative error.
Measured exposure vs. true exposure assuming additive error model and multiplicative error model (adapted from [17])
Use of a two-dimensional Monte Carlo method for estimation of exposures
In practice, the error structure of exposure estimation is usually complex and contains various types of errors, although one type usually predominates. In such cases, more advanced statistical methods are needed to account for the complex error structures in risk analyses. A Monte Carlo simulation procedure (i.e., repeated drawing of random samples from probability distributions of various exposure estimation parameters) could be used to generate multiple exposure estimates per individual (e.g., [8, 18, 19]). In this section, we introduce an exposure estimation approach called the two-dimensional Monte Carlo method (2DMC), which is an advanced approach compared to other forms of Monte Carlo methods widely used for quantitative uncertainty analysis in radiation dose reconstruction. By applying 2DMC in exposure estimation, information on both shared and unshared uncertainties are presented in the form of multiple alternative realizations of possibly true exposure estimate vectors. Each realization of a possibly true exposure estimate vector represents a set of different values of shared and unshared parameters. These multiple realizations of possibly true exposure estimate vectors allow researchers to use various statistical approaches to account for shared and unshared sources of exposure estimates of uncertainties in exposure-response analyses. This method allows researchers to use information about both shared and unshared uncertainties in exposure estimates in risk analyses. Although this method is time-consuming and challenging, it is often necessary for performing certain types of advanced statistical analyses of exposure-response accounting for errors in exposure estimates. The statistical methods that account for exposure estimation errors in exposure-response analyses are introduced in the later section, and are all described based on exposure estimates obtained by 2DMC. Although not all of them require that they be performed based on the 2DMC procedure, we use this setting for the convenience of comparison.
The 2DMC method is a simulation-based exposure reconstruction strategy that properly maintains the separation between shared uncertainties in exposure estimates among the entire cohort or the cohort’s subset, and the unshared, individual uncertainties. The concept of 2DMC is first mentioned in [20] while detailed implementation procedures were proposed by [7]. Although it had originally been proposed as a radiation dose reconstruction method, 2DMC could also be applied in other exposure scenarios in which the estimation procedure is complex and shared uncertainties are expected to be relatively large. By applying 2DMC, the parameters shared by cohort or subgroup members are fixed in the outer loop while the unshared parameters are simulated in the inner loop. Each run of the outer loop pass will generate a set of simulated exposure values for the N cohort members. For example, if the outer loop pass is run M times, it will result in a final estimated exposure Dest in a matrix form as below:
where N is the sample size of the cohort. Thus, M sets of exposure are estimated for the entire cohort.
We use W to denote the full set of input data that is needed to determine the estimated exposure Dest, where W does not represent a single variable but include all the variables needed in exposure estimation. Then, for example, in a dosimetry system developed to estimate radiation doses, W may include residence history, exposed age, intake of milk contaminated with radionuclides, etc. [21]. We use \( f\left({D}_1^{tr},\dots, {D}_N^{tr}|W\right) \) to denote the joint distribution of true exposure for all cohort members, given all input data that is needed in exposure estimation. The aim of the exposure estimation procedure is thus to draw samples from \( f\left({D}_1^{tr},\dots, {D}_N^{tr}|W\right) \) as potential exposure estimates. For 2DMC, where shared parameters are first fixed in the outer loop and the correlations among individuals are held, each estimated exposure vector \( {D}_r^{est}\ \left(r=1,\dots, M\right) \) is sampled from the joint distribution \( f\left({D}_1^{tr},\dots, {D}_N^{tr}|W\right) \) for all members of the cohort [21, 22]. Therefore, the estimated exposure matrix Dest in (1) is constructed by sampling \( \left({D}_1^{est},\dots, {D}_N^{est}\right) \) for M times.
Each estimated set of exposures for the entire cohort \( \left({D}_1^{est},\dots, {D}_N^{est}\right) \) based on 2DMC maintains the shared information among individuals and can possibly be the true exposure vector. When full-likelihood methods, such as the Monte Carlo Maximum Likelihood method and the Bayesian model averaging method, are applied to explore exposure-response relationship using the entire estimated sets of exposure, the overall effect of uncertainties in exposure estimates can be quantified [7]. Goodness of fit tests with respect to the cohort vector of individual exposure estimates and the cohort vector of individual disease incidence (or mortality) is used to distinguish between cohort exposure estimates that are plausible versus those that are not.
Statistical methods to account for exposure estimate errors in exposure-response analyses
Below, we will review the four main statistical methods to account for effects of errors in exposure estimation on risk estimates. Each section presents a short description of the methods to estimate functions and associated variances, followed by examples and advantages and limitations. For more details, readers are referred to primary references. Examples of studies which successfully used these methods are provided in Tables 2 (radiation epidemiology studies) and 3 (studies of other environmental exposures).
Regression calibration
Regression calibration is a replacement method [23] that substitutes the unobserved true exposure value Dtr by a calibration function E(Dtr ∣ Dest) in the regression of the health outcome Y on true exposure Dtr. The method could be easily applied to different types of data, including survival and binomial [24,25,26,27,28,29,30]. The general procedure of regression calibration can be summarized by the following three steps:
-
1)
Estimate the calibration function E(Dtr ∣ Dest);
-
2)
Fit a regression of Y on E(Dtr ∣ Dest) instead of the unobserved true exposure Dtr;
-
3)
Adjust the variance of the risk estimates to account for steps 1) and 2).
The method of estimation of calibration function E(Dtr ∣ Dest) depends on the data sources. In situations where internal validation data or data on unbiased instrumental variables are available, the calibration function could be directly estimated by the regression of Dtr on Dest or by the regression of an unbiased instrumental variable on the estimated exposure [3].
When repeated estimates of exposure are available, the calibrated function could be estimated by the so-called linear approximation [3]. Suppose we have M replicates of exposure estimate for ith individual \( \left({D}_{i1}^{est},\dots, {D}_{iM}^{est}\ \right) \) and consider an additive classical error model: Dest = Dtr + U. The variance of error term U is then estimated by
where \( {\overline{D}}_{i.}^{est} \) is the mean of M replicates for ith individual. The best linear approximation to Dtr given Dest is given by
where μT and μest are the means of Dtr and Dest, respectively. Both of these variables could be estimated by the overall sample average \( \frac{\sum_{i=1}^N{\overline{D}}_{i.}^{est}}{N} \), and the variance of the true exposure \( {\sigma}_T^2 \) is estimated by
The formulas (2)–(4) above are based on the simple case which only considers a relationship between a single exposure D and outcome Y in a risk model. When other covariates X (usually assumed to be estimated without errors, e.g., age, gender, etc.) are included in the risk model, the calibration function would change to E(Dtr| Dest, X). A matrix form of the linear approximation of E(Dtr| Dest, X) could be found in [3]. For a multiplicative error model, the log transformation is used to convert it to an additive one. The method introduced above can then be directly applied to the log-transformed data. Statistical software such as Stata [31] could be used to calculate the adjusted standard error as well as the confidence interval. Although other methods are available to adjust the variance (see [3]), bootstrap is recommended for large data sets based on the speed of computations [32].
The regression calibration method has been used in several radiation epidemiological studies [9, 23, 33,34,35,36]. For example, a multiplicative error model was considered for estimated thyroid doses in studies of those exposed to the Chornobyl (Chernobyl) accident [9, 15, 34, 37]. By assuming that the error term was log-normally distributed, the calibration function E(Dtr| Dest) was obtained based on the conditional distribution of f(Dtr| Dest), which also follows a log-normal distribution. In analyses of Chornobyl data, risk analyses using regression calibration method to adjust for uncertainties in doses, had estimated excess odds ratios which were 7–11% higher in the Ukrainian cohort [34] and 13% higher in the Belarusian cohort [9] compared to conventional analyses without accounting for dose uncertainties.
Regression calibration method is also widely used in nutritional studies. A recent systematic review of measurement error-correction approaches in nutritional epidemiology, showed that 71 of 76 studies adjusted for exposure measurement errors by regression calibration method [38]. Nutrient intake measurements frequently have errors because they are usually assessed based on self-reported food frequency questionnaires (FFQ) [39, 40]. To apply a regression calibration method to adjust for the measurement errors in FFQ, researchers typically collect additional data for a reference variable in a subset of the population from the main study. The reference variable is usually measured by multiple 24-h dietary recalls, or some biomarkers, such as urinary nitrogen for protein intake [40,41,42,43,44]. Regression of this reference variable on dietary variable from the FFQ is treated as an estimate of the calibration function E(Dtr ∣ Dest). Table 3 presents examples of studies that used regression calibration to adjust for exposure estimation errors.
Simulation-extrapolation
The simulation-extrapolation (SIMEX) method is a simulation-based method that is implemented in two steps: a simulation step and an extrapolation step [45]. The simulation step seeks to explore the relationship between errors in exposure estimation and an estimator of interest. Based on this relationship, the error-free estimate of risk parameter is obtained by setting the variance of the error term to zero in the extrapolation step. In this case, the “error-free” estimate here does not imply a perfect estimate of the risk parameter but a parameter estimator. A log-transformation could also be applied to generate an additive error when a multiplicative error model is considered [3].
In the simulation step, a set of pre-selected parameters (ξ1, … , ξT), such that 0 ≤ ξ1 < ξ2 < … < ξT are used as the scale factors to construct pseudo-errors. A “contaminated” exposure data set (i.e., the data set to which extra errors are manually added) could be generated for each scale factor ξt:
where i = 1, … , N; t = 1, … , T; Ui is sampled from \( N\left(0,{\sigma}_u^2\right) \) and \( {\sigma}_u^2 \) could be estimated using repeated data as eq. (2). Based on the “contaminated” data \( \left({Y}_i,{D}_{(t),i}^{est,\ast}\right) \), a naïve parameter \( \widehat{\beta}\left({\xi}_t\right) \) estimate could be obtained by fitting a regression model.
After the simulation step, the risk parameter estimate is obtained \( \widehat{\beta}\left({\xi}_t\right) \) for each pre-selected scale factor ξt, where \( \widehat{\beta}\left({\xi}_t\right) \) could be treated as a function of ξt. It is assumed that an extrapolation function, G(∙), is used to capture the relationship between the risk parameter estimate \( \widehat{\beta}\left({\xi}_t\right) \) and the scale factor ξt, that is, \( \widehat{\beta}\left({\xi}_t\right)=G\left({\xi}_t;\gamma \right) \), where γ is the parameter in function G(∙). The extrapolation step is then summarized as follows:
1) Estimate the parameter γ in the extrapolant function G(ξt; γ).
2) Obtain the SIMEX estimate for the risk parameter: \( {\widehat{\beta}}_{SIMEX}=G\left({\xi}_t=-1;\widehat{\gamma}\right) \).
During the extrapolation step, it is important to decide how to choose the extrapolation function G(∙). Cook and Stefanski [45] suggested three different extrapolation functions which include a linear extrapolation G(ξ; γ) = γ1 + γ2ξ, a linear quadratic extrapolation G(ξ; γ) = γ1 + γ2ξ + γ2ξ2, and a nonlinear extrapolation function (also called the rational linear extrapolant) \( G\left(\xi; \gamma \right)={\gamma}_1+\frac{\gamma_2}{\gamma_3+\xi } \). These extrapolants provide a relatively good approximation for any particular estimator.
The estimate of the standard error of the SIMEX estimator could be obtained via a bootstrap procedure, a Jackknife procedure [46], or a sandwich estimator [3]. SIMEX estimator with the estimated standard error could be obtained using statistical software such as Stata [31] or the R package “simex” [47].
SIMEX or extended SIMEX have been applied in some air pollution studies to adjust for errors in exposure estimates (e.g., [48, 49]). For example, a recent study of exposures to particulate matter (PM) estimated individual exposures using data from multiple monitoring stations within a certain area, which could potentially introduce some errors. After adjusting for exposure estimation errors by extended SIMEX, the estimated effect of PM < 2.5 μm in diameter (PM2.5) on birth weight increased by 56.7% in Alexeeff et al. [49] compared to analyses without adjustments for errors in exposure estimation. A radiation epidemiological study exploring a relationship between individual colon dose from gamma radiation and solid cancer deaths [50] reported that the estimated excess relative risk per gray (ERR/Gy) increased by 38.4% after accounting for dose uncertainties by SIMEX, compared to an increase of 6.7% after adjustment by regression calibration. Similar increases in risk estimates were reported in a study of effects of bone marrow doses on the risk of death from leukemia in survivors of atomic bombings in Japan [50]. After adjusting for dose uncertainties by SIMEX, the estimated ERR/Gy increased by 19.6%, compared to an increase of 7.3% after adjustment using regression calibration method (see Table 3 for details).
Monte Carlo Maximum Likelihood
The estimated exposure matrix Dest from equation (1) from the 2DMC dosimetry system can be treated as a sample drawn from the conditional distribution of true exposure given the input data f(Dtr| W). Because W represents the observed values of all the data that are used to determine the exposure estimates, we could estimate an observed likelihood f(Y| W; α, β) in the exposure-response analysis [21], where α and β are the parameters of covariates and exposure, respectively. The basic idea behind the Monte Carlo Maximum Likelihood (MCML) method is to obtain a maximum likelihood estimate of the risk parameter β based on the observed likelihood f(Y| W; α, β) [21, 22] from multiple dose vectors. The observed likelihood can be expressed as
where \( {E}_{D^{tr}\mid W}\left[\bullet \right] \) indicates the expectation under the conditional distribution of the true exposure Dtr given the full set of input data W and f(Y| Dtr; α, β) represents the exposure-response model that describes the relationship between response and true exposure value [21]. Since the estimated exposure Dest can be treated as multiple samples drawn from the conditional distribution f(Dtr| W), the observed likelihood can be estimated by averagingdexposure vectors:
where \( {D}_r^{est}\ \left(r=1,\dots, M\right) \) is the estimated exposure vector for the entire cohort. For a set of pre-selected values of β, [β1, … , βK], the profile likelihood of β is expressed as
Then the maximum likelihood estimate of β is the β value that maximizes the profile likelihood: \( {\widehat{\beta}}_{MLE}={argmax}_{\beta}\left[L\left({\beta}_k\right)\right] \). The likelihood ratio test statistic, \( -2\ln \left[L\left(\beta \right)\right]+2\ln \left[L\left({\widehat{\beta}}_{MLE}\right)\right] \), has an asymptotic χ2 distribution with one degree of freedom [21] and can be used to estimate a confidence interval.
For a complex dosimetry system, simple (unweighted) average might not produce precise values for point estimate and confidence interval for β since only a few exposure vectors will have reasonable goodness-of-fit to the response. In such cases, it would be better to implement MCML based on weighted average of profile likelihood function with respect to the goodness-of-fit measure such as Akaike information criterion (AIC) and Bayesian information criterion (BIC).
The MCML method has been used in many radiation studies. For example, in the 15-country study of cancer risks of nuclear workers [21], a time-period- and facility-specific bias factor was introduced to calculate possible true doses. The uncertainties in this bias factor were shared across all individuals who worked in the same facility during the specified time period. In analyses with MCML, the estimated ERR per unite dose (ERR/Sievert (Sv)) was reduced by 10.4% compared to the unadjusted estimate (see Table 2).
Bayesian model averaging
Kwon et al. (2016) proposed a Bayesian model averaging (BMA) method to account for uncertainties in exposure estimates [51]. This method uses a data augmentation approach to the multiple estimated exposure vectors obtained from 2DMC by introducing an exposure vector selection parameter, say γ (γ = 1, … , M). Bayesian inference could be treated as a learning process from the opinion of the unknown parameters (i.e., prior distribution) and the data at hand (i.e., likelihood). By first sampling one value of the vector selection parameter γ from its prior distribution, one of M exposure vectors will be selected as the “best fit” to update likelihood information. Iteratively, the updated likelihood information will update the probability distribution of γ. Similar updating process is applied to all the parameters. The posterior samples of the parameter of interest could then be obtained via Markov Chain Monte Carlo (MCMC) calculations by various sampling algorithms, such as Gibbs sampling [52] or Metropolis-Hastings [53].
The selection of prior distributions for each parameter depends on the prior knowledge and interpretation of the parameter. For example, when the response variable is binary, i.e., Yi~Bernoulli(1, pi), the parameter pi represents the probability of Yi = 1. In this case, a beta distribution is usually considered as the prior distribution of pi, because the beta distribution is defined on the interval [0, 1] which matches the natural probability range (between 0 and 1). In the BMA method, parameter γ indicates which exposure vector is selected in likelihood calculation, and given a multinomial distribution with probability vector π = (π1, … , πM) as its prior distribution. Multinomial distribution is a multivariate generalization of binomial distribution, which describes a trial with multiple possible outcomes. Since we have M sets of possibly true exposure vectors, it is appropriate to consider a multinomial distribution for γ. A Dirichlet distribution is often combined with a multinomial distribution to define the prior of the probability vector in multinomial distribution. In our case, each parameter in the probability vector π = (π1, … , πM) represents the probability of selecting the corresponding exposure vector in likelihood calculation. For example, π1 = 0.6 indicates that the first exposure vector has 60% chance to be selected to update the likelihood. Therefore, a prior distribution of Dirichlet(1, … , 1) for hyper-parameter vector π = (π1, … , πM) is considered and it indicates that every exposure vector \( {D}_r^{est}={\left[{D}_{1r}^{est},\dots, {D}_{Nr}^{est}\right]}^T \) has an equal a priori probability to be selected as the best fitting vector in the likelihood calculation. For additional details of BMA method see Kwon et al. [51].
Several radiation epidemiological studies have applied the BMA method to account for uncertainties in dose estimation [8, 9, 54]. For example, Land et al. (2015) examined the risk of radiation-related thyroid nodules in individuals who lived downwind from the Semipalatinsk Nuclear Test Site in Kazakhstan and accounted for complex uncertainties in dose estimation by using the BMA method [8]. Compared to conventional regression using a point “best estimate” dose [55], the BMA method increased the ERR per unit dose (ERR/Gy) estimate for the internal exposure, which was considered to have a large amount of shared uncertainties, by more than three times (see Table 2).
Representative studies
Tables 2 and 3 present a selection of representative studies from radiation epidemiology and other environmental epidemiological studies, respectively. The presented studies applied at least one of the four methods to account for exposure estimation errors we reviewed above. Whenever possible, we looked for studies that used multiple statistical methods on same dataset.
In the majority of studies, risk estimates adjusted for exposure estimation uncertainties changed by +/− 100% compared to model without such adjustments, with the exception of two studies (Land et al. (2015) in Table 2 and Wang and Song (2016) in Table 3) that doubled/tripled the naïve risk estimates. Epidemiological textbooks state that random errors in exposure estimation lead to attenuation of exposure-response relationship. Thus, we expect that after accounting for exposure estimation uncertainties, risk estimates should increase. Accounting for Berkson error will usually lead to a wider confidence interval but would not bias risk estimates in linear models because Berkson error is usually caused by group averaging (i.e., E(Dtr| Dest) = Dest) and is considered independent of estimated exposure values. However, in studies presented in Tables 2 and 3, the changes in risk estimates were not always away from the null. This could be due to complex error structures in different datasets or to different statistical methods applied. For example, BMA method works well when shared errors are substantial. However, it might “over-adjust” risk estimates if shared errors are small to only moderate in exposure estimation. Similarly, when shared errors are large, applying regression calibration or SIMEX could lead to “under-adjustment” of the uncertainties in exposure estimate.
Discussion
In this paper, we provided a detailed description of four main methods to account for effects of uncertainties in exposures on exposure-response estimates used in radiation epidemiology (regression calibration, simulation-extrapolation (SIMEX), Monte Carlo maximum likelihood (MCML) and Bayesian model averaging (BMA)). Some of these methods have successfully been applied in several studies of environmental exposures (Table 3).
Regression calibration is easy to perform and works well when E(Dtr| Dest) can be approximated reasonably well (e.g., when validation data or data on an unbiased instrumental variable of exposure are available) or when a linear model is used for risk analysis. For example, linear ERR model is often used in radiation epidemiology to explore dose-response relationships and regression calibration works well for adjustment of risk estimates for uncertainties in exposure estimates. However, it is relatively weak for highly nonlinear models [3] or complex uncertainty structures [54]. For example, in radiation epidemiological studies, a complex uncertainty structure includes shared errors that usually cannot be ignored. However, in regression calibration, the individual exposure vector \( \left({D}_{i1}^{est},\dots, {D}_{iM}^{est}\ \right) \) is treated as a vector of replicated estimates for ith subject and its mean is used as a best estimate of true exposure in regression calibration. In such case, the correlation between subjects (i.e., the shared information) is not accounted for, even if the estimated exposure is obtained from the 2DMC procedure. In other epidemiological studies, such as nutritional studies, shared error is not considered as critical in exposure estimation. Obtaining data from validation studies or data on unbiased instrumental variables is relatively easy in these studies, which makes the calibration function E(Dtr| Dest) much easier to implement. Therefore, regression calibration method is a strong tool for these studies to correct for exposure estimation uncertainties.
Compared to regression calibration, SIMEX does not require an assumption about a distribution of the unknown true exposures and therefore would produce a relatively robust estimator [15]. Also, SIMEX is easy to perform because only a naïve estimator using estimated exposure values is used and no additional data are needed. However, SIMEX estimator can be affected by the variance of error term and the choice of extrapolation functions [37, 50]. We need to know the error variance or be able to estimate it precisely, or the results would not be accurate. SIMEX has the same weakness as the regression calibration method when a complex uncertainty structure is considered, because it also uses the individual exposure vector in the analysis.
In contrast to regression calibration and SIMEX, full-likelihood methods such as MCML and BMA use the possible true exposure vector for the entire cohort \( \left({D}_{1r}^{est},\dots, {D}_{Nr}^{est}\ \right)\ \left(r=1,\dots, M\right) \) in exposure-response analyses, and therefore the shared information between subjects is preserved. Unlike regression calibration and SIMEX methods, which rely on the variance of the error term of exposure estimates, MCML and BMA methods use each vector of exposure estimates as a possible true exposure vector for the entire cohort. However, these methods are computationally intensive and must be applied based on 2DMC exposure estimates. Specifically, MCML estimation is based on values of likelihood on the profile likelihood function at specified grid points (e.g., 100 points) for parameter of interest for each exposure vector. Computational burdens will be large when the number of parameters of interest is more than two since choosing range and grid point is cumbersome and the number of likelihood evaluations will grow exponentially. Meanwhile, different choices of range and grid points for the likelihood evaluation would have an impact on the accuracy of point estimation (i.e., proximity to the true value) and confidence interval estimation. We might not obtain the accurate estimation results from inappropriate choices of range and sparse grid points.
When the shared uncertainties are relatively modest (e.g., [9, 54]), the full-likelihood methods are expected to work similarly to regression calibration. As demonstrated in Table 2, the regression calibration, MCML, and BMA methods had roughly similar results of reduced excess odds ratio per Gy (EOR/Gy) by 13, 2 and 23%, respectively, compared to the EOR/Gy from the models with no adjustment for dose uncertainties in studies of thyroid cancer after the Chornobyl accident [9]. The relatively small amount of shared errors is considered to be the cause of these modest effects from the application of adjustment methods in the exposure-response analyses. Unlike regression calibration and SIMEX methods, for which variance of exposure estimation errors is required, MCML and BMA methods require less information because each exposure estimate vector used in likelihood calculation is a possible true exposure vector for the entire cohort. However, if the shared uncertainties are substantial (e.g., same biased measuring device is applied to a group of people), the full likelihood methods such as MCML and BMA would perform better than regression calibration and SIMEX (see studies by Land et al. (2015) and Stayner et al. (2007), Table 2). The majority of the reviewed studies show relatively moderate changes (within 100%) in risk estimates after accounting for uncertainties in exposure estimates except for the two studies which doubled/tripled the naïve estimates [8, 56]. However, because the majority of risk estimates from studies of environmental exposures only show an excess of risk in exposed over unexposed of less than 100% (relative risks less than 2.0), the error in risk estimates of this magnitude is important. The risk estimates from analyses that do not account for uncertainties in exposure estimates could be significantly biased, and confidence in their accuracy overly optimistic. If analyses accounting for uncertainties in exposure estimates are not feasible, at least the potential effects of uncertain exposure estimates on final results should be discussed in environmental epidemiological studies when risk estimates are reported [5].
Other methods have been developed to account for uncertainties in exposure estimation in epidemiological studies at the stage of data analysis. Zhang et al. (2017) described a corrected confidence interval (CCI) approach to correct inflated variances of risk parameters estimated by the Poisson regression model due to uncertainties in the dosimetry system [57]. The CCI approximates an asymptotic distribution of parameter estimates in Poisson ERR model using multiple exposure vectors from the Monte Carlo dosimetry system. The CCI includes a variance-covariance matrix between multiple exposure vectors and mean exposure vector in the calculation of variances of parameters in the Poisson risk model. If exposure estimation uncertainty is large, then the corrected variances should be larger than the naïve variance estimates, which do not take account of exposure estimation uncertainties. Exposure-response analyses are performed with a mean exposure value of multiple exposure vectors using a regular Poisson ERR model to obtain an unbiased estimate of the risk parameter. Then, CCI is obtained by using corrected variances. The CCI is always wider than that of naïve approach due to the inflated variance estimate.
The CCI approach has a big disadvantage when exposure estimation uncertainties are very large compared to MCML and BMA. When exposure estimation uncertainties are small or moderate, using a variance-covariance matrix between multiple exposure vectors and mean exposure vector reflects uncertainty, since each exposure vector has a very similar goodness-of-fit for the outcome. When exposure estimation uncertainty is large, the variance-covariance matrix between multiple exposure vectors and the mean exposure vector is excessively large and produces an unreasonably wide 95% confidence interval. In this situation, only a few exposure vectors provide a relatively strong goodness-of-fit while most others have a poor goodness-of-fit. Both MCML and BMA take account of this fact, and only a few exposure vectors contribute to the estimation of ERR and corresponding confidence interval. Using the variance-covariance matrix between multiple exposure vectors and the mean exposure vector as proposed by Zhang et al. (2017) does not incorporate this mechanism and thus produces an unnecessarily large variance for the corrected confidence interval.
Another method which has been used to account for uncertainties in exposure estimation at the stage of data analysis is a Multi-Model Inference (MMI) method, e.g. [58,59,60]. In order to avoid a biased result based on a single risk model, the MMI method combines risk estimates from multiple plausible exposure-response models by assigning a weight to each model. This method could provide a comprehensive evaluation of model uncertainties in risk estimates [5]. Conceptually, this method is similar to BMA and MCML in that uncertainty in the use of multiple realizations of possibly true model parameter values used to estimate individual exposure is similar to uncertainty in the use of multiple model structures or equations to estimate exposure.
Conclusions
Although a single type of error may dominate in environmental epidemiological studies, uncertainties in exposure estimates for the entire cohort are often represented by more complex structures. Comprehensive consideration of potential error structures in the exposure estimates is important when developing an exposure estimation protocol because it can lead to improved exposure-response relationship by eliminating biases that can occur when uncertainties are ignored. If the exposure assessment is relatively simple and performed independently across individuals, unshared errors are more likely to be introduced. In such cases, using regression calibration and SIMEX methods with repeated estimates of exposure would work well to account for exposure estimation uncertainties in risk analyses. However, if the exposure assessment requires applying the same measurement device or using the same estimation parameters/models for a group of people, shared uncertainties are more likely to be introduced. In such cases, a more complicated exposure estimation method, i.e., 2DMC, needs to be considered. Although the 2DMC procedure was originally developed for radiation dose reconstruction, it could be easily used in other field of environmental epidemiology. Using exposure estimates from the 2DMC simulations, the MCML and BMA methods are able to account for exposure estimation uncertainties when shared errors are substantial. The methods reviewed in this paper are suitable to account for estimation errors in various situations of uncertain exposure estimates in environmental epidemiology. More analyses of uncertainties in exposure estimation should be conducted and the effects of uncertain exposure estimates on risk estimates should be discussed in environmental epidemiological studies when risk estimates are reported.
Abbreviations
- 2DMC:
-
Two-dimensional Monte Carlo
- AIC:
-
Akaike information criterion
- BIC:
-
Bayesian information criterion
- BMA:
-
Bayesian model averaging
- CCI:
-
Corrected confidence interval
- EOR:
-
Excess odds ratio
- EPA:
-
The U.S. Environmental Protection Agency
- ERR:
-
Excess relative risk
- FFQ:
-
Food frequency questionnaire
- Gy:
-
Gray
- MCMC:
-
Markov chain Monte Carlo
- MCML:
-
Monte Carlo maximum likelihood
- MMI:
-
Multi-model inference
- NRC:
-
National Research Council
- PM:
-
Particulate matter
- SIMEX:
-
Simulation-extrapolation
- Sv:
-
Sievert
References
Merrill RM. Environmental epidemiology: principles and methods. Sudbury: Jones & Bartlett Publishers; 2009.
Pearce N, Blair A, Vineis P, Ahrens W, Andersen A, Anto JM, Armstrong BK, Baccarelli AA, Beland FA, Berrington A, et al. IARC monographs: 40 years of evaluating carcinogenic hazards to humans. Environ Health Perspect. 2015;123(6):507–14.
Carroll RJ, Ruppert D, Crainiceanu CM, Stefanski LA. Measurement error in nonlinear models: a modern perspective. New York: Chapman and Hall/CRC; 2006.
IARC: Monographs on the evaluation of carcinogenic risks to humans. A review of human carcinogens. D. Radiation. In: International Agency for Research on Cancer (IARC) ed., vol. 100 (D). World Health Organization, International Agency for Research on Cancer: Lyon, France; 2012.
United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR): Sources and Effects of Ionizing Radiation. UNSCEAR 2012 Report to the General Assembly. In: (United Nations Scientific Committee on the Effects of Atomic Radiation), editor. Annex B: Uncertainties in risk estimates for radiation-induced cancer. New York: United Nations; 2015.
Gilbert ES. The impact of dosimetry uncertainties on dose-response analyses. Health Phys. 2009;97(5):487.
Simon SL, Hoffman FO, Hofer E. The two-dimensional Monte Carlo: a new methodologic paradigm for dose reconstruction for epidemiological studies. Radiat Res. 2014;183(1):27–41.
Land CE, Kwon D, Hoffman FO, Moroz B, Drozdovitch V, Bouville A, Beck H, Luckyanov N, Weinstock RM, Simon SL. Accounting for shared and unshared dosimetric uncertainties in the dose response for ultrasound-detected thyroid nodules after exposure to radioactive fallout. Radiat Res. 2015;183(2):159–73.
Little MP, Kwon D, Zablotska LB, Brenner AV, Cahoon EK, Rozhko AV, Polyanskaya ON, Minenko VF, Golovanov I, Bouville A. Impact of uncertainties in exposure assessment on thyroid cancer risk among persons in Belarus exposed as children or adolescents due to the Chernobyl accident. PLoS One. 2015;10(10):e0139826.
Hofer E. How to account for uncertainty due to measurement errors in an uncertainty analysis using Monte Carlo simulation. Health Phys. 2008;95(3):277–90.
Smith TJ, Kriebel D. A biologic approach to environmental assessment and epidemiology. New York: Oxford University Press; 2010.
U.S. Environmental Protection Agency (EPA). Exposure factors handbook 2011 edition (Final). Washington, DC: US Environmental Protection Agency; 2011.
National Research Council (NRC). Science and decisions: advancing risk assessment. Washington, DC: National Academies Press; 2009.
Armstrong BG. Effect of measurement error on epidemiological studies of environmental and occupational exposures. Occup Environ Med. 1998;55(10):651–6.
Masiuk S, Kukush A, Shklyar S, Chepurny M, Likhtarov I: Radiation risk estimation: based on measurement error models. Walter de Gruyter GmbH & Co KG; 2017.
Rhomberg LR, Chandalia JK, Long CM, Goodman JE. Measurement error in environmental epidemiology and the shape of exposure-response curves. Crit Rev Toxicol. 2011;41(8):651–71.
Heid I, Küchenhoff H, Miles J, Kreienbrock L, Wichmann H. Two dimensions of measurement error: classical and Berkson error in residential radon exposure assessment. Journal of Exposure Science and Environmental Epidemiology. 2004;14(5):365.
Drozdovitch V, Minenko V, Golovanov I, Khrutchinsky A, Kukhta T, Kutsen S, Luckyanov N, Ostroumova E, Trofimik S, Voillequé P. Thyroid dose estimates for a cohort of Belarusian children exposed to 131I from the Chernobyl accident: assessment of uncertainties. Radiat Res. 2015;184(2):203–18.
Likhtarov I, Kovgan L, Masiuk S, Talerko M, Chepurny M, Ivanova O, Gerasymenko V, Boyko Z, Voillequé P, Drozdovitch V. Thyroid cancer study among Ukrainian children exposed to radiation after the Chornobyl accident: improved estimates of the thyroid doses to the cohort members. Health Phys. 2014;106(3):370.
Simon TW. Two-dimensional Monte Carlo simulation and beyond: a comparison of several probabilistic risk assessment methods applied to a superfund site. Human and Ecological Risk Assessment: An International Journal. 1999;5(4):823–43.
Stayner L, Vrijheid M, Cardis E, Stram DO, Deltour I, Gilbert SJ, Howe G. A Monte Carlo maximum likelihood method for estimating uncertainty arising from shared errors in exposures in epidemiological studies of nuclear workers. Radiat Res. 2007;168(6):757–63.
Stram DO, Kopecky KJ. Power and uncertainty analysis of epidemiological studies of radiation-related disease risk in which dose estimates are based on a complex dosimetry system: some observations. Radiat Res. 2003;160(4):408–17.
Pierce DA, Stram DO, Vaeth M, Schafer DW. The errors-in-variables problem: considerations provided by radiation dose-response analyses of the A-bomb survivor data. J Am Stat Assoc. 1992;87(418):351–9.
Carroll RJ, Stefanski LA. Approximate quasi-likelihood estimation in models with surrogate predictors. J Am Stat Assoc. 1990;85(411):652–63.
Gleser L. Improvements of the naive approach to estimation in nonlinear errors-in-variables regression models. Contemp Math. 1990;112:99–114.
Clayton D. Models for the analysis of cohort and case-control studies with inaccurately measured exposures. In: Statistical models for longitudinal studies of health; 1992. p. 301–31.
Prentice R. Covariate measurement errors and parameter estimation in a failure time regression model. Biometrika. 1982;69(2):331–42.
Armstrong B. Measurement error in the generalised linear model. Communications in Statistics-Simulation and Computation. 1985;14(3):529–44.
Rosner B, Willett W, Spiegelman D. Correction of logistic regression relative risk estimates and confidence intervals for systematic within-person measurement error. Stat Med. 1989;8(9):1051–69.
Rosner B, Spiegelman D, Willett W. Correction of logistic regression relative risk estimates and confidence intervals for measurement error: the case of multiple covariates measured with error. Am J Epidemiol. 1990;132(4):734–45.
Hardin JW, Schmiediche H, Carroll RJ. The simulation extrapolation method for fitting generalized linear models with additive measurement error. Stata J. 2003;3(4):373–85.
Hardin JW, Schmiediche H, Carroll RJ. The regression-calibration method for fitting generalized linear models with additive measurement error. Stata J. 2003;3(4):361–72.
Little M, Hoel D, Molitor J, Boice J Jr, Wakeford R, Muirhead C. New models for evaluation of radiation-induced lifetime cancer risk and its uncertainty employed in the UNSCEAR 2006 report. Radiat Res. 2008;169(6):660–76.
Little MP, Kukush AG, Masiuk SV, Shklyar S, Carroll RJ, Lubin JH, Kwon D, Brenner AV, Tronko MD, Mabuchi K. Impact of uncertainties in exposure assessment on estimates of thyroid cancer risk among Ukrainian children and adolescents exposed from the Chernobyl accident. PLoS One. 2014;9(1):e85723.
Pierce DA, Stram DO, Vaeth M. Allowing for random errors in radiation dose estimates for the atomic bomb survivor data. Radiat Res. 1990;123(3):275–84.
Pierce DA, Væth M, Cologne JB. Allowance for random dose estimation errors in atomic bomb survivor studies: a revision. Radiat Res. 2008;170(1):118–26.
Kukush A, Shklyar S, Masiuk S, Likhtarov I, Kovgan L, Carroll RJ, Bouville A. Methods for estimation of radiation risk in epidemiological studies accounting for classical and Berkson errors in doses. The international journal of biostatistics. 2011;7(1):1–30.
Bennett DA, Landry D, Little J, Minelli C. Systematic review of statistical approaches to quantify, or correct for, measurement error in a continuous exposure in nutritional epidemiology. BMC Med Res Methodol. 2017;17(1):146.
Keogh RH, White IR. A toolkit for measurement error correction, with a focus on nutritional epidemiology. Stat Med. 2014;33(12):2137–55.
Kipnis V, Subar AF, Midthune D, Freedman LS, Ballard-Barbash R, Troiano RP, Bingham S, Schoeller DA, Schatzkin A, Carroll RJ. Structure of dietary measurement error: results of the OPEN biomarker study. Am J Epidemiol. 2003;158(1):14–21.
Ferrari P, Roddam A, Fahey M, Jenab M, Bamia C, Ocké M, Amiano P, Hjartåker A, Biessy C, Rinaldi S. A bivariate measurement error model for nitrogen and potassium intakes to evaluate the performance of regression calibration in the European prospective investigation into Cancer and nutrition study. Eur J Clin Nutr. 2009;63(S4):S179.
Freedman LS, Schatzkin A, Midthune D, Kipnis V. Dealing with dietary measurement error in nutritional cohort studies. J Natl Cancer Inst. 2011;103(14):1086–92.
Prentice RL, Pettinger M, Tinker LF, Huang Y, Thomson CA, Johnson KC, Beasley J, Anderson G, Shikany JM, Chlebowski RT. Regression calibration in nutritional epidemiology: example of fat density and total energy in relationship to postmenopausal breast cancer. Am J Epidemiol. 2013;178(11):1663–72.
Subar AF, Kipnis V, Troiano RP, Midthune D, Schoeller DA, Bingham S, Sharbaugh CO, Trabulsi J, Runswick S, Ballard-Barbash R. Using intake biomarkers to evaluate the extent of dietary misreporting in a large sample of adults: the OPEN study. Am J Epidemiol. 2003;158(1):1–13.
Cook JR, Stefanski LA. Simulation-extrapolation estimation in parametric measurement error models. J Am Stat Assoc. 1994;89(428):1314–28.
Stefanski LA, Cook JR. Simulation-extrapolation: the measurement error jackknife. J Am Stat Assoc. 1995;90(432):1247–56.
Lederer W, Küchenhoof H. A short introduction to the SIMEX and MCSIMEX. R News. 2006;6/4:26–31.
Kumar N. The exposure uncertainty analysis: the association between birth weight and trimester specific exposure to particulate matter (PM2. 5 vs. PM10). International journal of environmental research and public health. 2016;13(9):906.
Alexeeff SE, Carroll RJ, Coull B. Spatial measurement error and correction by spatial SIMEX in linear regression models when using predicted air pollution exposures. Biostatistics. 2016;17(2):377–89.
Allodji RS, Schwartz B, Diallo I, Agbovon C, Laurier D, de Vathaire F. Simulation–extrapolation method to address errors in atomic bomb survivor dosimetry on solid cancer and leukaemia mortality risk estimates, 1950–2003. Radiat Environ Biophys. 2015;54(3):273–83.
Kwon D, Hoffman FO, Moroz BE, Simon SL. Bayesian dose–response analysis for epidemiological studies with complex uncertainty in dose estimation. Stat Med. 2016;35(3):399–423.
Gelfand AE, Smith AF. Sampling-based approaches to calculating marginal densities. J Am Stat Assoc. 1990;85(410):398–409.
Hastings WK. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57(1):97–109.
Little MP, Kwon D, Doi K, Simon SL, Preston DL, Doody MM, Lee T, Miller JS, Kampa DM, Bhatti P. Association of chromosome translocation rate with low dose occupational radiation exposures in US radiologic technologists. Radiat Res. 2014;182(1):1–17.
Land C, Zhumadilov Z, Gusev B, Hartshorne M, Wiest P, Woodward P, Crooks L, Luckyanov N, Fillmore C, Carr Z. Ultrasound-detected thyroid nodule prevalence and radiation dose from fallout. Radiat Res. 2008;169(4):373–83.
Wang CY, Song X. Robust best linear estimator for cox regression with instrumental variables in whole cohort and surrogates with additive measurement error in calibration sample. Biom J. 2016;58(6):1465–84.
Zhang Z, Preston DL, Sokolnikov M, Napier BA, Degteva M, Moroz B, Vostrotin V, Shiskina E, Birchall A, Stram DO. Correction of confidence intervals in excess relative risk models using Monte Carlo dosimetry systems with shared errors. PLoS One. 2017;12(4):e0174641.
Schöllnberger H, Kaiser J-C, Jacob P, Walsh L. Dose–responses from multi-model inference for the non-cancer disease mortality of atomic bomb survivors. Radiat Environ Biophys. 2012;51(2):165–78.
Walsh L, Schneider U. A method for determining weights for excess relative risk and excess absolute risk when applied in the calculation of lifetime risk of cancer from radiation exposure. Radiat Environ Biophys. 2013;52(1):135–45.
Walsh L, Kaiser JC. Multi-model inference of adult and childhood leukaemia excess relative risks based on the Japanese A-bomb survivors mortality data (1950–2000). Radiat Environ Biophys. 2011;50(1):21–35.
International Programme on Chemical Safety (IPCS). Uncertainty and data quality in exposure assessment. In: World Health Organization; 2008.
Edwards JK, Keil AP. Measurement error and environmental epidemiology: a policy perspective. Current environmental health reports. 2017;4(1):79–88.
Hoffmann S, Laurier D, Rage E, Guihenneuc C, Ancelet S. Shared and unshared exposure measurement error in occupational cohort studies and their effects on statistical inference in proportional hazards models. PLoS One. 2018;13(2):e0190792.
Kesminiene A, Evrard A-S, Ivanov VK, Malakhova IV, Kurtinaitis J, Stengrevics A, Tekkel M, Anspaugh LR, Bouville A, Chekin S. Risk of hematological malignancies among Chernobyl liquidators. Radiat Res. 2008;170(6):721–35.
Beulens JW, Rimm EB, Ascherio A, Spiegelman D, Hendriks HF, Mukamal KJ. Alcohol consumption and risk for coronary heart disease among men with hypertension. Ann Intern Med. 2007;146(1):10–9.
Molina-Montes E, Wark PA, Sánchez MJ, Norat T, Jakszyn P, Luján-Barroso L, Michaud DS, Crowe F, Allen N, Khaw KT. Dietary intake of iron, heme-iron and magnesium and pancreatic cancer risk in the European prospective investigation into cancer and nutrition cohort. International journal of cancer. 2012;131(7):E1134.
Beydoun MA, Kaufman JS, Ibrahim J, Satia JA, Heiss G. Measurement error adjustment in essential fatty acid intake from a food frequency questionnaire: alternative approaches and methods. BMC Med Res Methodol. 2007;7(1):41.
Acknowledgements
None.
Funding
This work was supported by the National Cancer Institute/NIH grant R01CA197422 (LBZ).
Availability of data and materials
Not applicable.
Author information
Authors and Affiliations
Contributions
YW and LBZ designed and performed research, analyzed data and wrote the paper. OH, IA and DK contributed to the analysis of data and preparation of the paper. BT and RG participated in the preparation of the paper. All authors reviewed and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Wu, Y., Hoffman, F.O., Apostoaei, A.I. et al. Methods to account for uncertainties in exposure assessment in studies of environmental exposures. Environ Health 18, 31 (2019). https://doi.org/10.1186/s12940-019-0468-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12940-019-0468-4