Abstract
Background
Sample size planning for longitudinal data is crucial when designing mediation studies because sufficient statistical power is not only required in grant applications and peer-reviewed publications, but is essential to reliable research results. However, sample size determination is not straightforward for mediation analysis of longitudinal design.
Methods
To facilitate planning the sample size for longitudinal mediation studies with a multilevel mediation model, this article provides the sample size required to achieve 80% power by simulations under various sizes of the mediation effect, within-subject correlations and numbers of repeated measures. The sample size calculation is based on three commonly used mediation tests: Sobel’s method, distribution of product method and the bootstrap method.
Results
Among the three methods of testing the mediation effects, Sobel’s method required the largest sample size to achieve 80% power. Bootstrapping and the distribution of the product method performed similarly and were more powerful than Sobel’s method, as reflected by the relatively smaller sample sizes. For all three methods, the sample size required to achieve 80% power depended on the value of the ICC (i.e., within-subject correlation). A larger value of ICC typically required a larger sample size to achieve 80% power. Simulation results also illustrated the advantage of the longitudinal study design. The sample size tables for most encountered scenarios in practice have also been published for convenient use.
Conclusions
Extensive simulations study showed that the distribution of the product method and bootstrapping method have superior performance to the Sobel’s method, but the product method was recommended to use in practice in terms of less computation time load compared to the bootstrapping method. A R package has been developed for the product method of sample size determination in mediation longitudinal study design.
Similar content being viewed by others
Background
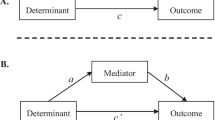
Mediation analysis is a statistical method that helps researchers to understand the mechanisms underlying the phenomena they study. It has broad application in psychology, prevention research, and other social sciences. A simple mediation framework (see Fig. 1) involves three variables: the independent variable, dependent variable and mediating variable [4, 27]. The aim of mediation analysis is to determine whether the relation between the independent and dependent variables is due, wholly or in part, to the mediating variables. Since the seminal work of Baron and Kenney [4], extensive research has been conducted in mediation analysis, including that of [7, 22, 25]; [34]; and [18], among others. A comprehensive review of mediation analysis can be found in the book by [27].
When planning a mediation study, the investigator commonly determines the required sample size. An appropriately chosen sample size is critical for the success of the study. If the sample size is too small, the study may lack adequate statistical power to detect an effect size of practical importance, which leads the investigator to incorrectly conclude that an efficacious intervention is inefficacious. Reviews of the psychological literature suggest that insufficient statistical power is a common problem in psychological studies [1, 29, 30]. On the other hand, an unnecessarily large sample size is wasteful and increases the duration of the study. Because of the importance of sample size, funding agencies such as the National Institutes of Health routinely require investigators to justify the sample size for funded projects.
Unfortunately, sample size determination is not straightforward for mediation analysis. No simple formula is available to carry out this task. Using Monte Carlo simulations, Fritz and MacKinnon [14] investigated power calculations for the simple mediation model and provided guidance in choosing sample sizes for mediation studies with independent data. Their results, however, are not applicable to longitudinal studies, in which data are correlated.
A longitudinal study design is common in psychological and social research [13]. Compared with a cross-sectional study design, the longitudinal design requires fewer subjects and allows investigators to study the trajectory of each subject. In longitudinal studies, repeated measures are collected from each subject over time. Since measures collected from the same subject are more likely to be similar when compared to those collected from other subjects, data from the same subject tend to be correlated. Analyzing such correlated data requires special statistical methods, such as the multilevel model [33]. In this article, assuming a multilevel mediation model and using Monte Carlo simulation, we investigate sample size determination for longitudinal mediation studies. Our objective is to provide practical guidance and easy-to-use R software to help researchers determine the sample size when designing longitudinal mediation studies.
Methods
This section starts by formulating single-level mediation model, then multilevel mediation model for longitudinal data is described. We focus on lower-level multilevel mediation model and relevant model assumptions are discussed.
Simple single-level mediation model
Let Y denote the dependent (or outcome) variable, X denote the independent variable, and M denote the mediating variable (or mediator). A single-level mediation model (Fig. 1) can be expressed in the form of three regression equations:
where β c quantifies the relation between the independent variable and dependent variable (i.e., the total effect of X on Y); \( {\beta}_{c^{\prime }} \) quantifies the relation between the independent variable and dependent variable after adjusting for the effect of the mediating variable (i.e., the direct effect of X on Y adjusted for M); β b quantifies the relation between the mediating variable and dependent variable after adjusting for the effects of the independent variable; β a measures the relation between the independent variable and mediating variable; β01, β02, and β03 are intercepts; and ε1, ε2, and ε3 are error terms that follow normal distributions with mean 0 and respective variances of \( {\sigma}_1^2,{\sigma}_2^2 \), and \( {\sigma}_3^2 \).
The mediation effect can be defined by two ways: β c − βc' and β a β b [16, 17, 27]. For the single-level mediation model, the two definitions of the mediation effect are equivalent [28], but they are generally different in the multilevel mediation models we will describe.
Multilevel mediation model for longitudinal data
For correlated longitudinal data, the simple mediation model, which assumes independence of observations, is not appropriate. Using the single-level mediation model for longitudinal data leads to biased estimates of standard errors and confidence intervals [3].
Multilevel mediation modeling is a powerful technique for analyzing mediation effects in longitudinal data. Multilevel models assume that there are at least two levels in the data, an upper level and a lower level. The lower-level units (e.g., repeated measures) are often nested within the upper-level units (e.g., subjects). Assuming that the lower-level units are random, also known as random effects, multilevel models appropriately account for correlations among the observations from the same subject, and yield valid statistical inference. For a comprehensive coverage of multilevel modeling techniques, see the book by Raudenbush & Bryk [33].
The multilevel mediation model is much more complex than the single-level model because mediation effects can occur at the different model levels. Two kinds of mediation, upper-level mediation and lower-level mediation, can be distinguished in the context of multilevel mediation models [5]. In upper-level mediation, the initial causal variable for which the effect is mediated is an upper-level variable. In lower-level mediation, the mediator is a lower-level variable. Krull [21] and MacKinnon [22] offered examples of upper-level mediation, while [18] studied lower-level mediation, in which the mediation links varied randomly across the upper-level units. In this study, we focus on a specific type of lower-level mediation model (Fig. 2) that is appropriate for analyzing longitudinal studies. In this model, an initial variable X is mediated in the lower level (i.e., measurement level), but the mediator M and outcome Y are affected by upper-level (i.e., subject level) variations. A simple scenario for this model is a longitudinal experimental study in which subjects are randomly assigned to a treatment (time-invariant) or the multiple treatments can be assigned to a same subject in cross-over design (i.e., initial variable X, in this paper, variable X is treated as time-varying), and mediating variable M, such as a psychosocial measure, is believed to change individual behavior (i.e., dependent variable Y) over time.
The lower-level mediation model
Let X ij , Y ij , and M ij denote the independent variable, dependent variable, and mediating variable, respectively, for the ith observation from the jth subject. The lower-level mediation model in Fig. 2 can be expressed in the form of the following two-level regression equations,
where at the lower (or within-subject) level, similar to the simple single-level mediation model, β c measures the total effect of the independent variable on the dependent variable; βc' measures the direct effect of the independent variable on the dependent variable, adjusted for the mediating variable; β b measures the effect of the mediating variable on the dependent variable, adjusted for the independent variable; β a measures the effect of the independent variable on the mediating variable; and β01j, β02j, and β03j are subject-specific intercepts that differ from subject to subject, as reflected by the subscript j in these parameters. These subject-specific intercepts are also known as random intercepts. The terms ε1ij, ε2ij, and ε3ij are lower-level (or within-subject) error terms that follow normal distributions with a mean of zero and respective variances \( {\sigma}_1^2,{\sigma}_2^2 \), and \( {\sigma}_3^2 \). At the upper (or between-subject) level γ1, γ2, and γ3 are overall or population average intercepts; and u1j, u2j, and u3j are upper-level (between-subject) error terms that follow normal distributions with a mean of zero and respective variances \( {\tau}_1^2,{\tau}_2^2 \), and \( {\tau}_3^2 \).
In the multilevel model, the upper-level errors induce within-subject correlations. Let y ij and \( {y}_{i^{\prime_j}} \) denote the i-th and i′-th measures for the same subject j, then y ij and \( {y}_{i^{\prime_j}} \) are correlated as
Such within-subject correlation is often measured by the intraclass correlation coefficient (ICC), which is defined as
Under the above two-level mediation model, the value of ICC for Y is given by
Larger values of ICC represent strong within-subject correlations, i.e., measures from the same subject are more similar. When ICC = 0, measures from the same subject are independent.
Due to the within-subject correlation, the two definitions of the mediation effects, β c − βc' and β a β b , are generally not equivalent in multilevel models [21], although they are equivalent in the single-level mediation model. The different behaviors of multilevel and single-level models are caused by the fact that the weighting matrix used to estimate the multilevel model is typically not identical to single-level equations. The non-equivalence between β c − βc' and β a β b , however, is unlikely to be problematic because the difference between the two estimates is typically small and unsystematic and tends to vanish at large sample sizes [21]. In this article, we focus on β a β b as the measure of the mediation effect.
Test of the mediation effect
As the independence assumption is violated, conventional statistical methods, such as the ordinary least squares method, are not appropriate for estimating the multilevel mediation model. Instead, maximum likelihood methods and/or empirical Bayes methods are typically used. Let \( {\widehat{\beta}}_a \) and \( {\widehat{\beta}}_b \) denote the maximum likelihood estimates of β a and βb, respectively. Then, the maximum likelihood estimate of the mediation effect is given by \( {\widehat{\beta}}_a{\widehat{\beta}}_b \). To test whether the mediation effect β a β b equals zero, three approaches can be taken.
Sobel’s method
Sobel’s method is a widely used test of the mediation effect, based on the first-order multivariate delta method [35, 36]. In this approach, assuming \( {\widehat{\beta}}_a \)and \( {\widehat{\beta}}_b \)are independent, the standard deviation of \( {\widehat{\beta}}_a{\widehat{\beta}}_b \) is estimated by
where \( {\widehat{s}}_{\beta_a}^2 \)and \( {\widehat{s}}_{\beta_b}^2 \)are the squared standard errors of \( {\widehat{\beta}}_a \) and \( {\widehat{\beta}}_b \), respectively. The 100(1-α)% confidence interval (CI) of the mediation effect is given by
where z1 − α/2 is the (1 − α/2)th quantile of the standard normal distribution. If α = 0.05, the familiar 95% CI results. If this CI does not contain zero, we reject the null hypothesis and conclude that the mediation effect is statistically significant.
Sobel’s method relies on the assumption that \( {\widehat{\beta}}_a{\widehat{\beta}}_b \), the product of two normal random variables \( {\widehat{\beta}}_a \) and \( {\widehat{\beta}}_b \), is normally distributed. However, several studies have shown that the distribution of the product of two normal random variables is not actually normal, but skewed [23]. The violation of the normality assumption compromises the performance of Sobel’s method and leads to invalid CIs [26]. To address this problem, [26] discussed several improved CIs that account for the fact that \( {\widehat{\beta}}_a{\widehat{\beta}}_b \) is not normally distributed, including the CI based on the distribution of the product of two normal random variables and the CI based on the bootstrap method [6, 34].
Distribution of the product method
Instead of assuming the normality of \( {\widehat{\beta}}_a{\widehat{\beta}}_b \), the distribution of the product method proposed by MacKinnon and Lockwood (2001) constructs the CI of the mediation effect based on the distribution of the product of two normal random variables. Although such a distribution does not take a simple closed form, Meeker et al. [31] provided tables of critical values for this distribution that can be used to construct the CI. Alternatively, the critical values can also be obtained based on the empirical distribution of the product of two normal random variables through Monte Carlo simulations. Let δ lower and δ upper denote critical values that correspond to the lower and upper bounds of the CI, then the CI of the mediation effect is given by
Bootstrap method
Another approach for constructing the CI without imposing a normal assumption on \( {\widehat{\beta}}_a{\widehat{\beta}}_b \) is the bootstrap method [11]. The bootstrap method, based on resampling, is useful for finding the standard error and forming CIs for estimates when their sampling distributions are unknown. In this study, we use the percentile bootstrap [6] to construct the CI for the mediation effect. We repeatedly resample the original data with replacement, obtaining the so-called bootstrap samples. For each of the bootstrap samples, we estimate the mediation effect using the maximum likelihood method. These estimates form the empirical distribution of the mediation effect. Let qα/2 and q1 − α/2 denote the (α/2)th and (1 − α/2)th percentiles of this empirical distribution; then the 100(1 − α)% CI of the mediation effect is given by
When conducting bootstrap resampling for the multilevel mediation model, in principle, we should resample both the upper-level (subjects) and lower-level (measures) units. However, in a multilevel context, we should be careful of not breaking the structure of the dataset, therefore, a resampling scheme for multilevel models must take into account the hierarchical data structure. There are three approaches can be applied to bootstrap two-level models: the parametric bootstrap, the residual bootstrap, and the cases bootstrap. We chose the cases bootstrap since it requires minimal assumptions of hierarchical dependency in the data being assumed to be specified correctly. de Leeuw & Meijer [9] suggest that when the number of lower-level units (measures) is small, the approach of resampling only the upper level and keeping the lower level intact yields more accurate estimates. In our simulation, the number of lower-level units is small (i.e., 2 to 5), thus we only resampled the upper-level units. To be specific, the algorithm for cases bootstrap is as follows:
-
1.
Draw a sample of size J with replacement from the upper level units; that is, draw a sample {\( {j}_k^{\ast },k=1,\cdots, J \)} (with replacement) of upper level numbers.
-
2.
For each k, draw a sample of entire cases, with replacement, from (the original) upper level unit \( j={j}_k^{\ast } \). This sample has the same size \( {n}_k^{\ast }={n}_{j_k^{\ast }}={n}_j \) as the original unit from which the cases are drawn. Then, for each k, we have a set of data {(\( {Y}_{ik}^{\ast },{X}_{ik}^{\ast },{M}_{ik}^{\ast } \)),\( i=1,\cdots, {n}_k^{\ast } \)}.
-
3.
Compute estimates for all parameters of the two-level model.
-
4.
Repeat steps 1–3 B times.
Simulation study
We conducted a simulation study to determine the sample size that is needed to achieve 80% power when using Sobel’s method, the distribution of the product method, and the bootstrap method for longitudinal mediation studies. In our simulation, we varied three factors. The first one is the effect size of the mediation effect \( {\widehat{\beta}}_a{\widehat{\beta}}_b \). We considered four values of β a and β b : 0.14, 0.26, 0.39 and 0.59, respectively corresponding to smaller, medium, halfway (between medium and large), and large effect sizes. These values yielded 16 combinations of effect sizes of the mediation effect. Another factor is the ICC. We considered five values of ICC, 0.1, 0.3, 0.5, 0.7 and 0.9, to cover various within-subject correlations from low to high. The last factor is the number of repeated measures. We considered 2, 3, 4 and 5 repeated measures for each subject. For other parameters, we set the overall interceptsγ2and γ3 as zero. Since there were no repeated measurements in Fritz et al. [14] and the samples were all drawn from a standard normal distribution, for fair comparisons, we set marginal variances of Y ij and M ij , that is, \( {\sigma}_2^2+{\tau}_2^2 \) and \( {\sigma}_3^2+{\tau}_3^2 \), as 1. Based on the definition of ICC, we have\( {\tau}_2^2={\tau}_3^2= ICC \).
To simulate data, we first simulated the independent variable X from the standard normal distribution, then generated random intercepts β02j and β03j according to eqs. (7) and (9). Conditional on the values of β02j and β03j, we generated the dependent variable Y and mediating variable M according to eqs. (6) and (8).
To determine the power of the three test methods, under each of the parameter settings, we generated 1000 simulated datasets, and applied the methods to each of the datasets to test the mediation effect. We calculated the power of the methods as the proportion of tests that rejected the null hypothesis of no mediation effects, i.e., the CI excluded zero. For the bootstrap method, we based the construction of the CI on 500 bootstrap samples.
To determine the sample size that yields 80% power, we started with an initial guess of the sample size. If we found the power achieved with that sample size to be too low, we increased the sample size; and if we found the power to be too high, we decreased the sample size. We repeated this procedure until the sample size allowed us to reach the level of power nearest to 80%.
Results
Tables 1, 2, 3, 4 and 5 show the sample sizes necessary to achieve 80% power under five different ICCs (ICC = 0.1, 0.2, 0.4, 0.6, 0.9). For completeness, results with other ICCs, say, 0.3, 0.5, 0.7, and 0.8, are also shown, which can be found in the Additional file 1: Tables S1- S4, respectively. In each table, the 16 mediation effect sizes are denoted by two letters, with the first one referring to the size of β a , and the second letter referring to the size of β b . We use S for small (0.14), M for medium (0.39), L for large (0.59) and H for halfway (0.26) between large and medium effect sizes, e.g., the effect size ML indicates β a = 0.39 and β b = 0.59.
Among the three methods of testing the mediation effects, Sobel’s method required the largest sample size to achieve 80% power. Bootstrapping and the distribution of the product method performed similarly and were more powerful than Sobel’s method, as reflected by the relatively smaller sample sizes. For instance, when the mediation effect size was medium (i.e., SM) and the ICC was 0.2, with 4 repeated measures, Sobel’s method required 191 subjects to achieve 80% power, whereas the distribution of the product and bootstrap methods required 188 and 185 subjects, respectively, to achieve the same power.
For all three methods, the sample size required to achieve 80% power depended on the value of the ICC (i.e., within-subject correlation). A larger value of ICC typically required a larger sample size to achieve 80% power. For example, under the design with two repeated measures and using the distribution of the product method, to detect a small effect size of SS, a sample size of 299 was needed when ICC = 0.1, while a sample size of 420 was needed when ICC = 0.4.
Simulation results also illustrated the advantage of the longitudinal study design. Compared with the results reported by Fritz and MacKinnon [14] for the cross-sectional study, the required sample size under the longitudinal design was substantially smaller. When the ICC was low, such as 0.1, the required sample size under the longitudinal study design was a fraction of that under the cross-sectional design, and was approximately equal to the sample size of the cross-sectional study divided by the number of repeated measures. For example, under the longitudinal design with three repeated measures and using the distribution of the product method, the sample size under the longitudinal design was 215 to detect a small effect size of SS, which was approximately one-third of that required under the cross-sectional design (667). Even when the ICC was relatively high, we still observed dramatic sample size savings. For example, when ICC = 0.6 and using the bootstrap method, to detect the mediation effect size SM, the cross-sectional design required 422 subjects, while the longitudinal design with 4 repeated measures only required 351 subjects. This observation is in accordance to findings in literatures [19].
Figure 3 shows the type I error rates for the sample sizes corresponding to 5 examples of zero mediation effects when ICC = 0.3 for three repeated measures. A parameter combination of zero/zero (ZZ) had error rates around zero for all numbers of observations and sample sizes across the mediation tests. The distribution of the product method had the most precise rates; whereas Sobel’s method had less type I error probability and bootstrapping inflated the error rates in the case of a zero/0.59 (ZL) parameter, as with small sample sizes. However, the rates approached 0.05 when the number of sample sizes increased. Other scenarios taking various ICCs and repeated measures showed results similar to those in Fig. 3 and they are not shown in the paper.
Discussion
Assuming a two-level mediation model and using Monte Carlo simulations, we determined the sample sizes required to achieve 80% power for longitudinal mediation studies under various practical settings. The simulation results provide guidance for researchers when choosing appropriate sample sizes in the design of longitudinal mediation studies. Our simulations also show that the distribution of the product and bootstrap methods are more powerful than Sobel’s method for testing the mediation effect. In addition, the required sample size is closely related to the ICC. A high ICC generally requires a larger sample size to detect a given effect size. The simulation results show that when the ICC is high, above 0.8 for instance, the required sample sizes in these scenarios are close to the values provided in Fritz et al. [14], suggesting that we should choose cross-sectional studies instead of longitudinal studies since the former is relatively easy to conduct but does not lose power. However, in real studies, especially in psychotherapy clinical trial studies, a meta-analysis of ICCs found that ICCs varied widely, ranging from 0 to 0.729, with an average around 0.08 [8]. Similar results have been found in clinical trial data [12, 20] and clinical practice data [24, 32, 37]. In studies in the field of education, small ICCs are also common [15], with 0.20 as a median value.
Another interesting finding for multilevel mediation is that the power of testing the mediation effect depends on not only the overall value of the mediation effects β a β b , but also the values of the individual regression coefficients β a and β b . For instance, the sample size required to detect the effect size of LS is different from that required to detect the effect size SL. In other words, the sample size depends on the position of the effect sizes. Such a “positioning” effect for testing the mediation effect in multilevel mediation depends on the ICC. A high ICC leads to a stronger positioning effect. For example, in Table 5, when ICC = 0.9, detecting the effect size SL requires 568 subjects, while detecting the effect size LS only requires 213 subjects. The positioning effect does not appear in the single-level mediation model, which can be viewed as an extreme case of the multilevel model with ICC = 0. In the single-level mediation model, the required sample size (or power) only depends on the value of β a β b , but not the individual values of β a and β b [14]. For example, the number of subjects needed to detect the effect size LS was equal to that required to detect the effect size SL. The different behavior of multilevel mediation compared to single-level mediation is due to the within-cluster correlation in the multilevel model. Therefore, when conducting power calculations for longitudinal mediation studies, in addition to the mediation effect β a β b , it is equally important to report the effect size of β a and β b .
Our simulation studies showed that the bootstrap and the distribution of the product methods have similar performance in testing the mediation effect. However, as the bootstrap is much more computer-intensive and time-consuming, we recommend using the distribution of the product method in practice. One limitation is that in the paper, coefficients β c , β a , β b and βc′ in the model were treated as fixed-effects coefficients only. More flexible model by treating these as random-effects variables and two-level random-slopes model can also be considered. Another limitation is that in practice, effects size estimates are just estimates, not the true values, so uncertainty needs to be considered in the effect size estimates for sample size planning. Interested readers can consult the papers by [2, 10] for more information. There is a recent paper [38] discusses power and sample size for mediation model in longitudinal studies, however, in their model, the mediator was assumed to be time-invarying instead of time-variant in our research.
Conclusion
Mediation analysis using longitudinal data allows researchers to investigate biological pathways and identifies their direct and indirect contribution to interested outcome variable. However, though this method is common in psychological and social research, sample size determination is still a challenging problem. This paper gives a way of using multilevel model for longitudinal data to provide the sample size under various sizes of the mediation effect, within-subject correlations and numbers of repeated measures via simulations by using three methods, Sobel, distribution of product and bootstrap. We found that the bootstrap and distribution of the product methods had comparable results and were more powerful than the Sobel’s method in terms of relatively smaller sample sizes. We recommend to use the distribution of product method due to its less computational load. For the mediation model of longitudinal data, the sample size depended on the ICC (i.e., the intra-subject correlation), number of repeated measurements, “position” of β a and β b . Sample size tables for commonly encountered scenarios in practice were also provided for researchers’ convenient use.
References
Abraham WT, Russell DW. Statistical power analysis in psychological research. Soc Personal Psychol Compass. 2008;2(1):283–301.
Anderson SF, Maxwell SE. Addressing the "replication crisis": using original studies to design replication studies with appropriate statistical power. Multivar Behav Res. 2017:1–20.
Barcikowski R. Statistical power with group mean as the unit of analysis. J Educ Stat. 1981;6:267–85.
Baron RM, Kenny DA. The moderator-mediator variable distinction on social psychological research: conceptual, strategic, and statistical considerations. J Pers Soc Psychol. 1986;51:1173–82.
Bauer DJ, Preacher KJ, Gil KM. Conceptualizing and testing random indirect effects and moderated mediation in multilevel models: new procedures and recommendations. Psychol Methods. 2006;11:142–63.
Bollen KA, Stine R. Direct and indirect effects: classical and bootstrap estimates of variability. Sociol Methodol. 1990;20:115–40.
Collins LM, Graham JW, Flaherty BP. An alternative framework for defining mediation. Multivar Behav Res. 1998;33:295–312.
Crits-Christoph P, Mintz J. Implication of therapist effects for the design and analysis of comparative studies of psychotherapies. J Consult Clin Psychol. 1991;59:20–6.
de Leeuw J, Meijer E. Handbook of multilevel analysis. New York: Springer; 2008.
Du H, Wang L. A Bayesian power analysis procedure considering uncertainty in effect size estimates from a meta-analysis. Multivar Behav Res. 2016;51(5):589–605.
Efron B. Bootstrap methods: another look at the jackknife. Ann Stat. 1979;7:1–26.
Elkin I, Falconnier L, Martinovich Z, Mahoney C. Therapist effects in the NIMH Treatment of Depression Collaborative Research Program. Psychother Res. 2006;16:144–60.
Frees EW. Longitudinal and panel data: analysis and applications in the social sciences. Cambridge: Cambridge University Press; 2004.
Fritz MS, Mackinnon DP. Required sample size to detect the mediated effect. Psychol Sci. 2007;18:233–9.
Hox JJ. Multilevel analysis: techniques and applications. Mahwah, NJ: Erlbaum; 2002.
Judd CM, Kenny DA. Estimating the effects of social interventions. Cambridge: Cambridge University Press; 1981a.
Judd CM, Kenny DA. Process analysis: estimating mediation in treatment evaluations. Eval Rev. 1981b;5:602–19.
Kenny DA, Korchmaros JD, Bolger N. Lower level mediation in multilevel models. Psychol Methods. 2003;8:115–28.
Killip S, Mahfoud Z, Pearce K. What is an Intracluster correlation coefficient? Crucial concepts for primary care researchers. Ann Fam Med. 2004;2(3):204–8. https://doi.org/10.1370/afm.141
Kim D-M, Wampold BE, Bolt DM. Therapist effects in psychotherapy: a random effects modeling of the NIMH TDCRP data. Psychother Res. 2006;16:161–72.
Krull JL, MacKinnon DP. Multilevel mediation modeling in group-based intervention studies. Eval Rev. 1999;23:418–44.
Krull JL, Mackinnon DP. Multilevel modeling of individual and group level mediated effects. Multivar Behav Res. 2001;36:249–77.
Lomnicki ZA. On the distribution of product of random variables. J R Stat Soc. 1967;29:513–24.
Lutz, Wolfgang; Leon, Scott C.; Martinovich, Zoran; Lyons, John S.; Stiles, William B. Therapist effects in outpatient psychotherapy: a three-level growth curve approach. J Couns Psychol, Vol 54(1), Jan 2007, 32–39.
MacKinnon DP, Dwyer JH. Estimating mediated effects in prevention studies. Eval Rev. 1993;17:144–58.
MacKinnon DP, Lockwood CM, Williams J. Confidence limits for the indirect effect: distribution of the product and resampling methods. Multivar Behav Res. 2004;39:99–128.
MacKinnon DP. Introduction to statistical mediation analysis. New York: Lawrence Erlbaum Associates; 2008.
MacKinnon DP, Warsi G, Dwyer JH. A simulation study of mediated effect measures. Multivar Behav Res. 1995;30:41–62.
Maxwell SE. The persistence of underpowered studies in psychological research: causes, consequences, and remedies. Psychol Methods. 2004;9(2):147.
Maxwell SE, Kelley K, Rausch JR. Sample size planning for statistical power and accuracy in parameter estimation. Annu Rev Psychol. 2008;59:537–63.
Meeker WQ Jr, Cornwell LW, Aroian LA. The product of two normally distributed random variables. In: Kennedy WJ, Odeh RE, editors. Selected tables in mathematical statistics, vol. VII. Providence, RI: American Mathematical Society; 1981.
Okiishi J, Lambert MJ, Nielsen SL, Ogles BM. Waiting for Supershrink: an empirical analysis of therapist effects. Clinical Psychology and Psychotherapy. 2003;10:361–73.
Raudenbush SW, Bryk AS. Hierarchical linear models: applications and data analysis methods. 2nd ed. Newbury Park, CA: Sage; 2002.
Shrout PE, Bolger N. Mediation in experimental and nonexperimental studies: new procedures and recommendations. Psychology Methods. 2002;7:422–45.
Sobel ME. Asymptotic confidence intervals for indirect effects in structural equation models. Sociol Methodol. 1982;13:290–312.
Sobel ME. Direct and indirect effects in linear structural equation models. Sociological Methods and Research. 1987;16:155–67.
Wampold BE, Brown GS. Estimating variability in outcomes attributable to therapists: a naturalistic study of outcomes in managed care. J Consult Clin Psychol. 2005;73:914.
Wang C, Xue X. Power and sample size calculations for evaluating mediation effects in longitudinal studies. Stat Methods Med Res. 2016 Apr;25(2):686–705.
Acknowledgements
The authors thank the associate editor and two reviewers for very insightful and constructive comments that substantially improved the article.
Funding
Yuan’s research was partially supported by grants CA154591, CA016672, and 5P50CA098258 from the National Cancer Institute. Miao’s research was partially supported by Military Health Care Key Projects during the Twelfth Five-year Plan Period. The above funds supported the authors to conduct statistical analysis, program code for producing results and write the manuscript and interpret the results.
Availability of data and materials
Not applicable.
Author information
Authors and Affiliations
Contributions
HP: idea for the study, programming, interpretation of results, writing of manuscript. YY: idea for the study, results checking, interpretation of results, writing of manuscript. SL: idea for the study, interpretation of results, writing of manuscript. DM: interpretation of results, writing of manuscript. All authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Ethics approval and consent to participate
Not applicable. This work contains no human data.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Additional file
Additional file 1:
Estimated numbers of required subjects with ICC = 0.3, 0.5, 0.7 and 0.8. (DOCX 27 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Pan, H., Liu, S., Miao, D. et al. Sample size determination for mediation analysis of longitudinal data. BMC Med Res Methodol 18, 32 (2018). https://doi.org/10.1186/s12874-018-0473-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12874-018-0473-2