Abstract
Background
It is important to quantify the dose response for a drug in phase 2a clinical trials so the optimal doses can then be selected for subsequent late phase trials. In a phase 2a clinical trial of new lead drug being developed for the treatment of rheumatoid arthritis (RA), a U-shaped dose response curve was observed. In the light of this result further research was undertaken to design an efficient phase 2a proof of concept (PoC) trial for a follow-on compound using the lessons learnt from the lead compound.
Methods
The planned analysis for the Phase 2a trial for GSK123456 was a Bayesian Emax model which assumes the dose-response relationship follows a monotonic sigmoid “S” shaped curve. This model was found to be suboptimal to model the U-shaped dose response observed in the data from this trial and alternatives approaches were needed to be considered for the next compound for which a Normal dynamic linear model (NDLM) is proposed. This paper compares the statistical properties of the Bayesian Emax model and NDLM model and both models are evaluated using simulation in the context of adaptive Phase 2a PoC design under a variety of assumed dose response curves: linear, Emax model, U-shaped model, and flat response.
Results
It is shown that the NDLM method is flexible and can handle a wide variety of dose-responses, including monotonic and non-monotonic relationships. In comparison to the NDLM model the Emax model excelled with higher probability of selecting ED90 and smaller average sample size, when the true dose response followed Emax like curve. In addition, the type I error, probability of incorrectly concluding a drug may work when it does not, is inflated with the Bayesian NDLM model in all scenarios which would represent a development risk to pharmaceutical company.
The bias, which is the difference between the estimated effect from the Emax and NDLM models and the simulated value, is comparable if the true dose response follows a placebo like curve, an Emax like curve, or log linear shape curve under fixed dose allocation, no adaptive allocation, half adaptive and adaptive scenarios. The bias though is significantly increased for the Emax model if the true dose response follows a U-shaped curve.
Conclusions
In most cases the Bayesian Emax model works effectively and efficiently, with low bias and good probability of success in case of monotonic dose response. However, if there is a belief that the dose response could be non-monotonic then the NDLM is the superior model to assess the dose response.
Similar content being viewed by others
Background
An ongoing and serious challenge facing the pharmaceutical industry is the high failure rate in the late phase of drug development [1]. It has been reported that approximately 50% of Phase 3 clinical trials fail and the main explanations are the wrong dose being selected or poor understanding of the dose response in Phase 2 trials [1, 2]. Therefore, it is critical to identify the correct dose in Phase 2 clinical trials to improve the Phase 3 success rate and thus increase research and development productivity [3, 4].
An assessment of dose response normally starts with a linear or nonlinear regression of a drug response for given doses [5]. Many biological activities follow a 4-parameter logistic model, and the Emax model is a special case of the 4-parameter logistic model [3]. Among the possible dose response models, Emax model is one of the most widely applied models relating drug concentrations to effects [3]. In practice, the Emax model assumes the drug effect is proportional to the dose, i.e. the bigger the dose, the bigger the effect. Thomas et al. [6] showed that majority of dose response models in the dose response of small molecule compounds were Emax models based on dose response curves from a single company and there were two cases reported a likely U-shaped dose response that Emax model failed to fit [6].
As the name implies a U-shaped dose response is a dose response where there is a down-turn of the clinical dose-response relationship at higher doses. In the context of the problem being investigated, we had a prior belief from a lead compound, where a U-shaped dose response was observed, that the dose response for the follow-on compound in the same drug class may also be U-shaped. For this reason, a U-shaped dose-response is considered to be pharmacologically plausible for the follow-on compound as well as for the reason that a U-shaped dose response had been seen in other biological treatments for RA [7,8,9,10].
There are a number of dose response models available to handle the non-monotonic U-shaped dose response relationships [4]. One alternative is the Normal Dynamic Linear Model (NDLM) which originated in time series modelling and is a method for model smoothing using information borrowed from neighbouring doses [11]. Berry [12] then proposed the NDLM model for the adaptive designs and in the post-herpetic neuralgia trial, Smith et al. [13] applied a Bayesian NDLM model to a pharmaceutical drug trial where patients were randomised to a dose based on the dose response model estimated from a posterior distribution. A Bayesian NDLM model was also used in an Acute Stroke Therapy by Inhibition of Neutrophils (ASTIN) trial [14]. In the ASTIN trial patients were allocated 1 of 15 doses, or a placebo, adaptively based on the response and the study allowed for early termination for efficacy or futility based on posterior probability using a Bayesian NDLM model. In the ASTIN trial, a Markov chain Monte Carlo approach was used to derive a posterior distribution for the model parameters which informed the estimation of the ED95. In addition, there have been other applications of NDLM model such as in in phase 2/3 study for dose selection of diabetes drug development [15].
For the study being planned there was an interest in the comparisons of both Emax model and NDLM models for the dose response assessment in a Phase 2a trial in patients with rheumatoid arthritis (RA). The Phase 2a trial was initially designed to investigate the treatment effect of different dose levels of GSK123456, using Bayesian Emax model which was used to guide the Bayesian analysis in searching for the dose levels targeting at ED90 for future cohorts. The compound later failed since a U-shaped like curve was observed in the dose response. The Emax model makes an assumption of a monotonic dose response relationship which was seemed to be violated in this trial.
A follow-on compound GSK654321, which is in the same drug class of GSK123456, is in development. The chance for GSK654321 having a U-shaped curve cannot be ruled out, therefore the emphasis of this manuscript is to find a suitable dose response model and design for future Phase 2a design of GSK654321, which would provide reasonable design operating characteristics under both monotonic dose response and non-monotonic dose response. In the following section, two main statistical models (Emax and NDLM) for estimating a dose response relationship are described and compared in a Phase 2a trial in patients with rheumatoid arthritis (RA). Also to use extensive simulations to show how the two models perform under a fixed and adaptive designs under a variety of assumed dose-response profiles with a focus on U-shaped response curve, a pharmacologically plausible dose response curve in GSK654321.
Methods
Background of clinical trials in RA patients
A primary endpoint of a typical Phase 2 clinical trial is the change from baseline in DAS28 score. DAS28 is a measure of disease activity score and the number 28 refers to the 28 joints that are examined in this assessment.
To calculate the DAS28 [16], a clinician will:
-
1.
count the number of swollen joints (out of the 28);
-
2.
count the number of tender joints (out of the 28);
-
3.
take blood to measure the erythrocyte sedimentation rate (ESR) or C reactive protein (CRP);
-
4.
ask the patient to make a ‘global assessment of health’ (indicated by marking a 10 cm line between very good and very bad).
The results from these four domains are then combined to produce an overall disease activity score ranging from 2 to 10, with a higher score indicating more disease activity. A DAS28 of greater than 5.1 implies active disease, less than 3.2 low disease activities, and less than 2.6 as remission.
Bayesian Emax model
The Emax model is a widely applied model relating drug concentrations to effects [3] and was planned for the analysis of dose response in the Phase 2a trial.
The Emax model is written as
where ΔDAS28 is the change in DAS28 score from baseline at day 56 post-randomisation, E0 is the basal effect corresponding to the response when the drug dose is equal to 0, Emax is the maximum achievable increase or decrease over placebo response, ED50 is the dose which produces 50% of the effect. All the doses were half-log spaced at design stage with exception of 20 mg/kg. The maximum dose level across the study cohorts is 30 mg/kg. The 30 mg/kg dose is the maximum tolerated dose for the study based on prior studies. If the posterior mean of ED90 exceeded 30 mg/kg, the maximum planned dose of 30 mg/kg is used. The priors of model parameters E0 and Emax follow a Normal distribution with large variance i.e. N(0,1E4) and the prior distribution of ED50 are N(3,1E2). The prior on σ2 is an inverse gamma distribution (IG(0.5,0.7). Markov Chain Monte Carlo (MCMC) were used to simulate the posteriors distribution: 2500 samples were used to estimate the model parameter after burn-in of 500. A larger burn-in was run and didn’t significantly improve the model fitting and estimation parameters.
The parameters of interest for the Emax model can be estimated by maximum likelihood estimation (MLE) and Bayesian methods – we chose this approach as Bayesian statistics [17] integrates information into the computation of the posterior probability of parameters, using the accumulated data observed so far for later doses and prior information for the early doses. In addition, the parameters from Bayesian method are displayed as distributional profile - which can be useful to illustrate uncertainty - and offer a robust estimation of parameters in complicated model [17].
Bayesian normal dynamic linear model (NDLM)
A NDLM can be used to fit to estimate the dose-response relationship. The description of the NDLM used in the analysis is shown below,
where ΔDAS28 is the observed individual change in DAS28 score from baseline at day 56 post-randomisation at Dosej. The likelihood of DAS28 at day 56 change from baseline follows a Normal distribution with mean (θj) for each Dosej and with variance of σ2, the Dosej is assumed to be spaced equally. θj is the estimated treatment effect at Dosej. Furthermore, θj has a linear relationship with neighboring θj−1 with intercept θj−1 and slope of δj−1. θ1 is the untreated or placebo response when the drug dose is equal to 0 and both θ1 and δ1 follow Normal distributions. Similar to Emax model, the coefficients for the NDLM model can be estimated from maximum likelihood methods [18] and Bayesian methods – we used the Bayesian NDLM method because Bayesian methods offer robust estimation of parameters with complicated models and provides better model fitting in both monotonic and non-monotonic dose response [17].
The prior distribution on θ has a vague Normal distribution with a large variance estimated from inverse-gamma distribution (IG(0.5, 72). The prior distributions on σ2 and the evoluation variance σθ 2 and σδ 2 are inverse-gamma distribution (IG(0.5, 72).
Motivating study
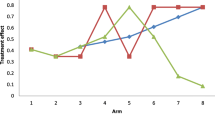
An initial Phase 2a Proof-of-concept (PoC) study was undertaken to demonstrate whether a new drug, GSK123456, achieves a certain level of pre-designated efficacy at a planned dose in RA [19]. The first part (Part A) of this PoC study was a learning phase with single dose escalation using a cohort randomised trial [19]. Patients were randomised within each cohort to either placebo or an active dose of GSK123456. Only the starting dose in cohort 1 was pre-defined and subsequent doses for other cohorts were selected using a Bayesian dose response Emax model [19]. A U-shaped dose response curve for DAS28 change from baseline was observed with the highest response at 3 mg/kg (Fig. 1). A consequence of this was the estimation of ED90 was suboptimal with higher variability.
Mean and estimated dose response of mean change in DAS28 scores from baseline using Bayesian Emax and NDLM models. The mean changes in DAS28 score between the doses were connected with a straight line in solid blue lines; the data are for illustration purpose so the error bars are not presented. Emax model is displayed as red dash/dotted line and NDLM model as green dotted line
A dose response in a new class of compound or target is generally unknown due to the biology and is not well understood, especially the drug is never being tested in healthy volunteers or patients. Further pharmacokinetic and pharmacodynamics data suggests the U-shaped curve may be due to moderate binding affinity and rapid off-rate of GSK123456 as compared to the higher affinity OSM receptor causing a protein carrier effect [19].
The follow-on compound GSK654321 is in the same drug class. It binds to the same binding site as GSK123456 and it is believed to have therapeutic properties but with higher potency. Therefore, the chance of U-shaped dose response cannot be ruled out. It is important to highlight however that Emax was the pre-specified analysis. Given the U-shaped curves being pharmacologically plausible in the follow-on compound GSK654321, there is a strong desire to compare and adopt a more flexible model, such as NDLM model, to handle both monotonic and non-monotonic dose response in the design and analysis consideration.
We have observed how Emax model was suboptimal in modelling the dose response. We then applied a model – NDLM – retrospectively, we know should work for the observed data and then demonstrated it was superior. For NDLM to be prospectively planned for GSK654321 there is need first to do further evaluations of its properties in the context of a RA PoC study design in the possible presence of non-monotonicity.
In next sections, we will explore the NDLM model, to compare the performance of the Emax model and the NDLM under various assumptions about the shape of the dose response curves - flat curve, Emax like curve, Log-linear curve and U-shaped curve.
Simulation
Dose response models in the evaluation
For the simulations four true dose response profiles (Fig. 2) are used for the primary endpoint, change in DAS28 score from baseline to day 56, to mimic the wide range of dose response scenarios likely to be observed and be analysed as dose response methods in clinical practice. In all models, the placebo effect (on the background of MTX) was set to be −0.5. That is a change in DAS28 score from baseline to day 56 post-randomisation of −0.5 points i.e. a small decline/improvement is disease activity. The error term ε was assumed to be independently Normally distributed with a mean of 0 and a variance of 1.44 for Emax, Log linear and U-shaped curve, which was the estimated variance from PoC study of GSK123456 (Fig. 2), the error term has variance 0.25 for placebo like response.
Profile 1 | Flat curve: ΔDAS28 = −0.5 + ε |
Profile 2 | Emax curve:y ΔDAS28 = −0.5–1.7*Dose/(2.5 + Dose) + ε, ED50 is 2.5. |
Profile 3 | Log linear curve: ΔDAS28 = −0.5 -log(Dose + 1) + ε |
Profile 4 | U-shaped curve: ΔDAS28 follows a predefined U shaped curve with: ΔDAS28 = (−0.5,-0.7,-1.6,-1.8,-1.2,-1, −0.6) for dose 0, 0.03, 0.3, 3, 10, 20, and 30 mg/kg respectively. |
The four true Dose-response profiles used in the simulations. The model profiles include a placebo like flat curve which is denoted in blue and is fixed at −0.5 for all dose levels, a dose proportional Emax model in red, a log-linear model in green, and a U-Shaped model in purple. The label for the vertical axis is the change in DAS28 score from predose at day 56 post-randomisation
These four profiles were chosen as plausible dose responses for the new compound in development GSK654321 ranging from a null effect (Profile 1) to what was previously observed with GSK123456 (Profile 4).
The scenarios of fixed design simulation and adaptive design simulation are discussed in the next section. The two basic designs set up are a fixed design and an adaptive design. The fixed design assumes that all six doses and placebo are allocated to a fixed number of patients. No adaptations are adopted in this design. In the adaptive design, the subjects are allocated according to the dose responses of all the subjects enrolled in the study.
Design of the Simulation Study
The range of doses is between 0.03 mg/kg to 30 mg/kg. The design is a parallel design and the total target sample size is 64. The goal of the trial is to characterise the dose-response curve at various doses. The fixed design assumes that all 6 doses are allocated to a fixed number of patients with no interim analysis or adaptation of the dose. In the adaptive simulation, the subjects are allocated due to the subjects’ response in the study at the end of each cohort.
Decisions regarding success and futility of the trial at completion are made based on the probability of DAS28 relative to control greater than clinically significant difference (a decrease of 0.95 as measured by DAS28 change from baseline between placebo and treatment). The positive difference of placebo and treatment is used to facilitate the positive effect and probability calculation. All the designs except fixed scenarios include 8 cohorts, with 8 patients in each cohort (2 on placebo and 6 on active treatment).
An adaptive design was used in the PoC design of GSK123456 and is considered as a better option than fixed design since it increases the chance of stopping a failed compound and expediting a good one as well as potentially maximizing the information on the doses which are most interest to carry forward for later development. For GSK654321 the study design has not been finalised. The wish therefore was to evaluate modelling the dose response using NDLM or Emax for different options for the study design which we have detailed. The follow-on compound GSK654321 is in the same drug class as GSK123456 which demonstrated good safety and tolerability in the PoC study [19], so there is no single dose escalation planned for the PoC study in GSK654321.
ED90 is defined as the dose to achieve 90% of maximum DAS28 response with the lower dose chosen if there are multiple values. In this calculation the maximum response is estimated from the maximal DAS28 effect at all doses. The 90% (ED90) of maximum response is then calculated as the lowest nominal dose in which is closest to the estimated dose that achieves 90% of maximal efficacy. The following fixed design as well as adaptive design scenarios are considered in the design options and evaluations.
Scenario 1 | Fixed design; the design is non-adaptive, the study allocates 8 patients to receive doses of GAK654321 (0.03, 0.3, 3, 10, 20 and 30 mg/kg) and 16 patients to receive placebo. There is no interim stopping and adaptation in the fixed design. The evaluation of final success will occur at the end of the study. |
Scenario 2 | No adaptive allocation; the ratio of patients (100% of the planned sample size) randomized into each study dose (placebo, 0.03, 0.3, 3, 10, 20 and 30 mg/kg) are 2:1:1:1:1:1:1. The placebo is given to a fixed proportion of the sample size allocation to ensure there is enough power for treatment comparisons vs. placebo. There are a total of 8 cohorts (6 treated +2 placebo) and the interim analysis will occur between cohorts, for example, at 8 patients, 16 patients, 24 patients, 32 patients (50%), 40 patients (62.5%) and 48 patients (75%) enrolled and complete the primary endpoint assessment (day 56 post-randomisation DAS28 score). The study is evaluated with the interim study success and interim study futility. |
Scenario 3 | Half adaptive, the first 50% of subjects are fixed allocated using pre-defined allocation ratio of treatments and placebo followed by adaptive allocation for the rest of the subjects based on the posterior distribution of dose around ED90; the placebo is given to a fixed proportion of the sample size allocation to ensure we have enough power for treatment comparisons vs. placebo. The fixed proportion is 25% of the total sample size. For each study dose (0.03, 0.3, 3, 10, 20 and 30 mg/kg), the 4 patients (50% of the planned sample size) will be randomized first, prior to any interim analysis. The dose response curve will then be fitted using the dose response model and ED90 is estimated. For each subject randomised into the study afterwards, the dose level will be randomized to the dose close to the ED90 dose response. The interim analysis will occur at 32 patients (50%), 40 patients (62.5%) and 48 patients (75%) that complete the primary endpoint assessment. The study is evaluated for interim study success and interim study futility. |
Scenario 4 | Adaptive allocation after the first cohort. In the fully adaptive simulation, the placebo is given a fixed proportion of the sample size allocation to ensure there is enough power for treatment comparisons vs. placebo. The fixed proportion is 25% of the total sample size. The dose response curve will be fitted using the dose response model and ED90 is estimated. For each subject randomised into the study afterwards, the dose level will be randomized to the dose close to ED90 dose response. The interim analysis will occur between cohorts, for example, at 8 patients, 16 patients, 24 patients, 32 patients (50%), 40 patients (62.5%) and 48 patients (75%) enrolled and complete the primary endpoint assessment. The study is evaluated for interim study success and interim study futility. |
The simulation and analysis are performed using a data simulation and analysis software - FACTs (Fixed and Adaptive Clinical Trial Simulator) version 2.1 and 4.05 developed by Tessella and Berry Consultant. Simulated data are fitted using similar Emax model and NDLM models as described in Eqs. 1 and 2. It is possible that the choice of informative prior impacts the simulation results [20], for consistency and comparison purpose, a vague prior is chosen in the calculation and simulation. The priors for the Emax model parameters Eo and Emax are vague and follow a Normal distribution with large variance. Thus, the prior of model parameter E 0 is N(0,1E4) and the prior distribution of ED50 is N(3,1E2). The vague prior distribution of evolution variance for NDLM model is inverse-gamma distribution (IG(0.5, 72). Additionally, selected informative priors are explored in the simulations. The simulation starts with fixed seed and all results are based on 5000 simulations. The number of simulations and number of MCMC simulations as 2500 with burn-in of 500 are chosen based on the estimated minimum precision.
Decision criteria in adaptive design simulation
Decision criteria for interim success, interim futility, final success and final futility in the adaptive design simulation are displayed in Table 1. For the fixed design, the final success is based on at least 95% posterior probability that the dED90 dose achieves a drug effect greater than the control or placebo, otherwise it is final futility. For all other adaptive design (scenario 2, 3, and 4), the decision criteria of the interim success, interim futility, final success and futility are presented in Table 1.
When there is truly is no effect or a placebo like effect, the Type I error rate is calculated based on the chance of rejecting the null hypothesis (when it is true). In the context of this simulation it would also be the chance of incorrectly accepting that the drug has a dose response, the false positive rate, and the statistical bias.
Results
Design comparisons using simulation
The results from the simulations giving the probability of interim and final success and failure in fixed design (S1), no adaptive allocation (S2), half-adaptive (S3) and fully adaptive (S4) using Bayesian Emax model and NDLM model are displayed in Table 2.
For Emax like true dose response, the total probability of success is 98% and 98% in fixed design; 93% vs. 91% in No-Adaptive Allocation design, 99% vs. 97% under Half Adaptive scenario and 95% vs. 96% under Adaptive Allocation scenario for Emax and NDLM models respectively. The average sample sizes in the trials are less in the No-Adaptive Allocation design, half adaptive and adaptive design than fixed design. Similar results and trends are also shown for log linear dose response curve.
The Type I error is inflated in Bayesian NDLM model in all scenarios under the current prior. The higher Type I error could potentially lead to a false investment decision and further work when a compound does not truly have an effect. Though the inflation of type I error rate is not a regulatory risk for a Phase 2a study it is a potential risk to the sponsor. The Phase 2a study is still an investigative study so the consequences risks are less and once the final study design is established the simulations will need to be reinvestigated with the decision criteria (as described in Table 1) set so the Type I error is controlled.
Table 3 displays the additional operating characteristics of the model fitting to the data that were analysed using the Emax model and NDLM model for Half Adaptive (S3) design. The proportion of times the dose being selected as ED90 are displayed with each of the four curves. The ED90 of the true Emax curve is likely to be between 20 and 30 mg/kg. Similar results for No adaptive (S2) and fully adaptive (S4) are presented in Additional file 1: Table S1 and Table S2 respectively.
Results from the simulations show that the Bayesian Emax model is able to find the correct dose for ED90 almost 100% of time (proportion of ED90 as 20 and 30 mg/kg) when the true response is either an Emax curve or log linear curve, comparing to approximately 61%–83% using Bayesian NDLM model. If the true dose response relationship is assumed to follow a U-shaped curve, the proportion of simulations selecting the ED90 as 0.3 and 3 mg/kg are 0% vs 82% in non-adaptive design, 0% vs 90% in Half-adaptive setting and 0% vs 91% in Adaptive setting using Emax model and NDLM model respectively when the true ED90 is around 2.5 mg/kg. NDLM is able to identify the correct ED90 doses 58% or 76% of the time when the true response is an Emax or log linear curve respectively.
All the simulated results seem to indicate that the Emax model performs better when the dose responses are monotonic and the NDLM model is a more robust approach in all four types of model and is superior to identify the correct ED90 doses when the true response followed a U−shaped curve.
In earlier comparisons of the Emax and NDLM models, the same decision rules were applied and to assess the type I errors. To facilitate for a fair comparison of power without the need for recalibrating type I error at each design, Receiver Operating Characteristic curves (ROC curve) for the fixed design (S1) and half-adaptive (S3) are presented in Figs. 3 and 4 respectively. The ROC curves draw a plot of the true positive rate against the false positive rate for the different possible decision criteria. Since any increase in sensitivity is accompanied by a decrease in specificity, the ROC shows the tradeoff between sensitivity and specificity. For each design, the true positive rates from Bayesian Emax and NDLM model at assumed U-shaped, Emax or Loglinear curves are plotted against the corresponding false positive rates from flat curve. The closer the curve follows the left border and the top border of the ROC space, it shows the better sensitivity given specificity. Similar ROC curves for non-adaptive (S2) and adaptive (S4) design are presented in supplemental material.
Receiver operating characteristic ROC curve display the true positive rate (statistical power) and false positive rate for Bayesian Emax (red) and NDLM model (blue) under Fixed design (S1). Bayesian Emax (blue dashed line) and NDLM model (red solid line) and dose response following a U-Shaped, b Emax or c Loglinear curve
Receiver operating characteristic ROC curves display the true positive rate (statistical power) and false positive rate for Bayesian Emax (red) and NDLM model (blue) under Half adaptive design (S3). Bayesian Emax (blue dashed line) and NDLM model (red solid line) and dose response following a U-Shaped, b Emax or c Loglinear curve
Under half adaptive design, the ROC curve of Bayesian Emax model is closer to the left and top borders than NDLM model when the assumed curves follow Emax or loglinear curves, so Emax model performs better. When the type I error rate is at 5%, the true positive rate of to Bayesain Emax model is approximately at 97% for both Emax curve and loglinear curve and the true positive rate is 90% and 85% for both Emax curve and loglinear curve using NDLM model. For U-shaped curve, the Bayesian NDLM model performed better than Emax model. The results are in line with earlier conclusion that Emax model outperforms if dose response is monotonical and NDLM model is better when the dose response is U-shaped.
Assessment of bias
The assessment of statistical bias through simulation at each dose level (placebo, 0.03, 0.3, 3, 10, 20, and 30 mg/kg) is calculated as the difference in the estimated mean response using Emax or NDLM models against the assumed true response profile (at each dose level). The difference from the true dose response profile is estimated for each simulation. The mean difference - and bias - is taken as the mean difference for the dose response from the truth across all 5000 simulations.
The Bayesian Emax model is compared to the NDLM model under four profiles of true dose response being Emax curve (Fig. 3a), flat curve (Fig. 3b), log linear curve (Fig. 3c), and U-shaped curve (Fig. 3d) for each of the four design scenarios: fixed design, no adaptive (S2), half adaptive (S3) and fully adaptive (S4).
Under the fixed design and no adaptive allocation and assumption of true dose response as Emax like curve (Fig. 5a) or log linear (Fig. 5c) shape curve, there is less bias (absolute bias) of mean response at lower dose levels using the NDLM model in comparison to the Bayesian Emax model. The bias using Emax model is less if the true dose response data follow a placebo like response (Fig. 5b) than NDLM model and the absolute values of all bias are less than 0.02. If the true dose response curve is a U Shaped non-monotonic curve (Fig. 5d), the bias is much bigger at 0.3 mg/kg and 3 mg/kg if analysing using the Emax model (0.6510 in Emax model vs. -0.0062 at 0.3 mg/kg in the NDLM model; 0.7523 in Emax model vs. 0.0155 at 3 mg/kg in the NDLM model), since the Emax model makes the assumption of monotonic changes and still fits the line between the lowest dose and highest dose, ignoring the U-shaped response.
The statistical bias based on the fixed Design and design with adaptations. The statistical bias is based on each planned dose group (placebo, 0.03, 3, 10, 20, and 30 mg/kg) under four scenarios of design setting as fixed design, no adaptive (Scenario 2), half adaptive (Scenario 3) and fully adaptive (Scenario 4). The true dose responses follow dose profiles of a: Emax curve; b: flat curve; c: log linear curve and d: U-shaped curve
Under the half adaptive allocation design and the assumption of true dose response as an Emax like curve or log linear shape curve, similar to fixed design, there are less bias (absolute bias) of mean response at lower dose levels but more bias at 20 mg/kg using the NDLM model in comparison to the Bayesian Emax model. The individual bias from each dose level shows that Emax model tends to underestimate the dose response effect while NDLM tends to overestimate the effect in the mean response. The bias using Emax model is less if the true dose response data follow a placebo like response than NDLM model and the absolute values of all bias are less than 0.06. If the true dose response curve is a U-Shaped non-monotonic curve, the bias is much bigger at 0.3 mg/kg and 3 mg/kg if analysing using the Emax model (0.7182 in Emax model vs. 0.0656 at 0.3 mg/kg in the NDLM model; 0.8835 in Emax model vs. 0.0992 at 3 mg/kg in the NDLM model) for the same reason described earlier.
Under the fully adaptive allocation design and the assumption of the true dose response as an Emax like curve, the bias of the Bayesian Emax model and NDLM model is similar. The individual bias from each dose level shows that Emax model tends to underestimate the mean response effect at 0.03, 0.3 and 30 mg/kg while NDLM tends to overestimate the effect at 3 and 20 mg/kg in the mean response. The biases are also similar if the true dose response data follow a log linear curve and Emax model tends to underestimate the mean response while NDLM tends to overestimate the mean response. NDLM model also overestimate the mean response if the true response is placebo like curve. If the true dose response curve is a U-Shaped non-monotonic curve, the bias is much bigger at 0.3 mg/kg and 3 mg/kg if analysing using the Emax model (0.8013 in Emax model vs. 0.1170 at 0.3 mg/kg in the NDLM model; 0.9678 in Emax model vs. 0.1553 at 3 mg/kg in the NDLM model).
Amongst all the designs, a hybrid approach of half adaptive design with fixed allocation at 50% subjects before any adaptive allocation seems to have the most reasonable operating characteristics and will be considered to carry forward for GSK654321. To further explore the impact of the analysis methods additional simulations were undertaken to examine the impact of choice of informative priors but anchored in the single half adaptive design (S3). The results for the Emax model are given below in Table 4.
The probability of success, as measure of posteriors probability of treatment effect (difference between treatment and placebo) greater than zero, increased in all dose response curves with 100%, 99, 59% success if the dose response follows a Emax model, Loglinear model and U-shaped curve. The type I error rate is inflated to 8% in Emax model with the informative prior. This inflated type I error rate would need to be communicated to the study team who may consider this to be too high a development risk.
Additional simulations for the NDLM model were performed to examine the impact of informative prior on the half adaptive design (S3) and are displayed below with two prior choices a) the evolution variance has prior of Inverse Gamma (IG) distribution (IG(0.5,0.5)) and b) IG(2,4).
The additional simulations seem to show that the NDLM model fitting is sensitive to the choice of evolution variance and the probably of success and type I error are impacted by the choice of priors such that with an informative prior, type I error was reduced to as low as 7% with little impact of the probability of success in other dose response curve. These considerations need to be weighed up by the study team. If the Type I error is important then the priors may be further investigated to reduce these to an acceptable level.
To compare the goodness of model fitting, deviance information criteria (DIC) results were calculated for both Emax and NDLM model based on dataset from single simulation in Half adaptive design. DIC was penalized for overfitting with additional parameters in the model. The DIC for NDLM model was 181.1 in comparison to 187.0 for Emax model, which further showed that there was no overfitting in NDLM model.
Summary of model comparison: Emax model versus NDLM model
If dose response follows a monotonic response i.e. Emax or log linear curve, both Bayesian Emax and NDLM models have good operating characteristic in the probability of success at interim and final analysis. However, a Bayesian Emax model performs better with higher probability of success than NDLM model in all the scenarios.
If the dose effects change non-monotonically in a U-shaped dose response curve, the power measured as the probability of success of the Bayesian Emax model is 26% vs 92% using the NDLM model in fixed design, 24% vs 80% in No-adaptive design, 16% vs 88% in Half-Adaptive design and 24% vs 86% in Adaptive design. The NDLM model significantly improves the probability of success compared to the Emax model in all four design simulations.
Under the same decision criteria, the Type I error rates are elevated to 12% for half-adaptive or fully adaptive scenario and to 18% for a non-adaptive scenario when analysing using the NDLM model, while the type I error is generally under control below 5% using Emax model. An inflated Type I error rate signals that the NDLM model is over-sensitive and is thus inflating the number of false positive trials. When controlling Type I error, it was shown from ROC curves that the statistical power is 8–10% lowers in NDLM model if the dose response follows Emax or Loglinear curves but much better in case of U-shaped curve. Analysis of the NDLM model led to a significant increase in the statistical power of detecting the treatment difference, when the true dose response is non-monotonic, compared to the Bayesian Emax Model. The probability of success using NDLM model was similar regardless of which underlying true dose-response profile was assumed, but less sensitivity in the analysis of selecting the dose response of ED90 and an increase in the statistical bias, compared to the Bayesian Emax model. The Bayesian Emax model excelled with a higher probability of selecting ED90 and a smaller average sample size, when the true dose response followed Emax like curve, compared to NDLM model.
Though there were some variations, the bias is comparable if the true dose response follows a placebo like curve, Emax like curve, or log linear shape curve under the no adaptive allocation, half adaptive and adaptive scenarios. The bias for Emax is significantly increased if the true dose response is assumed to follow a U-shaped non-monotonic curve.
Discussion
Due to the fact that the results for a PoC RA study of a drug in the same class followed a U-shaped dose response there was a wish to investigate if the analysis could be improved for a new compound in development. Of particular interest, in context with the development for GSK654321, the NDLM model was able to maintain the probability of success even in the case of a non-monotonic dose response.
We were conscious that the design of GSK654321 was driven by a single study for a lead compound, GSK123456, the analysis of which seemed to show a U-shaped dose response and the U-shaped dose response was deemed pharmacologically plausible [19]. Given the limitations of the NDLM model when the response is not U-shaped we decided to undertake further investigations of the U-shaped dose response in a literature review to assess the likelihood - based on the literature - of seeing this dose response relationship. It is shown that it is plausible to observe a U-shaped curve in the study with RA patients [21, 22]. Thomas et al. [6] showed that in the majority of cases the observed means could be well described using a Bayesian Emax model and Emax is one of the best models to estimate the dose response if data follows Emax curve, however, while biological exposure response relationships are often monotonic, down-turns of the clinical dose-response relationship at higher doses have been observed, one example in biologics development is the immunogenicity observed at high dose in the patients treating with biologicals. Therefore, we recommend to routinely consider a U-shaped dose-response model unless U-shaped profiles can be excluded with certainty at the trial design stage.
The work in this manuscript was inspired by the PoC design of the follow-on compound after the U-shaped curve was found in earlier clinical trial, which Bayesian Emax model was used. We aim to compare it with a more flexible NDLM model in the PoC design of the follow-on compound. Systematic literature search was conducted in the databases Google scholar, PubMED and web of science (WoS) and there was limited existing Literature in the comparison of Emax and NDLM model. Work by Jane Temple [23, 24] was deemed relevant but, within the parameters of the simulation undertaken by the authors although the research of Temple was of interest the work could not be generalised to the study being planned and described in this paper. This work demonstrated that both Bayesian NDLM model and Emax model detect a dose response well but Bayesian NDLM tends to have the highest power in the probability of detecting a clinical response than Emax model in the non-monotonical dose response.
It was also shown in the research of Temple that Bayesian NDLM tended to underestimate the response at lower doses, therefore resulting in higher doses being selected, however, our simulation showed a similar or better model fitting in Bayesian NDLM model than Emax model within the context of Phase 2a design. In addition, we found out that the adaptive design being proposed seemed to perform better with smaller average sample size but there was little difference in different allocation methods using NDLM model. These results agree with the finding in Temple [23, 24].
It has been reported that a Bayesian logistic model, especially with hierarchical longitudinal modelling with unbounded priors, often does not converge well [25, 26], posing a significant risk to dose escalation analysis. However, the NDLM model is a good alternative to the Emax model at the expense of pharmacological meaning in model parameters like maximal response Emax and ED50. This is to use an alternative, less complicated, modelling such as the linear model, power model etc. or a non-parametric model, such as the spline model or NDLM model. This will reduce the risk of non-convergence. A more Informative distribution on priors that constrain the parameter space to reasonable values would help the convergence for both models [27].
The main cause for concern with NDLM was the inflation of the Type I error. To minimise this problem, the decision criteria or informative prior may need to be adjusted to control the Type I error if the same decision rules are used in the comparison. After controlling for the type I error rate at 5%, the statistical powers of Emax model are ~8% higher than that of NDLM models in Emax and Log-linear dose responses, which was further supported by ROC results. The NDLM model works better when dose response follows U-shaped curve. Further work would be required therefore for any individual study to optimise the design characteristics. It is also acknowledged that NDLM model did not have high specificity in finding ED90 compared with the Emax model when the data follow Emax model.
It should be noted that the methods described in this paper were anchored in a single RA example with the simulations and results presented only applicable to this case study which motivated our work. This is of particular importance if different dose responses are anticipated or are of importance for an evaluation. Even for this case study there would be a need for further work once the study design has been finalised. In cases where a U-shaped curve is expected or there is potential physiological/pharmacological rationale of down-turn response, Bayesian NDLM model is generally recommended and this conclusion can be generalized to other case studies. In addition, our methods of evaluation in finding the best design could be generalised to other clinical trials to offer a solution to expedite drug development.
Conclusion
An adaptive design, especially a half-adaptive design, is more a efficient design than a fixed design due to an increased chance of a dose being selected being the ED90 dose and due to the reduced s average sample size being use in the clinical trial. In most cases the Bayesian Emax model works effectively and efficiently, with low bias and good probability of success when there is a monotonic dose response. However, if there is a belief that the dose response could be non-monotonic based on prior knowledge as in our case study - where a compound in the same class seemed to have non-monotonic dose responses - then the NDLM is the superior model to assess the dose response. Within the parameters of the simulation the NDLM model was shown to be flexible with the ability to handle a wide variety of dose-responses, including monotonic and non-monotonic relationships.
Abbreviations
- ASTIN:
-
Acute stroke therapy by inhibition of neutrophils
- CRP:
-
C reactive protein
- DAS28:
-
Disease activity score based on 28 joints
- ESR:
-
Erythrocyte sedimentation rate
- FACTs:
-
Fixed and adaptive clinical trial simulator
- MCMC:
-
Markov chain Monte Carlo
- NDLM:
-
Normal dynamic linear model
- PoC:
-
Proof-of-concept
- R&D:
-
Research and development
- RA:
-
Rheumatoid Arthritis
- WoS:
-
Web of Science
References
Hay M, Thomas DW, Craighead JL, Economides C, Rosenthal J. Clinical development success rates for investigational drugs. Nat Biotechnol. 2014;32(1):40–51.
Arrowsmith J, Miller P. Trial watch: phase II and phase III attrition rates 2011-2012. Nat Rev Drug Discov. 2013;12(8):569.
Pinheiro JC, Bretz F, Branson M. Analysis of Dose–Response Studies—Modeling Approaches in Dose Finding in Drug Development 2006. New York: Springer; p.146–171.
FDA Draft Guidance. Dose response information to support drug registration. 1994.
Ting N. Dose Finding in Drug Development. New York: Springer-Verlag; 2006.
Thomas N, Sweeney K, Somayaji V. Meta-analysis of clinical dose–response in a large drug development portfolio. Stat Biopharmaceutical Res. 2014;6:302–17.
Calabrese EJ, Baldwin LA. U-shaped dose-response in biology, toxicology and public health. Annu Rev Public Health. 2001;22:15–33.
Reynolds AR. Potential Relevance of Bell-Shaped and U-Shaped Dose-Responses for the Therapeutic Targeting of Angiogenesis in Cancer. Dose-Response. 2010;8(3):253–284.
Owen SC, Doak AK, Ganesh AN, Nedyalkova L, McLaughlin CK, Shoichet BK, Shoichet MS. Colloidal drug formulations can explain “bell-shaped” concentration–response curves. ACS Chem Biol. 2014;9(3):777–84.
Almstrup K, Fernández MF, Petersen JH, Olea N, Skakkebaek NE, Leffers H. Dual effects of phytoestrogens result in u-shaped dose-response curves. Environ Health Perspect. 2002;110(8):743–8.
West M, Harrison PJ. Bayesian forecasting and dynamic models. New York: Springer-Verlag; 1997.
Berry DA, Mueller P, Grieve AP, Smith MK, Parke T, Krams M. Bayesian designs for dose-ranging drug trials. Case studies in Bayesian statistics. 2002; v5. Springer-Verlag, New York, 99-181.
Grieve, AP, and Krams, M, 2005. ASTIN: a Bayesian adaptive dose-response trial in acute stroke. Clinical trials (London, England), 2(4), pp.340–351-358, 364–378.
Smith MK, Jones I, Morris MF, Grieve AP, Tan K. Implementation of a Bayesian adaptive design in a proof of concept study. Pharm Stat. 2006;5(1):39–50.
Skrivanek Z, Berry S, Berry D, Chien J, Geiger MJ, et al. Application of adaptive design methodology in development of a long-acting glucagon-like Peptide-1 analog (Dulaglutide): statistical design and simulations. J Diabetes Sci Technol. 2012;6(6):1305–18.
Fransen J, Stucki G, et al. Rheumatoid arthritis measures. Disease activity score (DAS), disease activity Score-28 (DAS28), rapid assessment of disease activity in rheumatology (RADAR), and rheumatoid arthritis disease activity index (RADAI). Arthritis & Rheumatism. 2003;49:S214–24.
Carlin BP, Louis, TA. Bayesian Methods for Data Analysis (Third Edition). Boca Raton, Florida: Chapman and Hall/CRC; 2008.
Newman KB. Modelling Population Dynamics: Model Formulation, Fitting and Assessment Using State-space Methods. New York: Springer-Verlag; 2014.
Choy EH, Bendit M, McAleer D, Liu F, Feeney M, Brett S, Zamuner S, Campanile A, Toso J. Safety, tolerability, pharmacokinetics and pharmacodynamics of an anti- oncostatin M monoclonal antibody in rheumatoid arthritis: results from phase 2 randomized, placebo-controlled trials. Arthritis Res Ther. 2013;15(5):R132.
Spiegelhalter DJ, Abrams KR and Myles JP, Bayesian Approaches to Clinical Trials and Health-Care Evaluation. Hoboken, New Jersey: John Wiley & Sons; 2004.
Stohl W, Merrill JT, et al. Efficacy and safety of Belimumab in patients with rheumatoid arthritis: a phase II, randomized, double-blind, placebo-controlled, dose-ranging study. J Rheumatol. 2013;40(5):579–89.
Behrens F, Tak PP, Østergaard M, Stoilov R, Wiland P, Huizinga TW, Burkhardt H. MOR103, A human monoclonal antibody to granulocyte–macrophage colony-stimulating factor, in the treatment of patients with moderate rheumatoid arthritis: results of a phase Ib/IIa randomised, double-blind, placebo-controlled, dose-escalation trial. Ann Rheum Dis. 2015;74(6):1058–64.
Temple J. and Jennison C. Bayesian Adaptive Design, Design and Analysis of Experiment Workshop 2011. Newton, UK.
Temple J. Adaptive Designs for Dose-Finding Trials. Bath UK: University of Bath; 2012.
Raftery AE, Lewis SM. The number of iterations, convergence diagnostics and generic metropolis algorithms. In Practical Markov chain Monte Carlo (Gilks W. R., Spiegelhalter D. J., and Richardson S), pp. 115–130. 1995 London: Chapman and Hall.
Heydari J, Lawless C, Lydall DA, Wilkinson DJ. Bayesian hierarchical modelling for inferring genetic interactions in yeast. J R Stat Soc Ser C Appl Stat. 2016;65(3):367–93.
Brain P, Kirby S, Larionovc R. Fitting Emax models to clinical trial dose–response data when the high dose asymptote is ill defined. Pharmaceut Statist. 2014;13:364–70.
Acknowledgements
The authors would like to thank all members of GSK123456 PoC study team, specifically Dr. Daren Austin who led the design of the PoC study of GSK123456. The authors also would like to thank the reviewers for their helpful and constructive comments that improved this manuscript.
Funding
Not Applicable.
Availability of data and materials
The PoC data will not be shared as they are proprietary information.
Author information
Authors and Affiliations
Contributions
FL executed and performed the statistical analysis of PoC study of GSK123456. FL, SAJ, and SJW participated in the method comparison and assisted in the drafting of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not Applicable.
Consent for publication
Not Applicable.
Competing interests
FLis employee and shareholder of GlaxoSmithKline. SAJ and SJW have no declarations.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Additional file
Additional file 1:
Supplemental materials provide additional results to supplement the main manuscript, including the two tables and two figures to discuss the proportional of doses being selected as ED90 and ROC curves in non-adaptive and fully adaptive scenarios. (DOCX 47 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Liu, F., Walters, S.J. & Julious, S.A. Design considerations and analysis planning of a phase 2a proof of concept study in rheumatoid arthritis in the presence of possible non-monotonicity. BMC Med Res Methodol 17, 149 (2017). https://doi.org/10.1186/s12874-017-0416-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12874-017-0416-3