Abstract
Background
When developing a prediction model for survival data it is essential to validate its performance in external validation settings using appropriate performance measures. Although a number of such measures have been proposed, there is only limited guidance regarding their use in the context of model validation. This paper reviewed and evaluated a wide range of performance measures to provide some guidelines for their use in practice.
Methods
An extensive simulation study based on two clinical datasets was conducted to investigate the performance of the measures in external validation settings. Measures were selected from categories that assess the overall performance, discrimination and calibration of a survival prediction model. Some of these have been modified to allow their use with validation data, and a case study is provided to describe how these measures can be estimated in practice. The measures were evaluated with respect to their robustness to censoring and ease of interpretation. All measures are implemented, or are straightforward to implement, in statistical software.
Results
Most of the performance measures were reasonably robust to moderate levels of censoring. One exception was Harrell’s concordance measure which tended to increase as censoring increased.
Conclusions
We recommend that Uno’s concordance measure is used to quantify concordance when there are moderate levels of censoring. Alternatively, Gönen and Heller’s measure could be considered, especially if censoring is very high, but we suggest that the prediction model is re-calibrated first. We also recommend that Royston’s D is routinely reported to assess discrimination since it has an appealing interpretation. The calibration slope is useful for both internal and external validation settings and recommended to report routinely. Our recommendation would be to use any of the predictive accuracy measures and provide the corresponding predictive accuracy curves. In addition, we recommend to investigate the characteristics of the validation data such as the level of censoring and the distribution of the prognostic index derived in the validation setting before choosing the performance measures.
Similar content being viewed by others
Background
Prediction models are often used in the field of healthcare to estimate the risk of developing a particular health outcome. These prediction models have an important role in guiding the clinical management of patients and monitoring the performance of health institutions [1, 2]. For example, models have been developed to predict the risk of in-hospital mortality following heart valve surgery and to predict the risk of developing cardiovascular disease within the next 10 years [3, 4]. Given their important role in health research, it is essential that the performance of a prediction model is evaluated in data not used for model development, using appropriate statistical methods [5, 6]. This model evaluation process is generally termed ‘model validation’ [7, 8]. The general idea of validating a prediction model is to establish that it performs well for new patients. Different types of validation process have been discussed in the literature [5,6,7,8]. The most commonly used processes include (i) splitting a single dataset (randomly or based on time) into two parts, one of which is used to develop the model and the other used for validation, (internal or temporal validation) and (ii) validating the model using a new dataset collected from a relevant patient population in different centres (external validation). Of the two approaches, external validation investigates whether a prediction model is transportable (or generalisable) to new patients.
When validating a prediction model, the predictive performance of the model is commonly addressed by quantifying: (i) the ‘distance’ between the observed and predicted outcomes (overall performance); (ii) the ability of the model to distinguish between low and high risk patients (discrimination); (iii) the agreement between the observed and predicted outcomes (calibration) [8]. Performance measures based on these concepts are well established for risk models for binary outcomes [1, 9, 10], but that is not the case for risk models for survival outcomes (survival prediction models) where censoring complicates the validation process [6].
Several performance measures have been suggested for use with survival prediction models. However, a few of these are not appropriate for use with validation data without modification. Also, some require specification of a clinically appropriate time-point or region to match the aims of the validation study. Some of these performance measures have been reviewed previously [11,12,13,14,15,16,17], although only two of the reviews were in the context of model validation. These were Hielscher et al. who reviewed ‘overall performance’ measures, and Schmid and Potapov who reviewed discrimination measures [12, 16]. Consequently, it is still unclear which performance measures should be routinely used in practice when validating survival prediction models using external data.
A good performance measure should be unbiased in the presence of censoring in the validation data. If this were not the case, the level of censoring would affect the evaluation of model performance and a high level of censoring might lead to an over-optimistic verdict regarding the performance of the prediction model. In addition, a good measure should be straightforward to interpret and, ideally, should be easy to implement or available in widely used software.
The aim of this paper is to review all types of performance measures (overall performance, discrimination and calibration) in the context of model validation and to evaluate their performance in simulation datasets with different levels of censoring and case-mix. Where necessary, measures have been modified to allow their use with validation data and a case study is provided to describe how these measures can be estimated in practice. Recommendations are then made regarding the use of these measures in model validation.
Methods
Data
Two datasets, which have previously been used to develop clinical prediction models, were used as the basis of the simulation study. They differ with respect to event rates, level of censoring, types of predictors and amount of prognostic information.
Breast cancer data
This dataset contains information on 686 patients diagnosed with primary node positive breast cancer from the German Breast Cancer Study [18]. The outcome of interest is recurrence-free survival time and the dataset contains 299 (44%) events. The median follow-up time is 3 years. The predictors are age, number of positive lymph nodes, progesterone receptor concentration, tumour grade (1–3), and hormone therapy (yes/no). These data have been analysed previously by Sauerbrei and Royston and their Model III was used as the basis for simulation [19]. That is, the continuous predictors were all transformed using fractional polynomials (FPs) and tumour grade was dichotomised (1/2–3). Number of positive lymph nodes and progesterone receptor concentration were each modelled using one FP term whereas age was modelled using two FP terms.
Hypertrophic cardiomyopathy data
This dataset contains information on a retrospective cohort of 1504 patients with hypertrophic cardiomyopathy (HCM) from a single UK cardiac centre [20]. The outcome of interest is sudden cardiac death or an equivalent event, i.e., a composite outcome and the dataset contains just 84 (6%) events. The median follow-up time is over 6 years. The predictors of interest are age, maximal wall thickness, left atrial diameter, left ventricular outflow gradient, family history of sudden cardiac death (yes/no), non-sustained ventricular tachycardia and unexplained syncope (yes/no). The prediction model produced by O’Mahony et al. was used as the basis for simulation [20]. In particular, maximal wall thickness was modelled using linear and quadratic terms.
Prediction models for survival outcomes
Prediction models for survival outcomes are commonly developed using the Cox proportional hazards model and hence this model was used in the simulations [5, 21]. The Cox model
models the hazard h(t|x) at time t as a product of a nonparametric baseline hazard h 0(t) and the exponential of the prognostic index η = β 1 x 1 + … + β p x p = β T x. The latter is a linear combination of p predictor values with regression coefficients β 1, …, β p providing weights. The predictive form of this model can be written in terms of the survival function as
where S(t|x) is the probability of surviving beyond time t given predictors x, and S 0(t) is the baseline survivall function at time t, where S 0(t) = exp[−∫ t0 h 0(u)du]. To make predictions at a specific time-point τ, one requires estimates \( \widehat{\boldsymbol{\beta}} \) and \( {\hat{S}}_0\left(\tau \right) \).
Performance measures for survival prediction models
Measures were selected for investigation on the basis of their performance in previous reviews [11,12,13,14,15,16], their ease of interpretation, and their availability, or ease of implementation, in statistical software. The selected performance measures are now described in the context of model validation. All measures were implemented in Stata using either built-in or user-written routines [22].
Measures of overall performance
Six measures of ‘overall performance’ were selected, of which four are based on predictive accuracy and two on explained variation [14]. These ‘R2-type’ measures typically take values between 0 and 1, though negative values may be possible in validation data if the prediction model is out-performed by the null model that has no predictors. This issue is discussed later.
The measures based on predictive accuracy were Graf et al’s R2 measure and its integrated counterpart [23], Schemper and Henderson’s R2 measure [24], and a modified version of the latter based on Schmid et al. [25]. The measures based on explained variation were Kent and O’Quigley’s R2 PM [26], and Royston and Sauerbrei’s R2 version of their separation statistic D [27]. Nagelkerke’s R2 measure was not considered due to its known poor performance in the presence of censoring [26, 28].
Graf et al’s R2 BS and R2 IBS
The R2 BS measure proposed by Graf et al. is based on quantifying prediction error at a time-point τ using a quadratic loss function [21]. Specifically, R 2 BS (τ) = 1 − BS(τ|X)/BS(τ) where
is the prediction error at time τ for the prediction model and I(T > τ) is the individual survival status at this time-point. Similarly, BS(τ) is the prediction error for the null model at the same time-point, and is based on the survival function \( \hat{\mathrm{S}}\left(\uptau \right) \) from the null model. The integrated version, R 2IBS (τ), is defined in a similar way to R 2BS (τ) but involves integrating both BS(t|x) and BS(t) over the range [0, τ].
The calculation of prediction errors for both of these models in validation data requires estimates of the corresponding baseline survival functions. This, however, is rarely provided by model developers [6]. One solution might be to estimate these survival functions by re-fitting the Cox model with the PI as the sole predictor in the validation data. This is the approach that we took when calculating R2 BS and R2 IBS, and the R2 SH and R2 S measures described below.
Schemper and Henderson’s R2 SH and Schmid et al’s R2 S
The R2 measure proposed by Schemper and Henderson (denoted here by R2 SH) is similar to Graf et al’s R2 IBS but is based on an absolute loss function [24]. This loss function was chosen to reduce the impact of poorly predicted survival probabilities, which are likely to occur in the right tail of the survival distribution. Specifically, R 2 SH (τ) = 1 − D(τ|x)/D(τ), where
is the prediction error at time τ for the prediction model and W(τ) = 1/∫ τ0 f(t)dt is a weight function to compensate for the measure being defined only on (0, τ). Similarly, D(τ) is the prediction error for the null model.
Schmid et al. prove that Schemper and Henderson’s estimator of D(τ|x) and D(τ) is not robust to model misspecification and suggest an improved estimator [25]. We estimated a summary measure, denoted by R2 S, based on this estimator.
Kent and O’Quigley’s R2 PM
Kent and O’Quiqley’s proposed their R2 PM measure for the Cox model based on the definition of R2 for linear regression [26]. That is,
seeks to quantify the proportion of variation in the outcome explained by the predictors in the prediction model, where σ 2 ϵ ≅ π 2/6 is the variance of the error term in an equivalent Weibuill model [13].
This measure does not use the observed survival times directly in its calculation and instead relies on the prediction model being correctly specified. As a result, R2 PM could be misleading if an apparent strong relationship between the outcomes and predictors in development data is not reproduced in validation data. To overcome this deficiency, we suggest re-calibrating the prediction model to the validation dataset before calculation of R2 PM. This procedure will tend to reduce the value of R2 PM and is described later.
Royston and Sauerbrei’s R2 D
Royston and Sauerbrei’s R2 D is similar to R2 PM but is based on the authors’ own D statistic, a measure of prognostic separation described later. That is,
\( {R}_D^2=\frac{D^2/{\kappa}^2}{D^2/{\kappa}^2+{\sigma}_{\epsilon}^2} \),
where \( \kappa =\sqrt{8/\pi} \) [27]. The ratio D 2/κ 2 is an estimator of Var(η), provided that η is Normally distributed.
Measures of discrimination
Four measures of discrimination were selected, of which three are based on concordance and one on prognostic separation. Discrimination measures assess how well a model can distinguish between low- and high- risk patients, and concordance measures in particular quantify the rank correlation between the predicted risk and the observed survival times. Concordance measures usually take values between 0.5 and 1, where a value of 0.5 indicates no discrimination and a value of 1 indicates perfect discrimination. The selected concordance measures were those of Harrell [29], Uno et al. [30], and Gönen and Heller [31], and the selected prognostic separation measure was Royston and Sauerbrei’s D statistic [27].
Harrell’s CH
The concordance probability is the probability that of a randomly selected pair of patients (i,j), the patient with the shorter survival time has the higher predicted risk. Formally,
where ηi and ηj are the prognostic indices for patients i and j, and Ti and Tj are the corresponding survival times. Harrell’s estimator CH considers all usable pairs of patients for which shorter time corresponds to an event and estimates CH as the proportion of these pairs for which the patient with the shorter survival time has the higher predicted risk [31]. A modified version of this estimator, CH(τ), restricts the calculation to include just those patient pairs where T i < τ and may provide more stable estimates [29, 30]. This truncated version may also be preferred if one were primarily interested in the discrimination of a prediction model over a specified period, for example within 5 years [20].
Uno et al’s CU
In the presence of censoring CH and CH(τ) are biased, even under independent censoring, as they ignore patient pairs where the shorter observed time is censored [15, 32]. Due to this deficiency, Uno et al. [30] proposed a modified estimator CU(τ) that uses weightings based on the probability of being censored. Furthermore, like CH(τ), the calculation may also be restricted to include just those patient pairs where T i < τ. Uno et al. found that their estimator was reasonably robust to the choice of τ, but noted that the standard error of the estimate could be quite large if τ were chosen such that there was little follow-up or few events beyond this time point [29].
Gonen and Heller’s CGH
Gönen and Heller proposed an alternative estimator CGH based on a reversed definition of concordance [30],
which is the probability that of a randomly selected pair of patients (i, j), the patient with the higher predicted risk has the shorter survival time. To avoid bias caused by censoring, their estimator is a function of the model parameters and the predictor distribution and assumes that the proportional hazards assumption holds.
As with R2 PM, CGH does not use the observed event and censoring times in its calculation and relies on the prediction model being correctly specified [15]. Therefore, we suggest re-calibrating the prediction model to the validation dataset before calculating CGH.
Royston and Sauerbrei’s D
The D statistic is a discrimination measure that quantifies the observed separation between subjects with low and high predicted risk [27]. Specifically, D estimates κσ, where σ is the standard deviation of the prognostic index and \( \kappa =\sqrt{8/\pi} \). The scale factor κ enables D to be interpreted as the log hazard ratio that compares two equal-sized risk groups defined by dichotomising the distribution of the patient prognostic indices at the median value.
Measures of calibration
One calibration measure was selected, the commonly used calibration slope proposed by van Houwelingen [33], which is based on the analogous measure for binary outcomes [34, 35].
Calibration slope
The calibration slope is simply the slope of the regression of the observed survival outcomes on the predicted prognostic index [33]. It is estimated by fitting a Cox model to new survival outcomes with the predicted prognostic index, \( \hat{\eta} \), as the sole predictor in the model
Values of \( {\hat{\alpha}}_1 \) close to 1 suggest that the prediction model is well calibrated. Moderate departures from 1 indicate that some form of model re-calibration may be necessary. In particular, \( {\hat{\alpha}}_1<<1 \) suggests over-fitting in the original data with predictions that may be too low for low risk patients or too high for high risk patients.
A brief summary of the performance measures is given in Table 1.
Results
Case study to illustrate the performance measures
A case study is now presented using the breast cancer data in order to describe how the performance measures may be evaluated in a validation setting. The dataset was split randomly into two parts with two thirds of the data used for model development and one third used for model validation. A Cox model was fitted to the development data using the same predictors as in Sauerbrei and Royston’s Model III [19] and the predicted prognostic index was calculated for all patients in the validation data using the estimated regression coefficients \( \hat{\upbeta} \). The values of all performance measures are shown in Table 2 with 95% confidence intervals estimated using the bootstrap techniques based on 200 bootstrap samples. For those measures that require specification of a time-point τ, 3 years was deemed to be clinically appropriate. This was also the median follow-up time.
The estimated prediction errors used to estimate R2 BS and R2 IBS are shown in Fig. 1a. The errors for the prediction and null models are similar for the first 12 months after which the superiority of the prediction model is evident. The corresponding prediction errors used to estimate R2 SH appear similar in shape although the magnitude of the errors are larger due to the use of an absolute loss function (Fig. 1b). The prediction errors used to estimate R2 S are almost indistinguishable from those used to estimate R2 SH (results not shown). R2 IBS, R2 SH and R2 S were estimated after averaging the prediction errors over the first 3 years. As expected R2 SH and R2 S are very similar, and both are slightly larger than R2 IBS. R2 BS was estimated using just the prediction errors at 3 years in Fig. 1a. Its value is larger than that of R2 IBS as the separation between the prediction errors is close to its maximum at this time-point.
To estimate R2 PM in the valids first re-calibrated for reasons explained earlier. That is, the Cox model \( \mathrm{h}\left(\mathrm{t}\Big|\hat{\upeta}\right)={\mathrm{h}}_0\left(\mathrm{t}\right) \exp \left(\upalpha \hat{\upeta}\right) \) was fitted to the validation data, where \( \hat{\upeta} \) is the predicted prognostic index calculated using the regression coefficients estimated in the development data. R2 PM was then estimated using \( {\hat{\upalpha}}^2\mathrm{V}\mathrm{a}\mathrm{r}\left(\hat{\upeta}\right) \) rather than \( \mathrm{V}\mathrm{a}\mathrm{r}\left(\hat{\upeta}\right) \). No such re-calibration is required to estimate R2 D since, unlike R2 PM, it uses the observed survival outcomes in the validation data. The values of R2 PM and R2 D are very similar and noticeably larger than the measures based on predictive accuracy (Table 2). We note that a naïve calculation (without re-calibration) of R2 PM would have produced a much larger value of 0.292, which would have provided an over-optimistic quantification of the model’s predictive performance.
The concordance measures CH and CU were estimated using all usable pairs in which shorter time corresponds to an event, and CGH was estimated after re-calibrating the prediction model to the validation data as described above. The values of these 3 measures are all reasonably similar and would lead to similar conclusions in practice (Table 2). A naïve estimation of CGH (without re-calibration) would have produced a much larger value of 0.696. Restricting the estimation of CH and CU by censoring survival times in the validation data at 3 years produces slightly higher values for both measures, suggesting that the risk model has slightly better discrimination when considering survival over just the first 3 years. The D statistic suggests that the prediction model provides a reasonably high amount of prognostic separation (Table 2). Specifically, if one were to form two risk groups of equal size in the validation data, then the corresponding hazard ratio would be exp(0.998) = 2.71. The calibration slope estimate of 0.76 (equal to the \( \hat{\upalpha} \) estimated during the re-calibration process above) suggests that the prediction model has been slightly over-fitted. We note that, in practice, one can detect and adjust for model over-fitting during model development.
The selected measures all provide useful information. R2 IBS, R2 SH, and R2 S, provide a summary measure quantifying the improvement in predictive accuracy offered by the prediction model over the null model. The R2 BS measure is more appropriate if one is interested in predictive accuracy at a specific time-point, which is sometimes the case in practice. The prediction error curves provide additional insight into the performance of the prediction model at different time-points. R2 PM and R2 D, which both quantify explained variation, produced very similar values though calculation of R2 PM required a re-calibration of the prediction model. The concordance measures CH, CU and CGH produced similar estimates, though calculation of CGH required the prediction model to be re-calibrated. Additionally, if required, the calculation of CH and CU can be restricted which may be appropriate if one wishes to quantify the discrimination of a prediction model before a specified time-point. Finally, the D statistic produces an intuitive quantification of prognostic separation and the calibration slope provides a succinct indication of whether the prediction model is over-fitted or not.
Evaluation of the performance measures using simulation
Following the case study, a simulation study was performed to investigate how robust the measures are with respect to both censoring and the characteristics of the validation data. The simulation design is now described.
Simulation scenarios
The simulation study is based on the breast cancer and HCM datasets described earlier. For both datasets, development and validation datasets were generated by simulating new outcomes based on a true model and combining these with the original predictor values. Models were fitted in the development data and the performance measures estimated in the validation data. Measures which require a choice of time-point τ (including CH and CU) used 3 years for the breast cancer data and 5 years for the HCM data. These values were chosen as they are close to the respective median follow-up times in the original datasets and are conventional choices for survival data. In practice, the choice of time-point would be clinically motivated and based on the underlying research question.
The performance measures were investigated over a range of scenarios to mimic real situations. For all simulations, validation data were constructed to have one of three different risk profiles (denoted low, medium, and high). The use of different risk profiles reflect the fact that, in practice, the characteristics of the patients in the development and validation data may differ [36]. In particular, the event rate for patients in the validation data may be higher or lower than that for patients in the development data due to differences in case-mix.
Four levels of random censoring were considered for the validation datasets (0, 20, 50, and 80%) which combined with the risk profiles, results in a total of 12 validation scenarios for each clinical dataset. The development datasets were generated with no censoring. 5,000 pairs of development and validation datasets were generated for each scenario.
Generating new survival and censoring times
Survival times were generated using the Weibull distribution as below
where η and γ are the observed regression prognostic indices and shape parameter respectively (both used here as the proxy of the true values) and u is a uniformly distributed random variable on (0, 1). For the breast cancer data, the prognostic indices and shape parameter were obtained by fitting a Weibull proportional hazards model using the same predictors as in Sauerbrei and Royston’s Model III [19]. For the HCM data, the prognostic indices were based on the regression coefficients estimated by O’Mahony et al. [20] and just the shape parameter was estimated using a Weibull model with the prognostic index specified as an offset.
To introduce random censoring, additional Weibull distributed censoring times were simulated using tc = (−log(u)/λ)1/γ where different choices of the scalar λ were used to give different proportions of censoring. A subject was considered to be censored if their censoring time was shorter than their survival time.
Generating validation data with different risk profiles
The three different risk profiles were created in the validation data, by first splitting the patients into tertile risk groups based on their true prognostic index η. It is assumed that the first tertile group consists of low-risk patients, the second medium risk, and the third high-risk patients. The three risk profiles for the validation data were created in the following way:
-
a)
low risk profile: 80% of the patients were sampled (without replacement) from the low-risk group, 50% from the medium-risk group, and 20% from the high-risk group;
-
b)
medium risk profile: 50% of the patients were sampled from the low-risk group, 50% from the medium-risk group, and 50% from the high-risk group;
-
c)
high risk profile: 20% of the patients were sampled from the low-risk group, 50% from the medium-risk group, and 80% from the high-risk group.
This sampling procedure was performed before generating each validation dataset and resulted in validation datasets that were half the size of the original datasets. In contrast, no sampling of patients was performed when generating the development datasets; all patients were used.
The prognostic indices were approximately normally distributed for all risk profiles and for both datasets. There was slight skewness, particularly in the low and medium risk profile datasets. For example, the (average) skewness in the HCM datasets was 0.8 (low risk profile), 0.4 (medium) and 0.1 (high). There was a similar trend in the breast cancer datasets, although the values were lower. The variance was largest for the medium profile datasets which was to be expected considering the sampling scheme. This suggests that the medium profile datasets contained more prognostic information than the low and high profile datasets. Finally, there was more prognostic information in the breast cancer data, as evidenced by the wider range of the corresponding prognostic indices.
Simulation results
Table 3 shows the mean values of the overall performance measures over 5000 simulations for the breast cancer data, for the four levels of censoring and three risk profiles. The three summary measures based on predictive accuracy (R2 IBS, R2 SH and R2 S) produced very similar values and were all unaffected by censoring. The values of these measures were highest for the medium risk profile simulations, where the patient characteristics were essentially the same in the development and validation samples, and lowest for the low risk profile simulations. Variability increased with increasing censoring, as expected, and was highest for R2 IBS. This can clearly be seen in Fig. 2 which shows the distribution of the values of the performance measures over the 5000 simulations (a few negative values were deleted to aid clarity). R2 BS, evaluated at 3 years, was also unaffected by censoring and achieved higher values in the medium risk profile simulations. R2 BS also produced some negative values (4%) when censoring was 80%. The two measures based on explained variation (R2 PM and R2 D) produced similar values that were twice as large as the values obtained for R2 IBS, R2 SH and R2 S. R2 PM was unaffected by censoring but R2 D increased slightly as censoring increased. The relationships between the various overall performance measures are shown in Fig. 3 for the medium risk profile scenario. In particular, there was excellent agreement between the R2 SH and R2 S measures which weakened as censoring increased (ρ = 0.54 for 80% censoring). Also, there was good agreement between R2 PM and R2 D which seemed little affected by censoring (ρ = 0.95). Very similar relationships were seen for the low and high risk scenarios (results not shown).
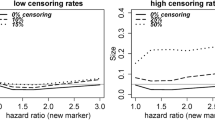
Table 4 shows the mean values of the discrimination and calibration measures for the breast cancer data. The Harrell and Uno c-indices were estimated twice, first using all usable patient pairs (CH and CU) and second by restricting the calculations by censoring times greater than 3 years (CH(3) and CU(3)). For 0% censoring, the CH and CGH mean values were very similar, and the CH and CU estimates were identical by definition. CH tended to increase as censoring increased, whereas CU and particularly CGH were little affected. CGH was the least variable of these three estimates. The variability in CH and CU was similar except for 80% censoring where the variability in CU was far larger (Fig. 4). The increased variability was probably due to large values of the weights caused by the high degree of censoring. The mean value of CH(3) (and CU(3)) was slightly larger than that for CH which suggests that the models were better able to discriminate within the first 3 years compared to across the whole follow-up period. Both CH(3) and CU(3) were relatively stable with respect to censoring, and the variability of both measures was similar. The calibration slope and particular the D statistic showed a slight tendency to increase with censoring. The relationships between the discrimination measures are shown in Fig. 5 for the medium risk profile scenario. In particularly, there was reasonable agreement between the concordance measures and D. The strong relationship between CH and CH(3) for 80% censoring is explained by the fact that there were few observed failure times above 3 years with this level of censoring. Very similar relationships were seen for the low and high risk breast cancer scenarios (results not shown).
The results for the overall performance measures for the HCM data can be seen in Table 5 and Fig. 6. The mean values were all lower than the corresponding values for the breast cancer data. In particular, the predictive accuracy values were considerably lower due to the relatively low number of events (5%) that occurred before 5 years. In addition there were many negative R2 IBS and R2 BS values (11 and 9% respectively). R2 D was affected by censoring in the low and medium risk profile simulations which may be explained by skewness in the prognostic index [6]. For example, the prognostic index was most skewed in the low risk profile HCM simulations, which is where greatest effect of censoring was observed. The relationships between the overall performance measures were similar, and often slightly stronger, than those seen in the breast cancer simulations (results not shown).
The results for the discrimination and calibration measures for the HCM data can be seen in Table 6 and Fig. 7. As with the overall performance measures, the discrimination values were all lower than the corresponding values for the breast cancer data. CH was again badly affected by censoring. In addition, D, like R2 D, was also affected by censoring in the low and medium risk profile simulations. Also notable is the increased variability of the CH(5) and CU(5) measures compared to their unrestricted counterparts. This again is due to the relatively low number of events that occurred before 5 years and the consequent low number of patient pairs used to estimate both measures. Again, the relationships between the discrimination measures were similar to those seen in the breast cancer simulations (results not shown). In particular, there was excellent agreement between CGH and D (ρ = 0.99).
Discussion
The aim of this research was to review some of the promising performance measures for evaluating prediction models for survival outcomes, modify them if necessary for use with external validation data, and perform a simulation study based on two clinical datasets in order to make practical recommendations.
Measures based on predictive accuracy quantify the predictive ability of the prediction model, relative to a null model with no predictors, on a percentage scale and can be readily communicated to health researchers. The measures investigated in this study (R2 IBS, R2 BS, R2 SH and R2 S) may be estimated for any survival prediction model provided that both the prognostic index and baseline survival function are available, although R2 SH also implicitly assumes that the model is correctly specified [12]. If the baseline survival function is not available, which is usually the case in practice [6], then one approach might be to estimate it using the validation data. This is a pragmatic choice as the baseline survival function is rarely presented in practice by model developers. An alternative, arguably better, approach would be to estimate the baseline survival function for the prediction model (with covariates), but not the null model, using the development data. This alternative approach was investigated in the case study and produced very similar results (not shown). A negligible difference in the baseline survival function is also reported in [6] when it was estimated using development and validation data separately. Similarly, for predictions from a null model, which are required for these measures, we suggest using the Kaplan-Meier estimate from the validation data.
Again for these measures, a choice of time-point is also required since the summary measures (R2 IBS, R2 SH and R2 S) are estimated over a specified range and R2 BS is estimated at a specified time-point. In practice, the choice of time-point will be guided by the clinical research question and the length of follow-up. For example, it is common for risk to be estimated at 5 years [4, 20]. The four predictive accuracy measures studied were not affected by censoring in the simulation study. In addition, the three summary measures (R2 IBS, R2 SH and R2 S) produced very similar values on average. However, the variability of R2 IBS was much greater than R2 SH and R2 S which suggests that use of the latter two measures might be preferred in practice if a summary measure is required. Hielscher et al. compared two of these measures, R2 IBS and R2 SH, and had similar findings [12].
The measures based on explained variation (R2 PM and R2 D) may be estimated for any proportional hazards model provided that the prognostic index is available, although we suggest that the prediction model is re-calibrated to the validation data before calculation of R2 PM to ensure that the survival times in the validation data are used in its calculation. Both measures provided very similar values in our simulations. R2 PM was robust to censoring, but R2 D tended to increase with censoring if the prognostic index was skewed.
Concordance measures are routinely used in practice since the concept of correctly ranking patient pairs can be readily communicated to health researchers [5]. CH and CU can be estimated for any survival prediction model that is able to rank patients. In addition, the calculation of CU may also be restricted to a specified range of time, which may be useful to match with clinical aims or to compare concordance across different datasets. The calculation of CH may also be restricted though it is not clear how often this is done in practice [37]. CGH has a similar interpretation to the other concordance measures but requires that the model is correctly specified. As with R2 PM, we suggest that the prediction model is re-calibrated to the validation data before calculation of CGH to ensure that the survival times in the validation data are used. Harrell’s CH, in its unrestricted form, is probably the most used concordance measure in practice [5]. However, it was affected by censoring, which is a finding noted by others [16]. Specifically, CH tended to increase for moderate to high levels of censoring, which is not an uncommon scenario with medical data, and is therefore likely to give an over-optimistic view of a prediction model’s discriminatory ability. Therefore, it cannot be recommended in such scenarios. In contrast, both CU and CGH were reasonably stable in the presence of censoring. CGH was the less variable of the two measures as a consequence of it being model-based [16]. The restricted versions of CH and CU were little affected by censoring but care needs to be taken when selecting the time-point to ensure that the time period contains a reasonable number of events.
The remaining discrimination measure D has an appealing interpretation as it can be communicated as a (log) relative risk between low and high risk groups of patients. It requires that the proportional hazards assumption holds and that the prognostic index is normally distributed. As with R2 D it may be affected by censoring if the prognostic index is skewed [27]. The sole calibration measure under investigation, the calibration slope, was robust to censoring. It assumes that the proportional hazards assumption holds although more general approaches are described by van Houwelingen [33, 38].
Conclusions
Harrell’s CH is routinely reported to assess discrimination when survival prediction models are validated [5]. However, based on our simulation results, we recommend that CU is used instead to quantify concordance when there are moderate levels of censoring. Alternatively, CGH could be considered, especially if censoring is very high, but we suggest that the prediction model is re-calibrated first. The restricted version of CH may also be used provided that the time-point is chosen carefully. We also recommend that D is routinely reported to assess discrimination since it has an appealing interpretation, although the distribution of the prognostic index would need to be checked for normality. ‘Overall performance’ measures are perhaps under used in practice. Our recommendation would be to use any of the predictive accuracy measures and provide the corresponding predictive accuracy curves. In particular, R2 SH and R2 S have relatively low variability. The calibration slope is a useful measure of calibration and recommended to report routinely. In addition, one could investigate calibration graphically, for example by comparing observed and predicted survival curves for groups of patients [6]. Finally, we also recommend to investigate the characteristics of the validation data such as the level of censoring and the distribution of the prognostic index derived in the validation setting before choosing the performance measures.
Abbreviations
- FP:
-
Fractional Polynomial
- HCM:
-
Hypertrophic Cardiomyopathy
References
Omar RZ, Ambler G, Royston P, et al. Cardiac surgery risk modeling for mortality: a review of current practice and suggestions for improvement. Ann Thorac Surg. 2004;77:2232–7.
Moons KGM, Royston P, Vergouwe Y, et al. Prognosis and prognostic research: what, why and how? Br Med J. 2009;338:1317–20.
Ambler G, Omar RZ, Royston P, et al. Generic, simple risk stratification model for heart valve surgery. Circulation. 2005;112:224–31.
Hippisley-Cox J, Coupland C, Vinogradova Y, et al. Predicting cardiovascular risk in England and Wales: prospective derivation and validation of QRISK2. Br Med J. 2008;336:1475–82.
Collins GS, de Groot JA, Dutton S, et al. External validation of multivariable prediction models: a systematic review of methodological conduct and reporting. BMC Med Res Methodol. 2014;14:40.
Royston P, Altman DG. External validation of a Cox prognostic model: principles and methods. BMC Med Res Methodol. 2013;13:33.
Harrell FE. Regression Modeling Strategies. Springer. 2001.
Steyerberg EW. Clinical Prediction Models: A Practical Approach to Development, Validation and Updating. New York: Springer; 2009.
Steyerberg EW, Vickers AJ, Cook NR, et al. Assessing the performance of prediction models: a framework for traditional and novel measures. Epidemiology. 2009;21(1):128–38.
Royston P, Altman DG. Visualizing and assessing discrimination in the logistic regression model. Stat Med. 2010;29(24):2508–20.
Schemper M, Stare J. Explained variation in survival analysis. Stat Med. 1996;15:1999–2012.
Hielscher T, Zucknick M, Werft W, Benner A. On the prognostic value of survival models with application to gene expression signatures. Stat Med. 2009;29(7–8):818–29.
Choodari-Oskooei B, Royston P, Parmar MKB. A simulation study of predictive ability measures in a survival model I: Explained variation measures. Stat Med. 2012;31(23):2627–43.
Choodari-Oskooei B, Royston P, Parmar MKB. A simulation study of predictive ability measures in a survival model II: explained randomness and predictive accuracy. Stat Med. 2012;31(13):2644–59.
Pencina MJ, D’Agostino RB, Song L. Quantifying discrimination of Framingham risk functions with different survival C statistics. Stat Med. 2012;31(15):1543–53.
Schmid M, Potapov S. A comparison of estimators to evaluate the discriminatory power of time-to-event models. Stat Med. 2012;31(23):2588–609.
Austin PC, Pencinca MJ and Steyerberg EW. Predictive accuracy of novel risk factors and markers: A simulation study of the sensitivity of different performance measures for the Cox proportional hazards regression model. Stat Methods Med Res.2015, in press.
Schmoor C, Olschewski M, Schumacher M. Randomized and non-randomized patients in clinical trials: experiences with comprehensive cohort studies. Stat Med. 1996;15:263–71.
Sauerbrei W, Royston P. Building multivariable prognostic and diagnostic models: transformation of the predictors by using fractional polynomials. J R Stat Soc A Stat Soc. 1999;162:71–94.
O’Mahony C, Jichi F, Pavlou M, et al. A novel clinical risk prediction model for sudden cardiac death in hypertrophic cardiomyopathy (HCM-RISK). Eur Heart J. 2014;35:2010–20.
Cox DR. Regression models and life tables. J R Stat Soc Ser B. 1972;34:187–220.
Stata Corporation. Stata Statistical Software, Release 13. College station: Tex: Stata Corporation; 2013.
Graf E, Schmoor C, Sauerbrei W, Schumacher M. Assessment and comparison of prognostic classification schemes for survival data. Stat Med. 1999;18:2529–45.
Schemper M, Henderson R. Predictive accuracy and explained variation in Cox regression. Biometrics. 2000;56:249–55.
Schmid M, Hielscher T, Augustin T, Gefeller O. A robust alternative to the Schemper-Henderson estimator of prediction error. Biometrics. 2011;67(2):524–35.
Kent J, O’Quigley J. Measures of dependence for censored survival data. Biometrika. 1988;75(3):525–34.
Royston P, Sauerbrei W. A new measure in prognostic separation in survival data. Stat Med. 2004;23:723–48.
Nagelkerke NJD. A Note on a General Definition of the Coefficient of Determination. Biometrika. 1991;78:691–2.
Harrell FE, Lee KL, Mark DB. Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing error. Stat Med. 1996;15(4):361–7.
Uno H, Cai T, Pencina MJ, D'Agostino BD, Wei LJ. On the C-statistics for evaluating overall adequecy of risk prediction procedures with censored survival data. Stat Med. 2011;30:1105–17.
Gönen M, Heller G. Concordance probability and discriminatory power in proportional hazards regression. Biometrika 2005;92(4):1799–09.
Kaziol JA. The concordance index C and the Mann-Whitney parameter Pr(X > Y) with randomly censored data. Biom J. 2009;51(3):467–74.
van Houwelingen HC. Validation, calibration, revision and combination of prognostic survival models. Stat Med. 2000;19:3401–15.
Cox DR. Two Further Applications of a Model for Binary Regression. Biometrika. 1958;45:562–5.
Miller ME, Hui SL, Tierney WM. Validation techniques for logistic regression models. Stat Med. 1991;10(8):1213–26.
Justice AC, Covinsky KE, Berlin JA. Assessing the Generalizability of Prognostic Information. Ann Intern Med. 1999;130:515–24.
Pencina MJ, D’Agostino RB. Overall C as a measure of discrimination in survival analysis: model specific population value and confidence interval estimation. Stat Med. 2004;23:2109–23.
Choodari-Oskooei B, Royston P, Parmar MKB. The extension of total gain (TG) statistic in survival models: properties and applications. BMC Med Res Methodol. 2015;15:50.
Acknowledgements
The authors would like to thank Drs Constantinos O’Mahony and Perry Elliott for allowing their data to be used data for simulation purposes. Also the authors would like to thank two reviewers and editor for their suggestions which strengthen the paper a lot.
Funding
This work was undertaken at University College London/University College London Hospitals who received a proportion of funding from the United Kingdom Department of Health’s National Institute for Health Research Biomedical Research Centres funding scheme. In addition, Babak Choodari-Oskooei is funded by Medical Research Council, grant number 532193-171339.
Availability of data and materials
The breast cancer dataset is available in a public domain at http://biostat.mc.vanderbilt.edu/DataSets under the authority of the department of biostatistics, Vanderbilt University, USA. and sudden cardiac death data is available on request from Professor Perry Elliott at email: perry.elliott@ucl.ac.uk.
Authors’ contributions
GA and MSR carried out the statistical analysis and simulation studies, and drafted the manuscript. BCO and RO input into the manuscript. All authors read and approved the final manuscript.
Competing interests
The authors declare that they have no competing interests.
Consent to publication
Not applicable.
Ethics approval and consent to participate
As the breast cancer dataset is freely available in public domain at http://biostat.mc.vanderbilt.edu/DataSets and is permitted to use in research publication, the ethics approval consent statement from the ethical review committees at German Breast Cancer Study Group has been available to the authority who made the data available for public use. Again, Professor Perry Elliott (with email perry.elliott@ucl.ac.uk) has given his consent to use HCM dataset for research paper and approval from ethical review committees at Heart Hospital, UK.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Rahman, M.S., Ambler, G., Choodari-Oskooei, B. et al. Review and evaluation of performance measures for survival prediction models in external validation settings. BMC Med Res Methodol 17, 60 (2017). https://doi.org/10.1186/s12874-017-0336-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12874-017-0336-2