Abstract
Background
Previous reviews have focussed on the rationale for employing the stepped wedge design (SWD), the areas of research to which the design has been applied and the general characteristics of the design. However these did not focus on the statistical methods nor addressed the appropriateness of sample size methods used.This was a review of the literature of the statistical methodology used in stepped wedge cluster randomised trials.
Methods
Literature Review. The Medline, Embase, PsycINFO, CINAHL and Cochrane databases were searched for methodological guides and RCTs which employed the stepped wedge design.
Results
This review identified 102 trials which employed the stepped wedge design compared to 37 from the most recent review by Beard et al. 2015. Forty six trials were cohort designs and 45 % (n = 46) had fewer than 10 clusters. Of the 42 articles discussing the design methodology 10 covered analysis and seven covered sample size. For cohort stepped wedge designs there was only one paper considering analysis and one considering sample size methods. Most trials employed either a GEE or mixed model approach to analysis (n = 77) but only 22 trials (22 %) estimated sample size in a way which accounted for the stepped wedge design that was subsequently used.
Conclusions
Many studies which employ the stepped wedge design have few clusters but use methods of analysis which may require more clusters for unbiased and efficient intervention effect estimates. There is the need for research on the minimum number of clusters required for both types of stepped wedge design. Researchers should distinguish in the sample size calculation between cohort and cross sectional stepped wedge designs. Further research is needed on the effect of adjusting for the potential confounding of time on the study power.
Similar content being viewed by others
Background
Randomised Controlled Trials (RCTs) are the gold standard for evaluating the effectiveness of an intervention [1]. However sometimes individual randomisation is not convenient or in some situations even possible [2]. For example, some interventions can only be delivered at the group, community or organisational level whereas for other interventions there is the risk of contamination of individuals in the control arm with those in the intervention arm. Cluster randomised controlled trials (CRCTs) provide an approach to overcome these issues by randomising participants to either the intervention or control condition in groups rather than as individuals. The most common type of CRCT is referred to as a parallel design because clusters in each arm receive their respective intervention regime at the same time but independently of each other.
CRCTs have become very common in health related research and the statistical implications of conducting a study in this manner have been well documented [2–8]. The most important implication of randomising clusters instead of individuals is that observations from individuals within a cluster may be correlated (i.e. not independent). There are also circumstances where conducting a parallel CRCT is not possible. For some interventions the cost of simultaneous implementation to multiple clusters may be too high or logistically impractical [9, 10]. For other interventions, especially those already proven in individual level RCTs, some authors have argued that it is unethical to withhold the treatment from entire clusters [11, 12]. Withholding an intervention which has not yet proven to be effective is not considered to be unethical but this is often not the perception of individuals, organisations or units which may constitute the clusters for a CRCT, or even ethics committees. Consistent with this perception and the experience of the authors of this paper, recruitment of clusters such as hospitals is easier if the cluster is guaranteed to get the intervention at some stage [13].
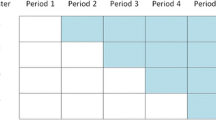
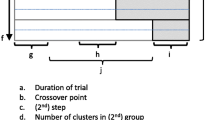
The stepped wedge design (SWD) offers a potential solution to these logistical and ethical problems. In a SWD every cluster begins in the control condition and every cluster receives the intervention by the end of the study. This is achieved through the following process. Before the trial begins, the period of data collection is organised into two or more sequences of measurements. All of the sequences have the first measurement in the control condition and all have the last measurement in the intervention condition, but the time at which clusters within a sequence change from the control to the intervention condition is different for each sequence. Clusters are randomised to these sequences so that each sequence contains at least one cluster. Figure 1 contains a diagrammatic representation of a stepped wedge CRCT where the intervention is implemented in two clusters at each “step” which we define as a point in time where at least one cluster has changed from control to intervention condition. There is a measurement occasion on both sides of every step, and when there are enough steps the overall picture looks somewhat like a wedge, giving the design its name. Despite the fact that publications of trials using the SWD have increased rapidly since its first recognised use in Gambia in 1986 [9, 14] very little attention has been paid to the fact that there are two sub categories of the SWD which differ depending on how data on participants within clusters are obtained. If at each new measurement occasion outcomes are measured on a different randomly selected set of participants in each cluster then the study is a cross sectional SWD. If outcomes at each time point are obtained from the same participants within clusters the trial is a cohort SWD.
The SWD does have some drawbacks however. It may take longer to conduct than a parallel CRCT and almost always involves more measurements overall [15] which in the cohort SWD might result in a greater burden on the participants. Unlike the parallel CRCT, the SWD also requires that the chosen method of analysis adjusts for the potential confounding effect of time [11, 16–19]. So far there has been limited exploration of the methods of analysis in the context of the SWD, particularly with respect to the adjustment for time. Previous reviews have focussed on the rationale for employing the SWD, the areas of research which the SWD has been applied to, and have described the general characteristics of the design [9, 10, 20]. These reviews also reported that a variety of statistical methods have been used in the analysis of stepped wedge CRCTs but they have not addressed the appropriateness of methods used to calculate the sample size. Given the substantial increase in the use of this design in recent years the aim of this review is to describe the methodological literature on SWDs and how these methods have been applied in practice.
One option for analysing individual level data in either a parallel CRCT or a SWD is to use a generalised linear mixed model (GLMM). The term mixed arises because these models estimate both fixed effects, which are the deterministic part of the model forming the regression line, and random effects, which estimate the stochastic variation of individual clusters around the conditional mean of the clusters. Models of this type are interchangeably referred to as mixed, hierarchical, multilevel or random effects models [21] and for the purposes of this paper these will hereafter be referred to simply as GLMMs. Another popular approach to the analysis of individual level data from CRCTs and SWDs is to use the generalised estimating equation (GEE) framework [22]. Unlike GLMMs which model the variance and covariance arising from correlated data directly, the GEE method primarily aims to model the population averaged effects while accounting for the correlation indirectly. The drawback of this approach is that GEEs suffer from inflated type I error rates when there are too few clusters [23]. The fact that many SWDs involve only a few clusters seems to be overlooked in previous reviews as well as in current papers on methods of analysis and sample size calculation [20, 24]. As part of this review we discuss the implication of the small number of clusters on the analysis and sample size calculation. Specifically we aimed to investigate: 1) the statistical methods that are currently recommended for use for the analysis of stepped wedge CRCTs; 2) the methods currently recommended for sample size/power estimation; 3) which methods of analysis for SWDs have been used in practice, and 4) which methods of sample size/power estimation for SWDs have been used in practice.
Methods
Search strategy
In October 2013 the Medline, Embase, and Cochrane databases were searched for the terms step wedge, stepped wedge, staged introduction, phased implementation, staggered implementation, phased recruitment, stepwise recruitment and one way crossover. The resulting titles and abstracts were scanned for eligibility by a single reviewer. When more information was required the article was obtained. The search was updated in June 2015 and included the additional terms dynamic wait list, roll-out randomized, one directional cross-over and randomised multiple baseline design. Also added to this review are the papers from the series in August 2015 in the journal Trials which covered the SWD.
Eligibility criteria
Papers were considered to be eligible for the review if they were written in the English language and were divisable into one of two categories. The first category, corresponding to aims 1) and 2), included papers which contained methodological details about the SWD itself that could be generalised to any such trial. Specifically papers had to include detailed coverage of either the pros and cons of choosing to use the SWD over other designs, variations of the SWD, settings in which the SWD was suitable, the methods of statistical analysis arising directly from the SWD or the methods for estimation of study power/sample size. The second category of papers, corresponding to aims 3) and 4), had to contain an example or protocol of a clustered trial using a SWD with at least two steps.
Data extraction and analysis
From the methodological (first category) papers we recorded the names of the authors, the year of publication and the relevant issues arising from the SWD that were presented in detail. We also examined the reference lists of eligible papers for additional papers which the search strategy had missed.
From papers describing the conduct of a trial that used the SWD (second category) we extracted the names of the authors, the year of publication, the number of clusters (unit of randomisation) and the number of steps. Where possible we also obtained the method used for sample size estimation, the method used for analysis of the primary outcome and whether or not time was adjusted for in that analysis. In addition to this we categorised the study as either a cross-sectional or cohort SWD based on the definition above. We followed the PRISMA guidelines for reporting systematic reviews where relevant [25].
Results
Literature search yield
Figure 2 shows the literature search procedure described below. After removal of duplicates the search terms yielded a total of 1517 abstracts. 1349 of these were excluded because they were considered to be irrelevant. We excluded a further seven of the 168 remaining potentially eligible papers because they did not offer enough detail on the methodology related to the SWD and also did not provide an example of a stepped wedge trial. One of those excluded specified that the study was a stepped wedge trial in the abstract but no more detail was given about the study design, other than that it was a cross sectional intervention study. We identified an additional 11 papers from the reference lists of the 154 eligible papers. There were 42 papers eligible for the methodology category (as shown in Table 1), 130 papers which contained details of a trial implementing the SWD at the cluster level and one paper which was included in both categories [26]. From the 131 papers containing implementations of the SWD we identified 102 distinct trials (see Table 2).
Methodological papers
A detailed examination of the statistical analysis approach for SWD was provided by 10 of the 42 papers which covered methodology [24, 26–32]. The paper by Hussey and Hughes [29] is the most widely cited of these and specifies a GLMM with a random intercept for clusters as the recommended method of analysis; however this applies only to the cross-sectional SWD. Hussey and Hughes also suggest that a GEE or a linear mixed model of the cluster summaries can be used and it is a noteworthy feature of this paper that the analysis methods were examined in both the equal cluster size and unequal cluster size scenarios. Both the GEE and GLMM models that Hussey and Hughes examined used the jack-knife variance estimate [33] instead of the robust variance estimator (RVE) because of the limited number of clusters in their motivating example, which was a trial planned with 24 county health districts in Washington state [34]. Scott et al. [30] suggest that a GEE is most appealing because of the marginal interpretation of model parameters and the lack of assumptions required about the latent variable distributions which are specified as random effects in GLMM. The defining feature of the Scott et al. paper is the comparison of four methods of small sample (small because of few clusters) corrections to the GEE modelling approach. Moulton et al. [26] outline an approach to the analysis of a SWD using a Cox proportional hazards model adjusting for clustering by either bootstrapping or using the RVE. Other authors also suggested the use of a GLMM or a GEE [24, 26, 27, 31, 32, 35] but some had different views on how the fixed or random effects should be specified. For example both Wyman et al. [32] and Van den Heuvel et al. [31] advocate the use of random effects for time in addition to the random intercept whereas Fok et al. [27] outline a random intercept model with an interaction term between time and intervention as a fixed effect. Gruber et al. take a causal modelling approach to the analysis and outline how to estimate the complier average causal effect from a stepped wedge trial [28]. They also note that the SWD has the advantage over parallel CRCTs in the testing of identification assumptions required to use the instrumental variables estimator. Finally Davey et al. use 3 examples (2 GLMMs and a Cox PH model) to explore potential analyses of cohort SWDs [35]. They also discuss the possible drawbacks that many of the simpler models possess; the secular trend and intervention effect is the same for all clusters. To that end they discuss the potential for additional random effects, particularly a random intervention by cluster term. However they do not discuss the potential analysis problems associated with smaller SWDs, such as the lack of statistical power required to fit the more complex models being suggested.
There were seven papers which offered a method of calculating power or sample size [15, 16, 26, 29, 36–38]. Hussey and Hughes suggest a method for calculating the study power of a cross sectional stepped wedge design based on a Wald test of the intervention effect from a weighted least squares analysis [29]. Hemming et al. extend the Hussey and Hughes method to several variations of the cross sectional SWD such as those which do not measure the outcome from every cluster at every step [37]. This generic method also encompasses the parallel CRCT and variations of it so that comparing the power of different cross sectional designs is more straightforward. Hemming and Girling also produced the user written program steppedwedge in the software package Stata [39] which can calculate the power for a variety of SWDs with continuous, binary or rate outcomes [40]. Woertman et al. proposed a formula for the design effect of a SWD based on the Hussey and Hughes method which when multiplied by the estimated sample size required for an individually randomised trial would yield the required number of subjects in the SWD [16]. Unfortunately this method applied the cross sectional SWD model to a cohort SWD trial and is potentially misleading because the correlation within subjects over time is therefore assumed to be zero, which is unlikely [41, 42]. Rhoda et al. also build on the work by Hussey and Hughes to derive a formula for the variance of the intervention effect estimator for both the SWD and a parallel CRCT with the same number of measurement times [15]. They take the ratio of these variances to compare the power of the two designs and present the conditions in terms of the number of steps and the values of the intra-cluster correlation (ICC) for which the SWD is more powerful than the parallel CRCT and vice versa. Moulton et al. outline a method in which the design effect is calculated based on the log-rank test statistic using information about the coefficient of variation (CV) of the outcome, which they obtained from pilot data [26]. Brown et al. present a power calculation based on a GLMM with a Poisson distributed outcome that has a random intercept and random slope for time [36]. Finally Baio et al. present a simulation based procedure for sample size estimation [38]. These authors raise some very important issues about sample size estimation in stepped wedge trials that have not been discussed anywhere else. The first issue is that existing methods do not account for secular trends and the failure to do so when such a trend exists overestimates study power. The second important point is that additional random effects, such as a random intervention effect, decrease study power considerably.
Twenty eight of the 42 papers included in the methodology category did not include any detail on the methods for analysis or sample size estimation. The most informative of these is the paper by Copas et al. [43]. These authors discuss the key features of the SWD in detail and defined 3 types of SWD based on the recruitment of patients within clusters. These are the cross-sectional, closed cohort and open cohort SWDs. Other papers discuss how the SWD potentially increases statistical power [16, 36, 41, 42, 44] while some discuss the need to adjust for the potential confounding effect of time [11, 16–19]. Further papers discussed broader aspects of the SWD such as the motivations for its use [19, 42, 45], the advantages and disadvantages of its use, or the possible settings for which the SWD is suited (see Table 1).
Examples of stepped wedge cluster RCTs
Consistent with three previous reviews of the SWD [9, 10, 20] the number of steps in the identified studies ranged between 2 and 36 with a median of 4. The number of clusters randomised varied even more, ranging from between 2 and 506. In contrast to the latest review [20] which found the median number of clusters per trial was 17 we found that the median was 12 and indeed most trials were modest in terms of the number of clusters with 64 % (n = 65) of the studies sampling fewer than 20 clusters and almost half (n = 46, 45 %) sampling fewer than 10. There were slightly more (n = 56, 55 %) studies which sampled participants in a cross sectional manner whereas the remainder were designed such that participants were repeatedly sampled as in a cohort SWD. Publications of trials using the SWD have increased rapidly in the past few years; more than three quarters (n = 101/131) of the papers in Table 2 were published since the beginning of 2012.
Method of analysis
The method of statistical analysis used varied between studies. Whilst it is not clear if this is due to a lack of agreement on how to analyse the data from a SWD or because of the variety of applications of the SWD or some combination of the two, the majority of studies chose to adjust for the longitudinal nature of the SWD with either GLMMs (n = 60, 59 %) or GEEs (n = 17, 17 %). The remainder used a variety of methods including generalised linear models (GLM) with robust variance estimators [46–48], Cox proportional hazards modelling [26, 49–52], paired t-tests [53, 54], χ2 tests [54, 55], McNemar’s test [56], Wilcoxon rank sum test/Mann-Whitney U test [57, 58], Analysis of covariance (ANCOVA) [58, 59], Analysis of variance (ANOVA) [60], Discourse mapping [61], GLM’s with cluster as a fixed effect [62–70] and GLM’s without any reported effort to adjust for clustering [71–75]. For some studies the method of analysis was unclear [14, 76–79]. The potential confounding effect of time was explored in 61 of the 102 (60 %) studies and either adjusted for in the primary analysis or found not to be correlated with the outcome. For the remaining studies time was not mentioned in the context of confounding and it is unknown whether or not this factor was adjusted for.
Sample size
Of the 79 (77 %) studies which did estimate sample size prospectively, 27 (26 %) of these did so by first determining the design effect based on the ICC as if the study were a parallel CRCT. The method outlined by Hussey and Hughes [29] was used in 22 (22 %) studies and the design effect method proposed by Woertman [16] was used in 3 studies. However 11 of these studies were cohort SWDs and these methods only apply to the cross sectional SWD. There were eight studies which simulated the power based on the method of analysis chosen [63, 64, 80–86] whilst one study used the coefficient of variation from pilot data to estimate the required sample size [26]. Seven studies calculated sample size without consideration for the effect of clustering [14, 47, 58, 59, 71, 73, 87–89]. There was one study which calculated the sample size retrospectively [56] and 22 (22 %) which either did not include details of, or did not estimate the sample size.
Discussion
This review confirmed that use of the SWD has increased substantially in recent years [20]. Reasons for the increased use have been speculated on in the past [10] but one appealing advantage which is often cited, is the ability of the SWD to maintain the same power with fewer clusters than the parallel CRCT [16, 36, 41, 78, 90]. However this is only true when the comparison is between the parallel CRCT with a single measurement period and the SWD with its multiple measurements. When both the parallel CRCT and the SWD have the same number of cross-sectional measurements, the latter is more powerful only when there are a sufficient number of steps [15]. It is unknown if this is the case for the cohort SWD and given the high proportion of cohort SWD studies (45 %) this is an area which needs more research. We would also like to point out that the ethical justification for the SWD may differ between the cohort and cross sectional SWD. All clusters will eventually receive the intervention in both designs but only half the participants will receive the intervention in a balanced cross-sectional SWD, since cluster members will be in the control phase until after the intervention has been implemented in their cluster. Thus even in a SWD the intervention can be withheld from participants. Only the cohort SWD will guarantee that all participants eventually receive the intervention.
Broadly speaking the recommended method of statistical analysis is a choice of either a GLMM or a GEE, both of which have a long history of use in parallel cluster RCTs. To date there has been little investigation into the minimum number of clusters required for a SWD. This is particularly important since this review demonstrated that the stepped wedge design was often used with a small number of clusters. Nearly half of stepped wedge cluster RCTs had fewer than 10 clusters which is a perilously low number for both unbiased estimation and statistical power for each of the recommended methods of analysis. For example the variance of the regression estimates from a GEE using only the robust variance estimator will generally be underestimated when the number of clusters is fewer than 50 [91]. It is possible to reduce the number of clusters needed if the correlation structure is correctly specified, but in general this structure is not known. Even the small sample methods such as the jack-knife method require 20 or more clusters to estimate the variance of the intervention effect with enough precision [91] and Scott et al. found only one of the methods of small sample adjustment which maintained coverage with as few as 10 clusters [30]. GLMM models also require a sufficient number of clusters in order to estimate the random effects. Snijders and Bosker [92] suggest that these models not be used when the number of clusters is fewer than 10 and results from the simulations of Baio et al. [38] suggest that under ideal circumstances a GLMM with only a random intercept might require as few as 8 clusters if the outcome is a count with a Poisson distribution. However as the number of cluster level random effects included in the model increases so too does the number of clusters required for adequate estimation. Although we agree with the rationale for the strong recommendation by Davey et al [35] that a “random intervention by cluster term” be added to the analysis, we must point out that many SWDs do not have a sufficient number of clusters to estimate this additional random effect accurately. For other methods of analysis, such as the cluster summaries method proposed by Hussey and Hughes [29], it is unknown how many clusters are required as a minimum. We suggest that researchers be aware that there will be a lower limit because the gain in power associated with more measurement periods diminishes as the number of measurement times increases [29], whereas reducing the number of clusters results in a relatively large loss of power for smaller trials. More simply put, between cluster information cannot be traded for within cluster information ad infinitum. While the lower limit to the number of clusters for a SWD is unknown, it will depend on several factors including whether the model is linear or non-linear and how balanced the clusters are in terms of size.
Time is another factor that must be considered in the analysis of a SWD because the study design itself induces an association between time and the intervention. If there is also an association between time and outcome, either directly or due to other predictors of the outcome changing over time then this meets the definition of a confounder. Many authors have correctly pointed out that the method of analysis needs to adjust for time [11, 16–19] but the impact of doing so on the statistical power of the analysis has only been investigated by Baio et al. [38]. These authors have found that adjusting for a time effect results in a loss of statistical power. This needs to be accounted for in future sample size estimates for SWDs but at present the best method of estimating the required sample size for a SWD, particularly the cohort design is to simulate the power based on the method of analysis proposed while also including time (as a fixed or random effect) in the chosen model.
Conclusions
Statistical methodology for SWDs continues to lag behind what is implemented in practice. Many SWDs might also be underpowered or even biased because they contain too few clusters for the chosen method of analysis. Further research is needed on the minimum number of clusters required to conduct both types of SWD, as well as on the most appropriate method of analysis for stepped wedge CRCTs when there are few clusters. Another methodological deficiency is the lack of research for the cohort SWD, and the lack of a clear distinction between it and the cross-sectional SWD to the point where trialists are confusing the methods of sample size calculation for cross-sectional SWDs and cohort SWDs. Researchers need to be aware that the cohort and cross sectional SWD require different approaches to sample size estimation and that the SWD should not be employed solely on the basis of a ‘simple’ power estimate which takes no account of the complex design. There is also need for further research on the effect of adjusting for time on the study power and therefore sample size estimates, which will impact the studies with small numbers of clusters the greatest. Finally we point out that it is yet to be proven if the SWD is more powerful than an equivalent parallel CRCT when all of the complexities of the design, such as time adjustment, are accounted for in the statistical analysis.
Abbreviations
ANCOVA, ANalysis of COVAriance; ANOVA, ANalysis Of VAriance; CRCT, cluster randomised controlled trial; GEE, generalised estimating equation; GLM, generalised linear model; GLMM, generalised linear mixed model; ICC, intra-cluster correlation; RCT, randomised controlled trial; RVE, robust variance estimator; SWD, stepped wedge design
References
Pocock SJ. Clinical trials: a practical approach. Chichester: Wiley; 1983.
Hayes RJ, Moulton LH. Cluster Randomised Trials. Boca Raton: Chapman & Hall; 2009.
Donner A, Klar N. Design and Analysis of Cluster Randomization Trials in Health Research. London: Arnold; 2000
Hayes RJ, Bennett S. Simple sample size calculation for cluster-randomized trials. Int J Epidemiol. 1999;28(2):319–26.
Donner A. Some Aspects of the Design and Analysis of Cluster Randomization Trials. J R Stat Soc: Ser C: Appl Stat. 1998;47(1):95–113.
Wears RL. Advanced statistics: statistical methods for analyzing cluster and cluster-randomized data. Acad Emerg Med. 2002;9(4):330–41.
Murray DM. Design and Analysis of GroupRandomized Trials. New York: Oxford University Press Inc; 1998.
Campbell MJ, Walters SJ. How to design, analyse and report cluster randomised trials in medicine and health related research. Chichester: Wiley-Blackwell; 2014.
Brown CA, Lilford RJ. The stepped wedge trial design: a systematic review. BMC Med Res Methodol. 2006;6:54.
Mdege ND et al. Systematic review of stepped wedge cluster randomized trials shows that design is particularly used to evaluate interventions during routine implementation. J Clin Epidemiol. 2011;64(9):936–48.
Handley MA, Schillinger D, Shiboski S. Quasi-experimental designs in practice-based research settings: design and implementation considerations. J Am Board Fam Med. 2011;24(5):589–96.
Weijer C et al. The Ottawa Statement on the Ethical Design and Conduct of Cluster Randomized Trials. PLoS Med. 2012;9(11):e1001346.
Melis RJ et al. Pseudo cluster randomization performed well when used in practice. J Clin Epidemiol. 2008;61(11):1169–75.
The Gambia Hepatitis Intervention Study. The Gambia Hepatitis Study Group. Cancer Res. 1987;47(21):5782–7.
Rhoda DA et al. Studies with staggered starts: multiple baseline designs and group-randomized trials. Am J Public Health. 2011;101(11):2164–9.
Woertman W et al. Stepped wedge designs could reduce the required sample size in cluster randomized trials. J Clin Epidemiol. 2013;66(7):752–8.
Hemming K et al. Stepped wedge cluster randomized trials are efficient and provide a method of evaluation without which some interventions would not be evaluated. J Clin Epidemiol. 2013;66(9):1058–9.
Haines T et al. A novel research design can aid disinvestment from existing health technologies with uncertain effectiveness, cost-effectiveness, and/or safety. J Clin Epidemiol. 2014;67(2):144–51.
Brown C et al. An epistemology of patient safety research: a framework for study design and interpretation. Part 2. Study design. Qual Saf Health Care. 2008;17(3):163–9.
Beard E et al. Stepped wedge randomised controlled trials: systematic review of studies published between 2010 and 2014. Trials. 2015;16:353.
Austin PC. Estimating multilevel logistic regression models when the number of clusters is low: a comparison of different statistical software procedures. Int J Biostat. 2010;6(1):Article 16.
Liang K-Y, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73(1):13–22.
Kauermann G, Carroll RJ. A Note on the Efficiency of Sandwich Covariance Matrix Estimation. J Am Stat Assoc. 2001;96(456):1387–96.
Hemming K et al. The stepped wedge cluster randomised trial: rationale, design, analysis, and reporting. BMJ. 2015;350:h391.
Moher D et al. Preferred Reporting Items for Systematic Reviews and Meta-Analyses: The PRISMA Statement. PLoS Med. 2009;6(7):e1000097.
Moulton LH et al. Statistical design of THRio: a phased implementation clinic-randomized study of a tuberculosis preventive therapy intervention. Clin Trials. 2007;4(2):190–9.
Fok CC, Henry D, Allen J. Research Designs for Intervention Research with Small Samples II: Stepped Wedge and Interrupted Time-Series Designs. Prev Sci. 2015;16(7):967–77.
Gruber JS et al. Estimation of treatment efficacy with complier average causal effects (CACE) in a randomized stepped wedge trial. Am J Epidemiol. 2014;179(9):1134–42.
Hussey MA, Hughes JP. Design and analysis of stepped wedge cluster randomized trials. Contemp Clin Trials. 2007;28(2):182–91.
Scott JM, et al. Finite-sample corrected generalized estimating equation of population average treatment effects in stepped wedge cluster randomized trials. Stat Methods Med Res. 2014.
Van den Heuvel, E.R., R.J. Zwanenburg, and C.M. Van Ravenswaaij-Arts, A stepped wedge design for testing an effect of intranasal insulin on cognitive development of children with Phelan-McDermid syndrome: A comparison of different designs. Stat Methods Med Res, 2014.
Wyman PA et al. Designs for Testing Group-Based Interventions with Limited Numbers of Social Units: The Dynamic Wait-Listed and Regression Point Displacement Designs. Prev Sci. 2015;16(7):956–66.
Lipsitz SR, Laird NM, Harrington DP. Using the jackknife to estimate the variance of regression estimators from repeated measures studies. Commun Stat Theory Methods. 1990;19(3):821–45.
Golden MR et al. Uptake and Population-Level Impact of Expedited Partner Therapy (EPT) on Chlamydia trachomatis and Neisseria gonorrhoeae: The Washington State Community-Level Randomized Trial of EPT. PLoS Med. 2015;12(1):1–22.
Davey C et al. Analysis and reporting of stepped wedge randomised controlled trials: synthesis and critical appraisal of published studies, 2010 to 2014. Trials. 2015;16:358.
Brown CH et al. Dynamic wait-listed designs for randomized trials: new designs for prevention of youth suicide. Clin Trials. 2006;3(3):259–71.
Hemming K, Lilford R, Girling AJ. Stepped-wedge cluster randomised controlled trials: A generic framework including parallel and multiple-level designs. Stat Med. 2015;34(2):181–96.
Baio G et al. Sample size calculation for a stepped wedge trial. Trials. 2015;16(1):1–15.
StataCorp. Stata 13 Base Reference Manual. College Station, TX: Stata Press; 2013.
Hemming K, Girling A. A menu-driven facility for power and detectable-difference calculations in stepped-wedge cluster-randomized trials. Stata J. 2014;14(2):363–80.
de Hoop E, Woertman W, Teerenstra S. The stepped wedge cluster randomized trial always requires fewer clusters but not always fewer measurements, that is, participants than a parallel cluster randomized trial in a cross-sectional design In reply. J Clin Epidemiol. 2013;66(12):1428.
Hemming K, Girling A. The efficiency of stepped wedge vs. cluster randomized trials: stepped wedge studies do not always require a smaller sample size. J Clin Epidemiol. 2013;66(12):1427–8.
Copas AJ et al. Designing a stepped wedge trial: three main designs, carry-over effects and randomisation approaches. Trials. 2015;16:352.
Kotz D et al. The stepped wedge design does not inherently have more power than a cluster randomized controlled trial. J Clin Epidemiol. 2013;66(9):1059–60.
Davis MP, Mitchell GK. Topics in research: structuring studies in palliative care. Curr Opin Support Palliat Care. 2012;6(4):483–9.
Larsen DA et al. Population-wide malaria testing and treatment with rapid diagnostic tests and artemether-lumefantrine in southern zambia: a community randomized step-wedge control trial design. Am J Trop Med Hyg. 2015;92(5):913–21.
Bacchieri G et al. A community intervention to prevent traffic accidents among bicycle commuters. Rev Saude Publica. 2010;44(5):867–75.
Hill AM et al. Fall rates in hospital rehabilitation units after individualised patient and staff education programmes: a pragmatic, stepped-wedge, cluster-randomised controlled trial. Lancet. 2015;385(9987):2592–9.
Durovni B et al. Effect of improved tuberculosis screening and isoniazid preventive therapy on incidence of tuberculosis and death in patients with HIV in clinics in Rio de Janeiro, Brazil: a stepped wedge, cluster-randomised trial. Lancet Infect Dis. 2013;13(10):852–8.
Golub JE et al. Long-term protection from isoniazid preventive therapy for tuberculosis in HIV-infected patients in a medium-burden tuberculosis setting: the TB/HIV in Rio (THRio) study. Clin Infect Dis. 2015;60(4):639–45.
Bouwsma EV et al. The cost effectiveness of a tailored, web-based care program to enhance postoperative recovery in gynecologic patients in comparison with usual care: protocol of a stepped wedge cluster randomized controlled trial. JMIR Res Protoc. 2014;3(2):e30.
Pearse R. Enhanced peri-operative care for high-risk patients (EPOCH) trial: a stepped wedge cluster randomised trial of a quality improvement intervention for patients undergoing emergency laparotomy. Lancet. 2015.
Due TD et al. The effectiveness of a semi-tailored facilitator-based intervention to optimise chronic care management in general practice: a stepped-wedge randomised controlled trial. BMC Fam Pract. 2014;15:65.
Grunewaldt KH et al. Working memory training improves cognitive function in VLBW preschoolers. Pediatrics. 2013;131(3):e747–54.
Doherty S et al. National project seeking to improve pain management in the emergency department setting: findings from the NHMRC-NICS National Pain Management Initiative. Emerg Med Australas. 2013;25(2):120–6.
Viera AJ, Garrett JM. Preliminary study of a school-based program to improve hypertension awareness in the community. Fam Med. 2008;40(4):264–70.
Skrovseth SO et al. Data-Driven Personalized Feedback to Patients with Type 1 Diabetes: A Randomized Trial. Diabetes Technol Ther. 2015;17(7):482–9.
Somerville M et al. From local concern to randomized trial: the Watcombe Housing Project. Health Expect. 2002;5(2):127–35.
Barton A et al. The Watcombe Housing Study: the short term effect of improving housing conditions on the health of residents. J Epidemiol Community Health. 2007;61:771–7.
Schnelle JF et al. Reducing and managing restraints in long-term-care facilities. J Am Geriatr Soc. 1992;40(4):381–5.
Dilworth S et al. Examining clinical supervision as a mechanism for changes in practice: a research protocol. J Adv Nurs. 2014;70(2):421–30.
Mouchoux C et al. Impact of a multifaceted program to prevent postoperative delirium in the elderly: the CONFUCIUS stepped wedge protocol. BMC Geriatr. 2011;11:25.
van den Broek IV et al. Evaluation design of a systematic, selective, internet-based, Chlamydia screening implementation in the Netherlands, 2008-2010: implications of first results for the analysis. BMC Infect Dis. 2010;10:89.
van den Broek IV et al. Effectiveness of yearly, register based screening for chlamydia in the Netherlands: controlled trial with randomised stepped wedge implementation. BMJ. 2012;345:e4316.
Cowan JF et al. Early ART initiation among HIV-positive pregnant women in central Mozambique: a stepped wedge randomized controlled trial of an optimized Option B+ approach. Implement Sci. 2015;10(1):61.
Craine N et al. A stepped wedge cluster randomized control trial of dried blood spot testing to improve the uptake of hepatitis C antibody testing within UK prisons. Eur J Public Health. 2015;25(2):351–7.
Groshaus H et al. Use of clinical decision support to improve the quality of care provided to older hospitalized patients. Appl Clin Inform. 2012;3(1):94–102.
Kelly PJ et al. Study protocol: a stepped wedge cluster randomised controlled trial of a healthy lifestyle intervention for people attending residential substance abuse treatment. BMC Public Health. 2015;15(1):465.
Weiner M et al. A web-based generalist-specialist system to improve scheduling of outpatient specialty consultations in an academic center. J Gen Intern Med. 2009;24(6):710–5.
Williamson A et al. Supporting Policy In health with Research: an Intervention Trial (SPIRIT)-protocol for a stepped wedge trial. BMJ Open. 2014;4(7):e005293.
Ciliberto MA et al. Comparison of home-based therapy with ready-to-use therapeutic food with standard therapy in the treatment of malnourished Malawian children: a controlled, clinical effectiveness trial. Am J Clin Nutr. 2005;81(4):864–70.
Mosha F et al. Evaluation of the effectiveness of a clean delivery kit intervention in preventing cord infection and puerperal sepsis among neonates and their mothers in rural Mwanza Region. Tanzania Tanzan Health Res Bull. 2005;7(3):185–8.
Patel MP et al. Supplemental feeding with ready-to-use therapeutic food in Malawian children at risk of malnutrition. J Health Popul Nutr. 2005;23(4):351–7.
Haugen AS et al. Effect of the World Health Organization checklist on patient outcomes: a stepped wedge cluster randomized controlled trial. Ann Surg. 2015;261(5):821–8.
Ononge S, Campbell O, Mirembe F. Haemoglobin status and predictors of anaemia among pregnant women in Mpigi, Uganda. BMC Res Notes. 2014;7:712.
Badenbroek IF et al. Design of the INTEGRATE study: effectiveness and cost-effectiveness of a cardiometabolic risk assessment and treatment program integrated in primary care. BMC Fam Pract. 2014;15:90.
Bailey IW, Archer L. The impact of the introduction of treated water on aspects of community health in a rural community in Kwazulu-Natal, South Africa. Water Sci Technol. 2004;50(1):105–10.
Banga FR et al. The impact of transmural multiprofessional simulation-based obstetric team training on perinatal outcome and quality of care in the Netherlands. BMC Med Educ. 2014;14:175.
Proeschold-Bell RJ et al. Use of a randomized multiple baseline design: rationale and design of the spirited life holistic health intervention study. Contemp Clin Trials. 2013;35(2):138–52.
Brimblecombe J et al. Stores Healthy Options Project in Remote Indigenous Communities (SHOP@RIC): a protocol of a randomised trial promoting healthy food and beverage purchases through price discounts and in-store nutrition education. BMC Public Health. 2013;13:744.
Fuller C et al. The Feedback Intervention Trial (FIT)--improving hand-hygiene compliance in UK healthcare workers: a stepped wedge cluster randomised controlled trial. PLoS One. 2012;7(10):e41617.
Bailey FA et al. Intervention to improve care at life’s end in inpatient settings: The BEACON trial. J Gen Intern Med. 2014;29(6):836–43.
Palmer VJ et al. The CORE study protocol: a stepped wedge cluster randomised controlled trial to test a co-design technique to optimise psychosocial recovery outcomes for people affected by mental illness in the community mental health setting. BMJ Open. 2015;5(3):e006688.
Stern A et al. Pressure ulcer multidisciplinary teams via telemedicine: a pragmatic cluster randomized stepped wedge trial in long term care. BMC Health Serv Res. 2014;14:83.
Tielsch JM et al. Designs of two randomized, community-based trials to assess the impact of alternative cookstove installation on respiratory illness among young children and reproductive outcomes in rural Nepal. BMC Public Health. 2014;14:1271.
van Daalen FV et al. A cluster randomized trial for the implementation of an antibiotic checklist based on validated quality indicators: the AB-checklist. BMC Infect Dis. 2015;15(1):134.
Lilly CM et al. Hospital mortality, length of stay, and preventable complications among critically ill patients before and after tele-ICU reengineering of critical care processes. JAMA. 2011;305(21):2175–83.
Priestley G et al. Introducing Critical Care Outreach: a ward-randomised trial of phased introduction in a general hospital. Intensive Care Med. 2004;30(7):1398–404.
Strijbos MJ et al. Design and methods of the Hospital Elder Life Program (HELP), a multicomponent targeted intervention to prevent delirium in hospitalized older patients: efficacy and cost-effectiveness in Dutch health care. BMC Geriatr. 2013;13:78.
Kotz D et al. Use of the stepped wedge design cannot be recommended: a critical appraisal and comparison with the classic cluster randomized controlled trial design. J Clin Epidemiol. 2012;65(12):1249–52.
Mancl LA, DeRouen TA. A covariance estimator for GEE with improved small-sample properties. Biometrics. 2001;57(1):126–34.
Snijders TAB, Bosker RJ. Multilevel Analysis: An Introduction to Basic and Advanced Multilevel Modeling. 2nd ed. Sage Publications Ltd; 1999.
Bellan SE et al. Statistical power and validity of Ebola vaccine trials in Sierra Leone: a simulation study of trial design and analysis. Lancet Infect Dis. 2015;15(6):703–10.
Beard E et al. Stepped wedge randomised controlled trials: systematic review of studies published between 2010 and 2014. Trials. 2015;16(1):1–14.
Fatemi Y, Jacobson RM. The stepped wedge cluster randomized trial and its potential for child health services research: a narrative review. Acad Pediatr. 2015;15(2):128–33.
Hargreaves JR et al. Five questions to consider before conducting a stepped wedge trial. Trials. 2015;16:350.
Hargreaves JR et al. How important is randomisation in a stepped wedge trial? Trials. 2015;16:359.
Keriel-Gascou M et al. A stepped wedge cluster randomized trial is preferable for assessing complex health interventions. J Clin Epidemiol. 2014;67(7):831–3.
Kotz D et al. Researchers should convince policy makers to perform a classic cluster randomized controlled trial instead of a stepped wedge design when an intervention is rolled out. J Clin Epidemiol. 2012;65(12):1255–6.
Mdege ND et al. There are some circumstances where the stepped-wedge cluster randomized trial is preferable to the alternative: no randomized trial at all. Response to the commentary by Kotz and colleagues. J Clin Epidemiol. 2012;65(12):1253–4.
Mdege ND, Kanaan M. Response to Keriel-Gascou et al. Addressing assumptions on the stepped wedge randomized trial design. J Clin Epidemiol. 2014;67(7):833–4.
Pater J et al. Future research and methodological approaches. Ann Oncol. 2011;22 Suppl 7:vii57–61.
Prost A et al. Logistic, ethical, and political dimensions of stepped wedge trials: critical review and case studies. Trials. 2015;16:351.
Sanson-Fisher RW et al. Evaluation of systems-oriented public health interventions: alternative research designs. Annu Rev Public Health. 2014;35:9–27.
Schelvis RM et al. Evaluation of occupational health interventions using a randomized controlled trial: challenges and alternative research designs. Scand J Work Environ Health. 2015;41(5):491–503.
van der Tweel I, van der Graaf R. Issues in the use of stepped wedge cluster and alternative designs in the case of pandemics. Am J Bioeth. 2013;13(9):23–4.
Viechtbauer W et al. Response to Keriel-Gascou et al.: higher efficiency and other alleged advantages are not inherent to the stepped wedge design. J Clin Epidemiol. 2014;67(7):834–6.
Wolkewitz M et al. Interventions to control nosocomial infections: study designs and statistical issues. J Hosp Infect. 2014;86(2):77–82.
Zhan Z et al. Strengths and weaknesses of a stepped wedge cluster randomized design: Its application in a colorectal cancer follow-up study. J Clin Epidemiol. 2014;67(4):454–61.
Aoun S et al. Supporting family caregivers to identify their own needs in end-of-life care: Qualitative findings from a stepped wedge cluster trial. Palliat Med. 2015;29(6):508–17.
Aoun S et al. Enabling a family caregiver-led assessment of support needs in home-based palliative care: Potential translation into practice. Palliat Med. 2015;29(10):929–38.
Aoun S et al. Implementing and evaluating the impact of the carer support needs assessment tool (CSNAT) in community palliative care in Australia. Palliat Med. 2014;28(6):606.
Aoun SM et al. The Impact of the Carer Support Needs Assessment Tool (CSNAT) in Community Palliative Care Using a Stepped Wedge Cluster Trial. PLoS One. 2015;10(4):e0123012.
Austin L, Ewing G, Grande G. Facilitating a shift to comprehensive carer-led assessment in palliative home care: The CSNAT approach. Palliat Med. 2014;4(1):612–3.
GrandeG.E, et al. Assessing the impact of a Carer Support Needs Assessment Tool (CSNAT) intervention in palliative home care: a stepped wedge cluster trial. BMJ Support Palliat Care, 2015.
Lo AC et al. Prevalence of molecular markers of drug resistance in an area of seasonal malaria chemoprevention in children in Senegal. Malar J. 2013;12:137–7.
Bailet LL et al. Emergent literacy intervention for prekindergarteners at risk for reading failure. J Learn Disabil. 2009;42(4):336–55.
Bashour HN, et al. The effect of training doctors in communication skills on women’s satisfaction with doctor-woman relationship during labour and delivery: a stepped wedge cluster randomised trial in Damascus. BMJ Open, 2013. 3(8).
Bennett PN et al. The impact of an exercise physiologist coordinated resistance exercise program on the physical function of people receiving hemodialysis: a stepped wedge randomised control study. BMC Nephrol. 2013;14(1):204.
Bernabe-Ortiz A et al. Launching a salt substitute to reduce blood pressure at the population level: a cluster randomized stepped wedge trial in Peru. Trials. 2014;15:93.
Brown BB et al. Clinician-led improvement in cancer care (CLICC)--testing a multifaceted implementation strategy to increase evidence-based prostate cancer care: phased randomised controlled trial--study protocol. Implement Sci. 2014;9:64.
Brownell MD et al. Long-term benefits of full-day kindergarten: a longitudinal population-based study. Early Child Dev Care. 2015;185(2):291–316.
Chavane L et al. Implementation of evidence-based antenatal care in Mozambique: a cluster randomized controlled trial: study protocol. BMC Health Serv Res. 2014;14:228.
Chinbuah MA et al. Impact of community management of fever (using antimalarials with or without antibiotics) on childhood mortality: a cluster-randomized controlled trial in Ghana. Am J Trop Med Hyg. 2012;87(5 Suppl):11–20.
Chinbuah MA et al. Impact of treating young children with antimalarials with or without antibiotics on morbidity: a cluster-randomized controlled trial in Ghana. Int Health. 2013;5(3):228–35.
Crain AL et al. Designing and implementing research on a statewide quality improvement initiative: the DIAMOND study and initiative. Med Care. 2013;51(9):e58–66.
Solberg LI et al. Partnership research: a practical trial design for evaluation of a natural experiment to improve depression care. Med Care. 2010;48(7):576–82.
Dainty KN et al. A knowledge translation collaborative to improve the use of therapeutic hypothermia in post-cardiac arrest patients: protocol for a stepped wedge randomized trial. Implement Sci. 2011;6:4.
Morrison LJ et al. Improving Use of Targeted Temperature Management After Out-of-Hospital Cardiac Arrest: A Stepped Wedge Cluster Randomized Controlled Trial. Crit Care Med. 2015;43(5):954–64.
De Allegri M et al. Step-wedge cluster-randomised community-based trials: an application to the study of the impact of community health insurance. Health Res Policy Syst. 2008;6:10.
Gnawali DP et al. The effect of community-based health insurance on the utilization of modern health care services: evidence from Burkina Faso. Health Policy. 2009;90(2-3):214–22.
Turner J et al. A randomised trial of a psychosocial intervention for cancer patients integrated into routine care: the PROMPT study (promoting optimal outcomes in mood through tailored psychosocial therapies). BMC Cancer. 2011;11:48.
Dreischulte T et al. A cluster randomised stepped wedge trial to evaluate the effectiveness of a multifaceted information technology-based intervention in reducing high-risk prescribing of non-steroidal anti-inflammatory drugs and antiplatelets in primary medical care: the DQIP study protocol. Implement Sci. 2012;7:24.
Dryden-Peterson S et al. An augmented SMS intervention to improve access to antenatal CD4 testing and ART initiation in HIV-infected pregnant women: A cluster randomized trial. PLoS One. 2015;10(2):e0117181.
Duijster D et al. Associations between oral health-related impacts and rate of weight gain after extraction of pulpally involved teeth in underweight preschool Filipino children. BMC Public Health. 2013;13:533.
Monse B et al. The effects of extraction of pulpally involved primary teeth on weight, height and BMI in underweight Filipino children. A cluster randomized clinical trial. BMC Public Health. 2012;12:725.
Durovni B et al. Impact of Replacing Smear Microscopy with Xpert MTB/RIF for Diagnosing Tuberculosis in Brazil: A Stepped-Wedge Cluster-Randomized Trial. PLoS Med. 2014;11(12):e1001766.
Trajman A et al. Impact on Patients’ Treatment Outcomes of XpertMTB/RIF Implementation for the Diagnosis of Tuberculosis: Follow-Up of a Stepped-Wedge Randomized Clinical Trial. PLoS One. 2015;10(4):e0123252.
Emond YE et al. Improving the implementation of perioperative safety guidelines using a multifaceted intervention approach: protocol of the IMPROVE study, a stepped wedge cluster randomized trial. Implement Sci. 2015;10(1):3.
Enns E et al. A controlled quality improvement trial to reduce the use of physical restraints in older hospitalized adults. J Am Geriatr Soc. 2014;62(3):541–5.
Etchells E et al. Real-time automated paging and decision support for critical laboratory abnormalities. BMJ Qual Saf. 2011;20(11):924–30.
Fernald LCH, Gertler PJ, Neufeld LM. Role of cash in conditional cash transfer programmes for child health, growth, and development: an analysis of Mexico’s Oportunidades. Lancet. 2008;371(9615):828–37.
Franklin BD et al. The effect of the electronic transmission of prescriptions on dispensing errors and prescription enhancements made in English community pharmacies: A naturalistic stepped wedge study. BMJ Qual Saf. 2014;23(8):629–38.
Gerritsen DL et al. Act In case of Depression: the evaluation of a care program to improve the detection and treatment of depression in nursing homes. Study Protocol BMC Psychiatry. 2011;11:91.
Leontjevas R et al. Process evaluation to explore internal and external validity of the “Act in Case of Depression” care program in nursing homes. J Am Med Dir Assoc. 2012;13(5):488 e1–8.
Leontjevas R et al. A structural multidisciplinary approach to depression management in nursing-home residents: a multicentre, stepped-wedge cluster-randomised trial. Lancet. 2013;381(9885):2255–64.
Leontjevas R et al. More insight into the concept of apathy: a multidisciplinary depression management program has different effects on depressive symptoms and apathy in nursing homes. Int Psychogeriatr. 2013;25(12):1941–52.
Gruber JS et al. A stepped wedge, cluster-randomized trial of a household UV-disinfection and safe storage drinking water intervention in rural Baja California Sur, Mexico. Am J Trop Med Hyg. 2013;89(2):238–45.
Gucciardi E et al. Will Mobile Diabetes Education Teams (MDETs) in primary care improve patient care processes and health outcomes? Study protocol for a randomized controlled trial. Trials. 2012;13:165.
Haines TP et al. Study protocol for two randomized controlled trials examining the effectiveness and safety of current weekend allied health services and a new stakeholder-driven model for acute medical/surgical patients versus no weekend allied health services. Trials. 2015;16(1):133.
Haukka E et al. Efficacy of temporary work modifications on disability related to musculoskeletal pain or depressive symptoms-study protocol for a controlled trial. BMJ Open. 2015;5(5):e008300.
Hayden MK et al. Prevention of colonization and infection by klebsiella pneumoniae carbapenemase-producing enterobacteriaceae in long-term acute-care hospitals. Clin Infect Dis. 2015;60(8):1154–61.
Hill AM et al. A stepped-wedge cluster randomised controlled trial for evaluating rates of falls among inpatients in aged care rehabilitation units receiving tailored multimedia education in addition to usual care: A trial protocol. BMJ Open. 2014;4(1):e004195.
Horner C et al. The longitudinal prevalence of MRSA in care home residents and the effectiveness of improving infection prevention knowledge and practice on colonisation using a stepped wedge study design. BMJ Open. 2012;2(1):e000423.
Howlin P et al. The effectiveness of Picture Exchange Communication System (PECS) training for teachers of children with autism: a pragmatic, group randomised controlled trial. J Child Psychol Psychiatry. 2007;48(5):473–81.
Hunter SB et al. Continuous quality improvement (CQI) in addiction treatment settings: design and intervention protocol of a group randomized pilot study. Addict Sci Clin Pract. 2014;9(1):1–11.
Husaini BA et al. A church-based program on prostate cancer screening for African American men: reducing health disparities. Ethn Dis. 2008;18(2 Suppl 2):S2-179-84.
Killam WP et al. Antiretroviral therapy in antenatal care to increase treatment initiation in HIV-infected pregnant women: a stepped-wedge evaluation. AIDS. 2010;24(1):85–91.
Kitson AL et al. The prevention and reduction of weight loss in an acute tertiary care setting: protocol for a pragmatic stepped wedge randomised cluster trial (the PRoWL project). BMC Health Serv Res. 2013;13:299.
Schultz TJ et al. Does a multidisciplinary nutritional intervention prevent nutritional decline in hospital patients? A stepped wedge randomised cluster trial. e-SPEN J. 2014;9(2):e84–90.
Kjeken I et al. Evaluation of a structured goal planning and tailored follow-up programme in rehabilitation for patients with rheumatic diseases: protocol for a pragmatic, stepped-wedge cluster randomized trial. BMC Musculoskelet Disord. 2014;15:153.
Li S et al. Rational and design of a stepped-wedge cluster randomized trial evaluating quality improvement initiative for reducing cardiovascular events among patients with acute coronary syndromes in resource-constrained hospitals in China. Am Heart J. 2015;169(3):349–55.
Liddy C et al. Improved delivery of cardiovascular care (IDOCC) through outreach facilitation: study protocol and implementation details of a cluster randomized controlled trial in primary care. Implement Sci. 2011;6:110.
Maheu-Giroux M, Castro MC. Do malaria vector control measures impact disease-related behaviour and knowledge? Evidence from a large-scale larviciding intervention in Tanzania. Malar J. 2013;12(1):422.
Marrin K et al. Option Grids to facilitate shared decision making for patients with Osteoarthritis of the knee: protocol for a single site, efficacy trial. BMC Health Serv Res. 2014;14:160.
Marshall T et al. Mixed methods evaluation of targeted case finding for cardiovascular disease prevention using a stepped wedged cluster RCT. BMC Public Health. 2012;12:908.
Mhurchu CN et al. Effects of a free school breakfast programme on children’s attendance, academic achievement and short-term hunger: results from a stepped-wedge, cluster randomised controlled trial. J Epidemiol Community Health. 2013;67(3):257–64.
Ni Mhurchu C et al. Effects of a free school breakfast programme on school attendance, achievement, psychosocial function, and nutrition: a stepped wedge cluster randomised trial. BMC Public Health. 2010;10:738.
Muntinga ME et al. Implementing the chronic care model for frail older adults in the Netherlands: study protocol of ACT (frail older adults: care in transition). BMC Geriatr. 2012;12:19.
Palmay L et al. Hospital-wide rollout of antimicrobial stewardship: A stepped-wedge randomized trial. Clin Infect Dis. 2014;59(6):867–74.
Pickering BW et al. The implementation of clinician designed, human-centered electronic medical record viewer in the intensive care unit: a pilot step-wedge cluster randomized trial. Int J Med Inform. 2015;84(5):299–307.
Poldervaart JM et al. The impact of the HEART risk score in the early assessment of patients with acute chest pain: design of a stepped wedge, cluster randomised trial. BMC Cardiovasc Disord. 2013;13(1):77.
Rasmussen CD et al. Prevention of low back pain and its consequences among nurses’ aides in elderly care: a stepped-wedge multi-faceted cluster-randomized controlled trial. BMC Public Health. 2013;13:1088.
Reuther S et al. Effect evaluation of two types of dementia-specific case conferences in German nursing homes (FallDem) using a stepped-wedge design: study protocol for a randomized controlled trial. Trials. 2014;15:319.
Roy A et al. Universal HIV testing in London tuberculosis clinics: a cluster randomised controlled trial. Eur Respir J. 2013;41(3):627–34.
Solomon E et al. The Devon Active Villages Evaluation (DAVE) trial: study protocol of a stepped wedge cluster randomised trial of a community-level physical activity intervention in rural southwest England. BMC Public Health. 2012;12:581.
Solomon E et al. The Devon Active Villages Evaluation (DAVE) trial of a community-level physical activity intervention in rural south-west England: a stepped wedge cluster randomised controlled trial. Int J Behav Nutr Phys Act. 2014;11:94.
Suman A et al. Cost-effectiveness of a multifaceted implementation strategy for the Dutch multidisciplinary guideline for nonspecific low back pain: design of a stepped-wedge cluster randomised controlled trial. BMC Public Health. 2015;15:522.
Tiono AB et al. The AvecNet Trial to assess whether addition of pyriproxyfen, an insect juvenile hormone mimic, to long-lasting insecticidal mosquito nets provides additional protection against clinical malaria over current best practice in an area with pyrethroid-resistant vectors in rural Burkina Faso: study protocol for a randomised controlled trial. Trials. 2015;16(1):1–12.
Tirlea L, Truby H, Haines TP. Investigation of the effectiveness of the “Girls on the Go!” program for building self-esteem in young women: trial protocol. SpringerPlus. 2013;2:683.
Tirlea L, Truby H, Haines TP. Pragmatic, Randomized Controlled Trials of the Girls on the Go! Program to Improve Self-Esteem in Girls. Am J Health Promot, 2015.
Toftegaard BS, Bro F, Vedsted P. A geographical cluster randomised stepped wedge study of continuing medical education and cancer diagnosis in general practice. Implement Sci. 2014;9:159.
Ward J et al. STI in remote communities: improved and enhanced primary health care (STRIVE) study protocol: a cluster randomised controlled trial comparing ‘usual practice’ STI care to enhanced care in remote primary health care services in Australia. BMC Infect Dis. 2013;13(1):1–9.
Williams AL et al. The effect of work-based mentoring on patient outcome in musculoskeletal physiotherapy: study protocol for a randomised controlled trial. Trials. 2014;15:409.
Wilrycx GK et al. Mental health recovery: evaluation of a recovery-oriented training program. Sci World J. 2012;2012:820846.
Zwijsen SA et al. Grip on challenging behaviour: a multidisciplinary care programme for managing behavioural problems in nursing home residents with dementia. Study protocol. BMC Health Serv Res. 2011;11:41.
Zwijsen SA et al. Coming to grips with challenging behavior: A cluster randomized controlled trial on the effects of a multidisciplinary care program for challenging behavior in Dementia. J Am Med Dir Assoc. 2014;15(7):531.e1–531.e10.
Zwijsen SA et al. Grip on challenging behavior: Process evaluation of the implementation of a care program. Trials. 2014;15(1):302.
Zwijsen SA et al. Coming to grips with challenging behaviour: a cluster randomised controlled trial on the effects of a new care programme for challenging behaviour on burnout, job satisfaction and job demands of care staff on dementia special care units. Int J Nurs Stud. 2015;52(1):68–74.
Van de Steeg L et al. The effect of a complementary e-learning course on implementation of a quality improvement project regarding care for elderly patients: a stepped wedge trial. Implement Sci. 2012;7:13.
van de Steeg L et al. Can an e-learning course improve nursing care for older people at risk of delirium: a stepped wedge cluster randomised trial. BMC Geriatr. 2014;14:69.
van Holland BJ et al. Sustained employability of workers in a production environment: design of a stepped wedge trial to evaluate effectiveness and cost-benefit of the POSE program. BMC Public Health. 2012;12:1003.
ᅟ
ᅟ
Funding
None.
Availability of data and materials
The data we used are contained in Tables 1 and 2 of the manuscript but because this is a systematic review it can be found in the Medline, Embase, PsycINFO, CINAHL and Cochrane databases using the search terms outlined in the search strategy.
Authors’ contributions
DB, PM and CD designed the study, DB undertook the literature search and data extraction. DB, PM, CD and MC drafted the manuscript and approved the final manuscript.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Ethics approval and consent to participate
Not applicable.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Barker, D., McElduff, P., D’Este, C. et al. Stepped wedge cluster randomised trials: a review of the statistical methodology used and available. BMC Med Res Methodol 16, 69 (2016). https://doi.org/10.1186/s12874-016-0176-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12874-016-0176-5