Skip to main content
Download PDF

StressGenePred: a twin prediction model architecture for classifying the stress types of samples and discovering stress-related genes in arabidopsis

BMC Genomics volume 20, Article number: 949 (2019) Cite this article

Abstract

Background

Recently, a number of studies have been conducted to investigate how plants respond to stress at the cellular molecular level by measuring gene expression profiles over time. As a result, a set of time-series gene expression data for the stress response are available in databases. With the data, an integrated analysis of multiple stresses is possible, which identifies stress-responsive genes with higher specificity because considering multiple stress can capture the effect of interference between stresses. To analyze such data, a machine learning model needs to be built.

Results

In this study, we developed StressGenePred, a neural network-based machine learning method, to integrate time-series transcriptome data of multiple stress types. StressGenePred is designed to detect single stress-specific biomarker genes by using a simple feature embedding method, a twin neural network model, and Confident Multiple Choice Learning (CMCL) loss. The twin neural network model consists of a biomarker gene discovery and a stress type prediction model that share the same logical layer to reduce training complexity. The CMCL loss is used to make the twin model select biomarker genes that respond specifically to a single stress. In experiments using Arabidopsis gene expression data for four major environmental stresses, such as heat, cold, salt, and drought, StressGenePred classified the types of stress more accurately than the limma feature embedding method and the support vector machine and random forest classification methods. In addition, StressGenePred discovered known stress-related genes with higher specificity than the Fisher method.

Conclusions

StressGenePred is a machine learning method for identifying stress-related genes and predicting stress types for an integrated analysis of multiple stress time-series transcriptome data. This method can be used to other phenotype-gene associated studies.

Background

Recently, cellular molecule measurement technologies, such as microarray [1] and RNA-seq [2], can be used to measure the expression levels of tens of thousands of genes in a cell. Using these technologies, biologists have measured the change in gene expression levels under stress treatment over time. These time-series data are now available in databases such as ArrayExpress [3] and GEO [4]. To analyze of time-series transcriptome data, various methods were developed based on machine learning techniques such as linear regression, principal component analysis (PCA), naive Bayes, k-nearest neighbor analysis [5], simple neural network [6, 7], naive Bayes methods [8], and ensemble model [9].

However, existing methods were designed to analyze gene expression data of a single stress, not of multiple stresses. Analyzing gene expression data of multiple stresses can identify stress-responsive genes with higher specificity because it can consider the effect of interference between stresses. However, since no method of integrating multiple stress gene expression data has been developed, this study aims to develop a method for an integrated analysis of transcriptome of multiple stress types.

Motivation

For the integrated analysis of transcriptome data of multiple stress, heterogeneous time-series analysis is should be considered [10]. Heterogeneous time-series analysis is a problem to analyze four-dimensional data of experimental condition (sample tissue, age, etc.), stress, time, and gene, where experimental condition axis and time axis are different among multiple time-series samples. Heterogeneous time-series analysis is explained in detail in the next section.

Many algorithms have been developed to analyze gene expression data. However, as far as we are aware of, there is no readily available machine learning algorithm for predicting stress types and detecting stress-related genes from multiple heterogeneous time-series data. Support vector machine (SVM) models are known to be powerful and accurate for classification tasks. Recently, SVMs are extended for multi-class problems and also for regression prediction. However, applying SVM for predicting stress-related genes and associating with phenotypes is not simple since the essence of the problem is to select small number of genes relevant to a few phenotypes. In fact, there is no known readily available prediction method for this research problem. Principal component analysis (PCA) is designed for predicting traits from the same structured input data, but it is not designed to analyze heterogeneous time-series data. Random forest (RF) is a sparse classification method, so how significant a gene is associated with stress is hard to be evaluated. Naive Bayes method [8] can measure the significance of genes, but it is not suitable for heterogeneous time-series data input. Clustering is one of the widely used machine learning approaches for gene expression data analysis. The STEM clustering method [11] clusters genes according to changes in expression patterns in time-series data analysis, but does not accept heterogeneous time-domain structure data.

Thus, we designed and implemented a neural network model, StressGenePred, to analyze heterogeneous time-series gene expression data of multiple stresses. Our model used feature embedding methods to address the heterogeneous structure of data. In addition, the analysis of heterogeneous time-series gene expression data, on the computational side, is associated with the high-dimension and low-sample-size data problem, which is one of the major challenges in machine learning. The data consists of a large number of genes (roughly 20,000) and a small number of samples (about less than 100). To deal with the high-dimension and low-sample-size data problem, our model is designed to share a core neural network model between twin sub-neural network models: 1) biomarker gene discovery model 2) stress type prediction model. These two submodels perform tasks known in the computer field as feature (i.e., gene) selection and label (i.e., stress type) classification, respectively.

Materials

Multiple heterogeneous time-series gene expression data

Multiple stress time-series gene expression data is a set of time-series gene expression data. The k-th time-series gene expression data, Dk, contains expression values for three dimensional axes: gene axis, \(G_{k}=\{g_{k1},\dots,g_{k|G_{k}|}\}\), time axis, \(T_{k}=\{t_{k1},\dots,t_{k|T_{k}|}\}\), experimental condition axis, \(F_{k}=\{f_{k1},\dots,f_{k|F_{k}|}\}\). However, the structure and values of time dimension and experimental condition dimension can be different in multiple samples, called “heterogeneous time-series data.”

  1. 1.

    Heterogeneity of time dimension. Each time-series data may have different number of time points and intervals.

  2. 2.

    Heterogeneity of experimental condition dimension. Each time-series data may have different experimental conditions, such as tissue, temperature, genotype, etc.

The time-series gene expression datasets of four stress types

In this paper, we analyze multiple heterogeneous time-series data of four major environmental stresses: heat, cold, salt and drought. We collected the 138 sample time-series data related to the four types of stress from ArrayExpress [3] and GEO [4]. Figure 1 shows the statistics of the collected dataset. The total dataset includes 49 cold, 43 heat, 33 salt, and 13 drought stress samples, and 65% of the time-series data are measured at only two time points. Every time point in each time-series data contains at least two replicated values.

Fig. 1
figure 1

Dataset statistic summary. The number of stress types (left) and the frequency of time points (right) in the 138 sample time-series gene expression data of four stress types

Full size image

Methods

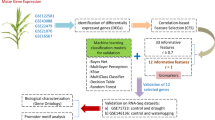
StressGenePred is an integrated analysis method of multiple stress time-series data. StressGenePred (Fig. 2) includes two submodels : a biomarker gene discovery model (Fig. 3) and a stress type prediction model (Fig. 4). To deal with the high-dimension and low-sample-size data problem, both models share a logical correlation layer with the same structure and the same model parameters. From a set of transcriptome data measured under various stress conditions, StressGenePred trains the biomarker gene discovery model and the stress type prediction model sequentially.

Fig. 2
figure 2

StressGenePred’s twin neural network model architecture. The StressGenePred model consists of two submodels: a biomarker gene discovery model (left) and a stress type prediction model (right). The two submodels share a “single NN layer”. Two gray boxes on the left and right models output the predicted results, biomarker gene and stress type, respectively

Full size image
Fig. 3
figure 3

Biomarker gene discovery model. This model predicts biomarker genes from a label vector of stress type. It generates an observed biomarker gene vector from gene expression data (left side of the figure) and a predicted biomarker gene vector from stress type (right side of the figure), and adjusts the weights of the model by minimizing the difference (“output loss” at the top of the figure)

Full size image
Fig. 4
figure 4

Stress type prediction model. This model predicts stress types from a vector of gene expression profile. It generates a predicted stress type vector (left side of the figure) and compares it with a stress label vector (right side of the figure) to adjust the weights of the model by minimizing the CMCL loss (“output loss” at the top of the figure)

Full size image

Submodel 1: biomarker gene discovery model

This model takes a set of stress labels, Y, and gene expression data, D, as input, and predicts which gene is a biomarker for each stress. This model consists of three parts: generation of an observed biomarker gene vector, generation of a predicted biomarker gene vector, and comparison of the predicted vector with the label vector. The architecture of the biomarker gene discovery model is illustrated in Fig. 3, and the process is described in detail as follows.

Generation of an observed biomarker gene vector

This part generates an observed biomarker vector, Xk, from gene expression data of each sample k, Dk. Since each time-series data is measured at different time points under different experimental conditions, a time-series gene expression data must be converted into a feature vector of the same structure and the same scale. This process is called feature embedding. For the feature embedding, we symbolize the change of expression before and after stress treatment by up, down, or non-regulation. In detail, a time-series data of sample k is converted into an observed biomarker gene vector of length 2n, Xk={xk1,…,xk2n}, where xk2n−1∈{0,1} is 1 if gene n is down-regulation or 0 otherwise, xk2n∈{0,1} is 1 if gene n is up-regulation or 0 otherwise. For determining up, down, or non-regulation, we use the fold change information. First, if there are multiple expression values measured from replicate experiments at a time point, the mean of expression values is calculated for the time point. Then, the fold change value is computed by dividing the maximum or minimum expression values for a time-series data by the expression value at first time point. After that, the gene whose fold change value >0.8 or <1/0.8 is considered as up or down regulation gene. The threshold value of 0.8 is selected empirically. When the value of 0.8 is used, the fold change analysis generates at least 20 up or down regulation genes for all time-series data.

Generation of a predicted biomarker gene vector

This part generates a predicted biomarker gene vector, \(X^{\prime }_{k}\), from stress type label Yk. \(X^{\prime }_{k}=\{x^{\prime }_{k1}, \ldots, x^{\prime }_{2kn}\}\) is a vector of the same size as the observed biomarker gene vector Xk. The values of Xk` means up or down regulation as same as Xk. For example, xk2n−1=1 means gene n is predicted as a down-regulated biomarker, or xk2n=1 means gene n is predicted as a up-regulated biomarker, for a specific stress Yk.

A logical stress-gene correlation layer, W, measures the weights of association between genes and stress types. The predicted biomarker gene vector, \(X_{k}^{\prime }\), is generated by multiplying stress type of sample k and the logical stress-gene correlation layer, i.e., Yk×W. In addition, we use the sigmoid function to summarize the output values between 0 to 1. The stress vector, Yk, is encoded as one-hot vector of l stresses, where each element indicates whether the sample k is each specific stress type or not. Finally, the predicted biomarker gene vector, \(X_{k}^{\prime }\), is generated like below:

$$\begin{array}{*{20}l} X^{\prime}_{k} = sigmoid(Y_{k} \times W) &= \frac{1}{1+exp(-Y_{k} \times W)} \\[0.4em] where ~~ W &= \left(\begin{array}{llll} w_{11} & w_{12} & \ldots & w_{1n} \\ \ldots & \ldots & \ldots & \ldots \\ w_{l1} & w_{l2} & \ldots & w_{ln} \end{array}\right) \end{array} $$

The logical stress-gene correlation layer has a single neural network structure. The weights of the logical stress-gene correlation layer are learned by minimizing the difference between observed biomarker gene vector, Xk, and predicted biomarker gene vector, \(X^{\prime }_{k}\).

Comparison of the predicted vector with the label vector

Cross-entropy is a widely-used objective function in logistic regression problem because of its robustness to outlier-including data [12]. Thus, we use cross-entropy as the objective function to measure the difference of observed biomarker gene vector, Xk, and predicted biomarker gene vector, \(X^{\prime }_{k}\), as below:

$$\begin{array}{*{20}l} loss_{W} = & - \sum\limits^{K}_{k=1} \left(X_{k} log (sigmoid(Y_{k}W)) \right.\\[-0.5em] &\left. \;\; + (1 - X_{k}) log (1-sigmoid(Y_{k}W)) \right) \end{array} $$

By minimizing the cross-entropy loss, logistic functions of the output prediction layer are learned to predict the true labels. Outputs of logistic functions can predict that a given gene responds to only one stress or to multiple stresses. Although it is natural for a gene to be involved in multiple stresses, we propose a new loss term because we aim to find a biomarker gene that is specific to a single stress. To control relationships between genes and stresses, we define a new group penalty loss. For each feature weight, the penalty is calculated based on how much stresses are involved. Given a gene n, a stress vector gn is defined as gn=[gn1,gn2,...,gnl] with l stresses and gnl=max(wl,2n,wl,2n+1). Then, the a group penalty is defined as \((\sum (g_{n}))^{2}\). Since we generate the output with a logistic function, gnl will have a value between 0 and 1. In other words, if gn is specific to a single stress, the group penalty will be 1. However, if the gene n reacts to multiple stresses, the penalty value will increase quickly. Using these characteristics, the group penalty loss is defined as below:

$$loss_{group} = \alpha \sum\limits^{N}_{n=1} \left(\sum\limits^{L}_{l=1} g_{nl}\right)^{2}$$

On the group penalty loss, hyper-parameter α regulates effects of group penalty terms. Too large α imposes excessive group penalties, so genes that respond to multiple stresses are linked only to a single stress. On the other hand, if the α value is too small, most genes respond to multiple stresses. To balance this trade-off, we use well-known stress-related genes to allow our model to predict the genes within the top 500 biomarker genes at each stress. Therefore, in our experiment, the α was set to 0.06, and the genes are introduced in “Ranks of biomarker genes and the group effect for gene selection” section.

Submodel 2: stress type prediction model

From biomarker gene discovery model, the relationships between stresses and genes are obtained by stress-gene correlation layer W. To build stress type prediction model from feature vectors, we utilize the transposed logical layer WT and define a probability model as below:

$$A_{k} = sigmoid \left(X_{k} W^{T}\right)$$
$$A_{kl} = sigmoid \left(\sum\limits^{N}_{i=1} x_{ki} w_{il} \right) $$

Matrix W is calculated from a training process of the biomarker gene discovery model. Ak means an activation value vector of stress types, and it shows very large deviations depending on the samples. Therefore, normalization is required and performed as below:

$$A^{norm}_{k} = \frac{A_{k}}{\sum\limits^{N}_{n}{x_{kn}}} $$

For the logistic filter, these normalized embedded features vectors encapsulate average weight stress-feature relationship values that reduce variances among the vectors with different samples. As another effect of the normalization, absolute average weights are considered rather than relative indicator like softmax. So, false positive rates of predicted stress labels can be reduced. Using the normalized weights \(A^{norm}_{k}\), logistic filter is defined to generate a probability as below:

$$g_{k}(A^{norm}_{k}) = \frac{1}{1+b_{l} \times exp(A^{norm}_{k}-a_{l})} $$

where a and b are general vector parameters of size L of logistic model g(x).

Learning of this logistic filer layer is started with normalization of the logistic filter outputs. This facilitates learning by regularizing the mean of the vectors. Then, to minimize loss of positive labels and entropy for negative labels, we adopted the Confident Multiple Choice Learning(CMCL) loss function [13] for our model as below:

$$\begin{array}{*{20}l} loss_{CMCL} &(Y_{k}, g(A^{norm}_{k})) = \\ &\sum\limits^{K}_{k=1} \left((1-A^{norm}_{k})^{2} - \beta \sum\limits^{L}_{l \neq Y_{k}} log(A^{norm}_{k}) \right) \end{array} $$

To avoid overfitting, a pseudo-parameter β is set by recommended setting from the original CMCL paper [13]. In our experiments, β=0.01≈1/108 is utilized.

Results

In this paper, two types of experiments were conducted to evaluate the performance of StressGenePred.

Evaluation of stress type prediction

StressGenePred was evaluated for the task of stress type prediction. The total time-series dataset (138 samples) was divided randomly 20 times to build a training dataset (108 samples) and a test dataset (30 samples). For the training and test datasets, a combination analysis was performed between two feature embedding methods (fold change and limma) and three classification methods (StressGenePred, SVM, and RF). The accuracy measurement of the stress type prediction was repeated 20 times.

Table 1 shows that feature embedding with fold change is more accurate in the stress type prediction than limma. Our prediction model, StressGenePred, more correctly predicted the stress types compared to other methods.

Table 1 Result of stress type prediction
Full size table

Then, we further investigated in which cases our stress type prediction model predicted incorrectly. We divided the total dataset into 87 samples of training dataset and 51 samples of test dataset (28 cold stress and 23 heat stress samples). Then, we trained our model using training dataset and predicted stress types for the test dataset. Figure 5 shows three of 51 samples were predicted wrong in our model. Among them, two time-series data of cold stress type were predicted salt then cold stress types, and those samples were actually treated to both stresses [14]. This observation implied our prediction was not completely wrong.

Fig. 5
figure 5

Stress type prediction result. Above GSE64575-NT are cold stress samples and the rest are heat stress samples. E-MEXP-3714-ahk2ahk3 and E-MEXP-3714-NT samples are predicted wrong in our model, but they are not perfectly predicted wrong because they are treated to both salt and cold stress [14]

Full size image

Evaluation of biomarker gene discovery

The second experiment was to test how accurately biomarker genes can be predicted. Our method was compared with Fisher’s method. The p-value of Fisher’s method was calculated using the limma tool for each gene for each stress types (heat, cold, drought, salt). The genes were then sorted according to their p-value scores so that the most responsive genes came first.

Then, we collected known stress-responsive genes of each stress type in a literature search, investigated EST profiles of the genes, and obtained 44 known biomarker genes with high EST profiles. We compared the ranking results of our method and Fisher method with the known biomarker genes. The Table 2 shows that 30 of 44 genes ranked higher in the results of our method than the Fisher method. Our method was better in the biomarker gene discovery than Fisher method (p=0.0019 for the Wilcoxon Signed-Rank test).

Table 2 Gene rank comparison
Full size table

Our method is designed to exclude genes that respond to more than one stress whenever possible and to detect genes that only respond to one type of stress. To investigate how this works, we collected genes known to respond to more than one stress. Among them, we excluded genes that resulted in too low a ranking (>3,000) for all stress cases.

When comparing the results of our method to the Fisher method for these genes, 13 of 21 genes ranked lower in the result of our method than Fisher method (Table 3). This suggests that our model detects genes that respond only to one type of stress. Figure 6 shows a plot of changes in expression levels of some genes for multiple stresses. These genes responded to multiple stresses in the figure.

Fig. 6
figure 6

Visualization of gene expression for multiple stress associated genes. Genes that were investigated to be responsive to multiple stresses. In the visualization results, these genes responded to multiple stresses and were not suitable for biomarker genes of a single stress

Full size image
Table 3 Rank comparison of multiple stress-responsive genes
Full size table

Literature-based investigation for discovered biomarker genes

In order to evaluate whether our method found the biomarker gene correctly, we examined in literature the relevance of each stress type to the top 40 genes. Our findings are summarized in this section and discussed further in the discussion section.

In the case of heat stress, we identified heat-related genes, including HSFA2, which are known to play an essential role in the plant’s heat response. Heat shock protein genes such as HSP101, HSP15.7, HSP17.6, HSP20-like, Hsp21, Hsp22, Hsp70B, and Hsp70T-2 we have identified are known to be highly related to heat stress. Mitochondrial heat shock protein genes such as AtHSP23.6 and MTHSC70-2 and chloroplast position genes such as HSP21 have also been identified. We predicted NADH dehydrogenases of energy metabolism which are related to heat stress.

In the case of salt stress, we have identified previously known ABA-related genes, such as ABI2, ABF1, HAI1 and HAI2, and late embryonic development-rich protein genes, such as AtLEA4-5, LEA7. Water biomarker genes as ATD18, NAC019, NAC047 and RAP2.6 were identified. We have also identified genes of common stress-response class genes, such as ALDH7B4 and ALDH2B7, AtMYB74, CYP707A1, and CYP94B3.

In the case of cold stress, we identified ADS2, AtGolS3, FP6, FRO3, GSTU18, UDP-glucosyl transferase, some lipid metabolism-related genes that are involved in a rearrangement of physical properties of the plasma membrane and cell wall. In addition, we identified genes related to development such as AGL20, BBX29, and GI. We also identified water biomarker genes such as ABF1, BBX25, and RAP2.1.

Finally, in the case of drought stress, we confirmed the involvement of well-known genes such as HIS1-3, NAC019 and SAUR63. Besides, we were able to identify common biomarker genes such as development-related AGL19 and CYP89A9. In addition, we predicted genes involved in microorganism development and differentiation such as ATHB-7, BRS1, GAMMA-VPE, GOLS2, MEE3, and PDCB3.

Discussion

In this section, we discuss gene-stress relationship in depth, referring to the current literature.

Biological function of heat stress-responsive genes

For heat stress, our model identified HSFA2, Hsp21, Hsp22, Hsp70B, Hsp70T-2, HSP101, HSP20-like, HSP17.6, HSP15.7, and NADH dehydrogenases. In heat stress, HSFA2 takes an essential part of heat response and may relate with histone methylation. HSFA2 is highly inducible and a direct target of HSFA1. HSFA2 is known to bind to the promoter of Hsp22 in vitro experiments [15]. Hsp22 is an endomembrane-localized protein during heat stress [16]. Hsp70 family proteins are well-known proteins, however functionally diversified. Hsp21 is small heat shock protein, which required for the development of chloroplasts [17] and associates with the thylakoid membranes [18]. HSP70 is a molecular chaperone and support plastid protein translocation [19]. HSP70b may involve a protein accumulation in the cytosol [20] and inducible by heat shock, not by low temperature [21]. HSP101 is a member of the Hsp100/ClpB family of proteins, is thought to be involved in disaggregation of misfolded proteins [22]. HSP101 protects protein translation factors during heat stress [23]. HSP17.6 is induced by heat and osmotic stress, and overexpression of AtHSP17.6A increase salt and drought tolerance in Arabidopsis [24]. Hsp17.6CII is a peroxisome-localized catalase chaperone [23]. Also, HSP15.7 is inducible by heat shock and high light, detected in peroxisome [25]. Interestingly, both the chloroplast-located genes HSP21 and mitochondrial heat shock proteins such as AtHSP23.6 and MTHSC70-2 were identified.

Biological function of cold stress-responsive genes

For cold stress, our model predicted many genes involved in plasma membrane fluidity and cell wall rigidity. ADS2 gene adjusts the composition of membrane lipids, and confer chilling and freezing tolerance in Arabidopsis [26]. AtGolS3 codes galactinol synthase 3 which is only induced by cold stress and target of DREB1A [27]. FP6 is farnesylated protein 6, interacts with ACBP2, and the transgenic plants showed overexpression had Cd(II) tolerance [28]. FRO is an iron chelate reductase, and FRO3 is predicted to involve in iron metabolism and iron reduction in the root [29].

Biological function of salt stress-responsive genes

For salt stress, our model identified ABI2, ABF1, HAI1, HAI2, LEA7, AtLEA4-5, NAC019, NAC047, ATD18, RAP2.6, CYP707A1, CYP94B3, AtMYB74, ALDH7B4 and ALDH2B7 genes. In salt stress, many genes of downstream signal transduction or possibly related with ABA such as ABI2, ABF1, HAI1 and HAI2, late embryogenesis abundant proteins like LEA7 and AtLEA4-5. ABI2 is a protein phosphatase 2C, interacts with SOS2 and inhibits SOS2 activity [30]. ABI2 involved in ABA-mediated transcription of chloroplast genes and link nitrate uptake and utilization [31]. ABF1 regulates the induction of DREB2A [17] and is necessary for seedling establishment during winter. Expression of ABF1 is induced by cold, heat, and ABA [32]. HAI1 has roles in decreasing the low water potential signaling that controls proline and osmoregulatory solute accumulation [33]. HAI1 is involved in feedback regulation of ABA signaling and HAI2 is a positive regulator of ABA and related to cell signaling mediated by ABA [34]. Late embryogenesis abundant proteins like LEA7 could protect the plasma membrane or organellar membrane. Its activity occurs at cytosol exposed side of the membrane [35]. AtLEA4-5 is a member of small, hydrophilic protein group, showing high expression levels in response hyperosmotic, drought, and ABA treatment [36]. NAC is a water stress-responsive transcription factor. NAC019 has ABRE-like motifs, and the motifs could induce expression in response to stress. NAC019 promoter interacts with a key mediator of ABA expression, ABI4, AP2 family transcription factors [37]. ATD18, also known as RAB18, is dehydrin family protein and required for ABA signal transduction. ATD18 expression is repressed by ethylene treatment [38]. RAP2.6 is induced by salt and osmotic stress. RAP2.6 promoter contains ABRE, DRE, MYBR, W-box, RAVbox, so seems like it may be an essential intersection in biotic and abiotic signaling [39]. CYP707A1 is a member of cytochrome P450 CYP707A family encoding ABA-8’-hydroxylases. CYP707As are working as structure modifiers of metabolites responsive to the abiotic stress, exogenous ABA treatment, and dehydration [40].

Biological function of drought stress-responsive genes

For drought stress, our model predicted many of early response genes against water stress. HIS1-3 has histone H1 globular domain and is expressed by dehydration and ABA [41]. SAUR63 is a member of early auxin-responsive genes family, promoting organ elongation by auxin stimulation in Arabidopsis [42]. AGL19 is expressed by a short-day photoperiod and vernalization [43]. Gamma-VPE is a type of vegetative VPE and induced during senescence, wounding, and pathogen infection [44]. Gamma-VPE has a cysteine protease activity and may be involved in plant hypersensitive cell death [41]. GOLS2 increase galactinol biosynthesis and improve oxidative stress tolerance. This gene regulated by HsfA3 [45]. AtGolS2-expressing transgenics displayed significantly improved drought tolerance [46]. MEE3 (Maternal Effect Embryo arrest 3) is a subfamily of single-MYB transcription factor and related to regulation of early photomorphogenesis [47]. BRS1 is involved in brassinosteroid signaling pathway. This gene was expressed strongly in the root and related to plant root development [48]. BRS1 gene encodes a serine carboxypeptidase II-like protein, secreted and active serine carboxypeptidase [49].

Stress responsive transcription factors

We examined genes that change expression levels with respect to temperature stress. Some of these genes were transcription factors, and they did not appear for other type stress because our predictive model predicted genes specifically associated with specific stresses. But what we can observe is that TFs, such as ARF, ERF, bZIP, which are involved in plant hormonal reactions, can be activated at both high and low temperatures when there are temperature-related stresses. Our model predicted NAD4L and NAD5 (NADH dehydrogenase subunits 4L and 5) and several unknown genes encoded in the mitochondrial genome that only affected heat stress. Some genes in mitochondria may be involved in the initial transcriptional response when under heat stress. In the case of salt and drought stress, we predicted two TF genes, HD-ZIP (ATHB-5; AT2G468) and NAC (ANAC019: AT1G5289), which are associated with both stresses. These two genes are likely to respond early to water-related stress. NAC domain TF is prominent in salt stress, but not drought stress. We observed SAURs (small auxin upregulated RNA) in drought stress, which means that it is a small RNA that is actively involved in plant physiological regulation during long-term water deficiency.

Diversity of responses to multiple stresses

In this study, we selected four different types of stress to find and classify the affected genes. The effects of these environmental stresses are overwhelming, but they do not define specific parts of metabolism and physiological consequences. The characteristics of the four stresses we studied have in common with the physiological response associated with water. Although they react differently depending on the signaling pathways of each stress, they do not have complete separation because of the commonalities associated with using water. Many of the biomarker genes we have found have been shown to respond to multiple stresses, and have shown a variety of phenotypes for different stresses in plants that have been transfected with mutations or recombinant genes. The APX gene is a gene that responds to all four stresses, and other genes such as AREB, AtRIP, DREB, Gols and MAPs are well known as genes that respond to multiple stresses. In this study, the genes involved in the specific stresses we predicted were either identical in other stresses or related to multiple complex stresses.

Conclusion

This study presented StressGenePred, a method of analyzing a set of time-series transcriptome data for multiple types of stress. StressGenePred consists of twin classification models to achieve two analytic goals. The biomarker gene discovery model aims to discover genes that respond to specific stresses. The goal of the stress type prediction model is to classify samples into four types of stress, heat, cold, drought, and salt. The key problem in this study is to train the StressGenePred model from high-dimension (approximately 20,000 genes) and low-sample-size data (138 sample data in the study). Analysis of high-dimension and low-sample-size data is a difficult computational problem that many researchers are studying.

In order to be trained with a small number of data, StressGenePred is designed to use a simplified architecture (only one logical layer) with a small number of parameters. StressGenePred is also designed so that twin classification models share the same logical layer and its parameters. In twin classification models, the logical layer is used symmetrically with respect to input and output. For example, the input and output in the biomarker gene discovery model are stress and genes, respectively, and the stress type prediction model is vice versa. When the logical layer is shared by both classification models, the parameters of the logical layer are trained redundantly in both models, reducing the number of data required.

In experiments using Arabidopsis stressed gene expression data, StressGenePred detected known stress-related genes at a higher rank compared to Fisher’s method. StressGenePred showed better performance than random forest and support vector machine in stress type prediction.

Availability of data and materials

The data information and source codes of StressGenePred are available at https://github.com/bhi-kimlab/StressGenePred.

Abbreviations

CMCL:

Confident multiple choice learning

DEG:

Differentially expressed gene

FC:

Fold change

GEO:

Gene expression omnibus

PCA:

Principal component analysis

RF:

Random forest

RNA-seq:

Ribonucleic acid-sequencing

SVM:

Support vector machine

References

  1. Eisen MB, Brown PO. DNA arrays for analysis of gene expression. Methods Enzymol. 1999; 303:179–205.

    CAS  PubMed  Article  Google Scholar 

  2. Wang Z, Gerstein M, Snyder M. RNA-Seq: a revolutionary tool for transcriptomics. Nat Rev Genet. 2009; 10(1):57–63.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  3. Kolesnikov N, Hastings E, Keays M, Melnichuk O, Tang YA, Williams E, Dylag M, Kurbatova N, Brandizi M, Burdett T, et al. ArrayExpress update—simplifying data submissions. Nucleic Acids Res. 2014; 43(D1):1113–6.

    Article  CAS  Google Scholar 

  4. Edgar R, Domrachev M, Lash AE. Gene Expression Omnibus: NCBI gene expression and hybridization array data repository. Nucleic Acids Res. 2002; 30(1):207–10.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  5. Lan H, Carson R, Provart NJ, Bonner AJ. Combining classifiers to predict gene function in Arabidopsis thaliana using large-scale gene expression measurements. BMC Bioinformatics. 2007; 8(1):358.

    PubMed  PubMed Central  Article  CAS  Google Scholar 

  6. Ko D, Xu W, Windle B. Gene function classification using NCI-60 cell line gene expression profiles. Comput Biol Chem. 2005; 29(6):412–9.

    CAS  PubMed  Article  Google Scholar 

  7. Tong D-L. Hybridising Genetic Algorithm-Neural Network (GANN) in marker genes detection. In: 2009 International Conference on Machine Learning and Cybernetics. Vol. 2. Hebei: IEEE: 2009. p. 1082–1087.

    Google Scholar 

  8. Wu M-Y, Dai D-Q, Shi Y, Yan H, Zhang X-F. Biomarker identification and cancer classification based on microarray data using laplace naive bayes model with mean shrinkage. IEEE/ACM Trans Comput Biol Bioinforma. 2012; 9(6):1649–62.

    Article  Google Scholar 

  9. Ko D, Windle B. Enriching for correct prediction of biological processes using a combination of diverse classifiers. BMC Bioinformatics. 2011; 12(1):189.

    PubMed  PubMed Central  Article  Google Scholar 

  10. Ahn H, Jung I, Chae H, Kang D, Jung W, Kim S. HTRgene: integrating multiple heterogeneous time-series data to investigate cold and heat stress response signaling genes in Arabidopsis. In: 2018 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). Madrid: IEEE: 2018. p. 393–8.

    Google Scholar 

  11. Ernst J, Bar-Joseph Z. STEM: a tool for the analysis of short time series gene expression data. BMC Bioinformatics. 2006; 7(1):191.

    PubMed  PubMed Central  Article  CAS  Google Scholar 

  12. Prager MH. Comparison of logistic and generalized surplus-production models applied to swordfish, Xiphias gladius, in the north Atlantic Ocean. Fish Res. 2002; 58(1):41–57.

    Article  Google Scholar 

  13. Lee K, Hwang C, Park KS, Shin J. Confident multiple choice learning. In: Proceedings of the 34th International Conference on Machine Learning. Vol. 70. International Convention Centre, Sydney: PMLR: 2017. p. 2014–23.

    Google Scholar 

  14. Jeon J, Kim J. Arabidopsis response Regulator1 and Arabidopsis histidine phosphotransfer Protein2 (AHP2), AHP3, and AHP5 function in cold signaling. Plant Physiol. 2013; 161(1):408–24.

    CAS  PubMed  Article  Google Scholar 

  15. Lämke J, Brzezinka K, Bäurle I. HSFA2 orchestrates transcriptional dynamics after heat stress in Arabidopsis thaliana. Transcription. 2016; 7(4):111–4.

    PubMed  PubMed Central  Article  CAS  Google Scholar 

  16. Helm KW, Schmeits J, Vierling E. An endomembrane-localized small heat-shock protein from Arabidopsis thaliana. Plant Physiol. 1995; 107(1):287.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  17. Ohama N, Sato H, Shinozaki K, Yamaguchi-Shinozaki K. Transcriptional regulatory network of plant heat stress response. Trends Plant Sci. 2017; 22(1):53–65.

    CAS  PubMed  Article  Google Scholar 

  18. Bernfur K, Rutsdottir G, Emanuelsson C. The chloroplast-localized small heat shock protein Hsp21 associates with the thylakoid membranes in heat-stressed plants. Protein Sci. 2017; 26(9):1773–84.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  19. Chotewutmontri P, Bruce BD. Non-native, N-terminal Hsp70 molecular motor recognition elements in transit peptides support plastid protein translocation. J Biol Chem. 2015; 290(12):7602–21.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  20. Aparicio F, Thomas CL, Lederer C, Niu Y, Wang D, Maule AJ. Virus induction of heat shock protein 70 reflects a general response to protein accumulation in the plant cytosol. Plant Physiol. 2005; 138(1):529–36.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  21. Sung DY, Vierling E, Guy CL. Comprehensive expression profile analysis of the Arabidopsis Hsp70 gene family. Plant Physiol. 2001; 126(2):789–800.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  22. Tonsor S, Scott C, Boumaza I, Liss T, Brodsky J, Vierling E. Heat shock protein 101 effects in A. thaliana: genetic variation, fitness and pleiotropy in controlled temperature conditions. Mol Ecol. 2008; 17(6):1614–26.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  23. Merret R, Carpenier M-C, Favory J-J, Picart C, Descombin J, Bousquet-Antonelli C, Tillard P, Lejay L, Deragon J-M, Charng Y-y. Heat-shock protein HSP101 affects the release of ribosomal protein mRNAs for recovery after heat shock. Plant Physiol. 2017; 174(2):1216–25.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  24. Sun W, Bernard C, Van De Cotte B, Van Montagu M, Verbruggen N. At-HSP17. 6A, encoding a small heat-shock protein in Arabidopsis, can enhance osmotolerance upon overexpression. Plant J. 2001; 27(5):407–15.

    CAS  PubMed  Article  Google Scholar 

  25. Li J, Hu J. Using co-expression analysis and stress-based screens to uncover arabidopsis peroxisomal proteins involved in drought response. PLoS ONE. 2015; 10(9):1–13.

    Google Scholar 

  26. Shi Y, Ding Y, Yang S. Cold signal transduction and its interplay with phytohormones during cold acclimation. Plant Cell Physiol. 2014; 56(1):7–15.

    PubMed  Article  CAS  Google Scholar 

  27. Taji T, Ohsumi C, Iuchi S, Seki M, Kasuga M, Kobayashi M, Yamaguchi-Shinozaki K, Shinozaki K. Important roles of drought-and cold-inducible genes for galactinol synthase in stress tolerance in Arabidopsis thaliana. Plant J. 2002; 29(4):417–26.

    CAS  PubMed  Article  Google Scholar 

  28. Gao W, Xiao S, Li H-Y, Tsao S-W, Chye M-L. Arabidopsis thaliana acyl-CoA-binding protein ACBP2 interacts with heavy-metal-binding farnesylated protein AtFP6. New Phytol. 2009; 181(1):89–102.

    CAS  PubMed  Article  Google Scholar 

  29. Wu H, Li L, Du J, Yuan Y, Cheng X, Ling H-Q. Molecular and biochemical characterization of the Fe (III) chelate reductase gene family in Arabidopsis thaliana. Plant Cell Physiol. 2005; 46(9):1505–14.

    CAS  PubMed  Article  Google Scholar 

  30. Ohta M, Guo Y, Halfter U, Zhu J-K. A novel domain in the protein kinase SOS2 mediates interaction with the protein phosphatase 2C ABI2. Proc Nat Acad Sci. 2003; 100(20):11771–6.

    CAS  PubMed  Article  PubMed Central  Google Scholar 

  31. Léran S, Edel KH, Pervent M, Hashimoto K, Corratgé-Faillie C, Offenborn JN, Tillard P, Gojon A, Kudla J, Lacombe B. Nitrate sensing and uptake in Arabidopsis are enhanced by ABI2, a phosphatase inactivated by the stress hormone abscisic acid. Sci Signal. 2015; 8(375):43.

    Article  CAS  Google Scholar 

  32. Sharma PD, Singh N, Ahuja PS, Reddy TV. Abscisic acid response element binding factor 1 is required for establishment of Arabidopsis seedlings during winter. Mol Biol Rep. 2011; 38(8):5147–59.

    CAS  PubMed  Article  Google Scholar 

  33. Bhaskara GB, Nguyen TT, Verslues PE. Unique drought resistance functions of the highly ABA-induced clade A protein phosphatase 2Cs. Plant Physiol. 2012; 160(1):379–95.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  34. Lim CW, Kim J-H, Baek W, Kim BS, Lee SC. Functional roles of the protein phosphatase 2C, AtAIP1, in abscisic acid signaling and sugar tolerance in Arabidopsis. Plant Sci. 2012; 187:83–8.

    CAS  PubMed  Article  Google Scholar 

  35. Candat A, Paszkiewicz G, Neveu M, Gautier R, Logan DC, Avelange-Macherel M-H, Macherel D. The ubiquitous distribution of late embryogenesis abundant proteins across cell compartments in Arabidopsis offers tailored protection against abiotic stress. Plant Cell. 2014; 26(7):3148–66.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  36. Olvera-Carrillo Y, Campos F, Reyes JL, Garciarrubio A, Covarrubias AA. Functional analysis of the group 4 late embryogenesis abundant proteins reveals their relevance in the adaptive response during water deficit in Arabidopsis. Plant Physiol. 2010; 154(1):373–90.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  37. Hickman R, Hill C, Penfold CA, Breeze E, Bowden L, Moore JD, Zhang P, Jackson A, Cooke E, Bewicke-Copley F, et al. A local regulatory network around three NAC transcription factors in stress responses and senescence in Arabidopsis leaves. Plant J. 2013; 75(1):26–39.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  38. Tanaka Y, Sano T, Tamaoki M, Nakajima N, Kondo N, Hasezawa S. Ethylene inhibits abscisic acid-induced stomatal closure in Arabidopsis. Plant Physiol. 2005; 138(4):2337–43.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  39. Zhu Q, Zhang J, Gao X, Tong J, Xiao L, Li W, Zhang H. The Arabidopsis AP2/ERF transcription factor RAP2. 6 participates in ABA, salt and osmotic stress responses. Gene. 2010; 457(1):1–12.

    CAS  Article  PubMed  Google Scholar 

  40. Okamoto M, Kuwahara A, Seo M, Kushiro T, Asami T, Hirai N, Kamiya Y, Koshiba T, Nambara E. CYP707A1 and CYP707A2, which encode abscisic acid 8’-hydroxylases, are indispensable for proper control of seed dormancy and germination in Arabidopsis. Plant Physiol. 2006; 141(1):97–107.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  41. Rea M, Zheng W, Chen M, Braud C, Bhangu D, Rognan TN, Xiao W. Histone H1 affects gene imprinting and DNA methylation in Arabidopsis. Plant J. 2012; 71(5):776–86.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  42. Chae K, Isaacs CG, Reeves PH, Maloney GS, Muday GK, Nagpal P, Reed JW. Arabidopsis SMALL AUXIN UP RNA63 promotes hypocotyl and stamen filament elongation. Plant J. 2012; 71(4):684–97.

    CAS  PubMed  Article  Google Scholar 

  43. Kang M-J, Jin H-S, Noh Y-S, Noh B. Repression of flowering under a noninductive photoperiod by the HDA 9-AGL 19-FT module in Arabidopsis. New Phytol. 2015; 206(1):281–94.

    CAS  PubMed  Article  Google Scholar 

  44. Kuroyanagi M, Yamada K, Hatsugai N, Kondo M, Nishimura M, Hara-Nishimura I. Vacuolar processing enzyme is essential for mycotoxin-induced cell death in Arabidopsis thaliana. J Biol Chem. 2005; 280(38):32914–20.

    CAS  PubMed  Article  Google Scholar 

  45. Song C, Chung WS, Lim CO. Overexpression of heat shock factor gene HsfA3 increases galactinol levels and oxidative stress tolerance in Arabidopsis. Mol Cells. 2016; 39(6):477.

    CAS  PubMed  PubMed Central  Article  Google Scholar 

  46. Himuro Y, Ishiyama K, Mori F, Gondo T, Takahashi F, Shinozaki K, Kobayashi M, Akashi R. Arabidopsis galactinol synthase AtGolS2 improves drought tolerance in the monocot model Brachypodium distachyon. J Plant Physiol. 2014; 171(13):1127–31.

    CAS  PubMed  Article  Google Scholar 

  47. Hamaguchi A, Yamashino T, Koizumi N, Kiba T, Kojima M, Sakakibara H, Mizuno T. A small subfamily of Arabidopsis RADIALIS-LIKE SANT/MYB genes: a link to HOOKLESS1-mediated signal transduction during early morphogenesis. Biosci Biotechnol Biochem. 2008; 72(10):2687–96.

    CAS  PubMed  Article  Google Scholar 

  48. Deng Q, Wang X, Zhang D, Wang X, Feng C, Xu S. BRS1 function in facilitating lateral root emergence in Arabidopsis. Int J Mol Sci. 2017; 18(7):1549.

    CAS  PubMed Central  Article  Google Scholar 

  49. Zhou A, Li J. Arabidopsis BRS1 is a secreted and active serine carboxypeptidase. J Biol Chem. 2005; 280(42):35554–61.

    CAS  PubMed  Article  Google Scholar 

Download references

Acknowledgements

The authors would like to thank those who conducted stress treatment experiments, measured gene expression data, and published the data in databases.

About this supplement

This article has been published as part of BMC Genomics Volume 20 Supplement 11, 2019: Selected articles from the IEEE BIBM International Conference on Bioinformatics & Biomedicine (BIBM) 2018: genomics. The full contents of the supplement are available online at https://bmcgenomics.biomedcentral.com/articles/supplements/volume-20-supplement-11.

Funding

This work and publication costs were supported by National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT (No. NRF-2017M3C4A7065887), and the Collaborative Genome Program for Fostering New Post-Genome Industry of the National Research Foundation (NRF) funded by the Ministry of Science and ICT (MSIT) (No. NRF-2014M3C9A3063541). This work was supported for W.J. by the Agenda program (No. PJ014307), Rural Development of Administration of Republic of Korea.

Author information

Author notes

  1. Dongwon Kang and Hongryul Ahn contributed equally to this work.

Authors and Affiliations

  1. Department of Computer Science and Engineering, Seoul National University, Seoul, Republic of Korea

    Dongwon Kang, Hongryul Ahn, Sangseon Lee & Sun Kim

  2. Interdisciplinary Program in Bioinformatics, Seoul National University, Seoul, Republic of Korea

    Chai-Jin Lee & Sun Kim

  3. Department of Crop Science, Konkuk University, Seoul, Republic of Korea

    Jihye Hur & Woosuk Jung

  4. Bioinformatics Institute, Seoul National University, Seoul, Republic of Korea

    Sun Kim

Authors
  1. Dongwon Kang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hongryul Ahn
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sangseon Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Chai-Jin Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jihye Hur
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Woosuk Jung
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Sun Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

SK, WJ, DK, and HA designed the project. HA collected data and HA and DK discussed the task. SK, DK, and SL designed and discussed the method. DK implemented the method and performed evaluation analysis. WJ and JH performed biological interpretation of results. WJ, JH, DK, HA, and CJL found the related reference. DK, WJ, SK, HA, and CJL wrote the article. All authors read and approved the final manuscript.

Corresponding authors

Correspondence to Woosuk Jung or Sun Kim.

Ethics declarations

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare that they have no competing interests.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Kang, D., Ahn, H., Lee, S. et al. StressGenePred: a twin prediction model architecture for classifying the stress types of samples and discovering stress-related genes in arabidopsis. BMC Genomics 20, 949 (2019). https://doi.org/10.1186/s12864-019-6283-z

Download citation

  • Published:

  • DOI: https://doi.org/10.1186/s12864-019-6283-z

Keywords

  • Arabidopsis
  • Stress
  • Transcriptome
  • Time-series
  • Machine learning