Abstract
Background
The notion of centrality is used to identify “important” nodes in social networks. Importance of nodes is not well-defined, and many different notions exist in the literature. The challenge of defining centrality in meaningful ways when network edges can be positively or negatively weighted has not been adequately addressed in the literature. Existing centrality algorithms also have a second shortcoming, i.e., the list of the most central nodes are often clustered in a specific region of the network and are not well represented across the network.
Methods
We address both by proposing Ablatio Triadum (ATria), an iterative centrality algorithm that uses the concept of “payoffs” from economic theory.
Results
We compare our algorithm with other known centrality algorithms and demonstrate how ATria overcomes several of their shortcomings. We demonstrate the applicability of our algorithm to synthetic networks as well as biological networks including bacterial co-occurrence networks, sometimes referred to as microbial social networks.
Conclusions
We show evidence that ATria identifies three different kinds of “important” nodes in microbial social networks with different potential roles in the community.
Similar content being viewed by others
Background
The concept of centrality is foundational in social network theory and its underlying motivation is to find the most important or “critical” nodes in a large complex social network [1]. In this type of network, one may be interested in finding the most influential or the most popular individual. A search engine may want to rank the hits resulting from a search, depending on how well linked it is in the network. In a terror network, an agency may be interested in finding the ringleader or the top leadership. Thus, “centrality” can have multiple meanings, and different metrics and methods are worth exploring.
With the advent of systems biology approaches, large-scale biological networks have become commonplace. Gene regulatory networks [2] model the interactions between genes, while protein-protein interaction (PPI) networks [3] represent the interaction of proteins. Microbial social networks [4–6] attempt to model the complex interactions between microbes within a microbial community, such as those that inhabit the human gut or those that can be found in diseased coral.
It is well known that microbes in a community interact. These interactions may occur through the use of quorum sensing molecules, other signalling molecules, metabolites and/or toxins [7–9]. However, lacking the access to precise interaction information in sampled microbial communities, it has been suggested that bacterial co-occurrence networks inferred from metagenomic studies are a crude form of microbial social networks [4, 6]. A bacterial co-occurrence network [10] is an undirected, weighted network with nodes that represent bacterial taxa present in the community and edges that correspond to how strongly the two taxa tend to co-occur (i.e., co-infect) in the sampled communities. Edge weights can be positive or negative lying in the range [−1,+1]. We show an example of this in Fig. 1, using data from a lung microbiome study. Green edges indicate positive correlations and red edges indicate negative ones, with edge thickness indicating strength of correlations. We visualize results using the Fruchterman-Reingold algorithm [11] within Cytoscape [12]. Even a cursory visual inspection of the network suggests the presence of dense subgraphs representing strongly co-occurring groups of bacteria (referred to as clubs [6]). In co-occurence networks, strong green edges suggest the likelihood of cooperation, while strong red edges suggest competition.
The following questions arise naturally in these investigations. Is it possible to identify bacterial taxa that drive or control the behavior of the community through their interactions? Can the first infectors or colonizers of the community be identified? What is the effect of disrupting a node or edge of such a biological network? All the above questions highlight the importance of studying central nodes in biological networks [13]. We suggest three notions of centrality that are potentially important to biological networks, and especially to microbial social networks. The work in this paper addresses all three notions:
-
1.
For each club (high density subgraph), we refer to a dominant node as a leader node [14], or an entity responsible for connecting many individuals and driving the behavior of the club.
-
2.
We define a villain node as one that has many strong negative edges to a club. Unity against a common enemy is a frequent theme in social networks [15].
-
3.
Nodes that connect two or more dense subgraphs (clubs) are referred to as bridge nodes. In general social networks, this would correspond to someone who has the ability to link different social circles [15].
Centrality concepts [16, 17] can be classified into three categories: degree centrality, closeness centrality, and betweenness centrality. Degree centrality assumes that the most important nodes have high connectivity or degree. It is useful in identifying popular individuals in a social network. Closeness centrality interprets centrality with respect to a distance metric, identifying nodes that are centrally located. This would be useful in identifying where to place an important network resource (e.g., fire station or database server). Betweenness centrality defines a central node as one that lies on many shortest paths. Betweenness centrality would help identify important junctions in a complex train or information flow network. Other approaches define an entity’s centrality by the importance of its friends in the social network. Eigenvector-based approaches [16] for centrality extend the ideas of degree and closeness centrality by explicitly defining the centrality of a node in terms of the importance of its neighbors. Google’s PageRank algorithm [18] is an example of this approach. In this paper, we will propose an algorithm that combines and generalizes these concepts.
Most of these approaches also generalize to weighted social networks, where edge weights represent the strength of the relationship or influence between nodes. Distance-based methods like closeness and betweenness extend trivially. Degree can be generalized to weighted degree. The original version of PageRank assumes edge weights of 0 and 1, but subsequent attempts have been made to generalize the algorithm to weighted networks [19]. However, not many generalize readily to networks with negative edge weights, which is an important characteristic of real social networks because it helps distinguish between “indifference” and “dislike”. PageTrust [20] extends PageRank to handle negative edges but, since all final centralities are positive, it becomes difficult to distinguish a villain vs. a node with few friends as they both have low values. The PN-Centrality algorithm [21] of Everett and Borgatti fixes this problem but, as an eigenvector-based approach, tends to be biased toward nodes in highly dense subgraphs, thus distorting centrality information. Degree centrality has this same difficulty with cliques or dense subgraphs having many strong edges. Closeness centrality tends to have a cluster of nodes with high centrality with values decreasing from there, biasing a particular area of the network. Betweenness centrality is better at identifying bridges but not leaders or villains.
In this work we present ATria, an iterative centrality algorithm that addresses the shortcomings mentioned above and combines aspects of economic theory, social network theory, and path-based algorithms [22]. We investigate methods that avoid the above shortcomings by iteratively removing nodes with highest centrality along with some of the neighborhood edges before finding the node with the next highest centrality, using social network theory to determine the appropriate edges to remove. The goal of ATria is to find leaders, villains and bridges within a signed, weighted social network. We will verify that ATria is able to produce these results by testing a wide-range of networks including some simple synthetic examples, a scale-free network [23], and biological networks, such as gene expression, PPI, and microbial social networks.
Methods
Our proposed algorithm incorporates economic theory to reflect the fact that our interest in leader, villain and bridge nodes is based on their benefit (good or bad) to the network as a whole. Conjecturing possible interpretations, a leader node can be interpreted as a dominant member of a club, by being a major producer or consumer of some resource (e.g., a metabolite) that benefits other club members. A villain node may either represent a common enemy against which members of a club unite, or the producer of some byproduct (e.g., toxin) that is harmful to all members of a club. Bridge nodes may represent taxa that provide a beneficial (or harmful) resource to more than one club. Alternatively, they could be an important part of a cascade of events in a process.
Our starting point for an economic model is the Payoff Model proposed by Jackson and Wolinsky [24], which analyzes the efficiency and stability of an economic network where every node in the network provides some payoff to every other node. They use this approach to determine nodes that receive the highest pay (meaning, the largest benefit from their connections), representing payoff for a node i in network G with uniform edge weights 0<δ<1 by the following:
In the above model, w ii represents an amount of starting “capital” for node i. They use w ij to represent an innate significance of node j to node i. The second term multiplies w ij by a factor that is exponential in t ij , the number of links in the shortest path between i and j. If 0<δ<1, this term ensures that the payoff contribution for node i is higher for nodes j that are closer. The shortest path between i and j will thus result in the highest pay for i from j, and is the only pay that is used. The final term c ij represents a cost (instead of a payoff) for node i to maintain a direct connection to a neighboring node j. In summary, closer nodes contribute more, but direct connections incur a cost.
The intuition behind the connection between the payoff model and centrality is as follows. If (a) all nodes start with the same capital (i.e., w ii =0), (b) nodes do not contain any intrinsic value to one another before the algorithm runs (i.e., w ij =w ji =1), and (c) there is no cost to maintain direct connections (i.e., c ij =0) then the network is symmetric. This implies that in an undirected network the amount of “pay” received by a node (positive or negative) is the same as the amount they are providing to other nodes. Pay thus becomes a direct measurement of a node’s benefit to the network.
Extended payoff model
In designing our algorithm ATria, we take the symmetric algorithm by Jackson and Wolinsky and extend it in the following ways to encapsulate more general social networks:
-
1.
We allow for edge weights to be non-uniform. Therefore, instead of all weights being equal to δ, the edge weights are 0<δ ij <1. As a consequence, in the second term of Eq. 1 we replace \(\phantom {\dot {i}\!}\delta ^{t_{ij}}\) by the product of the δ values along the path of maximum pay between node i and node j.
-
2.
We incorporate negative edge weights, under the limited assumption that all weights are in the range −1<δ ij <1. With negative edges, a node receives a negative benefit from its connection with a neighbor. However, a path with two negative edges will result in a positive payoff, since the total payoff from a path is the product (not sum) of its edge weights.
-
3.
Centrality is computed iteratively. The most central node is found first, with ties broken arbitrarily. This node is then deleted along with some of the edges in its neighborhood. The centrality values are then recomputed for all the nodes. Although ties are broken arbitrarily, this does guarantee that the list of the most central nodes are not occupied by nodes that are all close to each other. Hence, ATria will find central nodes from all across the network.
Our modified equation, after removing c ij , is thus:
where P(i,j) is the path of maximum pay magnitude between i and j.
A major deviation from the payoff model is that our algorithm computes the centrality values incrementally as opposed to all at once. Therefore, even if the node with the highest u i (G) value may be judged the most central node in the first iteration, the node with the second highest value in the first iteration will not end up as the second most central node, unless it is the highest in the second iteration.
Consider the example in Fig. 2. In this network, the payoff model would compute node B as being the most central to the network, but then would compute A as the second most central and C as the third most central. While this may make sense for the payoff model itself (both A and C receive large benefits from B), it has some shortcomings from the point of view of centrality to say that A and C are the next most important nodes, since most of their pay comes as a result of B. ATria would first find B as the most central node as a leader of the first triad, but it would then find D as the second most central node as a leader of the second triad.
This happens because the edges incident on B are deleted after B is determined as having the highest centrality. The logic here is to remove all dependencies on the most central node before computing the next most central node. Also for every triad involving two of these incident edges, we remove the third edge if both incident edges have the same sign and the third edge is positive. This is backed up by social network literature [15], which states that two nodes with a mutual friend (in this case the leader B) or enemy (a villain) will tend to become friends as a result, meaning their connection is coincidental and resulting not from their own importance but the importance of the leader or villain. Such a triad with an even number (zero or two) of negative edges is said to be stable, a necessary condition for social network balance.
Incorporating non-uniform edge weights
The first change that we make to the Payoff Model, as mentioned, is incorporating non-uniform edge weights. In the unweighted (or uniformly weighted) case, the shortest path between i and j is guaranteed to have the fewest number of edges; this may not be true any longer, as illustrated in Fig. 3(a).
Non-Uniform Weighted Networks. a An example social network with non-uniform positive edge weights. In this situation, the payoff between A and C is larger via their indirect connection through B (0.56) compared with their direct connection to each other (0.2). b An example network with non-uniform positive and negative edge weights. Nodes can now gain and lose from each other
To incorporate this change, we use a modified form of Dijkstra’s Algorithm. In particular, the length of a path is the product of its lengths, and the best path is the one with the maximum (not minimum) product. Note that since all edge weights are between 0 and 1, the products can only decrease in magnitude as the path gets longer. Such a modified Dijkstra’s algorithm when started at node i, will help compute P(i,j) for all j, thus computing u i (G) (see Eq. 2).
Incorporating negative edge weights
When negative edge weights are present in the network, we have a possibility for nodes to gain and lose from each other depending on the path along which the effect takes place. Similar to the path of maximum gain, we consider the path of maximum loss as more significant to a node’s centrality as opposed to one of a smaller loss. However, there may be pairs of nodes between which there is a positive length path as well as a negative length path. Consider the network in Fig. 3(b). There are two paths between A and D: A – C – D, and A – B – C – D with path lengths of 0.2×−0.5=−0.1 and −0.8×0.7×−0.5=0.28, respectively. One causes a gain, the other incurs a loss.
Dijkstra’s algorithm is modified so that for every starting node i, we simultaneously keep track of two quantities: the length of the path of highest gain to node j, and length of the path of highest loss to node j. This covers situations like in Fig. 3(b) where the path of highest gain from A to D includes a path of highest loss from A to C and a path of highest loss from C to D. We then modify the RELAX step in Dijkstra’s algorithm [25] as follows: when relaxing edge (j,k), if its weight is positive, then we use the maximum gain due to node j to update the maximum gain due to node k and the maximum loss due to node j to update the maximum loss due to node k. On the other hand, if its weight is negative, then we use the maximum gain due to node j to update the maximum loss due to node k and the maximum loss due to node j to update the maximum gain due to node k.
To incorporate both gain and loss, we modify our payment equation to set P(i,j)=G(i,j)+L(i,j), where G(i,j) is the length of the path of maximum gain between i and j and L(i,j) is the length of the path of maximum loss (negative or zero). So our final payment equation for ATria becomes:
Results and discussion
In order to test ATria, we run our algorithm on sample networks alongside five other centrality algorithms: betweenness, closeness, degree, and the eigenvector-based approaches PageRank (PageTrust if the graph has negative weights) and PN. To be fair we use weighted degree centrality, and for running Dijkstra’s algorithm for closeness and betweenness centrality we compute distance by taking the negative logarithm of the absolute value of an edge (so larger edge magnitudes carry smaller weights, yielding shorter paths).
Networks with cliques
Single clique
We begin by studying weighted cliques. The first is a non-uniform weighted clique of size four with a leader A (in Fig. 4(a)). The second is the same clique but with the addition of a villain node E (Fig. 4(b)). Finally, we show a uniform-weighted clique of rival groups in Fig. 4(c), where the most central node will be a leader to one group and a villain to the other. While ATria agreed with all other algorithms on the most central node for all three examples, only ATria clearly identified A as the leader in (a), E as the villain in (b), and A (arbitrarily, but the point remains) as leader and villain in (c). It does this by setting all other centralities to zero, thus assuming that all remaining connections result from connections to these nodes.
Multiple cliques
Figure 5 shows our first example of a multiple-clique network, which is the non-uniform weighted network from Fig. 2 that has two positive triads connected by a weaker positive edge. In this figure we compare the results of all six algorithms, color coding individual centrality values against a normal distribution (red=maximum, violet=minimum, blue and green respectively two and one standard deviations left of the mean, yellow one to the right, orange two to the right). Degree, PageRank and PN all biased the tighter-connected first triad, while betweenness and closeness biased the triad bridges. As discussed earlier, ATria computed B as most central (first triad leader), and D as second (second triad leader). E is then arbitrarily chosen as third over C. ATria thus favors leaders above bridges if triad edges are stronger than their connections. This holds independent of the sign of the connections. If the connection edge CE was stronger than the triads, ATria would choose C as most central for a positive CE (C is in the tighter triad and has closer friends) and E as most central for a negative CE (for this same reason, more nodes are harmed by its competition with C).
Comparison on Two-Triad Social Network. A comparison of ATria with five other centrality algorithms on the network from Fig. 2. Red nodes are the most central
Figure 6 shows a more extreme example, which contains one clique of ten nodes and another of one hundred nodes. All edges have random positive weights in the range (0,1). Note that ATria is able to immediately pick out both leaders, ranking the leader of the larger clique with a much higher centrality than that of the smaller. All other approaches tend to favor one of the two cliques. We summarize these results in Table 1.
Synthetic network with clubs
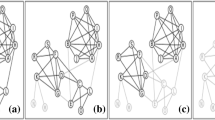
We now develop a synthetic network to illustrate the type of network for which ATria is most beneficial, with five cliques of random sizes between 16 and 20. We randomly choose one leader node for each of three of the cliques, and one villain node for each of the other two. We connect leaders to their clique using random edge weights in the range [0.85,1), and villains using (−1,−0.85]. Edges between other nodes are between 0.75 and the lower of the two edges with the leader or villain. We choose a number of bridge nodes equal to half the size of the largest clique and connect them to a random node in two random cliques using a random weight in the range [0.75,1). We run all six algorithms on this network and show our results in Fig. 7. As can be seen, ATria was able to immediately pick out leaders, villains and bridges and set all other centralities to zero.
This situation also illustrates challenges with other centrality approaches for this type of network. Betweenness was the only other algorithm able to somewhat separate leaders, villains, and bridges since in this example they reside on most high pay paths, but for this same reason also counted clique nodes connected to bridges (in some cases even above leaders and villains). Closeness centrality biased the cliques connected by the most bridges, and degree biased the tightest connected cliques. PageTrust and PN found the two villains (low centralities by design) and PN also found the top two leaders (the second less obvious), but then biased their cliques and lost the third. We summarize these results in Table 2.
Biological networks
We now demonstrate ATria’s results on three types of biological networks. The first, shown in Fig. 8(a) is a synthetic scale-free network of 1000 nodes. We use this as an overarching example of a network that is common across many areas of biology, including PPIs, cell signalling pathways [26], and neural networks [27]. The second, in Fig. 8(b), is a gene co-expression network (GEO:GSE31012) from a species of oyster under different salinity conditions. Finally as our largest example in Fig. 8(c), we run a yeast PPI [28] (BioGrid:S288c) consisting of 5526 nodes. Note that the PPI is by definition uniformly weighted and positive, since proteins either interact or do not interact.
Scale-free networks are known for the presence of critical hub nodes, which ATria also ranks with the highest centrality. The co-expression network shows that with more realistic biological data, ATria can still find leaders and villains across the network. The transcription factor Nuclear Y-Subunit Alpha (NYFA, [29]) was ranked #7 by ATria. This was found first by degree and PN centrality, but no other algorithms found transcription factors in their top ten. However, while degree and PN centrality then biased central nodes around this transcription factor, ATria was able to find a protein TRIM2 (#2) from the Tripartite Motif (TRIM, [30]) family, which no other algorithm found. TRIM2 helps bind the molecule Ubiquitin to proteins as a tag for later modification [31]. ATria discovered Ubiquitin itself as #4 in the yeast PPI. A specific type of modification for which Ubiquitin binds to proteins is degradation in the proteasome, and ATria also found Rpn11 (#7), which is responsible for removing Ubiquitin from proteins before entering the proteasome [32]. These results exhibit agreement with Cicehanover, Hershko and Rose in their discovery of Ubiquitin-mediated proteolysis and its regulation of numerous critical cellular processes including the cell cycle [33], helping them win the 2004 Nobel Prize in Chemistry.
Microbial social network
We now show the results of ATria and the five other centrality algorithms on the co-occurence network assembled from human lung microbiome data, from Fig. 1. These results are shown in Fig. 9.
Comparison on Microbial Social Network. A comparison of ATria to the other five centrality algorithms on the co-occurence network assembled from lung microbiome data, from Fig. 1
For this network, both degree and PN centrality restricted the highest ranked nodes to the tightest club in the center of the network. Closeness centrality tended to bias the center of the largest connected component, with centrality decreasing as nodes were more out of this loop. Betweenness centrality was heavily biased towards bridges in the largest connected component. The only other algorithm that was able to find central nodes in multiple clubs was PageTrust; however, ATria was able to better isolate one or two nodes in each club, followed by the bridges.
Based on the results of ATria, the bacterial taxa most likely to be producing a critical metabolite would be: F. Burkholderiaceae (the most central node, leader of the tightest club in the middle), F. Erysipelotrichaceae (#2, leader of the club just to the south), Bifidobacterium (#4, leader of the club to the southwest), and Atopobium (#6, leader of the southernmost component). F. Prevotellaceae (#3) is a villain of the tightest knit club which is likely to be in competition for a resource (possibly the same metabolite) that many bacteria in this club need. Bridge nodes such as Prevotella (#5, connecting many nodes in the two northernmost clubs) and Selenomonas (#8, part of a central bridge connecting the southwestern clubs to the largest connected component) could be producing a metabolite that benefits multiple clubs. Interestingly, ATria also found C.Gammaproteobacteria (#7), which is an enemy bridge between the largest club and the rest of this largest connected component. This could indicate competition with its counterpart Fusobacteria as critical to the network structure.
Conclusions
Our results demonstrate that the application of economic models using payoffs can be useful to computing centrality in a signed and weighted social network when finding important leader, villain and bridge nodes. We built ATria as an iterative extension of a payoff model using social networking principles and in the process overcome shortcomings of existing algorithms for computing centrality, identifying central nodes across the network as opposed to many in the same vicinity. We verifed these results using scale-free networks and synthetic networks with both positive and negative edge weights, both of which are particularly relevant in biological networks, and finally real biological networks including a bacterial co-occurence network (or Microbial Social Network).
As future work, we would like to explore extensions of ATria to directed networks, as while uncommon in the social networking field would be useful when applied to biological networks. We also would immediately like to explore the idea of interference [34] to show and analyze the effects of removing ATria’s highly central nodes from our networks. Finally, since the time complexity of ATria is more expensive than other centrality algorithms (see Table 3) due to recomputing centralities n times in the worst case, we have developed a module of ATria for the Graphics Processing Unit (GPU) and plan on releasing this open-source as part of a larger microbial analysis pipeline.
Abbreviations
- ATria:
-
Ablatio Triadum
- GPU:
-
Graphics processing unit
- PPI:
-
Protein-Protein Interaction
- TRIM:
-
Tripartite motif
References
Newman MEJ. Networks: an introduction. Oxford: Oxford University Press; 2010.
Davidson E, Levin M. Gene regulatory networks. Proc Natl Acad Sci U S A. 2005; 102(14):4935.
Schwikowski B, Uetz P, Fields S. A network of protein-protein interactions in yeast. Nat Biotech. 2000; 18(12):1257–61.
Ackerman J. The ultimate social network. Sci Am. 2012; 306(6):36–43.
Atkinson S, Williams P. Quorum sensing and social networking in the microbial world. J R Soc Interface. 2009; 6(40):959–78.
Fernandez M, Riveros JD, Campos M, Mathee K, Narasimhan G. Microbial “Social Networks”. BMC Genomics. 2015; 16(11):S6. (Special Issue).
Bassler BL, Wright M, Showalter RE, Silverman MR. Intercellular signalling in Vibrio Harveyi: sequence and function of genes regulating expression of luminescence. Mol Microbiol. 1993; 9(4):773–86.
Williams SCP. Microbial social networks. HHMI Bulletin. 2013; 26(3):1–6.
Pereira CS, Thompson JA, Xavier KB. Ai-2-mediated signalling in bacteria. FEMS Microbiol Rev. 2013; 37(2):156–81.
Kim PJ, Price ND. Genetic Co-Occurrence Network across Sequenced Microbes. PLoS Comput Biol. 2011; 7(12):1002340.
Fruchterman TMJ, Reingold EM. Graph drawing by force-directed placement. Softw Pract Experience. 1991; 21(11):1129–64.
Shannon P, Markiel A, Ozier O, Baliga NS, Wang JT, Ramage D, Amin N, Schwikowski B, Ideker T. Cytoscape: A software environment for integrated models of biomolecular interaction networks. Genome Res. 2003; 13(11):2498–504.
Koschutzki D, Schreiber F. Centrality analysis methods for biological networks and their application to gene regulatory networks. Gene Regul Syst Bio. 2008; 2:193–201.
Wu Q, Qi X, Fuller E, Zhang CQ. Follow the leader: A centrality guided clustering and its application to social network analysis. Sci World J. 2013; 2013:1–9.
Easley D, Kleinberg J. Networks, Crowds, and Markets: Reasoning About a Highly Connected World. Cambridge: Cambridge University Press; 2010.
Bonacich P. Power and centrality: A family of measures. Am J Sociol. 1987; 92:1170–82.
Boldi P, Vigna S. Axioms for centrality. Internet Math. 2014; 10:222–62.
Brin S, Page L. Reprint of: The anatomy of a large-scale hypertextual web search engine. Comput Netw. 2012; 56(18):3825–33.
Xing W, Ghorbani A. Weighted PageRank algorithm. In: Proceedings of the Second Annual Conference on Communication Networks and Services Research. Washington: IEEE: 2004. p. 305–14.
de Kerchove C, Van Dooren P. The PageTrust algorithm: How to rank web pages when negative links are allowed? In: Proceedings SIAM Data Mining Conference (SDM2008). Atlanta: SIAM: 2008. p. 346–52.
Everett MG, Borgatti SP. Networks containing negative ties. Soc Networks. 2014; 38:111–20.
Cickovski T, Peake E, Aguiar-Pulido V, Narasimhan G. ATria: A novel centrality algorithm applied to biological networks. In: International Conference on Computational Advances in Bio and Medical Sciences (short Abstract). ICCABS ’15. Miami: IEEE: 2015. p. 1.
Barabási AL, Albert R. Emergence of scaling in random networks. Science. 1999; 286(5439):509–12.
Jackson MO, Wolinsky A. A strategic model of social and economic networks. J Econ Theory. 1996; 71(1):44–74.
Cormen T, Leiserson C, Rivest R, Stein C. Introduction to Algorithms. Cambridge: MIT press; 2009.
Albert R. Scale-free networks in cell biology. J Cell Sci. 2005; 118(21):4947–57.
Watts DJ, Strogatz SH. Collective dynamics of’small-world’networks,. Nature. 1998; 393(6684):409–10.
Park D, Singh R, Baym M, Liao CS, Berger B. Isobase: a database of functionally related proteins across PPI networks. Nucleic Acids Res. 2011; 39(suppl 1):295–300.
Maity SN, de Crombrugghe B. Role of the ccaat-binding protein cbf/nf-y in transcription. Trends Biochem Sci. 1998; 23(5):174–8.
Reymond A, Meroni G, Fantozzi A, Merla G, Cairo S, Luzi L, Riganelli D, Zanaria E, Messali S, Cainarca S, Guffanti A, Minucci S, Pelicci PG, Ballabio A. The tripartite motif family identifies cell compartments. EMBO J. 2001; 20:2140–51.
Consortium TU. Uniprot: a hub for protein information. Nucleic Acids Res. 2015; 43(D1):204–12.
Worden EJ, Padovani C, Martin A. Structure of the Rpn11-Rpn8 dimer reveals mechanisms of substrate deubiquitination during proteasomal degradation. Nat Struct Mol Biol. 2014; 21(3):220–7.
Ciechanover A, Hershko A, Rose I. For the Discovery of Ubiquitin-Mediated Protein Degradation. 2004. Available at http://www.nobelprize.org/nobel_prizes/chemistry/laureates/2004/. Accessed 2015.
Scardoni G, Petterlini M, Laudanna C. Analyzing biological network parameters with CentiScaPe. Bioinformatics. 2009; 25(21):2857–9.
Cickovski T, Aguiar-Pulido V, Huang W, Mahmoud S, Narasimhan G. Lightweight microbiome analysis pipelines In: Guzman FO, I. R. Ruiz GSLP, editors. International Work Conference on Bioinformatics and Biomedical Engineering. IWBBIO ’16. Granada: Springer: 2016. p. 225–7.
Acknowledgements
The authors acknowledge the help of Michael Campos, Cameron Davis, Mitch Fernandez, Wenrui Huang, Lawrence Irvin, Kalai Mathee, Jingan Qu, Juan Daniel Riveros, Victoria Suarez-Ulloa, and Camilo Valdes in many useful discussions.
Funding
The work of Giri Narasimhan was partially supported by a grant from Florida Department of Health (FDOH 09KW-10) and a grant from the Alpha-One Foundation. The work of Vanessa Aguiar-Pulido was supported by the College of Engineering and Computing at Florida International University. Trevor Cickovski was funded by a Faculty Development Grant from Eckerd College. Publication charges for this article will be paid through personal funds of the authors.
Availability of data and material
ATria is now part of the PluMA [35] analysis pipeline, available along with all applicable data for this study at http://biorg.cs.fiu.edu/pluma/ for download. In addition, we have placed a small version with single ATria executions from this paper at http://biorg.cs.fiu.edu/pluma/atria.
Authors’ contributions
This work was conducted by the Bioinformatics Research Group (BioRG) at Florida International University managed by GN and spearheaded by TC. All authors contributed to all portions of this project. All authors read and approved the final manuscript.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Ethics approval and consent to participate
Not applicable.
About this supplement
This article has been published as part of BMC Bioinformatics Volume 18 Supplement 8, 2017: Selected articles from the Fifth IEEE International Conference on Computational Advances in Bio and Medical Sciences (ICCABS 2015): Bioinformatics. The full contents of the supplement are available online at https://bmcbioinformatics.biomedcentral.com/articles/supplements/volume-18-supplement-8.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Author information
Authors and Affiliations
Corresponding author
Additional information
From Fifth IEEE International Conference on Computational Advances in Bio and Medical Sciences(ICCABS 2015) Miami, FL, USA. 15-17 October 2015
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver(http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Cickovski, T., Peake, E., Aguiar-Pulido, V. et al. ATria: a novel centrality algorithm applied to biological networks. BMC Bioinformatics 18 (Suppl 8), 239 (2017). https://doi.org/10.1186/s12859-017-1659-z
Published:
DOI: https://doi.org/10.1186/s12859-017-1659-z