Abstract
Purpose
Ridesourcing services have become popular recently and play a crucial role in Mobility as a Service (MaaS) offers. With their increasing importance, the need arises to integrate them into travel demand models to investigate transport system-related effects. As strong interdependencies between different people’s choices exist, microscopic and agent-based model approaches are especially suitable for their simulation.
Method
This paper presents the integration of shared and non-shared ridesourcing services (i.e., ride-hailing and ride-pooling) into the agent-based travel demand model mobiTopp. We include a simple vehicle allocation and fleet control component and extend the mode choice by the ridesourcing service. Thus, ridesourcing is integrated into the decision-making processes on an agent’s level, based on the system’s specific current performance, considering current waiting times and detours, among other data.
Results and Discussion
In this paper, we analyze the results concerning provider-related figures such as the number of bookings, trip times, and occupation rates, as well as effects on other travel modes. We performed simulation runs in an exemplary scenario with several variations with up to 1600 vehicles for the city of Stuttgart, Germany. This extension for mobiTopp provides insights into interdependencies between ridesourcing services and other travel modes and may help design and regulate ridesourcing services.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.1 Introduction
Ridesourcing services have become increasingly popular during the past years and already play an important role in the transport system in many places. Sometimes such services are discussed as a solution to alleviate congestion by car traffic or to complement public transport as part of a Mobility as a Service (MaaS) offer. Yet, many questions arise concerning the design and the effects of these new mobility options: City administrations are concerned with their impacts and discuss setting regulations. Service providers are not sure which offer could be most successful. Furthermore, these services influence the use of other travel modes, such as car, bicycle or public transport. Such interdependencies are generally examined with travel demand models. However, as ridesourcing services present high correlations between demand and service supply, it has been difficult to integrate them into these models. In this paper, we present an approach to integrate modeling of ridesourcing services in an agent-based travel demand model, where the exact properties of the ridesourcing service, as well as other mobility options people may have, are taken into account. This allows making assessments of ridesourcing services, including their respective impact on the rest of the transport system.
In general terms, ridesourcing services provide individual rides. Rides are performed on request by users, and users pay a fee that is above mere compensation for the driver [17]. Two different principles of ridesourcing services exist. On the one hand, services may provide vehicles to be used exclusively by one person plus her or his possible companions. In this study, we use the term ride-hailing to refer to these services. On the other hand, the service provider may combine the ride requests of different people with similar origins and destinations into one vehicle. Thus, different people may ride together on parts of their ride. In this paper, we refer to such services with the term ride-pooling.
As ridesourcing services work on request by users, they are considered to be part of the field of mobility-on-demand. This field includes other services such as carsharing, bikesharing, public transport, and microtransit [18]. In contrast, Mobility as a Service (MaaS) describes the combination of different transportation modes within one platform offered to the user through a joint interface. MaaS may, but does not need to, include mobility-on-demand options [11].
This paper is structured as follows: In the following section, we present how ridesourcing services are modeled in travel demand models. Then, we give a short overview of the travel demand modeling framework mobiTopp. Subsequently, we present the outline of our model extensions for ridesourcing and present the scenario for evaluation. This is followed by the results of exemplary variations for the operation of ridesourcing fleets of different types and sizes within the city of Stuttgart (Germany). Finally, we critically review the limitations of our method, discuss further possible enhancements and draw conclusions on applications.
2 Background
In the literature, there are different approaches for the modeling of ride-pooling and ride-hailing services in the context of travel demand models. However, many methods do not fully integrate ridesourcing services into travel demand modeling but perform ex-post calculations on the possible bundling of trips. This may be combined with a new mode choice option and thus new demand for the ridesourcing service, creating an iterative process. An example is the PTV MaaS Modeller [16]. The demand from a (macroscopic) Visum model is disaggregated and subsequently bundled into rides. This is done with an algorithm used in logistics that solves a sequence of vehicle routing problems. Another modeling approach is presented by Friedrich et al. [8]. In their algorithm, ride-pooling tours are created within the aggregated travel demand software Visum. The core of this algorithm is to investigate if new ride requests can be integrated into the shortest trip route of an already planned tour. However, this approach simulates groups of people instead of agents and vehicles.
In agent-based models, such as SimMobility and MATSim, extensions to model ridesourcing services and other dynamic modes exist [15] [12]. In SimMobility, automated mobility-on-demand services are integrated in the pre-day-simulation which iterates towards an optimum, meaning that in mode choice decisions, only experienced travel times and cost are considered [2]. MATSim also uses an iterative approach based on experienced cost or benefits [1]. Using MATSim, an algorithm to check how ride requests can be included into an already existing tour in order to simulate a fleet of shared taxis was developed [5]. Also, an alternative approach to modeling a ride-hailing scenario with autonomous vehicles to replace all privately owned cars exists [4]. However, runs with 100% population may become challenging computing-wise, as a high number of iterations is required to achieve reliable results. Furthermore, MATSim does not directly perform mode choice in the sense of discrete choice theory. By doing so, such models may be used to determine willingness-to-pay measures as well as the value of time.
In the following, we present an integrated approach with discrete choice models for mode choice in an agent-based environment in which the whole population (100%) can be simulated in a rather small computing time. This way, we simulate interdependencies between the requests of different agents and the possible waiting and travel time, and thus mode choice on an individual level.
3 Travel demand model development and evaluation framework
3.1 Travel demand model mobiTopp
mobiTopp is an activity- and agent-based travel demand model, in which every person, household and car of the study area is modeled [13, 14]. People are modeled as individual decision-taking agents. The decisions are taken situation-dependent based on the current location, the agent’s properties and the interaction with other agents. mobiTopp consists of two parts, the initialization (so-called long-term module) and the simulation (so-called short-term module). In the long-term module, the synthetic population with its agents is modeled, i.e., the population with its attributes such as place of residence, car ownership and occupational status. This is based on structural data and representative samples of activity patterns, among others. In the short-term-module, travel demand based on the long-term module is modeled. Travel behavior is simulated by applying destination and mode choice models sequentially for each trip of an agent. For the destination choice, two types of activities are distinguished: activities at fixed locations (previously set during initialization, e.g., working location) and flexible locations (e.g., leisure and shopping). A mode choice follows the destination choice for each trip.
By default, mobiTopp supports five travel modes: walking, cycling, public transport, car as driver, and car as passenger. The actual choice set for each situation consists of a subset of these five modes, considering the availability of each mode. For instance, if one car is available in a household, only one household member at a time can use it as a driver. The mode choice itself is made by a Multinomial Logit Model using the choice set of the available modes. The utility function may contain variables like distance, travel time, travel cost, transit pass ownership, and sociodemographic variables.
mobiTopp is released open-source with multiple extensions and has been used in several projects already, with different objectives of study. A model of the Region of Stuttgart has been built and used for several problems, e.g., analyzing the effects of electric and hybrid cars on electricity demand [19], gaining more insights into public transport passenger trips [6] as well as station-based and free-floating carsharing [10]. By combining mobiTopp with MATSim, it is also possible to use a complete agent-based toolchain [7]. Furthermore, mobiTopp models for the area of Karlsruhe (Germany) and Hamburg (Germany) are being developed.
3.2 New Ridesourcing extension
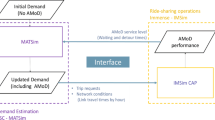
In standard mobiTopp, the travel times and costs for each mode and origin-destination-pair are provided through static matrices differentiated in several time periods a day. For regular modes this is sufficient. For ridesourcing particularly strong interdependencies between the actions of different person agents exist. This is because the vehicle tours are planned on-demand based on the requests. This influences the vehicles’ locations and the vehicles’ tours, which in turn influence travel and waiting times for other person agents. Consequently, the approach of static matrices, which are calculated before the simulation start, is not sufficient for these services.
Therefore, new methods (classes) to handle a fleet of vehicles are introduced. They gather the most suitable vehicle for a given ride request and determine travel and waiting times dependent on the current locations by the vehicles and the current bookings by other agents. These new classes return this information during the mode choice by an agent. The agent is not required to book at this moment. Instead, first the travel and waiting time for all modes is gathered, then the decision for a specific mode is performed. If the ridesourcing mode is chosen, the ride is booked and this booking is considered in the tour of the vehicle and as such considered in future requests by other agents.
There are several possibilities of how the vehicle fleet is managed in detail, which determines how users are assigned to vehicles and thus the calculation of travel and waiting times. We include a simple algorithm for both ride-hailing and ride-pooling, which uses an insertion-based heuristic. Vehicles for ride-pooling may take several users at a time and may perform detours to pick them up, which affects the travel or waiting time of other users. In contrast, rides in ride-hailing vehicles are performed strictly chronologically by the time of their requests.
The vehicles are assigned in a fixed manner to the ride requests, i.e. no re-assignment between the vehicles to the passengers to optimize the bundling of requests is performed. The travel times between the traffic analysis zones are retrieved by origin-destination matrices. However, for every pick-up and drop-off action, extra time is added, which represents the time required for the vehicle to stop at a suitable location and for passengers to enter or leave the vehicle.
Several operator-related features have been implemented and may be configured. An overview on these configuration parameters is given in Table 1.
The maximum tolerated waiting time is configured with the parameter tmax _ waiting. If the best offer among all ridesourcing vehicles exceeds this waiting time, this ridesourcing service is not available, i.e., the ridesourcing request is rejected.
Rides of different users are only pooled in one vehicle if the required detours for pick-up and drop-off do not exceed certain thresholds. These thresholds are defined relative to the originally planned waiting and travel times for those users who are impacted by the detour because of delayed departure (additional waiting time) or delayed trip travel time (additional travel time). The maximum additional waiting time is defined with the parameter tmax _ increase, waiting and the maximum additional travel time with the parameter tmax _ increase, travel. If picking up a user would imply a larger detour, the ride request is rejected.
The cost calculation for the trip may be based on costs per minute of ride ct(t), distance between origin and destination cs(s) and a base fee cbase. The price offered to the agent is the sum of these cost components or (if this is smaller) the maximum costs defined with the parameter cmax.
A rather simple algorithm for relocating unused vehicles is also included. This is handled with predefined relocation destination zones, which must be seen as zones with high demand and sufficient parking infrastructure. As soon as the last agent has alighted a vehicle and no other ride is registered for that vehicle, the vehicle will move in an empty run after a customizable waiting time (twait _ until _ relocation). Within the current implementation, the destination of this empty run is the closest relocation destination zone. Other strategies which, e.g., consider the current demand, could be implemented as well.
This algorithm can be extended to include more advanced strategies, concerning e.g., the relocation or re-optimization of vehicles. Alternatively, an external vehicle fleet management with more sophisticated vehicle control strategies can be connected to mobiTopp.
3.3 Evaluation scenario
The ridesourcing service schemes simulated for this paper are based on a mobiTopp model for the region of Stuttgart [9]. The model consists of around 2.7 million agents, which represent the whole population of that region. However, in the following, we focus on the city of Stuttgart only, which is the inner part of the region. The basic model is extended by a ridesourcing service using the algorithm described before. The mode choice model parameters used for ridesourcing services are, in this study, the same as those used for public transportation. The present model also differs from the original model with respect to simulation duration: we simulate one day (Monday) only instead of a full week.
For our analyses, we use six different model variations with different ridesourcing service schemes. We implemented an exclusive ride-hailing service in two variations and implemented a ride-pooling service in three variations. For comparison, we further have a business as usual (BAU) variation without any ridesourcing service. Except for fleet size, and in one variation the pricing, the configurations are identical. The operating area is the city of Stuttgart – only trips with both origin and destination inside of Stuttgart can be made with these services. Around 1.6 million trips fulfill this criterion. We further defined 20 relocation zones throughout that area, which are also used as initial positions of the vehicles. For ride-pooling, the vehicles have a capacity of four passengers. For ride-hailing, the capacity per vehicle is one passenger.
Costs for a ridesourcing trip are calculated distance-based at 0.60 € per kilometer (cs = 0.60 €, ct = 0). A fee of cbase = 1 € is added for each booking to avoid that too short trips are performed with the service. Each trip has a maximum price of cmax = 10 €. These costs are similar to public transport prices. In reality, these prices might be too low for the exclusively used ride-hailing service; however, we used these values to compare more easily the results of the different service types. For the variation with elevated price, the values are multiplied with 1.5, giving cs = 0.90 €, cbase = 1.5 € and cmax = 15 €.
After a waiting time of 10 min (twait _ until _ relocation), empty vehicles move to the closest relocation zone. For the ride-pooling service, the maximum detour allowed for one trip is 15 min for travel time (tmax _ increase, travel) and 10 min for waiting time (tmax _ increase, waiting).
4 Results
4.1 Internal effects of different ridesourcing schemes
In Table 2 we show different key figures related to the ridesourcing services in the different variations. They are based on trips made with the ridesourcing services only. The overall booking numbers show an almost linear increase in proportion to the number of vehicles. This observation lends plausibility to the assumption of an even higher potential demand for ride-pooling services. While the ride-pooling vehicles show between 103 and 115 bookings per vehicle, the number of bookings for the ride-hailing service is between 65 and 72. The number of vehicle kilometers traveled is higher for the ride-hailing service compared to the ride-pooling service. At the same time, the passenger-kilometer numbers are roughly doubled for the ride-pooling service. This is explained by the different occupancy of the vehicles. While the ride-pooling services show around 2.2 to 2.4 passengers per vehicle, for the ride-hailing service this figure is around 0.9. The decreased amount of vehicle kilometers for the ride-pooling service can be explained with the fact that due to the higher number of bookings, more “dead” times for pick-up and drop-off occur in which the vehicles do not move.
The average occupancy decreases with more vehicles available. This is plausible, as with more vehicles, more vehicles exist that cover the demand. The average distance traveled per booking decreases with an increasing number of vehicles. This co-relates to a decreasing average length of detours within each tour. A higher number of vehicles probably leads to optimized tour planning and lower mileage.
The mean distances between the origin and destination of the rides are similar for both service types. However, due to the detours required for pick-up and drop-off actions, the effective distance traveled, as well as the average travel time per booking is significantly higher for ride-pooling.
The ride-hailing services show higher waiting times and lower average travel time. Consequently, the trip speed (based on the shortest path between origin and destination, i.e., not considering detours due to pick-ups or drop-offs in between), including waiting time, is higher for the ride-hailing services. The differences between the variations with elevated and regular price are very small: while the costs per trip increase proportionally to the price change, the other figures hardly change. This is explained with a low price sensitivity in the mode choice parameters used in this model.
Figure 1 shows the distribution of distances within the ride-pooling variations with different vehicle fleet sizes. While the proportion of trips from 9 km onwards is nearly identical, differences are notable on shorter trips. Ride-pooling is more intensely used for trips of up to two (200 vehicles) or three kilometers (1600 vehicles). Furthermore, for ride-pooling with an increasing number of vehicles, the proportion of short trips increases while the proportion of longer trips decreases. We explain this as follows: With a larger fleet the waiting time is less, as it is more probable that a vehicle is close by. As slight time changes have a larger relative impact on short travel times, ride-pooling becomes more attractive for short trips.
The usage of the vehicles over the course of a day in the different variations is presented in Fig. 2, using the mean occupancy by all vehicles. It is well observable that while in the 200 vehicles variations the occupancy reaches its maximum values at around 6.00 h, the 1600 vehicles variations start to have these between 7.00 and 8.00 h. Generally, the mean occupancy is highest in the ride-pooling variation with 200 vehicles, reaching a mean occupancy of up to three passengers per vehicle simultaneously. The 1600 vehicles ride-pooling variation has slightly lower values, and from 20.00 h it lowers significantly. The ride-hailing variations have values slightly below 1. These values do not lower significantly at the end of the day for the 1600 vehicles variation, which shows that they are still utilized.
In Fig. 3 we show the number of passengers over the course of the day for the ride-pooling services. It is observable that at around 24.00 h approximately 50% of the vehicles have only zero or one passenger in the 1600 vehicles variation. In contrast, the same number of vehicles is filled with three or four passengers at the 200 vehicles variation. Thus, while there is still sufficient demand to fill the 200 vehicles, the 1600 vehicles are not needed anymore at this time of the day.
Figure 4 shows an example of one random vehicle from the variation with 1600 vehicles. The figure shows its activities in one day, presenting pick-up and drop-off events, empty runs, and utilization rates on an individual level. Based on the data available for the movements of each vehicle during one day, it would also be possible to show spatial representations (e.g., for the areas the vehicle is moving in to carry passengers in the course of time).
4.2 External effects of different ridesourcing service schemes
The change of the share at the trip-based modal split per mode in the different variations is shown in Fig. 5. It is calculated based on the trips performed in the city area and shows the relative change of the modal split of each mode compared to the BAU variation (i.e., a value of − 10% means that the share of this mode is lowered by 10%). It is observable that – with the given configuration – the shares of public transport and car as passenger are influenced most by ride-pooling. For ride-hailing, car as passenger is much less influenced. Furthermore, slight differences can be observed regarding the 1600 vehicles ride-pooling variations with different price levels: at higher price level, the bike share is less impacted, while car as driver is chosen less often. Further analysis on the reasons of these findings may be undertaken with the data of the simulations.
In Table 3 the changes of vehicle miles traveled for the modes “car as driver” and the ridesourcing modes in the different variations compared to the BAU variation are presented. For the given services, the amount of additionally driven vehicle kilometers of the ridesourcing modes surpasses the saved vehicle kilometers by the car mode, most notably for the ride-hailing services. Table 4 shows the changes of passenger miles traveled per mode. While the overall number of passenger kilometers remains roughly equal, the mileage of public transport is decreased most in all variations. As no realistic parameters for mode choice were used for these simulations, these results should not be overinterpreted but must be seen as a demonstration for possible analysis.
5 Discussion
The new extension for mobiTopp allows to model ridesourcing services with full integration into mode choice. With different fleet sizes, we get different service quality (travel times, waiting time, costs), which has a direct impact on the usage of the ridesourcing mode as well as on the usage of other travel modes. The results presented above show that the extension works as expected and is sensitive to changes of input parameters such as fleet size and costs.
Due to the microscopic approach of the modeling framework, service configuration parameters such as fleet size, maximum waiting times, or detour factors can be used in a similar way as they are used in real services – it is not required to recalculate these properties to fit them into the model. Therefore actual service schemes can be simulated relatively easily in the model.
The ridesourcing services can be analyzed with a wide range of possibilities. We can evaluate the services and their effects in a macroscopic way, analyzing times and points of high demand. Additionally, due to having the vehicles as agents, we can gather performance data on microscopic level, analyzing the occupancy of vehicles during the course of the day and other aspects. Further analysis on different phenomena may be performed (e.g., spatial or temporal analysis of the occupancy).
Concerning effects on other modes, we see that in our simulations mostly public transport and “car as passenger” decrease when ridesourcing services are introduced. This is due to the mode choice parameters and the ridesourcing configuration used in this example model. The model configuration is set in such a manner that cost changes only have a small impact on the probability of usage. We did not provide realistic results on modal shifts in this paper but presented the simulation results as a technical demonstrator. For future work it is necessary to carry out additional surveys on customers’ willingness to pay and other factors influencing the usage potential of ridesourcing services (e.g., using stated choice interviews). Calibrating the model using realistic mode choice parameters, among other aspects, would then enable to study effects of real services.
Currently, the mode choice is made based on the waiting and travel time offered to the agent at the time of the ride request. However, due to detours by bookings that occur afterwards, travel time for ride-pooling is around 30% higher at the end of the trip. This is currently not considered in the mode choice. In reality, people would know that they have to consider a certain detour factor, or the provider would already include a certain extra time when the person performs his booking. An approach to overcome this may be through adding a detour factor to the travel and waiting time.
Even though the computing performance was not in the focus of the development yet, we are able to simulate relatively huge fleets in 100% models with satisfying computing time (e.g., one simulation day with 1600 ride-pooling vehicles with high demand in 77 h). We estimate that due to the strong interdependencies between the choices of different agents and because the vehicles have a rather small capacity (compared to other means of public transport), using 100% models is necessary for simulating ride-sourcing services. Compared to other simulation frameworks, no or only a small number of iterations is needed. Therefore, performing simulation runs with the whole population (100% models) is feasible. To simulate even larger fleets and to be able to analyze more variations, further research and development in improving the efficiency of the algorithms and in speeding up the simulation would be required.
Many further questions may be investigated using this modeling approach. This includes integrating other aspects to assess welfare impacts of different MaaS schemes, as done in [3]. It is possible to simulate ride-pooling and ride-hailing services simultaneously, the effects of such coexistence could be analyzed. Different fleet control algorithms may be evaluated. Additionally, we think that further research regarding understanding the distinguishing factors of different service schemes is needed. In mobiTopp, it is possible to simulate full MaaS schemes, including a transit pass ownership, intermodal trips, and other mobility-on-demand services. Performing such simulations bears further potentials.
6 Conclusions
As ridesourcing services are gaining popularity and importance, the need arises to incorporate them into travel demand models. For these individual services, a microscopic travel demand model is the most suitable option in transportation planning. This paper has shown how these services may be simulated in the microscopic travel demand model mobiTopp and which possible analyses result from this integration. With this module, besides research, city planning authorities and mobility service providers are able to scale future mobility solutions by modeling, as well as determine effects and interdependencies with other transport modes. In this paper, we demonstrated the possible options for analyses using a scenario with five different fleet sizes for ride-pooling and ride-hailing services operating in the city of Stuttgart.
There are several limitations in the results of the presented scenario, which thus mainly served as a technical demonstrator. Most of all, we used the same decision parameters for the mode choice of public transport and ridesourcing services. In the future, these parameters will be replaced by data gained from surveys explicitly covering the use of ride-hailing and ride-pooling vehicles. In addition to the analyses described above, with this additional data we will be able to show more realistic results concerning the expected demand changes and mode shifts within the different scenarios.
The results could be used both in planning and in supplying ridesourcing solutions. Running simulations with different prices for these services would lead to different demand, which lead to different detour factors and variations in costs. Service providers could plan their services according to their goals and then test these goals using mobiTopp simulations. Thus, services can be optimized with regards to costs and profits as well as to meet demand as best as possible.
With this newly developed module for the travel demand model mobiTopp new mobility services can be modeled in a detailed and complex fashion as shown in the paper. Shortly, we will offer the ridesourcing module as an open-source extension. Researchers, service providers and other possible users will then be able to simulate such services including interdependencies with the rest of the transport system.
Availability of data and materials
The software framework mobiTopp is released in the following repository: https://github.com/ifv-mobitopp/mobitopp. The ridesourcing extension will be published there during 2021. The datasets used for building the model are not publicly available due to intellectual property by several parties. The simulation results analyzed during the current study are available from the corresponding author on reasonable request.
Abbreviations
- BAU:
-
Business as usual
- MaaS:
-
Mobility as a Service
References
Balmer, M., Meister, K., & Nagel, K [K.]. (2008). Agent-based simulation of travel demand: Structure and computational performance of MATSim-T. ETH, Eidgenössische Technische Hochschule Zürich, IVT Institut für Verkehrsplanung und Transportsysteme.
Basu, R., Araldo, A., Akkinepally, A., Biran, B., Basak, K., Seshadri, R., … Ben-Akiva, M. (2018). Automated mobility-on-demand vs. mass transit: A multi-modal activity-driven agent-based simulation approach. Transportation Research Record Journal of the Transportation Research Board, 2672(8), 608–618. https://doi.org/10.1177/0361198118758630.
Becker, H., Balac, M., Ciari, F., & Axhausen, K. W. (2020). Assessing the welfare impacts of shared mobility and mobility as a service (MaaS). Transportation Research Part A: Policy and Practice, 131, 228–243. https://doi.org/10.1016/j.tra.2019.09.027.
Bischoff, J., & Maciejewski, M. (2016). Simulation of City-wide replacement of private cars with autonomous taxis in Berlin. Procedia Computer Science, 83, 237–244. https://doi.org/10.1016/j.procs.2016.04.121.
Bischoff, J., Maciejewski, M., & Nagel, K. K. (2017). City-wide shared taxis - a simulation study in Berlin. In 2017 IEEE 20th international conference on intelligent transportation systems (ITSC), (pp. 275–280). IEEE. https://doi.org/10.1109/ITSC.2017.8317926.
Briem, L., Buck, H. S., Mallig, N., Vortisch, P., Strasser, B., Wagner, D., & Zündorf, T. (2017). Integrating public transport into mobiTopp. Procedia Computer Science, 109, 855–860. https://doi.org/10.1016/j.procs.2017.05.401.
Briem, L., Mallig, N., & Vortisch, P. (2019). Creating an integrated agent-based travel demand model by combining mobiTopp and MATSim. Procedia Computer Science, 151, 776–781. https://doi.org/10.1016/j.procs.2019.04.105.
Friedrich, M., Hartl, M., & Magg, C. (2018). A modeling approach for matching ridesharing trips within macroscopic travel demand models. Transportation, 45(6), 1639–1653. https://doi.org/10.1007/s11116-018-9957-5.
Hautzinger, H., Kagerbauer, M., Mallig, N., Pfeiffer, M., & Zumkeller, D. (2013). Mikromodellierung für die region Stuttgart - Schlussbericht.
Heilig, M., Mallig, N., Schroeder, O., Kagerbauer, M., & Vortisch, P. (2018). Implementation of free-floating and station-based carsharing in an agent-based travel demand model. Travel Behaviour and Society Advance online publication, 12, 151–158. https://doi.org/10.1016/j.tbs.2017.02.002.
Jittrapirom, P., Caiati, V., Feneri, A.-M., Ebrahimigharehbaghi, S., González, M., & Narayan, J. (2017). Mobility as a service - a critical review of definitions, assessments of schemes, and key challenges. Urban Planning, 2(2), 13–25. https://doi.org/10.17645/up.v2i2.931.
Maciejewski, M. (2016). Dynamic transport services. In A. Horni, K. Nagel, & K. Axhausen (Eds.), The multi-agent transport simulation MATSim, (pp. 145–152). Ubiquity Press. https://doi.org/10.5334/baw.23.
Mallig, N., Kagerbauer, M., & Vortisch, P. (2013). Mobitopp – A modular agent-based travel demand modelling framework. Procedia Computer Science, 19, 854–859. https://doi.org/10.1016/j.procs.2013.06.114.
Mallig, N., & Vortisch, P. (2017, July 17). Modeling travel demand over a period of one week: The mobiTopp model. http://arxiv.org/pdf/1707.05050v1
Nahmias-Biran, B., Oke, J., Kumar, N., Basak, K., Araldo, A., Seshadri, R., … Ben-Akiva, M. (2019). From traditional to automated mobility on demand - a comprehensive framework for modeling on-demand services in SimMobility. Transportation Research Record, 2536, 036119811985355. https://doi.org/10.1177/0361198119853553.
Nökel, K. (2018). Modeling ride pooling within state-of-the-art travel demand models. Transportation Research Board. Transportation Research Board, Annual Meeting Poster Session.
SAE International (2018–09). Taxonomy and Definitions for Terms Related to Shared Mobility and Enabling Technologies (Surface Transportation Recommended Practice J3163).
Shaheen, S., Cohen, A., Stocker, A., & Martin, E. (Eds.). (2019). Mobility on demand - a smart, sustainable, and equitable future. Transportation Research Board http://www.trb.org/Main/Blurbs/179157.aspx.
Weiss, C., Heilig, M., Mallig, N., Chlond, B., Franke, T., Schneidereit, T., & Vortisch, P. (2017). Assessing the effects of a growing electric vehicle fleet using a microscopic travel demand model. European Journal of Transport and Infrastructure Research EJTIR, 17(3), 330–345. https://doi.org/10.18757/ejtir.2017.17.3.3200.
Acknowledgements
Not applicable.
Funding
Some basic algorithms were developed within several projects. However, this study was undertaken independently.
Author information
Authors and Affiliations
Contributions
The authors confirm contribution to the paper as follows: literature review: GW, MH; study concept, design and programming: GW, TH, LB; interpretation of results: GW, TH, MH, LB, MK, PV; draft manuscript preparation: GW, MH, TH, LB. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
This publication was prepared independently and contains theoretical assumptions, thus the authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Paper prepared for publication in the European Transport Research Review (ETRR) – Topical Selection: Developing Mobility as a Service – User, operator and governance perspectives (Springer Open, 2020).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wilkes, G., Briem, L., Heilig, M. et al. Determining service provider and transport system related effects of ridesourcing services by simulation within the travel demand model mobiTopp. Eur. Transp. Res. Rev. 13, 34 (2021). https://doi.org/10.1186/s12544-021-00493-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12544-021-00493-3