Abstract
We study the problem of making algorithmic statistical inferences about the dynamics of city traffic. Our data is based on loop detector counts of observed vehicles in various roads in the city of Tampere, Finland. We show that meaningful correlations can be found between traffic asymmetries at different measurement locations. The traffic asymmetry is the difference of the traffic counts of the opposite directions of a road. The correlations can be further quantified by estimating how much they effect on the average values of the traffic asymmetries at the neighbouring locations. Conditional expectations, both sample and binormal model-based versions are useful tools for quantifying this effect. The uncertainty bounds of conditional expectations of the binormal model distribution are extremely useful for outlier detection. Furthermore, conditional expectations of the multinormal distribution model can be used to recover missing data with bounds to uncertainty.
Similar content being viewed by others
1 Introduction
People’s travel behavior is initiated by the need to travel and then choosing the mode, route and time for trips. Travel behavior can be expressed in transport planning and management by origin-destination matrices (OD), [1]. OD-matrices have generally been estimated based on travel behavior surveys and interviews. Loop detectors, for example, allow short-term estimation by using real-time data on the traffic situation. The accuracy of traffic information is a key factor for road users’ decision making.
Information on traffic dynamic predictions is beneficial in traffic management centers (TMC) and operations. Especially, with the development of Cooperative Intelligent Transport Systems (C-ITS) and automated and connected vehicles, traffic could be further optimized and rerouted based on the current traffic situation. When a risk for a congestion arises, the vehicles could be rerouted either automatically or by providing real-time route information to the drivers and vehicles [2].
The motivation of this work is to provide a statistically robust algorithmic framework for automated analysis of loop detector data. This framework is applied to loop detector counts of observed vehicles at various crossroads in the city of Tampere, Finland. In our case, the traffic counts are easily available data since non-intrusive loop detectors are widely deployed, for example, near traffic lights. There are more than 80 signalized intersections in the city of Tampere. Counts of observed vehicles are, in principle, unbiased as noted in Hazelton and Parry [3]. Finally, there are usually no privacy issues, therefore traffic counts can be made available as open data. Thus, traffic count data are worth utilizing even when other data is the primary data.
The fundamental observation in our work is that the traffic counts at two different, sufficiently close, mutually relevant locations in the same 15-minute time window are correlated. This is because some vehicles are detected in the two chosen places and are included in the counts at these locations. If the correlations were only due to the detection of the same vehicles, they would be linearly proportional to the average amount of the common vehicles. The real situation turned out to be more complicated since the traffic volumes increase or decrease everywhere approximately simultaneously according to the time of the day. There is a need to extract a detectable traffic stream from the general traffic activity.
One way to identify detectable traffic streams is to observe the asymmetry in the traffic streams in the opposite directions of a road. We will show that positive results can be achieved with statistically robust methods; the correlations can be found and further quantified by estimating how much they affect on the average values of traffic asymmetries at neighboring locations. Conditional expectations, both the sample version and the analytical version based on the binormal model, were found to be useful tools for quantifying this effect. The binormal distribution is a simple and transparent model for the observed traffic asymmetry data and its parameters can be estimated with well-known robust methods. Its application in this context is justified by the Central Limit Theorem. The most useful feature of the conditional expectation computed from binormal model is that the uncertainty of it can be quantified explicitly and efficiently.
The contributions of this paper are the following. First, we change the focus from traffic counts to asymmetry and volume, and use (multi)normal distributions as a baseline model for them. We estimate the multinormal parameters, including correlation, in a robust manner. We show three applications of the proposed approach. First, the correlation matrices of the asymmetries are used to restrict the solution space of the OD matrix estimation problem. Second, the conditional expectations of asymmetries are used further to quantify how much asymmetry in one location can be assumed to effect on the asymmetry in another location. Third, the multinormal model can be used to reconstruct missing data according to the traffic dynamics of nearby locations. Especially, our proposed reconstruction can be equipped with confidence intervals. While our research problem set-up has similarities with, for example, [4], our contribution is complementary to existing methodology and we focus more on automated and robust methods.
This paper is structured as follows. First, in Section 2 we discuss briefly the related work. A brief description of the data is given in Section 3. Our suggested methodology is explained in Section 4 and example applications of the methodology are shown in Section 5. Conclusions are drawn in Section 6. Additionally, for the convenience of the reader, the formulae from the binormal and trinormal models for the conditional expectations are presented in the Additional file 1.
2 Related work
Origin – destination (OD) traffic volumes in a transportation network are valuable information for traffic management and development. However, the estimation of the OD traffic volumes is a challenging task due to various observability and identifiability problems, see [5]. Shao et al. [6] reviews different models and assumptions utilized in the literature in the context of estimating OD pairs with day-to-day traffic counts. Castillo et al. [7] discuss in detail traffic random variables and models. In the OD estimation context Hazelton [8] proposed a multivariate normal model for the link counts, based on the underlying overdispersed Poisson process, in order to increase the model flexibility with a moderate amount of parameters. He applied the model in a Bayesian estimation framework with the real data of 14 days. Lam et al. [9] modelled hourly flows and flow increments in the city of Hong Kong by normal distributions. In the context of traffic equilibrium assignment problems Shao et al., [10] utilized independent normal distributions for OD flows. Later Duthie, Unnikrishnan and Waller, [11] utilized a truncated multivariate normal model for OD pairs and addressed dependencies in OD demands. Sun, Zhang and Yu, [4] used mixtures of multinormal models and causal Bayesian networks for short-term traffic forecasting.
Most of the conventional OD demand estimation models utilize only the first-order statistical properties, but using the second-order property of the traffic counts can alleviate the difficulty of identifiability, [6] and [12]. However, the use of the second-order statistics brings the challenge of separating the correlation due to traffic flows from the general correlation due to increased/decreased activity during different hours of the day. Indeed, the flow-induced correlation - the key information in OD matrix estimation - can easily be hidden/overdriven by the correlation due to other reasons than the traffic flows. Therefore, OD demand estimation benefits from preliminary studies of data that can identify potential flows between OD pairs in a robust way. Ignoring the covariance between different OD pairs leads to an overestimation of the variance of traffic demand, [6], Section 4.1.4.
We foresee that combinations of various methods yield the best outcomes in short-term traffic predictions. Thus, we review shortly also recent developments using machine-learning techniques. Considering machine-learning methods, both parametric and non-parametric approaches have been applied in the literature. Moussavi-Khalkhali and Jamshidi, [13] used similar loop detector data and they attempt to predict traffic flows with the use of Multi-Layer Perceptrons and Principal Component Analysis. Recently, the most prominent approaches have revolved around Bayesian Networks and, above all, Neural Networks. Fusco et al. [14] use mobile GPS-based data on travel speeds and concentrate on the application of Bayesian Networks and Neural Networks to resolve short-term traffic predictions. Morris, Antoniades and Took [15] have car accident data and combine Bayesian Networks and Neural Networks specifically for the prediction of traffic accidents. Wang et al. [16] have traffic flow data and target the challenge of short-term traffic prediction through the utilization of ensemble methods accompanied with Neural Networks to improve the robustness and stability of their predictions. Tang et al. [17] attempt to improve their predictions of traffic information by employing a Fuzzy Neural Network accompanied with k-means clustering and Takagi-Sugeno fuzzy rules.
3 Description of the data
The data we use consist of the number of vehicles per time window observed in a few roads in the centre of the city of Tampere, Finland. The data was derived from traffic loop detectors embedded in the road surface. The loop detectors are connected to sensors, registering the amount of vehicles passing the location with the change in inductance in the loop. The sensors detect a vehicle by comparing the loop’s inductance to a pre-set threshold. The original data produced by the loop detectors has the unit vehicles/hour. The data is registered irregularly in a few minute intervals. The data were preprocessed to have constant 15-minute intervals, and are interpreted as the number of cars per a 15-minute time slot. This interpretation is roughly correct, but there have been some interpolations and averaging in the process. The data was prepared by the company InfoTripla (www.infotripla.fi). InfoTripla also provided precise and valuable information about traffic conditions like speed limits, locations of the main construction works, parking lots and shopping areas in Tampere during the years 2011-2017.
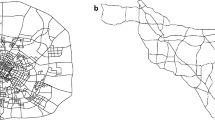
Figure 1 shows a part of the center of the city of Tampere, Finland, surrounded by the six measurement points located at Tampella, Satakunnansilta, Hämeensilta, Ratina, Pispala and Santalahti. There is a closed area with these six measurement points at the boundary. In this paper, the bounded city area will be referred to as the area of interest (AoI). These measurement points consist of loop detectors in both directions; therefore the entering and exiting directions are separated.
These six measurement points should have captured practically all vehicular traffic that entered or exited the bounded area during the four-year data collection period 2011 – 2014. The availability of traffic count data from Ratina was rather limited due to construction works, instead we were forced to use data collected from nearby locations, Satamakatu and Tampereen valtatie. Ratina is in between these two alternative locations and we know that the traffic characteristics at Ratina had to be similar to them. These alternative non-optimal locations did not capture all of the traffic; we know that, on long-term average, approximately 1-2 vehicles/minute were non-detected.
Due to the geographical location of the AoI there is some amount of east-west directed through-traffic. There are only few main roads or streets inside the AoI.
4 Methodology
In this section, we describe our methodologies for the automated analysis of traffic counts. We start with some notations.
The notations \(x_{i}^{(j)}\) and \(y_{i}^{(j)}\) are used for the number of vehicles per the i:th time slot and at the locationj, j=1,…,6. The \(x_{i}^{(j)}\) always indicates the number of vehicles that enter the AoI and \(y_{i}^{(j)}\) always refers to exiting vehicles. Since all locations are handled in a similar way, the location index (j) is sometimes dropped in the notation unless different locations are considered simultaneously. The time of the i:th slot is denoted by ti with the interpretation that the time stamp represents the end time of the slot. For example, ti=16:15 refers to the number of vehicles observed at the given day between 16:00−16:15.
4.1 Transformation of the data
At each location j we study the transformed data
The transformation (1) is bijective
so there is no loss of information in this step. The difference zi=xi−yi is called the (traffic) asymmetry and the sum vi=xi+yi is called the (traffic) volume. Since xi≥0 and yi≥0 the inequality −yi≤zi≤xi always holds. Due to limited space, in this paper we concentrate on applications of asymmetry but the same methodology framework can be applied to volumes as well. Figure 2 shows a scatter plot example of the transformation (1). The data in Fig. 2 consist of the first 10 000 available pairs \(\left (x_{i}^{(j)},y_{i}^{(j)}\right)\) from location j=Tampella.
A visual example of the transformation (1)
If \(z_{i}^{(j)}=x_{i}^{(j)}-y_{i}^{(j)}>0\), the number of the vehicles inside the AoI increased during the time slot ti at location j and, if \(z_{i}^{(j)}<0\), the number of the vehicles inside decreased. Thus, asymmetry is a measure of excess/shortfall at location j during the time slot ti when the AoI is considered as a reservoir of vehicles. If \(z_{i}^{(j)}\approx 0\) then, no matter how big the volume \(x_{i}^{(j)}+y_{i}^{(j)}\) is, the total of the vehicles inside AoI is not essentially affected by the traffic at j. Another justification behind this transformation is explained in Section 4.4. In [18] the asymmetry and the volume transform were utilized with a similar data but in a different problem set-up.
4.2 The Normal distribution as a baseline model
The empirical distributions of the asymmetries zi (and volumes) are typically unimodal, symmetric, light tailed and well approximated by the normal distribution. This is not a coincidence since the observed asymmetry values zi at any location j and at any time ti can be considered as sums of large number of possibly slightly correlated random variables with bounded small variances. The Central Limit Theorem (CLT) dictates that the distributions of zi should be approximately normally distributed [19]. Therefore, the normal distribution will be used as a baseline model for the asymmetries.
In an automated analysis, the parameters of the normal distribution model must be estimated in a robust manner. The reason for this is that the CLT-based argument for the normal distribution model covers only non-mixed cases. The observed data includes also observations that are mixed in the sense that any incident that restricts traffic anywhere nearby a loop detector can increase or decrease the number of observed vehicles in the detector. Thus, the observed data is a mixture of at least two qualitatively different sources of randomness and the use of ordinary sample means and sample variances is not justified for data from contaminated distributions, see [20] for further reasons. The next section discusses some technical details about robust estimation used in the proposed framework.
4.3 Robust estimation of the parameters of the Normal distribution model
Robust statistics is a well-developed area of statistics. In [20] robust estimators are heuristically defined as follows. Robust estimators should be statistically efficient at the assumed model, stable in the sense that small deviations in the model assumptions should impair the performance only slightly, and they should have high breakdown point meaning that somewhat larger deviations from the assumed model do not cause a catastrophe (see Section 1.2 in [20]). Any chosen robust estimator is always a compromise of these properties, including also conceptual clarity and computational issues.
The sample median is a well-known robust estimate of the mean μ of the normal distribution. If the data vary symmetrically around μ it is also reasonably efficient. Well-known robust estimators of the scale parameter σ (standard deviation) include the interquartile range (IQR) that has the following justification. If Φμ,σ is the cumulative distribution function (CDF) of the normal distribution N(μ,σ2) and Φ0,1 is the CDF of N(0,1), then the ratio of IQRs of these distributions is
and, since \(\Phi _{0,1}^{-1}(0.75)-\Phi _{0,1}^{-1}(0.25)\approx 1.3489795\), an estimator of the σ is just IQRn/1.3489795 where IQRn=Q3−Q1 is the sample IQR. The sample IQR is the difference of the 3rd sample quartile Q3 and the 1st sample quartile Q1. Again, symmetric variation around the mean is benefical for the efficiency of this simple estimator. The 2nd sample quartile Q2 is the sample median.
Conceptually three robust values, the sample quartilesQ1, Q2 and Q3, provide robust estimates of the two parameters μ and σ of the normal distribution, if the assumption of the normal distribution is valid and the data typically vary symmetrically around the mean. Moreover, the quartile skewness, defined as
can be used to indicate lack of symmetry in the quartile scale. In practice, it means that the fitted normal distribution typically fits the body of the empirical distribution well. There is deliberately no attempt to try to fit the normal model to the tails of the empirical distribution.
4.4 Robust estimation of the correlation
To understand the correlation (association, dependence) between the asymmetries of two locations the Spearman’s correlation coefficient is used as a complementary tool to the ordinary linear correlation coefficient. See [21] for the definition and Section 8.3 of [20] for the properties of the Spearman’s correlation. Spearman’s correlation ρS is a measure of monotone correlation. If the data are possibly contaminated, it is better suited for the data analysis than the linear correlation coefficient ρ. The sample version of ρS is denoted as rS and it is more robust against outliers than the sample version r of ρ. Linear correlation is a special case of monotone correlation and if linear correlation is true, the usually rS≈r. There is a negligible bias towards 0 in rS in that case and rS has slightly larger variance than r. In the binormal model case, this is straightforward to test by simulations. If the assumption of linear correlation is not true then the sample value r can be misleading while the sample value rS is meaningful as long as the monotone correlation, a concept with much wider extent, is plausible. As long as we do not know whether there are bivariate outliers or contamination in the data we trust more on rS than on r.
The simplest assumption for the main cause of the correlation is that the same vehicles are observed in two places, first in and then out. The 15-minute slot is sufficiently long so that a vehicle can enter and exit the AoI during the same slot at any two locations j and k. This specific kind of causality is the target to estimate. Note that an alternative explanation, in which totally different vehicles enter than exit, is always possible. However, being a significant and regular phenomenon such a coordinated common behaviour would require a more complicated explanation.
However, there are several other causes for the correlation between any two traffic streams. Other causes for correlation include such effects which appear in daily profile at every measurement point. For example: silent hours at night 0:00-06:00, rush hours around 8:00 and 16:00 during the working days and relatively silent moment just before early lunchtime 11:00 during the working days. In these cases the amounts of observed vehicles per slot are either increasing or decreasing everywhere and this shows up as always positive correlation in pairs like \(\left (x_{i}^{(j)},x_{i}^{(k)}\right)\), \(\left (y_{i}^{(j)},y_{i}^{(k)}\right)\) and \(\left (x_{i}^{(j)},y_{i}^{(k)}\right)\). This happens even in the cases in which the amount of the same cars in the two locations and in the directions in question must be practically zero. With the 15 minute granularity these effects are practically simultaneous. Ideally, our causal assumption can be expected to produce linear correlations. However, this is not necessarily true for the other causes. Either the above listed other common causes typically increase or decrease traffic amounts everywhere so that their combined effect should still be monotone. The use of rS to complement r is even more justified by this.
Another justification for the transformation (1) can now be expressed as follows: while the other common causes of correlation affect both xi and yi, the effect of other common causes diminishes when the difference xi−yi is considered and increases when the sum xi+yi is considered. That is, the differences xi−yi are less affected by the other common causes and they are easier to use when the assumed causal cause of the correlation is studied. Therefore, we use values
with different locations j and k.
The negative correlation in (2) tells something about the dynamics of the traffic. For example, if there is an asymmetric burst of traffic coming in at Tampella then, simultaneously, there is likely an asymmetric burst of traffic going out at Santalahti and vice versa. This holds true independently of the time of the day or the day of the week. It is plausible to assume that, whenever significantly non-zero, this correlation is caused by typically detecting some amount of the same vehicles at these locations during the same time slot. In [18] the application of asymmetry and volume was in a different context and the directions were chosen so that a positive correlation was targeted.
The correlation matrices can be estimated between the asymmetries of different locations. Moreover, the Spearman’s rank correlation test, see [21], can be added to the estimation process so that the null hypothesis of independence of asymmetries between two locations can be tested. If there is no evidence to reject the null hypothesis ρS=0, that is, rS≈0 with the large enough sample size n, then we can set rS=0. The correlation matrix is symmetric with diagonal values 1.
4.5 Empirical conditional expectation
For integer-valued random variables U and V, and an integer a with \(\mathbb {P}\{V=a\}>0\), the conditional expectation \(\mathbb {E}(U|V=a)\) can be computed as
Analogously to this, assuming that \(\mathbb {P}\{V>a\}>0\), define
The last formula can be used to compute a sample version\(\mathbb {E}_{n}(U|V>a)\) as
where (ui,vi), i=1,…,n, is the bivariate sample of size n. The formula for \(\mathbb {E}_{n}(U|V\leq a)\) is obtained similarly. There are two sums included and it requires some computation. The computational complexity is \({\mathcal {O}}(n^{2})\). The sample estimates of the joint probability mass function of the pair (U,V) and of the sample CDF of V are needed. The robustness properties of (3) should improve compared to if conditioned on the event {V=a}, but this is out of the scope of this publication.
The sample version (3) is computed for all vmin<a<vmax, where vmin and vmax are the minimum and maximum observed values. Typically n<vmax−vmin so there is implicit interpolation included in the map \( a\mapsto \mathbb {E}_{n}(U|V> a)\) since a need not be an observed value. This map defines a piecewise constant curve. If U and V are independent, it follows from (3) that \(\mathbb {E}_{n}(U|V>a)=\mathbb {E}_{n}(U)\) for all a.
4.5.1 The multinormal model
Given a binormal or trinormal model for asymmetries at two or three locations, formulae for the conditional expectations (4) and (6) and, especially, their variances can be computed analytically. These are provided in this section. The formulae (5) and (7) of conditional variances are important since they quantify the confidence limits and, therefore, allow the automatic detection of observations that do not fit into (multi)normal models.
Linear regression which is based on conditional expectatation \(\mathbb {E}(U|V=~a)\) with multinormal models are discussed, for example, in Section 4.3 of [22], in Section 11.3 of [23] and Chapters 4 and 7 in [24]. The conditioning with an event of type {V>a} is more rare but it is used at least in [25] in the context of economical self-selection models. Similar mathematical formulae appear also in the context of truncated distributions [26–28] since truncating a distribution is equivalent to conditioning on an interval.
Assume (Z1,Z2) is binormally distributed with the mean vector μ=(μ1,μ2), variances \(\sigma _{1}^{2}>0\), \(\sigma _{2}^{2}>0\) and correlation −1<ρ<1. If \(a\in \mathbb {R}\), then
in which, to simplify the notation, we define \(\alpha =\alpha (a)=\frac {a-\mu _{2}}{\sigma _{2}}\) for all \(a\in \mathbb {R}\). The formula for the conditional variance is
Assume (Z1,Z2,Z3) is trinormally distributed with the mean values μi, variances \(\sigma _{i}^{2}>0\), i=1,2,3 and pairwise correlations ρij, i<j. The conditional expectation \(\mathbb {E}\left (Z_{1}|Z_{2}=z_{2}, Z_{3}=z_{3}\right)\) can be computed as
The conditional variance Var(Z1|Z2=z2,Z3=z3) can be computed from
5 Results
5.1 Quantifying correlations of asymmetries
At each location the asymmetries zi turned out to vary around a non-zero and time-dependent mean. That is, at each location the long-term average value of the vehicles that enter the AoI at the location in question is different from the long-term average number of vehicles that exit the area at the same location. It is quite common to enter and exit the AoI at different locations due to various reasons of, for example, travel to work places, schools, daycare and shopping malls.
The robust methods allow algorithmic detection of those observed values that do not fit well to the normal or binormal distribution model. Figure 3 shows examples, where the asymmetries and volumes of two locations, Tampella and Santalahti, are illustrated. In the horizontal and vertical directions, the grid lines area at the estimated univariate normal model values μi and at the distance σi from it, that is, μi+kσi, k=−4,…,4. In the bivariate case also the elliptical quantile curves [24] can be computed, in Fig. 3 95% and 99% quantile curves are drawn as examples. At this phase, the correlations are based on rS. The uni- and bivariate values that do not fit well to the models can now be algorithmically classified as those points that are two far away from the model means, univariate or bivariate cases.
Based on the approach described in Section 4.4 we made two correlation matrix models for the boundary location asymmetries. They correspond to different times of the week in a coarser granularity than 15 minutes. The values that do not fit into the normal model are ignored so that r≈rS. For simplicity, the non-zero correlations are categorized only in granularity of 1/4. First, between 06:00 and 10:00 on weekdays the correlation matrix model is given in (8)
The rows and columns are in the order 1=Tampella, 2=Satakunnansilta, 3=Hämeensilta, 4=Ratina, 5=Pispala and 6=Santalahti. The afternoon rush hour model of hours 15:00 - 21:00 on weekdays is presented in (9)
During the other times the asymmetries at the boundary of AoI are almost uncorrelated or even independent for all location pairs j,k=1,…,6, j≠k. The correlation matrix models are positive-definite matrices. Due to many zeroes we conclude that the effective dimensionality of traffic asymmetry correlations is smaller than the number of the measurement points.
We expect the correlation matrices of asymmetries (8) and (9) should be helpful for OD matrix estimation in the sense that their information can be used to restrict the solution space of the OD matrix estimation problem and, therefore, should improve the identifiability of the problem.
5.2 Inference about traffic dynamics
We show an example that we expect to be directly helpful for a TMC operator. In addition, it brings more insight and restrictions to the OD matrix estimation problem. The idea is to consider the maps
where \(\mu _{j}=\mathbb {E}(Z^{(j)})\), as a function of a. This quantifies how the asymmetry at the location k affects the expected value of the asymmetry at the location j, j≠k; the unit will be "vehicles". The condition {Z(k)>a} is the easiest to interpret when a>0, that is, when the amount of vehicles that enter AoI at the location k is larger than the amount of vehicles that exit. We then ask how much this affects to the expected asymmetry at the location j. It is also easier to interpret Z(j)−μj since it is balanced in the sense that \(\mathbb {E}(Z^{(j)}-\mu _{j})=0\). In Fig. 4 the vertical axis is this balanced asymmetry (BA).
Four examples of functions expressed by Equation (10), the sample and the model versions
Figure 4 shows four examples from Friday, between 8:00 and 8:45 with j=Tampella and k=Santalahti. The sample version and the model version with 95% confidence intervals are shown together. Obviously, some of the vehicles that enter at Santalahti during this period, exit at Tampella, see the map in Fig. 1. Next, write \(x_{i}^{(k)}=\left (x_{i}^{(k)}-z_{i}^{(k)} \right)+z_{i}^{(k)}\) to emphasize that we first speak of excess vehicles \(z_{i}^{(k)}>0\) only. We then assume that the balanced asymmetry directly indicates the expected number of those excess vehicles that entered at Santalahti and will exit at Tampella. The values in the vertical axis with the minus sign in the balanced asymmetry are interpreted as the contribution of Santalahti to the expected number of excess vehicles that exit at Tampella. We can therefore estimate the proportion of the excess vehicles that enter at Santalahti and exit at Tampella. Finally, we generalize this by assuming that this proportion is the same as the proportion of all vehicles \(x_{i}^{(k)}\) that enter at Santalahti and exit at Tampella at the given time. Thus, from \(z_{i}^{(k)}>0\) we can infer properties of \(x_{i}^{(k) }\).
The model and the sample versions together have some potential to predict since the model is very fast to compute with updated information. It is possible to produce the model prediction already before the end of the 15-minute time slot and this, we believe, should be helpful for a TMC operator. In that application case, the information content needs to be expressed in a simple message like “An exceptionally large flow of inbound traffic observed at Santalahti, expected outbound contribution at Tampella is xx vehicles during the next 15 minutes”.
5.3 Reconstructing missing data
The limited availability of data from Ratina forced us to consider various methods to reconstruct missing data. This problem is solvable to some extent with a trinormal model when applied to the traffic asymmetries and taking advantage of correlations in the nearby locations. We show an example that is based on the formula (11) below. Instead of Ratina we use Pispala in an asymmetry triple
as it is possible to compare (11) with true observed values. We use the observed asymmetries at Santalahti and Tampella to predict the traffic asymmetry at Pispala and compare it with the true asymmetry value of Pispala. We assume that data are not completely missing, that is, in formula (6) the estimates of the parameters (μ1,μ2,μ3) and (σ1,σ2,σ3) are available and also the estimates ρ12, ρ13 and ρ23 are available.
The linear model is
The histogram of the distribution of the error ζ1−z1, where z1 is the true value in Pispala, was very good, see Fig. 5 (b). The errors have the median of 0 vehicles and 75% of the predictions satisfy −17≤ζ1−z1≤17, and 95% of the predictions satisfy −37≤ζ1−z1≤36. There were 102 093 triples (z1,z2,z3) available in total. Since we required that z2∈[μ2−3σ2,μ2+3σ2] and z3∈[μ3−3σ3,μ3+3σ3] so that z2 and z3 are not outliers of the trinormal model, the prediction was performed 98 949 times. In the remaining 3 144 cases (3% of the triple data) the predictions may still be good but this occurs merely by chance.
Figure 5a shows an example of time series view of the predictions (11). The red curve joins the predictions ζ1 and the black dots are the true values z1. The vertical short gray lines indicate the interval \(\left [\zeta _{1}-2\sigma _{\zeta _{1}},\zeta _{1}+2\sigma _{\zeta _{1}} \right ]\) where \(\sigma _{\zeta _{1}}\) is computed from (7). The gray intervals quantify the uncertainty of the predictions. Under the null hypothesis that (z1,z2,z3) is a sample from the trinormal distribution, the true value should be in the interval approximately 95% of cases.
There are a couple of issues to notice. First, the asymmetry at Ratina correlates with that of Pispala. If we could include that correlation into the multinormal model, we would probably get even better predictions. On the other hand, it is not meaningful to include any such location in the multinormal prediction model that does not correlate with Pispala. The second issue is the ability to quantify the prediction uncertainty. The third issue is that even a block of contiguous missing data can be recovered as long as good estimates of the parameters (μ1,μ2,μ3) and (σ1,σ2,σ3) are available and the estimates ρ12, ρ13 and ρ23 are available. The main issue we want to emphasize is, however, the simplicity of the formulas (6) and (7), and of the trinormal model in general.
6 Conclusion and discussion
We have described an algorithmic framework to extract relevant information about traffic dynamics from short-term traffic count data in the case where the traffic counts in the opposite directions are available in two or more mutually relevant locations. In our case, the traffic counts were obtained by loop detectors, but any other technology can be used as well. Our proposed framework is based on several basic ideas. First, we selected mutually relevant locations. By mutually relevant, we mean locations where asymmetries can be assumed to correlate due to detecting a proportion of the same vehicles at these locations. Second, we performed the transformation (1) in order to change the focus to asymmetry and volume, and use (multi)normal distributions as a baseline model for them. Third, we estimated the multinormal parameters, including correlation, in a robust manner (2). The fourth idea is the sample version of conditional expectation (3) which is supported by the model-based estimates with confidence intervals.
We showed three applications of the proposed approach. First, the correlation matrices of the asymmetries can be used to restrict the solution space of the OD matrix estimation problem. Since an OD matrix must be compatible with the information that the correlation matrix has, the solution space of possible OD matrices is reduced. In this application, we believe that only the relative strengths of correlations of asymmetries at different locations are needed. The stronger the correlations are, the more restrictions they should provide and the more helpful they should be. The estimation of the correlation matrix requires a sufficient amount of data.
Second, the conditional expectations of asymmetries can be used further to quantify how much asymmetry in one location can be assumed to affect on the asymmetry in the another location. We utilized the possibility to model the joint distribution at different locations by the binormal distribution. We have chosen a truncation-based method to acquire a robust and purely algorithmic method to quantify the effect of the asymmetry at one location to another correlated location. Since this approach can potentially predict, and its computation is very fast, it is expected to be helpful for a TMC operator.
Third, the multinormal model can be used to reconstruct missing data at one location according to the traffic dynamics of nearby locations. This approach is clearly different from using local long-term averages for the construction of missing data. Especially, our proposed reconstruction can be equipped with confidence intervals. When data is used for any kind of decision-making and some of the data is missing, the most important input for the decision-making is to quantify the uncertainty due to the missing data. The only knowledge about the traffic characterisics of the location of the missing data that was needed are the parameters μ1, \(\sigma _{1}^{2}\) and mutual correlations ρ12 and ρ13. In the reconstruction, we assumed availability of the historical data but, if no data is available from the location, then justified guess estimates for the values of these parameters already yield estimates that may be useful.
Finally, there are plenty of remaining issues for further study. In this study we focused on asymmetry at the boundary locations and achieved some understanding of the through-traffic. However, the majority of the total traffic is not through-traffic and a future topic is to explore what occurs inside the AoI. The transformation (1) is meaningful still there, hence also (2) and (3).
Availability of data and materials
All datasets used and/or analysed during the current study are available from the corresponding author on reasonable request. Some of the datasets generated and/or analysed during the current study are available in the Zenodo repository, https://zenodo.org/record/2359339#.XR3tj-szapo.
References
Sheffi, Y. (1985). Urban Transportation Networks. Englewood Cliffs, NJ: Prentice Hall.
EU (2017). C-ITS Platform Phase II Final report. https://ec.europa.eu/transport/sites/transport/files/2017-09-c-its-platform-final-report.pdf. Accessed 3 Fed 2020.
Hazelton, M.L., & Parry, K. (2016). Statistical methods for comparison of day-to-day traffic. Transportation Research Part B, 92, 22–34.
Sun, S., Zhang, C., Yu, G. (2006). A Bayesian Network Approach to Traffic Flow Forecasting. IEEE Transactions on Intelligent Transportation Systems, 7(1), 124–132. https://doi.org/10.1109/TITS.2006.869623.
Yang, Y., Fan, Y., Wets, R.J.B. (2018). Stochastic travel demand estimation: Improving network identifiability using multi-day observation sets. Transportation Research Part B: Methodological, 107, 192–211. https://doi.org/10.1016/j.trb.2017.10.007.
Shao, H., Lam, W.H.K., Sumalee, A., Chen, A., Hazelton, M.L. (2014). Estimation of mean and covariance of peak hour origin–destination demands from day-to-day traffic counts. Transportation Research Part B: Methodological, 68, 52–75. https://doi.org/10.1016/j.trb.2014.06.002.
Castillo, E., Calviño, A., Nogal, M., Lo, H.K. (2014). On the Probabilistic and Physical Consistency of Traffic Random Variables and Models. Computer-Aided Civil and Infrastructure Engineering, 29(7), 496–517. https://doi.org/10.1111/mice.12061.
Hazelton, M.L. (2008). Statistical inference for time varying origin–destination matrices. Transportation Research Part B: Methodological, 42(6), 542–552. https://doi.org/10.1016/J.TRB.2007.11.003.
Lam, W.H.K., Tang, Y.F., Chan, K.S., Tam, M.-L. (2006). Short-term Hourly Traffic Forecasts using Hong Kong Annual Traffic Census. Transportation, 33(3), 291–310. https://doi.org/10.1007/s11116-005-0327-8.
Shao, H., Lam, W.H.K., Meng, Q., Tam, M.L. (2006). Demand-Driven Traffic Assignment Problem Based on Travel Time Reliability. Transportation Research Record, 1985(1), 220–230. https://doi.org/10.1177/0361198106198500124.
Duthie, J.C., Unnikrishnan, A., Waller, S.T. (2009). Influence of Demand Uncertainty and Correlations on Traffic Predictions and Decisions. Computer-Aided Civil and Infrastructure Engineering, 26(1), 16–29. https://doi.org/10.1111/j.1467-8667.2009.00637.x.
Hazelton, M.L. (2003). Some comments on origin-destination matrix estimation. Transportation Research Part A, 37, 811–822.
Moussavi-Khalkhali, A., & Jamshidi, M. (2014). Leveraging machine learning algorithm to perform online and offline highway traffic flow predictions. In 13th International Conference on Machine Learning and Applications. https://doi.org/10.1109/ICMLA.2014.75. IEEE.
Fusco, G., Colombaroni, C., Comelli, L., Isaenko, N. (2015). Short-term traffic predictions on large urban traffic networks: applications ofnetwork-based machine learning models and dynamic traffic assignment models. In Models and Technologies for Intelligent Transportation Systems (MT-ITS), 3.5. June 2015. Budapest, Hungary. https://doi.org/10.1109/MTITS.2015.7223242. IEEE.
Morris, D., Antoniades, A., Took, C.C. (2017). On making sense of neural networks in road analysis. In 2017 International Joint Conference on Neural Networks (IJCNN). https://doi.org/10.1109/IJCNN.2017.7966415. IEEE.
Wang, D., Xiong, J., Xiao, Z., Li, X. (2016). Short-term Traffic Flow Prediction based on Ensemble Real-time Sequential Extreme Learning Machine under Non-stationary Condition. In Vehicular Technology Conference (VTC Spring), 2016, IEEE 83rd. https://doi.org/10.1109/VTCSpring.2016.7504474. IEEE.
Tang, J., Liu, F., Zou, Y., Zhang, W., Wang, Y. (2017). An Improved Fuzzy Neural Network for Traffic Speed Prediction Considering Periodic Characteristic. IEEE Transactions on Intelligent Transportation Systems, 18(9), 2340–2350.
Kilpi, J., Koskinen, S., Scholliers, J. (2019). Detection of anomalies in urban traffic from open data. In 13th ITS European Congress : Fulfilling ITS promises ; Conference date: 03-06-2019 Through 06-06-2019. https://2019.itsineurope.com/. ERTICO - ITS Europe, (p. TP1916).
Serfling, R.J. (1980). Approximation Theorems of Mathematical Statistics. New York: Wiley.
Huber, P.J., & Ronchetti, E.M. (2009). Robust Statistics, 2nd edn. Hoboken, New Jersey: Wiley.
Zwillinger, D., & Kokoska, S. (2000). Standard Probability and Statistics Tables and Formulae. Boca Raton, Florida: Chapman & Hall/CRC.
Weisberg, S. (2005). Applied Linear Regression, 3rd edn. New York: John Wiley & Sons.
Casella, G., & Berger, R.L. (2002). Statistical Inference, 2nd edn. Pasific Grove, California: Duxbury.
Johnson, R.A., & Wichern, D.W. (2007). Applied Multivariate Statistical Analysis, 6th edn. New Jersey: Pearson Prentice Hall.
Maddala, G.S. (1983). Limited-Dependent and Qualitative Variables in Economics. UK: Cambridge University Press.
Barr, D.R., & Sherill, E.T. (1999). Mean and variance of truncated normal distributions. The American Statistician, 53(4), 357–361.
Johnson, N.L., & Kotz, S. (1972). Bivariate and Trivariate Normal Distributions, (pp. 84–131). New York: John Wiley & Sons, Inc.
Kotz, S., Balakrishnan, N., Johnson, N.L. (2005). Bivariate and Trivariate Normal Distributions, (pp. 251–348). New York: John Wiley & Sons, Inc.https://doi.org/10.1002/0471722065.ch46.
Acknowledgements
The authors would like to thank Aleksi Vesanto and Kimmo Ylisiurunen from InfoTripla for their valuable assistance.
Funding
This study was funded by the Academy of Finland project 294763 Stomograph. The authors have also been supported by ECSEL MegaMaRT2 Project and by the European Union’s Horizon 2020 project Transforming Transport, grant agreement No 731932.
Author information
Authors and Affiliations
Contributions
JK, IN, PK and FM all contributed in the general conception of the work and in the initial analysis of data. JK, IN and PK all contributed in the mathematical and statistical conception of the work. JK is responsible for the final mathematical and statistical approach of this study. JK has done the data analysis of this study. JK, IN, PK, FM and TR all contributed in drafting, writing and revising of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Additional file 1
Statistical appendix. The file contains statistical details of the formulae that are used in this study.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kilpi, J., Norros, I., Kuusela, P. et al. Robust methods and conditional expectations for vehicular traffic count analysis. Eur. Transp. Res. Rev. 12, 10 (2020). https://doi.org/10.1186/s12544-020-0399-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12544-020-0399-8