Introduction

Water is one of the planet’s most critical and life-sustaining resources [1, 2]. Water management is a significant concern due to rising water consumption and pollution [3, 4]. Accurate and timely rainfall forecasting is crucial for water resource management, irrigation planning, and reservoir operation [5]. Forecasting rainfall is crucial, because heavy rain frequently poses hydrological risks [6]. The nature of the atmospheric circulation system that generates rain makes rainfall forecasting difficult [7]. Physically based models commonly used for rainfall forecasting perform poorly when predicting rainfall 1 month in advance. However, rainfall forecasting 1 month in advance is crucial for water resource management. Consequently, hydrological modelers continuously attempt to develop a perfect model for rainfall prediction [8].

Soft computing techniques have been extensively used for parameter prediction and modeling in various fields of water resources, such as hydraulics [9], hydrology [10,11,12], and water quality [13, 14]. In addition, rainfall prediction methods based on soft computing have been frequently investigated in recent years [15, 16]. Soft computing models have been found to be quite effective at identifying nonlinear systems in a variety of engineering domains. Using various forms of soft computing, numerous studies have been conducted on rainfall forecasting. Rainfall was modeled by Mandal and Jothiprakash [17] utilizing a multilayer perceptron (MLP) neural network, a radial basis neural network (RBFNN), and a time-lagged recurrent network (TLRN). Regarding accuracy, the ANN models performed better than the regression models.

Hipni et al. [18] modeled rainfall using ANFIS and support vector machine (SVM) models. They observed that the ANFIS model could provide accurate estimates of rainfall. Nourani and Komasi [19] examined the performance of integrated geomorphological adaptive ANFIS (IGAANFIS) in modeling rainfall and reported that it outperformed the other models. Akrami et al. [20] compared the ANFIS and ANN rainfall prediction models. According to their findings, the ANFIS provided greater accuracy than the ANN model. They utilized various time delays between time (t) and time (t–4) (scale: month).

Mehdizadeh et al. [21] estimated monthly rainfall time series using gene express programming autoregressive conditional heteroscedasticity. The outcomes demonstrated that the new method was more precise than gene expression programming. Mehr and Nourani [22] compared multi-gene-genetic programming (MGGP) and genetic programming (GP) for estimating seasonal rainfall and demonstrated that the MGGP is more accurate than the GP. Ouyang and Lu [23] predicted monthly rainfall using MGGP, echo state network, and SVM models. In terms of predicting monthly rainfall, the results indicated that the MGGP performed poorly compared to other models.

Recent research has demonstrated that combining soft computing models with preprocessing and optimization algorithms can boost their performance. Adiwjaya (2015) improved rainfall forecasting by combining ANN with evolutionary algorithms. Feng et al. [24] combined the wavelet technique with SVM and ANN and demonstrated that the wavelet SVM (WSVM) model outperformed others. Yaseen et al. [25] investigated the application of integrated ANFIS model with the firefly optimization algorithm (FFA) and revealed that the FFA-optimized ANFIS is more accurate in stream-flow forecasting than standalone ANFIS. Mehr et al. [26] investigated the combination of SVM and FFA for rainfall forecasting. According to the results, the new model generated accurate precipitation forecasts.

Pham et al. [27] developed ANN–particle optimization (PSO) and SVM–PSO models for predicting rainfall. The results indicated that the SVM–PSO was the most accurate model. Basha et al. [28] predicted rainfall using auto-regressive integrated moving average (ARIMA), ANN, and SVM. The outcomes revealed that the ANN model outperformed the ARIMA model. Aknier (2021) developed an ANN model for rainfall forecasting. The Levenberg–Marquardt algorithm was employed to adjust ANN parameters. The study reported that the ANN provided accurate results. Ahmed et al. (2021) developed different hybrid models including MLP–HGSO, MLP–NRO and MLP–EO for estimation of stream flow for High Aswan dam. They used data of 130 years for training and testing of the developed models. They concluded that the NRO was the best optimization algorithm that improves the capability of MLP model for hydrological modeling. Ruma et al. [29] used PSO to enhance the performance of ANN and LSTM for water level prediction in one of Bangladesh rivers. They concluded that the PSO could enhance the performance of the LSTM better than the ANN.

Wang et al. [30] combined wavelet packet decomposition (WPD) and an extreme learning machine (ELM) model. They stated that the WPD enhanced the ELM model’s effectiveness. Kumar et al. [31] coupled biogeography-based optimization (BBO) models with ELM and deep neural network models. They selected the inputs using partial autocorrelation function (PACF). They reported that the ELM–BBO was a reliable tool for risk mitigation. Li et al. [32] designed the pruned ELM (OP–ELM) to forecast rainfall. Different activation functions of the OP–ELM model were utilized. The OP–ELM was highly capable of predicting rainfall.

The review above indicates that the soft computing model integrated with an optimized algorithm performs better than the standalone model in terms of rainfall modeling. However, the performance of such a hybrid model varies greatly depending on the optimization algorithm chosen. Consequently, it is essential to evaluate the performance of various optimization algorithms after their incorporation into soft computing models. In this study, new and conventional optimization algorithms were compared in terms of their performance in enhancing the accuracy of soft computing models for rainfall forecasting.

The RBFNN has numerous benefits. While MLP models can have multiple hidden layers, the RBFNN models have one. Therefore, it is faster and can converge sooner. In addition, RBFNN models offer simplicity of implementation and high precision. There are various machine learning models for predicting rainfall, such as optimized ANFIS and ELM models. However, adjusting these models’ unknown parameters may be time-consuming and challenging. These unknown parameters may increase the values of model uncertainty. Consequently, the current study employs optimized MLP and RBFNN models for rainfall forecasting.

This study evaluates the effectiveness of new optimization algorithms in training ANNs and analyzes the uncertainty of new RBF and MLP models. Monthly rainfall with varying time lags was used as input parameters to predict rainfall 1 month in advance. Several models were developed using different input combinations that include time lags ranging from months (t–1) to (t–9), where (t–1) was used as input for the first model and (t–1) and (t–2) for the second model and so on. The main objectives and novelties of the current paper are as follows:

  1. (1)

    Developing a new hybrid models of MLP and RBFNN using meta-heuristic algorithms, Henry gas solubility optimization (HGSO), bat algorithm (BA) and particle swarm optimization (PSO) for predicting long-term rainfall.

  2. (2)

    Developing the transient probability matrix (TPM) rainfall for identifying rainy days, where the TPM can be used as an early warning system to identify and motoring of the flood and drought periods.

  3. (3)

    The principal component analysis (PCA) was used to preprocess the data, where it is considered as the best tool to decide the best-input data.

Materials and methods

Materials

Study area

In Peninsular Malaysia, the Sara Station (station A) is located at latitude 5o 25ˊ and longitude 101° 25ˊ, while the Banding Station (station B) is located at latitude 5o 30ˊ and longitude 101° 30ˊ. Figure 1 depicts the locations of stations on a map of peninsular Malaysia. According to the Koppen classification, both stations have climates characterized by tropical rainforests. The average monthly rainfall was obtained from station A and station B for the period January 2001 to January 2014 to develop the models. The monthly rainfall time series for both stations are depicted in Fig. 2a, b. The models developed in the current study can be applied to other global regions. These models can predict other variables, such as groundwater level, temperature, runoff, and sediment. In addition, these models can be used to predict various variables under climate change conditions. Since the water resource management is important for the basin, these stations are chosen.

Fig. 1
figure 1

Location map of rainfall stations

Full size image
Fig. 2
figure 2

Time series of rainfall stations

Full size image

Data preprocessing and input selection

Principal component analysis (PCA) was used to reduce a large number of input variables to a manageable number [33, 34]. PCA transforms a collection of correlated variables into a collection of principal components (uncorrelated variables). The initial PCA accounts for as much information variability as possible. PCA searches for a linear combination of input variables to extract the maximum data variance. This study used PCA to select inputs in various time lags from month (t–1) to month (t–9).

Methods

Artificial neural network (ANN) models

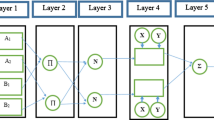
ANN is a technique based on the workings of the human nervous system [35]. MLP is one of the most significant ANN models for predicting meteorological variables. It is composed of individual processing units called neurons. The neurons in the MLP structure are arranged in distinct layers. When applied to problems, ANNs do not require prior knowledge of atmospheric conditions [36]. They can circumvent the limitations of empirical models. The neurons of the first layer receive the input variables (x0). Neurons can learn complicated features via hidden layers. A weight (w0) associated with each input is considered in the structure of the MLP model. Each neuron also has a bias. Additional inputs to neurons are classed as biases (b). By generating weight values, ANNs build associations between input and output data. The MLP output is obtained by applying the nonlinear activation function to the weighted input sum (Fig. 3).

Fig. 3
figure 3

a Computation process in the MLP and b The details of the structure of the MLP model

Full size image

The weights and biases must be updated to minimize the error predictions. Different algorithms are used to optimize the network parameters. The learning algorithms can be categorized into two groups. The first group employs optimization algorithms, while the second employs conventional numerical optimization techniques. Although numerous optimization algorithms for training ANNs have been studied in the past, the problem of local minima remains unsolved. Consequently, novel MLP and RBFNN methods based on new optimization algorithms are proposed in this article [37].

Henry gas solubility optimization (HGSO)

Hashim et al. [38] introduced a new optimization technique based on Henry’s law, termed HGSO. The algorithm’s performance was evaluated on benchmark functions, a speed reducer design problem, and real-world engineering difficulties. In the experiments, particle swarm optimization (PSO), genetic algorithm (GA), gravitational search algorithm (GSA), whale optimization algorithm (WHOA), and cuckoo search algorithm (CSA) performed poorly. HGSO can imitate Henry’s law behavior. Local optimums are omitted through this method. Henry’s law determines how soluble low-solubility gases are in liquids. First, the population (number of gases) and position of gases are initialized using the following equation:

$$X_i \left( {t + 1} \right) = X_{\min } + r\left( {X_{\max } - X_{\min } } \right)$$
(1)

where Xi denotes the position of ith gas, N is the population size, r represents a random number, Xmin and Xmax are bounds of the problem, t is the iteration number, and \(X_i \left( {t + 1} \right)\) denotes the new position at the t + 1 iteration.

The population gases are divided into equal categories based on their number. Because the gases in each group are comparable, Henry’s constant value for each group is the same. Every gas has its own unique Henry’s law constant. Henry’s law constant for every gas is proportional to the gas concentration in liquid form and partial pressure in the gas phase. Henry’s law states that the amount of dissolved gas in a given volume of liquid is proportional to its partial pressure above the liquid. Each cluster j is analyzed to determine the optimal gas in its class with the highest equilibrium phase. Different ranks of gases are used to identify the optimal gas for the swarm. Equation (2) is used to update Henry’s coefficient:

$$\begin{gathered} H_j \left( {t + 1} \right) = H_j \left( t \right) \times \exp \left( { - C_j \times \left( {\frac{1}{T_t } - \frac{1}{T^\theta }} \right)} \right),T_t = \exp \left( {\frac{ - t}{{{\text{iter}}}}} \right) \hfill \\ H_j \left( t \right) = l_1 \times {\text{rand}}\;\left( {0,1} \right),P_{ij} = l_2 \times {\text{rand}}\;\left( {0,1} \right),C_j = l_3 \times {\text{rand}}\;\left( {0,1} \right) \hfill \\ \end{gathered}$$
(2)

where \(H_j\) denotes Henry’s coefficient of cluster j, T represents temperature, \(T^\theta\) is constant (298.5), \(P_{ij}\) represents partial pressure, Cj denotes enthalpy of dissolution, l1 is constant (0.05), l2 is constant (100), and l3 is constant (0.01). The solubility is updated based on the following equation:

$$S_{i,j} \left( t \right) = K \times H_j \left( {t + 1} \right) \times P_{i,j} \left( t \right)$$
(3)

where \(S_{i,j} \left( t \right)\) denotes gas i’s solubility in cluster j’s, \(P_{i,j}\) represents gas i’s partial pressure in cluster j. The position of gases is updated using the following equation:

$$\begin{aligned} X_{i,j} \left( {t + 1} \right)\; = & \;X_{i,j} \left( t \right) + F \times r \times \gamma \times \left( {X_{i,{\text{best}}} \left( t \right) - X_{i,j} \left( t \right)} \right) + F \times r \times \alpha \times \left( {S_{i,j} \left( t \right) \times X_{i,{\text{best}}} \left( t \right) - X_{i,j} \left( t \right)} \right) \\ \gamma \; = & \;\beta \times \exp \left( { - \frac{{F_{{\text{best}}} \left( t \right) + \varepsilon }}{{F_{i,j} \left( t \right) + \varepsilon }}} \right),\varepsilon = 0.5 \\ \end{aligned}$$
(4)

where \(X_{i,j}\) denotes the position of gas i in cluster j, r is a random constant, t is iteration time, \(X_{i,{\text{best}}} \left( t \right)\) denotes the optimal gas, \(F_{i,j}\) is the objective function of gas i in cluster j, \(X_{i,{\text{best}}} \left( t \right)\) denotes the optimal gas in the group, \(\beta\) is constant, \(F_{{\text{best}}}\) is the objective function of the optimal gas, \(F_{i,j}\) represents the objective function of gas i in cluster j, \(\alpha\) is the effect of other gases on gas i in cluster j equal to 1, and F denotes the flag that alters the search gas’ direction. Finally, Eq. (9) is used to rank and choose the quantity of the worst gases:

$$N_u = N \times \left( {{\text{rand}}\left( {c_2 - c_1 } \right) + c_1 } \right),c_1 = 1,c_2 = 0.2$$
(5)

where \(N_u\) denotes the number of worst gases, and N represents the number of gases.

Equation (10) is used to update the worst gases’ position:

$$G_{i,j} = G_{\min \left( {i,j} \right)} + r \times \left( {G_{\max \left( {i,j} \right)} - G_{\min \left( {i,j} \right)} } \right)$$
(6)

where \(G_{i,j}\) denotes gas i’s position in cluster j, r is a random number, and \(G_{\max \left( {i,j} \right)}\) and \(G_{\min \left( {i,j} \right)}\) are the bounds of the problem.

Particle swarm optimization (PSO)

PSO is utilized in various optimization domains and integrated with other algorithms. This algorithm uses particles to determine the optimal solution. The achieved and optimal swarm positions are utilized to identify each particle. Equations (7, 8) change the positions of the particles as follows [39]:

$$v_i^{t + 1} = \omega v_i^t + c_1 r_1 \left( {xBest_i^t - x_i^t } \right) + c_2 r_2 \left( {gBest_i^t - x_i^t } \right)$$
(7)
$$x_i^{t + 1} = x_i^t + v_i^t .t$$
(8)

where \(x{\text{Best}}\) denotes the best particle position, g represents the best group position, \(\omega\) is inertia weight, c1 and c2 are acceleration coefficients, and \(\omega\) denotes the inertia coefficient. PSO’s stochastic features ensure that the solution space is exploited.

Bat algorithm (BA)

The BA is an optimization algorithm based on swarm intelligence introduced by Yang [40]. The algorithm mimics the echolocation behavior of bats.

Bats employ echolocation to locate prey and avoid obstacles. Bats utilize the temporal difference between emission and environmental reflection to locate prey. The bats’ volume decreases from a high positive value to a low constant value. Virtual bats are used to produce novel solutions for the bat algorithm:

$$f_i = f_{\min } + \left( {f_{\max } - f_{\min } } \right)\beta$$
(9)
$$v_i^t = v_i^{t - 1} + \left( {x_i^{t - 1} - x_\ast } \right)f_i$$
(10)
$$x_i^t = x_i^{t - 1} + v_i^t$$
(11)

where \(v_i^t\) denotes velocity, \(x_i^t\) represents location, t is iteration, \(x_\ast\) denotes the optimal solution, \(\beta\) is a random value, and \(f_{\min }\) and \(f_{\max }\) are min and max frequency, respectively.

The loudness and pulsation rate must be changed to manage the exploitation and exploration stages. To this end, Eq. 16 is used to calculate the pulsation rate and loudness parameters:

$$\begin{gathered} A_i^{t + 1} = \alpha A_i^t \hfill \\ r_i^{t + 1} = r_i^0 .\left( {1 - e^{ -^{\gamma t} } } \right) \hfill \\ \end{gathered}$$
(12)

where \(A_i^{t + 1}\) denotes the average loudness of all bats, \(r_i^{t + 1}\) represents the pulsation rate at time t + 1, \(\alpha\) and \(\gamma\) are a constant and initial loudness, respectively, and \(r_i^0\) is the initial pulsation rate.

Locally, the random walk is used to determine a new position for each bat:

$$x_{new} = x_\ast + \varepsilon A^t$$
(13)

Optimization algorithm for training RBFNN and MLP

Each candidate ANN (MLP and RBFNN) is encoded as a dimensional vector for each member (particle, gas, and bat). Vectors consist of a set of weights connecting the first layer to the hidden layer, a set of weights connecting the second layer to the final layer, a set of biases, a set of widths of hidden neurons, and a set of centers of hidden neurons. To assess the objective function value of the candidate RBFNN and MLP networks, the RMSE is computed over all training data for each member. The workflow of the optimization algorithms used in this article to train the MLP and RBFNN is outlined in the steps below:

  1. 1.

    Initialization: A predefined number of particles, bats, and gases show a possible RBFNN and MLP network.

  2. 2.

    An objective function evaluates the equality of generated RBFNN and MLP networks. The provided search agents (weights, biases, widths, and centers) are first assigned to MLP and RBFNN networks, and then the networks are evaluated. The RMSE is a popular objective function in integrated ANNs. Based on the training data, the training algorithm attempts to construct the MLP and RBFNN with the lowest RMSE value possible.

  3. 3.

    The position of each agent is updated.

  4. 4.

    Levels 2 to 3 are iterated until the maximum number of iterations is achieved. Finally, the RBFNN and MLP models with the minimum RMSE are tested on the unobserved part of the data.

The current study’s MLP–HGSO model contains one hidden layer. There were four hidden neurons. A process of trial and error was used to determine the number of hidden neurons and layers. Moreover, there were four hidden neurons in RBFNN–HGSO, obtained using a trial-and-error method (Fig. 4).

Fig. 4
figure 4

Flowchart of the developed models

Full size image

Evaluation of models performance

To evaluate and compare the results of the developed models in this study, different statistical indices were used, including mean absolute error (MAE), percentage of BIAS (PBIAS) and Nash–Sutcliffe efficiency (NSE). The equations of these statistical indices are shown as follows:

$$\mathrm{MAE}= \frac{1}{n}\sum_{i=1}^{n}\left({y}_{i}-{y}_{i}^{-}\right)$$
(14)
$$\mathrm{PBIAS}= \sum_{i=1}^{n}\left({y}_{i}- {y}_{i}^{-}\right)*100/\sum_{i=1}^{n}{y}_{i}$$
(15)
$$\mathrm{NSE}=1- \left[\sum_{i=1}^{n}{\left({y}_{i}- {y}_{i}^{-}\right)}^{2}/\sum_{i=1}^{n}{\left({y}_{i}- {y}_{mean}\right)}^{2}\right]$$
(16)

where \({y}_{i}\) is the observed value, \({y}_{i}^{-}\) is the predicted value, \({y}_{\mathrm{mean}}\) is the mean value of the data and n is the total number of data [39, 41, 42].

Results and discussion

Taguchi model

The Taguchi model is one of the commonly applied methods for adjusting the parameters of optimization algorithms. In this model, some experiments are considered based on different integrations of some effective parameters to achieve the best integrations of effective parameters. Taguchi’s model uses some special orthogonal arrays (OR). The OR are special cases of the fractional factorial design. In this model, there are two important parameters: noise parameters and controllable parameters. Analyzing the results employs the signal-to-noise ratio. To implement the Taguchi model for adjusting the parameters of optimization algorithms, it is necessary to identify the parameters with the most significant impact on the output. Table 1 outlines the algorithm’s parameters that were determined for this purpose. To conduct the experiments in the Taguchi model, it is necessary to determine the parameter values that result in good fitness.

Table 1 Parameters of the algorithm implemented in this study
Full size table

Consequently, the parameter values are determined using a trial-and-error approach. Next, considering the available degrees of freedom, an appropriate orthogonal array is selected. Since the minimization problem is considered, the signal-to-noise ratio can be calculated through the following equation:

$$\frac{S}{N} = - 10\log \left( {{\text{objective}}\left( {\,{\text{function}}} \right)} \right).$$
(17)

In this study, 4, 5, and 2 parameters were selected for the PSO, BA, and HGSO, respectively, using the Taguchi model with four levels. Based on L16, L16, and L16 orthogonal arrays, 16 experiments were performed for the PSO, BA, and HGSO parameters, respectively. The outputs of tuning parameters using the Taguchi model are presented in Table 1.

PCA results

Inputs to the various soft computing models were selected based on the past monthly average rainfall. As shown in Table 2, the total number of experimental input data is nine, including rainfall at t–1 (previous month) to t–9 (9 previous months). The PCA was applied to data from 2001 to 2014 to obtain PCs and reduce the dimension of the input data. Table 3 displays the selected important components. Eigenvalues larger than one indicate significant components, where significant components must be retained. The variance described indicates what percentage of its component’s data can describe the variability of raw rainfall inputs. It was determined that the first five PCs accounted for 80% of the total variance, so the input was set to 5. Table 3 displays the loading matrix of the input variables for these components. Greater loading indicates that input data describe more information. The results indicate that the first five components are strongly correlated with the five sets of lagged input data [R (t–1), R (t–2), R(t–3), R(t–4), and R (t–5)].

Table 2 Input data and Eigen vectors
Full size table
Table 3 Loading matrix for input variables
Full size table

Statistical results for soft computing models

The PSO, BA, and HGSO were combined with a standalone MLP model to develop new models for forecasting monthly rainfall at two stations based on antecedent values. Three important indices including the MAE, NSE, and PBIAS were used. They illustrate the disparity between measured and observed data. These indices serve to assess the performance of models. In addition, the calculation of these indices is straightforward.

As shown in Table 4, using the MLP–HGSO model, as an illustration, the MAE value for station 1 during the testing period is 0.712 mm. Table 4 demonstrates that the MLP–HGSO model is more accurate than the other soft computing models. Table 4 clearly demonstrates that the MLP–BA model outperforms the MLP–PSO model. Regarding the obtained results of MLP and RBFNN models for two stations, it could be concluded that the MLP outperforms the RBFNN. The MAE = 0.812 mm and PBIAS = 0.27 values reflected in the RBFNN–HGSO outputs for the testing level exceeded the accuracy level of the MLP–HGSO developed with the same inputs.

Table 4 Statistical indexes for different soft computing models
Full size table

In terms of the RMSE and PBIAS indices, Table 4 shows that the MLP–HGSO model has the lowest values when compared to other applied soft computing models. According to Table 4, the RBFNN–HGSO model with lower MAE and PBIAS values is more accurate than the other RBFNN models. However, the MLP–HGSO model has the lowest RMSE and PBIAS values among the other models. In addition, Table 4 demonstrates that the RBFNN–HGSO model outperforms the RBFNN–PSO and RBFNN–BA across all performance metrics. Moreover, the HGSO appears to be a more effective optimization tool than the PSO and BA for improving results.

Taylor diagram (TD) for soft computing models

TDs are graphical representations of mathematical models that highlight the most realistic models. TD is used to evaluate the degree of accuracy between simulated and observed data using standard deviation, RMSE, and Pearson’s coefficient of correlation. According to the findings, the MLP–HGSO model is more accurate than the other soft computing models (Fig. 5). The MLP–HGSO and RBFNN–HGSO are found to be closer to the reference point (observed data).

Fig. 5
figure 5

TD for soft computing models

Full size image

Gradient color curves

Figure 6 depicts the RMSE–observation standard deviation ratio (RSR) values. As can be seen, the maximum MLP–HGSO RSR values at stations 1 and 2 are 0.25 and 0.2, respectively. The HGSO model outperforms the BA and PSO models. According to a previous literature review (Braga et al. 2018), model performance is deemed “satisfactory” if RSR ≤ 0.7 [43]. Various reports indicate that the model’s performance can be deemed “very good” if RSR ≤ 0.5. In addition, the R2 analysis indicates that the MLP–HGSO model is more closely aligned with the observed data compared to other models.

Fig. 6
figure 6

Gradient color curves for soft computing models

Full size image

Transient probability matrix rainfall

The Markov chain is a mathematical model that explains stochastic processes and offers probability information on phase transitions. In n time steps, the probability of moving from state i to state j is given as [17]:

$$P\left[ {X_{t + 1} = i_{t + 1} |X_t = i_t ,....,X_0 = i_0 } \right] = \Pr \left[ {X_{t + 1} = i_{t + 1} |X_t = i_t } \right]$$
(18)

where Xt denotes a random variable, i0, i1, i2,…,it+1 represents the state at each time and \(P\left( {x_{t + 1} = j|X_t = i} \right) = p_{ij}\) is the transition probability from phase i at time t to phase j at time t + 1:

$$p= \left[{p}_{ij}\right]=\left[\begin{array}{cc}{p}_{11}& {p}_{1s}\\ {p}_{s1}& {p}_{ss}\end{array}\right]$$
(19)

where \(0 \le p_{ij} \le 1,\sum_{j = 1}^s {p_{ij} } = 1,s:{\text{the}}\;\left( {\,{\text{number}}} \right)\,{\text{of}}\;\left( {\,{\text{state}}} \right)\)

Given the strong performance of the newly implemented hybrid MLP–HGSO model, future research could include the hybrid MLP–HGSO model to forecast other hydrological variables in the short and long run. To avoid duplication of discussions, station 1 was selected as a representative example for analyzing rainfalls. A state matrix, which is a row matrix, displays the probabilities for each state. For instance, the steady-state matrix (0.77, 0.23) indicates that station 1’s precipitation follows the probability distribution (Table 5).

Table 5 Stable probability matrix for stations
Full size table

In 2001, the probability of precipitation on a given month at station 1 was 0.77, and the probability of dryness on a given month at station 1 was 0.23. The predicted monthly rainfall used in this article was derived from the observed data at stations 1 and 2 for the years 2001–2014, a period of 13 years. Notably, MLP–PSO and RBFNN–PSO were omitted from Table 5 due to their significantly inferior estimates compared to MLP–HGSO, RBFNN–HGSO, MLP–BA, and RBFNN–BA. The results indicate that the rainfall pattern of MLP–HGSO closely resembles those of observed data. For example, the predicted rainfall values of MLP–HGSO and observed data reveal that the highest rainfall for station 1 occurred in 2001 with a probability of 0.77 and that the highest rainfall for station 2 occurred in 2007 and 2009 with the same probability. Other values also demonstrate that the MLP–HGSO model is superior to other alternatives.

When modelers encounter incomplete, noisy, or small data sets, signal decomposition is a useful performance-enhancing technique. Optimization algorithms, preprocessing techniques, and decomposition methods can improve the performance of ML models. Our data are reliable and complete; thus, optimization and principal component analysis are used to enhance model performance. The models produced the best results without error index-based decomposition techniques. A set of input variables carefully selected can aid forecasting models in capturing the nonlinear characteristics of runoff data. However, ensemble empirical mode decomposition with the MLP model is combined to determine the difference between MLP–EMD and MLP models.

The ensemble empirical mode decomposition (EEMD) is a useful tool for preprocessing data. The EMD generates a finite number of oscillatory modes from the original time series data. Every oscillatory mode is described by an intrinsic mode function (IMF). Depending on the data-driven mechanism, the IMF can be derived directly from the data. An EMD algorithm converts a time series into IMF modes through a shifting process. More details about the EMD can be found in Wang et al. (2015). The results of MLP–HGSO with and without EMD are displayed in Table 3. As shown in the table, MLP–HGSO–EMD does not significantly improve MLP–HGSO performance.

Since robust optimization algorithms and PCA were used to improve the performance of MLP models, the MLP–HGSO results are reliable without an EMD model. At the first station, the MLP–HGSO–EMD and MLP–HGSO models had training MAEs of 0.685 and 0.687 mm, respectively. At the testing level, the MLP–HGSO–EMD and MLP–HGSO models had MAE values of 0.710 and 0.712 Table 6.

Table 6 Comparison of MLP–HGSO–EMD with MLP–HGSO
Full size table

This research found that optimization algorithms play a crucial role in modeling. They can improve the output prediction accuracy of machine learning models. To select the optimal input scenarios, developers should employ methods, such as PCA. However, there are a variety of ways to define optimal features. The gamma test is a reliable method for selecting inputs. Since the optimization algorithms use different operators, the MLP and RBFNN models have different accuracy. Moreover, these models are highly adaptable.

The modelers can integrate these models with climate scenarios to predict targets under climate change conditions. The models of the current paper can be used for predicting spatial and temporal variation of rainfall in different regions. Figure 7 shows the boxplot models at the testing level. At the Sara Station, the median of the observed data, MLP–HGSO, RBFNN–HGSO, MLP–BA, RBFNN–BA, MLP–PSO, and RBFNN–PSO, M5Tree and multivariate adaptive regression splines (MARS) was 478 mm, 486.5 mm, 494.5 mm, 502 mm, 529. 4mm, 534 mm, 536 mm, 541 mm, and 544 mm, respectively. At the Banding Station, the median of the observed data, MLP–HGSO, RBFNN–HGSO, MLP–BA, RBFNN–BA, MLP–PSO, and RBFNN–PSO, M5Tree and multivariate adaptive regression splines (MARS) was 189 mm, 190 mm, 192 mm, 202 mm, 205. 4mm, 207 mm, 209 mm, 212 mm, and 221 mm, respectively.

Fig. 7
figure 7

Boxplots of models for comparing models

Full size image

Acharya et al. [44] used multi-model ensemble using ELM for monsoon rainfall forecasting over south peninsular India and the correlation coefficient (R) of simple arithmetic mean (EM), singular value decomposition-based multiple linear regression (SVD–MLR) and ELM in the test stage were found to be − 0.34, 0.47 and 0.63, respectively. Beheshti et al. [45] used three different algorithms, centripetal accelerated PSO (CAPSO), a gravitational search algorithm and an imperialist competitive algorithm in training ANN for forecasting monthly rainfall in Johor State, Malaysia. Among the available methods, the MLP–CAPSO provided the best accuracy in the test stage with R value of 0.9103. Helali et al. [46] forecasted rainfall using generalized regression ANN (GRNN), ANN, least square SVM and multi-linear regression (MLR) for 1–6-month lead times. The best GRNN, MLP, LSSVM, and MLR models gave the R values of 0.65, 0.74, 0.48, and 0.74 in the test stage, respectively. In the presented study, the best model MLP–HGSO accurately forecasted the monthly rainfalls with an efficiency of 0.90 and 0. 92 for the first and second stations, respectively.

Concerning water resources management, the outcomes offer valuable insights for policymakers aiming to ensure fair water resource distribution, especially in densely populated, water-scarce regions in Malaysia. With the use of rainfall forecasts, water managers can make well-informed decisions regarding water resource management. This may include adjusting water releases from reservoirs to enhance storage capacity based on anticipated inflow or implementing water conservation measures to safeguard water supplies during drought conditions [47]. In addition, rainfalls forecasts can aid in establishing early warning systems for floods and droughts, guiding water management strategies to alleviate the impact of weather-related disasters [46].

Conclusion

Rainfall is critical to irrigation and hydrological projects. This study explores the potential of hybrid soft computing models (MLP–PSO, MLP–BA, MLP–HGSO, RBFNN–BA, RBENN–PSO, and RBFNN–HSO). Monthly rainfall data from two Malaysian stations were used as model inputs. In terms of efficiency, the hybrid MLP–HGSO model outperformed the MLP–BA, MLP–PSO, RBFNN–BA, RBFNN–PSO, and RBFNN–HGSO models. The RFNN–HGSO outputs for the testing level reflected a value of MAE = 0.812 mm and PBIAS = 0.27, which was also more accurate than the MLP–HGSO developed with the same inputs.

The MLP–HGSO predicted and observed rainfall values revealed that the highest rainfall was observed in 2012, with a probability of 0.72. Given the newly implemented hybrid MLP–HGSO model’s strong performance, further research could include using the hybrid MLP–HGSO model to forecast other hydrological variables in the short and long run.

The current paper’s challenges and limitations are data collection, adjusting computer systems and models, and determining the best input scenarios. It is recommended that the current models be tested in different climate zones and compared with other soft computing models could be adopted to find more precision results in rainfall modeling. In addition, another limitation of the present study is that conducted using rainfall data of two stations, it can be further augmented to use data of more stations (greater number of observations) to obtained better prediction results. In addition, the models are currently being researched for use as early warning systems in various regions. Some of the ML models are heavy and hence require huge computational resources and large computing time, and therefore, the proposed method can be compared with other ML methods which has simpler structure so as to see if the solution of the investigated problem is possible with simpler ML method. On the other hand, with the advanced technology (parallel computing), it is possible to use more complex ML models in real-time applications.