Abstract
Recently, the synthesis of oxidized holey graphene with the chemical formula C2O has been reported (J. Am. Chem. Soc. 2024, 146, 4532). We herein employed a combination of density functional theory (DFT) and machine learning interatomic potential (MLIP) calculations to investigate the electronic, optical, mechanical and thermal properties of the C2O monolayer, and compared our findings with those of its C2N counterpart. Our analysis shows that while the C2N monolayer exhibits delocalized π-conjugation and shows a 2.47 eV direct-gap semiconducting behavior, the C2O counterpart exhibits an indirect gap of 3.47 eV. We found that while the C2N monolayer exhibits strong absorption in the visible spectrum, the initial absorption peaks in the C2O lattice occur at around 5 eV, falling within the UV spectrum. Notably, we found that the C2O nanosheet presents significantly higher tensile strength compared to its C2N counterpart. MLIP-based calculations show that at room temperature, the C2O nanosheet can exhibit remarkably high tensile strength and lattice thermal conductivity of 42 GPa and 129 W/mK, respectively. The combined insights from DFT and MLIP-based results provide a comprehensive understanding of the electronic and optical properties of C2O nanosheets, suggesting them as mechanically robust and highly thermally conductive wide bandgap semiconductors.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nanoporous graphene lattices, in recent years have garnered significant attention in both scientific research and industrial applications due to their appealing physical and chemical properties and versatile capabilities. Graphene [1,2,3], the two-dimensional (2D) form of sp2 carbon atoms, is renowned for its exceptional mechanical strength and flexibility [4], ultrahigh thermal conductivity [5, 6], and intriguing electronic and optical properties [7,8,9,10], however is a semimetal and thus lacks a semiconducting electronic nature. This inherent electronic characteristic poses a limitation on the graphene applications, as the presence of an appropriate electronic band gap is crucial for most advanced applications in nanoelectronics, optoelectronics, and catalysis. Introducing ordered porosities into graphene, like making graphene-kirigami [11], -nanomesh [12], antidot [13, 14] or nanoporous graphene [15, 16], have been already employed to develop an appropriate band gap in the electronic structure of graphene [17,18,19], which have been proven to boost efficiency for diverse chemical processes [20,21,22] and other advanced technologies, like the DNA sequencing [23,24,25]. In addition to the semiconducting electronic nature, another key advantage of nanoporous graphene lattices lies in their high surface area to volume ratio, providing abundant active sites for various chemical reactions, adsorption processes, making them as more efficient candidate for applications such as catalysis, gas separation, and energy storage. In 2015, the wet-chemical reaction technique enabled the fabrication of a nanoporous C2N lattice with semiconducting electronic properties [26]. Worth noting that because of the existence of the covalent interactions in nanoporous graphene lattices, they are expected to show remarkably high mechanical strength, lower than that of the graphene, but comparable, resulting in remarkable structural stability.
In a latest breakthrough in the synthesis of nanoporous carbon-based nanomembranes, an oxidized holey graphene with a chemical formula of C2O, was fabricated through an irreversible nucleophilic aromatic substitution reaction [27]. From a practical standpoint, assessing the various physical properties of the C2O nanosheets is crucial to determine their suitability across diverse applications. While the electronic and optical properties of 2D materials are usually key features for their applications, a thorough examination of their thermal and mechanical properties is likewise important. Due to the critical importance of thermal management in nanoelectronics [28,29,30], semiconducting nanosheets with higher thermal conductivity are particularly desirable. Additionally, mechanical properties are vital as they determine the stability and flexibility of nanomembranes under mechanical loads during operation, directly impacting overall durability of nanodevices. To efficiently explore the aforementioned properties, we employed a synergistic approach, combining first-principles density functional theory (DFT) calculations with classical modeling based on machine learning interatomic potentials (MLIPs). This comprehensive analysis allowed us to evaluate the structural, electronic, optical, mechanical, thermal expansion, and lattice thermal conduction properties of the pristine and suspended C2O monolayer.
2 Computational methods
The Vienna Ab-initio Simulation Package (VASP) [31, 32] was utilized, employing the generalized gradient approximation (GGA) and PBE exchange correlation functional [32] and DFT-D3 [33] van der Waals (vdW) dispersion for different computations, including the structural optimizations, ab-initio molecular dynamics (AIMD) simulations, analyses of mechanical properties, and electronic structure calculations. As discussed in our previous study [34], the inclusion of DFT-D3 [33] vdW dispersion correction can enhance the accuracy of the modeling results for nanoporous nanosheets. The plane wave cutoff energy was set as 500 eV, while the self-consistency convergence criterion energy was set at 10–4 and 10–6 eV, for geometry optimizations and analysis of electro-optical properties, respectively. In order to achieve geometry optimization and stress-free structures, adjustments were made to atomic positions and lattice sizes by using the conjugate gradient algorithm until the Hellman–Feynman forces on each atom reduced to below 0.002 eV/Å on each atom. The nanosheets were positioned in the XY-plane and in order to remove interactions between neighboring cells in the Z direction, around 15 Å vacuum space was introduced. The deformation potential theory was utilized to estimate the carrier mobilities limited by acoustic phonon scattering in C2N and C2O monolayers. The carrier mobilities were calculated using the formula: \(\frac{{{\text{e}}\hbar^{3} C_{2D} }}{{{\text{KT}}\left( {m_{e}^{*} } \right)^{2} \left( {E_{i} } \right)^{2} }}\), where, K is the Boltzmann constant, ℏ represents the reduced Planck’s constant, \(C_{2D}\) and \(m_{e}^{*}\) stand for the elastic modulus and the effective mass of the carrier along the transport direction, respectively. \(E_{i}\) signifies the deformation potential constant of the carrier due to the acoustic phonons for the i-th edge band along the transport direction (\(E_{i}\) = \(\frac{{\Delta E_{i} }}{{\Delta l/l_{0} }}\)). Here, \(\Delta E_{i}\) represents the change in the absolute energy position of ith edge band, \(l_{0}\) is the lattice constant along the transport direction, and \(\Delta l\) is the deformation of \(l_{0}\). The light absorption properties were analyzed by calculating their frequency-dependent dielectric matrix, by neglecting the local field effects, on the basis of the random phase approximation, using the same methodology as our previous works [34, 35].
A moment tensor potential (MTP) [36] was fitted to investigate the structural, dynamical, thermal and mechanical properties of the C2O monolayer, using the MLIP package [37]. The training dataset was prepared by the AIMD calculations over the stress-free and stretched unitcells under varying temperatures, using the same methodology of our recent works [38, 39], adopting a time step of 1 fs, NVT ensemble, DFT-D3 correction and 2 × 2 × 1 K-point grid. The complete AIMD datasets with 3200 configurations was equally subsampled to 640, and an MTP with a cutoff distance of 3.5 Å was trained using the two-step passive training approach [40].The phonon dispersion relation was obtained by utilizing the refined MTP, employing 3 × 3 × 1 supercells and applying the small displacement technique from the PHONOPY package [41], as detailed in our previous study [42]. VESTA [43] and OVITO [44] free packages were employed to illustrate the atomic structures.We utilized the LAMMPS package [45] to examine thermal and mechanical properties based on the trained MTP, with a time step of 0.5 fs. We assumed a fixed thickness of 3.5 Å for the C2N and C2O monolayers, according to the experimental report [27]. Non-equilibrium molecular dynamics (NEMD) simulations on the basis of the trained MTP were carried out to evaluate the length-dependent lattice thermal conductivity of the C2O monolayer, using the same approach as that discussed in our previous studies [46,47,48].
3 Results and discussion
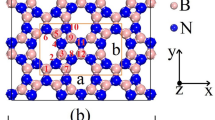
Figure 1 illustrates the top view of the crystal structure of the extensively studied C2N monolayer. The C2N monolayer features a topologically flat structure characterized by a hexagonal primitive cell and the symmetry group P6/MMM (No. 191). Despite having different conjugation characteristics, the C2O monolayer shares a similar crystal structure with the C2N counterpart. The two monolayers can be envisioned as benzene rings covalently bonded together within the same plane, facilitated by doubly coordinated nitrogen or oxygen atoms, resulting in the formation of flat structures. The resulting networks are porous, and in the case of C2O, the pores resemble the structure of graphene embedded 18-Crown-6 ether [49]. In order to investigate the comparative synthesis favorability of the C2O and C2N monolayers, we calculated their polymerization energy. According to an experimental report [27], the C2O lattice was simply synthesized by the self-condensation reaction of trichlorophloroglucinol: 2C6O3Cl3H3 → 6C2O + 6HCl. While there are several synthesis routes for the synthesis of C2N [50, 51], we adopted the condensation reaction between hexaaminobenzene and hexaketocyclohexane, resulting in: C6N6H12 + C6O6 → 6C2N + 6H2O. To calculate the polymerization energies of the C2N and C2O monolayers, we employed the following formulas:
(a) Constructing molecules and (b) top view of crystal structures of C2O and C2N monolayers. Both the hexagonal primitive cell and the smallest rectangular cell of each one are also shown. The most stable structures appear completely planar. The thin gray lines in this figure represent carbonaceous backbone of the C2X monolayers
For the C2N monolayer:
For the C2O monolayer:
In these equations, Etot(C2N) and Etot(C2O) represent the total electronic energies of a formula unit of the C2N and C2O monolayers, respectively. All other terms correspond to the total energies of their isolated precursor molecules. The process for the C2N nanosheet formation is found to be 4.01 eV exothermic, whereas that for the C2O counterpart is by 1.85 eV endothermic, indicating that the C2N monolayer formation is thermodynamically more favorable. Shifting our focus to the structural properties of the two monolayers, the optimized lattice constants for the C2O and C2N monolayers are 8.24 and 8.33 Å, respectively. The calculated lattice constant for the C2N is in good agreement with previous theoretical reports (8.325 Å [52] and 8.33 Å [53]), and that of the C2O monolayer is also very close to the experimentally determined value of 8.25 Å [27]. Examination of bond lengths in both C2O and C2N monolayers reveal that despite of the slightly longer lattice constant in the C2N lattice, C–C bond lengths in C2N (1.43 and 1.47 Å) are slightly more elongated than their counterparts in the C2O lattice (1.39 and 1.40 Å). This preliminary observation suggests that the C2O sheet may exhibit higher mechanical strength compared to the C2N lattice. Moreover, the C–C bond lengths in C2O (1.39 and 1.40 Å) are almost identical to those found in isolated benzene molecules (1.39 Å [54]). Notably, the C-O bonds in C2O are single bonds with a bond length of 1.38 Å, while the C–N bonds in C2N are partial double bonds with a bond length of 1.33 Å. These observations in bond lengths in C2O and C2N monolayers can be explained by considering their different π-conjugation characteristics. In the C2N structure, each nitrogen atom exhibits sp2 hybridization. This configuration allows one electron to contribute to the π-system of the adjacent ring, while the nitrogen's lone pair remains in the plane of the sheet, localized within the pore. In the C2O nanosheet, however, oxygen atoms and their lone pairs adopt a tetrahedral configuration due to sp3 hybridization. This difference in hybridization between nitrogen and oxygen atoms in the respective monolayers results in distinct electronic properties. The C2N monolayer features delocalized π-conjugation, arising from a network of fused aromatic rings. In contrast, the C2O counterpart contains oxygen-linked rings that interrupt the aromaticity between benzene units, thus confining π-conjugation to the individual benzene rings. The difference in π-conjugation characteristics between the two systems is expected to yield distinct physico-chemical and electronic properties in each. The difference in π-conjugation characteristics between the two systems is expected to yield distinct physico-chemical and electronic properties in each.
Replacing all nitrogen atoms in C2N monolayer with oxygen atoms, introduces six additional electrons into each primitive cell, while also disrupting the π-conjugation. These dual alterations are anticipated to induce significant changes in the electronic structure from C2N to C2O. To investigate the electronic structures of C2O and C2N monolayers, we conducted band structure calculations using both PBE and HSE06 functionals. In Fig. 2, we present the HSE06 band structure alongside partial and projected density of states (PDOS), as well as the charge density distribution of the valance band maximum (VBM) and conduction band minimum (CBM) of each of C2N to C2O nanosheets. Based on the data depicted in Fig. 2, single layer C2N emerges as a direct gap semiconductor, exhibiting an HSE06 (PBE) band gap of 2.47 (1.67) eV at the Γ point. This band gap value agrees with previous reports (2.46 and 2.47 eV) [55,56,57]. The corresponding band gap in the C2O monolayer increases to 3.47 (2.23) eV, with the VBM shifting to the K point, resulting in an indirect band gap. The increased band gap in C2O, compared to C2N, is likely attributed to the disruption of delocalized π-conjugation upon substituting nitrogen atoms with oxygen atoms. Although there are differences in their band structures, both C2N and C2O monolayers exhibit dispersed valence and conduction bands, suggesting potentially high carrier mobilities for both systems. To gain further insights into the electronic structure of C2N and C2O, we conducted a detailed analysis of their PDOS and charge density distribution of their VBMs and CBMs. Based on the data presented in Fig. 2c, both VBM and CBM of C2N exhibit delocalized π-characteristics. In the case of C2O, as shown in Fig. 2d the VBM also demonstrates delocalized π-characteristics, albeit it can be conceptualized as an antibonding interaction between the lowest energy π-molecular orbital of a benzene ring and the purely pz-orbitals of the surrounding oxygen atoms, as per the crystal orbital bond index (COBI) analysis conducted using LOBSTER [58]. The occupation of such antibonding states leads to the disruption of π-conjugation within the C2O layer by breaking down the π bond between carbon and oxygen atoms. This form of orbital hybridization aids in avoiding anti-aromaticity, and consequently, instability in the oxygen-containing rings between benzene units. Further confirmation is provided by observing that the hydrogenation of pore nitrogen atoms in the C2N sheet results in nearly identical dispersion patterns for the three top valance bands as in the C2O counterpart. It is noteworthy that hydrogenated C2N is isoelectronic with C2O. In fact, both materials avoid the anti-aromaticity of the linker ring at the expense of sacrificing delocalized π-conjugation. The CBM, however, represents an in-plane σ state, indicative of an anti-bonding interaction between the benzene ring and its surrounding oxygen. The distinct nature of band edge states in C2N and C2O monolayers may lead to varying electronic behaviors in response to in-plane strains.
Carrier mobility is a fundamental parameter in semiconductor physics, defining the speed at which charge carriers move under an electric field. This parameter directly impacts the performance of electronic devices based on 2D materials, from transistors to optoelectronic devices, making it essential for advancing nanoelectronics and next-generation technologies. Mobility is profoundly constrained by scattering phenomena within materials, with lattice vibrations constituting a primary source. These scattering events, arising from lattice vibrations, govern intrinsic mobility and establish the upper limit for defect-free 2D materials. We utilized the deformation potential theory (DPT) method to assess the intrinsic charge carrier mobility within the C2N and C2O monolayers. It is worth noting that a prior study found that unlike many other 2D materials, the electron mobility in the C2N monolayer at room temperature is primarily influenced by optical phonons rather than acoustic phonons [58]. However, the DPT theory we apply in our work to examine carrier mobilities accounts only for scattering from longitudinal acoustic (LA) phonon modes. Despite this limitation, we believe that a comparative analysis of acoustic (LA) phonon-limited mobility in the two systems of the C2N and C2O nanosheets remains valuable. For computational ease, we adopted the smallest rectangular cell for each monolayer to compute the electron and hole mobilities along in-plane directions (X(armchair) and Y(zigzag) directions). The resulting carrier mobilities and associated quantities using the rectangular cells for the C2N and C2O monolayers are summarized in Table 1. Analysis of the data in Table 1 reveals that the C2N monolayer displays a maximum electron mobility of 47,640 cm2 V−1 s−1, significantly surpassing its maximum hole mobility of 1844 cm2 V−1 s−1. Our calculated electron mobilities are consistent with those previously reported for the acoustic phonon-limited electron mobilities of the C2N monolayer (greater than 104 cm2 V−1 s−1) [58]. It is evident that replacing nitrogen atoms with oxygen atoms markedly suppresses the electron mobility to 684 cm2 V−1 s−1. However, despite significant alterations in effective masses and deformation potentials, the hole mobility remains almost intact.
We next investigate the optical properties of the C2N and C2O monolayers by calculating their absorption coefficients (α(ω)) using the HSE06-based method. Figure 3 illustrates the absorption coefficients of the C2N and C2O monolayers under light incidence along the Z-direction and polarization along the zigzag and armchair directions. Since the materials feature isotropic hexagonal lattices, the calculated absorption coefficients remain the same along zigzag and armchair directions. A quick examination of the figure reveals that C2N displays notably high absorption coefficients (105 cm−1) within the visible region of the light spectrum, in which the first absorption peak appears at 2.62 eV, slightly exceeding its calculated band gap value. In contrast, the first absorption peak of C2O occurs at a higher energy of 5.07 eV, significantly surpassing its band gap. Our thorough analysis suggests that the shift of the first absorption peak compared to the band gap, can be attributed to the indirectness of the band gap. In this study, due to the large unit cell of the C2O monolayer, excitonic effects have not been incorporated into the analysis of electronic and optical properties, potentially impacting the accuracy of predictions [59,60,61]. This aspect can be an important topic for oncoming studies.
We next explore the mechanical/failure responses of the C2O monolayers with the DFT and MTP-based model, and compare the obtained results with those of the C2N counterpart. The mechanical responses were examined using the uniaxial tensile loading. In this regard within the DFT and MTP-based methods, at the ground state without the temperature effect, the conjugate gradient algorithm coupled with the box-relaxation in the perpendicular direction of loading was employed, to ensure the accurate satisfaction of the uniaxial stress condition. From a modelling point of view, it is crucial that the trained MLIP model accurately reproduces the stress–strain curve up to the ultimate tensile strength point and the failure mechanism as well, which are critical information for the design of nanodevices. As depicted in Fig. 4, the uniaxial stress–strain curves of the C2O monolayer predicted by the DFT and the MTP-based model are compared, confirming the remarkable precision of the developed MLIP in scrutinizing the direction-dependent mechanical response of the C2O nanosheet. It is useful to highlight that since geometry optimizations were carried out rather than lengthy molecular dynamics calculations, the conducted MTP calculations for a rectangular 2 × 2 × 1 supercell was accomplished with a negligible computational cost, earlier than the completion of the first self-consistent loop of the DFT calculations, using the same computational resource. The tensile strengths of the C2O monolayer along the armchair(zigzag) directions are predicted to be 55.8(63.8) GPa, which are distinctly higher than the corresponding values of the 37.4(50.0) GPa predicted for the C2N counterpart. As discussed earlier, this is consistent with observed shorter C–C bond lengths in the C2O lattice. Failure mechanism analysis shown in Fig. 4 insets, reveals that for the uniaxial loading along the armchair, the failure first happen by homonuclear C–C bond breakages in the central hexagonal rings for both of the C2N and C2O monolayers. Along the zigzag direction, the rupture however initiates by the breakages of the C-O bonds in the C2O monolayers, whereas for the C2N counterpart, it happens along the C–C bonds. From the presented results shown in Fig. 4, it can be also concluded that the developed classical model could also precisely reproduce the direction dependent failure mechanism in the C2O monolayer. After ensuring the accuracy of the trained MTP, we then evaluate the mechanical properties of the C2O nanosheets at 300 K by considering over 1000 atoms. In this case, the quasi-static uniaxial tensile loading was employed, utilizing the Nosé–Hoover barostat and thermostat method (NPT) to satisfy the uniaxial stress conditions, as detailed in our previous studies [38, 39]. The tensile strengths of the C2O monolayer at room temperature along the armchair(zigzag) directions are predicted to be 44.4(42.0) GPa, which are close to the value of 42 GPa, reported with MTP for the C2N lattice at room temperature [62]. It was nonetheless observed that the failure mechanism stays consistent with that observed at the ground state. The MLIP-based molecular dynamics calculations confirm remarkably high tensile strength of the nanoporous C2O monolayer, which is almost half of the that predicted for the pristine graphene [38].
a, b Predicted uniaxial stress–strain responses of the C2O monolayer by the MTP and DFT loaded along the armchair and zigzag directions, respectively. c Uniaxial stress–strain response of the C2N monolayer by the DFT method. d Predicted uniaxial stress–strain curves of the C2O monolayer at 300 K. Atomic configurations over every panel illustrate the failure mechanism
We now turn our attention to investigate the lattice thermal conductivity and dynamical stability of the C2O nanosheet. The phonon dispersion curve of the C2O monolayer predicted using the fitted MTP is shown in Fig. 5a, demonstrating the absence of imaginary frequencies across all three acoustic phonon and optical branches. This observation indicates the desired structural stability of the fully planar configuration of the C2O lattice. Originating from the Γ point three acoustic phonon modes initiate, with the out-of-plane mode exhibiting quadratic relationships, while the two in-plane counterparts display linear dispersions, reminiscent of those observed in single-layer graphene and many other 2D materials [42]. In Fig. 5b the MTP-based NEMD predictions for the length effects on the room temperature phononic thermal conductivity of the C2O nanosheet is plotted, assuming a thickness of 3.5 Å according to the experimental report [27]. In the NEMD simulations, after the initial equilibration with the NPT method, a few rows of atoms at both ends were fixed and then the remaining of the system was then divided into 22 sections along the heat transport direction, with a 20 K temperature difference applied between the two ends using the NVT method. The remaining part of the system was simultaneously simulated using the constant energy ensemble (NVE) method. Lattice thermal conductivity was determined for each system using 1D Fourier's law, considering the imposed heat flux under NVT conditions and the resulting averaged temperature gradient along the sample's length, as mentioned in our previous studies [46,47,48]. In consistency with NEMD results for the C2N monolayer [57, 63], an increasing trend in the predicted lattice thermal conductivity appears by increasing the nanosheet length up to 300 nm. As a firmly established method, utilizing NEMD predictions for samples of finite lengths \(L\) and \(\kappa_{L}\), one can estimate the diffusive phononic thermal conductivity κ∞, as a function of the phonons’ mean free path (Λ) via [64]:
As depicted in Fig. 5b, based on the fitted line to the NEMD data points using the aforementioned relationship, the room temperature diffusive lattice thermal conductivity of the C2O monolayer is estimated to be 129 ± 8 W/mK. This value is noticeably higher than the previous theoretical predictions of the 85 and 82 W/mK for the C2N counterpart, respectively, using the NEMD with MTP [62] and Boltzmann transport equation coupled with DFT [65] calculations. The high lattice thermal conductivity and wide band gap of the C2O nanosheet, suggest them as promising candidates for the enhancement of the polymeric materials thermal conductivity, particularly appealing for the thermal managements in nanoelectronics.
We finally examine the thermal expansion behavior of the C2O monolayer using the MTP-based model, using the same methodology as that validated in our previous study [63]. Thermal expansion coefficients were evaluated based on the temperature dependency of the projected area (A) using the \(\frac{1}{A}\frac{dA}{{dT}}\) relation [63, 64]. To establish this relationship, we conducted seven independent calculations with uncorrelated initial velocities using the large system with 3528 atoms. The projected areas at various temperatures were averaged, and a polynomial curve was fitted to determine the thermal expansion coefficients [63, 64]. In Fig. 6, the thermal expansion coefficients of the single-layer C2O and C2N (data taken from Ref. [66]) are compared. At room temperature, the thermal expansion coefficients for the suspended C2O and C2N monolayers are predicted to be relatively close, − 12.2 and − 9.4 × 10−6 K−1 [66], respectively. When analyzing the predicted thermal expansion coefficients, it becomes evident that at low temperatures, the thermal expansion coefficients of the C2O monolayer are significantly more negative than its C2N counterpart. However, as the temperature increases, the negative thermal expansion coefficient of the C2O nanosheets decreases more conspicuously than that of the C2N, and approaches to the zero value at around 900 K. This observation suggests that at temperatures below 400 K, the contractions along in-plane directions because of the out-of-plane wrinkles formations, are more considerable in the C2O monolayer than the C2N counterpart. However, as temperature increases, the out-of-plane deflections of the C2O nanosheet becomes more limited. The presented results indicate high flexibility of the C2O nanomembranes, particularly at low temperatures.
Thermal expansion coefficients of the suspended C2O and C2N (data taken from Ref. [66]) monolayers as a function of temperature. The side views of the equilibrated C2O monolayers at different temperatures are also illustrated, with color coding representing the out-of-plane displacements of atoms with respect to the center of atomic mass
4 Concluding remarks
Inspired by the latest synthesis of the oxidized holey graphene with a chemical formula of the C2O, through irreversible nucleophilic aromatic substitution reaction [27], herein comprehensive first-principles calculations were carried out to explore the electronic, optical, mechanical, and thermal properties of the single-layer and free-standing C2O, and compared the acquired findings with those of the C2N monolayer. The comparison of C2N and C2O nanosheets underscores their unique electronic and optical properties. Delocalized π-conjugation in the C2N contributes to its direct band gap and superior electron mobilities. Switching from N to O in the C2O monolayer, considerably suppresses the electron mobility but maintains hole mobility. While the C2N monolayer exhibits a strong light absorption in the visible spectrum, the initial absorption peaks in the C2O lattice occur at around 5 eV, falling within the UV spectrum. Without taking the temperature effects into account, the tensile strengths of the C2O monolayer along the armchair(zigzag) directions are predicted to be 55.8(63.8) GPa, which are distinctly higher than the predicted values of 37.4(50.0) GPa for the C2N counterpart. It is predicted that the C2O nanosheet can exhibit remarkably high tensile strengths over 42 GPa at 300 K. Furthermore, the room temperature lattice thermal conductivities of the C2O monolayer is estimated to be 129 ± 8 W/mK, which is also noticeably higher than previous theoretical reports [62, 65] of around 85 W/mK for the C2N nanosheet. Analysis of the thermal expansion behavior of the C2O monolayer confirms its remarkable thermal flexibility. Presented results, for the first time, highlight the remarkably high tensile strength and thermal conductivity, decent thermal flexibility, strong absorption in UV region of light and wide band gap semiconducting nature of the C2O nanosheets, highly promising for applications in nanoelectronics, nanophotonics, polymer nanocomposites and thermal management systems.
Data availability
Data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Novoselov KS, Geim AK, Morozov SV, Jiang D, Zhang Y, Dubonos SV, Grigorieva IV, Firsov AA. Electric field effect in atomically thin carbon films. Science. 2004;306:666–9. https://doi.org/10.1126/science.1102896.
Geim AK, Novoselov KS. The rise of graphene. Nat Mater. 2007;6:183–91. https://doi.org/10.1038/nmat1849.
Castro Neto AH, Peres NMR, Novoselov KS, Geim AK, Guinea F. The electronic properties of graphene. Rev Mod Phys. 2009;81:109–62. https://doi.org/10.1103/RevModPhys.81.109.
Lee C, Wei X, Kysar JW, Hone J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science (80-). 2008;321:385–8. https://doi.org/10.1126/science.1157996.
Ghosh S, Calizo I, Teweldebrhan D, Pokatilov EP, Nika DL, Balandin AA, Bao W, Miao F, Lau CN. Extremely high thermal conductivity of graphene: prospects for thermal management applications in nanoelectronic circuits. Appl Phys Lett. 2008. https://doi.org/10.1063/1.2907977.
Balandin AA, Ghosh S, Bao W, Calizo I, Teweldebrhan D, Miao F, Lau CN. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008;8:902–7. https://doi.org/10.1021/nl0731872.
Berger C, Song Z, Li T, Li X, Ogbazghi AY, Feng R, Dai Z, Marchenkov AN, Conrad EH, First PN, de Heer WA. Ultrathin epitaxial graphite: 2D electron gas properties and a route toward graphene-based nanoelectronics. J Phys Chem B. 2004;108:19912–6. https://doi.org/10.1021/jp040650f.
Liu M, Yin X, Ulin-Avila E, Geng B, Zentgraf T, Ju L, Wang F, Zhang X. A graphene-based broadband optical modulator. Nature. 2011;474:64–7. https://doi.org/10.1038/nature10067.
Withers F, Dubois M, Savchenko AK. Electron properties of fluorinated single-layer graphene transistors. Phys Rev B Condens Matter Mater Phys. 2010. https://doi.org/10.1103/PhysRevB.82.073403.
Liu B, Zhou K. Recent progress on graphene-analogous 2D nanomaterials: properties, modeling and applications. Prog Mater Sci. 2019;100:99–169. https://doi.org/10.1016/J.PMATSCI.2018.09.004.
Blees MK, Barnard AW, Rose PA, Roberts SP, McGill KL, Huang PY, Ruyack AR, Kevek JW, Kobrin B, Muller DA, McEuen PL. Graphene kirigami. Nature. 2015;524:204–7. https://doi.org/10.1038/nature14588.
Bai J, Zhong X, Jiang S, Huang Y, Duan X. Graphene nanomesh. Nat Nanotechnol. 2010. https://doi.org/10.1038/nnano.2010.8.
Pedersen TG, Flindt C, Pedersen J, Mortensen NA, Jauho AP, Pedersen K. Graphene antidot lattices: designed defects and spin qubits. Phys Rev Lett. 2008;100:136804. https://doi.org/10.1103/PhysRevLett.100.136804.
Eroms J, Weiss D. Weak localization and transport gap in graphene antidot lattices. New J Phys. 2009;11:095021. https://doi.org/10.1088/1367-2630/11/9/095021.
Celebi K, Buchheim J, Wyss RM, Droudian A, Gasser P, Shorubalko I, Il Kye J, Lee C, Park HG. Ultimate permeation across atomically thin porous graphene. Science (80-). 2014. https://doi.org/10.1126/science.1249097.
Moreno C, Vilas-Varela M, Kretz B, Garcia-Lekue A, Costache MV, Paradinas M, Panighel M, Ceballos G, Valenzuela SO, Peña D, Mugarza A. Bottom-up synthesis of multifunctional nanoporous graphene. Science (80-). 2018. https://doi.org/10.1126/science.aar2009.
Sinitskii A, Tour JM. Patterning graphene through the self-assembled templates: Toward periodic two-dimensional graphene nanostructures with semiconductor properties. J Am Chem Soc. 2010. https://doi.org/10.1021/ja105426h.
Oswald W, Wu Z. Energy gaps in graphene nanomeshes. Phys Rev B Condens Matter Mater Phys. 2012. https://doi.org/10.1103/PhysRevB.85.115431.
Mortazavi B, Lherbier A, Fan Z, Harju A, Rabczuk T, Charlier J-C. Thermal and electronic transport characteristics of highly stretchable graphene kirigami. Nanoscale. 2017;9:16329–41. https://doi.org/10.1039/c7nr05231f.
Choi K, Droudian A, Wyss RM, Schlichting K-P, Park HG. Multifunctional wafer-scale graphene membranes for fast ultrafiltration and high permeation gas separation. Sci Adv. 2018. https://doi.org/10.1126/sciadv.aau0476.
Akhavan O. Graphene nanomesh by ZnO nanorod photocatalysts. ACS Nano. 2010. https://doi.org/10.1021/nn1007429.
Paul RK, Badhulika S, Saucedo NM, Mulchandani A. Graphene nanomesh as highly sensitive chemiresistor gas sensor. Anal Chem. 2012. https://doi.org/10.1021/ac3012895.
Avdoshenko SM, Nozaki D, Gomes Da Rocha C, González JW, Lee MH, Gutierrez R, Cuniberti G. Dynamic and electronic transport properties of DNA translocation through graphene nanopores. Nano Lett. 2013;5:1969–76. https://doi.org/10.1021/nl304735k.
Scheicher RH, Grigoriev A, Ahuja R. DNA sequencing with nanopores from an ab initio perspective. J Mater Sci. 2012;47:7439–46. https://doi.org/10.1007/s10853-012-6671-0.
Prasongkit J, Feliciano GT, Rocha AR, He Y, Osotchan T, Ahuja R, Scheicher RH. Theoretical assessment of feasibility to sequence DNA through interlayer electronic tunneling transport at aligned nanopores in bilayer graphene. Sci Rep. 2015;5:17560. https://doi.org/10.1038/srep17560.
Mahmood J, Lee EK, Jung M, Shin D, Jeon I-Y, Jung S-M, Choi H-J, Seo J-M, Bae S-Y, Sohn S-D, Park N, Oh JH, Shin H-J, Baek J-B. Nitrogenated holey two-dimensional structures. Nat Commun. 2015;6:6486. https://doi.org/10.1038/ncomms7486.
Kim J, Kim S, Park J, Kang S, Seo DJ, Park N, Lee S, Kim JJ, Lee WB, Park J, Lee J-C. Covalent-frameworked 2D crown ether with chemical multifunctionality. J Am Chem Soc. 2024;146:4532–41. https://doi.org/10.1021/jacs.3c11182.
Shahil KMF, Balandin AA. Thermal properties of graphene and multilayer graphene: applications in thermal interface materials. Solid State Commun. 2012;152:1331–40. https://doi.org/10.1016/j.ssc.2012.04.034.
Fu Y, Hansson J, Liu Y, Chen S, Zehri A, Samani MK, Wang N, Ni Y, Zhang Y, Zhang Z-B, Wang Q, Li M, Lu H, Sledzinska M, Torres CMS, Volz S, Balandin AA, Xu X, Liu J. Graphene related materials for thermal management. 2D Mater. 2019;7:12001. https://doi.org/10.1088/2053-1583/ab48d9.
Balandin AA. Thermal properties of graphene and nanostructured carbon materials. Nat Mater. 2011;10:569–81. https://doi.org/10.1038/nmat3064.
Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B. 1996;54:11169–86. https://doi.org/10.1103/PhysRevB.54.11169.
Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. 1996;77:3865–8. https://doi.org/10.1103/PhysRevLett.77.3865.
Grimme S, Antony J, Ehrlich S, Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J Chem Phys. 2010;132:154104. https://doi.org/10.1063/1.3382344.
Mortazavi B, Shahrokhi M, Shojaei F, Rabczuk T, Zhuang X, Shapeev AV. A first-principles and machine-learning investigation on the electronic, photocatalytic, mechanical and heat conduction properties of nanoporous C5N monolayers. Nanoscale. 2022;14:4324–33. https://doi.org/10.1039/D1NR06449E.
Mortazavi B, Shojaei F, Shahrokhi M, Azizi M, Rabczuk T, Shapeev AV, Zhuang X. Nanoporous C3N4, C3N5 and C3N6 nanosheets; novel strong semiconductors with low thermal conductivities and appealing optical/electronic properties. Carbon N Y. 2020;167:40–50. https://doi.org/10.1016/j.carbon.2020.05.105.
Shapeev AV. Moment tensor potentials: a class of systematically improvable interatomic potentials. Multiscale Model Simul. 2016;14:1153–73. https://doi.org/10.1137/15M1054183.
Ivan Novikov AS, Gubaev K, Podryabinkin E. The MLIP package: moment tensor potentials with MPI and active learning. Mach Learn Sci Technol. 2021;2:025002. https://doi.org/10.1088/2632-2153/abc9fe.
Mortazavi B, Silani M, Podryabinkin EV, Rabczuk T, Zhuang X, Shapeev AV. First-principles multiscale modeling of mechanical properties in graphene/borophene heterostructures empowered by machine-learning interatomic potentials. Adv Mater. 2021;33:2102807. https://doi.org/10.1002/adma.202102807.
Mortazavi B, Shojaei F, Shapeev AV, Zhuang X. A combined first-principles and machine-learning investigation on the stability, electronic, optical, and mechanical properties of novel C6N7-based nanoporous carbon nitrides. Carbon N Y. 2022;194:230–9. https://doi.org/10.1016/j.carbon.2022.03.068.
Mortazavi B, Zhuang X, Rabczuk T, Shapeev AV. Atomistic modeling of the mechanical properties: the rise of machine learning interatomic potentials. Mater Horizons. 2023;10:1956–68. https://doi.org/10.1039/D3MH00125C.
Togo A, Tanaka I. First principles phonon calculations in materials science. Scr Mater. 2015;108:1–5. https://doi.org/10.1016/j.scriptamat.2015.07.021.
Mortazavi B, Novikov IS, Podryabinkin EV, Roche S, Rabczuk T, Shapeev AV, Zhuang X. Exploring phononic properties of two-dimensional materials using machine learning interatomic potentials. Appl Mater Today. 2020;20:100685. https://doi.org/10.1016/j.apmt.2020.100685.
Momma K, Izumi F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J Appl Crystallogr. 2011;44:1272–6. https://doi.org/10.1107/S0021889811038970.
Stukowski A. Visualization and analysis of atomistic simulation data with OVITO–the open visualization tool. Model Simul Mater Sci Eng. 2009;18:015012. https://doi.org/10.1088/0965-0393/18/1/015012.
Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J Comput Phys. 1995;117:1–19. https://doi.org/10.1006/jcph.1995.1039.
Mortazavi B, Novikov IS, Shapeev AV. A machine-learning-based investigation on the mechanical/failure response and thermal conductivity of semiconducting BC2N monolayers. Carbon N Y. 2022;188:431–41. https://doi.org/10.1016/j.carbon.2021.12.039.
Mortazavi B, Shojaei F, Yagmurcukardes M, Shapeev AV, Zhuang X. Anisotropic and outstanding mechanical, thermal conduction, optical, and piezoelectric responses in a novel semiconducting BCN monolayer confirmed by first-principles and machine learning. Carbon N Y. 2022;200:500–9. https://doi.org/10.1016/j.carbon.2022.08.077.
Mortazavi B, Podryabinkin EV, Roche S, Rabczuk T, Zhuang X, Shapeev AV. Machine-learning interatomic potentials enable first-principles multiscale modeling of lattice thermal conductivity in graphene/borophene heterostructures. Mater Horizons. 2020;7:2359–67. https://doi.org/10.1039/D0MH00787K.
Guo J, Lee J, Contescu CI, Gallego NC, Pantelides ST, Pennycook SJ, Moyer BA, Chisholm MF. Crown ethers in graphene. Nat Commun. 2014;5:5389. https://doi.org/10.1038/ncomms6389.
Tian Z, López-Salas N, Liu C, Liu T, Antonietti M. C2N: a class of covalent frameworks with unique properties. Adv Sci. 2020;7:2001767. https://doi.org/10.1002/advs.202001767.
Mahmood J, Lee EK, Jung M, Shin D, Jeon IY, Jung SM, Choi HJ, Seo JM, Bae SY, Sohn SD, Park N, Oh JH, Shin HJ, Baek JB. Nitrogenated holey two-dimensional structures. Nat Commun. 2015. https://doi.org/10.1038/ncomms7486.
Yong Y, Cui H, Zhou Q, Su X, Kuang Y, Li X. C2N monolayer as NH3 and NO sensors: a DFT study. Appl Surf Sci. 2019;487:488–95. https://doi.org/10.1016/j.apsusc.2019.05.040.
Zuntu Abdullahi Y, Yoon TL, Lim TL. Elastic and electronic properties of C2N monolayer: first-principles calculation. Mater Res Express. 2019;6:25601. https://doi.org/10.1088/2053-1591/aae9ca.
Bacon GE, Curry NA, Wilson SA, Spence R. A crystallographic study of solid benzene by neutron diffraction. Proc R Soc Lond Ser A Math Phys Sci. 1997;279:98–110. https://doi.org/10.1098/rspa.1964.0092.
Ashwin Kishore MR, Ravindran P. Tailoring the electronic band gap and band edge positions in the C2N monolayer by P and As substitution for photocatalytic water splitting. J Phys Chem C. 2017;121:22216–24. https://doi.org/10.1021/acs.jpcc.7b07776.
Ashwin Kishore MR, Larsson K, Ravindran P. Two-dimensional CdX/C2N (X = S, Se) heterostructures as potential photocatalysts for water splitting: a DFT study. ACS Omega. 2020;5:23762–8. https://doi.org/10.1021/acsomega.0c02804.
Mortazavi B, Rahaman O, Rabczuk T, Pereira LFC. Thermal conductivity and mechanical properties of nitrogenated holey graphene. Carbon N Y. 2016;106:1–8. https://doi.org/10.1016/j.carbon.2016.05.009.
Maintz S, Deringer VL, Tchougréeff AL, Dronskowski R. LOBSTER: a tool to extract chemical bonding from plane-wave based DFT. J Comput Chem. 2016;37:1030–5. https://doi.org/10.1002/jcc.24300.
Shu H. Two Janus Ga2STe monolayers and their electronic, optical, and photocatalytic properties. Phys Chem Chem Phys. 2023;25:7937–45. https://doi.org/10.1039/D3CP00070B.
Shu H, Guo J. Enhanced stability and tunable optoelectronic properties of silicon–carbon monolayers by strain and surface functionalization. J Mater Chem C. 2024;12:5916–25. https://doi.org/10.1039/D4TC00401A.
Shu H, Guo J. Strain effects of stability, transport, and electro-optical properties of novel Ga2TeS monolayer. J Mater Sci. 2024;59:2403–15. https://doi.org/10.1007/s10853-024-09348-3.
Arabha S, Rajabpour A. Thermo-mechanical properties of nitrogenated holey graphene (C2N): a comparison of machine-learning-based and classical interatomic potentials. Int J Heat Mass Transf. 2021;178(2021):121589. https://doi.org/10.1016/j.ijheatmasstransfer.2021.121589(accessedJune2.
Hatam-Lee SM, Rajabpour A, Volz S. Thermal conductivity of graphene polymorphs and compounds: from C3N to graphdiyne lattices. Carbon N Y. 2020;161:816–26. https://doi.org/10.1016/j.carbon.2020.02.007.
Schelling PK, Phillpot SR, Keblinski P. Comparison of atomic-level simulation methods for computing thermal conductivity. Phys Rev B. 2002;65:1–12. https://doi.org/10.1103/PhysRevB.65.144306.
Ouyang T, Xiao H, Tang C, Zhang X, Hu M, Zhong J. First-principles study of thermal transport in nitrogenated holey graphene. Nanotechnology. 2017;28:1–7. https://doi.org/10.1088/1361-6528/28/4/045709.
Mortazavi B, Rajabpour A, Zhuang X, Rabczuk T, Shapeev AV. Exploring thermal expansion of carbon-based nanosheets by machine-learning interatomic potentials. Carbon N Y. 2022;186:501–8. https://doi.org/10.1016/j.carbon.2021.10.059.
Acknowledgements
F.S. thanks the Persian Gulf University Research Council, Iran, for the support of this study. B. M. and X. Z. appreciate the funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy within the Cluster of Excellence PhoenixD (EXC 2122, Project ID 390833453). B. M. is greatly thankful to the VEGAS cluster at Bauhaus University of Weimar and the cluster system team at the Leibniz University of Hannover, for providing the computational resources.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
FS: conceptualization, data curation, formal analysis, investigation, methodology, resources, software, validation, writing—original draft. QZ: methodology, writing—review and editing. XZ: funding acquisition. BM: conceptualization, data curation, formal analysis, investigation, methodology, resources, software, validation, writing—original draft, writing—review and editing.
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shojaei, F., Zhang, Q., Zhuang, X. et al. Remarkably high tensile strength and lattice thermal conductivity in wide band gap oxidized holey graphene C2O nanosheet. Discover Nano 19, 99 (2024). https://doi.org/10.1186/s11671-024-04046-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s11671-024-04046-0