Abstract
While control banding has been identified as a suitable framework for the evaluation and the determination of potential human health risks associated with exposure to nanomaterials (NMs), the approach currently lacks any implementation that enjoys widespread support. Large inconsistencies in characterisation data, toxicological measurements and exposure scenarios make it difficult to map and compare the risk associated with NMs based on physicochemical data, concentration and exposure route. Here we demonstrate the use of Bayesian networks as a reliable tool for NM risk estimation. This tool is tractable, accessible and scalable. Most importantly, it captures a broad span of data types, from complete, high quality data sets through to data sets with missing data and/or values with a relatively high spread of probability distribution. The tool is able to learn iteratively in order to further refine forecasts as the quality of data available improves. We demonstrate how this risk measurement approach works on NMs with varying degrees of risk potential, namely, carbon nanotubes, silver and titanium dioxide. The results afford even non-experts an accurate picture of the occupational risk probabilities associated with these NMs and, in doing so, demonstrated how NM risk can be evaluated into a tractable, quantitative risk comparator.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Background
Control banding has been identified [1, 2] as a suitable framework in which concerned stakeholders can evaluate and determine the risks of nanomaterials (NMs) to human health. Despite a broad consensus on the approach, there are no significant implementations that have a widespread support. This is because of known [3–5] inconsistencies in characterisation, toxicological measurement and exposure tests that are especially difficult to map using a risk tool. The low volume of quality data relevant to NM risk measurements presents further difficulties in the hazard potential. Widespread recognition that the hazard potentials of NMs can vary depending on chemistry, physicochemical characteristics, concentration and the mode and time of exposure.
Several unique control banding (CB) solutions have been identified [6] that utilize exposure and hazard banding to evaluate occupational risk for nanomaterials. Each CB tool offers alternative methodologies in order to estimate the exposure potential and hazard, and hence classify the prevailing risk within a ranking matrix. For example, NanoSafer [7] combines a hazard evaluation derived from data provided by technical information sheets, with an exposure assessment determined by the occupational setting and production rates to provide case-specific risk assessment of manufactured nanomaterials. Similarly, the Nano-Evaluris [8] CB solution assesses occupational inhalation risk pertaining to nanopowders by combining hazard and exposure band estimates with protective measures taken, process emission evaluation and frequency of use. The physical form (solid, liquid, powder or aerosol) of a manufactured nanomaterial is used to determine the exposure/emission potential within the French agency for food, environmental, and occupational health and safety (ANSES) [9] CB framework, with the hazard band allocated according to the classification of the bulk or analogous material according to the classification, labelling and packaging (CLP) regulation. While CB tools are effective in classifying risk and establishing risk management protocols 6, current applications have been criticised regarding their inability to produce transparent or easily communicable risk forecasts. Alternative frameworks employ multi criteria decision analysis (MCDA) and weight of evidence (WoE) approaches, which enable expert judgement and experimental data to be incorporated into the risk assessment [10–12]. Indeed, for regulatory purposes, MCDA-based tools may provide a more appropriate way to address issues surrounding data uncertainty [13, 14]. However, the uncertainties underlying the use of expert opinion to interpret the quality of experimental evidence or to establish weights for criterion in MCDA approaches may prove to have a critical effect on the resultant assessment [11]. Finally, methodologies borrowing from the finance industry [15], value of information and portfolio decision analysis can also be employed with some success.
Bayesian networks (BNs) can be utilised to overcome these limitations. BNs offer a reliable method for NM risk estimation owing to their ability to capture data sets that have a probability distribution of values or even missing values. These omissions are commonly observed in toxicological investigations related to NM risk characterisation and assessment. Furthermore, BNs allow for the incorporation of expert opinion where data are lacking, and has the functionality to refurbish these assessments as new experimental data becomes available. The model can incorporate NM-specific physicochemical characteristics, exposure potential and hazard components relevant to NMs for all exposure routes. In this article, we demonstrate the use of BN in occupational settings (e.g. inhalation exposure). The risk estimation is transparent and can be used to prioritize further testing to increase accuracy. More detailed NM characterisation, toxicological and exposure information will produce a more accurate risk estimation.
This framework enables proactive, iterative risk assessment through its underlying Bayesian interpretation of probability. Probability is subjective representing a degree of belief that is updated as information or data is acquired. In scarce data environments, new experimental data and relevant data from literature to have a strong influence on posterior probabilities as the process is updated via the learning algorithm. This, we believe, is a strength over the existing quantitative MCDA approaches [11] as the uncertainty attributed to expert opinion diminishes as additional experimental data are acquired. The margin of exposure (or MOE) of a NM is the ratio of its no-observed-adverse-effect level (NOAEL) to its predicted dose. Within a BN, the MoE can then be mapped to a control banding framework that affords even non-experts an accurate picture of the risk profile associated with a particular NM. Furthermore, the value of the risk forecast is easily translated into a decision-making framework by applying the US Environmental Protection Agency (USEPA)-defined [16] inflection point of 1 (or 100% in percentage terms) to determine whether a specific NM poses a hazard to human health.
Methods
We apply our methodology to NMs made from silver (Ag), titanium dioxide (TiO2) and carbon nanotubes (CNTs) and focus on occupational exposure. For all three NMs, we source data from the US National Institute for Occupational Safety and Health (NIOSH) exposure recommendation reports [17–19] and EU funded research consortia [20–22] and then map the estimated risk to a control banding solution using our model. To test the validity of our approach, we run the model using a sample set of data from a European research consortium database [23].
BNs are a class of probabilistic models originating from the Bayesian statistics and decision theory combined with graph theory [24, 25], which are able to model dependencies between variables. They were developed as a probabilistic structure in 1921 for the analysis of crop failure [26] and re-invented by many researchers under numerous pseudo-names such as causal network, belief network and influence diagram [27]. Modern applications of BNs are used in the fields of medicine [28], information technology and engineering [29], food fraud prediction [30] and environmental and human health risk assessment [31–36].
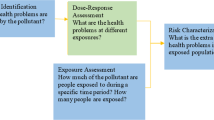
BNs offer an adaptive risk evaluation framework on two separate levels. First, the model structure and parameterization can be refined as contemporary research grows and improves the underlying assumptions used in the preliminary model formulations. Second, BNs are easily updatable as new scientific data becomes available by means of learning and updating model parameters and probability distributions via Bayes’ theorem [37]. The ability to incorporate a variety of traditional (i.e. experimental data) and non-traditional knowledge bases such as expert judgement, mechanistic or physical relationships and simulated data into the parameterization process of a BN appeals to the task of modelling complex systems in data-scarce environments, such as the NM risk assessment arena [38]. Using BNs, a generalised risk assessment model (Fig. 1) can be followed for the purpose of risk characterization of potentially hazardous substances and then applied to a control banding framework.
The transferability of the BN modelling framework to the NM risk assessment paradigm such as control banding is characterised by its mathematical flexibility in terms of probability elicitation (mechanical, empirical or expert judgement), its ability to adapt to new information and its capacity to produce probabilistic forecasts in low, and often missing data environments. Any variable (node) in the graphical structure may have any number of parents, including no parents. However, by increasing the number of parents with multiple states conditionally linked to a specific node, the number of conditional probabilities or parameters, to be estimated grows exponentially. While this may pose an issue as the structure grows in complexity, there are strategies to approximate the conditional probability tables which have proven adequate for these instances in the form of noisy probability distributions [39]. For example, there is a widespread uncertainty in the identification of hazard, or more precisely, in determining the lowest threshold for hazard identification. In applying BN, we resort to expert elicitation from both primary (SANOWORK http://cordis.europa.eu/project/rcn/102461_en.html) and secondary (NIOSH) data to ascertain input parameters and the influence thereof on predecessors and successors in the causal network leading to risk characterisation. Expert interpretations in terms of the potential for human health risk [40] are then incorporated in a BN where the uncertainty of risk-associated variables are described as probability distributions [41].
In line with Bergamaschi et al. (2015) [42], the following NM characteristics were selected as model parameters that contribute to hazard: size, surface area, chemical reactivity, surface charge, solubility and morphology. These were selected following an appraised of the literature and selected based on their influence in the particle’s toxicological profile. They [ibid] also detail the hazard or effect consequence of each physicochemical characteristic. We also categorize NMs as carcinogenic, mutagenic or toxic for reproduction (CMR) [43]. The choice of physicochemical characteristics is based on extant literature but of course there is no clear consensus within that literature set. BNs, however, can be configured to accommodate diverse user opinions on specific hazard impacts and multiple other parameters although a consensus or default assumption would make the prediction better.
For toxicants, a threshold exposure level can be derived, below which it is assumed there is no statistically significant adverse effect to human health. As a point of departure for this, the no-observed-adverse-effect level (NOAEL) is usually derived in animal studies, then a safety or uncertainty factor is applied (usually 100) to determine the dose considered safe for humans. In the absence of an experimentally determined NOAEL, the quantity lowest-observed-adverse-effect level (LOAEL) can be used as is the lowest dose tested for a potential hazard. Alternatively, the benchmark dose (BMD) [44, 45] method can be employed. We will use the term occupational exposure limit (OEL) term as the upper boundary on acceptable dose concentrations. NIOSH periodically disseminate new scientific data relating to potential occupational hazard from NMs (such as scientifically derived NOAELs) and recommend occupational exposure limits. There is, however, considerable disparity between recommended OELs proposed by NIOSH, regulatory bodies and academia. For example, current recommendations relating to CNTs range from 1 to 50 μm/m3 [17]. NMs’ human occupational exposure potential is the probabilistic measure of the propensity of the NM to enter the human body by inhalation, ingestion or dermal pathways. For NMs, there remains substantial ambiguity as regards the most relevant exposure metric [4, 46–48]. This remains a challenge as only a limited number of the nanomaterial parameters can be determined reliably [4, 49]. We have used the expectation–maximization (EM) learning algorithm in the BN to refine the conditional probabilities in parameterization of the risk assessment model using literature and experimental data. We also demonstrate the learning ability of BNs to handle risk data for CNT, Ag and TiO2 NMs as new scientific data and/or expert knowledge becomes available. For example, recommended OELs and occupational exposure data provided in the NIOSH reports [17–19] are used to learn the parameters within their corresponding nodes.
Within each node of the BN, we incorporate experience to measure the confidence attributed to the conditional probabilities inferred via specialist data sources. Any initial subjective choices of data can be refined to reduce bias using more data from diverse sources. This learning-through-experience feature allows us to continually define the sensitivity of the models’ parameters to new information. The idea is that if a given expert (or a group of experts) has a low confidence in their initial data choice, new information would make a considerable impact on this initial estimate and support the subsequent data with better confidence and experience. Once the model is updated with case data, the experience value corresponding to each state within a node coincides with the number of cases that have been observed.
Results
Figure 2 summarises the 12 key physicochemical characteristics identified by us as influential variables for defining the potential exposure and toxicity of pristine CNT; the figures for Ag and TiO2 are available as supplementary data. This includes the discretized states and causal links between these states. The presence of a surface coating is also included as it is experimentally proven to induce changes in the state of specific structural determinants of hazard when compared to an uncoated, pristine state [42]. The degree of agglomeration/aggregation and dispersibility are additional characteristics known to be important factors in the causal chain of assigning NMs risk potential [40]. Conditional relationships, signified by directed arrows starting from the influential parent nodes and ending at the child nodes, are determined by expert opinions derived from relevant contemporary literature [17–22] and SANOWORK [32, 40]. For example, the directed arrow from Degree of Aggregation to Particle Size implies that the rate at which NMs attach to other NMs of the same type has a direct impact on the NM’s size distribution. Marginal variables (i.e. the nodes with no network parents, (Coating, pH and Contamination)) are assumed to be represented by uniform distributions for unbiased parameterization when adequate knowledge is lacking [32].
Graphical structure and parameterization for the physicochemical characteristics component of the CNT Bayesian network. Each node displays the variable name (top), possible states (left) and the % probability of being in a specific state inferred from the conditional probability table for the node with associated bar chart (centre, right). Directed arrows symbolise the conditional relationship between parent and child nodes. Continuous variables display the centre of the probability distribution and its variance. The parameter data was sourced from the National Institute for Occupational Safety and Health (NIOSH) and the EU Project, SANOWORK
The exposure potential component is conditionally linked to the physicochemical characteristics component via parent nodes dispersibility and solubility (Fig. 2). The relationship is inferred from the expert opinion (NIOSH reports) used in developing the influence diagram [40]. The NMs Concentration in Air variable is discretized into intervals that gradually increase in range as the value of the variable increases to offer increased granularity at the left tail of the distribution where the likelihood of occurrence is greater.
Both exposure potential and dose-response assessments are incorporated in the BNs to generate a quantitative forecast of risk with parameterization (Fig. 2). Two distinct dose-response assessment models have been tested for carcinogenic (linear model) and non-carcinogenic (threshold model) toxicants [41, 50] via the OEL and are directly parameterized by its parent node CMR. Integrating both of these dose-response assessment ideologies into the Bayesian framework enables us to create a risk assessment model that accounts for both inter-batch and experimental inconsistencies in the relevant data, and also captures the uncertainty surrounding the toxicity potential of many NMs [51].
We define the margin of exposure as the hazard quotient (HQ), quantified by dividing the exposure potential of NMs concentration in air by the threshold value OEL. The resultant value represents the initial deterministic risk forecast generated by the BN risk assessment model. If the forecasted exposure level is greater than the threshold dose, i.e. HQ > 100%, there exists potential risks of adverse human health implications for the particular NM. The HQ can be refined through a robust learning process in BN and offers a coherent and quantifiable human health risk assessment. It consolidates exposure, hazard and dose-response assessments into a single risk forecast.
Discussion
For CNTs, Ag and TiO2 NMs, we created a database of information based on the NIOSH and EU research reports on each material [17–22]. Each NIOSH report referenced numerous publications from which the secondary data was sourced. We created 46 rows of CNT data, 39 rows of Ag data and 55 rows of TiO2 data. All references and data are available as supplementary data. The datasets contained high levels of missing data as is typical of data from different sources. The results are plotted in a heat map (Fig. 3) and show the estimated risk of each material using the BN approach.
At a glance, we can see from Fig. 3 that CNTs, Ag and TiO2 NMs exhibit increasing levels of risk as we would anticipate. The heat map can be superimposed onto a control banding solution that could exhibit hazard and exposure rows and columns, this may be particularly suitable for labelling purposes or a decision-making process. The relatively wide confidence bands are indicative of the amount and quality of the available data. Clearly, more data sources with less missing data will strengthen the degree of certainty.
To further validate our approach, we then applied the same BN approach to a primary data source, the SANOWORK database. This is, in effect, an out-of-sample test to check the accuracy of the learned system. We include these results in Fig. 3. The results from the secondary and primary data are consistent with expectations with the out-of-sample results falling within the 90% confidence interval.
Conclusions
Our BN approach has empirically found a solution to measuring the risk of NMs which has been a particularly vexing problem across the lifecycle of manufactured NMs. In this article, we have used secondary data from research articles cited by the NIOSH occupational exposure reports and EU research consortia to estimate the risk of CNTs, Ag and TiO2 and to map these results to a control banding solution that is intuitive and accessible to a wide variety of interested parties. The approach identified here is applied with a particular bias on human health factors, particularly in an occupational setting but there is no reason not to extend the approach to include a more general human health and environmental risks. To be sure, a greater discussion surrounding the input parameters and causal relationships is inevitable, but if a consensus can be found then, by definition, we have a template for a database design that can be used by experts in categorization, exposure assessment and toxicology. Where more data from research and industry published to this template, then the accuracy of risk measurement would quickly increase.
Our approach is a quantitative solution that offers a more objective approach than subjective, semi-quantitative methods. In addition to offering an alternative in the continuum of risk modelling approaches (e.g. mechanistic, statistical, Bayesian and decision-analytic [13]) for NM risk, our BN tool could also be used in conjunction with a weight of evidence [10] approach and/or multi criteria decision analysis methodologies [52]. With a quantitative result, users will be in a position to reduce exposure pathways or ameliorate hazard profiles by engineering the NM through coating (say). This BN approach is a particularly powerful approach when combined with material modelling and safety by design paradigms. By modelling the physicochemical properties of proposed NMs, an estimate of the potential risk increase/reduction of the resultant material can be derived. It may also be developed as a tool to promote occupational safety standards and extended to examine all NM lifecycle risks. With this said, the strength of BN approach derives from a consensus view on the variables and a resultant standardised database. The corollary of disperse, heterogeneous datasets with a wide variability in material properties will limit the potential of BN techniques. Therefore, national and supranational efforts to standardise nanomaterial information sets are highly desirable.
Abbreviations
- BMD:
-
Benchmark dose
- BN:
-
Bayesian Networks
- CB:
-
Control Banding
- CLP:
-
Classification, Labelling and Packaging
- CMR:
-
Carcinogenic, Mutagenic, or toxic for Reproduction
- CNT:
-
carbon nanotube
- EM:
-
Expectation–Maximization
- HQ:
-
Hazard Quotient
- MCDA:
-
Multi Criteria decision Analysis
- MoE:
-
Margin of Exposure
- NIOSH:
-
National Institute for Occupational Safety and Health
- NM:
-
Nanomaterial
- NOAEL:
-
No Observed Adverse Effect Level
- OEL:
-
Occupational Exposure Limit
- USEPA:
-
US Environmental Protection Agency
- WoE:
-
Weight of Evidence
References
Mullins M, Murphy F, Baublyte L, McAlea EM, Tofail SA (2013) The insurability of nanomaterial production risk. Nat Nanotechnol 8(4):222–224
ISO (2011) Nanotechnologies -- Occupational risk management applied to engineered nanomaterials -- Part 2: Use of the control banding approach
Savolainen K, Backman U, Brouwer D, Fadeel B, Fernandes T, Kuhlbusch T, et al. (2013). Nanosafety in Europe 2015–2025: towards safe and sustainable nanomaterials and nanotechnology innovations. Finnish Institute of Occupational Health, Helsinki.
Bouwmeester H, Lynch I, Marvin HJ, Dawson KA, Berges M, Braguer D et al (2011) Minimal analytical characterization of engineered nanomaterials needed for hazard assessment in biological matrices. Nanotoxicology 5(1):1–11
Johnston H, Pojana G, Zuin S, Jacobsen NR, Møller P, Loft S et al (2013) Engineered nanomaterial risk. Lessons learnt from completed nanotoxicology studies: potential solutions to current and future challenges. Crit Rev Toxicol 43(1):1–20
Subramanian V, Semenzin E, Hristozov D, den Zondervan-van Beuken E, Linkov I, Marcomini A (2015) Review of decision analytic tools for sustainable nanotechnology. Environment Systems Decisions 35(1):29–41
Jensen KA, Saber AT, Kristensen HV, Koponen IK, Liguori B, Wallin H (2013) NanoSafer vs. 1.1-nanomaterial risk assessment using first order modeling, 6th International Symposium on Nanotechnology, Occupational and Environmental Health
Bouillard JX, Vignes A (2014) Nano-Evaluris: an inhalation and explosion risk evaluation method for nanoparticle use. Part I: description of the methodology. J Nanopart Res 16(2):1–29
Ostiguy C, Riediker M, Triolet J, Troisfontaines P, Vernez D (2010) Development of a specific control banding tool for nanomaterials. Expert committee (CES) on physical agents French Agency for Food, Environmental, and Occupational Health and Safety, Maisons-Alfort Cedex
Hristozov DR, Zabeo A, Foran C, Isigonis P, Critto A, Marcomini A et al (2014) A weight of evidence approach for hazard screening of engineered nanomaterials. Nanotoxicology 8(1):72–87
Hristozov D, Zabeo A, Jensen KA, Gottardo S, Isigonis P, Maccalman L, et al. (2016) Demonstration of a modelling-based multi criteria decision analysis procedure for prioritization of occupational risks from manufactured nanomaterials. Nanotoxicology. (just-accepted):1–48.
Tervonen T, Linkov I, Figueira JR, Steevens J, Chappell M, Merad M (2009) Risk-based classification system of nanomaterials. J Nanopart Res 11(4):757–766
Keisler J, Linkov I (2014) Environment models and decisions. Environment Systems Decisions 34(3):369
Linkov I, Anklam E, Collier ZA, DiMase D, Renn O (2014) Risk-based standards: integrating top–down and bottom–up approaches. Environment Systems Decisions 34(1):134–137
Bates ME, Keisler JM, Zussblatt NP, Plourde KJ, Wender BA, Linkov I (2015). Balancing research and funding using value of information and portfolio tools for nanomaterial risk classification. Nat Nanotechnol 11:198–203
US-EPA (2014) Framework for Human Health Risk Assessment to Inform Decision Making
NIOSH (2011). Occupational exposure to titanium dioxide. National Institute for Occupational Safety and Health, Cincinnati.
NIOSH (2013). Occupational exposure to carbon nanotubes and nanofibers. National Institute for Occupational Safety and Health, Cincinnati.
NIOSH (2015). Health effects of occupational exposure to silver nanomaterials. National Institute for Occupational Safety and Health, Cincinnati.
Aschberger K, Johnston HJ, Stone V, Aitken RJ, Hankin SM, Peters SA et al (2010) Review of carbon nanotubes toxicity and exposure—appraisal of human health risk assessment based on open literature. Crit Rev Toxicol 40(9):759–790
Christensen FM, Johnston HJ, Stone V, Aitken RJ, Hankin S, Peters S et al (2010) Nano-silver–feasibility and challenges for human health risk assessment based on open literature. Nanotoxicology 4(3):284–295
Christensen FM, Johnston HJ, Stone V, Aitken RJ, Hankin S, Peters S et al (2011) Nano-TiO2–feasibility and challenges for human health risk assessment based on open literature. Nanotoxicology 5(2):110–124
SANOWORK. SANOWORK (Safe Nano Worker Exposure Scenarios) 2015.
Bonafede CE, Giudici P (2007) Bayesian networks for enterprise risk assessment. Physica A: Statistical Mechanics Applications 382(1):22–28
Nielsen TD, Jensen FV (2007) Bayesian networks and decision graphs. Springer New York, Information Science and Statistics
Wright S (1921) Correlation and causation. J Agric Res 20(7):557–585
Heckerman D, Mamdani A, Wellman MP (1995) Real-world applications of Bayesian networks. Commun ACM 38(3):24–26
Wiegerinck WAJJ, Kappen HJ, ter Braak EWMT, ter Burg WJPP, Nijman MJ, O YL, et al. (1999). Approximate inference for medical diagnosis. Pattern Recognition Letters. 20(11–13):1231–9.
Jensen FV, Nielson TD (2007) Bayesian networks and decision graphs. Springer, New York
Bouzembrak Y, Marvin HJ (2016) Prediction of food fraud type using data from rapid alert system for food and feed (RASFF) and Bayesian network modelling. Food Control 61:180–187
Goulding R, Jayasuriya N, Horan E (2012) A Bayesian network model to assess the public health risk associated with wet weather sewer overflows discharging into waterways. Water Res 16(16):4933–4940
Money ES, Reckhow KH, Wiesner MR (2012) The use of Bayesian networks for nanoparticle risk forecasting: model formulation and baseline evaluation. Sci Total Environ 426:436–445
Money ES, Barton LE, Dawson J, Reckhow KH, Wiesner MR (2014) Validation and sensitivity of the FINE Bayesian network for forecasting aquatic exposure to nano-silver. Sci Total Environ 473:685–691
Low-Kam C, Telesca D, Ji Z, Zhang H, Xia T, Zink JI et al (2015) A Bayesian regression tree approach to identify the effect of nanoparticles’ properties on toxicity profiles. Ann Appl Stat 9(1):383–401
Winkler D, Burden F, Yan B, Weissleder R, Tassa C, Shaw S et al (2014) Modelling and predicting the biological effects of nanomaterials. SAR QSAR Environ Res 25(2):161–172
Linkov I, Massey O, Keisler J, Rusyn I, Hartung T (2015) From“ weight of evidence” to quantitative data integration using multicriteria decision analysis and Bayesian methods. Alternatives Animal Experimentation: ALTEX 32(1):3–8
Wiesner MR, Bottero JY (2011) A risk forecasting process for nanostructured materials, and nanomanufacturing. Comptes Rendus Physique 12(7):659–688
Hendren CO, Lowry M, Grieger KD, Money ES, Johnston JM, Wiesner MR et al (2013) Modeling approaches for characterizing and evaluating environmental exposure to engineered nanomaterials in support of risk-based decision making. Environ Sci Technol 47(3):1190–1205
Pearl J (2014) Probabilistic reasoning in intelligent systems: networks of plausible inference: Morgan Kaufmann
Morgan K (2005) Development of a preliminary framework for informing the risk analysis and risk management of nanoparticles. Risk Anal 25(6):1621–1635
Kandlikar M, Ramachandran G, Maynard A, Murdock B, Toscano WA (2007) Health risk assessment for nanoparticles: a case for using expert judgment. J Nanopart Res 9:137–156
Bergamaschi E, Murphy F, Poland CA, Mullins M, Costa AL, McAlea E, et al. (2015). Impact and effectiveness of risk mitigation strategies on the insurability of nanomaterial production: evidences from industrial case studies. Wiley Interdiscip Rev Nanomed Nanobiotechnol 7(6):839–85. doi:10.1002/wnan.1340
World Health Organization (2013). Agents classified by the IARC monographs. World Health Organization, International Agency for Research on Cancer. http://monographs.iarc.fr/ENG/Classification. Last Accessed 2016.
U.S. EPA, (Environmental Protection Agency) (2012). Benchmark Dose Technical Guidance.
Sa E (2009) Use of the benchmark dose approach in risk assessment 1 guidance of the scientific committee. EFSA J 1150:1–72
Sharifi S, Behzadi S, Laurent S, Forrest ML, Stroeve P, Mahmoudi M (2012) Toxicity of nanomaterials. Chem Soc Rev 41(6):2323–2343
Braakhuis HM, Cassee FR, Fokkens PH, de la Fonteyne LJ, Oomen AG, Krystek P, et al. (2015). Identification of the appropriate dose metric for pulmonary inflammation of silver nanoparticles in an inhalation toxicity study. Nanotoxicology 10(1):63–73
Simkó M, Nosske D, Kreyling WG (2014) Metrics, dose, and dose concept: the need for a proper dose concept in the risk assessment of nanoparticles. Int J Environ Res Public Health 11(4):4026–4048
Laborda F, Bolea E, Cepriá G, Gómez MT, Jiménez MS, Pérez-Arantegui J et al (2016) Detection, characterization and quantification of inorganic engineered nanomaterials: a review of techniques and methodological approaches for the analysis of complex samples. Anal Chim Acta 904:10–32
Calabrese EJ, Baldwin LA (2003) Toxicology rethinks its central belief. Nature 421(6924):691–692
Savolainen K, Backman U, Brouwer D, Fadeel B, Fernandes T, Kuhlbusch T et al (2013) Nanosafety in Europe 2015–2025: towards safe and sustainable nanomaterials and nanotechnology innovations. Finnish Institute of Occupational Health, Helsinki
Linkov I, Bates ME, Canis LJ, Seager TP, Keisler JM (2011) A decision-directed approach for prioritizing research into the impact of nanomaterials on the environment and human health. Nat Nanotechnol 6(12):784–787
Funding
This work was partially funded by the European Commission’s Seventh Framework Programme, The Sustainable Nanotechnologies (SUN) project. Grant no. 604305.
Authors’ contributions
FM and BS carried out the main part of the data analysis and configuration. MM contributed to the structure and context. HB, HM and YB contributed ideas from biosciences. AC and ST provided categorization input and data. RD provided environmental input. VS provided toxicological input. All authors read and approved the final manuscript.
Competing interests
Prof. Vicki Stone currently receives research grants from Byk/Altana and GlaxoSmithKline. Via a number of EU FP7 funded projects I collaborate with industrial partners including BASF and Plasmachem. Her research group in the past has received research grants or consultancy funding from a number of industrial companies including British Petroleum, GlaxoSmithKline, Octel, Unilever and BHP Billiton, Powergen, National Power, Sandoz Pharma and ECETOC. No other author has an interest to declare.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Murphy, F., Sheehan, B., Mullins, M. et al. A Tractable Method for Measuring Nanomaterial Risk Using Bayesian Networks. Nanoscale Res Lett 11, 503 (2016). https://doi.org/10.1186/s11671-016-1724-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s11671-016-1724-y