Introduction

Dowel-type connections are the most commonly used connections in glulam structures. The mechanical performance of dowel-type connections plays a significant role for the load-resisting performance of the structure. Usually, nails, bolts, screws, or tubes can be used as the fasteners for dowel-type connections. However, the fabrication techniques and behaviors of these connections differ a lot. Bolts are often used as fasteners in dowel-type connections. For traditional bolted connections, the bolts usually go through the pre-drilled holes in both the glulam and the slotted-in steel plate to make these two components connected. Relative research shows a few shortcomings for traditional bolted connections, such as low rotational stiffness, insufficient moment-resisting capacity, and unpredictable brittle failure, which result in unfavorable lateral load-resisting performance for the glulam structures [1,2,3,4,5]. Therefore, some reinforcing methods were proposed in order to improve the mechanical performance of the bolted connections. Based on the idea of reinforcing the glulam in the perpendicular-to-grain direction, Blass and Bejtka [6], Lam et al. [7], and Gehloff et al. [8] investigated the performance of self-tapping screws (STS)-reinforced bolted connections with a series of experiments, and results showed the STS could effectively mitigate the crack propagation and improve the ductility of the connections. Meanwhile, both the moment-resisting and the energy dissipation capacities were increased. With the similar idea, plain round rods (PRP), locally cross-laminated members and fiber-reinforced polymer (FRP) were also used to reinforce the glulam in the perpendicular-to-grain direction, and experimental together with numerical results showed obvious enhancement on the mechanical performance of bolted connections [9,10,11]. On the other hand, glued plywood plates, weft knitted textiles, and steel inserts were used to reinforce the wood region around the dowel holes, and the results showed the load-resisting capacity and the ductility of the connections were improved [12,13,14]. In addition, wedge angles were used to reinforce a kind of hybrid timber beam-to-tubular steel column bolted connection by Karagiannis et al. [15]. The pretension technique and energy dissipation devices were introduced into the bolted connection to provide a re-centering force for the glulam connections by Li et al. [16].

Except for the development of traditional bolted connections, research was also conducted to investigate the mechanical performance of some novel dowel-type connections. Steel tubes were used as fasteners and densified veneer wood was glued to the glulam to prevent wood splitting by Leijten et al. [17]. A kind of dowel-type connection using slotted-in compressed wooden plate and compressed wooden dowels instead of the steel plate and bolts for traditional bolted connections was investigated by Jung et al. [18, 19]. Araki et al. [20] proposed a new connection using hollow steel tubes as fasteners. The tubes were inserted through the slotted-in steel plate and were fixed to the wood member with resin injection. A kind of pre-stressed tube bolted connection, in which the pre-stressed bolts went through the steel tubes to connect the slotted-in steel plate and the glulam beam more effectively was investigated by He et al. [21]. Research results showed these connections could provide better performance compared with traditional bolted connections, but problems might exist such as the complex assembling process of the tubes and the steel dowels.

Recently, the fastener of coach screws was used in the connections of timber-concrete or timber-steel composite members, and research was carried out to investigate the mechanical performance of these kinds of connections [22,23,24]. Relative research results showed that the screwed connections might overcome the disadvantage of low rotational stiffness for traditional bolted connections because of the tight contact between the screws and the screw holes. The factors influencing the performance of coach screws, such as the diameter of the screws and the wood species, were studied by Smith et al. [25]. The load-resisting capacity and the load-slip characteristics of the coach screwed connections in the timber-concrete composites were studied by Symons et al. [26], Sebastian et al. [27], Jiang et al. [28], and Du et al. [29]. The mechanical performance of both lap laminated veneer lumber (LVL)-steel composite connections and cross-laminated timber (CLT)-steel composite connections with coach screws was investigated by Hassanieh et al. [30, 31]. Furthermore, hysteretic performance of the connections with both bolts and screws as fasteners in CLT shear walls was investigated by Li et al. [32] and Sun et al. [33].

A kind of dowel-type connection using coach screws as fasteners was investigated in this paper. The connection consisted of the glulam beam, a π-shaped steel, and the coach screws. The coach screws were drilled into the glulam through holes in the clamps of the π-shaped steel. It could avoid the clearance between the fasteners and the pre-drilled holes, and was also a relatively efficient way of assembling. To investigate the mechanical performance of this kind of screwed connection and compare its behavior with traditional bolted connections, monotonic and cyclic loading tests were conducted. The failure modes, moment-resisting capacity, ductility ratio, stiffness degradation, and equivalent viscous damping ratio were analyzed and reported. The mechanical performance of the bolted connection and the screwed connection was compared.

Materials and test methods

Two kinds of dowel-type connections with different fasteners were designed. One was the bolted connection (BC) and the other was the coach screwed connection (CSC), as shown in Figs. 1, 2. The BC specimen is composed of a T-shaped slotted-in steel and the glulam beam which is connected with the web of the T-shaped slotted-in steel with bolts. The CSC specimen is composed of a π-shaped steel and the glulam beam which is connected with the clamps of the π-shaped steel with coach screws. The geometric dimension of the glulam beams was the same for both the BC specimens and the CSC specimens. Therefore, the influence of different fasteners can be studied by analyzing these specimens. Both the BC specimens and the CSC specimens were divided into 2 groups. The first group had two replicates (named BC1, BC2 or CSC1, CSC2, respectively) and was tested under monotonic loading protocol. The second group had one replicate (named BC3 or CSC3, respectively) and was tested under cyclic loading protocol.

Fig. 1
figure 1

Configuration of the bolted connection. a T-shaped slotted-in steel. b The BC specimen

Full size image
Fig. 2
figure 2

Configuration of the coach screwed connection. a π-shaped steel. b The CSC specimen

Full size image

Materials

The glulam beams were fabricated by No. 2 stress-graded Douglas fir dimensional lumber. The air-dry density of the dimension lumber was 509 kg/m3 and the moisture content was 10.57% on average. The parallel-to-grain modulus of elasticity, parallel-to-grain compressive strength, and perpendicular-to-grain compressive strength of the dimension lumber were 11,742 MPa, 46.00 MPa, and 6.69 MPa, respectively. Both the T-shaped steel and the π-shaped steel were made of mild carbon structural steel Q235B with a nominal yielding strength of 235 MPa conforming to Chinese Standard for Design of Steel Structures [34]. The bolts were 8.8 grade bolts with a length of 180 mm (the length of the thread part was 40 mm), and the outer diameter of the bolts was 12 mm. The coach screws were imported hexagonal coach screws (08A grade) made by the Rothoblaas company with a length of 80 mm (the length of the thread part was 64 mm), and the outer diameter of the screws was 8 mm. Particularly, the characteristic yielding moment-resisting capacity and the tensile-resisting capacity of the screws were 1.69 × 10–2 kN·m and 15.7 kN, respectively.

Specimen design

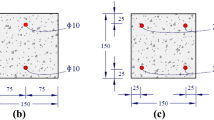
The configurations of the BC specimens and the CSC specimens are illustrated in Fig. 3. The specimens are full scale. The glulam beams were 200 × 150 mm in cross-section and 1000 mm in length. The cross section size of the beam was chosen based on a common size in glulam structures. Both the BC specimens and the CSC specimens were designed according to Structural Timber Design to Eurocode 5 [35], to have the same design moment-resisting capacity as the glulam beam. The connection details, such as the spacing, end, and edge-distance of bolts or coach screws, also met the requirements of literature [35]. For the BC specimens, the diameter of the pre-drilled holes was 13.5 mm in the glulam and 12.5 mm in the web of the T-shaped steel, respectively. The oversized pre-drilled holes in the glulam made it convenient to assemble different structural components with bolts, because the rough inner surface of the pre-drilled holes in the glulam and the alignment error of the pre-drilled holes might affect the assembling if small size of pre-drilled holes was used. However, the clearance between the bolts and the pre-drilled holes in the glulam makes the bolted connection rotate with low stiffness in the initial stage. Pre-drilled holes in the end plate of the T-shaped steel were 18.5 mm in diameter because high strength bolts with 18 mm in diameter were used to connect the BC specimens with the rigid foundation beam. The thicknesses of the end plate and the web were 20 and 16 mm, respectively. In addition, there was a gap of 20 mm between the end plate and the bottom of the glulam beam, which was designed to avoid the compaction between them.

Fig. 3
figure 3

Configurations of the specimens. a The BC specimens. b The CSC specimens

Full size image

For the CSC specimens, the diameter of the pre-drilled holes was 8.5 mm in the clamps of the π-shaped steel. There are also pre-drilled holes in the glulam beam, which were about 5.5 mm in the diameter. However, holes in the glulam did not need locating accurately or cutting through the glulam compared to those of the bolted connections, and the size of the pre-drilled holes was smaller than that of the coach screws. This is because the thread of the coach screws made themself able to be drilled into the glulam, and these pre-drilled holes were only for the ease of drilling. Therefore, oversized pre-drilled holes were not necessary and it would not affect the assembling if the drilling precision was not that high. Furthermore, because there is almost no clearance between the screws and the screw holes, this kind of connection could effectively resist the applied load with high rotational stiffness even in the initial stage. Pre-drilled holes in the end plate of the π-shaped steel were the same as the BC specimens and the high strength bolts with 18 mm in diameter were also used to connect the specimens with the rigid foundation beam. The thicknesses of the end plate and the clamps were 24 and 16 mm, respectively. The designed gap between the end plate and the glulam beam was 20 mm, which was the same as the BC specimens.

Test methods

As illustrated in Fig. 4, both the BC specimens and the CSC specimens were rotated by 90° to be loaded availably with the specific loading equipment. The specimens were fixed on the rigid foundation beam using high strength bolts. The lateral load was applied through the electro-hydraulic servo loading system with the actuator. The load range is  ±  300 kN and the displacement range is  ± 250 mm, respectively. The rotation angles of the glulam beam and the T-shaped steel (or π-shaped steel) were calculated using the horizontal displacements collected by the linear voltage displacement transducers (LVDTs). LVDT 1 was used to record the horizontal displacement of the actuator. LVDT 3, 5 were used to calculated the rotation of the glulam beam, and LVDT 2, 4 were used to calculated the rotation of the steel clamps or slotted-in web.

Fig. 4
figure 4

Test set-up and measurement arrangement

Full size image

For the monotonic loading test, the displacement-controlled loading method was used with the loading rate of 5 mm/min based on ASTM D1761-12 [36]. The test would be stopped either when the applied load falls to 80% of the ultimate load or when the tested specimen severely damaged.

For the cyclic loading test, the CUREE displacement-controlled reciprocating loading method was used with the loading rate of 60 mm/min based on ASTM E2126-11 [37]. The loading regime is illustrated in Fig. 5 and the reference displacement ∆ is determined as 60% of the ultimate loading displacement under the monotonic loading test. At first, 6 loading cycles were performed with equal displacement amplitude of 0.05∆. Then, the subsequent loading included the primary cycles and the trailing cycles, wherein the displacement amplitude of the primary cycle successively increased from 0.075∆ to 2.0∆ (i.e., 0.075∆, 0.1∆, 0.2∆, 0.3∆, 0.4∆, 0.7∆, 1.0∆, 1.5∆, 2.0∆, respectively). After each primary cycle, a series of trailing cycles were implemented as 75% of the primary cycle’s amplitude. Especially, there were 6 trailing cycles after the primary cycles of 0.075∆ and 0.1∆, 3 trailing cycles after the primary cycles of 0.2∆ and 0.3∆, and 2 trailing cycles after the primary cycles of 0.4∆, 0.7∆, 1.0∆, 1.5∆, and 2.0∆.

Fig. 5
figure 5

CUREE loading protocol

Full size image

Results and discussion

Monotonic loading test

Specimen BC1, BC2, CSC1, and CSC2 were tested under monotonic loading protocol. The moment–rotation curves are depicted in Fig. 6 through the data recorded by the loading equipment and the LVDTs.

Fig. 6
figure 6

Moment–rotation curves under monotonic loading protocol. a The BC specimens. b The CSC specimens

Full size image

For the BC specimens, small sound of cracking was heard and the relative slip between the web of the T-shaped slotted-in steel and the glulam beam was observed in the initial loading stage. Because of the existed clearance between the bolts and the bolt holes in the glulam, the moment–rotation curves showed relatively low stiffness in the initial stage. As the contact between the bolts and the bolt holes was complicated, the range of this low stiffness segment was unpredictable. Previous experimental research on bolted beam-to-column connections [9, 21, 38] had shown that this stage of low stiffness ranged from 0° to 0.7° on average. From this point, the test results were more reliable. With the increase of the applied load, the rotation of the glulam beam became obvious and the slip between the web and the beam became larger. Because the bolts had already contacted with the bolt holes tightly, the curves presented a relatively high stiffness until obvious plasticity occurred in the specimens. The first crack appeared either on the tension or the compression side of the glulam beam. Then, the cracks slowly spread to the upper part of the beam and occurred on both the tension and the compression sides. Large sound of cracking could be heard. At last, as shown in Fig. 7a, splitting cracks on the tension side developed rapidly and the load applied to the specimens descended suddenly, so the loading was terminated. As depicted in Fig. 6a, the plastic stage of the BC specimens was not obvious and the stiffness in the final segment of the curves was relatively high before failure, which conformed to the previous research of Yu [38]. It could be explained by that the diameter of bolts was relatively big while the distance from the bolts to the end of the glulam beam was small, thus resulting in large transverse tensile stress and brittle splitting failure of the glulam. That is also one of the reasons why traditional bolted connections have a relatively low moment-resisting capacity and poor ductility. It was noticed that specimen BC2 had a lower moment-resisting capacity and the latter part of the curve fluctuated obviously compared with specimen BC1. Through observation in the test, an initial defect of the wood knot was found on the path of a crack and accelerated the spread of the crack, making specimen BC2 behaved worse than specimen BC1. After the experiments, the specimens were disassembled to further study the deformation modes of the bolts, as shown in Fig. 7b. Bolts in the top edge zones presented the most severe deformation which conformed to the “one-hinge” yielding mode. To explain the mechanism, the bolts were thought to resist the shear force and the bending moment in the same time caused by the lateral load, and the rotation center could be assumed to be the geometric center of the bolts group. Therefore, the magnitude of the force caused by the bending moment of one bolt was linear to the distance from the rotation center to this bolt, and the direction of this force was perpendicular to the line going through the rotation center and the bolt. On the other hand, the force caused by shear was assumed to be distributed averagely to each bolt and pointed parallel to the direction of the shear force. Finally, the resultant force was obtained by adding the force caused by the bending moment and the force caused by shear according to the rule of vectors, which could be concluded that the top edge bolts suffered the biggest force. Therefore, the deformation of the top edge bolts was the most obvious.

Fig. 7
figure 7

Failure modes of the BC specimens. a Failure of the glulam. b Deformation of bolts

Full size image

For the CSC specimens, the initial stiffness was much higher than that of the BC specimens without the initial low stiffness stage, as shown in Fig. 6b. The initial linear segment of the moment–rotation curves indicated that the specimens were under elastic stage. Contrary to the BC specimens, because the coach screws were drilled into the glulam beam, which made no initial clearance between the screws and the screw holes, the screws contacted tightly with the wood fibers and worked effectively as soon as the external force applied to the specimens. With the increase of the applied load, relative slip was observed between the clamps of the π-shaped steel and the glulam beam. The glulam beam rotated obviously. The sound of cracking could be heard but cracks were not able to be observed because of the covering of the clamps. The slope of the curves became smaller, meaning that plasticity developed in the specimens. The applied load continued to increase and the cracks became visible, which extended from the area under the clamps to the upper part of the glulam beam. Then, more cracks developed and the screws in the top edge zone were sheared. The applied load could hardly rise any more. Finally, the splitting crack on the tension side of the glulam beam propagated rapidly and the applied load descended suddenly, so the loading was terminated. The relative slip between the clamps and the glulam beam was as large as 20 mm. In contrast with the BC specimens, the moment–rotation curves of specimen CSC1 and specimen CSC2 were similar due to the fact that there was no unpredictable initial low stiffness stage or significant initial defect in the CSC specimens. The CSC specimens presented an obvious plastic segment in the curves, which meant the plasticity developed more effectively compared with the BC specimens. This could be explained by that the relatively small diameter of screws relieved the large transverse tensile stress for the bolted connections, so the ductile embedment failure together with the brittle splitting failure happened during loading, as shown in Fig. 8a. Therefore, the failure of CSC specimens was more ductile. The shear failure, “one-hinge” and “two-hinge” yielding failures were observed in the top, bottom and edge zones, as illustrated in Fig. 8b. The different degrees of damage in screws could be explained with the same mechanism as the BC specimens, which was the addition of the force caused by the bending moment and the force caused by shear.

Fig. 8
figure 8

Failure modes of the CSC specimens. a Failure of the glulam. b Deformation of screws

Full size image

Mechanical properties, such as the initial stiffness (Ke), the yielding moment (My), and the ductility ratio (μ), can be calculated based on the Y&K method [39]. The results are listed in Table 1, in which θy is the corresponding rotation angle of My; Mp is the maximum moment and θp is the corresponding rotation angle; Mf is the failure moment and θf is the corresponding rotation angle; and μ is equal to θf divided by θy. Because the initial stage of the BC specimens was unpredictable and the stiffness was quite low, if the initial stage was considered when applying the Y&K method, some problems might happen. For example, the stiffness in the plastic stage might be much bigger than that of the elastic stage, and the yielding moment would be also underestimated, which were not reasonable to describe the behavior of the BC specimens. Therefore, the initial stage of low stiffness was not considered when using the Y&K method.

Table 1 Mechanical properties calculated based on Y&K method
Full size table

The initial stiffness of the CSC specimens was 133% higher than that of the BC specimens on average, which was mainly improved by the tight contact between the screws and the screw holes. The yielding moment of the CSC specimens was 22% higher that of the BC specimens. The yielding rotation angle of the CSC specimens was 59% lower than that of the BC specimens, and this was because the BC specimens had to experience the initial stage of low stiffness until the yielding point. The ultimate moment and the failure moment of the CSC specimens were 93% and 87% higher than those of the BC specimens, respectively. The ultimate rotation angle and the failure rotation angle of the CSC specimens were 39% and 54% higher than those of the BC specimens, respectively. It showed that the performance after yielding of the CSC specimens was better than that of the BC specimens. Although the BC specimens and the CSC specimens had the similar yielding moments, the ultimate and the failure moments of the CSC specimens were much higher, which could serve as a safety margin. The initial stage of low stiffness for the BC specimens made it a higher yielding rotation angle, but after yielding the BC specimens failed quickly and could hardly develop the plasticity effectively, so the ultimate and the failure rotation angles were smaller than those of the CSC specimens. For the same reason, ductility of the BC specimens was also worse than that of the CSC specimens. To describe the ductility performance exactly, the ductility ratio was used. Ductility ratio of 5.3 for the CSC specimens, which was greater than 4, indicated the CSC specimens had a good ductile performance [40]. In contrast, ductility ratio of 1.41 meant it tended to be a brittle failure for the BC specimens. In general, the moment-resisting capacity and the ductility of the coach screwed connections improved a lot compared with the bolted connections.

Cyclic loading test

Specimen BC3 and specimen CSC3 were tested under cyclic loading based on CUREE loading protocol. The hysteretic loops are depicted in Fig. 9. Under cyclic loading protocol, the specimens failed similarly to those under monotonic loading protocol, except that failure on both sides of the glulam was similar because either side of the specimens could be in tension or compression under cyclic loading protocol.

Fig. 9
figure 9

Hysteretic loops. a Specimen BC3. b Specimen CSC3

Full size image

Compared with specimen BC3, the hysteretic loop of specimen CSC3 was plumper, and the pinching phenomenon was gentler. The total energy dissipation was calculated, equal to the area enclosed by the hysteretic loop. As illustrated in Fig. 10, the energy at each displacement amplitude included the energy dissipated both in the primary circle and the trailing cycles. Specimen BC3 failed in the primary cycle of 1.5∆ and the hysteretic curve was not complete for this cycle, so the total energy dissipated of 1.5∆ was unable to calculate. The hysteretic loops and the total energy dissipation indicated a better energy dissipation capacity of specimen CSC3. The skeleton curves also presented the characteristics of high initial stiffness and good ductility of the CSC specimens, as those shown under monotonic loading protocol.

Fig. 10
figure 10

Total energy dissipation

Full size image

To further study the performance of the specimens under cyclic loading protocol, the stiffness degradation and the equivalent viscous damping ratio (EVDR for short) were analyzed. The secant stiffness (Ki) of each primary cycle can be calculated using Eq. (1), where  + Mi and − Mi are the positive and negative peak moment of the i-th primary cycle, respectively;  + θi and − θi are the rotation angles corresponding to  + Mi and − Mi. The EVDR (εeq) can be calculated based on Eq. (2), where Ed is the dissipated energy in a primary cycle; Ep is the available potential energy in a primary cycle. The calculated results are illustrated in Fig. 11.

$$K_{i} = \frac{{| + M_{i} | + | - M_{i} |}}{{| + \theta_{i} | + | - \theta_{i} |}}$$
(1)
$$\varepsilon_{{{\text{eq}}}} = \frac{{E_{{\text{d}}} }}{{2\pi E_{{\text{p}}} }}$$
(2)
Fig. 11
figure 11

Stiffness degradation and EVDR of the specimens. a Stiffness degradation. b EVDR

Full size image

As can be observed in Fig. 11, the performance of stiffness degradation and EVDR of specimen CSC3 was better than those of specimen BC3.Specimen BC3 failed in the primary cycle of 1.5∆ and the hysteretic curve was not complete for this cycle, so the EVDR of 1.5∆ was unable to calculate.

From the displacement amplitude of 0.2–0.4∆, the rotation angle of specimen BC3 was relatively small but contained a large part of low stiffness. Therefore, the secant stiffnesses in this range were relatively low. After the displacement amplitude of 0.4∆, as the bolts and the bolt holes contacted more and more tightly, the secant stiffness began to increase until the displacement amplitude of 1.0∆. Then, large cracks were observed and propagated gradually, so the secant stiffness started to decrease, which indicated the damage accumulation in specimen BC3. On the other hand, the energy dissipation capacity that can be described by the EVDR mainly depends on the deformation of the bolts, the compression between the bolts and the bolt holes, and the friction among the bolts, the web of the T-shaped slotted-in steel, and the glulam beam. With the displacement amplitude increasing until 0.4∆, the contact among each component became more and more sufficient, while cracks did not occur in the specimen, so the energy dissipation capacity continued to increase. After the displacement amplitude of 0.4∆, cracks spread gradually in the specimen, which was not conducive to the compression between the bolts and the glulam beam. In addition, the effect of cyclic loading caused looseness between the glulam and the web, thus reducing the friction between them. Therefore, the capacity of energy dissipation kept decreasing.

For specimen CSC3, it showed a high secant stiffness and energy dissipation capacity in the initial loading stage, which could be explained by the tight contact among the screws, glulam beam and the clamps of the π-shaped steel. As the displacement amplitude increased in the following primary cycles, plasticity developed in the screws as well as in the wood fibers. Then, cracks appeared and propagated gradually. Therefore, the secant stiffness continued to decrease. Similar to specimen BC3, the energy dissipation capacity of specimen CSC3 depends on the deformation of the screws, the compression between the screws and the screw holes, and the friction among the screws, clamps and the glulam beam. With the increase of the displacement amplitude, plastic deformation and the appeared cracks made the contact insufficient, which also led to the failure of the screws and larger cracks in the final loading stage. The effect of cyclic loading also caused looseness between the glulam and the clamps. As a result, the secant stiffness and the EVDR kept decreasing. However, the secant stiffness and the EVDR were still larger than those of specimen BC3 under different displacement amplitudes.

Conclusions

A kind of dowel-type connection with hexagonal coach screws as fasteners was investigated. Monotonic and cyclic loading experiments were carried out to study the mechanical performance of this kind of connection and its load-resisting properties were further compared with traditional bolted connections. The failure modes, moment-resisting capacity, and hysteretic performance were obtained and compared. It can be concluded the following:

  • (1) Under monotonic loading protocol, the failure modes of the bolted connections were the splitting failure on the tension side of the glulam beam, and the “one-hinge” yield failure was observed in the top edge bolts. However, for the screwed connections, the failure modes of the glulam beam were the splitting failure on the tension side together with embedment failure of the screw holes. In addition, shear failure, “one-hinge” yielding failure and “two-hinge” yielding failure were observed in coach screws.

  • (2) The initial stiffness, yielding moment, ultimate moment, and ductility ratio of the screwed connections were respectively 133%, 22%, 93%, and 276% larger than those of the bolted connections. Especially, the screwed connections could overcome the disadvantages of low initial stiffness and low ductility existed in bolted connections. And the higher ultimate moment-resisting capacity could serve as the safety margin.

  • (3) The hysteretic loops of the screwed connection were plumper, and the pinching effect was gentler compared to those of the bolted connection. The energy dissipation capacity of the screwed connection was also better compared to the bolted connection.

It should also be noted that the sample size in this study is relatively limited. Therefore, the influence of material variabilities on the mechanical performance of the bolted connection and the screwed connection may not be fully considered. Further research is still needed to investigate the mechanical behavior of the screwed connection.