1 Introduction

A stabilization platform detects any position change of the equipment on it through a sensitive element, compensates for the deviation in the position of the equipment through attitude adjustment, and isolates the equipment from the influence of the environment to keep it relatively stable in inertial space [1,2,3,4]. According to the type of mechanism, a platform can be classified into a series or parallel stabilization platform [5, 6]. A series stabilization platform is simple to control and has a low design cost [7]. Thus, they are widely used in fields such as laser positioning, satellite communication, missile guidance, and for unmanned reconnaissance aircrafts. In contrast, a parallel stabilization platform is driven by multi-axis coupling and has the characteristics of a strong bearing capacity and high stiffness and therefore has a wide range of application scenarios in high-precision operations such as weapon launches and maritime rescues [8,9,10,11]. By adopting the electro-hydraulic driven platform with the advantages of its high power/weight ratio, fast response speed and small cumulative error, however, the motion control accuracy of the stabilization platform can be greatly improved [12,13,14,15].

Mechanical vibrations can cause dynamic deformation and relative motion of platform structures, thereby increasing the stress and fatigue loads on various components of the platform. This subsequently affects the stability, control accuracy, and service life of the platform, and in severe cases, can even lead to structural damage [16,17,18]. Therefore, to further improve the performance of parallel stabilization platforms, it is important to study their vibration characteristics [19, 20]. There are three methods for studying the vibration characteristics: the simulation analysis method [21,22,23], theoretical analysis method [24] and experimental analysis method [25]. The simulation analysis method is used to analyze the vibration characteristics after solving the characteristic value of the finite element analysis of the structure [26,27,28]. Therefore, it is widely used to analyze the vibration characteristics of complex mechanical systems. The experimental analysis method is used to estimate the modal parameters of the mechanism through the frequency response function measured in practice and it is also used to verify the results of the simulation and theoretical analysis [29, 30]. The theoretical analysis method is used to analyze the vibration characteristics based on the dynamic equation and the analytical solution of the vibration response [31, 32]. It can quantitatively analyze the vibration characteristics of a mechanism and is a common method for the further study of mechanical vibrations. However, during the process of dynamic modeling, previous studies did not consider the influence of flexible stiffness [33, 34]. Moreover, with the development of the finite element method, hinge stiffness has gradually been studied, which has also led to a low computational efficiency with regards to dynamic calculations [35]. Additionally, the variation characteristics of the natural frequency and vibration response with respect to the position of the mechanism have not yet been studied.

Therefore, taking an electro-hydraulic driven 3-UPS/S parallel stabilization platform as research object, its mechanical-hydraulic coupling dynamic equation is established considering the hinge stiffness. Subsequently, the modal and resonant characteristics of the mechanism are studied. The theoretical model is verified through numerical simulations and modal tests. This study provides a theoretical basis for dynamic modal analysis and resonance research on parallel mechanisms.

2 Kinematic Analysis of Electro-hydraulic Driven 3-UPS/S Parallel Stabilization Platform

2.1 Position Analysis of Electro-hydraulic Driven 3-UPS/S Parallel Stabilization Platform

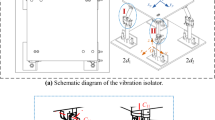
As shown in Figure 1(a), an electro-hydraulic driven 3-UPS/S parallel stabilization platform consists of a moving platform, supporting branch chain, static platform, and three driving branches. The coordinate system U−xyz is the fixed coordinate system of the moving platform and the coordinate system D−XYZ is the fixed coordinate system of the static platform.

Figure 1
figure 1

Coordinate system of electro-hydraulic 3-UPS/S parallel stabilization platform

Full size image

As shown in Figure 1(b), the local coordinate system di−xdiydizdi is established at the center of the universal joint, established at the center of the spherical hinge. Axes zdi and axis zui are in the same direction as the unit-direction vector ei of the driving branch. The rotation angles of the universal joint about axis xdi and axis ydi are, respectively, \(\theta_{{{\text{d}}i}}\) and \(\phi_{{{\text{d}}i}}\); the rotation angles of the spherical hinge about axis xui, axis yui and axis zui are, respectively, θui, \(\phi_{{{\text{u}} i}}\), \(\gamma_{{{\text{u}}i}}\); \(\psi_{{{\text{d}}i}}\), \(\psi_{{{\text{u}}i}}\) are the installation angles of the universal joint and the spherical hinge, respectively, which are determined by the platform structure.

The closed-loop equation of the drive chain can be expressed as:

$$l_{i} {\varvec{e}}_{i} = {}_{U}^{D} R{\varvec{u}}_{i}^{{\left\{ U \right\}}} - {\varvec{d}}_{i}^{{\left\{ D \right\}}} + {\varvec{u}}_{0} + {\varvec{u}},$$
(1)

where \(l_{i}\) is the length of the drive chain; \({\varvec{e}}_{i}\) is the unit direction vector of the drive chain; \(_{U}^{D} {\varvec{R}}\) is the rotation transformation matrix between the coordinate system U−xyz and the coordinate system D−XYZ; \({\varvec{u}}_{i}^{{\left\{ U \right\}}}\) is the vector from the center of the spherical hinge to the origin of the coordinate system U−xyz; \({\varvec{d}}_{i}^{{\left\{ D \right\}}}\) is the vector from the center of the universal joint to the origin of the coordinate system D−XYZ; \({\varvec{u}}_{0}\) is the initial displacement vector of the coordinate system U−xyz to the coordinate system D−XYZ; \({\varvec{u}}\) is the displacement vector of the coordinate system U−xyz to the coordinate system D−XYZ.

Thus, the equation for the drive chain length can be expressed as:

$$l_{i} = \left\| {_{U}^{D} {\varvec{Ru}}_{i}^{{\left\{ U \right\}}} - {\varvec{d}}_{i}^{{\left\{ D \right\}}} + {\varvec{u}}_{0} + {\varvec{u}}} \right\|.$$
(2)

The centroid position of the lower connecting rod of the drive chain can be expressed as:

$${\varvec{p}}_{{{\text{g}}i}} = {\varvec{d}}_{i}^{{\left\{ D \right\}}} + q_{i} {\varvec{e}}_{i} ,$$
(3)

where pgi is the position vector of the lower connecting rod centroid and \(q_{i}\) is the distance between the centroid of the lower connecting rod and the center of the universal joint.

The rotation transformation matrix between the local coordinate system di−xdiydizdi and the coordinate system D−XYZ can be expressed as:

$${}_{{d_{i} }}^{D} {\varvec{R}} = {\varvec{R}}(\psi_{{{\text{d}}i}} ,z_{{{\text{d}}i}} ){\varvec{R}}(\phi_{{{\text{d}}i}} ,y_{{{\text{d}}i}} ){\varvec{R}}(\theta_{{{\text{d}}i}} ,x_{{{\text{d}}i}} ).$$
(4)

Because axis zdi is in the same direction as the unit direction vector ei, zdi can be expressed as:

$$\left[ {\begin{array}{*{20}c} {e_{{{\text{x}}i}} } \\ {e_{{{\text{y}}i}} } \\ {e_{{{\text{z}}i}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sin \psi_{{{\text{d}}i}} \sin \theta_{{{\text{d}}i}} + \cos \psi_{{{\text{d}}i}} \sin \phi_{{{\text{d}}i}} \cos \theta_{{{\text{d}}i}} } \\ {\sin \psi_{{{\text{d}}i}} \sin \phi_{{{\text{d}}i}} \cos \theta_{{{\text{d}}i}} - \cos \psi_{{{\text{d}}i}} \cos \theta_{{{\text{d}}i}} } \\ {\cos \phi_{{{\text{d}}i}} \cos \theta_{{{\text{d}}i}} } \\ \end{array} } \right].$$
(5)

Thus, the rotation angle of the universal joint is:

$$\left\{ \begin{gathered} \phi_{{{\text{d}}i}} = \arctan (\frac{{e_{{{\text{x}}i}} \cos \psi_{{{\text{d}}i}} + e_{{{\text{y}}i}} \sin \psi_{{{\text{d}}i}} }}{{e_{{{\text{z}}i}} }}), \hfill \\ \theta_{{{\text{d}}i}} = - \arcsin (e_{{{\text{y}}i}} \cos \psi_{{{\text{d}}i}} - e_{{{\text{x}}i}} \sin \psi_{{{\text{d}} i}} ). \hfill \\ \end{gathered} \right.$$
(6)

If the local coordinate systems di−xdiydizdi and ui−xuiyuizui have the same direction, the rotation transformation matrix \({}_{{u_{i} }}^{D} {\varvec{R}}\) between the local coordinate system ui−xuiyuizui and the coordinate system D−XYZ can be obtained from Eq. (4). Thus, the rotation angle of the spherical hinge is:

$$\left\{ \begin{gathered} \phi_{{{\text{u}}i}} = \arctan (\frac{{\left( {{\varvec{R}}_{{{\text{F}}i}} } \right)_{1,3} }}{{\left( {{\varvec{R}}_{{{\text{F}}i}} } \right)_{3,3} }}), \hfill \\ \theta_{{{\text{u}}i}} = - \arcsin (\left( {{\varvec{R}}_{{{\text{F}}i}} } \right)_{2,3} ), \hfill \\ \gamma_{{{\text{u}}i}} = \arctan (\frac{{\left( {{\varvec{R}}_{{{\text{F}}i}} } \right)_{2,1} }}{{\left( {{\varvec{R}}_{{{\text{F}}i}} } \right)_{2,2} }}), \hfill \\ \end{gathered} \right.$$
(7)

where \({\varvec{R}}_{{{\text{F}}i}} = {\varvec{R}}\left( {\psi_{{{\text{u}}i}} ,z_{{{\text{u}}i}} } \right)_{U}^{{{\text{T}}D}} {\varvec{R}}^{{\text{T}}} {}_{{u_{i} }}^{D} {\varvec{R}}^{{\text{T}}}\).

2.2 Velocity Analysis of Electro-hydraulic Driven 3-UPS/S Parallel Stabilization Platform

By solving the first derivative with respect to time in Eq. (1), the velocity equation of the drive chain can be expressed as:

$$\dot{l}_{i} {\varvec{e}}_{i} + l_{i} {{\varvec{\omega}}}_{{{\text{z}}i}} \times {\varvec{e}}_{i} = {{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{i}^{{\left\{ U \right\}}} ,$$
(8)

where \({{\varvec{\omega}}}_{{{\text{z}}i}}\) is the angular velocity of the drive chain and \({{\varvec{\omega}}}_{{\text{u}}}\) is that of the moving platform.

Then, the Jacobian matrix between the drive chain and the moving platform is:

$${\varvec{J}}_{{\text{u}}} = \left[ {\begin{array}{*{20}c} {{}_{U}^{D} {\varvec{Ru}}_{1}^{{\left\{ U \right\}}} \times {\varvec{e}}_{1} } \\ {{}_{U}^{D} {\varvec{Ru}}_{2}^{{\left\{ U \right\}}} \times {\varvec{e}}_{2} } \\ {{}_{U}^{D} {\varvec{Ru}}_{3}^{{\left\{ U \right\}}} \times {\varvec{e}}_{3} } \\ \end{array} } \right].$$
(9)

By multiplying both sides of Eq. (8) by the unit direction vector ei, and expressing the result in the local coordinate system di−xdiydizdi, the result can be shown as follows:

$$\left[ {\begin{array}{*{20}c} {\left( {\omega_{{\text{z}}}^{{\left\{ {d_{i} } \right\}}} } \right)_{x} } \\ {\left( {\omega_{{\text{z}}}^{{\left\{ {d_{i} } \right\}}} } \right)_{y} } \\ 0 \\ \end{array} } \right] = \frac{1}{{l_{i} }}\left[ {\begin{array}{*{20}c} { - \left( {v_{{{\text{u}}i}}^{{\left\{ {d_{i} } \right\}}} } \right)_{y} } \\ {\left( {v_{{{\text{u}}i}}^{{\left\{ {d_{i} } \right\}}} } \right)_{x} } \\ 0 \\ \end{array} } \right],$$
(10)

where \(v_{{{\text{u}}i}}^{{\left\{ {d_{i} } \right\}}}\) represents the center velocity of the spherical hinge in the local coordinate system di−xdiydizdi.

The angular velocity of the drive chain is generated by the rotation of the universal joint, so the angular velocity of the drive chain rotation can be expressed in the local coordinate system di−xdiydizdi as:

$$\omega_{{\text{z}}} = \dot{\phi }_{{{\text{d}}i}} {\varvec{y}}_{{{\text{d}}i}} + \dot{\theta }{}_{{{\text{d}}i}}{\varvec{x}}_{{{\text{d}}i}} .$$
(11)

By representing the vector in Eq. (9) in the local coordinate system di−xdiydizdi, Eq. (9) can be expressed as:

$$\begin{aligned} {\varvec{\omega }}_{{\text{z}}}^{{\left\{ {d_{i} } \right\}}} & = \dot{\phi }_{{{\text{d}}i}} {\varvec{R}}\left( {\theta {}_{{{\text{d}}i}},x_{{{\text{d}}i}} } \right)^{{\text{T}}} {\varvec{R}}\left( {\phi {}_{{{\text{d}}i}},y_{{{\text{d}}i}} } \right)^{{\text{T}}} \left( {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } \right)^{{\text{T}}} \\ & + \dot{\theta }_{{{\text{d}}i}} {\varvec{R}}\left( {\theta {}_{{{\text{d}}i}},x_{{{\text{d}}i}} } \right)^{{\text{T}}} \left( {\begin{array}{*{20}c} 1 & 0 & 0 \\ \end{array} } \right)^{{\text{T}}} \\ & \approx \left( {\begin{array}{*{20}c} {\dot{\theta }_{{{\text{d}}i}} } & {\dot{\phi }_{{{\text{d}}i}} } & 0 \\ \end{array} } \right)^{{\text{T}}} . \\ \end{aligned}$$
(12)

By combining Eqs. (10)–(12), the angular velocity of the universal joint can be expressed as:

$$\left\{ \begin{gathered} \dot{\phi }_{{{\text{d}}i}} = - \frac{1}{{l_{i} }}\left( {{}_{U}^{{d_{i} }} {\varvec{R}}} \right)_{:,2} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{i}^{{\left\{ U \right\}}} } \right), \hfill \\ \dot{\theta }_{{{\text{d}}i}} = \frac{1}{{l_{i} }}\left( {{}_{U}^{{d_{i} }} {\varvec{R}}} \right)_{:,1} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{i}^{{\left\{ U \right\}}} } \right). \hfill \\ \end{gathered} \right.$$
(13)

Then, the Jacobian matrix of the universal joint is:

$${\varvec{J}}_{{{\text{fd}}}} = \left[ {\begin{array}{*{20}c} { - \frac{1}{{l_{1} }}\left( {{}_{U}^{{d_{1} }} {\varvec{R}}} \right)_{:,2} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{1}^{{\left\{ U \right\}}} } \right)} \\ { - \frac{1}{{l_{2} }}\left( {{}_{U}^{{d_{2} }} {\varvec{R}}} \right)_{:,2} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{2}^{{\left\{ U \right\}}} } \right)} \\ { - \frac{1}{{l_{3} }}\left( {{}_{U}^{{d_{3} }} {\varvec{R}}} \right)_{:,2} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{3}^{{\left\{ U \right\}}} } \right)} \\ \end{array} } \right],$$
(14)
$${\varvec{J}}_{{{\text{xd}}}} = \left[ {\begin{array}{*{20}c} {\frac{1}{{l_{1} }}\left( {{}_{U}^{{d_{1} }} {\varvec{R}}} \right)_{:,2} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{1}^{{\left\{ U \right\}}} } \right)} \\ {\frac{1}{{l_{2} }}\left( {{}_{U}^{{d_{2} }} {\varvec{R}}} \right)_{:,2} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{2}^{{\left\{ U \right\}}} } \right)} \\ {\frac{1}{{l_{3} }}\left( {{}_{U}^{{d_{3} }} {\varvec{R}}} \right)_{:,2} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{3}^{{\left\{ U \right\}}} } \right)} \\ \end{array} } \right].$$
(15)

Similarly, considering the motion transmission relationship between the spherical hinge and the moving platform, the angular velocity of the drive chain can be expressed as:

$${{\varvec{\omega}}}_{{\text{z}}} = {{\varvec{\omega}}}_{{\text{u}}} + \dot{\phi }_{{{\text{u}}i}} {\varvec{y}}_{{{\text{d}}i}} + \dot{\theta }{}_{{{\text{u}}i}}{\varvec{x}}_{{{\text{u}}i}} + \dot{\gamma }{}_{{{\text{u}}i}}{\varvec{z}}_{{{\text{u}}i}} .$$
(16)

By representing the vector in Eq. (14) in the local coordinate system ui−xuiyuizui, Eq. (14) can be expressed as follows:

$$\begin{aligned} {\varvec{\omega }}_{{\text{z}}}^{{\left\{ {u_{i} } \right\}}} & = {\varvec{\omega }}_{{\text{u}}}^{{\left\{ {u_{i} } \right\}}} + \dot{\gamma }{}_{{{\text{u}}i}}{\varvec{R}}\left( {\gamma {}_{{{\text{u}}i}},z_{{{\text{u}}i}} } \right)^{{\text{T}}} \left( {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right)^{{\text{T}}} \\ & + \dot{\phi }_{{{\text{u}}i}} {\varvec{R}}\left( {\gamma {}_{{{\text{u}}i}},z_{{{\text{u}}i}} } \right)^{{\text{T}}} {\varvec{R}}\left( {\theta {}_{{{\text{u}}i}},x_{{{\text{u}}i}} } \right)^{{\text{T}}} {\varvec{R}}\left( {\phi {}_{{{\text{u}}i}},y_{{{\text{u}}i}} } \right)^{{\text{T}}} \left( {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } \right)^{{\text{T}}} \\ & + \dot{\theta }{}_{{{\text{u}}i}}{\varvec{R}}\left( {\gamma {}_{{{\text{u}}i}},z_{{{\text{u}}i}} } \right)^{{\text{T}}} {\varvec{R}}\left( {\theta {}_{{{\text{u}}i}},x_{{{\text{u}}i}} } \right)^{{\text{T}}} \left( {\begin{array}{*{20}c} 1 & 0 & 0 \\ \end{array} } \right)^{{\text{T}}} {\text{ }} \\ & \approx {\varvec{\omega }}_{{\text{u}}}^{{\left\{ {u_{i} } \right\}}} + \left( {\begin{array}{*{20}c} {\dot{\phi }_{{{\text{u}}i}} } & {\dot{\theta }{}_{{{\text{u}}i}}} & {\dot{\gamma }{}_{{{\text{u}}i}}} \\ \end{array} } \right)^{{\text{T}}} . \\ \end{aligned}$$
(17)

By combining Eq. (11) and Eq. (17), the angular velocity of the spherical hinge can be expressed as:

$$\left\{ \begin{aligned} & \dot{\phi }_{{{\text{u}}i}} = - \frac{1}{{l_{i} }}\left( {{}_{U}^{{d_{i} }} {\varvec{R}}} \right)_{:,2} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{i}^{{\left\{ U \right\}}} } \right) - \left( {{}_{{u_{i} }}^{D} {\varvec{R}}} \right)_{:,1} \cdot {{\varvec{\omega}}}_{{\text{u}}} , \hfill \\ & \dot{\theta }_{{{\text{u}}i}} = \frac{1}{{l_{i} }}\left( {{}_{U}^{{d_{i} }} {\varvec{R}}} \right)_{:,1} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{i}^{{\left\{ U \right\}}} } \right) - \left( {{}_{{u_{i} }}^{D} {\varvec{R}}} \right)_{:,2} \cdot {{\varvec{\omega}}}_{{\text{u}}} , \hfill \\ & \dot{\gamma }_{{{\text{u}}i}} = \frac{1}{{l_{i} }}\left( {{}_{U}^{{d_{i} }} {\varvec{R}}} \right)_{:,3} \cdot {{\varvec{\omega}}}_{{\text{u}}} . \hfill \\ \end{aligned} \right.$$
(18)

Thus, the Jacobian matrix of the spherical hinge can be expressed as:

$${\varvec{J}}_{{{\text{gu}}}} = \left[ {\begin{array}{*{20}c} { - \left( {{}_{{u_{i} }}^{D} {\varvec{R}}} \right)_{:,3}^{{\text{T}}} } \\ { - \left( {{}_{{u_{i} }}^{D} {\varvec{R}}} \right)_{:,3}^{{\text{T}}} } \\ { - \left( {{}_{{u_{i} }}^{D} {\varvec{R}}} \right)_{:,3}^{{\text{T}}} } \\ \end{array} } \right],$$
(19)
$${\varvec{J}}_{{{\text{fu}}}} = \left[ {\begin{array}{*{20}c} { - \frac{1}{{l_{1} }}\left( {{}_{U}^{{d_{1} }} {\varvec{R}}} \right)_{:,2} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{1}^{{\left\{ U \right\}}} } \right)^{{\text{T}}} - \left( {{}_{{u_{i} }}^{D} {\varvec{R}}} \right)_{:,1}^{{\text{T}}} } \\ { - \frac{1}{{l_{2} }}\left( {{}_{U}^{{d_{1} }} {\varvec{R}}} \right)_{:,2} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{1}^{{\left\{ U \right\}}} } \right)^{{\text{T}}} - \left( {{}_{{u_{i} }}^{D} {\varvec{R}}} \right)_{:,1}^{{\text{T}}} } \\ { - \frac{1}{{l_{3} }}\left( {{}_{U}^{{d_{1} }} {\varvec{R}}} \right)_{:,2} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{1}^{{\left\{ U \right\}}} } \right)^{{\text{T}}} - \left( {{}_{{u_{i} }}^{D} {\varvec{R}}} \right)_{:,1}^{{\text{T}}} } \\ \end{array} } \right],$$
(20)
$${\varvec{J}}_{{{\text{xu}}}} = \left[ {\begin{array}{*{20}c} { - \frac{1}{{l_{1} }}\left( {{}_{U}^{{d_{1} }} {\varvec{R}}} \right)_{:,1} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{1}^{{\left\{ U \right\}}} } \right)^{{\text{T}}} - \left( {{}_{{u_{i} }}^{D} {\varvec{R}}} \right)_{:,2}^{{\text{T}}} } \\ { - \frac{1}{{l_{2} }}\left( {{}_{U}^{{d_{1} }} {\varvec{R}}} \right)_{:,1} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{1}^{{\left\{ U \right\}}} } \right)^{{\text{T}}} - \left( {{}_{{u_{i} }}^{D} {\varvec{R}}} \right)_{:,2}^{{\text{T}}} } \\ { - \frac{1}{{l_{3} }}\left( {{}_{U}^{{d_{1} }} {\varvec{R}}} \right)_{:,1} \cdot \left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{1}^{{\left\{ U \right\}}} } \right)^{{\text{T}}} - \left( {{}_{{u_{i} }}^{D} {\varvec{R}}} \right)_{:,2}^{{\text{T}}} } \\ \end{array} } \right].$$
(21)

By solving the first derivative with respect to time in Eq. (3), the result can be shown as follows:

$${\dot{\varvec{p}}}_{{{\text{g}}i}}^{{\left\{ {d_{i} } \right\}}} = q_{i} \left( {{{\varvec{\omega}}}_{{\text{z}}}^{{\left\{ {d_{i} } \right\}}} \times {\varvec{e}}_{i} } \right) = q_{i} \left( {\begin{array}{*{20}c} {\dot{\phi }_{{{\text{d}}i}} } & {\dot{\theta }_{{{\text{d}}i}} } & 0 \\ \end{array} } \right)^{{\text{T}}} .$$
(22)

Combining Eq. (13) and Eq. (22), the Jacobian matrix of the lower connecting rod is:

$${\varvec{J}}_{{{\text{g}}i}} = \left[ {\begin{array}{*{20}c} {\frac{{q_{i} }}{{l_{i} }}\left( {\left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{i}^{{\left\{ U \right\}}} } \right)\left( {{}_{U}^{{d_{i} }} {\varvec{R}}} \right)_{:,2} } \right)^{{\text{T}}} } \\ { - \frac{{q_{i} }}{{l_{i} }}\left( {\left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{i}^{{\left\{ U \right\}}} } \right)\left( {{}_{U}^{{d_{i} }} {\varvec{R}}} \right)_{:,1} } \right)^{{\text{T}}} } \\ {{\varvec{0}}^{1 \times 3} } \\ \end{array} } \right].$$
(23)

Similarly, the Jacobian matrix of the upper connecting rod is:

$${\varvec{J}}_{{{\text{h}}i}} = \left[ {\begin{array}{*{20}c} {\frac{{h_{i} }}{{l_{i} }}\left( {\left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{i}^{{\left\{ U \right\}}} } \right)\left( {{}_{U}^{{d_{i} }} {\varvec{R}}} \right)_{:,2} } \right)^{{\text{T}}} } \\ { - \frac{{h_{i} }}{{l_{i} }}\left( {\left( {{{\varvec{\omega}}}_{{\text{u}}} \times {}_{U}^{D} {\varvec{Ru}}_{i}^{{\left\{ U \right\}}} } \right)\left( {{}_{U}^{{d_{i} }} {\varvec{R}}} \right)_{:,1} } \right)^{{\text{T}}} } \\ {{\varvec{0}}^{1 \times 3} } \\ \end{array} } \right],$$
(24)

where hi is the distance between the centroid of the lower connecting rod and the center of the universal joint.

2.3 Dynamic Equation of Electro-hydraulic Driven 3-UPS/S Parallel Stabilization Platform

To derive the dynamic equation of an electro-hydraulic driven 3-UPS/S parallel stabilization platform, the following assumptions were made:

  1. (1)

    Errors in the processing and assembly processes were ignored.

  2. (2)

    The force of the drive chain on the moving platform was equivalent to the spring force along the expansion direction of the drive chain.

  3. (3)

    The passive joints of the mechanism adopted a ball-and-socket structure with rolling balls for point contact. Universal joints utilized needle-roller bearings. Therefore, friction at the passive joints of the mechanism was ignored.

The friction at the hydraulic cylinder in the mechanism is primarily manifested in the form of the viscous shear resistance of the hydraulic oil. Therefore, a fluid viscous damping coefficient was introduced during the process of establishing the equation. According to the virtual work principle, the virtual power acting on each component of the mechanism can be calculated as follows:

$$\begin{aligned} & {\updelta }p = \left( {{\varvec{f}}_{{\text{u}}} - {\varvec{k}}\Delta {\varvec{l}} - {\varvec{c\dot{l}}}} \right) \cdot {\updelta }{\varvec{l}} + \left( { - {\varvec{\ I}}_{{\text{u}}} {\dot{\varvec{\omega }}}_{{\text{u}}} - {{\varvec{\omega}}}_{{\text{u}}} \times {\varvec{\ I}}_{{\text{u}}} {{\varvec{\omega}}}_{{\text{u}}} } \right) \cdot {\updelta }{{\varvec{\omega}}}_{{\text{u}}} \hfill \\ & + \left( { - k_{{{\text{xd}}}} \Delta \theta_{{\text{d}}} } \right) \cdot {\updelta }\dot{\theta }_{{\text{d}}} + \left( { - k_{{{\text{fd}}}} \Delta \psi_{{\text{d}}} } \right) \cdot {\updelta }\dot{\psi }_{{\text{d}}} + \left( { - k_{{{\text{xu}}}} \Delta \theta_{{\text{u}}} } \right) \cdot {\updelta }\dot{\theta }_{{\text{u}}} \hfill \\ & + \sum\limits_{i = 1}^{3} {\left( { - m_{{{\text{g}}i}} {\varvec{\ddot{p}}}_{{_{{{\text{g}}i}} }}^{{\left\{ {di} \right\}}} \cdot {\updelta }{\dot{\varvec{p}}}_{{_{{{\text{g}}i}} }}^{{\left\{ {di} \right\}}} + \left( { - {\varvec{I}}_{{_{{{\text{g}}i}} }}^{{\left\{ {di} \right\}}} {\dot{\varvec{\omega }}}_{{_{{{\text{g}}i}} }}^{{\left\{ {di} \right\}}} - {{\varvec{\omega}}}_{{_{{{\text{g}}i}} }}^{{\left\{ {di} \right\}}} \times {\varvec{I}}_{{_{{{\text{g}}i}} }}^{{\left\{ {di} \right\}}} {{\varvec{\omega}}}_{{_{{{\text{g}}i}} }}^{{\left\{ {di} \right\}}} } \right) \cdot {\updelta }{{\varvec{\omega}}}_{{_{{{\text{g}}i}} }}^{{\left\{ {di} \right\}}} } \right)} \hfill \\ & + \sum\limits_{i = 1}^{3} {\left( { - m_{{{\text{h}}i}} {\varvec{\ddot{p}}}_{{_{{{\text{h}}i}} }}^{{\left\{ {di} \right\}}} \cdot {\updelta }{\dot{\varvec{p}}}_{{_{{{\text{h}}i}} }}^{{\left\{ {di} \right\}}} + \left( { - {\varvec{I}}_{{_{{{\text{h}}i}} }}^{{\left\{ {di} \right\}}} {\dot{\varvec{\omega }}}_{{_{{{\text{h}}i}} }}^{{\left\{ {di} \right\}}} - {{\varvec{\omega}}}_{{_{{{\text{h}}i}} }}^{{\left\{ {di} \right\}}} \times {\varvec{I}}_{{_{{{\text{h}}i}} }}^{{\left\{ {di} \right\}}} {{\varvec{\omega}}}_{{_{{{\text{h}}i}} }}^{{\left\{ {di} \right\}}} } \right) \cdot {\updelta }{{\varvec{\omega}}}_{{_{{{\text{h}}i}} }}^{{\left\{ {di} \right\}}} } \right)} \hfill \\ & + \left( { - k_{{{\text{fu}}}} \Delta \psi_{{\text{u}}} } \right) \cdot {\updelta }\dot{\psi }_{{\text{u}}} + \left( { - k_{{{\text{gu}}}} \Delta \gamma_{{\text{u}}} } \right) \cdot {\updelta }\dot{\gamma }_{{\text{u}}} = {\varvec{0}}, \hfill \\ \end{aligned}$$
(25)

where fu is the force matrix on the moving platform; k is the stiffness matrix of the drive chain; c is the damping matrix of the drive chain; Iu is the inertia matrix of the moving platform; \({{\varvec{\omega}}}_{{\text{u}}}\) is the angular velocity of the moving platform; mgi is the mass of the lower connecting rod; \({\varvec{p}}_{{_{{{\text{g}}i}} }}^{{\left\{ {di} \right\}}}\) is the displacement vector of the lower connecting rod; \({\varvec{I}}_{{_{{{\text{g}}i}} }}^{{\left\{ {di} \right\}}}\) is the inertia matrix of the lower connecting rod; \({{\varvec{\omega}}}_{{_{{{\text{g}}i}} }}^{{\left\{ {di} \right\}}}\) is the angular velocity of the lower connecting rod; mhi is the mass of the upper connecting rod; \({\varvec{p}}_{{_{{{\text{h}}i}} }}^{{\left\{ {di} \right\}}}\) is the displacement vector of the upper connecting rod; \({\varvec{I}}_{{_{{{\text{h}}i}} }}^{{\left\{ {di} \right\}}}\) is the inertia matrix of the upper connecting rod; \({{\varvec{\omega}}}_{{_{{{\text{h}}i}} }}^{{\left\{ {di} \right\}}}\) is the angular velocity of the upper connecting rod.

By ignoring the Coriolis and centrifugal forces, Eq. (25) can be simplified as follows:

$$\begin{gathered} \left( {{\varvec{f}}_{{\text{u}}} - {\varvec{kJ}}_{{\text{u}}} {\varvec{x}} - {\varvec{cJ}}_{{\text{u}}} {\dot{\varvec{x}}}} \right){\updelta }{\dot{\varvec{x}}} - \left( {k_{{{\text{x}}{\text{u}}}} {\varvec{J}}_{{{\text{xu}}}} {\varvec{x}}} \right)^{{\text{T}}} {\varvec{J}}_{{{\text{xu}}}} {\updelta }{\dot{\varvec{x}}} \hfill \\ - \left( {k_{{{\text{xd}}}} {\varvec{J}}_{{{\text{xd}}}} {\varvec{x}}} \right)^{{\text{T}}} {\varvec{J}}_{{{\text{xd}}}} {\updelta }{\dot{\varvec{x}}} - \left( {k_{{{\text{fd}}}} {\varvec{J}}_{{{\text{fd}}}} {\varvec{x}}} \right)^{{\text{T}}} {\varvec{J}}_{{{\text{fd}}}} {\updelta }{\dot{\varvec{x}}} \hfill \\ - \left( {k_{{{\text{fu}}}} {\varvec{J}}_{{{\text{fu}}}} {\varvec{x}}} \right)^{{\text{T}}} {\varvec{J}}_{{{\text{fu}}}} {\updelta }{\dot{\varvec{x}}} - \left( {k_{{{\text{gu}}}} {\varvec{J}}_{{{\text{gu}}}} {\varvec{x}}} \right)^{{\text{T}}} {\varvec{J}}_{{{\text{gu}}}} {\updelta }{\dot{\varvec{x}}} \hfill \\ - \sum\limits_{i = 1}^{3} {\left( {{\varvec{I}}_{{{\text{g}}i}} {{\varvec{\omega}}}_{{{\text{g}}i}} {\varvec{J}}_{{{\text{g}}i}} + {\varvec{I}}_{{{\text{h}}i}} {{\varvec{\omega}}}_{{{\text{h}}i}} {\varvec{J}}_{{{\text{h}}i}} } \right)} {\updelta }{\dot{\varvec{x}}} = {\varvec{0}}, \hfill \\ \end{gathered}$$
(26)

where \({\dot{\varvec{x}}} = {{\varvec{\omega}}}_{{_{{\text{u}}} }}^{{\text{T}}}\).

The components of \({{\varvec{\omega}}}_{{\text{u}}}\) are independent because the generalized coordinates are independent. Therefore, the coefficient should be equal to zero. The explicit dynamic equation for this mechanism is as follows:

$${\varvec{M\ddot{x}}} + {\varvec{C\dot{x}}} + {\varvec{Kx}} = {\varvec{0}},$$
(27)

where

$${\varvec{M}} = {\varvec{I}}_{{\text{u}}} + \sum\limits_{i = 1}^{3} {\left( {{\varvec{J}}_{{_{{{\text{g}}i}} }}^{{\text{T}}} {\varvec{I}}_{{{\text{g}}i}} {\varvec{J}}_{{{\text{g}}i}} + {\varvec{J}}_{{_{{{\text{h}}i}} }}^{{\text{T}}} {\varvec{I}}_{{{\text{h}}i}} {\varvec{J}}_{{{\text{h}}i}} } \right)} ,$$
(28)
$${\varvec{C}} = {\varvec{J}}_{{\text{u}}}^{{\text{T}}} {\varvec{cJ}}_{{\text{u}}} ,$$
(29)
$$\begin{gathered} {\varvec{K}} = {\varvec{J}}_{{\text{u}}}^{{\text{T}}} {\varvec{kJ}}_{{\text{u}}} + {\varvec{J}}_{{\theta {\text{d}}}}^{{\text{T}}} {\varvec{k}}_{{\theta {\text{d}}}} {\varvec{J}}_{{\theta {\text{d}}}} + {\varvec{J}}_{{\psi {\text{d}}}}^{{\text{T}}} {\varvec{k}}_{{\psi {\text{d}}}} {\varvec{J}}_{{\psi {\text{d}}}} \hfill \\ + {\varvec{J}}_{{\theta {\text{u}}}}^{{\text{T}}} {\varvec{k}}_{{\theta {\text{u}}}} {\varvec{J}}_{{\theta {\text{u}}}} + {\varvec{J}}_{{\psi {\text{u}}}}^{{\text{T}}} {\varvec{k}}_{{\psi {\text{u}}}} {\varvec{J}}_{{\psi {\text{u}}}} + {\varvec{J}}_{{\gamma {\text{u}}}}^{{\text{T}}} {\varvec{k}}_{{\gamma {\text{u}}}} {\varvec{J}}_{{\gamma {\text{u}}}} . \hfill \\ \end{gathered}$$
(30)

3 Free Vibration Analysis of Electro-hydraulic Driven 3-UPS/S Parallel Stabilization Platform

3.1 Modal Analysis of Electro-hydraulic Driven 3-UPS/S Parallel Stabilization Platform in Fixed Posture

The structural parameters of the electro-hydraulic driven 3-UPS/S parallel stabilization platform are listed in Table 1.

Table 1 Structural parameters of electro-hydraulic driven 3-UPS/S parallel stabilization platform
Full size table

Based on the parameters shown in Table 1, the modal and natural frequencies of the platform in the initial position α=0°, β=0°, γ=28° and the random position α=10°, β=10°, γ=28° are calculated, and the results are shown in Tables 2 and 3.

Table 2 Natural frequency and vibration mode at initial position
Full size table
Table 3 Natural frequency and vibration mode at random position
Full size table

After analyzing the data in Tables 2 and 3, the following conclusions can be drawn:

  1. (1)

    At the initial position, the natural frequency in the deflection direction was at the minimum, and the natural frequencies in the directions of the rotation and pitch were approximately equal.

  2. (2)

    There is a certain coupling relationship between the vibration responses in the pitching and rotation directions; however, the coupling relationship between them and the deflection direction is small.

  3. (3)

    By changing the position of the mechanism, the coupling of the vibration response in every direction was enhanced, and the natural frequencies of each order changed. This is because the Jacobian matrix of the mechanism changed and affected its mass and stiffness matrices.

  4. (4)

    When the position of the mechanism changed, the natural frequencies of each order changed differently. The first- and third-order natural frequencies increased, whereas the second-order natural frequencies decreased.

  5. (5)

    When the vibration frequencies were the first-, second-, and third-order natural frequencies, the maximum vibration responses appeared in the deflection, pitching, and rotation directions, respectively. Under actual operating conditions, the external excitation frequency is most likely to approach the first-order natural frequency; therefore, the mechanism is most prone to vibration in the deflection direction.

3.2 Natural Frequency Analysis in Workspace of Electro-hydraulic Driven 3-UPS/S Parallel Stabilization Platform

When the platform is used to maintain the stability of the horizontal direction of the equipment, the change range of the deflection angle is small, and the angle compensation is mainly performed through changes in the rotation and pitching directions. According to the workspace search theory, when the deflection angle is 28°, the change range of the pitch and rotating angles is the largest. Therefore, considering this position as the initial workspace, the natural frequency variation curve of the mechanism can be obtained as follows.

As shown in Figure 2, in the initial workspace, the natural frequencies of each order presented an obvious symmetry with the position change, and that for the first-order natural frequency was the most evident, corresponding to the movement in the deflection direction. When the mechanism gradually deviated from the initial position, the variation trends for the different orders of the natural frequencies were not the same. Meanwhile, the positions at which the maximum and minimum values of each order of the natural frequencies were obtained are different. In general, when the pitching angle is significantly different from the rotation angle, the natural frequency approaches its limit. However, the second-order natural frequency had a large value near the initial position. When the mechanism gradually deviated from the initial position through attitude compensation, the second-order natural frequency gradually decreased. In addition, the third-order of the natural frequency was the most sensitive to position changes, followed by the second-order of the natural frequency, and the first-order of the natural frequency was the least affected by position changes.

Figure 2
figure 2

Variation law for the natural frequencies in the initial workspace

Full size image

4 Force Vibration Analysis of Electro-hydraulic Driven 3-UPS/S Parallel Stabilization Platform

4.1 Vibration Response Analysis of Electro-hydraulic Driven 3-UPS/S Parallel Stabilization Platform

When the excitation frequency is close to the natural frequency of each order, the mechanism generates a resonance, which affects the compensation accuracy and control precision. Therefore, when the structural parameters remain unchanged, the vibration response of the mechanism at the random position α=10°, β=10°, γ=28° is solved. The torque matrix acting on the mechanism is expressed as follows:

$${\varvec{M}}_{{\text{U}}} = \left[ {\begin{array}{*{20}c} {80\cos \left( {\omega_{0} t} \right)} \\ {80\cos \left( {\omega_{0} t} \right)} \\ {80\cos \left( {\omega_{0} t} \right)} \\ \end{array} } \right].$$
(31)

The time-domain curve of the vibration response is shown in Figure 3. As shown in Figure 3, when subjected to an external harmonic excitation whose frequency is close to the natural frequency, the mechanism generates a resonance, and the steady-state response is a simple harmonic motion. When the excitation frequency was close to the first-, second-, or third-order natural frequencies, the angular displacement in the deflection, pitch, and rotation directions reached a maximum. When the external excitation frequency was close to the first-order natural frequency, the angular displacement of the mechanism in the rotation and pitching directions was approximately equal; however, when the angular displacement in the rotation or pitching directions reached the maximum, the angular displacement response in the other two directions was smaller, which is consistent with the main vibration mode.

Figure 3
figure 3

Time domain curves of forced vibrations

Full size image

The frequency-domain curve of the vibration response is shown in Figure 4. When the excitation frequency was close to the natural frequency of each order, the steady-state vibration response amplitude in each direction reached the maximum at the corresponding natural frequency. The maximum amplitudes of the vibration response were 0.932° in the deflection direction, 0.0213° in the pitching direction, and 0.0111° in the rotation direction. When the excitation frequency was close to the first-, second-, and third-order natural frequencies, the steady-state response amplitudes in each direction gradually decreased. When the excitation frequency was close to the first-order natural frequency, the steady-state vibration response in each direction was much larger than when the excitation frequency was close to the second- or third-order natural frequency. Thus, when the excitation frequency is close to the first-order natural frequency, the resulting resonance significantly influences the compensation and control accuracies.

Figure 4
figure 4

Frequency domain curves of forced vibrations

Full size image

4.2 Vibration Response Amplitude Analysis in Workspace of Electro-hydraulic Driven 3-UPS/S Parallel Stabilization Platform

The amplitude of the vibration response was also related to the position of the mechanism. Therefore, by keeping the theoretical parameters unchanged, the vibration response amplitude in the initial working space was calculated for when the excitation frequency was close to the first-order natural frequency, and the results are shown in Figure 5.

Figure 5
figure 5

Amplitudes of vibration response for \(\omega_{0} \approx \omega_{1}\)

Full size image

It can be seen from Figure 5 that when the excitation frequency is close to the first-order natural frequency, the amplitude curves of the vibration response in each direction show a certain symmetry, and that the locations at which the extreme values of the response amplitudes in each direction are obtained are not the same. In Figure 5(a), we show that the vibration response amplitude in the rotation direction was small when the pitch angle is approximately 0°. At this position, the vibration response amplitude in the rotational direction was insensitive to a position change in the pitching direction. Similarly, as shown in Figure 5(b), the vibration response amplitude in the pitch direction was relatively small when the pitch angle was approximately 0°. At this position, the vibration response amplitude in the pitch direction was insensitive to position changes in the rotation direction. When the mechanism gradually deviates from the initial position, the amplitude of the vibration response in the rotation and pitching directions gradually increases. When the difference between the rotation and pitch angles was large, the vibration response amplitudes in the rotation and pitching directions were large. As shown in Figure 5(c), when the position changed from the left to the right limit of the working space, the amplitude of the vibration response in the deflection direction increased gradually. When the excitation frequency was close to the first-order natural frequency, the vibration response amplitude in the deflection direction was much larger than those in the pitch and rotation directions, and the maximum value was greater than 1°. The vibration generated by the mechanism has a significant impact on the control accuracy.

5 Verification of Dynamic Theoretical Model of Electro-hydraulic Driven 3-UPS/S Parallel Stabilization Platform

5.1 Verification of Theoretical Free Vibration Model

To verify the correctness of the theoretical free vibration model, the natural frequency of the prototype was measured at the random position α=10°, β=10°, γ=28° using the pulse excitation method. A schematic of the experimental setup is shown in Figure 6. A force hammer strikes the moving platform to generate an impulse excitation force. The signal of the exciting force then enters the lower computer through the force sensor and voltage amplifier on the force hammer. The axial response signal of the prototype is collected by the acceleration sensor and input to the computer through the voltage amplifier and lower computer. The experimental prototype and test diagram are shown in Figures 7 and 8, respectively.

Figure 6
figure 6

Schematic diagram of modal experiment. 1−oil tank, 2−liquid level gauge, 3−liquid temperature gauge, 4−filter, 5−motor pump, 6−overflow valve, 7−check valve, 8−filter, 9−servo valve, 10−electro-hydraulic driven 3-UPS/S parallel stabilization platform prototype, 11−acceleration sensor, 12−force hammer, 13−lower computer, 14−computer

Full size image
Figure 7
figure 7

Electro-hydraulic drive 3-UPS/S parallel stabilization platform prototype

Full size image
Figure 8
figure 8

Modal test diagram

Full size image

The sampling frequency used in the experiment was 640 Hz; therefore, it met the sampling theorem, and the collected signals were reliable. The time-domain curves of the excitation and vibration signals collected during the experiment are presented in Figure 9.

Figure 9
figure 9

Time domain curve of the measured signal

Full size image

After processing the data shown in Figure 9, the spectral power density curve of the prototype response signal was obtained, as shown in Figure 10. The curve exhibited peaks at 26.31 Hz, 126.41 Hz and 141.88 Hz. A comparison of the theoretical and experimental values of the natural frequency is shown in Table 4. The maximum error between the theoretical and experimental values is 4.66%, which verifies the correctness of the theoretical model.

Figure 10
figure 10

Power spectral density of the system response

Full size image
Table 4 Comparison of theoretical and experimental values of the natural frequency
Full size table

5.2 Verification of Theoretical Forced Vibration Model

To verify the correctness of the theoretical forced vibration model of the mechanism, and taking the excitation frequency close to the first-order natural frequency as example, the fourth-order Runge-Kutta method was used to solve the time-domain and frequency-domain characteristic curves of the vibration response, and the results are shown in Figure 11.

Figure 11
figure 11

Time domain curve of steady-state response numerical solution

Full size image

As shown in Figure 11(a), when the excitation frequency is close to the first-order natural frequency, the time-domain curve of the numerical solution exhibits a stable simple harmonic motion, which is consistent with the results of the theoretical analysis. By comparing Figures 3(b) and 11(b), it can be seen that the numerical solutions of the maximum vibration response amplitude in the rotation, pitching, and deflection directions were 0.0627°, 0.0766° and 0.932° respectively. Correspondingly, the maximum vibration response amplitudes obtained from the theoretical calculations in each direction were 0.0626°, 0.0765° and 0.9316°, respectively. A comparison between the theoretical and numerical values of the maximum vibration response amplitude is shown in Table 5; the maximum error between the theoretical and numerical solutions is 0.16%, which verifies the correctness of the theoretical forced vibration model.

Table 5 Comparison of theoretical and numerical values of maximum vibration response amplitude
Full size table

6 Conclusions

  1. (1)

    The natural frequency is a function of the position of the mechanism. In the initial working space, the change in the natural frequency was symmetrical, and the position for obtaining the extreme value was not the same. With a change in position, the third-order natural frequency changed the most, followed by the second-order natural frequency, and the first-order natural frequency changed the least.

  2. (2)

    When the mechanism resonated with the external excitation of a simple harmonic motion, the steady-state resonance response presented a simple harmonic motion. When the excitation frequency was close to the first-, second-, and third-order natural frequencies, the amplitude of the vibration response reached a maximum in the deflection, pitching, and rotation directions, respectively.

  3. (3)

    The vibration response amplitude varied symmetrically in the initial working space. When the excitation frequency was close to the first-order natural frequency, the vibration response amplitude in the deflection direction was larger than that in the other two directions, and the value was close to 1°, which had a significant influence on the compensation and control accuracies.

  4. (4)

    A modal test and fourth-order Runge-Kutta numerical simulation were used to verify the theoretical model. The maximum error between the theoretical and experimental values was 4.66%, and the maximum error between the numerical and theoretical values was 0.16%, verifying the correctness of the theoretical model.