1 Introduction

Time synchronous averaging (TSA) is a powerful technique that extracts periodic components from a composite signal [1,2,3,4,5]. It is widely used in noise reduction and fault diagnosis [6,7,8,9,10]. In this method, segments separated by the exact period are averaged. Any component not synchronous with this period will be attenuated [11,12,13].

It is known that TSA works well only if all the segments are synchronized. Generally, an external trigger signal, provided by a tachometer, is used for synchronous sampling. This external reference signal should be stable so that effective synchronization can be obtained [14]. However, in some cases, installing a tachometer is difficult or impossible. If there is no reference signal available, it is necessary to estimate the fundamental frequency of the components to be extracted [15, 16]. While in practice, accurate estimation of the fundamental frequency is quite hard, and the rounding error needs to be considered [17].

There are many studies to improve the performance of TSA. Bonnardot et al. proposed a method for angular resampling by using the acceleration signal of a gearbox [18]. On this basis, an automatic TSA method was proposed, whose effectiveness depends on the local signal-to-noise ratio of mesh harmonics [19]. The time domain average scanning was presented to extract periodic components when no external reference signal exists. The fundamental frequency is obtained by searching within the possible range [20]. This optimization process can be adaptive [21]. Halim et al. combined TSA and wavelet transform to synchronize the data with the rotation period based on the reference peak [22]. Wu et al. eliminated the phase error by fractional delay filtering, but this method requires an accurate estimation of the fundamental frequency [23]. Guo et al. screened all segments according to the correlation coefficient, providing a new research route [24].

The above discussion indicates that TSA requires effective synchronization of segments. Therefore, this paper proposes time synchronous averaging based on the cross-power spectrum to cope with the current challenges. First, the original vibration signal is divided into equal-length segments. Then the phases of the segments are calculated and compensated, which means that the phase differences are eliminated. Finally, the synchronized segments are averaged. Numerical and experimental signals are presented to verify the proposed method.

This paper is organized as follows. Section 2 reviews the theory of time synchronous averaging, and Section 3 introduces the proposed method in detail. Section 4 studies the performance of the proposed method by numerical simulation. In Section 5, the experimental signal is provided for validating the proposed method. Section 6 shows the conclusions.

2 Time Synchronous Averaging

The basic theory of TSA is as follows. \(x(t)\) represents the original vibration signal of rotating machinery. Its discrete sequence can be expressed as \(x(n)(n = 0, \, 1, \, 2, \, \cdots )\), where \(x(n)\) is equivalent to \(x(n\Delta t)\). \(\Delta t\) denotes the sampling interval. The expression of TSA is

$$\left\{ \begin{gathered} y(n) = \frac{1}{N}\sum\limits_{r = 0}^{N - 1} {x(n + rM),} \hfill \\ n = 0, \, 1, \, \cdots , \, M - 1, \hfill \\ \end{gathered} \right.$$
(1)

where \(y(n)\) is the average signal, N is the number of segments, and M is the number of sampling points per segment.

The frequency response function of Eq. (1) can be expressed as:

$$H(f) = \frac{1}{N}\frac{{\sin ({{\uppi Nf} \mathord{\left/ {\vphantom {{\uppi Nf} {f_{0} }}} \right. \kern-0pt} {f_{0} }})}}{{\sin ({{\uppi f} \mathord{\left/ {\vphantom {{\uppi f} {f_{0} }}} \right. \kern-0pt} {f_{0} }})}}\exp ( - j\uppi (N - 1){f \mathord{\left/ {\vphantom {f {f_{0} }}} \right. \kern-0pt} {f_{0} }}),$$
(2)

where f0 is the fundamental frequency of the periodic components.

As illustrated in Figure 1, the typical shape of the frequency response function is like a comb. Therefore, TSA works like a comb filter with main lobes centered around integer multiples of the fundamental frequency. It is easy to find that the periodic components are unchanged, while the nonsynchronous components and noise are attenuated.

Figure 1
figure 1

Frequency response of TSA

Full size image

An external reference signal is usually needed to get the desired result. However, when no reference signal is available, TSA's performance will be limited by rounding and frequency estimation errors. The phase error caused by them can be expressed as:

$$\psi_{r,m} \approx 2\uppi mr\Delta M\frac{{f_{0} }}{{f_{s} }} + 2\uppi mr\frac{\Delta f}{{f_{o} }},$$
(3)

where m is the order of the component, \(\Delta M\) is the rounding error, \(\Delta f\) is the frequency estimation error, and fs is the sampling frequency.

It has been proved that the phase error will lead to a sharp attenuation of the periodic components. Detailed analyses can be found in Refs. [17, 20, 23].

3 Time Synchronous Averaging Based on Cross-Power Spectrum

3.1 Phase Detection Based on Cross-power Spectrum

For continuous signals \(x(t)\) and \(y(t)\), the expression of their cross-correlation function is:

$$R(\tau ) = \int_{ - \infty }^{ + \infty } x \left( t \right)\,y\left( {t - \tau } \right){\text{d}}t,$$
(4)

where \(\tau\) is the delay.

This function is mainly used to reflect the correlation of two different signals. After cross-correlation, components with the same frequency are enhanced, retaining the phase information, while the others get suppressed. Thus, the signal components of interest can be enhanced in this way. A phase-detection method based on the cross-power spectrum is introduced next.

To detect the phase of the fundamental component in the discrete vibration signal \(x(n)\), a reference cosine sequence is constructed as:

$$y_{0} (n) = \cos (2\uppi f_{0} n).$$
(5)

According to the definition of convolution, the cross-correlation function can be expressed as:

$$R(n) = x(n) * y_{0} ( - n),$$
(6)

where \(*\) denotes the convolution.

With the Fourier transform and time-domain convolution theorem, the cross-power spectrum can be calculated as:

$$P(k) = X(k)Y_{0}^{ * } (k),$$
(7)

where \(Y_{0}^{ * } (k)\) represents the complex conjugation of \(Y_{0} (k)\); \(X(k)\) and \(Y_{0} (k)\) represent the discrete Fourier transforms of \(x(n)\) and \(y_{0} (n)\), respectively.

The fundamental component in the vibration signal is thus enhanced. Its phase \(\varphi\) is equal to that of a complex number at the maximum amplitude of the cross-power spectrum. The expression is:

$$\left\{ \begin{gathered} \varphi = \arg (P(k_{0} )), \hfill \\ \left| {P(k_{0} )} \right| = \mathop {\max }\limits_{{0 < k < \uppi f_{s} }} \left( {\left| {P(k)} \right|} \right). \hfill \\ \end{gathered} \right.$$
(8)

This method strengthens the fundamental component through cross-correlation operation and extracts the phase from the cross-power spectrum. It has the advantages of strong adaptability, high precision, and small computation [25]. In addition, there is no limitation on the component of interest.

3.2 The Proposed Method

The detailed procedure of the proposed method can be divided into five steps, as shown in Figure 2.

Figure 2
figure 2

Flowchart of the proposed method

Full size image

Step 1: Some separate segments are obtained from the original signal by continuous and equispaced interception. The ith (\(i = 1, \, 2, \, \cdots , \, N\)) segment can be expressed as:

$$\left\{ \begin{gathered} x_{i} (n) = x[n + (i - 1)M], \hfill \\ n = 0, \, 1, \, \cdots , \, M - 1, \hfill \\ \end{gathered} \right.$$
(9)

where \(M = {\text{round}}({{f_{s} } \mathord{\left/ {\vphantom {{f_{s} } {f_{0} }}} \right. \kern-0pt} {f_{0} }})\).

Step 2: The phase-detection signal of the ith segment can be defined as:

$$\left\{ \begin{gathered} x_{i}^{{\text{p}}} (n) = x[n + (i - 1)M], \hfill \\ n = 0, \, 1, \, \cdots , \, f_{s} - 1. \hfill \\ \end{gathered} \right.$$
(10)

Step 3: The reference cosine sequence \(y_{0}^{{\text{p}}} (n)\), corresponding to the phase-detection signal obtained in Step 2, is constructed by Eq. (5). Then the cross-power spectrum \(P_{i} (k)\) is calculated according to Eq. (7). Finally, the phase \(\varphi_{i}\) can be calculated by Eq. (8). It will be used for phase compensation.

Step 4: The phase obtained in Step 3 is converted to the number of sampling points. The expression is:

$$N_{i} = {\text{round}}\left( {\frac{{\varphi _{i} }}{{2\pi f_{0} }}\,f_{s} } \right).$$
(11)

The phase differences among segments are eliminated by cyclic shift. This process can be expressed as follows:

$$x_{i}^{{\text{s}}} (n) = \left\{ \begin{gathered} x_{i} (n + M - N_{i} ),n < N_{i} , \hfill \\ x_{i} (n - N_{i} ),n \ge N_{i} , \hfill \\ n = 0, \, 1, \, \cdots , \, M - 1, \hfill \\ \end{gathered} \right.$$
(12)

where \(x_{i}^{{\text{s}}} (n)\) is the ith synchronized segment.

Step 5: All the synchronized segments are averaged.

$$y^{{\text{s}}} (n) = \frac{1}{N}\sum\limits_{i = 1}^{N} {x_{i}^{{\text{s}}} (n)} ,$$
(13)

where \(y^{{\text{s}}} (n)\) is the average signal of the proposed method.

4 Numerical Simulation

In this section, a numerical simulation is given to test the performance of the proposed method. Two existing TSA methods are introduced for comparison. They are original TSA (Method 1) and TSA based on a fractional delay filter (Method 2) proposed by Wu et al. [23]. The simulated signal comprises periodic components, nonsynchronous components, and noise. The expression is:

$$\left\{ \begin{gathered} x(t) = \sum\limits_{k} {A_{k} \cos (2\uppi kf_{0} t + \varphi_{k} )} + n(t), \hfill \\ k = 1, \, 3, \, 3.5, \, 5{, }5.7, \, 6, \, 8, \hfill \\ \end{gathered} \right.$$
(14)

where \(n(t)\) is the noise signal; \(A_{k}\) and \(\varphi_{k}\) are the amplitude and initial phase of the signal component with frequency kf0, respectively. Amplitudes are shown in Table 1, while initial phases can be set to any value. f0=31.05 Hz, and the sampling frequency is 16384 Hz.

Table 1 Amplitudes of the simulated signal
Full size table

The waveform of the simulated signal is shown in Figure 3.

Figure 3
figure 3

Simulated signal

Full size image

The frequency estimation error in actual situations should be considered, and the fundamental frequency of the simulated signal is estimated to be 31 Hz. The number of sampling points per segment is rounded to 529, and 40 segments are obtained by continuous interception.

The waveforms of segments 5 and 35 are shown in Figure 4(a). It can be observed that the two segments are not well synchronized. Figure 4(b) shows that the two segments almost overlap after phase detection and compensation.

Figure 4
figure 4

a Unsynchronized segments, b synchronized segments, c phases of all segments

Full size image

The phase before synchronization increases with the segment number, as shown in Figure 4(c). The maximum value is about 60°, leading to a sharp attenuation of the average result. After synchronization, all phases are stable around 0°, which means that the phase differences are eliminated.

Figure 5(a) shows the simulated signal in the frequency domain. The results of the three methods are shown in Figure 5(b)–(d). It is easy to find that the amplitudes of some harmonics in the results of Method 1 and Method 2 are obviously attenuated.

Figure 5
figure 5

Spectrum comparison: a Simulated signal, b Method 1, c Method 2, d Method 3

Full size image

Figure 6 gives the amplitude errors of the three methods based on Figure 5. It can be observed that the errors of Method 3 are the smallest.

Figure 6
figure 6

Amplitude errors of the three methods

Full size image

5 Experimental Validation

5.1 Set-up of the Experiment

We apply the proposed method to analyze the test-bench signal for further validation. The test bench is mainly composed of a motor, a parallel gearbox, a planetary gearbox, and a magnetic brake, as illustrated in Figure 7.

Figure 7
figure 7

Gearbox test bench

Full size image

In this experiment, a gear with one broken tooth is installed in the parallel gearbox to simulate the gear fault. The structure of the parallel gearbox and the fault gear are shown in Figure 8. B&K PULSE is used for data acquisition, and the accelerometer is PCB 608A11. The accelerometer is located on the housing of the parallel gearbox. Considering the requirement of frequency bandwidth, the convenience of calculating the time for spectrum analysis, and preset options for the instrument, we select the sampling frequency as 16384 Hz [26, 27]. The rotation speed of the motor is 1200 r/min. By searching in the frequency domain, the fundamental frequency of the input shaft is estimated to be 19.5 Hz.

Figure 8
figure 8

Parallel gearbox and broken gear

Full size image

5.2 Analysis of the Experimental Signal

The waveform of the experimental signal is shown in Figure 9, from which impacts caused by gear fault can be observed.

Figure 9
figure 9

Experimental signal

Full size image

For the experimental signal, the number of sampling points per segment is rounded to 840, and 90 segments are obtained by continuous interception. The waveforms of segments 5 and 85 are shown in Figure 10(a). It can be found that there is an impact in both segments, which is consistent with the fault feature. At the same time, it should also be noted that there is an obvious phase difference between the two impacts. Figure 10(b) shows the waveforms of the two segments after phase detection and compensation. They almost overlap.

Figure 10
figure 10

a Unsynchronized segments, b Synchronized segments, c Phases of all segments

Full size image

As shown in Figure 10(c), the phase differences after synchronization are close to 0°, which means that the segments are well synchronized.

Once a gear tooth is damaged, an impulsive vibration per revolution will be generated. As a result, detecting periodic impacts is a practical method for gear fault diagnosis.

Figure 11 shows the average waveforms of the three methods. It can be seen from Figure 11(c) that impacts appear once in a gear revolution, which indicates the presence of the gear fault. In contrast, the fault-induced impacts in the average waveforms of Method 1 and Method 2 are not strong enough. The gear fault is easier to be identified by the proposed method.

Figure 11
figure 11

Average waveforms: a Method 1, b Method 2, c Method 3

Full size image

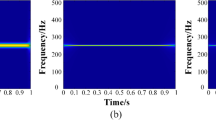
Figure 12(a) shows the spectrum of the experimental signal. Frequency components unrelated to gear fault can be misleading in fault diagnosis.

Figure 12
figure 12

Spectrum comparison: a experimental signal, b Method 1, c Method 2, d Method 3

Full size image

The spectrum results of the three methods are shown in Figure 12(b)–(d). The characteristic frequency of the gear fault and its harmonics can be clearly observed in Figure 12(d). Although these components can also be found from other two methods, they are severely attenuated.

As shown in Figure 13, the amplitude errors of the three methods are calculated. The result of Method 1 is the worst, and the amplitude error of 8x is as high as 45.8%. Due to the frequency estimation error, Method 2 can not reach the theoretical efficiency. Its maximum error is 22.9%. The maximum amplitude error of Method 3 is only 9.1%, which shows the superiority of the proposed method in extracting periodic components.

Figure 13
figure 13

Amplitude errors of the three methods

Full size image

6 Conclusions

  1. (1)

    A novel TSA method that is capable of synchronizing the separate segments without an external reference signal is proposed in this paper.

  2. (2)

    In numerical and experimental validations, the segments are well synchronized by the proposed method, and the periodic components are extracted.

  3. (3)

    Compared with other methods, the amplitude attenuation of the proposed method is less. The superiority of the proposed method in extracting periodic components with limited frequency estimation error is thus reflected.