1 Introduction

With the development of modern manufacturing industry, reverse engineering has been playing an increasingly important role in the fields of aviation, automobile and house appliance [1, 2]. The products in these fields are becoming more and more complex and irregular. If a part could be measured accurately and completely, its CAD model can be reconstructed correctly and efficiently. In the field of manufacturing, more and more product geometric dimensions also need to be measured quickly and accurately [3, 4]. To meet these requirements, visual-based measurement methods, such as laser beam probes and structured-light laser sensors have been widely used benefited from their attributes of non-contact, high-speed, and high-accuracy, etc. [5]. Laser beam sensors can be considered as a 1D sensor that outputs a distance value from the zero reading point. When the laser beam sensor is used for scanning, it is usually installed on the CMM. The transformation relationship from the 1D coordinate on the laser beam to the 3D coordinate of the CMM should be determined [6].

The structured light mainly consists of two categories of the line structured light and the plane structured light [7]. The plane structured light is a portable and efficient measurement approach. It can measure an area of a part at a time. Specifically, several areas on a part need to be plotted out before independent measurements of each area, and the collected data on different areas can then be merged using special algorithm [8, 9] or CAD systems, such as Rapidform and Polyworks. Compared with plane structured light, line structured light has high robustness to dark objects and highly reflective objects because of its good monochromaticity and high brightness [10].

In the line structure light 3D measurement technique, the measurement accuracy mainly depends on the laser light plane calibration. The main issue is to identify the relationship between the light plane and CCD array plane. To address this issue, a series of light plane calibration methods with different targets have been developed. Dependent on the requirements, 3D targets [11, 12], 2D targets [13,14,15] and 1D targets [16] could be applied to a variety of scenes.

However, the line structured light can only acquire one single line for each measurement, makes it difficult to obtain the full-view shape of the object through one-time measurement. It can realize non-contact 3D scanning only when it is integrated into CMMs or CNC machine tools [17]. The data collected by line structured light sensors, which is expressed in 2D format must be transformed into 3D format in world coordinate system. Xie et al. [18] proposed a five-axis system in which a laser line sensor is mounted on a PH10 rotary head and the PH10 is mounted on the Z-axis of a CMM. He mainly studied the relationship between the 2D coordinate system in the light plane and the CMM 3D world coordinate system, that is, the extrinsic parameters of structured light. Santolaria et al. [19] and Xie et al. [20] proposed a method for simultaneously calibrating intrinsic and extrinsic parameters of structured-light sensors respectively.

In addition to being mounted on a 3D mechanism, structured-light sensors can be positioned by other methods. In Ref. [21], a laser tracker and an industrial robot are used to provide position for structured-light sensor to obtain 3D data, which can achieve high position accuracy by using a highcost laser tracker. In Ref. [22], a turntable is used to provide rotation coordinates. This method is relatively flexible, but it can only measure small rotating objects. Optical positioning is a new method by using cameras, but the positioning accuracy is not easy to be controlled [23].

In recent years, handheld laser scanning technology has been developed rapidly and been widely used. Its main feature is that it can flexibly change the angle according to the characteristics of the object and measure all areas on the object. Moreover, it is not limited by the measurement range and can measure large objects [24]. However, before measurement, a large number of circular mark points must be pasted on the object in order to locate the measurement system. Therefore, this method is not very convenient in real-time measurement.

To overcome the bottleneck of measuring the parts with complex structure and features completely and efficiently, this paper presents a flexible scanning system by integrating a laser line sensor with an AACMM, as shown in Figure 1. The system can measure complicated parts by manually controlling the arms to change the orientation of the laser sensor, therefore accessing any area on the part.

Figure 1
figure 1

The integrated system of an AACMM and a laser line sensor

Full size image

In this study, the relationship between laser sensor and AACMM is similar to the hand-eye relationship of robot, which can be determined based on the position relationship between the end joint of the robot and the vision systems, including the binocular vision and monocular vision. In this case, a target is usually used as a calibration object, so that the vision system can observe the target and obtain the calibration point under the fixed target position, as a known condition to solve the hand–eye relationship. Yin et al. [25] proposed a method to calibrate the hand-eye relationship using a standard sphere. The feasibility of this method is that the motion of the robot can be controlled and the laser plane can be controlled to pass through the sphere center. Sharifzadeh et al. [26] calibrated the hand-eye relationship using a flat plate. It is also because the motion of the robot is controllable, the structured light projected onto the flat plate shows a circular pattern. Qin et al. [27] calculated the sensor rotational errors reversely from the data dislocation originating from the sensor without calibration, and then calibrated the sensor by mechanical adjustment and numerical compensation. In this method, the stitching of data depends on objects with special structure such as honeycomb cores. Yu et al. [28] calibrated the light plane of the line structured light using binocular cameras which simplifies the calibration process and improves the 3D measurement accuracy. When the calibration is completed, the camera 2 is removed. This method is reasonable in principle, but it is inconvenient in practical use.

2 System Modelling

An articulated arm CMM (AACMM) usually has six or seven rotation axes to access a point in 3D space from almost any direction. Figure 2 shows a simplified model of a six-axis articulated arm CMM. In this model, \({O}_{0}{X}_{0}{Y}_{0}{Z}_{0}\),…, \({O}_{5}{X}_{5}{Y}_{5}{Z}_{5}\) are the six coordinate frames located on each rotation axis, with \({O}_{0}{X}_{0}{Y}_{0}{Z}_{0}\) the base coordinate frame and \({O}_{6}{X}_{6}{Y}_{6}{Z}_{6}\) the coordinate frame of a touch probe. In Figure 1, the touch probe originally mounted on AACMM is replaced by a laser line sensor, while the definition of touch probe coordinates \({O}_{6}{X}_{6}{Y}_{6}{Z}_{6}\) still applies: \({O}_{6}\) is located at the position of the tip of the touch probe; \({Y}_{6}\) is parallel to the last axis (\({Z}_{5}\)) of the arm; \({Z}_{6}\) points towards the inwards direction along the touch probe; the remaining direction of \({X}_{6}\) can be determined by right-hand rule.

Figure 2
figure 2

Coordinate transformations of a six-axis AACMM

Full size image

For a commercial AACMM, the transformations from \({O}_{6}{X}_{6}{Y}_{6}{Z}_{6}\) to \({O}_{0}{X}_{0}{Y}_{0}{Z}_{0}\) can be performed based on SDK information provide by manufacturers. In another word, it is possible to directly obtain the coordinate of the touch probe \({O}_{6}\) and the direction vector of \({X}_{6}\), \({ Y}_{6}\) and \({Z}_{6}\) in the base coordinate frame \({O}_{0}{X}_{0}{Y}_{0}{Z}_{0}\). After calibration of intrinsic parameters of the laser sensor, a 2D coordinate frame \({O}_{\mathrm{L}}{Y}_{\mathrm{L}}{Z}_{\mathrm{L}}\) in the laser plane can be established, according to Figures 1 and 2. When the laser sensor is employed for scanning, 2D raw data points in the frame \({O}_{\mathrm{L}}{Y}_{\mathrm{L}}{Z}_{\mathrm{L}}\) are recorded. Since the transformation from \({O}_{6}{X}_{6}{Y}_{6}{Z}_{6}\) to \({O}_{0}{X}_{0}{Y}_{0}{Z}_{0}\) is known, once the transformation from \({O}_{\mathrm{L}}{Y}_{\mathrm{L}}{Z}_{\mathrm{L}}\) to \({O}_{6}{X}_{6}{Y}_{6}{Z}_{6}\) is determined, the scanned 2D data point can be then transformed into 3D data point in the base coordinate frame \({O}_{0}{X}_{0}{Y}_{0}{Z}_{0}\).

The articulated arm CMM adopted in this paper is Romer 2028, which has six axes. The communications between the AACMM and the computer are fulfilled through a USB interface. The computer can directly read twelve parameters from the AACMM. The sequence of the parameters reading from Romer 2028 is \((\begin{array}{ccc}{r}_{1}& {r}_{4}& {r}_{7}\end{array})\), \((\begin{array}{ccc}{r}_{2}& {r}_{5}& {r}_{8}\end{array})\), and \((\begin{array}{ccc}{r}_{3}& {r}_{6}& {r}_{9}\end{array})\), \((\begin{array}{ccc}{q}_{x}& {q}_{y}& {q}_{z}\end{array})\), corresponding to the direction vectors of \({X}_{6}\), \({ Y}_{6}\), \({ Z}_{6}\), and the coordinate of \({O}_{6}\) in the base coordinate frame \({O}_{0}{X}_{0}{Y}_{0}{Z}_{0}\). The matrix form is

$${{\varvec{T}}}_{0}^{6}=\left[\begin{array}{cc}\begin{array}{cc}{r}_{1}& {r}_{2}\\ {r}_{4}& {r}_{5}\end{array}& \begin{array}{cc}{r}_{3}& {q}_{x}\\ {r}_{6}& {q}_{y}\end{array}\\ \begin{array}{cc}{r}_{7}& {r}_{8}\\ 0& 0\end{array}& \begin{array}{cc}{r}_{9}& {q}_{z}\\ 0& 1\end{array}\end{array}\right].$$
(1)

Eq. (1) is the transformation from \({O}_{6}{X}_{6}{Y}_{6}{Z}_{6}\) to \({O}_{0}{X}_{0}{Y}_{0}{Z}_{0}\).

The transformation from \({O}_{\mathrm{L}}{Y}_{\mathrm{L}}{Z}_{\mathrm{L}}\) to \({O}_{6}{X}_{6}{Y}_{6}{Z}_{6}\) is a 2D to 3D transformation, which can be established as

$${{\varvec{T}}}_{6}^{{\varvec{L}}}=\left[\begin{array}{cc}\begin{array}{cc}{l}_{y} & {l}_{z}\end{array}& {t}_{x}\\ \begin{array}{cc}\begin{array}{c}{m}_{y}\\ {n}_{y}\\ 0\end{array}& \begin{array}{c}{m}_{z}\\ {n}_{z}\\ 0\end{array}\end{array}& \begin{array}{c}{t}_{y}\\ {t}_{z}\\ 1\end{array}\end{array}\right],$$
(2)

where \((\begin{array}{ccc}{l}_{y}& {m}_{y}& {n}_{y}\end{array})\) is the direction vector of \({Y}_{\mathrm{L}}\), \((\begin{array}{ccc}{l}_{z}& {m}_{z}& {n}_{z}\end{array})\) is the direction vector of \({Z}_{\mathrm{L}}\), \((\begin{array}{ccc}{t}_{x}& {t}_{y}& {t}_{z}\end{array})\) is the translation of \({O}_{\mathrm{L}}{Y}_{\mathrm{L}}{Z}_{\mathrm{L}}\) in \({O}_{6}{X}_{6}{Y}_{6}{Z}_{6}\). All parameters in Eq. (2) are unknown.

According to Eqs. (1) and (2), the system model is established to transform the 2D data point in \({O}_{\mathrm{L}}{Y}_{\mathrm{L}}{Z}_{\mathrm{L}}\) into 3D data point in \({O}_{0}{X}_{0}{Y}_{0}{Z}_{0}\) by

$${{\varvec{P}}}_{0}= {{\varvec{T}}}_{0}^{6}{{\varvec{T}}}_{6}^{{\varvec{L}}}{{\varvec{P}}}_{\mathbf{L}},$$
(3)

or

$$\left[\begin{array}{c}\begin{array}{c}{x}_{0}\\ {y}_{0}\end{array}\\ \begin{array}{c}{z}_{0}\\ 1\end{array}\end{array}\right]=\left[\begin{array}{cc}\begin{array}{cc}{r}_{1}& {r}_{4}\\ {r}_{2}& {r}_{5}\end{array}& \begin{array}{cc}{r}_{7}& {q}_{x}\\ {r}_{8}& {q}_{y}\end{array}\\ \begin{array}{cc}{r}_{3}& {r}_{6}\\ 0& 0\end{array}& \begin{array}{cc}{r}_{9}& {q}_{z}\\ 0& 1\end{array}\end{array}\right]\left[\begin{array}{cc}\begin{array}{c}{l}_{y}\\ {m}_{y}\end{array}& \begin{array}{cc}{l}_{z}& {t}_{x}\\ {m}_{z}& {t}_{y}\end{array}\\ \begin{array}{c}{n}_{y}\\ 0\end{array}& \begin{array}{cc}{n}_{z}& {t}_{z}\\ 0& 1\end{array}\end{array}\right]\left[\begin{array}{c}{y}_{\mathrm{L}}\\ {z}_{\mathrm{L}}\\ 1\end{array}\right],$$
(4)

where \({{\varvec{P}}}_{\mathbf{L}}\) is the coordinate of a point in \({O}_{\mathrm{L}}{Y}_{\mathrm{L}}{Z}_{\mathrm{L}}\), and \({{\varvec{P}}}_{0}\) is the coordinate of the same point in \({O}_{0}{X}_{0}{Y}_{0}{Z}_{0}\).

3 Calibration of \({{\varvec{T}}}_{\text 6}^{{\varvec{L}}}\)

In Eqs. (3) and (4), the parameters in \({{\varvec{T}}}_{0}^{6}\) are directly read from the articulated arm CMM, while the parameters in \({{\varvec{T}}}_{6}^{{\varvec{L}}}\) are unknown and need to be calibrated. \(({y}_{L},{z}_{L})\) is given by the laser line sensor, which is the coordinate of a point in \({O}_{\mathrm{L}}{Y}_{\mathrm{L}}{Z}_{\mathrm{L}}\), and \(({{x}_{0},y}_{0},{z}_{0})\) is the coordinate of the same point in \({O}_{0}{X}_{0}{Y}_{0}{Z}_{0}\). If \({{\varvec{T}}}_{0}^{6}\), \({{\varvec{T}}}_{6}^{{\varvec{L}}}\) and \(({y}_{L},{z}_{L})\) are all determined, \(({{x}_{0},y}_{0},{z}_{0})\) can be worked out.

\({{\varvec{T}}}_{6}^{{\varvec{L}}}\) and \({{\varvec{P}}}_{0}\) are the unknown parameters in Eq. (3). If \(({{x}_{0},y}_{0},{z}_{0})\) is always the same point during the process of calibration of \({{\varvec{T}}}_{6}^{{\varvec{L}}}\), the total number of unknown parameters in Eq. (4) is twelve, otherwise this number of unknown parameters in Eq. (4) is uncertain.

The calibration process is to build some sets of \({{\varvec{T}}}_{0}^{6}\) and \(({y}_{\mathrm{L}},{z}_{\mathrm{L}})\), which are then substituted into Eq. (4) to establish an equations set that further solves \({{\varvec{T}}}_{6}^{{\varvec{L}}}\) and \(({{x}_{0},y}_{0},{z}_{0})\). To ensure that \(\left({{x}_{0},y}_{0},{z}_{0}\right)\) does not change with the alternation of \({{\varvec{T}}}_{0}^{6}\) and \(({y}_{\mathrm{L}},{z}_{\mathrm{L}})\), a fixed point in \({O}_{0}{X}_{0}{Y}_{0}{Z}_{0}\) should be measured. In this paper when a fixed point is measured using the sensor, the measured \(({y}_{\mathrm{L}},{z}_{\mathrm{L}})\) in \({O}_{\mathrm{L}}{Y}_{\mathrm{L}}{Z}_{\mathrm{L}}\) and \({{\varvec{T}}}_{0}^{6}\) are defined as a “conjugate pair”. In principle, four conjugate pairs are sufficient to sovle the twelve unknown parameters. On the other hand, as \({O}_{\mathrm{L}}{Y}_{\mathrm{L}}{Z}_{\mathrm{L}}\) is an orthogonal coordinate frame, three constrains can be picked up from Eq. (4):

$$\left\{\begin{array}{l}{l}_{y}^{2}+{m}_{y}^{2}+{n}_{y}^{2}=1, \\ {l}_{z}^{2}+{m}_{z}^{2}+{n}_{z}^{2}=1, \\ {l}_{y}{l}_{z}+{m}_{y}{m}_{z}+{n}_{y}{n}_{z}=0.\end{array}\right.$$
(5)

Because of the nonlinearity of Eq. (5), using only these conditions to solve twelve unknown parameters will give a non-stable solution, and the accuracy of the solution can be affected seriously by the errors of conjugate pairs. In order to avoid these problems, more conjugate pairs should be established. Therefore, the calculation of \({{\varvec{T}}}_{6\boldsymbol{ }}^{{\varvec{L}}}\) becomes a non-linear constrained least-square optimization problem.

$$F=\sum_{i=1}^{n}{\left|{{\varvec{P}}}_{0{\varvec{i}}}-{{\varvec{T}}}_{0}^{6}{{\varvec{T}}}_{6}^{{\varvec{L}}}{{\varvec{P}}}_{{\varvec{L}}{\varvec{i}}}\right|}^{2}.$$
(6)

4 Conjugate Pairs Identification

In the calibration process, how to get “conjugate pairs” is the key problem. To solve this problem, a fixed point is measured several times by the sensor at different coordinates \(({y}_{\mathrm{L}},{z}_{\mathrm{L}})\) from different directions. In practice, it is difficult to project the laser stripe onto a fixed point by manually controlling the sensor.

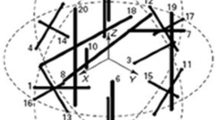
Usually, the center coordinate of a sphere can always be found by sphere fitting using the measured points on the surface of the sphere. Apart from sphere fitting, the center of the sphere can also be obtained by circle fitting if the laser plane passes through the sphere center. In this paper, a sphere is scanned with many lines captured as demonstrated in Figure 3, and the 2D data points on each line are applied to fit a circle. If the laser lines are dense enough, the circle with biggest radius would be corresponding to the position of the AACMM, where the laser plane passes through the center of the sphere. Fixed-point measurements by the laser line sensor can be therefore achieved. At the meantime, \({{\varvec{T}}}_{0}^{6}\) (AACMM position) and the center of the sphere \(({y}_{\mathrm{L}},{z}_{\mathrm{L}})\), i.e., a “conjugate pair” is obtained.

Figure 3
figure 3

(a) Scanning a sphere and fitting circle using the 2D points on the laser line, (b) Center of the circle with biggest radius correspongding to the center of the sphere

Full size image

After calibration, the measurement accuracy should be consistent with any AACMM coordinate and sensor value within their working ranges. Therefore, in the process of calibration each axis of the arm should be rotated within its range as large as possible. The laser plane intersects the sphere with different working region as shown in Figure 4. By substituting these conjugate pairs into Eq. (6), the twelve unknown parameters can be worked out.

Figure 4
figure 4

Different coordinates of the sphere center in the laser plane for building “conjugate pairs”

Full size image

It is important to note that the center of the sphere obtained in Figure 3 is not perfectly accurate. This is because that the scanning of the sphere is a handheld operation, and it would be difficult to manually maintain the constancy of both scanning speed and sensor orientation. On the other hand, since the sampling of the lines on the sphere is not continuous, the ground truth circle line corresponding to the biggest radius may not be captured. These inaccuracies in fixed-point measurements could cause errors in obtained conjugate pairs, thereby leading to errors in resultant \({\boldsymbol{ }{\varvec{T}}}_{6}^{{\varvec{L}}}\).

5 Searching the Optimal Solution of \({{\varvec{T}}}_{\text 6}^{{\varvec{L}}}\)

In Figure 3(b), the center of the circle with biggest radius corresponds to the center of the sphere. However, as mentioned in Section 4, it is difficult to get the circle that exactly passes through the center of the ball, which suggests that the \({{\varvec{T}}}_{6}^{{\varvec{L}}}\) obtained might not be an exact solution.

To find the accurate result of \({{\varvec{T}}}_{6}^{{\varvec{L}}}\), a searching optimization approach is proposed. Firstly, the form of \({{\varvec{T}}}_{6}^{{\varvec{L}}}\) is changed by reducing number of parameters in order to improve the efficiency of the search algorithm. In principle, the direction vectors \((\begin{array}{ccc}{l}_{y}& {m}_{y}& {n}_{y}\end{array})\) and \((\begin{array}{ccc}{l}_{z}& {m}_{z}& {n}_{z}\end{array})\) in \({{\varvec{T}}}_{6}^{{\varvec{L}}}\) can be expressed using three rotation angles. The rotation angles of \({O}_{\mathrm{L}}{Y}_{\mathrm{L}}{Z}_{\mathrm{L}}\) around three axes of \({O}_{6}{X}_{6}{Y}_{6}{Z}_{6}\) can be considered as \(\alpha\),\(\beta\) and \(\gamma\). Eq. (7) gives the detailed rotation matrix. Since \({Y}_{\mathrm{L}}\) and \({Z}_{\mathrm{L}}\) in \({O}_{\mathrm{L}}{Y}_{\mathrm{L}}{Z}_{\mathrm{L}}\) corresponds to \({Y}_{6}\) and \({Z}_{6}\) in \({O}_{6}{X}_{6}{Y}_{6}{Z}_{6}\), from Eqs. (2) and (7), a nonlinear equation set can be established in the form of Eq. (8). By solving this equation set, the rotation angle \(\alpha\),\(\beta\) and \(\gamma\) can be worked out, which reduces the number of the parameters in \({{\varvec{T}}}_{6}^{{\varvec{L}}}\) from nine to six.

$$\left[\begin{array}{ccc}\mathrm{cos}\beta \mathrm{cos}\gamma & -\mathrm{cos}\beta \mathrm{sin}\gamma & \mathrm{sin}\beta \\ \mathrm{sin}\alpha \mathrm{sin}\beta \mathrm{cos}\gamma +\mathrm{cos}\alpha \mathrm{sin}\gamma & -\mathrm{sin}\alpha \mathrm{sin}\beta \mathrm{sin}\gamma +\mathrm{cos}\alpha \mathrm{cos}\gamma & -\mathrm{sin}\alpha \mathrm{cos}\beta \\ -\mathrm{cos}\alpha \mathrm{sin}\beta \mathrm{cos}\gamma & \mathrm{cos}\alpha \mathrm{sin}\beta \mathrm{sin}\gamma +\mathrm{sin}\alpha \mathrm{cos}\gamma & \mathrm{cos}\alpha \mathrm{cos}\beta \end{array}\right],$$
(7)
$$\left\{\begin{array}{c}\begin{array}{c}{l}_{y}=-\mathrm{cos}\beta \mathrm{sin}\gamma , \\ {m}_{y}=-\mathrm{sin}\alpha \mathrm{sin}\beta \mathrm{sin}\gamma +\mathrm{cos}\alpha \mathrm{cos}\gamma ,\end{array}\\ \begin{array}{c}{n}_{y}=\mathrm{cos}\alpha \mathrm{sin}\beta \mathrm{sin}\gamma +\mathrm{sin}\alpha \mathrm{cos}\gamma , \\ {l}_{z}=\mathrm{sin}\beta , \end{array}\\ \begin{array}{c}{m}_{z}=-\mathrm{sin}\alpha \mathrm{cos}\beta , \\ {n}_{z}=\mathrm{cos}\alpha \mathrm{cos}\beta . \end{array}\end{array}\right.$$
(8)

As shown in Figure 5, the parameters \({t}_{x}\), \({t}_{y}\), \({t}_{z}\) solved in Section 4 and \(\alpha\), \(\beta\), \(\gamma\) solved from Eq. (8) are taken as initial values. The search process is to find the optimal results \(opt\_{t}_{x}\), \(opt\_{t}_{y}\), \(opt\_{t}_{z}\), \(opt\_\alpha\), \(opt\_\beta\) and \(opt\_\gamma\) from –range to +range. As long as the range setting is reasonable, the optimal value must be within this range. The green dot in the figure are the optimal results.

Figure 5
figure 5

Schematic diagram of initial value, search range and optimal value

Full size image

The search process is implemented through six-layer loops:

figure a

Where \({t}_{xref}\), \({t}_{yref}\), \({t}_{zref}\), \({\alpha }_{ref}\), \({\beta }_{ref}\), \({\gamma }_{ref}\) are the initial value of \({t}_{x}\), \({t}_{y}\), \({t}_{z}\), \(\alpha\), \(\beta\), \(\gamma\). Each parameter is changed from the corresponding initial value by small steps \({\Delta }_{tx}\), \({\Delta }_{ty}\), \({\Delta }_{tz}\), \({\Delta }_{\alpha }\), \({\Delta }_{\beta }\), \({\Delta }_{\gamma }\) in the six loops. All points on the circle lines captured for calibration are used to fit a sphere. Sph_fit \({(t}_{x}\), \({t}_{y}\), \({t}_{z}\), \(\alpha\), \(\beta\), \(\gamma\)) is the function which transforms the 2D data points in \({O}_{\mathrm{L}}{Y}_{\mathrm{L}}{Z}_{\mathrm{L}}\) into 3D data points in \({O}_{0}{X}_{0}{Y}_{0}{Z}_{0}\) using a group of \({(t}_{x}\),\({t}_{y}\),\({t}_{z}\),\(\alpha\),\(\beta\),\(\gamma\)), fits sphere using the 3D data points, and computes the distance between each 3D point to the fitted surface. S is the sum of the distance between each 3D point and the fitted surface and \({\mathrm{S}}_{\mathrm{min}}\) is the smallest value of S. The parameters corresponding to \({\mathrm{S}}_{\mathrm{min}}\) are \(opt\_{t}_{x}\), \(opt\_{t}_{y}\), \(opt\_{t}_{z}\), \(opt\_\alpha\), \(opt\_\beta\) and \(opt\_\gamma\), which are searched optimal parameters.

In order to reduce the total search time, the search algorithm were executed several times in a coarse-to-fine manner. Firstly, the search algorithm is performed with a larger step size to find a set of optimal values. Then, by taking the optimal values as new initial values, a finer search algorithm is carried out using smaller steps. In Section 6.1, four rounds of search optimizations were performed. As shown in Table 1, in each search process, the cycles number corresponding to each variable is 11, that is, from −5 to + 5. The searching steps of \({t}_{x}\), \({t}_{y}\), \({t}_{z}\) gradually decreases from 0.625 to 0.005, while the search steps of \(\alpha\), \(\beta\), \(\gamma\) gradually changes from 0.125° to 0.001°.

Table 1 Steps of the six parameters in the searching algorithm
Full size table

In this study, 40 lines are obtained on the sphere, and the number of points on each line is about 25, so the total number of points on the sphere is about 1000. The number of cycles corresponding to each variable is 11. Using i7-CPU for search operation, the time of one search is about 20 s, and the total time of four searches is 80 s.

6 Experimental Studies

6.1 Calibration Result

The AACMM adopted in this paper is Romer 2028, with the working diameter 2800 mm, repeatability 0.025 mm (3 \(\upsigma\)), and length accuracy 0.066 mm (3 \(\upsigma\)). The laser line sensor is self-made with the working depth 80 mm, and line length 65 mm. The repeatability is 0.008 mm, the measuring accuracy is 0.045 mm, and the standard working distance is 90 mm.

According to the proposed calibration method, 40 lines on the sphere are captured from different directions. Using obtained 40 conjugate pairs, the parameters in Eq. (2) are computed as:

$$\left[\begin{array}{cc}\begin{array}{cc}{l}_{y} & {l}_{z}\end{array}& {t}_{x}\\ \begin{array}{cc}\begin{array}{c}{m}_{y}\\ {n}_{y}\\ 0\end{array}& \begin{array}{c}{m}_{z}\\ {n}_{z}\\ 0\end{array}\end{array}& \begin{array}{c}{t}_{y}\\ {t}_{z}\\ 1\end{array}\end{array}\right]=\left[\begin{array}{ccc}-0.997642& 0.0314107& 1.079\\ 0.0596228& -0.043697& -3.465\\ \begin{array}{c}-0.033985\\ 0\end{array}& \begin{array}{c}-0.998555\\ 0\end{array}& \begin{array}{c}-211.168\\ 1\end{array}\end{array}\right].$$
(9)

The 2D data points on 40 measured lines are then transformed into 3D data points by substituting Eq. (9) into Eq. (4), and the 3D data points are employed to fit a sphere. Figure 6 demonstrates the distance between each point and the fitted surface. The biggest distance from the points outside the sphere and inside the sphere to the fitted surface are 0.483 mm and 0.576 mm, respectively.

Figure 6
figure 6

Error of the sphere fitted using the 3D data points transformed by the calibration result before searching optimization

Full size image

To improve the accuracy of the parameters in \({{\varvec{T}}}_{6}^{{\varvec{L}}}\), the searching algorithm was executed four times. The cycle index of each loop is always fixed at 11, while the incremental steps for each time are listed in Table 1.

The optimized result of current iteration will be taken as a reference value for the next iteration. The final optimized parameters are

$$\left[\begin{array}{cc}\begin{array}{cc}{l}_{y} & {l}_{z}\end{array}& {t}_{x}\\ \begin{array}{cc}\begin{array}{c}{m}_{y}\\ {n}_{y}\\ 0\end{array}& \begin{array}{c}{m}_{z}\\ {n}_{z}\\ 0\end{array}\end{array}& \begin{array}{c}{t}_{y}\\ {t}_{z}\\ 1\end{array}\end{array}\right]=\left[\begin{array}{ccc}-0.997193& 0.0348994& 1.465\\ 0.0644936& -0.048820& -3.170\\ \begin{array}{c}-0.038018\\ 0\end{array}& \begin{array}{c}-0.998197\\ 0\end{array}& \begin{array}{c}-211.604\\ 1\end{array}\end{array}\right].$$
(10)

The 2D data points on the 40 lines are also transformed into 3D data points by substituting Eq. (10) into Eq. (4), and the 3D data points are employed to fit a sphere. In Figure 7, the biggest distance from the point outside the sphere and inside the sphere to the fitted surface are 0.175 mm and 0.142 mm, respectively. It can be noticed that the accuracy the parameters in \({{\varvec{T}}}_{6}^{{\varvec{L}}}\) is greatly improved after the searching optimization.

Figure 7
figure 7

Error of the sphere fitted using the 3D data points transformed by the calibration result after searching optimization

Full size image

6.2 Error Analysis

The spatial accuracy of the AACMM is 0.066 mm (3 \(\upsigma\)), and the accuracy of the laser line sensor is 0.045 mm, which is usually considered as the error of a single scanned point. In this study, we test this error on a Hexagon bridge CMM. After the sensor is mounted on the CMM, the extrinsic parameters are calibrated. A sphere with the nominal radius 19.875 mm is scanned using the sensor. The scanned 3D data points are then applied to fit sphere with a fitted radius at 19.870 mm. The error between the nominal radius and the fitted radius is 0.005 mm, and the fitted radius is the result of all scanning point operations. We define this error as the systematic error of the sensor. While the biggest distance from the 3D points to the fitted sphere surface is 0.045 mm, it is regarded as the random error of the sensor.

The error of the AACMM and the laser sensor can cause errors in the process of calibration. Even if a fixed point is exactly measured, the errors in \({{\varvec{T}}}_{0}^{6}\) and \(({y}_{\mathrm{L}},{z}_{\mathrm{L}})\) can also cause errors in \({{\varvec{T}}}_{6}^{{\varvec{L}}}\). Since \(({y}_{\mathrm{L}},{z}_{\mathrm{L}})\) is achieved by circle fitting, the error of \(({y}_{\mathrm{L}},{z}_{\mathrm{L}})\) is much smaller than the sensor error, which suggests that the error of the AACMM is the main error source of calibration error. In summary, there exist four types of errors in this system, which are defined as follows:

\({err}_{A}\): Error of the AACMM,

\({err}_{SS}\): The systematic error of the laser sensor,

\({err}_{SR}\): Random error of the laser sensor,

\({err}_{C}\): Calibration error of the system.

The maximum total error of the system is

$$\begin{aligned} {err}_{Total}={err}_{A}+{err}_{SS}+{err}_{SR}+{err}_{C} &{=0.066+0.005+0.045+err}_{C}. \end{aligned}$$
(11)

Since the magnitude of \({err}_{C}\) is unknown, \({err}_{Total}\) cannot be directly calculated.

6.3 Accuracy Test

The measuring accuracy of the system is tested by scanning a plate and a reference sphere. The plate was scanned five times from different directions. For each scanning, only one or two joints of the AACMM were rotated, while other joints were kept fixed as far as possible. Firstly, the points on each scanned data patch are used to fit a plane, and the biggest distance from the points on each data patch to the corresponding fitted plane is defined as \({D}_{PPi}\) (i = 1, 2, 3, 4, 5), listed in Table 2. Then, the points on all five data patches are together utilized to fit a plane, and the biggest distance from the points on five data patches to the fitted plane is 0.193 mm.

Table 2 Biggest distance from the points on each data patch to the fitted plane
Full size table

The measurement error mainly depends on the error of the arm and the sensor, and the error of arm comes from the position errors of the six axes. When scanning the plate from one direction, only one or two joints of the AACMM were rotated with other joints kept fixed. Thus, the biggest distance from the points to the fitted plane is majorly affected by the error of the one or two joints and the sensor. On the other hand, the position error of the entire data patch is mainly caused by the position errors of other axes. If all five data patches are applied to fit a plane, the fitted error could be attributed to the position errors of the six axes and the sensor. As a result, fitted error of five data patches (around 0.193 mm) is significantly greater than errors in single data patch \({D}_{PPi}\).

The sphere was also scanned from five directions. At each direction, only one or two joints of the AACMM were rotated. The points on the edge of each data patch have greater errors, thereby removed from the data patch using the software Surfacer V10.0. Five spheres were fitted using the remaining points on each data patch, defined as \({SPH}_{i}\) (i = 1, 2, 3, 4, 5). In Table 3, \({R}_{i}\) represents the fitted radius, and \({D}_{PSi}\) (i = 1, 2, 3, 4, 5) gives the biggest distance from the points on each data patch to the corresponding fitted sphere. Then the points on five data patches are utilized to fit a sphere, defined as \({SPH}_{ALL}\). The biggest distance from the points to the fitted sphere is 0.219 mm, which is greater than \({D}_{PSi}\) in Table 3. The distances between the center of \({SPH}_{ALL}\) and the centers of \({SPH}_{i}\) are also given in Table 3.

Table 3 Biggest distance from the points on each data patch to the fitted sphere (mm)
Full size table

It can be seen from the above test:

  1. (1)

    According to Eq. (11), total errors of the system are 0.193 mm and 0.219 mm, corresponding to scanning a plate and a sphere from five directions, respectively.

  2. (2)

    In Table 3, \(\left|{SPH}_{ALL}-{SPH}_{i}\right|\) can represent the error between two data patches. Apparently, this error is caused by the position errors of different joints of the AACMM. Hence, \({err}_{A}\) is its main error source.

  3. (3)

    The \({R}_{i}\) in Table 3 is close to the nominal radius of the sphere, since \({R}_{i}\) is the radius of the fitted sphere by the data scanned from one direction. In this case, \({err}_{A}\) is much smaller than 0.066 mm, and \({err}_{SR}\) is greatly reduced after sphere fitting. Therefore, \({err}_{C}\) and \({err}_{SS}\) are the main error sources in \({R}_{i}\).

Typically, when measuring a complicated part, all joints are required to be rotated. In the above test, the total error of measuring a sphere is 0.219 mm. This error can be regarded as the measuring error of this system, since when scanning the sphere from five directions, all of the joints of the AACMM are rotated.

It can be found that the error of the AACMM is the main error source. It is worth noting that the calibration error is also an error source, but its magnitude cannot be found out.

7 Applications

To test the performance of this system, a model shown in Figure 8 is designed and manufactured with complex features of spheres, hole, square holes, and quadrangulars. Complete scanning of concave and convex semis-spheres can be achieved relatively easily. The four quadrangulars and the cylinder can be also completely measured from many directions. For circular and square holes, only the areas around the upper inside surface are scanned, as the deep areas cannot be accessed even though all the arms are rotated to try to find a suitable sensor orientation. Figure 9 shows the shaded form of the scanned data processed in Geomagic Studio 12. In this figure, there is no data on the deep area of the circular hole and the bottom of the square holes. As described in Section 1, the working principle of the sensor is based on triangulation method, which suggests that the projected light cannot be received by the CCD camera if there exists sheltering. In this test, when scanning the hole, it is the hole itself which shelters the reflected light. Therefore, in principle, the sensor cannot scan the deep area of a hole, even though the AACMM provides adequate flexibility to the sensor. To sum up, most features of the model are completely measured using the system. This indicates that the system is flexible and facilitate to measure a part from any necessary direction.

Figure 8
figure 8

Picture of the model with specially fabricated complex features

Full size image
Figure 9
figure 9

The shaped form of the measured data and the indication of some areas where cannot be scanned

Full size image

8 Conclusions

This paper presents a flexible scanning method by integrating laser line sensors with articulated arm coordinate measuring machines. For a commercial articulated arm CMM, the transformation from the touch probe coordinate frame to the AACMM base coordinate frame can be directly accessed. By establishing the transformation from the 2D sensor coordinate frame into the sixth coordinate frame, the 2D data can be transformed into 3D data in the AACMM base coordinate frame. In order to solve the transformation model, “conjugate pairs” are introduced and determined by fixing the scanned points. In this study, a sphere is scanned with the data points fitted to a circle. The particular circle with a biggest radius is then used to locate the laser plane that passes through the sphere center. To improve the accuracy of the transformation model, a searching approach is proposed to find the optimal solution. Experimental studies revealed that the measurement error is about 0.2 mm, which consist of the error of the AACMM, the sensor error, and the calibration error. The error of the AACMM is identified to be the main error source of the system, which leads to errors in conjugate pairs during calibration, as well as measurement errors during scanning. Its value varies with the number of the rotated axes, i.e., increasing the number of rotation axes could result in a greater error of the AACMM.

Therefore, when scanning an area of a part, the AACMM should be smoothly moved by rotating one or two arms. When the viewpoint of the sensor is not suitable for scanning, the orientation of the sensor should be changed by rotating other axes of the AACMM.