1 Introduction

The bus is prone to lateral instability under special driving conditions such as emergency turning on slippery roads because of the characteristics of large quality, high center of gravity and narrow wheelbase [1–4]. If this lateral instability phenomenon cannot be predicted accurately and be timely and effectively controlled, it will eventually lead to bus rollover accident [5]. Therefore, it is of great significance to study the active stabilization control (ASC) strategy of bus when turning on slippery roads [6–8]. In order to improve the vehicle curve driving stability and safety on slippery roads, the yaw stability control (YSC) system has been applied to achieve the vehicle ASC function [9]. Leonardo et al. designed a direct yaw moment controller based on the combination of feedforward and feedback [10]. Chen et al. determined the desired vehicle yaw moment by means of sliding mode control [11]. Avesta et al. proposed an active controller system to supervise the vehicle lateral dynamics and then designed a differential braking yaw moment controller [12]. Ding et al. proposed a YSC strategy for in-wheel electric vehicles by using the sliding mode and nonlinear disturbance observer methods [13, 14]. Although all the above studies have made outstanding contributions to the YSC system, the vehicle tire model, which shows high nonlinearity in the operation process of the ASC system [15–17], is not handled effectively. Even though some studies have established the vehicle dynamics model considering the tire nonlinear characteristics, the tire model adopted cannot effectively reflect the coupling relationship between the tire longitudinal force and lateral force, which will lead to the derived YSC strategy cannot achieve good performance in practical applications.

On the basis of the accurate vehicle model, the effectiveness of the YSC control algorithm can then be guaranteed. In the existing literatures, several methodologies have been applied to improve the vehicle YSC performance [18–21]. Among them, the sliding mode control (SMC) method has been widely applied due to its strong robustness against uncertainties and disturbance. However, the traditional SMC method still has drawbacks that limit its performance in real applications, thus much effort has been devoted to finding effective solutions to eliminate those drawbacks [22–24]. Based on the conclusions of the existing research, the adaptive nonsingular fast terminal sliding mode (ANFTSM) control method, which can both obtain fast finite time convergence and chattering elimination [25, 26], is applied in this work to effectively solve the direct yaw moment calculation problem of bus. As is known to all, the obtained direct yaw moment needs to be further achieved by distributing the braking forces of four wheels, thus the solution of the optimal allocation problem of the tire braking forces is also crucial. In Refs. [27–29], several algorithms have been proposed to achieve well allocation of the tire forces. However, we have found that the allocation algorithms used in the current research still take a long time to calculate, thus the real-time control, which is very important for the YSC system, cannot be guaranteed reliably.

In this paper, a novel YSC scheme which both includes a new tire model applied in the vehicle system modeling, a new control algorithm used to calculate the direct yaw moment and a new method used to guarantee the solving efficiency of the tire forces allocation is presented. Therefore, the main contributions of this research are as follows:

  • The STI tire model, which can effectively reflect the coupling relationship between the tire longitudinal force and the tire lateral force, is established based on experimental data and firstly adopted in the bus YSC system design.

  • The ANFTSM control algorithm, which has the merits of high robustness against uncertainty and external disturbance, fast transient response and finite time convergence, is firstly applied to solve the direct yaw moment calculation problem of the bus effectively.

  • The robust least-squares control allocation method, which can effectively guarantee the solving efficiency of complex optimization problem like the tire longitudinal forces allocation of each tire and restrain the uncertainty in control distribution effectiveness matrix, is firstly used to solve the optimal allocation problem of the tire forces.

The rest of this paper is organized as follows: Section 2 presents the establishment of the STI tire model based on experimental data firstly, and on this basis, a 7-DOF nonlinear dynamics model of bus is further introduced. In Section 3, the YSC strategy design based on ANFTSM method is provided. Section 4 shows how to solve the optimal allocation problem of the tire forces by using the robust least-squares allocation method. In Section 5, the TruckSim-Simulink co-simulation results are presented to verify the feasibility, effectiveness and practicality of the proposed YSC approach. Finally, the conclusions and future works are given in Section 6.

2 System Modeling

2.1 STI Tire Model

STI tire model is proposed by an American company, which named as “Systems Technologies Inc.” [30]. Compared with other tire models, the STI tire model can not only describe the tire nonlinear mechanical characteristics accurately, but also reflect the coupling relationship between the tire longitudinal force and the tire lateral force exactly [31], thus it is very suitable for the bus YSC system design in this study. To achieve the description of the STI tire model, an important variable must be defined firstly, i.e., the composite slip coefficient σ, which is expressed as [32]:

$$\sigma = \frac{{\uppi a_{p}^{2} \sqrt {k_{\alpha }^{2} \tan^{2} \alpha + k_{s}^{2} (s/1 - s)^{2} } }}{{8\mu F_{z} }},$$
(1)

where ap denotes the length of the tire contact patch, kα denotes the tire lateral stiffness, ks denotes the tire longitudinal stiffness, α denotes the tire sideslip angle, s denotes the tire longitudinal slip coefficient, μ is the road adhesion coefficient and Fz is the tire vertical load. In Eq. (1), the length of the tire contact patch can be further defined as [33]:

$$a_{p} = 0.0768\sqrt {F_{z} \cdot F_{zt} } /T_{w} (T_{p} + 5),$$
(2)

where Fzt is the tire design load, Tw is the tire width, Tp is the tire pressure. The tire lateral stiffness kα and the tire longitudinal stiffness ks in Eq. (1) can be measured by experimental tests. On this basis, to further consider the saturation effect of the tire longitudinal stiffness, a modified tire longitudinal stiffness ksm is defined as:

$$k_{sm} = k_{s} + (k_{\alpha } - k_{s} )\sqrt {\sin^{2} \alpha + \cos^{2} \alpha } ,$$
(3)

Based on the defined composite slip coefficient σ, a tire force saturation function can then be defined as:

$$f(\sigma ) = \frac{{C_{1} \sigma^{3} + C_{2} \sigma^{2} + (4/\uppi )\sigma }}{{C_{1} \sigma^{3} + C_{3} \sigma^{2} + C_{4} \sigma + 1}},$$
(4)

where C1, C2, C3 and C4 are the fixed coefficients, which can be obtained by fitting the experimental data. The function f (σ) is consistent with the mechanical properties of the tire force friction circle, thus it can reflect the tire force saturation characteristics effectively. Then, on the basis of the above equations, the standardized expressions of the tire longitudinal force and the tire lateral force of the STI tire model can be respectively described as:

$$\left\{ \begin{aligned} F_{x} & = \frac{{f(\sigma )k_{sm} s}}{{\sqrt {k_{\alpha }^{2} \tan^{2} \alpha + k_{sm}^{2} s^{2} } }}\mu F_{z} , \\ F_{y} & = \frac{{f(\sigma )k_{\alpha } \tan \alpha }}{{\sqrt {k_{\alpha }^{2} \tan^{2} \alpha + k_{sm}^{2} s^{2} } }}\mu F_{z} + Y_{\gamma } \gamma , \\ \end{aligned} \right.$$
(5)

where Fx represents the tire longitudinal force, Fy represents the tire lateral force, γ represents the tire camber angle, Yγ represents the tire camber coefficient, which is used to reflect the influence of the camber angle on the tire lateral force. According to Eq. (5), the coupling relationship between the tire longitudinal force and the tire lateral force under compound driving conditions can be reflected exactly.

To obtain the experimental data which can accurately reflect the nonlinear mechanical characteristics of the tire, the experimental tests are conducted through a flat-plate bench assisted by the KH Automotive Technologies (Guangzhou) Co., Ltd. Figure 1 shows the experimental setup of the tire mechanical characteristics tests.

Figure 1
figure 1

Experimental setup of the tire mechanical characteristics tests

Full size image

Based on the experimental data, the STI tire model parameters can then be fitted. According to the expressions of the tire forces, it is obvious that the fitting of the tire model parameters is actually to determine the fixed coefficients C1, C2, C3 and C4 in Eq. (4). Before achieving the fitting of the fixed coefficients, the tire lateral stiffness and the tire longitudinal stiffness need to be firstly measured by experimental tests. According to the test results, the tire lateral stiffness is finally determined as − 66463 N/rad and the tire longitudinal stiffness is finally determined as 84000 N/rad. On this basis, the value of the composite slip coefficient σ can then be calculated for different tire vertical loads, tire sideslip angles and tire longitudinal slip coefficients. Meanwhile, according to Eq. (5) and the experimental results of the tire forces, the value of the tire force saturation function can also be determined. Therefore, by combining the value of the composite slip coefficient and the value of the tire force saturation function, the fixed coefficients C1, C2, C3 and C4 can then be determined by using the curve fitting function in the Origin software. Take the case of the tire bench test under low road adhesion coefficient, the values of the four fixed coefficients C1, C2, C3 and C4 are finally determined as 10, 8.98, 10 and 0 respectively.

To verify the fitting accuracy, the comparison between the experimental results and the simulation results of the tire force saturation function is shown in Figure 2. It can be seen that the experimental results of the tire force saturation function are all distributed around the fitting curve, which shows that the fitting results are highly consistent with the experimental results. Figure 3 further shows the fitting residual of the tire force saturation function. It can be seen that most of the absolute values of the fitting residual are less than 0.15, which indicates that the fitting of the tire force saturation function in this work is trustworthy. Note that there are two other parameters that can also show the fitting effect, i.e., the R-squared and the adjusted R-squared. However, because of the residual diagram can show the fitting effect more intuitively, thus we only provide the fitting residual results in this paper.

Figure 2
figure 2

Comparison between the experimental results and the simulation results of the tire force saturation function

Full size image
Figure 3
figure 3

Fitting residual of the tire force saturation function

Full size image

2.2 Bus Dynamics Model

In this section, a 7-DOF bus dynamics model is established based on previous literatures [34–36], which includes the longitudinal motion, lateral motion, yaw motion and the rotational dynamics of four wheels. According to Newton’s theorem, the dynamic equations of the bus longitudinal, lateral and yaw motions can be established as follows [37]:

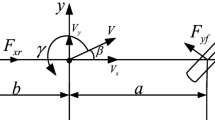
$$\left\{ \begin{aligned} m(\dot{v}_{x} - r \cdot \dot{v}_{y} ) & = (F_{xfl} + F_{xfr} )\cos \delta \\ & \quad - (F_{yfl} + F_{yfr} )\sin \delta + F_{xrl} + F_{xrr} , \\ m(\dot{v}_{y} + r \cdot v_{x} ) & = (F_{xfl} + F_{xfr} )\sin \delta \\ & \quad + (F_{yfl} + F_{yfr} )\cos \delta + F_{yrl} + F_{yrr} , \\ I_{z} \cdot \dot{r} & = [(F_{xfl} + F_{xfr} )\sin \delta + (F_{yfl} + F_{yfr} )\cos \delta ]a \\ & \quad + [(F_{xfr} - F_{xfl} )\cos \delta + (F_{yfl} - F_{yfr} )\cos \delta ]\frac{{t_{w1} }}{2} \\ & \quad + (F_{xrr} - F_{xrl} )\frac{{t_{w2} }}{2} - (F_{yrl} + F_{yrr} )b, \\ \end{aligned} \right.$$
(6)

where Fxij and Fyij are the tire longitudinal and lateral forces respectively, the first subscript i = f or r represent front and rear axles respectively, and the second j = l or r denote left and right wheels. m is the vehicle weight, vx and vy are the longitudinal and lateral velocities of the vehicle, δ is the front wheel steering angle, a is the distance from the center of the vehicle to the front axle, b is the distance from the center to the rear axle, tw1 and tw2 are the wheel bases of the front and rear axles, r is the vehicle yaw rate. Note that the tire longitudinal and lateral forces in Eq. (6) are calculated by the STI tire model which has been established in the previous section. To represent the lumped disturbance which includes the system uncertainties and external disturbance, a variable D(t) which is usually assumed to be a bounded function is defined as follows:

$$D(t) \le \delta_{0} ,$$
(7)

where δ0 is the upper bound of D(t).

In addition, the dynamic equations which represent the rotation of the four wheels are given by:

$$J \cdot \dot{\omega }_{k} = T - F_{xij} \cdot R,$$
(8)

where J is the moment of inertia of the wheel, ωk (k = 1, 2, 3, 4) represent the angular velocity of the four wheels, R is the wheel radius, Tk (k = 1, 2, 3, 4) represent the braking torques acted on the four wheels.

To more accurately reflect the vehicle load transfer effect during vehicle driving process, the tire vertical load can be calculated by combining the static tire vertical load and the load transfer effect caused by longitudinal and lateral acceleration. Thus, the related equations are expressed as Ref. [38]:

$$\left\{ \begin{aligned} F_{zfl} & = mg\frac{b}{2l} - m\dot{v}_{x} \frac{{h_{g} }}{2l} - m\dot{v}_{y} \frac{{h_{g} }}{{t_{w1} }} \cdot \frac{b}{l}, \\ F_{zfr} & = mg\frac{b}{2l} - m\dot{v}_{x} \frac{{h_{g} }}{2l} + m\dot{v}_{y} \frac{{h_{g} }}{{t_{w1} }} \cdot \frac{b}{l}, \\ F_{zrl} & = mg\frac{a}{2l} + m\dot{v}_{x} \frac{{h_{g} }}{2l} - m\dot{v}_{y} \frac{{h_{g} }}{{t_{w1} }} \cdot \frac{a}{l}, \\ F_{zrr} & = mg\frac{a}{2l} + m\dot{v}_{x} \frac{{h_{g} }}{2l} + m\dot{v}_{y} \frac{{h_{g} }}{{t_{w1} }} \cdot \frac{a}{l}, \\ \end{aligned} \right.$$
(9)

where hg is the height of the center of the bus, l is the length of the bus. In addition, the calculation of the tire sideslip angle of each wheel is given as follows:

$$\left\{ \begin{aligned} \alpha_{fl} & = \delta - \arctan \left( {\frac{{v_{y} + ar}}{{v_{x} - {{t_{w1} r} \mathord{\left/ {\vphantom {{t_{w1} r} 2}} \right. \kern-\nulldelimiterspace} 2}}}} \right), \\ \alpha_{rl} & = \delta - \arctan \left( {\frac{{v_{y} + ar}}{{v_{x} + {{t_{w1} r} \mathord{\left/ {\vphantom {{t_{w1} r} 2}} \right. \kern-\nulldelimiterspace} 2}}}} \right), \\ \alpha_{rl} & = - \arctan \left( {\frac{{v_{y} - br}}{{v_{x} - {{t_{w2} r} \mathord{\left/ {\vphantom {{t_{w2} r} 2}} \right. \kern-\nulldelimiterspace} 2}}}} \right), \\ \alpha_{rl} & = - \arctan \left( {\frac{{v_{y} - br}}{{v_{x} + {{t_{w2} r} \mathord{\left/ {\vphantom {{t_{w2} r} 2}} \right. \kern-\nulldelimiterspace} 2}}}} \right). \\ \end{aligned} \right.$$
(10)

Based on the above calculations for bus driving states, the wheel center speed of each wheel can then be obtained as follows [39, 40]:

$$\left\{ \begin{aligned} v_{t\_fl} & = \left( {v_{x} - \frac{{t_{w1} }}{2}r} \right)\cos \delta + (v_{y} + ar)\sin \delta , \\ v_{t\_fr} & = \left( {v_{x} + \frac{{t_{w1} }}{2}r} \right)\cos \delta + (v_{y} + ar)\sin \delta , \\ v_{t\_rl} & = v_{x} - \frac{{t_{w2} }}{2}r{\kern 1pt} ;\;v_{t\_rr} = v_{x} + \frac{{t_{w2} }}{2}r. \\ \end{aligned} \right.$$
(11)

Since the angular velocity and the wheel center speed of the four wheels have been calculated, the tire longitudinal slip coefficient can then be given by:

$$\left\{ \begin{aligned} s_{fl} & = \frac{{\omega_{fl} R - v_{t\_fl} }}{{v_{t\_fl} }},\;s_{fr} = \frac{{\omega_{fr} R - v_{t\_fr} }}{{v_{t\_fr} }}, \\ s_{rl} & = \frac{{\omega_{rl} R - v_{t\_rl} }}{{v_{t\_rl} }},\;s_{rr} = \frac{{\omega_{rr} R - v_{t\_rr} }}{{v_{t\_rr} }}. \\ \end{aligned} \right.$$
(12)

According to Eqs. (9)‒(12), it can be seen that the tire vertical load, the tire sideslip angle and the tire longitudinal slip coefficient can be calculated by the vehicle model in real time, thus on this basis, the tire longitudinal and lateral forces can be obtained through the established STI tire model, which lays an important foundation for the following YSC system design

3 YSC System Design Based on ANFTSM

3.1 System Overall Control Structure

The main control objective of the YSC system is to ensure that the bus driving states can follow the target values calculated by the reference model when tracking curve paths on slippery roads. In this driving condition, the main challenge for calculating an optimal direct yaw moment is that the tire-road friction force cannot both meet the requirements of tire longitudinal and lateral forces. Therefore, the first objective of the YSC system is to calculate the optimal direct yaw moment by considering the coupling relationship between the tire longitudinal force and the tire lateral force. On this basis, an effective allocation algorithm should be adopted to distribute the braking forces of the four wheels, thus the optimal direct yaw moment can be achieved. In this paper, to verify the feasibility, effectiveness and practicality of the proposed YSC approach, the TruckSim vehicle model, which can accurately reflect the bus nonlinear dynamic characteristics, is used to conduct the co-simulation with Simulink. Based on the above descriptions, the system overall control structure can be shown in Figure 4.

Figure 4
figure 4

Hierarchical control framework

Full size image

3.2 YSC System Design

In this section, the ANFTSM control method is proposed to eliminate the uncertainty and disturbance in the bus YSC system design process. For general nonsingular fast terminal sliding mode (NFTSM) controller, the upper bound of disturbance is usually assumed to be known, nevertheless this assumption is difficult to be satisfied in practical application. Therefore, the ANFTSM is adopted in this paper to estimate and compensate the effects of lumped uncertainty, so as to improve the performance of the YSC control system. The block diagram of the ANFTSM control method presenting the control principle is shown in Figure 5.

Figure 5
figure 5

Control principle of ANFTSM

Full size image

In the first step, according to the definition of general NFTSM, the following first-order terminal sliding mode variable is defined as [41–43]:

$$s = e + k_{1} \left| e \right|^{{\alpha_{1} }} {\text{sign}}(e) + k_{2} \left| {\dot{e}} \right|^{{\beta_{1} }} {\text{sign}}(\dot{e}),$$
(13)

where k1 and k2 are positive constants,1 < β1 < 2 and α1 > β1 and sign(⋅) is the signum function, e represents the system tracking error, which is always expressed as:

$$\left\{ \begin{aligned} e & = c_{1} (\beta - \beta_{d} ) + (1 - c_{1} )(\varphi - \varphi_{d} ), \\ \dot{e} & = c_{1} (\dot{\beta } - \dot{\beta }_{d} ) + (1 - c_{1} )(r - r_{d} ), \\ \ddot{e} & = c_{1} (\ddot{\beta } - \ddot{\beta }_{d} ) + (1 - c_{1} )(\dot{r} - \dot{r}_{d} ), \\ \end{aligned} \right.$$
(14)

where c1 is the weight coefficient used to determine the control specific proportion-n of the vehicle slip angle and the yaw rate, φ is the vehicle yaw angle. On this basis, the time derivative of the sliding mode variable defined by Eq. (13) can be obtained as:

$$\begin{aligned} \dot{s} & = \dot{e} + \alpha_{1} k_{1} \left| e \right|^{\alpha - 1} \cdot \dot{e} + \beta_{1} k_{2} \left| {\dot{e}} \right|^{\beta - 1} \cdot \ddot{e} \\ & = \dot{e} + \alpha_{1} k_{1} \left| e \right|^{\alpha - 1} \cdot \dot{e} \\ & \quad + \beta_{1} k_{2} \left| {\dot{e}} \right|^{\beta - 1} \cdot \left[ {c_{1} (\ddot{\beta } - \ddot{\beta }_{d} ) + (1 - c_{1} )(\dot{r} - \dot{r}_{d} )} \right]. \\ \end{aligned}$$
(15)

By further transform the expression of the vehicle yaw motion in Eq. (6) as:

$$\dot{r} = \frac{1}{{I_{z} }}\left[ {\frac{{t_{w1} }}{2}(F_{yfl} - F_{yfr} )\sin \delta + a(F_{yfl} + F_{yfr} )\cos \delta - b(F_{yrl} + F_{yrr} ) + M_{z} + D(t)} \right],$$
(16)

where Mz is the direct yaw moment, which is expressed as:

$$\begin{aligned} M_{z} & = a(F_{xfl} + F_{xfr} )\sin \delta \\ & \quad - \frac{{t_{w1} }}{2}(F_{xfl} - F_{xfr} )\cos \delta - \frac{{t_{w2} }}{2}(F_{xrl} - F_{xrr} ). \\ \end{aligned}$$
(17)

The lumped uncertainty in the YSC system has been proposed in Eq. (16), and its upper bound can be defined as the polynomial of tracking error and its derivative, which is expressed as follows [44]:

$$\delta_{0} = a_{0} + a_{1} \left| e \right| + a_{2} \left| {\dot{e}} \right|,$$
(18)

where a0, a1 and a2 are positive constants.

Combing Eqs. (15)‒(17) without consideration of the uncertainty, the system control law can be expressed as:

$$\dot{e} + \alpha_{1} k_{1} \left| e \right|^{\alpha - 1} \cdot \dot{e}+ \beta_{1} k_{2} \left| {\dot{e}} \right|^{\beta - 1} \cdot \left\{ {c_{1} (\ddot{\beta } - \ddot{\beta }_{d} ) + (1 - c_{1} )\left[ {\frac{1}{{I_{z} }}(P + M_{z} ) - \dot{r}_{d} } \right]} \right\} = 0, \\$$
(19)

where

$$P = \frac{{t_{w1} }}{2}(F_{yfl} - F_{yfr} )\sin \delta + a(F_{yfl} + F_{yfr} )\cos \delta - b(F_{yrl} + F_{yrr} ).$$
(20)

By satisfying Eq. (19), the YSC equivalent control law can be derived as:

$$\tau_{eq} = \frac{{I_{z} }}{{1 - c_{1} }}\left[ {(1 - c_{1} )\dot{r}_{d} - c_{1} (\ddot{\beta } - \ddot{\beta }_{d} ) - \frac{1}{{\beta_{1} k_{2} }}\left| {\dot{e}} \right|^{{2 - \beta_{1} }} \cdot {\text{sign}}(\dot{e})\left( {1 + \alpha_{1} k_{1} \left| e \right|^{{\alpha_{1} - 1}} } \right)} \right] - P.$$
(21)

In order to reduce the influence of uncertainty on the control performance, an adaptive switching law is employed to estimate the parameters of the upper bound of system uncertainty, which is expressed as follows:

$$\tau_{asw} = \frac{{I_{z} }}{{1 - c_{1} }}[ - ks - (\hat{a}_{0} + \hat{a}_{1} \left| e \right| + \hat{a}_{2} \left| {\dot{e}} \right| + \eta ) \cdot {\text{sign}}(s)],$$
(22)

where η > 0 is a small positive number, k > 0 is the switching gain, \(\hat{a}_{0}\), \(\hat{a}_{1}\) and \(\hat{a}_{2}\) are the estimates of a0, a1 and a2 respectively and the parameters are updated by the following adaptive laws:

$$\left\{ \begin{aligned} \dot{\hat{a}}_{0} & = \mu_{0} \left| s \right| \cdot \left| {\dot{e}} \right|^{{\beta_{1} - 1}} , \\ \dot{\hat{a}}_{1} & = \mu_{1} \left| s \right| \cdot \left| e \right| \cdot \left| {\dot{e}} \right|^{{\beta_{1} - 1}} , \\ \dot{\hat{a}}_{2} & = \mu_{2} \left| s \right| \cdot \left| {\dot{e}} \right|^{{\beta_{1} }} , \\ \end{aligned} \right.$$
(23)

where μ0, μ1 and μ2 are arbitrary positive numbers. Therefore, by combining the equivalent control law and the adaptive control law, the overall control law of ANFTSM for the direct yaw moment is designed as follows:

$$M_{z} = \tau_{eq} + \tau_{asw} .$$
(24)

Based on the conclusions of the existing research, the YSC control law based on ANFTSM can effectively avoid the singular problems and ensure the fast convergence of the control system. In addition, based on Lyapunov theory, the proof process of the control system stability can be analyzed as follows [45].

Proof

The following Lyapunov functions are defined as:

$$V = \frac{1}{2}s^{2} + \beta_{1} k_{2} \sum\limits_{i = 0}^{2} {\frac{1}{{2\mu_{i} }}} (\hat{a}_{i} - a_{i} )^{2} .$$
(25)

The time derivative of V can then be obtained as:

$$\dot{V} = s\dot{s} + \beta_{1} k_{2} \sum\limits_{i = 0}^{2} {\frac{1}{{\mu_{i} }}} (\hat{a}_{i} - a_{i} )\dot{\hat{a}}_{i} .$$
(26)

Substituting Eq. (25) into Eq. (26), it can be concluded that:

$$\begin{aligned} \dot{V} & = s(\dot{e} + \alpha_{1} k_{1} \left| e \right|^{{\alpha_{1} - 1}} \cdot \dot{e} + \beta_{1} k_{2} \left| {\dot{e}} \right|^{{\beta_{1} - 1}} \cdot \ddot{e}) \\ & \quad + \beta_{1} k_{2} \sum\limits_{i = 0}^{2} {\frac{1}{{\mu_{i} }}} (\hat{a}_{i} - a_{i} )\dot{\hat{a}}_{i} . \\ \end{aligned}$$
(27)

By further substituting Eq. (24) in Eq. (27), the above formula can be rewritten as:

$$\begin{aligned} \dot{V} & = \beta_{1} k_{2} \left| {\dot{e}} \right|^{{\beta_{1} - 1}} \left[ {D(t)s - ks^{2} - (\hat{a}_{0} + \hat{a}_{1} \left| e \right| + \hat{a}_{2} \left| {\dot{e}} \right| + \eta )\left| s \right|} \right] \\ & \quad + \beta_{1} k_{2} \sum\limits_{i = 0}^{2} {\frac{1}{{\mu_{i} }}} (\hat{a}_{i} - a_{i} )\dot{\hat{a}}_{i} . \\ \end{aligned}$$
(28)

Considering the adaptive updating laws shown in Eq. (23), Eq. (28) can be rewritten as:

$$\begin{aligned} \dot{V} & = \beta_{1} k_{2} \left| {\dot{e}} \right|^{{\beta_{1} - 1}} \left[ {D(t)s - ks^{2} - (\hat{a}_{0} + \hat{a}_{1} \left| e \right| + \hat{a}_{2} \left| {\dot{e}} \right| + \eta )\left| s \right|} \right] \\ & \quad + \beta_{1} k_{2} \left[ {(\hat{a}_{0} - a_{0} )\left| s \right| \cdot \left| {\dot{e}} \right|^{{\beta_{1} - 1}} + (\hat{a}_{1} - a_{1} )\left| s \right| \cdot \left| e \right| \cdot \left| {\dot{e}} \right|^{{\beta_{1} - 1}} + (\hat{a}_{2} - a_{2} )\left| s \right| \cdot \left| {\dot{e}} \right|^{{\beta_{1} - 1}} } \right]. \\ \end{aligned}$$
(29)

Simplifying Eq. (29) yields to the following equation:

$$\dot{V} = \beta_{1} k_{2} \left| {\dot{e}} \right|^{{\beta_{1} - 1}} \left[ {D(t)s - \eta \left| s \right| - ks^{2} - (a_{0} + a_{1} \left| e \right| + a_{2} \left| {\dot{e}} \right|)\left| s \right|} \right].$$
(30)

Combining the above equations, the system Lyapunov function satisfies:

$$\begin{aligned} \dot{V} & \le \beta_{1} k_{2} \left| {\dot{e}} \right|^{{\beta_{1} - 1}} \left[ {D(t)\left| s \right| - \eta \left| s \right| - ks^{2} - (a_{0} + a_{1} \left| e \right| + a_{2} \left| {\dot{e}} \right|)\left| s \right|} \right] \\ & \le \beta_{1} k_{2} \left| {\dot{e}} \right|^{{\beta_{1} - 1}} \left[ { - \eta \left| s \right| - ks^{2} } \right] \le 0. \\ \end{aligned}$$
(31)

According to the above analysis, it can be seen that the system state can asymptotically converge to zero along the sliding surface s = 0 in finite time, which proves the stability of the proposed ANFTSM control system.

4 Optimal Allocation of Tire Braking Forces

4.1 Description of the Dynamic Allocation Problem

The main objective of the dynamic allocation problem is to determine the optimal braking forces of the four wheels, thus the obtained direct yaw moment can be achieved [46–49]. However, it is obvious that the coupling relationship between the tire longitudinal force and the tire lateral force must be satisfied for a single wheel in the dynamic allocation process, thus the motion stability of the bus when tracking curve paths on slippery roads can be guaranteed. It is obvious that this treatment will make the dynamic allocation problem more difficult when considering the tire force constraints. Therefore, how to achieve the dynamic allocation of all the tire forces to achieve the desired yaw moment is a challenging research task [50–52]. In this work, considering the uncertainty in the tire force allocation problem and the problem-solving efficiency, the robust least-squares allocation method is utilized to solve the optimal allocation problem of the tire braking forces.

Based on the theory of robust least-squares allocation algorithm, an optimization objective needs to be solved, that is, Eq. (17) should be firstly transformed into Bu = v without considering the uncertainty and external disturbance. In this allocation rule, v is the desired yaw moment Mz, u is the actuator response, i.e., the braking forces of four wheels and B is the efficiency matrix. This treatment linearizes the relationship between u and v, and hence, the efficiency matrix B can be written as:

$$B = \left[ {\begin{array}{*{20}c} { - \frac{{t_{w1} }}{2}} & {\frac{{t_{w1} }}{2}} & { - \frac{{t_{w2} }}{2}} & {\frac{{t_{w2} }}{2}} \\ \end{array} } \right].$$
(32)

4.2 Weighted Least-Squares Allocation Method

Firstly, a reasonable objective function of the tire forces allocation should be defined, which is described as follows:

$$\mathop {\min }\limits_{u} J = u^{{\text{T}}} Wu,$$
(33)

where W is a diagonal matrix which considers the utilization ratio of the tire forces, whose element are given as follows:

$$w_{ij} = \frac{1}{{(\mu_{ij} F_{zij} )^{2} }},$$
(34)

where Fzij is the tire vertical load and μij is the road adhesion coefficient.

The essence of the optimization objective for Eq. (33) is to minimize the control energy consumption of the actuator, i.e., minimizing the braking force of the tire, so as to maintain a low tire utilization ratio and improve the stability margin of the tire. In order to simplify the operation process and reduce the calculation time, the above optimization problem can be further rewritten as follows:

$$\min \, J = \left\| {W_{v} (Bu - v)} \right\|_{2}^{2} + \left\| {W_{u} (u - u_{d} )} \right\|_{2}^{2} ,$$
(35)

where Wv and Wu are the weight matrix for the desired yaw moment and the tire braking forces respectively, and ud is the target control quantity of the actuator.

4.3 Robust Least-Squares Allocation Method

Although the weighted least-squares method is fast in calculation without considering the system uncertainty, in the case of uncertainty and external disturbance, this simplified method will reduce the allocation efficiency. Therefore, when the lumped uncertainty is fully considered, an uncertainty efficiency matrix ΔB should be introduced. In conclusion, the allocation error problem in Eq. (35) can then be transformed into the following robust least-squares allocation problem:

$$u_{RLSCA} = \arg \min \mathop {\max }\limits_{{\left\| {\Delta B} \right\|_{\infty } \le \rho }} \left\| {(B + \Delta B)u - v} \right\|,$$
(36)

where ΔB is the efficiency matrix used to reflect the system lumped uncertainty.

In order to solve this problem, the robust least-squares control allocation method is used, and then the allocation problem can be transformed into a second-order cone programming problem. In the first, when the variable u is in the definition field, a worst case residual can be defined as:

$$r(u) = \mathop {\max }\limits_{{\left\| {\Delta B} \right\|_{\infty } \le \rho }} \left\| {(B + \Delta B)u - v} \right\|.$$
(37)

According to the triangle inequality transformation, the above equation can be rewritten as:

$$r(u) \le \mathop {\max }\limits_{{\left\| {\Delta B} \right\|_{\infty } \le \rho }} (\left\| {Bu - v} \right\| + \left\| {\Delta Bu} \right\|) = \left\| {Bu - v} \right\| + \mathop {\max }\limits_{{\left\| {\Delta B} \right\|_{\infty } \le \rho }} \left\| {\Delta Bu} \right\|.$$
(38)

Then, the following assumptions can be given as:

$$\Delta B = \frac{\rho }{\left\| u \right\|}\varepsilon u^{{\text{T}}} ,$$
(39)

where

$$\varepsilon = \left\{ {\begin{array}{*{20}ll} {\frac{Bu - v}{{\left\| {Bu - v} \right\|}},} & {Bu \ne v,} \\ {{\text{unit}}\;{\text{norm}}\;{\text{vector}},} & {{\text{otherwise}}.} \\ \end{array} } \right.$$
(40)

Based on the above assumptions, the worst-case residual can be redefined as:

$$r(u) = \left\| {Bu - v} \right\| + \rho \left\| u \right\| \le \lambda ,$$
(41)

where λ is the upper bound of the minimum residual for the optimal solution of variable u in the definition domain.

In conclusion, the robust least-squares problem is then transformed into the following second-order cone optimization problem (SOCP):

$$\begin{aligned} & \quad \quad \quad \mathop {\min }\limits_{u,\tau ,\lambda } \lambda \\ & {\text{s}}.{\text{t}}.,\quad \left\{ \begin{aligned} & \left\| {Bu - v} \right\| \le \lambda - \tau , \\ & \rho \left\| u \right\| \le \tau , \\ & \underline{u} \le u \le \overline{u}, \\ \end{aligned} \right. \\ \end{aligned}$$
(42)

where τ is a real number, and λ > τ is satisfied. On this basis, the optimal solution uRLSCA to the aforementioned allocation problem shown in Eq. (42) can be given by [53]:

$$u_{RLSCA} = \left\{ {\begin{array}{*{20}ll} {(\mu I + B^{{\text{T}}} B)^{ - 1} B^{{\text{T}}} v,} & {{\text{if}}\;\mu = \frac{{(\lambda - \tau )\tau \rho^{2} }}{{\tau^{2} + \rho^{2} s}} > 0,} \\ {B^{ + } ,} &{{\text{else}}.} \\ \end{array} } \right.$$
(43)

5 Simulation Results and Analyses

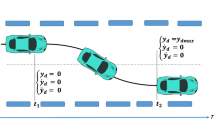
In this section, the effectiveness of the proposed YSC approach for bus is verified by simulation results. Since the YSC system is only activated under those driving conditions in which the tire-road friction force cannot both meet the requirements of the tire longitudinal and lateral forces, thus in this work, two simulation cases in which the road adhesion coefficients are 0.1 and 0.3, respectively are provided. By conducting efficient simulation comparisons, the parameters of the ANFTSM control system are as follows: c1 = 0.5, α1 = 2, β1 = 5/3, k1 = 1, k2 = 1, k = 50, η = 0.5, μ0 = 0.01, μ1 = 0.01, μ2 = 0.01. In the co-simulation process, the vehicle is assumed to track the double lane curve path on two slippery roads at fixed speed (35 km/h) and the target trajectory curve is shown in Figure 6. The vehicle parameters adopted in the TruckSim-Simulink co-simulation are given in Table 1.

Figure 6
figure 6

Target trajectory curves

Full size image
Table 1 Bus simulation parameters
Full size table

5.1 Simulation Results of the First Case (μ = 0.1)

The simulation results comparison of the vehicle slip angle, the vehicle yaw rate and the obtained direct yaw moment between the ANFSTM and the SMC are shown in Figure 7. As can be seen from Figure 7(a) and Figure 7(b), the peak values of the vehicle slip angle and the vehicle yaw rate controlled by the ANFTSM are decreased significantly compared with that controlled by the conventional SMC, among of which the absolute value of the vehicle slip angle peak value is reduced from 0.025 rad to 0.015 rad and the absolute value of the vehicle yaw rate peak value is reduced from 0.25 rad to 0.2 rad, which demonstrates the feasibility, effectiveness and practicality of the proposed YSC approach for vehicle tracking curve path on slippery road. Figure 6(c) shows the difference of the direct yaw moment between the ANFSTM and the SMC. It is obviously that the direct yaw moment calculated by the two methods is different, which illustrates that the proposed YSC approach in this work can effectively calculate the optimal direct yaw moment by considering the tire force constraints on slippery road.

Figure 7
figure 7

Simulation results comparison between the ANFTSM and the SMC (μ = 0.1)

Full size image

To achieve the direct yaw moment and guarantee the path tracking accuracy, the optimal allocation of the tire braking forces are also conducted. Figure 8 shows the allocation results of the tire braking forces of the four wheels. It can be seen that different tire forces are optimally allocated to achieve the direct yaw moment. In addition, as shown in the figures, when the vehicle is steering, the absolute values of the tire longitudinal forces of the left-front wheel and the left-rear wheel are large, while that of the right-front wheel and the right-rear wheel are small. This tire forces allocation results can not only realize the additional yaw moment, but also ensure that the overall load rate of the four wheels is maintained at a low level, so that the vehicle will not lose lateral stability.

Figure 8
figure 8

Tire forces allocation results based on the robust least-squares control allocation method (μ = 0.1)

Full size image

5.2 Simulation Results of the Second Case (μ = 0.3)

Similarly, the simulation results comparison of the vehicle slip angle, the vehicle yaw rate and the obtained direct yaw moment between the ANFSTM and the SMC for the second case are shown in Figure 9. As can be seen from Figure 9(a) and Figure 9(b), the peak values of the vehicle slip angle and the vehicle yaw rate controlled by the NFTSM are also decreased significantly compared with that controlled by the conventional SMC, among of which the absolute value of the vehicle slip angle peak value is reduced from 0.045 rad to 0.03 rad and the absolute value of the vehicle yaw rate peak value is reduced from 0.35 rad to 0.25 rad.

Figure 9
figure 9

Simulation results comparison between the ANFTSM and the SMC (μ = 0.3)

Full size image

The allocation results of the tire braking forces of the four wheels in the second case are shown in Figure 10. Compared with the allocation results of the tire forces shown in Figure 10, it can be seen that the tire forces of the four wheels in the second case are obviously larger than that in the first case, which is due to the larger road adhesion coefficients. In this case, the tire-road friction force increases. This phenomenon shows that the optimal allocation of the tire forces based on the robust least-squares control allocation method can effectively reflect the relationship between the tire longitudinal force and the tire lateral force and the tire force constraints on slippery road, thus the resulted tire forces can then be achieved through the actuators of the bus braking system in practical applications.

Figure 10
figure 10

Tire forces allocation results based on the robust least-squares control allocation method (μ = 0.3)

Full size image

6 Conclusions

  1. (1)

    The concrete expressions of the STI tire model are provided and the tire model parameters are fitted based on the experimental data with high accuracy.

  2. (2)

    A 7-DOF bus dynamics model, which includes the longitudinal motion, lateral motion, yaw motion and the rotational dynamics of four wheels, is established. In the model, the tire longitudinal and lateral forces are obtained through the established STI tire model.

  3. (3)

    The ANFTSM control method is proposed to eliminate the uncertainty and disturbance in the bus YSC system design process, and control system stability can be proved based on Lyapunov theory.

  4. (4)

    The robust least-squares allocation method is used to solve the optimal allocation problem of the tire forces, whose objective is to achieve the desired direct yaw moment through the effective distribution of the brake force of each tire. The allocation problem can be transformed into a second-order cone programming problem.

  5. (5)

    Two simulation cases in which the road adhesion coefficients are 0.1 and 0.3, respectively, are provided to verify the effectiveness of the proposed YSC approach for bus. The simulation results show that the peak values of the vehicle slip angle and the vehicle yaw rate controlled by the ANFTSM are decreased significantly compared with that controlled by the conventional SMC, which demonstrates the feasibility, effectiveness and practicality of the proposed YSC approach for bud tracking curve path on slippery road.