Abstract
Measurement of the effects of drugs, mediators and infectious agents on various models of lung disease, as well as assessment of lung function in the intact mouse has the potential for significantly advancing our knowledge of lung disease. However, the small size of the mouse presents significant challenges for the assessment of lung function. Because of compromises made between precision and noninvasiveness, data obtained may have an uncertain bearing on the mechanical response of the lung. Nevertheless, considerable recent progress has been made in developing valid and useful measures of mouse lung function. These advances, resulting in our current ability to measure sophisticated indices of lung function in laboratory animals, are likely to lead to important insights into the mechanisms of lung disease.
Similar content being viewed by others
Introduction
Much of our current understanding of the normal functioning of the lung and mechanisms of lung disease comes from studies utilizing animals. As one clear example, animal systems of a wide variety of species, including humans, provided the essential mechanistic proof of a link between inflammation and airways hyperresponsiveness that set the stage for current anti-inflammatory therapy [1]. Mice are now widely employed in lung research because of certain advantages this species is thought to provide [2]. Advantages of using mice include a well-understood immunologic system, the vast array of available reagents, a short reproductive cycle, a well-characterized genome, the advent of transgenic technology, and economic factors [2–4]. Using mice as models of human disease, in particular asthma, has certain shortcomings [2, 5] only some of which will be covered in this review. For any animal system to yield useful and valid insights into disease it must exhibit an appropriate phenotype. It has become apparent that the valid assessment of lung function in an animal as small as the mouse requires that a number of technical challenges be overcome.
The paucity of information on the measurement of lung function in the mouse has largely reflected the difficulty of measuring the necessary respiratory signals of flow, volume and transpulmonary pressure. This applies particularly to the small gas flows involved [6, 7]. However, the work of Martin et al in 1988 demonstrated that measurements of pulmonary resistance and compliance could be made in this small species [8]. At about the same time, Levitt and Mitzner clearly illustrated the utility of using mice to explore the genetics of hyperresponsiveness [9, 10]. Since these studies, the use of mice to study lung disease has increased dramatically and a number of approaches have been developed in the ensuing years for measuring lung function in mice in vivo. In this review we examine these various methods and discuss their respective attributes. Each approach represents a compromise between accuracy, non-invasiveness, and convenience [11].
Lung anatomy
One look through the microscope at a section of mouse lung (Figure 1) demonstrates that the mouse lung is considerably different in structure from the human lung, although relatively little has been published about the architecture of the mouse lung compared to other species. What is known about the structure of the mouse lung probably has important bearing on its function [12–14]. The total lung capacity (TLC) of the mouse is about 1 ml compared to 10 ml of the rat and 6,000 ml of a human. Like the human, there are 5 lobes in the right mouse lung, but unlike the human the mouse has only a single left lung. Also unlike the human lung, but similar to the rat, the mouse pleura is thin, yet it is strong enough to be inflated to considerably higher pressures than the 30 cm H2O normally associated with TLC (W Mitzner, personnel communications). The parenchyma of the mouse lung occupies a smaller fraction of the total lung than that of the rat but more than that of the human (mouse: 18%, rat: 24%, human: 12% lung volume). The alveoli of the mouse lung are smaller (80 μm mean linear intercept (MLI)) than those of the rat (MLI 100 μm) or human (MLI 210 μm). The blood-gas barrier thickness in the mouse (0.32 μm) is similar to that of the rat (0.38 μm) but somewhat smaller than that of the human (0.62 μm), which might have important implications for both gas exchange and parenchymal lung mechanics. The airways constitute a large percentage of the lung in mice (11%) compared to rats (5.7%). Cartilage is present in the mouse trachea but is less well organized than in other species; only the upper part of the trachea has the complete rings seen in other mammals and these rapidly change to plates as one proceeds distally. Mouse lungs have fewer respiratory bronchioles and airway generations (13–17 generations) than do human lungs (17–21 generations) with the airways of the mouse lung exhibiting a monopodial as opposed to dichotomous branching pattern. Two other significant features of the mouse lung are the thinness of the respiratory epithelium and the relatively large airway lumen [12, 14]. This large airway caliber is speculated to reduce the flow-resistive load that would otherwise result from the rapid respiratory rate (250–350 bpm) required by the mouse to maintain body temperature [15]. An important functional difference between mice and rats compared to humans is the paucity, or even complete absence, of submucosal glands and the presence of high numbers of Clara cells [12]. Exactly what significance all these anatomical features of the mouse lung have for lung function is speculative, but it has been our experience that the baseline airway resistance of mice that have been sensitized and challenged with antigen differs imperceptibly from that of control animals [16, 17]. This suggests that inflammatory processes that could compromise lung function in larger animals (e.g. humans) might have little effect in mice because of their relatively large airway size and/or lack of mucous glands.
Basic mechanical models of the lung
Measurement of the function of the lung, especially assessment of lung mechanics, is typically done in the context of a model of the lung [18–20]. The simplest model is a tube connected to a bellows (Figure 2A). This model works well for a single breathing frequency, but has major limitations when the changes in lung mechanics that occur with alterations in breathing frequency are considered. This is because the resistive and elastic properties of the lung are substantially dependent on breathing frequency. For example, the resistance of the lung falls as frequency increases over the range associated with normal breathing [21]. To model this type of mechanical behavior, spring-and-dashpot assemblies capable of simulating viscoelastic behavior need to be included in the model (Figure 2B). These basic models allow us to develop mathematical expressions, which can be used to quantitatively assess lung mechanics. The parameters of the models, that is, the resistive and elastic values of their individual components, constitute the endpoints we use to assess lung function experimentally.
Two common and basic mechanical models of the lung. A: A homogeneously ventilated model consisting of a single elastic balloon (elastance E) served by a single flow-resistive pipe (resistance R). B: A homogeneous model again with a single airway (resistance R 1), but with a Kelvin body consisting of two springs (E 1 and E 2) and a dashpot (resistance R2) to account for the viscoelastic behavior of the lung tissue.
The viscoelastic model in Fig. 2B does a substantially better job of describing frequency-dependent nature lung mechanics than the model in Fig. 2A. Nevertheless, the simple model in Fig. 2A still serves as the conceptual platform for most studies of lung mechanics and bronchial responsiveness. The mechanical behavior of this model is described by its equation of motion. This equation is based on simple physics and states that the force (pressure) applied to the model is equal and opposite to the opposing force (pressure) the model generates. The applied pressure, P, is that supplied either by the respiratory muscles or a mechanical ventilator. The opposing pressure is made up, in general, of three components: a resistive pressure (P res ), an elastic pressure (P el ), and an inertive pressure (P in ).
Thus,

P res is described by Ohm's law:

where R is the resistance of the lung and 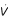 is flow of gas. P
el
is described by Hooke's law:
is flow of gas. P
el
is described by Hooke's law:

where E is lung elastance (equal to the inverse of compliance, C) and V is lung volume relative to functional residual capacity. P in comes into play only at frequencies well above those of normal breathing, while both P res and P in become negligible when frequency is extremely low. Thus, the equation of motion relevant to normal breathing is

The parameters R and E are both profoundly dependent on breathing frequency and lung volume.
Lung volume
The volume of the lungs has an important influence on its pressure-flow relationships. For example, an increase in lung volume stretches the airways open and so causes airway resistance to fall (tethering). This also makes it more difficult for the airways to narrow when the airway smooth muscle contracts, and represents an important mechanism by which the challenged lung can defend airway caliber [18, 22]. Unlike larger laboratory animals, the measurement of lung volume in the mouse is particularly problematic due to its small size. For example, when thoracic gas volume is measured using the conventional Boyle's Law technique, the volumes of air in the transducers used to measure plethysmographic and airway-opening pressures must be small relative to the lung volume, or significant measurement errors will occur. It has only recently been reported that measurement of functional residual capacity (FRC) by this approach is at all feasible [23]. The measurement of FRC with gas dilution is equally difficult, again due to the small size of the mouse lung, and there are only a few reports in the literature on the use of this technique [24]. Other studies of mouse lung volume have used a buoyancy approach [25], a degassing approach [26, 27], and even a CT scanner method has been reported [28]. None of these, however, is particularly practical for most study designs. Better techniques for measuring lung volumes in mice are certainly needed, so this will be a fruitful area for future research.
Lung elastance (compliance)
The component of the transpulmonary pressure loss that is out of phase with flow and in phase with volume, as well as the recoil pressure exerted by the lung under static conditions, are caused by the elastic forces within the lung. The loss of elastic recoil within the lung defines emphysema while an increase defines restrictive processes [18, 25]. The chest walls and other thoracic structures in mice are extremely compliant, so most elastic recoil measured in an intact animal can be attributed specifically to the lung. Moreover, the elastic recoil of the lung shows considerable genetic variability that needs to be taken into account in study designs [26]. The elastic recoil of the lung is conveniently assessed in terms of the quasi-static pressure-volume (PV) curve measured by inflating and deflating the lung in a step-wise fashion. The inspiratory limb of the curve traverses a path through values of P that are higher than those of the expiratory limb, the difference between the two limbs being termed hysteresis. Changes in the inspiratory limb of the PV curve that cause an increase in hysteresis are taken to indicate enhanced airway closure, such as that observed in humans after dry cold gas inhalation [29] and recapitulated in mice with allergic inflammation [30]. These changes in PV characteristics can be sensitive indicators of lung dysfunction and contribute to the genesis of hyperresponsiveness. The shape of the pressure volume relationship is one manifestation of the nonlinear characteristics of lung mechanics in the normal, unperturbed lung. Airflow resistance also exhibits alinear behavior as the airflow reaches high rates of flow as sudden changes in lumenal dimensions occur (e.g. vocal chords). The mouse lung exhibits alinear elastic (compliance) behavior that increases following antigen challenge, a change that is most consistent with reopening airways that were closed [29, 30]. Airflow is not alinear (i.e. laminar flow regimes) in either condition as it is highly unlikely turbulent flow occurs in mouse lungs due to the small airway diameters, unlike humans where turbulent flow is a common occurrence [30], pointing to a clear limitation of this species in exploring complex airflow conditions.
Phenotyping uncertainty principle
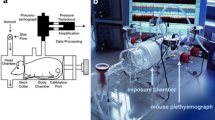
Accurate and valid measurement of lung mechanics in laboratory animals is a balancing act between measurement precision and maintenance of "natural" conditions. This situation is similar to the Heidelberg uncertainty principle of quantum mechanics which states that the measurement of a particle's position interferes with the measurement of its movement, and vice versa [31]. In a similar fashion, as we make more precise measurements of lung function in an animal, we are forced to constrain the animal's behavior in a way that departs from the maintenance of natural conditions [11]. At the extreme ends of this continuum are the measurements derived from the free roaming animal in a closed chamber, known as unrestrained plethysmography (UP), and the measurement of input impedance using forced oscillations performed in an anesthetized, tracheostomized animal (Figure 3).
Unrestrained plethysmography
This approach to assess lung function involves placing the subject into a small closed box and measuring the pressure changes within the box that occur as the animal breathes [7, 11, 32]. The animal is conscious and unrestrained. This technique currently enjoys wide popularity (for example see [33]) because 1) it is simple and 2) the mouse remains unharmed after the experiment. The endpoint is the heuristic variable known as Penh, which stands for 'enhanced pause'. It is important to note that there is no linkage between Penh and other variables that are derived from mechanical principles – Penh is merely an empirical derivative of the respiratory variations in box pressure [11]. While an earlier publication demonstrated reasonable correlations between Penh and invasive measures of lung mechanics [32], recent publications draw into serious question the validity of using Penh to measure lung function [7, 11, 34].
The pressure changes occurring within the box as the mouse breathes are derived first from gas compression and decompression within the thorax – an event linked to the state of lung mechanics – and second from humidification and warming of inspired gas – an event unrelated to lung mechanics. During bronchoconstriction, both components increase [7], but much of this increase is likely due to the increased stimulation to breathe that would arise from chemoreceptor receptors in the lung. Hence box pressure changes should be influenced by chemoreceptor sensitivity and genetics that control responses to chemo- or irritant- receptor stimulation and integration [11, 35]. Recent studies show that changes in Penh depart from mechanical changes during a state of increased box temperature [7, 34] in an exactly opposite way during exposure to hyperoxic conditions [34, 35] and temporarily [36]. These findings show that Penh is not a valid measurement of the lung function of the mouse except as a measure of patterns of respiration, and it has been known for a long time that patterns of respiration usually have little bearing on lung mechanics. Finally, a response in Penh may also be due to changes in nasal cavity resistance, as the upper airways are very significant contributors (50%) to total lung resistance and their contribution is likely to change depending on the experimental situation [32].
Lung impedance magnitude
The next step on the phenotyping uncertainty continuum (Figure 3) is the measurement of the magnitude of respiratory system or lung impedance. Lung impedance is a complex quantity having both real and imaginary parts (see section 'Forced oscillations and the constant phase model'), and its calculation requires rather sophisticated methods. The magnitude of impedance (|Z
rs
|), however, is easily determined simply as the ratio of the absolute value of the swing in pressure (ΔP) to the absolute value of the swing in flow (Δ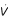 ) occurring over a breath, thus
) occurring over a breath, thus

As seen in the example in Figure 4, pressure is obtained by placing a pressure transducer at the airway opening, while flow is assumed to be constant as the animal is mechanically ventilated with a volume-cycled ventilator [9, 10, 37, 38]. When a bronchoactive agent is introduced, the peak pressure with each breath goes up, so |Z rs | increases commensurately. Hence, by merely measuring airway-opening pressure, a useful index of lung function is derived. This technique has been used because it is simple and gives a direct assessment of lung mechanics [9, 10, 37, 38].
Pulmonary impedance measurements in anesthetized mice. The diagram shows airway opening pressure plotted against time. Volume and flow excursions for each breath are maintained constant by use of a volume-cycled ventilator. Increases in the magnitude of lung impedance following acethycholine injection are assessed as the increase in pressure above baseline. Note the increased responsiveness in the A/J compared the C3He/J strain of mouse. APTI: Airway pressure time index. Used with permission [38].
The major disadvantage of this technique is that even though a direct measure of lung function is made, no insight is obtained as to where in the lung an abnormality might be located. This is a significant limitation if one wishes to explore the mechanisms of bronchoconstriction and whether it reflects, for example, central versus peripheral airways dysfunction. Nevertheless, this simple approach has produced significant advances in our understanding of the genetics of hyperresponsiveness [3, 9, 10].
Measurement of dynamic resistance (RL) and compliance (CL)
A classic approach to assessment of lung mechanics in animals is the measurement of dynamic lung resistance (R L ) and compliance (C dyn or C L ) [3, 8, 20, 38–40]. In the past, this approach was often used to assess central versus peripheral alterations in lung mechanics – a topic of considerable current interest. The calculation of R L and C dyn requires the measurement of intrathoracic pressure that, in larger animals, is obtained with an esophageal balloon or pleurel catheter, but in a mouse is obtained either by opening the chest or by making the reasonable assumption that the chest wall presents little mechanical load compared to that of the lung [26, 41, 42]. Flow is usually obtained with a pressure transducer but this approach is problematic when miniaturized to the mouse [7, 43]. Accordingly, flow is commonly derived from the differentiation of a volume signal, usually obtained from a body plethysmograph [8, 40]. The values of R L and C L are then derived by fitting the equation of motion (Equation 4) to measurements of pressure, flow and volume.
The measurement of R L and C L , while technically challenging, does yield additional insight into the mechanisms of bronchoconstriction over that provided by |Z rs |. Generally speaking, an increase in R L reflects both narrowing of the conducting airways and alterations in the lung periphery (heterogeneous narrowing or closure of distal airways together with changes in the intrinsic mechanical properties of the parenchyma). Decreases in CL, on the other hand, reflect only events in the lung periphery, particularly airway closure leading to lung unit derecruitment [44]. If the response to an intervention is limited largely to R L , then a relatively proximal location is implicated for the effect. By contrast, a selective change in C L is indicative of a more distal site of action [3, 8, 45]. As an example of this approach, R L and C L were clearly shown to be independent variables in mice treated with an antibody agonist for VLA-4, an adhesion protein of the eosinophil [45]. Furthermore, the genetic dependence of these variables suggests that the factors that control central airway function (reflected in R L ) are different from those that control peripheral airway function (reflected in C L ) [46].
Forced oscillations and the constant phase model
At the far end of the phenotyping uncertainty principle lies the forced oscillation technique (FOT) applied in anesthetized, paralyzed, tracheostomized animals to measure the complex input impedance (Z rs ) of the lungs [21]. We have already covered the concept that the magnitude of Zrs (|Z rs |) is a generalization of the changes of resistance and compliance, and that Zrs consists of two parts that are both functions of frequency. The real part of Z rs is directly related to the resistance and provides essentially the resistance of the respiratory system at the frequency in question. The imaginary part of Z rs is called the reactance and reflects respiratory compliance at frequencies below 20 Hz in the mouse. Thus, the FOT essentially provides R L and C L at each frequency contained in the flow signal applied to the lungs. This requires that the animal be oscillated with a complex flow wave produced by either a loudspeaker [34, 47, 48] or a computer-controlled piston [6, 7, 17]. The data of pressure and either flow or volume are converted into the frequency domain by the Fast Fourier transform, and their ratios calculated to yield the real and imaginary parts of Z rs (Figure 5).
The respiratory input impedance of the mouse. Open squares represent baseline conditions while closed circles show the result of administering an aerosol of methacholine. The solid and dashed lines are the fit provided by the constant-phase model (Eq. 6). Used with permission [17].
The key advantage of this approach, as compared to the determination of R L and C L or |Z rs |, is that Z rs can be fitted to a more complex model of the lung known as the constant-phase model [49] which makes a clearer distinction between central and peripheral events in the lung. The equation of motion of the constant-phase model is

where R
aw
is the resistance of the airways that are attached to the constant phase element, I
aw
is the inertance of the gas in the airways (which has negligible effect in the mouse below 20 Hz and can be ignored [17]), G
ti
is tissue resistance or damping, H
ti
is tissue elasticity, and i is  . As R
aw
is a measure of central airways resistance, it would be expected to change if the airways are significantly narrowed. By contrast, G
ti
reflects either changes in tissue physical properties or regional airways heterogeneity. If changes in R
aw
are small, then any changes in G
ti
most likely represent changes in the parenchyma or very small airways. Acute changes in H
ti
are likely to reflect lung derecruitment (airway closure) [44], whereas chronic changes in H
ti
would be expected to reflect changes in the intrinsic mechanical properties of the parenchyma. This technique is now being successfully and extensively used to assess lung mechanics of the mouse [17, 33, 50].
. As R
aw
is a measure of central airways resistance, it would be expected to change if the airways are significantly narrowed. By contrast, G
ti
reflects either changes in tissue physical properties or regional airways heterogeneity. If changes in R
aw
are small, then any changes in G
ti
most likely represent changes in the parenchyma or very small airways. Acute changes in H
ti
are likely to reflect lung derecruitment (airway closure) [44], whereas chronic changes in H
ti
would be expected to reflect changes in the intrinsic mechanical properties of the parenchyma. This technique is now being successfully and extensively used to assess lung mechanics of the mouse [17, 33, 50].
Tomioka et al [17] showed that Z rs can be used to track changes obtained with an even more invasive technique [51, 52] – the alveolar capsule – where resistance is partitioned into a central airway and a parenchymal tissue resistance component through the direct measurement of alveolar pressure (Figure 6). In this study, the disparate behaviours of R aw , G ti and H ti clearly show that these three quantities are independent parameters that access different aspects of lung function. For example, antigen exposure followed by methacholine challenge caused an enhancement of both G ti and H ti – measures of peripheral lung function – however, changes in R aw , reflecting central airways, were not significantly altered. The enhanced changes in G or H in this acute state may reflect three different mechanisms: derecruitment of lung units as airways close, temporal shifts of tissue movement, and inhomogenities of airflow distribution. Moreover these data point away from significant alterations in airway smooth muscle function and more towards enhanced or altered secretions that cause dysfunction in small airways. Interestingly, antigen challenge in either sensitized or unimmunized mice caused no significant changes in any of the parameters at baseline before methacholine challenge, likely due to the unique architecture of the mouse lung (see above).
The mechanical response of the mouse lung to methacholine in terms of the parameters of the constant-phase model (see Eq. 6 in text). The open squares correspond to control BALB/c mice, while the closed circles represent mice sensitized to and challenged with ovalbumin. Taken from [17] with permission.
We believe that the well-founded theoretical basis of the FOT, and its rigorous application in mice, will lead to considerable insight into the functioning of mouse models of lung disease.
Conclusion
Measurement of lung function in a creature as small as the mouse presents considerable technical challenges. However, with the exception of the measurement of absolute lung volume and the analysis of blood gases, we have now conquered the challenge of miniaturizing the instrumentation necessary for mouse lung function assessment. Application of advanced techniques such as the FOT coupled with constant-phase model analysis hold particular promise for improved characterization of lung responses to intervention and pathology. With these approaches, we can now unravel the mechanisms of airways dysfunction, the influence of genetics and the immunological factors that define the physionome of the mouse.
Abbreviations
- bpm:
-
breaths per minute
- C dyn :
-
dynamic compliance
- C L :
-
lung compliance
- E :
-
elastance
- FOT:
-
forced oscillation technique
- FRC:
-
functional residual capacity
- G :
-
tissue damping or tissue resistance
- H :
-
elasticity
- MLI:
-
mean linear intercept
- P :
-
pressure
- P res :
-
resistive pressure
- P el :
-
elastic pressure
- P in :
-
inertial pressure
- Penh:
-
enhanced pause
- R L :
-
resistance
- TLC:
-
total lung capacity
- UP:
-
unrestrained plethysmography
-
 :
: -
Flow
- Z RS or Z :
-
impedance of the respiratory system
- |Z rs |:
-
Magnitude of impedance
References
Wanner A, Abraham WM, Douglas JS, Drazen JM, Richerson HB, Sri RJ: Models of airway hyperresponsiveness. Am Rev Respir Dis 1990, 141:253–257.
Tu Y-P, Larsen GL, Irvin CG: Utility of murine systems to study asthma pathogenesis. Eur Respir Rev 1995, 29:224–230.
Drazen JM, Finn PW, De Sanctis GT: Mouse models of airway responsiveness: physiological basis of observed outcomes and analysis of selected examples using these outcome indicators. Annu Rev Physiol 1999, 61:593–625.
Gelfand E: Pro: mice are a good model of human airway disease. Am J Resp Crit Care Med 2002, 166:5–8.
Persson CG: Con: mice are not a good model of human airway disease. Am J Resp Crit Care Med 2002, 166:6–8.
Schuessler TF, Bates JHT: A computer-controlled research ventilator for small animals: design and evaluation. IEEE Trans Biomed Eng 1995, 42:860–866.
Lundblad KAL, Irvin CG, Adler A, Bates JHT: A reevaluation of the validity of unrestrained plethysmography in mice. J Appl Physiol 2002, 93:1198–1207.
Martin TR, Gerard NP, Galli SJ, Drazen JM: Pulmonary responses to bronchostrictor agonists in the mouse. J Appl Physiol 1988, 64:2318–2323.
Levitt RC, Mitzner W: Expression of airway hyperreactivity to acetylcholine as a simple autosomal recessive trait. FASEB J 1998, 2:2605–2608.
Levitt RC, Mitzner W: Autosomal recessive inheritance of airway hyperreactivity to 5-hydroxytryptamine. J Appl Physiol 1998, 67:1125–1132.
Bates JHT, Irvin CG: Measuring Lung Function in Mice: The Phenotyping Uncertainty Principle. J Appl Physiol 2003, 94:1297–1306.
McBride JT: Architecture of the tracheobronchial tree. In Treatise on Pulmonary Toxicology: Comparative Biology of the Normal Lung (Edited by: Parent RA). Boca Raton, Florida: CRC Press 1992, 49–61.
Valerius KP: Size-dependent morphology of the conductive bronchial tree in four species of myomorph rodents. J Morphol 1996, 230:291–297.
Gomes RFM, Bates JHT: Geometric determinants of airway resistance in two isomorphic rodent species. Respir Physiol Neurobiol 2002, 130:317–325.
Bennett FM, Tenney SM: Comparative mechanics of the mammalian respiratory system. Respir Physiol 1982, 49:131–140.
Cieslewicz G, Tomkinson A, Adler A, Duez C, Schwarze J, Takeda K, Larson KA, Lee JJ, Irvin CG, Gelfand EW: The late but not the early phase reaction in a murine model of asthma is dependent on IL-5 and tissue eosinophils. J Clin Invest 1999, 104:301–308.
Tomioka S, Bates JHT, Irvin CG: Airway and tissue mechanics in a murine model of asthma: alveolar capsules vs forced oscillations. J Appl Physiol 2002, 93:263–270.
Eidelman DN, Irvin CG: Airway mechanics in Asthma. In Asthma and Rhinitis 2 (Edited by: Busse WW). Holgate Street: Blackwell Science 2000, 1237–1247.
D'Angelo E: Dynamics. In Respiratory Mechanics. European Respiratory Monograph (Edited by: Milic-Emili J). European Respiratory Society 1999,4(12):54–67.
Rodarte JR, Rehder K: Dynamics of respiration. In Handbook of Physiology. The Respiratory System (Edited by: Macklem PT, Mead J). Bethesda, MD: American Physiological Society 1986,III(1):131–144.
Peslin R, Fredberg JJ: Oscillation mechanics of the respiratory system. In Handbook of Physiology. The Respiratory System (Edited by: Macklem PT, Mead J). Bethesda, MD: American Physiological Society 1986,III(1):145–178.
Irvin CG, Pak J, Martin RJ: Airway-parenchyma uncoupling in nocturnal asthma. Am J Respir Crit Care Med 2000, 161:50–56.
Lundblad KAL, Allen G, Irvin CG, Bates JHT: Reduced thoracic gas volume in a mouse model of acute lung injury. Am J Resp Crit Care Med 2001, 165:A785.
Takezawa J, Miller FJ, O'Neill JJ: Single breath diffusing capacity and lung volume in small laboratory animals. J Appl Physiol 1980, 48:1052–1059.
Fujita M, Shannon JM, Irvin CG, Fagan KA, Cool C, Augustin A, Mason RJ: Overexpression of tumor necrosis factor-alpha produces an increase in lung volumes and pulmonary hypertension. Am J Physiol Lung Cell Mol Physiol 2001, 280:L39-L49.
Tankersley CG, Rabold R, Mitzner W: Differential lung mechanics are genetically determined in inbred murine strains. J Appl Physiol 1999, 86:1764–1769.
Gross NJ: Mechanical properties of mouse lungs: effects of degassing on normal, hyperoxic and irradiated lungs. J Appl Physiol 1981, 51:391–398.
Mitzner W, Brown R, Lee W: In vivo measurement of lung volumes in mice. Physiol Genomics 2001, 4:215–221.
Kaminsky DA, Wenzel SE, Carcano C, Gurka D, Feldsien D, Irvin CG: Hyperpnea-induced changes in parenchymal lung mechanics in normal subjects and in asthmatics. Am J Respir Crit Care Med 1997, 155:1260–1266.
Wagers S, Lundblad L, Moriya HT, Bates JHT, Irvin CG: Non-linearities of respiratory mechanics during bronchoconstriction in mice with airway inflammation. J Appl Physiol 2002, 92:1802–1804.
Feynman RP, Leighton RB, Sands M: The Feynman Lectures on Physics: Quantum Mechanics (Edited by: Reading MA). Addison-Wesley 1965, III:1–11.
Hammelmann E, Schwarze J, Takeda K, Oshiba A, Larson GL, Irvin CG, Gelfand EW: Noninvasive measurement of airway responsiveness in allergic mice using barometric plethysmography. Am J Respir Crit Care Med 1997, 156:766–775.
Finotto S, Neurath MF, Glickman JN, Qin S, Lehr HA, Green HY, Ackerman K, Haley K, Galle PR, Szabo SJ, Drazen JM, De Sanctis GT, Glimcher LH: Development of spontaneous airway changes consistent with human asthma in mice lacking T-bet. Science 2002, 295:336–342.
Petak F, Habre W, Donati YR, Hantos Z, Barazzone-Argiroffo C: Hyperoxia-induced changes in mouse lung mechanics: forced oscillations vs. barometric plethysmography. J Appl Physiol 2001, 90:2221–2230.
Tankersley CG, Fitzgerald RS, Mitzner WA, Kleeberger SR: Hypercapnic ventilatory responses in mice differentially susceptible to acute ozone exposure. J Appl Physiol 1993, 75:2613–2619.
Albertine KH, Wang L, Watanabe S, Marathe GK, Zimmerman GA, McIntyre TM: Temporal correlation of measurements of airway hyperresponsiveness in ovalbumin-sensitized mice. Am J Physiol Lung Cell Mol Physiol 2002, 283:L219-L233.
Dixon NE, Brodie TG: Contribution to the physiology of the lungs. Part 1. The bronchial muscles, their inervation and the action of drugs upon them. J Physiol 1903, 29:97–173.
Ewart S, Levitt R, Mitzner W: Respiratory system mechanics in mice measured by end-inflation occlusion. J Appl Physiol 1995, 79:560–566.
DeSanctis GT, Merchant M, Beir DR, Dredge RD, Grobholz JK, Martin JR, Lander ES, Drazen JM: Quantitative locus analysis of airway responsiveness in A/J and C5+BL/6J mice. Nature Genetics 1995, 11:150–154.
Irvin CG, Tu YP, Sheller JR, Funk CD: 6-lipoxygenase products are necessary for ovalbumin-induced airway responsiveness in mice. Am J Physiol 1997, 272:L1053-L1058.
Vinegar A, Sinnett EE, Leith DE: Dynamic mechanisms determine functional residual capacity in mice, Mus musculus. J Appl Physiol 1979, 46:867–871.
Lai Y-L, Chou HC: Respiratory mechanics and maximal expiratory flow in the anesthetized mouse. J Appl Physiol 2000, 88:939–943.
Mortola JP, Noworaj A: Two-sidearm tracheal cannula for respiratory airflow measurements in small animals. J Appl Physiol 1983, 55:250–253.
Bates JHT, Irvin CG: Time dependence of recruitment and derecruitment in the lung: a theoretical model. J Appl Physiol 2002, 93:705–713.
Kanehiro A, Takeda K, Joetham A, Tomkinson A, Ikemura T, Irvin CG, Gelfand EW: Timing of administration of Anti-VLA-4 differentiates airway hyperresponsiveness in the central and peripheral airways in mice. Am J Respir Crit Care Med 2000, 162:1132–1139.
Takeda K, Haczku A, Lee JJ, Irvin CG, Gelfand EW: Strain dependence of airway hyperresponsiveness reflects differences in eosinophils localization in the lung. Am J Physiol Lung Cell Mol Physiol 2001, 281:L394-L402.
Hessel EM, Zwart A, Oostveen E, van Oosterhout AJM, Blyth DI, Nijkamp FP: Repeated measurement of respiratory function and bronchoconstriction in unanesthetized mice. J Appl Physiol 1995, 79:1711–1716.
Zwart A, Hessel EM: Oscillatory mechanics of the mouse respiratory system. Eur Respir Rev 1994, 4:182–186.
Hantos Z, Daroczy B, Suki B, Nagy S, Fredberg JJ: Input impedance and peripheral inhomogeneity of dog lungs. J Appl Physiol 1992, 72:168–178.
Ingenito EP, Mora R, Cullivan M, Marzan Y, Haley K, Mark L, Sonna LA: Decreased surfactant protein-B expression and surfactant dysfunction in a murine model of acute lung injury. Am J Respir Cell Mol Biol 2001, 25:35–44.
Gomes RFM, Shen X, Ramchandani R, Tepper RS, Bates JHT: Comparative respiratory system mechanics in rodents. J Appl Physiol 2000, 89:908–916.
Nagase T, Matsui H, Aoki T, Ouchi Y, Fukuchi Y: Lung tissue behavior in the mouse during constriction induced by methacholine and endothelin-1. J Appl Physiol 1996, 81:2373–2378.
Acknowledgements
The authors would like to acknowledge the support of NIH NHLBI grants HL 56638, HL 60793, PO1 HL 67004 and NCRR COBRE program PO1 RR-15557.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Irvin, C.G., Bates, J.H. Measuring the lung function in the mouse: the challenge of size. Respir Res 4, 1 (2003). https://doi.org/10.1186/rr199
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1186/rr199