Abstract
Background
Drafting in cetaceans is defined as the transfer of forces between individuals without actual physical contact between them. This behavior has long been surmised to explain how young dolphin calves keep up with their rapidly moving mothers. It has recently been observed that a significant number of calves become permanently separated from their mothers during chases by tuna vessels. A study of the hydrodynamics of drafting, initiated in the hope of understanding the mechanisms causing the separation of mothers and calves during fishing-related activities, is reported here.
Results
Quantitative results are shown for the forces and moments around a pair of unequally sized dolphin-like slender bodies. These include two major effects. First, the so-called Bernoulli suction, which stems from the fact that the local pressure drops in areas of high speed, results in an attractive force between mother and calf. Second is the displacement effect, in which the motion of the mother causes the water in front to move forwards and radially outwards, and water behind the body to move forwards to replace the animal's mass. Thus, the calf can gain a 'free ride' in the forward-moving areas. Utilizing these effects, the neonate can gain up to 90% of the thrust needed to move alongside the mother at speeds of up to 2.4 m/sec. A comparison with observations of eastern spinner dolphins (Stenella longirostris) is presented, showing savings of up to 60% in the thrust that calves require if they are to keep up with their mothers.
Conclusions
A theoretical analysis, backed by observations of free-swimming dolphin schools, indicates that hydrodynamic interactions with mothers play an important role in enabling dolphin calves to keep up with rapidly moving adult school members.
Similar content being viewed by others
Background
The problem of separation of mother-calf pairs in chase situations has become a serious concern in fishing-related cetacean mortality, in particular in the eastern tropical Pacific Ocean where tuna are fished with a purse-seine method, in which schools of dolphins are encircled with a fishing net to capture the tuna concentrated below [1]. The phenomenon of separation has been linked to the escape response of the mother, and has been described in detail in a pair of recent reports [2, 3]. The present study examines the hydrodynamics of dolphin mother-calf interactions, with the purpose of identifying possible reasons for loss of contact between mother and calf during chases.
The hydrodynamics of the drafting situation is extremely complex, as it deals with unsteady motions of two flexible bodies of different size, moving, while changing shape, at varying speeds and distances from the water surface and from each other, and periodically piercing the surface. In addition, there are several different preferred drafting positions for the calf [2], which appear at different ages and different modes of motion. These include the newborn being supported high on the mother's flank, within a few centimeters of her body, immediately following birth; this is sometimes called the 'neonate position'. It has been observed that neonates cannot control buoyancy well [2], and they tend to 'pop like corks' to the surface. Within a few hours the calf is moved down to a more lateral position (the 'echelon position'). This involves positioning of the infant within 10 cm of the mother's flank, with the neonate's dorsal fin a little anterior to, level with, or slightly behind, the mother's dorsal fin, and the neonate's body stationed vertically somewhere between the mother's upper body and mid-body. The echelon position is characterized by the infant making relatively few tail fluke movements as it 'drafts' alongside its mother, indicating a hydrodynamic advantage.
Older calves are seen more often in the 'infant position', which involves swimming under the mother's tail section with the neonate's head (or melon) lightly touching the mother's abdomen. Once they are several months old, calves swim in the echelon position about 40% of the time and swim in the infant position about 30% of the time. Gubbins et al. [4] report that at the age of 12 months, calves still spend about 50% of their time in close proximity to their mothers, with probabilities of 30% and 35% of finding a calf in the echelon or the infant position, respectively. Calves have apparently outgrown their dependence upon the mother by the end of the third year, and spend relatively little time in the echelon position, mainly swimming side by side with their mothers as adults do.
There is very little quantitative information on drafting in dolphins, and much of the extant data is qualitative (for example, 'close proximity' is not reported in actual distances in the different positions). Such data as do exist will be briefly reviewed here, and mentioned again when specifically used in the calculations later in this article.
The experimental comparisons used here are based on data for eastern spinner dolphins, Stenella longinostris, for which drafting situations (such as those discussed below and shown in Figure 1) were documented by aerial photography [5]; see Materials and methods section for further details. Physical data for the size and mass of dolphin calves and adults of several species are reviewed by Edwards [2], showing that the shape does not change significantly during growth, and thus the body shape from beak to caudal peduncle can be well approximated by a body of rotation of ellipsoidal shape and aspect ratio 6:1. (Data from [2] show that the actual aspect ratio decreases from about 6.3:1 for neonates, to 6:1 for adults.) Calves at birth are 85-90 cm long, while adults are up to about 190 cm [2], so that the mass ratio changes from 10:1 to 1:1 during the first three years of life. Drafting is observed at swimming speeds of up to 2.4 m/sec. For this aerobic speed range the ratio of swimming drag to gliding drag for dolphins is in the range 1 <β < 5, with the value of 3 applicable for average estimates [6].
Aerial photographs of swimming dolphins. (a) An actual leaping sequence; (b) several mother-calf pairs swimming at high speed. In (a), the calf performs a bad leap, resulting in a large splash (frame 4), slowing it down and losing the close connection required for drafting. The data in (b) are the basis for several of the entries in Table 4.
In some aerial records of mother-calf pairs moving at high speed, one can observe the calf moving from one side to the other obliquely behind the mother. This motion may be due to the bias in yaw that the calf experiences when moving on one side, and an attempt to 'even' this out, by periodically changing sides.
The first step in the analysis is to try to extract the dominant effects of the postulated hydrodynamic interaction and to build a simplified model, which will be able to give quantitative predictions for the major parameters, without losing relevance. This model can then serve as a building block for further, more complicated descriptions. This procedure is complicated, however, by the fact that empirical data are scarce and partial with large inherent errors. Such a model should be simple enough to be solvable by semi-analytic methods before delving into full numerical analysis, the accuracy of which will be compromised by the large scatter in experimental input data.
Obviously the model needs to be accurate and detailed enough to give useful results. Lang [7] made a list of possible interactions, based in part on the analysis by Kelly [8]. In the latter paper, it is assumed that the flow is described by classical solutions of two equal-sized spheres moving at the same speed, either in the direction of the line of centers, or perpendicular to this line [9, 10]. These solutions show the great advantage of the inviscid flow assumption, which allows linearization, and thus superposition of solutions, such that the two existing solutions can be combined to form the flow-field around two spheres at any orientation to the oncoming flow. While Kelly's work [8] showed that there is a possibility of one sphere producing a pressure field that can produce thrust on an object in certain neighboring areas, the spherical model is too crude to offer accurate enough insight into the forces on nearby elongate bodies, especially when there is a big size difference between the interacting bodies, as in neonate drafting. Kelly's results [8] are based on Lamb's [9] approximate method of reflections, which, as he mentions, results in errors of up to 12% for touching spheres, dropping to 0.3% at one radius separation. Since that work was performed, exact solutions for the two-sphere interaction have been calculated [11], but the differences do not qualitatively change the conclusions reached by Kelly [8], and therefore the two-sphere model is still not accurate enough to be a predictive, or even an explanatory, tool for drafting.
Results and discussion
The modeling process is started by looking at drafting in water far enough from the surface to neglect surface wave (Froude number) effects. Viscosity (boundary layer) effects are left out at this stage, allowing the use of the linear, potential flow model. This will allow superposition of solutions, as mentioned above. Effects of viscosity will be included where required at a later stage (see below). This is the equivalent of using the Kutta-Joukowski condition in airfoil theory [10], which simulates the results of viscous effects into an inviscid computation.
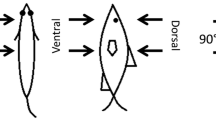
Next, assume that both mother and calf are moving without changing body shape - that is, with a fixed (rigid) body shape (no tail oscillations). On the basis of observations on several dolphin species, this shape is taken to be an oblate ellipsoidal shape of aspect ratio of about 6 (see Figure 2). Lang [7] used a similar approach, defining the body shape as a 6:1 ellipsoid with an added tail region, which adds 20% to the length and 20% to the total surface area. The effects of swimming motions are partly accounted for by adjusting the drag coefficient to include the effects of swimming, as mentioned in the Background section. Further effects of the swimming motions are discussed later.
Thus the drag on a swimming dolphin will be estimated as that of a 6:1 ellipsoid moving in the direction of its long axis, multiplied by 3, while a coasting dolphin will have the drag of a 6:1 ellipsoid. The drag on streamlined bodies at zero angle of attack (measured between the direction of motion and the animal's longitudinal axis) is well known [12]. The drag coefficient decreases only very slightly as the Reynolds number grows (that is, speed increases, or calf size changes with age), and also as the body aspect ratio changes slightly with age, as mentioned previously. These changes are small enough for us to take equal drag coefficients for both mother and calf.
The basic premise here is that drafting is advantageous as a result of the mother producing a flow-field that has areas of forward-moving water, resulting from a non-uniform pressure field. When the calf positions itself in these areas, it needs to produce less thrust, as the relative velocity it experiences is lower than the absolute speed of motion, and the energy required is roughly proportional to the relative velocity cubed. This is the same principle I and others used in developing models for fish schooling [13, 14], wave riding by dolphins [7, 15] and other drafting situations, such as duckling motions behind their mothers [16].
A series of cases simplified sufficiently to allow semi-analytical solutions (that is, solutions that do not require numerical analysis of the differential equations, but use computations to obtain numerical values of the solution functions) are now analyzed. The flow around ellipsoidal shapes is calculated. As mentioned above, these closely approximate dolphin shapes, when excluding fins. First a single ellipsoid is analyzed, and then two ellipsoidal shapes of equal or different sizes in close proximity.
Motion of a single ellipsoid
The first model developed here is of a single ellipsoid moving in still waters. The flow field obtained is an accurate representation of the force on each point in the flow field and can be seen as the flow field experienced by a body much smaller than the ellipsoid itself. Thus, such a calculation is a good approximation for the positioning of pilot fish in the vicinity of sharks, but less so for dolphin calves, which at birth are already about one half the length, and over one tenth of the mass, of an adult [2].
This model is only an approximation to the flow pressure distribution on a large body, showing the generally advantageous areas for calf positioning. Figure 3 shows the flow field around a moving 6:1 ellipsoid. The significant point to notice is the area in front of the body's equator, within the forward 20% of the length (to the left of x = -5) based at the body center of mass, in which there is a forward component of velocity forced upon the surrounding water. This is essentially the water being pushed out of the way by the approaching body. This is maximal directly in front of the body's 'nose', as the lateral component of velocity vanishes there (not shown). The lateral component grows, and the forward component is reduced, until at about x = -0.5 the forward component vanishes, and further downstream the x component of velocity becomes negative. This means that the area beyond the cone mentioned above is bad for the calf, as the relative velocity is larger. The negative longitudinal induced velocity is maximal at the ellipsoid equator, where the lateral component vanishes. Moving backwards, a symmetric situation is observed, with gradually growing lateral velocity and a smaller longitudinal component until, at about x = +4.5, the longitudinal velocity becomes positive, such that a second advantageous area for the calf is obtained. This flow is a result of water moving in after the body to fill the volume vacated as the body moves forward. The 'best' position again is directly behind the body, where the forward velocity is maximal, reaching the forward velocity of the body itself.
A snapshot description of the flow around a single ellipsoid moving from right to left at speed U. The length units are normalized by the maximum diameter of the 6:1 ellipsoid. Lines indicate the paths of individual fluid 'particles' as they are pushed out of the way and then 'sucked' back in after the body has moved forward. Arrows indicate the direction of motion.
But the positions identified here need to be carefully scrutinized to make sure that they are relevant when the simplifications in the model are taken into account. Thus, some of the 'best' positions predicted by this model are irrelevant. These are as follows: first, a position just ahead of the mother's nose, being 'pushed' forward; this position will not be adopted for several reasons, including that the pushing motions are unstable [17] and thus considerable energy and skill (not available to the calf) would be required to keep this position; also, this position would disturb the mother and interfere with her navigation. Second, a position just behind the mother's rear end. Again, in the real situation, the tail motions result in a different flow pattern, including a jet moving backwards relative to the mother's body, which cancels out the effect identified by the simplified model. Third, the zone adjacent to the body, behind the equator, is dominated by body motions when the animal is swimming, so that the horizontal line (actually a cylinder) tangent to the equator in Figure 3 delineates another zone in which this simple model is not relevant.
Thus, the actual best positions will be obliquely in front, and obliquely behind the mother's center-line. The forward position is less practical, for the reasons explained above, and so is used only in the first few hours after birth. The remaining preferred zone is obliquely behind the mother's equator, which is more reminiscent of the 'infant' position, to which we will return later. All positions, except directly in front of or behind the mother's center-line, experience lateral velocity components, which need to be compensated for by a lateral force if the calf is to swim in a straight line. Thus, an optimal trade-off between forward velocity contribution and loss due to sideways compensation can be found.
Two slender ellipsoidal shapes moving in proximity
Here, the analysis is based on the studies by Tuck and Newman [18], and Wang [19] of the interactions of forces and moments produced by two slender ships moving in close proximity, at low enough Froude numbers that the free surface can be assumed to be flat. Interestingly, they modeled the ships as being equivalent to axisymmetric bodies moving deep under the surface, which is very different than their original application, as ships are far from being submerged ellipsoids of revolution. Fortuitously, however, the model is directly applicable to the present case of two submerged dolphins, which are much closer to axisymmetric shapes. The actual motion of the mother-calf pair is now translated into the motion of two slender, ellipsoidal shapes moving at different velocities (Figure 4). The coordinate system as presented by Tuck and Newman [18], and Wang [19] is here adjusted to present requirements so that the calf is body 1 and the mother is designated body 2. A review of the basics of slender body theory is presented in the additional data file, with only the final equations required for actual calculations appearing below. The model thus describes the effect of the mother moving next to a calf, showing the forces on the calf.
As mentioned in the additional data file, each of the bodies can be defined by a distribution of doublets along the longitudinal axis

where we take

where d is the doublet strength, S i (x i ) is the cross sectional area, i = 1 describes the calf, I = 2 the mother, and D i is the maximum area of each at the equator. Without loss of generality, the calf is assumed to be non-moving and the mother moving at U2 relative to the calf.
After some rather complicated algebraic development (see the additional data file), one can finally obtain expressions for the forces by substituting equation (1) into equations (A-8) and (A-9) in the additional data file. The force in the longitudinal direction on the calf (that is, the force pushing the calf forward) is:

and the lateral (side) force (including the Bernoulli effect mentioned by Kelly [8]) is

where ρ is water density, ξ is the horizontal distance between center-lines, η is the lateral distance between center-lines, and the remainder of the terms also appear in Figure 4. The yawing moment on the calf (definitions and further discussion of the forces and moments on moving dolphins can be found in [20]) is

Some results of these calculations are presented in non-dimensional form, in Figure 5.
The forces on the calf calculated from equations (2) and (3). Definitions of the parameters appear in Figure 4. (a) The non-dimensional peak longitudinal force X max (thrust) on the calf as a function of the normalized lateral distance η/L1 from the mother, for different mother/calf size ratios (as indicated by the numbered arrows). The dashed red line indicates closest probable proximity. The ratios relevant here are from 1 (fully grown calf - the solid blue line) to 2 (neonate). (b) The non-dimensional peak lateral force on the calf, for different mother/calf size ratios, as a function of the normalized lateral distance η/L1 from the mother. The peak lateral force is obtained when the centers of mass of mother and calf are on a line perpendicular to the long axis (ξ = 0 in Figure 4). The curve marked 'wall effect' describes the lateral force on the calf when moving close to a wall, as in a tank. (c) The variation of forces and moments as one animal is placed at different normalized longitudinal positions relative to the other in the fore-aft direction. Positive values on the horizontal axis indicate that the mother's center is ahead of the calf. The lateral distance is one quarter of the calf's length. The curves marked X are the non-dimensional longitudinal force and Y is the normalized lateral (Bernoulli) force. Positive values indicate forward force and attraction, respectively, while negative values represent backward forces and repulsion, respectively. Two sets of curves are shown, for neonate calves (where the mother is twice as long; in solid blue), and for equal-sized animals (fully grown calf; dashed red line).
These results are now applied to the dolphin-drafting situation. The mother and calf are in the same horizontal plane, but the results are applicable also for depth differences, as the assumption is that both are approximated by bodies of revolution, so that all that is required is that the plane including the two center-lines is defined as the horizontal.
Figure 5a shows the non-dimensional peak longitudinal force on the calf, as a function of the normalized lateral distance from the mother. This force will appear at the position described before, when the calf centroid is slightly behind the mother's equator. Recalling that the newborn calf is roughly one half the length of the mother, L2/L1 is 2 at birth, so that the top line is applicable. Both mother and calf are approximately 6:1 ellipsoids, so that the minimal distance in terms of calf length is η/L1 = 0.16, with a value of 0.2-0.3 probably best to avoid collisions, beyond the first few hours after birth. The non-dimensional force can be seen to be about 3.3 at η/L1 = 0.3 for newborn calves, going down to about 1.3 for almost fully grown calves (when L2/L1 ≈ 1). The dotted red line in Figure 5a shows the probable minimal separation so that collision is avoided.
Figure 5b shows the peak lateral force that occurs when the equators of both are side by side, when ξ = 0. Comparing values from Figure 5a and Figure 5b, we see that the lateral force is three to five times times the longitudinal force. This is the so-called Bernoulli effect. The presence of the neighboring calf body causes the flow on the mother's body on the side closer to the calf to move faster, and thus produces a pressure drop - leading to a suction force 'pulling' the calf to the mother (and vice versa, but the effect on the mother is less important). This is significant mainly in the newborn and echelon positions. It is also used in 'bolting with infant' baby-snatching occurrences during the first weeks after birth, in which an adult female stranger swims by the mother-calf pair at high speed, attracting the calf [21]. Again, the dotted red line in Figure 5b shows the minimal distance to avoid collision. Here, higher ratios of length are calculated, to show the approach to the limit of moving next to a wall, which results in strong attraction.
Figure 5c is somewhat different, as it looks at how the effects change with relative longitudinal (fore-aft) positions of the two animals. In this case, two limiting cases are presented, the first where the calf is half the length of the mother (as for a neonate), and the second where both animals are the same size (adult). This figure is thus not to be used directly for calculating forces and moments, but is presented in order to show the preferential areas. Thus, looking first at the longitudinal force X and starting with the calf being far ahead of the mother (at the left side of the curve) the calf experiences a growing forward force, reaching a first maximum when its center-line is at the mother's head. This is one of the impractical maxima predicted by the single-ellipsoid model mentioned earlier. The forward force drops, and becomes negative, rising again to a zero value when the two animals are abreast of one another. When the mother's equator is somewhat ahead of the calf's, the maximal thrust is provided when the calf's center of mass is approximately at two-thirds of the mother's length. This probably corresponds to the infant and echelon positions. The position of the thrust maximum does not vary with the mother/calf size ratio. The fact that the relative position does not change as the calf grows is probably very useful, as the calf has to learn to find only one such position. The lateral force Y has full fore-aft symmetry. The maximal force is obtained when the animals are side by side, and is about three to four times as large as the maximal forward force, thus being the most dominant effect (the Bernoulli effect). This is especially important for very young calves, where it acts as a suction force keeping them by their mothers. Here again, the optimal position does not change with calf size.
Force calculations
To find the actual forces in specific cases, we need to define a normalizing coefficient based on specific data, to make the remaining terms in the integral dimension-free. This coefficient is obtained by taking all constants in equations (2) to (4) out of the integration. The coefficient is thus

Recalling that we assumed 6:1 ellipsoidal bodies of revolution for both mother and calf with no allometric changes during growth, the ratios S i /L i 2 can be calculated once and for all as

From [2] we see that drafting is observed at swimming speeds that are up to U = 2.4 m/sec. We take the mother's length to be about 1.9 m and the neonate's length as 0.95 m. Substituting these values into the equation for the non-dimensionalization factor K, we obtain for the neonate:
K = 1030*2.42*0.952*0.02182 = 2.54 (7)
A reasonable minimal distance between mother and calf center-lines is the sum of half the mother's thickest section plus half the calf's thickest section. This is 1.9/12 + 0.95/12 = 0.24 m for the neonate, and 2*1.9/12 = 0.32 m for a fully grown calf. The spacing parameter is therefore at best η/L1 = 0.25 for neonates and η/L1 = 0.17 for fully-grown calves.
The maximal forward force on the calf can now be obtained from Figure 5a. The non-dimensional value is about 4.16, so applying equation (7) it is found that the force is about 4.16*2.54 = 10.6 N. The maximal Bernoulli attraction is close to three times as large (the non-dimensional value for η/L1 = 0.25 and length ratio L2/L1 = 2, in Figure 5b, is about 12.1), at about 12.1*2.54 = 27.9 N.
These values can now be compared to viscous drag on the calf, recalling that the drag force is defined as D = 0.5ρ U2ACD' where A is the surface area and C D is the drag coefficient. At speeds of 2.4 m/sec the drag coefficient based on wetted area for a 6:1 ellipsoid is approximately 0.003 [12] in the longitudinal direction. The surface area of the 0.95 m calf is about 1.5 m2, so that the drag is about 12 N for the stretched body and about 36 N for the swimming calf. Comparing these drag estimates to the forward and lateral forces found previously, it is seen that the drafting forward force is close to 90% of the total drag force (that is, 10.6/12 for a coasting, stretched-straight calf) and the Bernoulli suction is much larger, but in a different direction. Thus, even when considering the enhanced drag when performing swimming motions, we see that the mother can provide a large proportion of the force required for a neonate. These numbers are reduced for larger calves, but this is again reasonable, as the larger calves are both more powerful and more adept at swimming. The cost to the mother is increased by the presence of the calf, obviously, as the curve for thrust (X) is antisymmetric.
Next, the effect of increased lateral distance between the center-lines of mother and calf is assessed. This is obtained from Figure 5a by moving along lines of constant L2/L1. As mentioned above, a reasonable minimal distance between mother and calf center-lines is the sum of half the mother's thickest section plus half the calf's thickest section. Table 1 shows the loss in forward force as the distance grows beyond 0.24 m by a quantity ε.
As shown above, the mother can provide close to 90% of the thrust needed for the calf to move at 2.4 m/sec when the mother and coasting calf move side by side, almost touching. Table 1 shows that even when they are laterally separated by 30 cm (two calf diameters) the mother can still provide 3.3/12 = 27% of the required thrust.
A similar calculation for full-grown calves, where L1 = 1.9 m, and L2/L1 = 1, appears in Table 2. The minimal distance is again taken to be the sum of the body half-thicknesses. This sum is now 1.9/12 + 1.9/12 = 0.317 m. The nominal non-dimensional distance is then η/L1 = 0.317/1.9 = 0.167. The factor K, from equation (5) is now K = 10.16, and this is used to generate the figures in Table 2, applying the values from Figure 5.
Tables 1 and 2 show that the gains from drafting are concentrated in an area close to the mother, with the slope of the decrease not changing as the calf grows. This is true also of the side forces, as shown in Table 3. As the thrust required for a fully grown calf is much (about four-fold) larger than for a neonate, however, the percentage gain is smaller, being about 62% (=29.8/(12*4) when ε = 0, and only 25% when ε = 30 cm. These percentages are for coasting, fully grown calves. We expect fully grown calves to swim most of the time, so that the drag is about three times as large, and the real savings will be only about 20%, at best. This probably helps explain why less drafting is observed as the calf grows: the relative gain decreases, while the calf has more stamina. On the other hand, this may lead to loss of contact in strenuous chase situations where the calf needs more help.
Similar results can be obtained for the side force and yawing moments. We only show the side force on the neonate, for which the Bernoulli effect is most important. This appears in Table 3, which is based on Figure 5b. Tables 1, 2, 3 show the effects of changes in lateral (in the horizontal plane) distance. In some of the aerial records of mother-calf pairs moving at high speed, however, one can observe the calf moving from one side to the other obliquely behind the mother. As mentioned previously, this motion may be due to the bias in yaw that the calf experiences when moving on one side, and an attempt to even this out by periodically changing sides.
The rapid decrease of the transmitted forces with lateral distance is a clear indication that forced 'running', as in chases by fishing vessels, can easily cause loss of the mother-calf connection. Moving at high speeds will require strenuous, large-amplitude motions by both mother and calf, so that in order not to interfere with each other they would have to enlarge the lateral distance, from almost touching (ε = 0) to a safe distance. Thus, a significant conclusion here is that long high-speed chases, where the drafting gain for the calf is much smaller as a result of the increased lateral distance, are much more dangerous. This is in addition to the fact that there is less time for catching up after an error in judgment by mother or calf. It is interesting to mention, in this context, that adult schooling dolphins, which are usually more widely dispersed, tend to move closer to each other when chased, perhaps attempting to use some of these hydrodynamic advantages. This is also observed in fish schools [13, 14].
Further hydrodynamic effects
In order to obtain an exact mathematical solution to the drafting problem, I had to make some simplifying assumptions: first, the propulsive motions were not accounted for; second, no free surface effects were considered (water of infinite depth); third, inviscid flow was assumed; and fourth, uniform velocity (no jumps) was assumed. The effects of relaxing these assumptions are now examined, to see what effect such relaxation has on the results presented above. Obviously, only rough estimates of these additional, complicated effects can be made.
Effects of propulsive motions
The propulsive motions of the mother and calf are now considered. These can be described as a vertical oscillation of the body and caudal flukes, with amplitude minimal at the shoulders, and growing as one moves rearwards. For example, Romanenko [22] presents a case in which the distribution of maximal vertical excursion along the body of Tursiops truncatus is approximated by

where h T is the maximal vertical excursion of the fluke and xn = x/L is the longitudinal coordinate measured from the beak, divided by the animal's length, L. The actual periodic excursions of the body center-line are h = h max sin(2πt/ν) where the amplitude h max is obtained from (8), ν is the frequency and t is time. As mentioned previously, the body swimming oscillations increase drag by a factor of about three [6, 20]. Thus, the hydrodynamic benefits of interaction, which do not increase due to the propulsive motions, are reduced by this factor. Presumably the calf will have a large swimming drag penalty factor, at least during the first few days and weeks of its life, until it masters the 'secrets' of efficient swimming and overcoming the effects of buoyancy. As a result, there is a clear advantage for the calf to swim in the 'burst-and-coast' mode [20, 23, 24], in which it swims by body oscillations for a short burst, then coasts for a while, repeating this behavior periodically.
In the burst-and-coast mode, the animal accelerates during the burst and decelerates during the coast. Thus, a calf using this mode of energy saving would appear to move relative to the mother. This would appear as forward motion during the burst, and slipping backwards during the coast. It might be difficult to observe this behavior, as the effectiveness of the burst-and-coast rises (more energy is saved) when the bursts are short and the velocity does not change appreciably [20]. For example, at an average swimming speed of about 3.2 m/sec, the energy required for burst-and-coast swimming is only 37% of that required for constant-speed swimming. This means that the swimming drag penalty for the calf is essentially eliminated at mother and calf cruising speeds, as the swimming drag would be only 3*0.37 = 1.11 times the coasting drag. At higher speeds, say about 6.4 m/sec, the best achievable saving is approximately 0.56, which means that the swimming drag on the calf, even when using burst-and-coast, would be 3*0.56 = 1.68 times the coasting drag. This is probably one of the reasons for calves becoming detached from mothers at higher swimming speeds: the cost increases by 1.68/1.11 = 1.51. This 51% increase in cost, when combined with the fact that the energy required goes up roughly as the speed cubed, means a 12-fold total increase in energy required (1.51 * 6.43/3.23 = 12.1) by the calf to keep up with the mother when the swimming speed doubles from 3.2 m/sec (fast cruising) to 6.4 m/sec (escape speeds).
It may seem that using burst-and-coast could be counter-productive, as the calf moves away from the rather narrow range of beneficial positions. This loss can be minimized if the calf starts the burst and accelerates when it is at the optimum position for maximum forward force, at about 65% of the mother's length where the acceleration is easiest (Figure 5c), and coasts when the surge force contribution drops, as it approaches the mother's center-line, thus dropping back to the more advantageous positions.
The propulsive motions cause a periodically varying pressure field, which affects the results shown previously in two additional ways. First, the fact that the body, and especially the caudal flukes, produce a backward-moving wake makes the zone directly behind the mother highly undesirable, as moving in that area means moving against a backward-flowing current (as in schooling [13, 14]). Thus, the calf should be located outside of two cones with apices at the mother's head and tail. The cone around the tail is larger, due to the larger vertical excursions, which puts the apex here further forward (Figure 6).
In the analysis for non-oscillating ellipsoids presented in the previous section, the effects are axially symmetric, such that any angular displacement between the line connecting the center-lines of mother and calf and the horizon gives the same result. It is clear, however, that moving closely above or directly below the mother is more difficult, because of the vertical body oscillations (and, in addition, the surface effects if the calf were to be above the mother). As a result, we see that the calf is limited to zones between approximately 45° above and below the mother's center-line. The next question addressed here is what are the preferred positions for the calf, in the vertical plane, relative to the mother.
Logvinovich showed (as cited in [22], page 135) that for slender bodies the pressure field around a circular cross section performing transverse oscillations is:

where p is the local pressure, p8 is the undisturbed pressure, ρ is the water density, and r and θ are polar (cylindrical) coordinates. Here the angle θ is measured from the vertical (see the front view in Figure 6c), t is time and V n is the vertical excursion velocity. V n can be related to the vertical excursion of the dolphin's body as

where U is the dolphin's forward speed [22] and h is defined in the paragraph following equation (8). Here, only the time-averaged angular dependence of the pressure is needed. This is defined by the factor 1 - 4sin2θ in equation (9). The added pressure is positive (repulsion) for 0° <θ < 30°, negative (attraction) for 30° <θ < 150° and positive again for 150° <θ < 180°. So, the calf should be within 60° upwards and downwards from the horizontal, relative to the mother, for the Bernoulli suction shown above to be most effective. Within this sector, the vertical motions of the mother increase the suction force. This increase grows as the calf's center of mass is located further backwards relative to the mother, but is canceled out by the larger excursions of the mother's body, which means that the deviations from the mean attractive force are larger and thus more difficult to adjust to. The conclusion is that the swimming motions actually increase the Bernoulli attraction somewhat, with the preferred position for this attractive force still roughly laterally to the mother's center of mass. More exact calculations of this contribution are not realistic, as the assumptions of slender body theory are relatively inaccurate in this situation, and are mainly used to show trends.
Looking at cases where the mother helps the calf, and not vice versa, the mother's propulsive motions are defined as a periodic vertical motion of the rear part of the body and caudal flukes. This motion produces forces, which are evident in the backwards-moving thrust component of the wake, that are, at least near the animal, distinct from the drag part of the wake. The thrust component appears as a reverse, thrust-type Kármán vortex street [14, 25]. The drag part is the shed boundary layer, an annular mass of water moving forward (relative to the earth). Far behind the dolphin these two components cancel out in the case of constant-speed swimming, as from Newton's law there is no net motion far from a body moving at constant speed.
In the study of fish schooling mentioned previously [13, 14], I showed that a following fish can save energy by choosing the right position relative to a leader. That analysis is fully applicable here after rotating the plane of motion by 90° to accommodate the vertical motions of the dolphin. The analysis is based on the fact that while the reverse Kármán vortex street produces an undulating backwards-moving jet, relative to the vortices, between the vortices it produces a forward-moving component of velocity outside that area. Translating this observation to the drafting situation, the area directly within the rectangle roughly defined by the extreme positions of the mother's caudal flukes during propulsive motions is an area of higher backwards velocity than elsewhere. This means that a calf that finds itself in the box defined by this rectangle and the longitudinal axis (see side-view in Figure 6a) will have to work against a higher current than if it were elsewhere. On the other hand, being either slightly above or below this box puts the calf in a position where it will need less energy to keep up with the mother. This effect is probably very important for suckling situations, especially for neonates. The real drag wake is obviously three-dimensional, such that it will appear as a series of tilted vortex rings, but the two-dimensional vortex street model, while probably quantitatively inaccurate, gives a good description of the preferable zones for the calf to occupy.
Recently some studies have appeared [26, 27] on fish utilizing regular Kármán vortex streets from fixed bodies. This is not directly relevant to the present situation, as the flow directions are reversed, but is useful as experimental evidence for using periodic vortices as a drafting accessory; thus, this serves as proof that such vortices are detectable and can be utilized. Actually, there is an additional small gain possible by using forward momentum in the boundary layer shed by the mother, when the calf is in the suckling position. The propulsive oscillations will result in boundary layer separation so that the suckling calf will be able to benefit from this layer. This gain is small, however, as will be shown by the following argument. The total boundary layer momentum shed per unit time is, at most, equal to the drag force on the mother. This boundary layer has an annular shape with elliptical cross section. Thus, the part that the calf will pass through is relatively small, and the gain is similarly small.
A rough estimate for a neonate with 16 cm diameter is presented next. The detached wake of the swimming mother has a total circumference of roughly πD m + 2*0.2L m where the subscript m stands for the mother; D m = 32 cm and L m = 1.9 m. The second term is due to the oscillations. So, the calf will pass through 16/(π*32 + 2*0.2*190) = 0.0625; the gain in thrust due to the shed boundary layer can therefore be, at best, 6.2% of the drag on the mother's fore-body (or about 3% of the total drag on the mother, which is approximately 12% of the neonate's drag at the same speed). It is important to mention here that this gain can be obtained even when the mother is coasting, so one can predict that suckling calves will preferentially draft during coasting.
Free surface effects
The main influence of the free surface of the water is to increase the energy required to move at a given speed as a result of the energy wasted on lifting the free surface. This can be roughly modeled by an increase in drag coefficient, by a factor of up to 5, depending on the ratio of depth to body hydraulic diameter, and on the swimming speed (Froude number); further details may be found in [28–30]. This means that the gains due to the different hydrodynamic effects discussed in this and the previous reports are reduced. When dolphins are relatively close to the surface the practical conclusion from the previous statement is that dolphin calves are expected to be deeper than the mother, in the lower quadrants shown in the front view in Figure 6c. Thus, the calf is expected to be at a depth equal to, or greater than, that of the mother, except when very young. As mentioned previously, neonates cannot control buoyancy well, and tend to 'pop like corks' to the surface [2]. In this case, being slightly above the mother's depth may help, in that the hydrodynamic suction towards the mother's body will help reduce the upwards force due to the positive buoyancy. Unfortunately, in chase situations the rate of breathing is increased, so that swimming has to occur closer to the surface. Thus, just when the calf needs the most assistance, the drag is increased beyond the nominal value because of wave drag.
Another free-surface effect stems from the fact that the interaction is negligible when in air, so that breaching effectively breaks up the drafting interaction. This effect is not too harmful for juveniles, as the ballistic motion the mother and calf perform means that if they leave the water together, and return together, they will be able to re-establish drafting. But infants, and especially neonates, who are less adept at porpoising, may either breach or return at non-optimal penetration angles (see analysis below, and Figure 7), increasing their drag and causing a speed differential. In addition, if the calf does not emerge from the water at the right angle, its aerial trajectory will be shorter. The calf will end up further behind the mother, and would then have to catch up.
Viscous flow
Viscous flow theory is required to estimate the original drag force on the animal, before calculating the interactive corrections. However, as we are interested in the mother-calf interactions here, we do not need this type of calculation. Furthermore, as the Reynolds numbers are large (R = O(106)), the boundary layer approximation is sufficiently accurate. This means that only thin layers of fluid are affected by viscosity. The thickness of these layers is not more than 1-3% of the body radius, so that the body may be assumed to be that much thicker and to move in inviscid fluid (displacement thickness model). At distances of 25-50% of body radius, where the calf may be found, the effects are therefore negligible, to the level of accuracy of the present discussion.
Synchronization of jumping
At high swimming speeds, dolphins usually resort to porpoising [20, 30]. To examine whether this might be a factor in separation, the surface-piercing event is broken up into five steps: step 1, horizontal swimming before the event; step 2, water exit; step 3, aerial motion; step 4, water return; and step 5, horizontal swimming after the event. Steps 1 and 5 are regular drafting situations and thus do not require specific consideration here. Step 3 is a ballistic trajectory for which the distance crossed in a jump is a function of speed and angle only, but not of animal mass (see equation 11)

Thus, if the mother-calf pair exits the water at the same speed and angle as each other, they will land in the same relative positions as when leaving. On exit, leaving at the wrong angle can reduce the distance crossed in the air; this effect, however, is very small. From equation (11), the maximum distance is achieved at 45°. Thus, the difference in distance is

and

For a calf jumping at 40° (a 5° difference), the decrease in distance jumped is only 0.015 (1.5%), and even if the calf jumped at 30° the difference in distance crossed by the center of mass, while out of the water, is 0.134 (13.4%). For 50°, from equation (13), the difference in distance crossed is again only 0.015 (1.5%) as the decrease is symmetrical with respect to the angular difference from the maximal 45°. The distance the mother can cross, when moving at 2.4 m/sec is, from equation (11), above, about 59 cm, and at 4 m/sec it is 1.63 m. Thus, even at the higher speed, a 15° error by the calf will result in only a 22 cm longitudinal displacement in landing.
Next, steps 2 and 4 are examined. If re-entry is at same penetration angle (the angle between the animal's long axis and the horizon) for both mother and calf, the only differences that may occur are a result of the spray energy being proportional to animal mass (equation 2 from [20])

Here, β is the ratio of swimming to gliding drag (usually about 3 for strenuous swimming, as mentioned previously); m is the added mass coefficient, which is a function of angle of incidence between the animal's long axis and the direction of motion. The added mass coefficient m ranges from about 0.2 for swimming in the longitudinal direction [31] to about 1.0 for broadside motion of smooth bodies of revolution, such as the ellipsoid. M is the animal mass and U the speed. The energy E j is proportional to animal mass so, all other parameters being equal, the energy lost by the smaller calf is less, but can be a higher proportion of the calf's energy store. For example, neonates can have less than 40% of the oxygen-storage capacity of adult dolphins [32]. This is probably a minor consideration, however, when compared to the effects of possible differences in attitude when leaving and re-entering the water.
The stretched straight dolphin was modeled as a 6:1 ellipsoidal body. The splash produced by such a shape, when penetrating water, is highly dependent on the angle between the body longitudinal axis and the angle of penetration, with the lowest value being, naturally, when these angles are equal (see Figure 7). This is roughly mirrored in the change in value of m as described above: the splash energy lost if the ellipsoid hits the water surface broadside, which is roughly proportional to the penetrating body's area parallel to the surface, will be at least five times that of the same ellipsoid moving in the direction of its long axis. This increase is even before accounting for separation of flow, and other drag-enhancing factors. Thus, leaving or re-entering the water at the wrong attitude (the angle between body axis and penetration angle not being zero) can result in massive slowing of the body.
Optimal exit and entry require that the animal change orientation in mid-air from roughly 45° above the horizon when exiting, to roughly 45° below the horizon for re-entry. In practice, dolphins are observed to exit at 30-45° [33], but this does not change the present argument. This pitching rotation of the body is easily achieved by adults and experienced juveniles, but may be more difficult for neonates, who can 'lose' twice, both on exit, as a result of carrying more water as spray on exit, thus slowing down, and on re-entry when they encounter much higher drag. Copying the mother's motions will probably enable the calf to exit smoothly, but water entry is probably more difficult. An additional point to note is that the infant position is harder to keep in acceleration towards leaping, as it requires synchronization of tail beats, so it makes sense for the calf to move to the echelon position when leap-burst-and-coast motion starts.
Comparison with existing observations
Observations of drafting in the literature have been sparse and mainly anecdotal, and almost no data of the accuracy and detail required were found. Data collected from flights over spinner dolphin groups [1] are the only reliable data found. Ten instances of assumed mother-calf pairs were found to be sufficiently clear to extract measurements. These are shown in Table 4; five of the mother-calf pairs appear in Figure 1b. These pairs were analyzed using the following procedure.
First, I assumed the larger animal in each pair to be the mother, and took its size to be 1.90 m [2] from nose to caudal peduncle. This defined the scale of the photograph. Using the same scale, and assuming that any possible depth differences between mother and calf were negligibly less than the altitude of the airborne camera so that parallax effects on the size could be neglected, I obtained the calf length L1 in Table 4 and the ratio of L2/L1. Using the same scaling, the lateral distance between center-lines of the mother and calf η and the non-dimensional value η / L1 were obtained. Next, the longitudinal displacement of centers of mass ξ was measured, and its value normalized by the mother's length ξ/L2. This displacement ξ/L2 was used to find the value of thrust (X) force from calculations such as those shown in Figure 5c. Figure 5c is calculated for two cases: that of equal-sized mother and calf, and for a 2:1 length ratio. As we see, for different-sized calves only the numerical values change, not the shape of the curve. Thus, we can find the value of the X force, relative to the maximum forward force, depending on the coordinate ξ/L2. From Figure 5c we see that the maximum is obtained approximately at ξ/L2 = 0.35, so that, for example, for pair A2, ξ/L2 = 0.22, so that X/X max = 0.90.
Next, we find the maximal thrust (X max ) for this case from Figure 5a, given the values for L2/L1 and η/L1. Taking again pair A2 as the example, we have L2/L1 = 1.48 and η/L1 = 0.36. From Figure 5a the ordinate is then Ordinate = 1.76. We now use equation (5) to obtain the actual force in newtons, assuming a swimming speed of 2.4 m/sec and the calf length of 1.28 m from Table 4. The force is then:
X = X max *0.9 = K* Ordinate* 0.9 (15)
Where, in this case,

So that X = 1.76*4.62*0.9 = 7.3 N.
Recalling that the drag on a newborn calf coasting at 2.4 m/sec was estimated at 12 N, and that the drag coefficient does not change because of geometric similarity, the drag increases simply with surface area (length squared). We can thus estimate the drag on a calf of length L1 coasting at 2.4 m/sec by equation (16)

which for the calf of pair A2 is 21.8 N.
So, we finally determine that, in this case, the drafting thrust is 7.3/21.8 = 0.33 of the force required for the calf to coast. This value appears as X/X req in Table 5. From this column we see that energy savings of up to 61% were available to the calves pictured, with only one case (A3) in which no thrust interaction was obtained. Table 6 summarizes the side-force interactions for these 10 pairs, showing large forces in some cases. There is no clear correlation between Bernoulli forces produced and calf size; one might be led to think that larger (or even relatively larger) Bernoulli forces would be produced by mothers with small calves, but this trend is not in evidence here. This Bernoulli force does not cause rapid attractive motions bringing the mother and calf to collision, as the drag coefficient in the broadside direction is at least five times the value for motion along the longitudinal axis [12].
Figure 1a shows a sequence of snapshots of a mother-calf pair leaping, in which the calf, probably a neonate, misjudged the attitude angle and so produced a large splash and ended up far behind the mother, in a zone where essentially no drafting gains are possible. This calf is therefore at risk of detachment and loss. Unfortunately, the recorded sequence ended as this point, so the later development of this situation is unknown.
Conclusions
Drafting has been shown to enable adult dolphins to help their young by reducing the forces required of the young for swimming. Several separate hydrodynamic effects join to produce this interaction. Under ideal conditions, the drafting force can counteract a large part of the drag experienced by a neonate calf. Examination of aerial photographs of eastern spinner dolphin mother-calf pairs shows that the predicted preferred positions for the calf to maximally benefit from these hydrodynamic effects are found in most cases. There is a need for more controlled experimental data to be able to improve the current model, especially where the effects of viscosity and free surface penetration are concerned, and to ascertain whether burst-and-coast motions are found when dolphins flee tuna fishermen. The clear implication for dolphin chases is that long chases at high speeds will result in an increased probability of separation of mother-calf pairs, as a result of a combination of fatigue on the calf's side, decreased help from the mother due to the larger body oscillations by both mother and calf, and the increased probability of erroneous leaping.
Materials and methods
Aerial photography
Images were taken in the eastern tropical Pacific Ocean from a Hughes 500D helicopter flying at approximately 60 knots (around 110 km/h) at about 250 m altitude (Figure 1a) and 220 m (Figure 1b). The camera was a 126 mm Chicago Aerial Industries KA-76 with a 152 mm lens, f = 5.6, and shutter speed 1/1200 sec, based on ambient light conditions, using Kodak Plus-X type 3404 black-and-white film. The images were converted to digital format by magnifying under the microscope by 1.25× (in each image, 1 mm is approximately 170 pixels).
Additional data file
The following is provided as an additional file: a brief overview of slender body theory used for the calculation of flow around a pair of slender bodies (Additional data file 1).
References
Archer F, Gerrodette T, Dizon A, Abella K, Southern S: Unobserved kill of nursing dolphins in a tuna purse seine fishery. Mar Mamm Sci. 2001, 17: 540-554.
Edwards EF: Behavioral contributions to separation and subsequent mortality of dolphin calves chased by tuna purse-seiners in the eastern tropical Pacific Ocean. Southwest Fisheries Center Administrative Report LJ-02-28 June. 2002
Edwards EF: Energetic consequences of chase by tuna purse-seiners for spotted dolphins (Stenella attenuata) in the eastern tropical Pacific Ocean. Southwest Fisheries Center Administrative Report LJ-02-29 June. 2002
Gubbins C, McGowan B, Lynn S, Hooper S, Reiss D: Mother-infant spatial relations in captive bottlenose dolphins, Tursiops truncatus. Mar Mamm Sci. 1999, 15: 751-765.
Perryman WL, Westlake RL: A new geographic form of the spinner dolphin, Stenella longirostris, detected with aerial photogrammetry. Mar Mamm Sci. 1998, 14: 38-50.
Skrovan RC, Williams TM, Berry PS, Moore PW, Davis RW: The diving physiology of bottlenose dolphins (Tursiops truncatus). II. Biomechanics and changes in buoyancy at depth. J Exp Biol. 1999, 202: 2749-2761.
Lang TG: Hydrodynamic analysis of Cetacean performance. In Whales, Dolphins and Porpoises. Edited by: Norris KS. 1966, Berkeley: University of California Press, 410-432.
Kelly HR: A two body problem in the echelon swimming of porpoise. Naval Ordnance Test Station Technical Note 40606-1. 1959
Lamb H: Hydrodynamics. 1932, New York: Dover, 6
Milne-Thomson LM: Theoretical Hydrodynamics. 1968, New York: Macmillan, 5
Weihs D, Small RD: An exact solution of the motion of two adjacent spheres in axisymmetric potential flow. Isr J Technol. 1975, 13: 1-6.
Hoerner SF: Fluid Dynamic Drag. 1965, Bricktown NJ: published by author
Weihs D: Hydromechanics of fish schooling. Nature. 1973, 241: 290-291.
Weihs D: Some hydrodynamical aspects of fish schooling. In Swimming and Flying in Nature. Edited by: Wu TYT, Brokaw CJ, Brennen C. 1975, New York: Plenum Press, 703-718.
Fish FE, Rohr JJ: Review of dolphin hydrodynamics and swimming performance. Space and Naval Warfare Systems Command Technical Report 1081, San Diego. 1999
Fish FE: Kinematics of ducklings swimming in formation: energetic consequences of position. J Exp Biol. 1995, 272: 1-11.
Weihs D: Stability versus maneuverability in aquatic locomotion. Integr Comp Biol. 2002, 42: 127-134.
Tuck EO, Newman JN: Hydrodynamic interactions between ships. In Proceedings of the 10th Symposium on Naval Hydrodynamics (ACR-204): Cambridge MA. Washington DC: Office of Naval Research. 1974, 35-58.
Wang S: Dynamic effects of ship passage on moored vessels. J Waterways Harbors Coast Eng Div (ASCE). 1975, 101: 247-258.
Weihs D: Dynamics of dolphin porpoising revisited. Integr Comp Biol. 2002, 42: 1071-1078.
Mann J, Smuts BB: Natal attraction: allomaternal care and mother-infant separations in wild bottlenose dolphins. Anim Behav. 1998, 55: 1097-1113. 10.1006/anbe.1997.0637.
Romanenko EV: Fish and Dolphin Swimming. 2002, Moscow: Pensoft, 127-
Weihs D: Energetic advantages of burst swimming of fish. J Theor Biol. 1974, 48: 215-229.
Fish FE, Fegely JF, Xanthopoulos CJ: Burst and coast swimming in schooling fish, with implications for energy economy. Comp Biochem Physiol. 1991, 100A: 633-637. 10.1016/0300-9629(91)90382-M.
Weihs D: Semi-infinite vortex trails and their relation to oscillating airfoils. J Fluid Mech. 1972, 54: 679-690.
Webb PW: Entrainment by river chub Nocomis micropogon and smallmouth bass Micropterus dolomieu on cylinders. J Exp Biol. 1998, 201: 2403-2412.
Liao JC, Beal DN, Lauder GV, Triantafyllou MS: The Kármán gait: novel body kinematics of trout swimming in a vortex street. J Exp Biol. 2003, 206: 1059-1073. 10.1242/jeb.00209.
Newman JN: Marine Hydrodynamics. 1977, Cambridge, MA: MIT Press
Hertel H: Structure, Form and Movement. 1966, New York: Reinhold
Au D, Weihs D: At high speeds dolphins save energy by leaping. Nature. 1980, 284: 548-550.
Webb PW, Weihs D, Eds: Fish Biomechanics. 1983, New York: Praeger Press
Noren SH, Lacave G, Wells RS, Williams TM: The development of blood oxygen stores in bottlenose dolphins: implications for diving capacity. J Zool (Lond). 2002, 258: 105-113. 10.1017/S0952836902001243.
Hui CA: Surfacing behavior and ventilation in free-ranging dolphins. J Mammal. 1989, 70: 833-835.
Acknowledgements
I thank Elizabeth Edwards for asking the questions that resulted in this paper and her careful and helpful monitoring of the project, F. Archer, W.F. Perrin, and S. Reilly for useful discussions, W. Perryman and K. Cramer for permitting the use of their unpublished photographs (Figure 1) and O. Kadri and T. Haimowitz (deceased) for helping with the calculations. This study was supported by NOAA/NMFS Southwest Fisheries Science Center.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
13061_2003_40_MOESM1_ESM.pdf
Additional data file 1: A brief overview of slender body theory used for the calculation of flow around a pair of slender bodies (PDF 38 KB)
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Weihs, D. The hydrodynamics of dolphin drafting. J Biol 3, 8 (2004). https://doi.org/10.1186/jbiol2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1186/jbiol2