Abstract
The comprehensive identification of cis-regulatory elements on a genome scale is a challenging problem. We develop a novel, steganalysis-based approach for genome-wide motif finding, called WordSpy, by viewing regulatory regions as a stegoscript with cis-elements embedded in 'background' sequences. We apply WordSpy to the promoters of cell-cycle-related genes of Saccharomyces cerevisiae and Arabidopsis thaliana, identifying all known cell-cycle motifs with high ranking. WordSpy can discover a complete set of cis-elements and facilitate the systematic study of regulatory networks.
Similar content being viewed by others
Background
The comprehensive identification and characterization of short functional sequence elements has become increasingly important as we begin to elucidate transcriptional regulation on a large scale. Transcriptional regulation involves a complex molecular network. The interaction of transcription factors (TFs) and cis-acting DNA elements determines the expression levels of different genes under various environmental conditions [1]. Deciphering such a network is to infer regulatory rules that can properly explain the expressions of different genes with the regulatory elements in their promoters and the presence of TFs [2, 3]. Therefore, a complete set of regulatory elements is essential for systematic analysis of transcriptional regulation networks on a genome-wide scale.
The discovery of cis-regulatory elements in a genome has been a challenging problem for decades. Most widely applied approaches first cluster genes into small groups with similar expression profiles or similar biological functions, and then search for common short sequences (or motifs) in the regulatory regions of the genes in a group. This is based on the assumption that coexpressed genes are more likely to be co-regulated. Many efficient algorithms, including multiple local alignment-based [4–7], word enumeration-based [8], and dictionary-based [9], have been developed to search for statistically significant motifs from a small number of sequences. Despite the success of these methods, this approach has noticeable limitations. Computational gene clustering is often inaccurate and subjective, in terms of what similarity measure to use and how many clusters to form. Importantly, many genes belonging to a common pathway may have similar expression patterns, but are not regulated by the same TFs. Furthermore, transcriptional regulation is combinatorial [1], in that a regulatory element needs to combine with various others to function under different conditions. This means that the same motif may appear in the promoters of genes that express or function differently. Therefore, clustering genes into small sets may split the genes containing a particular set of motifs into different clusters, which makes it difficult, if not impossible, to find all regulatory elements [10].
In recent years, comparative genome analysis has been successfully applied to the discovery of regulatory motifs [11, 12]. Taking advantage of sequence conservation in related species, this approach can effectively identify regulatory elements on a genome scale without any prior knowledge of co-regulation or gene function. This approach is limited in some situations, however. First, the species considered in a comparative analysis must be properly diversified evolutionarily. They must be evolutionarily separated long enough to allow nonfunctional elements to diverge. On the other hand, they must not be evolutionarily too far apart from one another so that functional elements remain conserved. For many applications, not many such genomes are available. Second and more important, there exist species-specific regulatory elements, which a comparative genomic method can hardly detect.
In this paper we propose a novel genome-wide approach to comprehensively identify regulatory elements from a single genome. Instead of clustering genes into groups, we use all the genes of interest together - for instance, the genes related to a particular biological process such as the cell cycle or the genes responding to a particular stress condition. In this approach, we first search for statistically over-represented motifs as completely as possible. We then use additional information, such as the coherency of expression profiles of genes containing a motif and the specificity of a motif to target genes, in order to evaluate the biological relevance of the extracted motifs so as to find truly functional regulatory elements.
We view this genome-wide motif-finding problem from a perspective of steganography and steganalysis. Steganography is a technique for concealing the existence of information by embedding the messages to be protected in a covertext to create a 'stegoscript' [13]. Steganalysis is the deciphering of a stegoscript by discovering the hidden message [13]. In this approach, we consider the regulatory regions of a genome as though they constituted a stegoscript with over-represented words (that is, regulatory elements) embedded in a covertext (that is, 'background' genomic sequences). We then model the stegoscript with a statistical model - a hidden Markov model [14] - consisting of a dictionary of motifs and a grammar. We progressively learn a series of models that are most likely to have generated the script. The final model is then used to decipher the stegoscript as well as to extract over-represented motifs. On the basis of this novel viewpoint, we have developed an efficient genome-wide motif-finding algorithm called WordSpy that can discover a large number of motifs from a large collection of regulatory sequences. Note that our technical approach of using a dictionary is inspired by the work of Bussemaker et al. [15], in which they introduced innovative ideas of segmenting sequences into words and building a dictionary of words from the sequences.
Our WordSpy method has several salient properties. First of all, by statistically modeling the regulatory regions as stegoscripts, WordSpy aims to discover a complete set of significant motifs. Therefore, instead of being trapped by some pseudo-motifs, for example, over-represented repeats, WordSpy includes them in its model, making it less vulnerable to spurious motifs. Second, WordSpy combines word counting and statistical modeling. It applies word counting to efficiently detect high-frequency words. It then enhances the representation of words by position weight matrices (PWMs) [16] to capture degenerate motifs. Third, WordSpy is able to detect discriminatory motifs that can be used to properly separate two sets of sequences. Finally, by incorporating gene-expression information and a genome-wide specificity analysis, we augment the basic algorithm in order to distinguish biologically relevant motifs from spurious ones, making the overall method practical for genome-wide identification of functional cis-regulatory elements, as we will demonstrate here.
We will first evaluate the method with an English stegoscript and 645 cell-cycle-related genes of Saccharomyces cerevisiae. We will then apply it to identify cell-cycle-related motifs from more than 1,000 genes in model plant, Arabidopsis thaliana. Furthermore, we will apply WordSpy as a discriminative motif-finding algorithm by incorporating TF location information - that is, chromatin immunoprecipitation DNA binding microarray (ChIP-chip) data - and build a dictionary of motifs for each known TF of budding yeast. Finally, we compare WordSpy with a set of existing methods on a benchmark that includes 56 well-curated sets of sequences and motifs in four species [17].
Results and discussion
Stegoscripts and the statistical model
The regulatory regions of a genome encode transcriptional regulatory information using regulatory elements embedded in background sequences. We can thus view the regulatory regions of the genes of interest as a stegoscript, which conceals the secret messages (cis-elements) with some covertext (background sequences). The hidden secret messages are typically more conserved and statistically over-represented than those in the covertext. This is particularly true for genomic regulatory sequences, where a small number of TFs regulate a large number of genes [1], making functional cis-elements over-represented.
Consider a set of regulatory sequences or a stegoscript S = (S1,S2,...,S
q
) where S
i
= (Si1Si2... ) and l
i
is the length of the ith (i = 1, 2,..., q) sequence. Deciphering the script is to annotate the sequences with a series of substrings χ = (x1,x2,...,x
t
), where x
j
denotes the jth substring with length l(x
j
), which can be a background word or a functional element. In general, a stegoscript is a product of a grammar, by which all possible scripts in the language can be generated by successively rewriting strings according to a set of rules. Therefore, we model the stegoscript statistically. The model captures regulatory motifs and background words by a dictionary, and specifies how the motifs and words are used to form the stegoscript by a grammar. Given the statistical model, χ is just the optimal parse over S using the words in the dictionary.
) and l
i
is the length of the ith (i = 1, 2,..., q) sequence. Deciphering the script is to annotate the sequences with a series of substrings χ = (x1,x2,...,x
t
), where x
j
denotes the jth substring with length l(x
j
), which can be a background word or a functional element. In general, a stegoscript is a product of a grammar, by which all possible scripts in the language can be generated by successively rewriting strings according to a set of rules. Therefore, we model the stegoscript statistically. The model captures regulatory motifs and background words by a dictionary, and specifies how the motifs and words are used to form the stegoscript by a grammar. Given the statistical model, χ is just the optimal parse over S using the words in the dictionary.
To accurately capture the transcriptional mechanism encoded in the regulatory regions requires a complicated grammar, which may be computationally not feasible. To reduce computational complexity, we consider that motifs are used independently. Therefore, we can use a stochastic regular grammar [18], which is equivalent to a hidden Markov model (HMM) [14]. Figure 1 illustrates the model. Beginning with a start symbol, a motif symbol M is produced with probability P
M
, or a background symbol B is generated with probability P
B
. From M, a degenerate motif W
i
is produced, with probability  , from the motif subdictionary, and an exact word w is generated with probability P(w|W
i
). The process for generating a background word from symbol B is similar. The generated word is then appended to the script that has been created so far and the process repeats until the whole script is created.
, from the motif subdictionary, and an exact word w is generated with probability P(w|W
i
). The process for generating a background word from symbol B is similar. The generated word is then appended to the script that has been created so far and the process repeats until the whole script is created.
A hidden Markov model for deciphering stegoscripts. It consists of two submodels, the 'secret message model' is for motifs and the 'covertext model' for background words. The blue boxes with dashed outlines each represent a word node, which is a combination of several position nodes. Node W b is a single-base node and always belongs to the covertext model. States S, B, and M do not emit any letter.
We formally write the model as G = {Ψ, Θ, I}, where Ψ = {P
B
,P
M
, } is the set of transition probabilities, Θ = {Θ
b
, Θ1, Θ2,..., Θ
n
} is a set of emission probabilities corresponding to the motifs and words in a dictionary D = {W
b
,W1,W2,...,W
n
}, and I = {
} is the set of transition probabilities, Θ = {Θ
b
, Θ1, Θ2,..., Θ
n
} is a set of emission probabilities corresponding to the motifs and words in a dictionary D = {W
b
,W1,W2,...,W
n
}, and I = { |W
i
∈ D} is a set of indicators, where
|W
i
∈ D} is a set of indicators, where

W
b
is the only word in the model that has a single base. As we never consider a word of single base as a functional element, W
b
is always a background word, that is,  is always set to 0.
is always set to 0.
The WordSpy algorithm
The central problem of deciphering a stegoscript is learning a statistical model with which a stegoscript was created. Assume that a stegoscript S was generated from an unknown model 〈D*, G*〉 of a dictionary D* and a grammar G*. With no prior knowledge of the true model, the maximum likelihood estimate, arg max〈D', G'〉 P(S|〈D', G'〉), is a good approximation of 〈D*, G*〉. However, it is difficult to directly search for arg max〈D', G'〉 P(S|〈D', G'〉), as a large number of words need to be discovered and many unknown parameters to be optimized. Therefore, we separate the learning process into two phases, 'word sampling' and 'model optimization', and adopt an incremental learning strategy to progressively capture short to long words and gradually build such a model (see Materials and methods).
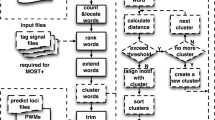
The procedure for learning the model and subsequently deciphering the regulatory sequences is shown in Figure 2. The overall algorithm starts with the simplest model 〈D1, G1〉 with only a background word W
b
in D1. At the kth iteration, the algorithm first runs word sampling to identify all over-represented words of length k. In this process, the algorithm scans the script S once to tabulate all the words of length k in S and their occurrences using a hash table. Every word in the table is then tested against the current best model  which contains over-represented motifs shorter than k. A word is considered over-represented if it occurs in S more often than expected by
which contains over-represented motifs shorter than k. A word is considered over-represented if it occurs in S more often than expected by  . Furthermore, the newly discovered words will be examined (to separate background words) and clustered, if necessary, to form degenerate preliminary motifs. All new words and motifs will be merged with the current best dictionary
. Furthermore, the newly discovered words will be examined (to separate background words) and clustered, if necessary, to form degenerate preliminary motifs. All new words and motifs will be merged with the current best dictionary  to form the next dictionary D
k
. The model is retrofitted to accommodate the new words, leading to the next grammar, G
k
. The new grammar G
k
is then optimized to fit the script. The word statistics are recalculated in the model optimization step and the insignificant words are discarded. The process repeats until the model covers words up to a predefined maximum length.
to form the next dictionary D
k
. The model is retrofitted to accommodate the new words, leading to the next grammar, G
k
. The new grammar G
k
is then optimized to fit the script. The word statistics are recalculated in the model optimization step and the insignificant words are discarded. The process repeats until the model covers words up to a predefined maximum length.
Components and flow diagram of WordSpy. Starting with k = 1 and a grammar G0 with a single word node W
b
in background, the algorithm goes through the following steps, represented by the red numbers on the figure. 1. Model Gk-1 is optimized to  which contains over-represented motifs shorter than k. 2. Use
which contains over-represented motifs shorter than k. 2. Use  as a base model to detect over-represented exact words of length k. 3. Choose over-represented words for word clustering. 4. Evaluate all the words. Select and add background words to the background model. On the basis of similarity, cluster the rest of the words to form degenerate preliminary motifs. 5. Add the preliminary motifs to the motif sub-dictionary and create a new grammar G
k
. 6. Optimize G
k
. 7. Apply optimized
as a base model to detect over-represented exact words of length k. 3. Choose over-represented words for word clustering. 4. Evaluate all the words. Select and add background words to the background model. On the basis of similarity, cluster the rest of the words to form degenerate preliminary motifs. 5. Add the preliminary motifs to the motif sub-dictionary and create a new grammar G
k
. 6. Optimize G
k
. 7. Apply optimized  to decipher the script and locate motifs.
to decipher the script and locate motifs.
The classification of real motifs and background words is important to the accuracy of the model. When no extra information is available, we resort to a word significant threshold to select putative motif words. We use the Z-score to quantify the over-representation of a word (see 'Word sampling' section in Materials and methods). If more information is available, such as gene-expression coherence in G-score and target gene specificity in Z g -score (see 'Motif evaluation' section in Materials and methods), more accurate classification can be made.
Deciphering an English stegoscript
We evaluated the performance of WordSpy with a stegoscript of English text that contains the first ten chapters (approximately 112,000 letters) of the novel Moby Dick embedded within randomly generated covertext (approximately 156,000 letters). This stegoscript was created by Bussemaker et al. [15]. We ran WordSpy with different Z-score thresholds to find words up to length 15. WordSpy reached its best performance with Z-score threshold 6. With covertext removed, the deciphered text contains 16,522 words. Among the total 18,930 words that appear at least twice in the original text, 13,435 (70.9%) words are 100% matched to their corresponding deciphered words, and 15,529 (82%) words overlap at least 50% with their corresponding deciphered words. Only 761 (4.6%) deciphered words match less than 50% to their counterparts in the original text. This result shows that WordSpy can accurately decipher the stegoscript and recover Moby Dick from the covertext with high specificity and sensitivity (see Additional data file 1 for a detailed analysis and more results).
Identifying yeast cell-cycle regulatory motifs
To evaluate the performance of WordSpy on biological sequences, we applied it to discover cis-regulatory elements of cell-cycle related genes of S. cerevisiae [19]. To avoid bias, we first removed homolog genes using WU-BLAST with an E-value threshold of 10-12, resulted in 645 genes in the final set. The promoter sequences were retrieved using the RSA tools [20]. We compared WordSpy with three other methods, MobyDick [15], RSA-tools [21] and Weeder [22], which can handle a large number of sequences. We tuned these programs to get their best possible parameters. The Z-score threshold for WordSpy was set to 3. The whole-genome analysis on the specificity of the motifs, Z g -scores, was performed with the promoters of all the genes in S. cerevisiae. We also used the yeast gene expression data collected in [23] to calculate the G-score for each motif. As shown in Table 1, all known cell-cycle-related cis-elements were identified with high ranking in either Z g -score or G-score. In contrast, MobyDick failed to discover three of them, and RSA-tools and Weeder missed four of them.
MBF and SBF are predominant TFs in the G1/S phase of the yeast cell-cycle. Their binding motifs, MCB (ACGCGT) and SCB (CRCGAAA) [24], are consistent with the top motifs discovered by WordSpy. Among 199 discovered motifs of length 7, AACGCGT ranks the first in both Z g -score and G-score, CGCGAAA is the second in G-score and the third in Z g -score, and CACGAAA ranks the 10th in Z g -score and the 17th in G-score. Another prominent motif GTAAACA (the 8th in Z g -score and the 10th in G-score) has been reported to be the binding motif of Fkh2 (or Fkh1) [25], which is involved in cell-cycle control during pseudohyphal growth and in silencing of MHRa [26]. WordSpy also identifies the binding motifs of Ace2/Swi5 and Met4/Met28 with high G-score ranking, and the binding motifs of Mcm1 and Ste12 with high Z g -score ranking.
Figure 3 displays the distribution of all discovered motifs of length 8 in reference to the Z g -score. The motifs that overlap with some known motifs by at least six nucleotides are displayed in a different color. This result shows that most of the top-ranking motifs based on the Z g -score resemble known motifs. To facilitate motif selection, we clustered similar motifs. The motifs were first sorted by Z g -score or G-score. From the highest to the lowest rankings, we took a motif that had not been clustered as a seed, and grouped it with all the motifs that shared a common substring of length 6 (out of 8 base pairs) with the seed or its reverse complementary. Combining the top 20 clusters of all motifs of length 8 based on Z g -score and G-score, all the known motifs are identified (see Tables 3 and 4 in Additional data file 1). All these encouraging results suggest that by combining Z g -score and G-score analysis, WordSpy can comprehensively identify real motifs from a large set of regulatory sequences with a high specificity.
Identifying Arabidopsiscell-cycle regulatory motifs
Cell-cycle regulation in plants is more complicated than that in yeast or even mammals. One possible explanation is that the sessile life-style of plants requires a more sophisticated mechanism for growth or development to adapt to adverse environmental conditions [27]. What makes the study of the cell-cycle in plants more appealing is that some plant cells have surprisingly long life spans and are extremely resistant to cancerous conditions. Understanding how plant cells are controlled during development may shed light on the control of human cell proliferation [27].
In this study, we applied WordSpy to identify regulatory elements of 1,081 cell-cycle regulated genes of A. thaliana, which were identified by a high-throughput expression profiling experiment [28]. After having removed homologous genes with an E-value threshold of 10-12, we had 1,030 genes left for analysis. The promoter sequences were obtained from TAIR database [29]. We ran WordSpy to find motifs with lengths up to 10. The Arabidopsis whole-genome transcription-profiling data under normal growth conditions from the Weigel lab [30] were used to calculate motif G-scores.
Figure 4 shows the distribution of 5,277 discovered over-represented words over gene specificity in Z g -score (x-axis) and gene expression coherence in G-score (y-axis). We considered words with a G-score greater than 0.2 as biologically significant, and used Z g -score thresholds of greater than 3.0 or less than -1.0 to select cell-cycle-related or unrelated motifs. With these criteria, motifs are split into six categories, as shown in Figure 4. The motifs in region I are putative cell-cycle-related motifs that we are mostly interested in. Region II also contains many putative binding motifs for cell-cycle genes, which may not be specific to cell-cycle processes. The motifs in region IV are putative motifs that are more plentiful in non cell-cycle genes. The motifs in regions III and V are the ones that are statistically significant although their target genes do not express coherently. We can consider the rest of the words in the middle region as background words as they do not satisfy either criterion.
Distribution of all discovered motifs from Arabidopsis cell-cycle-related genes. The x-axis is the genome Z-score (Z g -score) of a motif, which measures the motif's specificity to the cell-cycle genes. The y-axis is the G-score of a motif, which measures the coherency of the expression profiles of the genes whose promoters contain the motif.
There are 110 motifs in region I of Figure 4 (see Tables 5 and 6 in Additional data file 1). We clustered them to obtain 55 motifs (see Additional data file 2). We selected 14 of the 55 motifs, which are similar to some known motifs listed in the plant motif databases PLACE [31] and PLANTCARE [32], and present them in Figure 5.
Selected putative Arabidopsis cell-cycle-related motifs. ID, the ranking of a motif in the overall list. The third column gives the number of cell-cycle genes whose promoters contain the motif. The following four columns are the number of target genes in S and M phases of the cell cycle and the corresponding P value. GO analysis gives the functional group with the best P value, which is shown in the last column.
To further evaluate whether WordSpy can indeed find functional cis-regulatory elements, we analyzed these 55 clustered motifs with respect to different cell-cycle phases. The expressions of 247, 343, 131, and 247 of the 1,081 cell-cycle genes peak in G1, S, G2, and M phases, respectively [28]. On the basis of this target gene distribution in each phase, we calculated the specificity of each motif to every phase of the cell cycle. For example, 79 of 122 target genes containing motif 2 (ID = 2, Figure 5) are M-phase genes. When randomly selecting 122 genes from the set of cell-cycle genes, the chance to have 79 M phase genes is less than 3 × 10-14. Therefore, motif 2 is very likely to be an M-phase motif. Surprisingly, all the motifs in Figure 5 have very low p values in either M phase or S phase. More interestingly, most motifs with low p values in M phase match well with the mitotic-specific activation (MSA) elements (consensus YCYAACGGYY) [33], and the motifs with low p values in S phase resemble motifs E2F (TTTYYCGYY) [34], Octamer and Hexamer [35], which are known S-phase motifs.
Furthermore, to reveal possible functions for each of the 55 motifs, we calculated the enrichment of gene ontology (GO) terms [36] within the genes containing the motif (see Materials and methods). Figure 5 shows that almost every motif has some enriched functional categories (p value < 1e-2). The most common functional category is the cyclin-dependent protein kinase regulator activity (CDK). Interestingly, many motifs related to CDK are MSA elements or resemble MYB-like motifs, suggesting that MYB-like TFs regulate cyclin kinase-like proteins in G2M phase of the cell cycle. Motif 28 (TTCACCTAC, Figure 5) does not match with any known motif. However, all its 11 target genes peak in S phase, and all seven target genes with GO annotations are related to catalytic activity, implying that this is a novel functional motif. We report all new putative functional motifs in Additional data file 2.
MSA motifs are position dependent
The top four motifs of length 7 ordered by G-score - AGCCGTT, GACCGTT, ACCGTGG, and GGCGCCA - have both significant Z g -score (> 3.0) and G-score (> 0.2). The first three of these motifs resemble MSA elements (consensus CYAACGGYY) [33]. We investigated their position distribution on the promoters of the cell-cycle genes containing the motifs. The result is shown in Figure 6. Three MSA motifs - AGCCGTT, GACCGTT and ACCGTTG - are significantly over-represented near the transcription start sites (TSSs).
We further studied the most significant motif of length 10, ACTAGCCGTT, which is ranked the first in Z g -score (11.4) and the second in G-score (0.718) (see Table 5 in Additional data file 1). Figure 7 shows the expression patterns of the genes whose promoters contain ACTAGCCGTT on either strand. Both heat-map and profile chart demonstrate a highly coherent expression pattern, except for three outliers, AT3G61640, AT5G13100, and AT5G23480. Remarkably, the loci of the motif on these outliers are far away from their TSSs, as shown in Figure 8. Moreover, these cell-cycle genes, except the outliers, are all M-phase related according to the experiment in [28]. These results suggest that MSA motifs are position dependent, and usually close to TSSs.
Expression patterns of Arabidopsis genes associated with ACTAGCCGTT. The gene-expression profiles are highly coherent except three outliers - AT3G61640, AT5G13100, and AT5G23480. (a) Heat-map analysis of microarray expression patterns. (b) Profile analysis of microarray expression patterns. Expression profiles are clustered into two groups. The profiles in both red and blue have similar patterns, but the profiles in red have relatively low values.
E2F binding motifs may vary in cell-cycle related and unrelated genes
Various studies have shown that in addition to the cell cycle, the genes containing binding motif E2F appear in many functional categories including transcription, stress defense, and signaling [37]. As expected, we also identified many E2F-like motifs in region II. Table 2 shows the discovered motifs that match to the known E2F binding elements (consensus TTTYYCGYY) [34]. The motifs in cluster 1 are in the motif region I of Figure 4 with Z g -score greater than 3.0. This cluster of motifs corresponds to motif 8 in Figure 5. The motifs in cluster 2 are in the motif region II with Z g -score less than 3.0. Obviously, the motifs in cluster 1 are more specific to cell cycle than those in cluster 2. These two sets of motifs differ only by two nucleotides in their core sequences. The motifs that are more cell-cycle specific have 'GG' in the middle (TTTGGCGCC), whereas the motifs that are abundant in the genome contain 'CC' in their core sequences (TTTCCCGCC). Among the cell-cycle genes, TTTGGCGCC appears in 14 promoters and TTTCCCGCC in 10 promoters. In the whole genome, 100 genes have TTTGGCGCC in their promoters and 257 genes have TTTCCCGCC.
In summary, these observations indicate that the preferential cell-cycle-related E2F motif is TTTGGCGCC, and the non-cell-cycle related E2F motif is TTTCCCGCC. In other words, the E2F binding motifs differ based on whether or not they are cell-cycle related. Our results also demonstrate that the WordSpy method can detect such subtle and important difference in regulatory elements.
Finding discriminative motifs
Given two sets of scripts or sequences, a discriminative motif is such a motif that is over-represented in one script but not in the other. WordSpy is, in essence, an algorithm for finding discriminative motifs, because of its intrinsic feature of modeling motifs and background words in an integral model. Here, background words can be extracted from one set of sequences (negative set), while the discriminative motifs are identified from another set of sequences (positive set).
We applied WordSpy as a discriminative algorithm to find regulatory motifs in S. cerevisiae. We constructed positive and negative sequence sets based on the ChIP-chip experiments of Lee et al. [38]. For a particular TF, we selected as the positive dataset those promoters that the TF could bind to with p values < 0.01 in the ChIP-chip experiments and as the negative dataset those promoters with p values > 0.99. We also applied two widely used algorithms, MEME [5] and AlignACE [7] to the same data. MEME was executed with a sixth-order Markov model on the yeast noncoding regions as background. Table 3 lists the motifs that are closest to the known cell-cycle-related motifs from these three algorithms. As shown, WordSpy not only found all known motifs for each TF but also the known motifs of cofactors. MEME and AlignACE were able to find most known motifs, but missed some binding sites of cofactors.
Evaluation with a benchmark study
Recently, Tompa et al. [17] developed a benchmark of a set of well-curated regulatory sequences and cis-regulatory elements of budding yeast, fruit fly, mouse, and human for evaluating motif-finding algorithms. They introduced seven statistical measurements to assess the performance of 13 motif-finding programs. An interesting observation on their results is that the enumeration-based methods, represented by Weeder [22] and YMF [8], outperformed the model-based approaches, represented by MEME [5] and AlignACE [7].
Almost all the sets of sequences in the benchmark are relatively small; none of them has more than 35 sequences. Aimed at finding motifs from a large number of sequences, for example, more than 1,000 promoters of genes related to cell cycles in Arabidopsis, WordSpy was not originally designed to deal with a small number of sequences. Nevertheless, it can be used to find motifs from a small set of sequences and has a very competitive performance, as we show here. We applied WordSpy to the sets of sequences in the benchmark and compared it with the other programs studied by Tompa et al. [17]. For fair comparison, we did not use gene-expression information in WordSpy, but rather used only genomic sequences to calculate the Z g -scores. Moreover, although WordSpy discovered a set of motifs for each sequence set, we reported the most significant motif with some selection criteria. For all the experiments, we built a dictionary up to word length 10. Then we filtered out the motifs with Z g -scores less than 4. Finally, we selected the motif with the highest Z-score or Z g -score depending on their site distributions. We always chose the ones that are close to the TSSs.
Figure 9 shows the comparison results of WordSpy with the 13 programs (Weeder [22], YMF [8], RSA-tool [21], QuickScore [39], AlignACE [7], ANN-Spec [40], MEME [5], Consensus [6], MIRTA [41], GLAM [42], Improbizer [43], MotifSampler [44], SeSiMCMC [45]) on the seven statistics introduced in [17]. A detailed description of these statistics is available on the benchmark website [46]. As shown in Figure 9 and Additional data file 3, WordSpy outperforms the other programs by all the measures. Figure 10 shows true positive versus false positive in both nucleotide level and site level for all the programs. WordSpy has the highest numbers of true positives and relatively low numbers of false positives in both cases. The success of WordSpy may be due to the following reasons. First, WordSpy aims to discover all over-represented motifs; the chance of it missing a significant motif is low. Second, the Z g -scores computed in WordSpy help it to select the right motifs that are specific to a given set of sequences. Third, WordSpy uses a strategy of first searching for over-represented exact words and then combining them to form degenerate motifs. This strategy makes the motif representation in WordSpy more stringent than that in the other methods, and as a result, it has a smaller false-positive rate. Note that WordSpy performs better on the budding yeast and human datasets than on the fruit fly datasets.
The results of a comparison of 14 motif-detection programs on a benchmark study [17]. At the nucleotide level, sensitivity (nSn), positive predictive value (nPPV), performance coefficient (nPC), and correlation coefficient (nCC) were measured. With nTP, nFN, nFP and nTN as nucleotide-level true positive, false negative, false positive, and true negative, respectively, nSn = nTP/(nTP + nFN); nPPV = nTP/(nTP + nFP); nPC = nTP/(nTP + nFN + nFP); and nCC = (nTP·nTN - nFN·nFP)/ . At the site level, sensitivity (sSn), positive predictive value (sPPV), and average site performance (sASP) were measured. With sTP, sFN, sFP as site-level true positive, false negative, and false positive, respectively, sSn = sTP/(sTP + sFN); sPPV) = sTP/(sTP + sFP; and sASP = (sSn + sPPV)/2.
. At the site level, sensitivity (sSn), positive predictive value (sPPV), and average site performance (sASP) were measured. With sTP, sFN, sFP as site-level true positive, false negative, and false positive, respectively, sSn = sTP/(sTP + sFN); sPPV) = sTP/(sTP + sFP; and sASP = (sSn + sPPV)/2.
True positives and false positives of the 14 motif-detection programs compared. (a) Nucleotide-level true positive (nTP) is the number of nucleotide positions in both known sites and predicted sites; nucleotide-level false positive (nFP) is the number of nucleotide positions not in known sites but in predicted sites. (b) Site-level true positive (sTP) is the number of known sites overlapped by predicted sites; site-level false positive (sFP) is the number of predicted sites not overlapped by known sites.
Conclusion
We propose a new approach to the challenging problem of genome-wide motif finding, which combines a novel steganalysis method for discovering over-represented motifs and methods for selecting biologically significant motifs. By taking a steganalysis perspective on the motif-finding problem, we were able to accurately identify a large number of motifs of nearly optimal lengths. By considering all the genes of interest altogether, we avoided the problem of subjectively partitioning the genes into small clusters, which may make some motifs difficult to detect. By applying our approach to all cell-cycle-related genes in budding yeast and A. thaliana, we demonstrated its power as an effective genome-wide motif finding approach that compared favorably to many existing methods.
The core motif-finding algorithm, WordSpy, combines both word counting and statistical modeling. Like word-counting methods, WordSpy can simultaneously detect a large number of putative motifs. Unlike the existing word-counting methods, however, the wording-counting procedure of WordSpy is progressive and retrospective. It considers short to long words, adjusts the over-representation of shorter words after examining longer ones, and subsequently eliminates not truly over-represented shorter words. As a result, WordSpy produces fewer spurious motifs and is able to find motifs with optimal lengths. Furthermore, instead of using statistical models to characterize a small number of motifs with multiple local alignments, WordSpy models a large number of motifs, their compositions, and their usage to fit to the whole of the given sequences. Consequently, all significant words in regulatory regions can be identified.
WordSpy is a dictionary-based approach, which was initiated in the innovative MobyDick algorithm by Bussemaker et al. [15]. Nevertheless, we significantly extended their work in many important aspects. First, we took a novel steganographic view of the problem of motif finding. This allows us to combine a grammar with a dictionary in a statistical model to capture both conserved motifs and background words. Second, WordSpy accurately quantifies the over-representation of a word by considering the probability that the word can be generated by the best model that has been built so far, whereas MobyDick computes the over-representation by counting the occurrences of a word in a large synthetic dataset. Third, WordSpy considers only those words that occur in the given sequences without enumerating all possible words, which saves a substantial amount of computation, especially for long words.
In the current implementation of WordSpy, we assumed that the motifs and words in a dictionary were used independently. For some applications, however, spatial relationship among motifs may be biologically important. For such cases, we may resort to a more complex grammar, such as stochastic context-free or context-sensitive grammar [18]. However, the incurred computational cost could be prohibitively high for even small problems. A more efficient way to capture motif correlations is to construct motif modules using the motifs identified by a simple grammar model. Similar post-processing strategies have been proposed [47, 48].
In this research, we adopted two schemes to measure the biological significance of motifs. One is the expression coherence of the genes whose promoters contain a motif, and the other is the specificity of a motif to the genes of interest with respect to the rest of the genome. Similar ideas have been proposed [49]. As shown in this study, these two biological relevance measures are effective in identifying cell-cycle-related TF-binding motifs of yeast and A. thaliana. However, we need to caution that a high G-score may not necessarily and sufficiently mean a good motif, a similar restriction to the clustering-first approaches, and that gene-expression information may not be available for all genomes. Therefore, we suggest using the Z g -score as the major criterion, and the G-score and other information as supports.
In this study, we applied our approach to identify significant cis-elements from sequences of a single species. Like most algorithms that use information of a single species, WordSpy may be vulnerable to noisy promoter sequences as a result of the uncertainty of the annotation, especially in the genomes of higher eukaryotes. A comparative approach may have an advantage in such situations by utilizing conservation information from multiple species. Therefore, we will consider using evolutionary information to improve our method in future work. Nevertheless, computational tools for large-scale de novo motif finding for a single species are still important, especially for applications where no sequences of closely related species are available and for problems where species-specific motifs are needed. It is interesting to note that single-species motif finding can be competitive when compared with comparative genomics methods using multiple species [50].
Materials and methods
Word sampling
The goal of word sampling is to discover over-represented motifs as completely and accurately as possible. Word sampling determines the structure of the model and initializes its parameters. For biological sequences, a regulatory motif is usually represented by a series of position profiles, each of which is the distribution of four nucleotides at that position. In our model, the emission probability of each position node is equivalent to such a profile. However, such motifs, named as 'profile motifs', exist in a continuous space. It is almost impossible to comprehensively search for all over-represented profile motifs directly. Here, we combine methods of word counting and statistical modeling. We apply a word-counting method to detect over-represented words in the discrete sequence space of four nucleotides, and then cluster similar words to form a profile motif. All resulting profile motifs will be further improved in the model optimization phase.
We develop an efficient algorithm for word sampling to identify all over-represented words of length k in the sequence space against the optimal model  in linear time and linear space complexity. The algorithm scans the script S once, tabulates, using a hashing scheme, all exact words of length k in S, and computes their over-representativeness. A word is considered over-represented if it occurs more frequently in S than it could be generated by the current best model
in linear time and linear space complexity. The algorithm scans the script S once, tabulates, using a hashing scheme, all exact words of length k in S, and computes their over-representativeness. A word is considered over-represented if it occurs more frequently in S than it could be generated by the current best model  . We measure the over-representativeness by a Z-score. Let N
w
be the number of occurrences of a word w in S and random variable
. We measure the over-representativeness by a Z-score. Let N
w
be the number of occurrences of a word w in S and random variable  w
be the number of occurrences of w in a script with the same length as S which were supposedly generated by model
w
be the number of occurrences of w in a script with the same length as S which were supposedly generated by model  . Denote E(
. Denote E( w
) and σ(
w
) and σ( w
) as the mean and standard deviation of
w
) as the mean and standard deviation of  w
. The Z-score of w is defined as Z
w
= (N
w
- E(
w
. The Z-score of w is defined as Z
w
= (N
w
- E( ))/σ(
))/σ( w
). It is nontrivial to compute the statistics of random variable
w
). It is nontrivial to compute the statistics of random variable  w
. Consider a word w of length k in a sequence of length L generated by model
w
. Consider a word w of length k in a sequence of length L generated by model  . There are various ways to produce w using the model, for example, by concatenating words of a single letter, or by merging a word's suffix with another word's prefix. To compute the expected number of occurrences of w, E(
. There are various ways to produce w using the model, for example, by concatenating words of a single letter, or by merging a word's suffix with another word's prefix. To compute the expected number of occurrences of w, E( w
), we define
w
), we define  (i) (and respectively
(i) (and respectively  (j)) to be the set of words in
(j)) to be the set of words in  whose suffixes (and respectively prefixes) match the first i (and respectively the last j) letters of w. The expectation E(
whose suffixes (and respectively prefixes) match the first i (and respectively the last j) letters of w. The expectation E( w
) can be computed as
w
) can be computed as

where

and w[j,k] represents the subsequence of w from its jth to kth positions,  is the transition probability of motif W
u
, and
is the transition probability of motif W
u
, and  and
and  are the emission probabilities of the last i and first j positions of Θ
u
, respectively. The computation of σ(
are the emission probabilities of the last i and first j positions of Θ
u
, respectively. The computation of σ( w
) is complex and costly [51, 52]. Following the practice in the existing methods, in our current implementation, we approximate σ(
w
) is complex and costly [51, 52]. Following the practice in the existing methods, in our current implementation, we approximate σ( w
) by E(
w
) by E( w
).
w
).
All the words with Z-scores greater than a threshold are considered over-represented. Thereafter, all new words are classified into background words or motif words with some motif evaluation methods. Two evaluation methods will be described in the section on 'Motif evaluation' below. After evaluation, background words are added to background sub-dictionary of

. The motif words are further clustered to form profile motifs.
The current implementation of word clustering is a greedy algorithm. Let C = {w1,w2,...,w
m
} be a set of words of length k, sorted in a non-increasing order of their Z-scores. From the beginning to the end of list C, we take a word w
j
as a seed and search the words in C that match w
j
by at least κ letters, where κ is determined so that the chance of two random words of length k having κ matched letters is less than 0.001. All such matched words are then merged with w
j
and subsequently removed from the seed candidate list. The procedure terminates after all seeds have been examined. This heuristic assumes that the degeneracy is uniform over all positions of a motif. Regulatory motifs may, however, have one or two core parts that are more conserved than their flanking sequences, which sometimes may be 'do-not-care' positions. Fortunately, the current model  keeps all short but over-represented motifs that may include those possible cores of longer motifs. We can also make a nonuniform seed by parsing a word in C through
keeps all short but over-represented motifs that may include those possible cores of longer motifs. We can also make a nonuniform seed by parsing a word in C through  , finding some cores (substrings), fixing the seed at those core positions, and allowing mismatches at the other positions. Note that these word clusters are not final. During the model optimization, word clusters are dynamically changed as profile motifs are updated.
, finding some cores (substrings), fixing the seed at those core positions, and allowing mismatches at the other positions. Note that these word clusters are not final. During the model optimization, word clusters are dynamically changed as profile motifs are updated.
At the end of word sampling, the new profile motifs are added to the motif sub-dictionary of

(I W is set to 1) to form the next dictionary D k . The model is retrofitted to accommodate the new motifs, leading to the next grammar G k . The new model G k is then optimized in the model optimization phase. The overall process repeats until the model covers motifs up to the maximum length.
Model optimization
The goal of model optimization is to optimize the profile motifs as well as their usage probabilities. In this phase, motif statistics are recomputed and insignificant motifs are discarded. Given a stegoscript S and a grammar G
k
= (Ψ, Θ, I), where I has been determined in word sampling, an optimized grammar  can be derived using the expectation maximization (EM) algorithm [53].
can be derived using the expectation maximization (EM) algorithm [53].
Without loss of generality, we view a set of sequences as a long sequence S = s1s2...s
q
. Let  = (Ψ(t), Θ(t)) be G
k
's parameters in the tth iteration. We can adopt a dynamic programming forward-backward algorithm [14] to compute the most probable state when observing s
l
∈ S. Specifically, we compute the probability of observing s
l
at the jth position of a motif W given Ψ(t) and Θ(t) as follows,
= (Ψ(t), Θ(t)) be G
k
's parameters in the tth iteration. We can adopt a dynamic programming forward-backward algorithm [14] to compute the most probable state when observing s
l
∈ S. Specifically, we compute the probability of observing s
l
at the jth position of a motif W given Ψ(t) and Θ(t) as follows,

where W[j] is the jth position of W, f(μ) is the probability of observing S up to s
μ
(inclusive) given  , μ = i - k, ρ
W
= P
W
(I
W
P
M
+ (1 - I
W
)P
B
), and b(ν + 1) is the probability of observing S from Sν+ 1 (inclusive) to the end of S, ν = i - k + l(W), and l(W) is the length of W. Function f(i) can be recursively computed as f(i) =
, μ = i - k, ρ
W
= P
W
(I
W
P
M
+ (1 - I
W
)P
B
), and b(ν + 1) is the probability of observing S from Sν+ 1 (inclusive) to the end of S, ν = i - k + l(W), and l(W) is the length of W. Function f(i) can be recursively computed as f(i) =  ·τ
W
(i - l(W) + 1, i)·f(i - l(W)). Similarly b(i) can be computed as b(i) =
·τ
W
(i - l(W) + 1, i)·f(i - l(W)). Similarly b(i) can be computed as b(i) =  ·τ
W
(i, i + l(W) - 1)·b(i + l(W)). Evidently, P(S|
·τ
W
(i, i + l(W) - 1)·b(i + l(W)). Evidently, P(S| ) = f(q) = b(1).
) = f(q) = b(1).
With this posterior probability, we can easily have,

and  , where
, where  is the average number of W
i
likely to be observed and
is the average number of W
i
likely to be observed and  (ς, j) is the average number of letter ς likely to be observed at the jth position of W
i
, in all the possible parses of S given Ψ(t) and Θ(t). On the basis of the maximum likelihood principle, a model that fits the data better will have the following parameters,
(ς, j) is the average number of letter ς likely to be observed at the jth position of W
i
, in all the possible parses of S given Ψ(t) and Θ(t). On the basis of the maximum likelihood principle, a model that fits the data better will have the following parameters,

where Λ is the alphabet, ς ∈ Λ, j = 1,2,...,l(W i ), l(W i ) is the length of W i , and δ (x, y) equals 1 if x = y, or 0 otherwise. The model optimization is done iteratively using equations in (3) until convergence.
In this procedure, the computation of the forward-backward algorithm becomes more costly when the number of motifs in the dictionary increases because its time complexity is O(L·N), where L is the sequence length and N the size of the dictionary. We introduce a hash scheme to index a word w directly to the profile motifs that may emit w in the dictionary, which reduces the average cost of forward-backward algorithm to O(α L), where α is the average link length of the words in the hash table. The links are initially created during word clustering. When a profile motif is generated from a word cluster, every word in the cluster will add a link to the motif in its hash field. Because a word may appear in multiple clusters, its hash field may contain multiple links. These links will also be dynamically changed at the end of each iteration, as the profile motifs are updated.
Motif evaluation
WordSpy is designed to identify a complete list of putative motifs and usually gives a large number of significant words. How to separate true motifs from background words is critical. As the covertext consists of random strings, a proper Z-score threshold can be used to filter out most background words. However, the regulatory regions of a genome are not purely random. There exist many highly over-represented pseudo-motifs that make it harder to find real, functional motifs. Fortunately, functional motifs often have intrinsic properties that make them separable from spurious ones.
Specificity to the target promoters
An extracted motif cannot be considered as a genuine motif specific to the genes of interest if it is prevalent in other promoter regions of the genome. We utilize this property to discriminate real motifs from fake ones. This is done by a whole genome analysis with a Monte Carlo simulation of thousands of runs. In each run, a set of promoters are randomly selected from the genome and the occurrence of a motif is counted. A genome Z-score, shortened as Z g -score, is calculated to measure the specificity of the motif to the target promoters from which it was discovered with respect to randomly selected promoters. A high positive Z g -score is desired, as it means that the motif is unlikely to be a background word.
Gene-expression coherence
Statistically a set of genes sharing a motif will have more similar expression profiles than a set of arbitrary genes. Therefore, we can measure the likelihood of a motif being biologically meaningful by the coherence of the expressions of all the genes whose promoters contain the motif. We use the average coherence of pairwise gene expression to measure the coherence of a set of expression profiles. We call this measure the G-score, where G stands for genes. A higher G-score indicates a more biologically significant motif. The pairwise gene-expression coherence can be measured in many ways, such as Euclidean distances and Pearson correlation coefficients. Here, we present our results using Pearson correlation coefficients. We have also analyzed the expression coherence score in [49] and a normalized version of the G-score. Our results on yeast (see Additional data file 1) indicate that the simple Pearson correlation-coefficient G-score works slightly better than the other two.
GO functional analysis
To determine whether any GO terms are enriched in a specified list of genes, we use GO::TermFinder perl module[54] to calculate a p value with accumulative hypergeometric distribution,

where N is the total number of genes, M is the number of genes annotated to have a specific function, n is the number of genes tested, and k is the number of genes tested which are annotated to have the specific function. The p values are adjusted by Bonferroni corrections for multiple tests [55]. GO annotations of Arabidopsis were retrieved from TAIR database (version January 2006) [56]. The significantly enriched functional categories were discovered with a false-discovery rate (FDR) of less than 0.05 [57].
WordSpy webserver
An online server has been set up for the WordSpy algorithm to support direct access to the software at [58].
Additional data files
References
Lemon B, Tjian R: Orchestrated response: A symphony of transcription factors for gene control. Genes Dev. 2000, 14: 2551-2569.
Segal E, Yelensky R, Koller D: Genome-wide discovery of transcriptional modules from DNA sequence and gene expression. Bioinformatics. 2003, 19 Suppl 1: 273-282.
Tamada Y, Kim S, Bannai H, Imoto S, Tashiro K, Kuhara S, Miyano S: Estimating gene networks from gene expression data by combining Bayesian network model with promoter element detection. Bioinformatics. 2003, 19 Suppl 2: II227-II236.
Lawrence C, Altschul S, Bogouski M, Liu J, Neuwald A, Wooten J: Detecting subtle sequence signals: a Gibbs sampling strategy for multiple alignment. Science. 1993, 262: 208-214.
Bailey T, Elkan C: Unsupervised learning of multiple motifs in biopolymers using EM. Machine Learning. 1995, 21: 51-80.
Hertz G, Stormo G: Identifying DNA and protein patterns with statistically significant alignments of multiple sequences. Bioinformatics. 1999, 15: 563-577.
Hughes J, Estep P, Tavazoie S, Church G: Computational identification of cis-regulatory elements associated with groups of functionally related genes in Saccharomyces cerevisiae. J Mol Biol. 2000, 296: 1205-1214.
Sinha S, Tompa M: YMF: a program for discovery of novel transcription factor binding sites by statistical overrepresentation. Nucleic Acids Res. 2003, 31: 3586-3588.
Gupta M, Liu J: Discovery of conserved sequence patterns using a stochastic dictionary model. J Am Stat Assoc. 2003, 98: 55-66.
Zhang M: Large scale gene expression data analysis: a new challenge to computational biologists. Genome Res. 1999, 9: 681-688.
Kellis M, Patterson N, Endrizzi M, Birren B, Lander E: Sequencing and comparison of yeast species to identify genes and regulatory elements. Nature. 2003, 423: 241-254.
Wasserman W, Palumbo M, Thompson W, Fickett J, Lawrence C: Human-mouse genome comparisons to locate regulatory sites. Nat Genet. 2000, 26: 225-228.
Wayner P: Disappearing Cryptography. 2002, San Francisco, California:Morgan Kaufmann, 2
Durbin R, Eddy S, Krogh A, Mitchison G: Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. 1998, Cambridge: Cambridge University Press
Bussemaker H, Li H, Siggia E: Building a dictionary for genomes: identification of presumptive regulatory sites by statistical analysis. Proc Natl Acad Sci USA. 2000, 97: 10096-10100.
Stormo G: DNA binding sites: representation and discovery. Bioinformatics. 2000, 16: 16-23.
Tompa M, Li N, Bailey TL, Church GM, Moor BD, Eskin E, Favorov AV, Frith MC, Fu Y, Kent WJ, et al: Assessing computational tools for the discovery of transcription factor binding sites. Nat Biotechnol. 2005, 23: 137-144.
Hopcroft JE, Motwani R, Ullman JD: Introduction to Automata Theory, Languages, and Computation. 2000, Reading, MA:Addison-Wesley, 2
Spellman P, Zhang M, Lyer V, Anders K, Eisen M, abd D Botstein PB, Futcher B: Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol Biol Cell. 1998, 9: 3273-3297.
van Helden J, Andre B, Collado-Vides J: A web site for the computational analysis of yeast regulatory sequences. Yeast. 2000, 16: 177-187.
van Helden J, Rios AF, Collado-Vides J: Discovering regulatory elements in noncoding sequences by analysis of spaced dyads. Nucleic Acids Res. 2000, 28: 1808-1018.
Pavesi G, Mereghetti P, Mauri G, Pesole G: Weeder Web: discovery of transcription factor binding sites in a set of sequences from co-regulated genes. Nucleic Acids Res. 2004, W199-W203. 32 Web Server
Stuart J, Segal E, Koller D, Kim S: A gene coexpression network for global discovery of conserved genetic modules. Science. 2003, 302: 249-255.
Koch C, Moll T, Neuberg M, Ahorn H, Nasmyth K: A role for the transcription factors Mbp1 and Swi4 in progression from G1 to S phase. Science. 1993, 261: 1551-1557.
Kato M, Hata N, Banerjee N, Futcher B, Zhang M: Identifying combinatorial regulation of transcription factors and binding motifs. Genome Biol. 2004, 5: R56-
Hollenhorst P, Bose M, Mielke M, Müller U, Fox C: Forkhead genes in transcriptional silencing, cell morphology and the cell cycle: overlapping and distinct functions for FKH1 and FKH2 in Saccharomyces cerevisiae. Genetics. 2000, 154: 1533-1548.
Inzé D: Why should we study the plant cell cycle?. J Exp Bot. 2003, 54: 1125-1126.
Menges M, Hennig L, Gruissem W, Murray J: Genome-wide gene expression in Arabidopsis cell suspension. Plant Mol Biol. 2003, 53: 423-442.
TAIR database. [http://www.arabidopsis.org]
Schmid M, Davison T, Henz S, Pape U, Demar M, Vingron M, Scholkopf B, Weigel D, Lohmann J: A gene expression map of Arabidopsis thaliana development. Nat Genet. 2005, 37: 501-506.
Higo K, Ugawa Y, Iwamoto M, Korenaga T: Plant cis-acting regulatory DNA elements (PLACE) database. Nucleic Acids Res. 1999, 27: 297-300.
Lescot M, Dehais P, Thijs G, Marchal K, Moreau Y, van de Peer Y, Rouze P, Rombauts S: PlantCARE, a database of plant cis-acting regulatory elements and a portal to tools for in silico analysis of promoter sequences. Nucleic Acids Res. 2002, 30: 325-327.
Ito M, Iwase M, Kodama H, Lavisse P, Komamine A, Nishihama R, Machida Y, Watanabe A: A novel cis-acting element in promoters of plant B-type cyclin genes activates M phase specific transcription. Plant Cell. 1998, 10: 331-341.
Menges M, Hennig L, Gruissem W, Murray J: Cell cycle-regulated gene expression in Arabidopsis. J Biol Chem. 2002, 277: 41987-42002.
Chaubet N, Philipps G, Chaboute ME, Ehling M, Giot C: Nucleotide sequences of two corn histone H3 genes. Genomic organization of the corn histone H3 and H4 genes. Plant Mol Biol. 1986, 6: 253-263.
Harris MA, Clark JI, Ireland A, Lomax J, Ashburner M, Collins R, Eilbeck K, Lewis S, Mungall C, Richter J, et al: The Gene Ontology (GO) project in 2006. Nucleic Acids Res. 2006, 34 (Database issue): D322-D226.
Ramirez-Parra E, Fründt C, Gutierrez C: A genome-wide identification of E2F-regulated genes in Arabidopsis. Plant J. 2003, 33: 801-811.
Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK, Hannett NM, Harbison CT, Thompson CM, Simon I, et al: Transcriptional regulatory networks in Saccharomyces cerevisiae. Science. 2002, 298: 799-804.
Regnier M, Denise A: Rare events and conditional events on random strings. Discrete Math Theor Comput Sci. 2004, 6: 191-214.
Workman C, Stormo G: ANN-Spec: a method for discovering transcription factor binding sites with improved specificity. Pac Symp Biocomput. 2000, 5: 464-475.
Eskin E, Pevzner P: Finding composite regulatory patterns in DNA sequences. Bioinformatics. 2002, 18 (Suppl 1): S354-S363.
Frith MC, Hansen U, Spouge JL, Weng Z: Finding functional sequence elements by multiple local alignment. Nucleic Acids Res. 2004, 32: 189-200.
Ao W, Gaudet J, Kent WJ, Muttumu S, Mango SE: Environmentally induced foregut remodeling by PHA-4/FoxA and DAF-12/NHR. Science. 2004, 305: 1743-1746.
Thijs G, Lescot M, Marchal K, Rombauts S, Moor BD, Rouze P, Moreau Y: A higher-order background model improves the detection of promoter regulatory elements by Gibbs sampling. Bioinformatics. 2001, 17: 1113-1122.
Favorov AV, Gelfand MS, Gerasimova AV, Ravcheev DA, Mironov AA, Makeev VJ: A Gibbs sampler for identification of symmetrically structured, spaced DNA motifs with improved estimation of the signal length. Bioinformatics. 2005, 21: 2240-2245.
Assessment Statistics. [http://bio.cs.washington.edu/assessment/statistics.html]
Frith MC, Hansen U, Weng Z: Detection of cis-element clusters in higher eukaryotic DNA. Bioinformatics. 2001, 17: 878-889.
Sinha S, Nimwegen E, Siggia E: A probabilistic method to detect regulatory modules. Bioinformatics. 2003, 19 Suppl 1: 292-301.
Pilpel Y, Sudarsanam P, Church G: Identifying regulatory networks by combinatorial analysis of promoter elements. Nat Genet. 2001, 29: 153-159.
Siggia E: Computational methods for transcriptional regulation. Curr Opin Genet Dev. 2005, 15: 214-221.
Régnier M: A unified approach to word statistics. RECOMB (Proceedings of the Second Annual International Conference on Research in Computational Molecular Biology). 1998, 207-213. [DOI: 10.1145/279069.279116]
Reinert G, Schbath S, Waterman M: Probabilistic and statistical properties of words: an overview. J Comput Biol. 2000, 7: 1-46.
Dempster A, Laird N, Rubin D: Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc. 1977, 39: 1-38.
Boyle EI, Weng S, Gollub J, Jin H, Botstein D, Cherry JM, Sherlock G: GO::TermFinder - open source software for accessing Gene Ontology information and finding significantly enriched Gene Ontology terms associated with a list of genes. Bioinformatics. 2004, 20: 3710-3715.
Sokal R, Rohlf F: Biometry: The Principles and Practice of Statistics in Biological Research. 1995, New York: Freeman, 3
Berardini TZ, Mundodi S, Reiser L, Huala E, Garcia-Hernandez M, Zhang P, Mueller LA, Yoon J, Doyle A, Lander G, et al: Functional annotation of the Arabidopsis genome using controlled vocabularies. Plant Physiol. 2004, 135: 745-755.
Benjamini Y, Hochberg Y: Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc. 1995, 57: 289-300.
WordSpy. [http://cic.cs.wustl.edu/wordspy]
Dohrmann P, Voth W, Stillman D: Role of negative regulation in promoter specificity of the homologous transcriptional activators Ace2p and Swi5p. Mol Cell Biol. 1996, 16: 1746-1758.
Zhu J, Zhang M: SCPD: a promoter database of yeast Saccharomyces cerevisiae. Bioinformatics. 1999, 15: 607-611.
Dolan J, Kirkman C, Fields S: The yeast STE12 protein binds to the DNA sequence mediating pheromone induction. Proc Natl Acad Sci USA. 1989, 86: 5703-5707.
Blaiseau P, Thomas D: Multiple transcriptional activation complexes tether the yeast activator Met4 to DNA. EMBO J. 1998, 17: 6327-6336.
Acknowledgements
We are grateful to Gary Stormo and Hao Li for insightful comments on this work. Thanks to Harmen Bussemaker, Hao Li, and Eric Siggia for their MobyDick program. Thanks to Tompa et al. [17] for a motif-finding algorithm assessment benchmark and the corresponding website used in our study. The research was funded in part by NSF grants EIA-0113618 and IIS-0535257.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Wang, G., Zhang, W. A steganalysis-based approach to comprehensive identification and characterization of functional regulatory elements. Genome Biol 7, R49 (2006). https://doi.org/10.1186/gb-2006-7-6-r49
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1186/gb-2006-7-6-r49