Numerical solution of nonlinear stochastic differential equations using the block pulse operational matrices

Abstract

This article proposes an efficient numerical method for solving nonlinear stochastic differential equations. Using the operational matrices of block pulse functions, stochastic differential equations can be reduced to a system of algebraic equations. Computation of presented method is very simple and attractive. In addition, convergence analysis and numerical examples that illustrate accuracy and efficiency of the method are presented.

Introduction

Real problems are mathematically modeled by stochastic differential equations (SDE) or, in more complicated cases, by nonlinear stochastic differential equations of the Itô type. Most of these equations do not have analytical solution, so it is important to find their approximate solution. In recent years, some different numerical methods for solving stochastic differential or stochastic integral equations have been presented [1–8]. The topic of our study is the integral form of SDE as follows:

$$\begin{array}{ll}x\left(t\right)& =x_0+\underset{0}{\overset{t}{\int }}{k}_1(t,s)b(s,x(s\left)\right)\mathit{\text{ds}}+\underset{0}{\overset{t}{\int }}{k}_2(t,s)\sigma (s,x(s\left)\right)\mathit{\text{dB}}\left(s\right),\\ t& \in [0,1),\end{array}$$

(1)

where x₀ is a random variable independent of B(t), B = (B(t),t ≥ 0) is a Brownian motion, and stochastic process x is a strong solution of Equation 1 which is adapted to {г _t ,t ≥ 0} Furthermore, all Lebesgue’s and Itô’s integrals in Equation 1 are well defined [9].

Block pulse functions (BPFs) have been studied by many authors and applied for solving different problems [10–12]. In this paper, we used the stochastic operational matrix of BPFs for reducing the nonlinear stochastic differential equation to a set of algebraic equations.

The paper is ordered as follows: In ‘BPFs and their properties properties’ section, a brief review of the BPFs is presented. The ‘Implementation in stochastic integral equation’ section is devoted to the formulation of nonlinear SDE. In the ‘Error analysis’ section, convergence analysis of the method is discussed. In the ‘Numerical examples’ section, some numerical examples are provided. Finally, the ‘Conclusion’ section gives a brief conclusion.

BPFs and their properties

In this paper, BPFs are defined over [0,1). We consider m-set of BPFs as

$${\varphi }_i\left(t\right)=\left\{\begin{array}{ll}1& (i-1)h\le t<\mathit{\text{ih}},i=1,\dots ,m,\\ 0& \text{otherwise},\end{array}\right.$$

where $h=\frac{1}{m}$. The BPFs have the following properties:

• 1. Disjointness

  $${\varphi }_i\left(t\right){\varphi }_j\left(t\right)={\delta }_{\mathit{\text{ij}}}{\varphi }_i\left(t\right),$$

where i,j = 1,2,…,m and δ _ij  is the Kronecker delta.

• 2. Orthogonality

  $$\underset{0}{\overset{1}{\int }}{\varphi }_i\left(t\right){\varphi }_j\left(t\right)\mathit{\text{dt}}=h{\delta }_{\mathit{\text{ij}}},i,j=1,2,\dots ,m.$$

• 3. Completeness

If m → ∞, then the BPF set is complete, i.e., for every f ∈ L²([0,1)), Parseval’s identity holds,

$$\underset{0}{\overset{1}{\int }}{f}^2\left(t\right)\mathit{\text{dt}}=\sum _{i=1}^{\infty }{f}_i^2\parallel {\varphi }_i\left(t\right){\parallel }^2,$$

where

$$f_i=\frac{1}{h}\underset{0}{\overset{1}{\int }}f\left(t\right){\varphi }_i\left(t\right)\text{dt.}$$

(2)

Let

$$\Phi \left(t\right)={\left(\begin{array}{l}{\varphi }_1\left(t\right),{\varphi }_2\left(t\right),\dots ,{\varphi }_m\left(t\right)\end{array}\right)}^T,t\in [0,1),$$

so

$$\Phi \left(t\right){\Phi }^T\left(t\right)={\left(\begin{array}{llll}{\varphi }_1\left(t\right)& 0& \cdots & 0\\ 0& {\varphi }_2\left(t\right)& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\varphi }_m\left(t\right)\end{array}\right)}_{m\times m},$$

$${\Phi }^T\left(t\right)\Phi \left(t\right)=1,$$

and

$$\Phi \left(t\right){\Phi }^T\left(t\right)v=\tilde{v}\Phi \left(t\right),$$

where v is the m-vector, $\tilde{v}$ is the m × m matrix, and $\tilde{v}=\text{diag}\left(v\right).$ It is easy to see that

$${\Phi }^T\left(t\right)\mathrm{A\Phi }\left(t\right)={\widehat{A}}^T\Phi \left(t\right),$$

(3)

where A is the m × m matrix and ${\widehat{A}}^T$ is the m-vector with elements equal to the diagonal entries of matrix A.

An arbitrary real bounded function f(t), which is square integrable in the interval t ∈ [0,1), can be expanded as

$$f\left(t\right)\simeq {\widehat{f}}_m\left(t\right)=\sum _{i=1}^m{f}_i{\varphi }_i\left(t\right)={\Phi }^T\left(t\right)F,$$

(4)

where f _i  is the block pulse coefficient that is defined by (2). Let k(t,s) be a function of two variables in L² ([0,1) × [0,1)). It can be similarly expanded with respect to BPFs as

$$k(t,s)\simeq {\Phi }^T\left(t\right)K\Psi \left(s\right),$$

(5)

where Ψ(s) and Φ(t) are m₁,m₂-dimensional block pulse vectors, respectively. Also, K is the m₁ × m₂ block pulse coefficient matrix with

$$\begin{array}{ll}{k}_{\mathit{\text{ij}}}& =m_1{m}_2\underset{0}{\overset{1}{\int }}\underset{0}{\overset{1}{\int }}k(t,s){\varphi }_i\left(t\right){\psi }_j\left(s\right)\mathit{\text{dtds}},i=1,2,\dots ,m_1,\\ j& =1,2,\dots ,m_2.\end{array}$$

For convenience, we put m₁ = m₂ = m.

Lebesgue and Itô integral can be approximated as

$$\underset{0}{\overset{t}{\int }}\Phi \left(s\right)\mathit{\text{ds}}\simeq P\Phi \left(t\right)$$

(6)

and

$$\underset{0}{\overset{t}{\int }}\Phi \left(s\right)\mathit{\text{dB}}\left(s\right)\simeq P_s\Phi \left(t\right),$$

(7)

where operational matrices P and P _s  are given in [6]. So we can write

$$\underset{0}{\overset{t}{\int }}f\left(s\right)\mathit{\text{ds}}\simeq \underset{0}{\overset{t}{\int }}{F}^T\Phi \left(s\right)\mathit{\text{ds}}\simeq F^{T}P\Phi \left(t\right)$$

(8)

and

$$\underset{0}{\overset{t}{\int }}f\left(s\right)\mathit{\text{dB}}\left(s\right)\simeq \underset{0}{\overset{t}{\int }}{F}^T\Phi \left(s\right)\mathit{\text{dB}}\left(s\right)\simeq F^T{P}_s\Phi \left(t\right).$$

(9)

Implementation in stochastic integral equation

Using the block pulse operational matrices, first, we find the collocation approximation to the functions z₁(t) and z₂(t) defined by

$$z_1\left(t\right)=b\left(t,x\left(t\right)\right),z_2\left(t\right)=\sigma \left(t,x\left(t\right)\right).$$

(10)

From Equations 1 and 10, we get

$$x\left(t\right)=x_0+\underset{0}{\overset{t}{\int }}{k}_1(t,s)z_1\left(s\right)\mathit{\text{ds}}+\underset{0}{\overset{t}{\int }}{k}_2(t,s)z_2\left(s\right)\mathit{\text{dB}}\left(s\right),$$

(11)

and

$$\left\{\begin{array}{l}{z}_1\left(t\right)=b\left(t,x_0+\underset{0}{\overset{t}{\int }}{k}_1(t,s)z_1\left(s\right)\mathit{\text{ds}}+\underset{0}{\overset{t}{\int }}{k}_2(t,s)z_2\left(s\right)\mathit{\text{dB}}\left(s\right)\right),\\ z_2\left(t\right)=\sigma \left(t,x_0+\underset{0}{\overset{t}{\int }}{k}_1(t,s)z_1\left(s\right)\mathit{\text{ds}}+\underset{0}{\overset{t}{\int }}{k}_2(t,s)z_2\left(s\right)\mathit{\text{dB}}\left(s\right)\right).\end{array}\right.$$

(12)

We approximate z₁(t),z₂(t), and k _i (t,s),i = 1,2, by block pulse series as follows:

$$\begin{array}{ll}{z}_1\left(t\right)& \simeq {\widehat{z}}_1\left(t\right)=Z_1^T\Phi \left(t\right)={\Phi }^T\left(t\right)Z_1,\end{array}$$

(13)

$$\begin{array}{ll}{z}_2\left(t\right)& \simeq {\widehat{z}}_2\left(t\right)=Z_2^T\Phi \left(t\right)={\Phi }^T\left(t\right)Z_2,\end{array}$$

(14)

$$\begin{array}{ll}{k}_i(t,s)& \simeq \widehat{k_i}(t,s)={\Phi }^T\left(t\right)K_i\Phi \left(s\right),i=1,2,\end{array}$$

(15)

such that m-vectors Z₁, Z₂, and m × m matrix K _i  are block pulse coefficients of z₁(t) and z₂(t) and k _i (t,s), respectively. By substituting Equations 13 and 14 in Equation 11, we get

$$\begin{array}{ll}\underset{0}{\overset{t}{\int }}{k}_1(t,s)z_1\left(s\right)\mathit{\text{ds}}& \simeq \underset{0}{\overset{t}{\int }}{\Phi }^T\left(t\right)K_1\Phi \left(s\right){\Phi }^T\left(s\right)Z_1\mathit{\text{ds}}\\ ={\Phi }^T\left(t\right)K_1\underset{0}{\overset{t}{\int }}\Phi \left(s\right){\Phi }^T\left(s\right)Z_1\mathit{\text{ds}}\\ \simeq {\Phi }^T\left(t\right)K_1\underset{0}{\overset{t}{\int }}\widetilde{Z_1}\Phi \left(s\right)\mathit{\text{ds}}\\ \simeq {\Phi }^T\left(t\right)K_1\widetilde{Z_1}P\Phi \left(t\right);\end{array}$$

(16)

also, the Itô integral of Equation 11 can be written as

$$\begin{array}{ll}\underset{0}{\overset{t}{\int }}{k}_2(t,s)z_2\left(s\right)\mathit{\text{dB}}\left(s\right)& \simeq \underset{0}{\overset{t}{\int }}{\Phi }^T\left(t\right)K_2\Phi \left(s\right){\Phi }^T\left(s\right)Z_2\mathit{\text{dB}}\left(s\right)\\ ={\Phi }^T\left(t\right)K_2\underset{0}{\overset{t}{\int }}\Phi \left(s\right){\Phi }^T\left(s\right)Z_2\mathit{\text{dB}}\left(s\right)\\ \simeq {\Phi }^T\left(t\right)K_2\underset{0}{\overset{t}{\int }}\widetilde{Z_2}\Phi \left(s\right)\mathit{\text{dB}}\left(s\right)\\ \simeq {\Phi }^T\left(t\right)K_2\widetilde{Z_2}{P}_s\Phi \left(t\right),\end{array}$$

(17)

where ${\tilde{Z}}_1=\text{diag}\left(Z_1\right),{\tilde{Z}}_2=\text{diag}\left(Z_2\right)$. By substituting (16) and (17) into (12) and replacing ≃ with =, we obtain

$$\left\{\begin{array}{l}{Z}_1^T\Phi \left(t\right)=b\left(t,x_0+{\Phi }^T\left(t\right)K_1\widetilde{Z_1}P\Phi \left(t\right)+{\Phi }^T\left(t\right)K_2\widetilde{Z_2}{P}_s\Phi \left(t\right)\right),\\ Z_2^T\Phi \left(t\right)=\sigma \left(t,x_0+{\Phi }^T\left(t\right)K_1\widetilde{Z_1}P\Phi \left(t\right)+{\Phi }^T\left(t\right)K_2\widetilde{Z_2}{P}_s\Phi \left(t\right)\right).\end{array}\right.$$

(18)

Now, we collocate Equation 18 in m nodes $t_j=\frac{j}{m+1},j=1,\dots ,m,$ as

$$\left\{\begin{array}{l}{Z}_1^T\Phi \left(t_j\right)=b\left(t_j,x_0+{\Phi }^T\left(t_j\right)K_1\widetilde{Z_1}P\Phi \left(t_j\right)+{\Phi }^T\left(t_j\right)K_2\widetilde{Z_2}{P}_s\Phi \left(t_j\right)\right),\\ Z_2^T\Phi \left(t_j\right)=\sigma \left(t_j,x_0+{\Phi }^T\left(t_j\right)K_1\widetilde{Z_1}P\Phi \left(t_j\right)+{\Phi }^T\left(t_j\right)K_2\widetilde{Z_2}{P}_s\Phi \left(t_j\right)\right).\end{array}\right.$$

(19)

After solving nonlinear system (19), we obtain Z₁ and Z₂. Then, we can approximate the solution of Equation 11 as follows:

$$x\left(t\right)\simeq x_m\left(t\right)=x_0+{\Phi }^T\left(t\right)K_1\widetilde{Z_1}P\Phi \left(t\right)+{\Phi }^T\left(t\right)K_2\widetilde{Z_2}{P}_s\Phi \left(t\right).$$

(20)

Error analysis

In the following theorems, suppose that the functions b(x,y),σ(x,y) satisfy the Lipschitz and linear growth conditions such that

$$\left|b\right(t,x_1\left(t\right))-b(t,x_2\left(t\right)\left)\right|+|\sigma (t,x_1\left(t\right))-\sigma (t,x_2\left(t\right)\left)\right|\le L|x_1-x_2|$$

(21)

and

$$\left|b\right(t,x\left(t\right)\left)\right|+|\sigma (t,x\left(t\right)\left)\right|\le L(1+|x\left|\right).$$

(22)

Theorem 1

Let f (t) be an arbitrary real bounded function, which is square integrable in the interval [0,1), and$e\left(t\right)=f\left(t\right)-{\widehat{f}}_m\left(t\right)$, t ∈ [0,1), where${\widehat{f}}_m\left(t\right)=\sum _{i=1}^m{f}_i{\varphi }_i\left(t\right)$, is the block pulse series of f(t). Then,

$$\parallel e\left(t\right){\parallel }^2\le O\left(h^2\right).$$

Proof

See [8]. □

Theorem 2

Suppose that f(t,s) ∈ [0,1) × [0,1), and$e(t,s)=f(t,s)-{\widehat{f}}_m(t,s)$, (t,s) ∈ J, where${\widehat{f}}_m(t,s)=\sum _{i=1}^m\sum _{j=1}^m{f}_{\mathit{\text{ij}}}{\psi }_i\left(t\right){\varphi }_j\left(s\right)$, is the block pulse series of f(t,s) Then,

$$\parallel e(t,s){\parallel }^2\le O\left(h^2\right).$$

Proof

See [8]. □

Theorem 3

Let x(t) and x _m (t) be the exact solution and approximate solution of (1), respectively; furthermore, let conditions (21), (22), and (i) ∥x(t) ∥ ≤ M, t ∈ I = [0,1), (ii) ∥ k _i (t,s) ∥ ≤ M _i , (t,s) ∈ I × I, i = 1,2, hold; then,

$$\parallel x\left(t\right)-x_m\left(t\right)\parallel \to 0,$$

where

$$\parallel x\left(t\right){\parallel }^2=E\left|x\right(t){|}^2.$$

Proof

Let $e_i\left(t\right)=z_i\left(t\right)-{\widehat{z}}_i\left(t\right)$ be the error function, where z _i (t) is defined in (10) and ${\widehat{z}}_i\left(t\right),i=1,2$ is the approximated form of z _i (t) by BPFs, i.e.,

$${\widehat{z}}_1\left(s\right)=\widehat{b}\left(s,x_m\left(s\right)\right),{\widehat{z}}_2\left(s\right)=\widehat{\sigma }\left(s,x_m\left(s\right)\right),$$

and

$$z_1^m\left(s\right)=b\left(s,x_m\left(s\right)\right),z_2^m\left(s\right)=\sigma \left(s,x_m\left(s\right)\right).$$

From Lipschitz condition and Theorem 2, we get

$$\begin{array}{ll}\parallel z_i\left(t\right)-{\widehat{z}}_i\left(t\right)\parallel & \le \parallel z_i\left(t\right)-z_i^m\left(t\right)\parallel +\parallel {\widehat{z}}_i\left(t\right)-z_i^m\left(t\right)\parallel \\ \le L\parallel x\left(t\right)-x_m\left(t\right)\parallel +c_{i}h,\end{array}$$

(23)

where i = 1,2. Let e _m (t) = x(t) - x _m (t). We can write

$$\parallel e_m\left(t\right)\parallel \le \parallel I_1\parallel +\parallel I_2\parallel ,$$

(24)

where

$$\begin{array}{l}{I}_1=\underset{0}{\overset{t}{\int }}\left[k_1\right(t,s\left)z_1\right(s)-{\widehat{k}}_1(t,s\left){\widehat{z}}_1\right(s\left)\right]\mathit{\text{ds}},\\ I_2=\underset{0}{\overset{t}{\int }}\left[k_2\right(t,s\left)z_2\right(s)-{\widehat{k}}_2(t,s\left){\widehat{z}}_2\right(s\left)\right]\mathit{\text{dB}}\left(s\right).\end{array}$$

(25)

For I₁, we get

$$\begin{array}{ll}\parallel I_1\parallel & \le \underset{0}{\overset{t}{\int }}(\parallel k_1(t,s)\parallel \parallel z_1(s)-{\widehat{z}}_1(s)\parallel )\mathit{\text{ds}}+\underset{0}{\overset{t}{\int }}(\parallel {\widehat{z}}_1(s)\parallel \parallel k_1(t,s)\\ -{\widehat{k}}_1(t,s)\parallel )\mathit{\text{ds}},\\ \le M_1\left(L\underset{0}{\overset{t}{\int }}\parallel e_m\left(s\right)\parallel \mathit{\text{ds}}+c_{1}h\right)+c_{3}h\left(\underset{0}{\overset{t}{\int }}\parallel z_1\left(s\right)\right.\\ -\left.{\widehat{z}}_1\left(s\right)\parallel \mathit{\text{ds}}+\underset{0}{\overset{t}{\int }}\parallel z_1\left(s\right)\parallel \mathit{\text{ds}}\right)\\ \le L(M_1+c_{3}h)\underset{0}{\overset{t}{\int }}\parallel e_m\left(s\right)\parallel \mathit{\text{ds}}+O\left(h\right).\end{array}$$

(26)

From Itô isometry, we can write

$$\begin{array}{ll}\parallel I_2\parallel & \le \parallel \underset{0}{\overset{t}{\int }}\left[k_2\right(t,s\left)z_2\right(s)-{\widehat{k}}_2(t,s\left){\widehat{z}}_2\right(s\left)\right]\mathit{\text{dB}}\left(s\right)\parallel \\ \le \underset{0}{\overset{t}{\int }}\parallel k_2(t,s)z_2\left(s\right)-{\widehat{k}}_2(t,s){\widehat{z}}_2\left(s\right)\parallel \mathit{\text{ds}}\\ \le \underset{0}{\overset{t}{\int }}(\parallel k_2(t,s)\parallel \parallel z_2(s)-{\widehat{z}}_2(s)\parallel )\mathit{\text{ds}}+\underset{0}{\overset{t}{\int }}(\parallel {\widehat{z}}_2(s)\parallel \parallel k_2(t,s)\\ -{\widehat{k}}_2(t,s)\parallel )\mathit{\text{ds}},\\ \le M_2\left(L\underset{0}{\overset{t}{\int }}\parallel e_m\left(s\right)\parallel \mathit{\text{ds}}+c_{2}h\right)+c_{4}h\left(\underset{0}{\overset{t}{\int }}\parallel z_2\left(s\right)\right.\\ -\left.{\widehat{z}}_2\left(s\right)\parallel \mathit{\text{ds}}+\underset{0}{\overset{t}{\int }}\parallel z_2\left(s\right)\parallel \mathit{\text{ds}}\right)\\ \le L(M_2+c_{4}h)\underset{0}{\overset{t}{\int }}\parallel e_m\left(s\right)\parallel \mathit{\text{ds}}+O\left(h\right).\end{array}$$

(27)

Equations 26, 27, and 24 conclude that

$$\parallel e_m\left(t\right)\parallel \le \alpha \underset{0}{\overset{t}{\int }}\parallel e_m\left(s\right)\parallel \mathit{\text{ds}}+O\left(h\right),$$

(28)

where α = L(M₁ + c₃h) + L(M₂ + c₄h). Hence, from (28) and Gronwall inequality, we get

$$\parallel e_m\left(t\right)\parallel \le O\left(h\right)(1+\alpha \underset{0}{\overset{t}{\int }}{e}^{\alpha (t-s)}\mathit{\text{ds}}),t\in [0,1)$$

and then we get $h=\frac{1}{m}$; by increasing m, it implies ∥e _m (t) ∥ → 0 as m → ∞. □

Numerical examples

To illustrate efficiency and accuracy of presented method, we solve some real-world problems.

Example 1

A simple model for the size x of a population at time t is the model of exponential growth

$$\mathit{\text{dx}}\left(t\right)=\mathit{\text{ax}}\left(t\right)\mathit{\text{dt}},$$

(29)

where a is the growth coefficient. An appropriate modification of Equation 29 is given as a linear quadratic Verhulst equation:

$$\mathit{\text{dx}}\left(t\right)=x\left(t\right)(\lambda -x(t\left)\right)\mathit{\text{dt}},$$

(30)

where the population growth a is replaced by λ - x. By randomizing the parameter λ in Equation 30 to λ + σ ξ (t), where $\xi \left(t\right)=\frac{\mathit{\text{dB}}\left(t\right)}{\mathit{\text{dt}}}$ is a white noise of zero mean, we have the usual stochastic Verhulst equation describing more precisely the population dynamics

$$\mathit{\text{dx}}\left(t\right)=x\left(t\right)(\lambda -x(t\left)\right)\mathit{\text{dt}}+\sigma x\left(t\right)\mathit{\text{dB}}\left(t\right),$$

(31)

in which λ and σ are positive constants [13–15]. The exact solution of Equation 31 is given as follows [1]:

$$x\left(t\right)=\frac{x_0{e}^{(\lambda -\frac{1}{2}{\sigma }^2)t+\sigma B\left(t\right)}}{1+x_0\underset{0}{\overset{t}{\int }}{e}^{(\lambda -\frac{1}{2}{\sigma }^2)s+\sigma B\left(s\right)}\mathit{\text{ds}}}.$$

Let X _i  denote the block pulse coefficient of exact solution and Y _i  be the block pulse coefficient of computed solutions by the presented method. The error is defined as

$$\parallel E\parallel \infty ={\text{max}}_{1\le i\le m}|X_i-Y_i|.$$

In Table 1, ${\overline{x}}_E$ is the error mean and s _E  is the standard deviation of errors in k iteration. In addition, we consider x₀ = 0.5, λ = 1,and σ = 0.25.

Table 1 Mean, standard deviation, and confidence interval for error mean ( m = 32, k = 500)

Example 2

In finance, the Vasicek model is a mathematical model describing the evolution of interest rates. This model can be used for interest rate derivative valuation and also adapted for credit market. Vasicek’s pioneering work (1977), which is based on the Ornstein-Uhlenbeck process, is the first account of a bond pricing model that incorporates stochastic interest rate and can be also seen as a stochastic investment model. The short-term interest rate process${\left(r\right(t\left)\right)}_{t\in R^{+}}$ solves the equation

$$\mathit{\text{dr}}\left(t\right)=a(b-r(t\left)\right)\mathit{\text{dt}}+\sigma \mathrm{dB}\left(t\right),$$

(32)

where B(t),t ≥ 0 is a standard Brownian motion, d r(t) is the change in the short-term interest rate, a is the speed of mean reversion, b is the average interest rate, and σ is the volatility of the short rate. The main disadvantage is that, under Vasicek’s model, it is theoretically possible for the interest rate to become negative, which is an undesirable feature. This shortcoming was fixed in the Cox-Ingersoll-Ross (CIR) model. The CIR process is a Markov process with continuous paths defined by the following SDE:

$$\mathit{\text{dr}}\left(t\right)=\beta (\alpha -r(t\left)\right)\mathit{\text{dt}}+\sigma \sqrt{r\left(t\right)}\mathit{\text{dB}}\left(t\right).$$

(33)

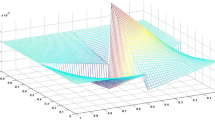
The parameter β corresponds to the speed of adjustment, α to the mean and σ to volatility. Equation 33 has no analytical solution. This process is widely used in finance to model short-term interest rate. The approximated solution by the presented method is shown in Figure 1.

Figure 1

Numerical results for β = 0 . 05, α = 0 . 3, σ = 0 . 002, and r (0) = 0 . 03.

Conclusion

The aim of the presented paper is to apply a method for solving nonlinear stochastic differential equations. The properties of the BPFs with the collocation method are used to reduce the problem to a system of nonlinear algebraic equations. The advantage of this method is the low cost of setting up the equations due to the properties of BPFs. For showing efficiency, the method is applied to some practical problems. The results show accuracy of the method.