Relativistic spin symmetry of the generalized Morse potential including tensor interaction

Abstract

The relativistic Dirac equation under spin symmetry is investigated for generalized Morse potential. We calculated the eigenvalues and the corresponding wave function by using the Nikiforov-Uvarov method. We also discussed two special cases: attractive radial and Deng-Fan potentials. We have also reported some numerical results and figures to show the effect of tensor interaction.

Introduction

The relativistic symmetries of the Dirac Hamiltonian had been discovered about 40 years ago. These symmetries have been recently recognized empirically in nuclear and hadronic spectroscopic [1]. However, within the framework of Dirac equation, the concepts of exact pseudospin symmetry occurs when the magnitude of the attractive Lorentz scalar potential S(r) and the repulsive vector potential V(r) are nearly equal but opposite in sign, i.e., S(r) ≈ -V(r) [2, 3]. Also, the approximate pseudospin symmetry is when the sum of the potential is Σ(r) = c _ps = const ≠ 0 [4]. The pseudospin symmetry used to feature deformed nuclei and the superdeformation to establish an effective shell model [5]. On the other hand, the spin symmetry is relevant in mesons [6] and occurs when the difference of the scalar S(r) and V(r) potentials are constant, i.e., Δ(r) = V(r) - S(r) = c _s = const ≠ 0 [3, 4]. The pseudospin symmetry refers to a quasi-degeneracy of single-nucleon doublets with non-relativistic quantum number $\left(n,l,j=l+\frac{1}{2}\right)$ and $\left(n-1,l+2,j=l+\frac{3}{2}\right),$ where n, l, j denote the single nucleon radial, orbital, and total angular momentum quantum numbers, respectively [7, 8]. Furthermore, the total angular momentum is $j=\tilde{l}+\tilde{s}$, where $\tilde{l}=l+1$ is the pseudo-angular momentum and $\tilde{s}$ is the pseudospin angular momentum [9].

The relativistic and non-relativistic quantum mechanics equations with different phenomenology have been considerably investigated in the recent years [10–25]. Ikhdair and Sever [19] have solved approximately the Dirac-Hulthen problem under spin and pseudospin symmetry limits including Coulomb-like tensor potential with an arbitrary spin-orbit coupling number κ. Also, Hamzavi et al. [20] studied the exact solutions of the Dirac equation for Mie-type potential and approximate solutions of the Dirac-Morse problem with Coulomb-like tensor potential and relativistic Morse potential with tensor interaction [21]. Similarly, Ikot [22] solved the generalized hyperbolical potential including a tensor potential for spin symmetry. The Morse potential is one of the convenient models for the potential energy of diatomic molecules. The Morse potential can be used to model interactions such as the interaction between an atom and a surface [23]. Berkdemir investigated the pseudospin symmetry in the relativistic Morse potential systematically by solving the Dirac equation by applying the Pekeris approximation to the spin-orbit coupling term [24]. The Morse potential (MP) is defined as [21]

$$V\left(r\right)=D_e\left[1-e^{-2\alpha \left(r-r_c\right)}\right],$$

(1)

where α is the screening parameter and D _e is the dissociation energy.

In this work, we introduced a novel potential and call it the New Generalized Morse-like potential (NGMP) model having the same behaviors as MP, attractive radial potential, and Deng-Fan potential models. It is defined as

$$V\left(r\right)=D_e\left[1-{\left(\frac{A+B{e}^{-\mathit{\alpha r}}}{C+D^{\prime }{e}^{-\mathit{\alpha r}}}\right)}^2\right],$$

(2)

where A, B, C, D′ are constant coefficients and the term in the bracket is the Mobius square potential proposed recently [25] (see Figure 1).

Figure 1

Behavior of potentials for α = 0.01 fm ^-1 , A = 1, B = -2, C = 1, D ′ = -1, D _e = -0.8 fm ^-1 .

The motivation of the present work is intend to investigate this potential including the Coulomb-like term under the spin symmetry limit and calculate the energy eigenvalues and the corresponding wave functions expressed in terms of the hypergeometric functions.

The organization of the paper is as follows. In the 'Parametric Nikiforov-Uvarov method’ section, we briefly introduced the NU method. The 'Dirac equation with a tensor coupling’ section is devoted to the Dirac equation with scalar and vector potential with arbitrary spin-orbit coupling number κ including tensor interaction under spin and pseudospin symmetry limits. The energy eigenvalue equation and corresponding wave functions for spin symmetry limit is obtained in the 'Spin symmetry limit’ section. A special case of the potential under investigation is discussed in the 'Special cases’ section. Finally, we give a brief conclusion in the 'Conclusions’ section.

Parametric Nikiforov-Uvarov method

The NU method is used to solve second-order differential equations with an appropriate coordinate transformation s = s(r) [26].

$${{\psi }^{″}}_n\left(s\right)+\frac{\tilde{\tau }\left(s\right)}{\sigma \left(s\right)}{{\psi }^{\prime }}_n\left(s\right)+\frac{\tilde{\sigma }\left(s\right)}{{\sigma }^2\left(s\right)}{\psi }_n\left(s\right)=0,$$

(3)

where σ(s) and $\tilde{\sigma }\left(s\right)$ are polynomials, at most of second degree, and $\tilde{\tau }\left(s\right)$ is a first-degree polynomial. To make the application of the NU method simpler and direct without need to check the validity of solution, we present a shortcut for the method. So, at first, we write the general form of the Schrödinger-like Equation (3) in a more general form applicable to any potential as follows [27]:

$${{\psi }^{\prime \prime }}_n\left(s\right)+\left(\frac{c_1-c_{2}s}{s\left(1-c_{3}s\right)}\right){{\psi }^{\prime }}_n\left(s\right)+\left(\frac{-{\xi }_1{s}^2+{\xi }_{2}s-{\xi }_3}{s^2{\left(1-c_{3}s\right)}^2}\right){\psi }_n\left(s\right)=0,$$

(4)

satisfying the wave functions

$${\psi }_n\left(s\right)=\varphi \left(s\right)y_n\left(s\right).$$

(5)

Comparing (4) with its counterpart (5), we obtain the following identifications:

$$\begin{array}{l}\tilde{\tau }\left(s\right)=c_1-c_{2}s,\sigma \left(s\right)=s\left(1-c_{3}s\right),\\ \tilde{\sigma }\left(s\right)=-{\xi }_1{s}^2+{\xi }_{2}s-{\xi }_3.\end{array}$$

(6)

Following the NU method [26–30], we obtain the following;

• (1) the relevant constant:

  $$\begin{array}{ll}{c}_4=\frac{1}{2}\left(1-c_1\right),& c_5=\frac{1}{2}\left(c_2-2c_3\right),\\ c_6=c_5^2+{\xi }_1,& c_7=2c_4{c}_5-{\xi }_2,\\ c_8=c_4^2+{\xi }_3,& c_9=c_3{c}_7+c_3^2{c}_8+c_6.\\ c_{10}=c_1+2c_4+2\sqrt{c_8}& c_{11}=c_2-2c_5+2\left(\sqrt{c_9}+c_3\sqrt{c_8}\right)\\ c_{12}=c_4+\sqrt{c_8}& c_{13}=c_5-\left(\sqrt{c_9}+c_3\sqrt{c_8}\right)\end{array}$$

  (7)

• (2) the essential polynomial functions:

  $$\pi \left(s\right)=c_4+c_{5}s-\left[\left(\sqrt{c_9}+c_3\sqrt{c_8}\right)s-\sqrt{c_8}\right],$$

  (8)
  $$k=-\left(c_7+2c_3{c}_8\right)-2\sqrt{c_8{c}_9},$$

  (9)
  $$\tau \left(s\right)=c_1+2c_4-\left(c_2-2c_5\right)s-2\left[\left(\sqrt{c_9}+c_3\sqrt{c_8}\right)s-\sqrt{c_8}\right],$$

  (10)
  $${\tau }^{\prime }\left(s\right)=-2c_3-2\left(\sqrt{c_9}+c_3\sqrt{c_8}\right)<0.$$

  (11)

• (3) the energy equation:

  $$\begin{array}{l}{c}_{2}n-\left(2n+1\right)c_5+\left(2n+1\right)\left(\sqrt{c_9}+c_3\sqrt{c_8}\right)\\ +n\left(n-1\right)c_3+c_7+2c_3{c}_8+2\sqrt{c_8{c}_9}=0.\end{array}$$

  (12)

• (4) the wave functions:

  $$\rho \left(s\right)=s^{c_{10}}{\left(1-c_{3}s\right)}^{c_{11}},$$

  (13)
  $$\varphi \left(s\right)=s^{c_{12}}{\left(1-c_{3}s\right)}^{c_{13}},c_{12}>0,c_{13}>0,$$

  (14)
  $$y_n\left(s\right)=P_n^{\left(c_{10},c_{11}\right)}\left(1-2c_{3}s\right),c_{10}>-1,c_{11}>-1,$$

  (15)
  $${\psi }_{\mathit{n\kappa }}\left(s\right)=N_{\mathit{n\kappa }}{s}^{c_{12}}{\left(1-c_{3}s\right)}^{c_{12}-\frac{c_{13}}{c_3}}{P}_n^{\left(c_{10}-1,\frac{c_{11}}{c_3}-c_{10}-1\right)}\left(1-2c_{3}s\right),$$

  (16)

where $P_n^{\left(\mu ,\nu \right)}\left(x\right),\mu >-1,\nu >-1$ and x ∈ [-1, 1] are Jacobi polynomials with

$$P_n^{\left(\alpha ,\beta \right)}\left(1-2s\right)=\frac{{\left(\alpha +1\right)}_n}{n!}{}_{2}F_1\left(-n,1+\alpha +\beta +n;\alpha +1;s\right),$$

(17)

and N _nκ is a normalization constant. Also, the above wave functions can be expressed in terms of the hypergeometric function as

$$\begin{array}{ll}{\psi }_{\mathit{n\kappa }}\left(s\right)=& N_{\mathit{n\kappa }}{s}^{c_{12}}{\left(1-c_{3}s\right)}^{c_{13}}\\ {}_2{F}_1\left(-n,1+c_{10}+c_{11}+n;c_{10}+1;c_{3}s\right),\end{array}$$

(18)

where c₁₂ > 0, c₁₃ > 0 and s ∈ [0, 1/c₃], c₃ ≠ 0. This method has been used extensively to solve various second-order differential equations in quantum mechanics such as Schrodinger equation, Klein-Gordon equation, Duffin-Kemmar-Petiau equation, spinless-Salpeter equation, and Dirac equations [31].

Dirac equation with a tensor coupling

The Dirac equation for spin $\frac{1}{2}$ particles moving in an attractive scalar potential S(r), a repulsive vector potential V(r) and a tensor potential U(r) in the relativistic unit (ℏ = c = 1) is [32]

$$\left[\overrightarrow{\alpha }.\overrightarrow{p}+\beta (M+S\left(r\right)-\mathit{i\beta }\overrightarrow{\alpha }.\widehat{r}U\left(r\right)\right]\psi \left(r\right)=\left[E-V\left(r\right)\right]\psi \left(r\right),$$

(19)

where E is the relativistic energy of the system, $\overrightarrow{p}=-i\overrightarrow{\nabla }$ is the three-dimensional momentum operator, and M is the mass of the fermionic particle. $\overrightarrow{\alpha },\beta$ are the 4 × 4. Dirac matrices given as

$$\overrightarrow{\alpha }=\left(\begin{array}{ll}0& {\overrightarrow{\sigma }}_{\mathit{i}}\\ {\overrightarrow{\sigma }}_{\mathit{i}}& 0\end{array}\right),\beta =\left(\begin{array}{ll}I& 0\\ 0& -I\end{array}\right),$$

(20)

where I is 2 × 2 unitary matrix and ${\overrightarrow{\sigma }}_{\mathit{i}}$ are the Pauli three-vector matrices,

$${\sigma }_1=\left(\begin{array}{ll}0& 1\\ 1& 0\end{array}\right),{\sigma }_2=\left(\begin{array}{ll}0& -i\\ i& 0\end{array}\right),{\sigma }_3=\left(\begin{array}{ll}1& 0\\ 0& -1\end{array}\right).$$

(21)

The eigenvalues of the spin-orbit coupling operator are $\kappa =\left(j+\frac{1}{2}\right)>0,\kappa =-\left(j+\frac{1}{2}\right)<0$ for unaligned $j=l-\frac{1}{2}$ and the aligned spin $j=l+\frac{1}{2}$, respectively. The set (H²,K,J²,J _z ) forms a complete set of conserved quantities. Thus, we can write the spinors as [33],

$${\psi }_{\mathit{n\kappa }}\left(r\right)=\frac{1}{r}\left(\begin{array}{ll}{F}_{\mathit{n\kappa }}\left(r\right)& Y_{\mathit{jm}}^l(\theta ,\phi \\ i{G}_{\mathit{n\kappa }}\left(r\right)& Y_{\mathit{jm}}^{\tilde{l}}\left(\theta ,\phi \right)\end{array}\right),$$

(22)

where F _nκ (r),G _nκ (r) represent the upper and lower components of the Dirac spinors. $Y_{\mathit{jm}}^l\left(\theta ,\phi \right),Y_{\mathit{jm}}^{\tilde{l}}\left(\theta ,\phi \right)$ are the spin and pseudospin spherical harmonics and m is the projection on the z-axis. With other known identities [34],

$$\begin{array}{l}\left(\overrightarrow{\sigma }.\overrightarrow{A}\right)\left(\left(\overrightarrow{\sigma }.\overrightarrow{B}\right)\right)=\overrightarrow{A}.\overrightarrow{B}+i\overrightarrow{\sigma }.\left(\overrightarrow{A}\mathit{x}\overrightarrow{B}\right),\\ \overrightarrow{\sigma }.\overrightarrow{p}=\overrightarrow{\sigma }.\widehat{r}\left(\widehat{r}.\overrightarrow{p}+i\frac{\overrightarrow{\sigma }.\overrightarrow{L}}{r}\right)\end{array}$$

(23)

as well as

$$\begin{array}{l}\left(\overrightarrow{\sigma }.\overrightarrow{L}\right)Y_{\mathit{jm}}^{\tilde{l}}\left(\theta ,\phi \right)=(\kappa -1)Y_{\mathit{jm}}^{\tilde{l}}(\theta ,\phi )\\ \left(\overrightarrow{\sigma }.\overrightarrow{L}\right)Y_{\mathit{jm}}^l\left(\theta ,\phi \right)=-(\kappa -1)Y_{\mathit{jm}}^l(\theta ,\phi )\\ \left(\overrightarrow{\sigma }.\widehat{r}\right)Y_{\mathit{jm}}^l\left(\theta ,\phi \right)=-Y_{\mathit{jm}}^{\tilde{l}}(\theta ,\phi )\\ \left(\overrightarrow{\sigma }.\widehat{r}\right)Y_{\mathit{jm}}^{\tilde{l}}\left(\theta ,\phi \right)=-Y_{\mathit{jm}}^l(\theta ,\phi )\end{array}$$

(24)

leads on to the two coupled first-order Dirac equation [34],

$$\left(\frac{d}{\mathit{dr}}+\frac{\kappa }{r}-U\left(r\right)\right)F_{\mathit{n\kappa }}\left(r\right)=\left(M+E_{\mathit{n\kappa }}-\mathrm{\Delta }\left(r\right)\right)G_{\mathit{n\kappa }}\left(r\right)$$

(25)

$$\left(\frac{d}{\mathit{dr}}-\frac{\kappa }{r}+U\left(r\right)\right)G_{\mathit{n\kappa }}\left(r\right)=\left(M-E_{\mathit{n\kappa }}+\mathrm{\Sigma }\left(r\right)\right)F_{\mathit{n\kappa }}\left(r\right),$$

(26)

where

$$\mathrm{\Delta }\left(r\right)=V\left(r\right)-S\left(r\right),$$

(27)

$$\mathrm{\Sigma }\left(r\right)=V\left(r\right)+S\left(r\right).$$

(28)

Eliminating F _nκ (r) and G _nκ in Equations (25) and (26), we obtain the second-order Schrödinger-like equation as

$$\left\{\begin{array}{l}\frac{d^2}{d{r}^2}-\frac{\kappa \left(\kappa +1\right)}{r^2}+\frac{2\mathit{\kappa U}\left(r\right)}{r}-\frac{\mathit{dU}\left(r\right)}{\mathit{dr}}-U^2\left(r\right)\\ -\left(M+E_{\mathit{n\kappa }}-\mathrm{\Delta }\left(r\right)\right)\left(M-E_{\mathit{n\kappa }}+\mathrm{\Sigma }\left(r\right)\right)\\ +\frac{\frac{\mathit{d\Delta }\left(r\right)}{\mathit{dr}}\left(\frac{d}{\mathit{dr}}+\frac{\kappa }{r}-U\left(r\right)\right)}{\left(M+E_{\mathit{n\kappa }}-\mathrm{\Delta }\left(r\right)\right)}\end{array}\right\}{F}_{\mathit{n\kappa }}\left(r\right)=0,$$

(29)

$$\left\{\begin{array}{l}\frac{d^2}{d{r}^2}-\frac{\kappa \left(\kappa -1\right)}{r^2}+\frac{2\mathit{\kappa U}\left(r\right)}{r}+\frac{\mathit{dU}\left(r\right)}{\mathit{dr}}-U^2\left(r\right)\\ -\left(M+E_{\mathit{n\kappa }}-\mathrm{\Delta }\left(r\right)\right)\left(M-E_{\mathit{n\kappa }}+\mathrm{\Sigma }\left(r\right)\right)\\ +\frac{\frac{\mathit{d\Sigma }\left(r\right)}{\mathit{dr}}\left(\frac{d}{\mathit{dr}}-\frac{\kappa }{r}+U\left(r\right)\right)}{\left(M+E_{\mathit{n\kappa }}-\mathrm{\Sigma }\left(r\right)\right)}\end{array}\right\}{G}_{\mathit{n\kappa }}\left(r\right)=0,$$

(30)

where $\kappa \left(\kappa -1\right)=\tilde{l}\left(\tilde{l}+1\right),\kappa \left(\kappa +1\right)=l\left(l+1\right)$.

Spin symmetry limit

In the spin symmetry limit, $\frac{\mathit{d\Delta }\left(r\right)}{\mathit{dr}}=0$ or Δ(r) = c _s = const [1–4]. Here, we take the new generalized Morse-like potential as

$$\mathrm{\Sigma }\left(r\right)=D_e\left[1-{\left(\frac{A+B{e}^{-\mathit{\alpha r}}}{C+D^{\prime }{e}^{-\mathit{\alpha r}}}\right)}^2\right],$$

(31)

in addition to a Coulomb tensor interaction [21],

$$U\left(r\right)=-\frac{H}{r};r\ge R_e,$$

(32)

where

$$H=\frac{Z_a{Z}_b{e}^2}{4\pi {\mathit{ϵ}}_0}$$

(33)

and A, B, C, D′, α are constant, R _e is the Coulomb radius, and Z _a , Z _b denote the charges of the projectile a and the target nuclei b[21] Now substituting Equations (31) and (32) into Equation (29) yields

$$\left\{\begin{array}{c}\frac{d^2}{d{r}^2}-\frac{\kappa \left(\kappa +1\right)}{r^2}-\frac{2\mathit{\kappa H}}{r^2}-\frac{H}{r^2}-\frac{H^2}{r^2}-\left(M+E_{\mathit{n\kappa }}-c_s\right)\\ \left(M-E_{\mathit{n\kappa }}+D_e\left[1-{\left(\frac{A+B{e}^{-\mathit{\alpha r}}}{C+D^{\prime }{e}^{-\mathit{\alpha r}}}\right)}^2\right]\right)\end{array}\right\}{F}_{\mathit{n\kappa }}\left(r\right)=0.$$

(34)

The good approximation for the centrifugal term is given as [35]

$$\begin{array}{ll}\frac{1}{r^2}& ={\alpha }^2{\left(\frac{C{e}^{-\mathit{\alpha r}}}{C+D^{\prime }{e}^{-\mathit{\alpha r}}}\right)}^2,\\ =\underset{\alpha \to 0}{lim}\left(\begin{array}{c}\frac{1}{r^2}+\frac{\alpha }{r}+\frac{5}{12}{\alpha }^2+\frac{1}{12}{\alpha }^{3}r+\frac{1}{240}{\alpha }^4{r}^2\\ -\frac{1}{720}{\alpha }^5{r}^3-\frac{1}{6045}{\alpha }^6{r}^4+O\left(r^5\right)\end{array}\right)\end{array}$$

(35)

where C = -D′, Equation (33) gives a good approximation for the centrifugal term (see in Figure 2). Performing a power series expansion and setting α → 0 gives the desired r^-2, as suggested by Greene and Aldrich [36]. Now, substituting Equation (35) into Equation (34) and defining a new variable s = e^-αr allows us to obtain

$$\begin{array}{ll}\frac{d^2{F}_{\mathit{n\kappa }}}{d{s}^2}& +\frac{\left(1+\frac{D^{\prime }}{C}s\right)}{s\left(1+\frac{D^{\prime }}{C}s\right)}\frac{d{F}_{\mathit{n\kappa }}}{\mathit{ds}}\\ +\frac{1}{s^2{\left(1+\frac{D^{\prime }}{C}s\right)}^2}\left[-A_0{s}^2+A_{1}s-A_2\right]F_{\mathit{n\kappa }}\left(s\right)=0,\end{array}$$

(36)

where

$$\begin{array}{l}{A}_0={\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)+\frac{{D^{\prime }}^2{\overline{\mathit{ϵ}}}^2}{C^2}-\frac{\tilde{\gamma }{B}^2}{C^2},\\ A_1=\left(2\frac{\mathit{AB}}{C^2}\tilde{\gamma }-\frac{2D^{\prime }{\overline{\mathit{ϵ}}}^2}{C}\right),A_2={\overline{\mathit{ϵ}}}^2-\tilde{\gamma }\frac{A^2}{C^2},\\ {\mathit{ϵ}}^2=\frac{\left[\left(M+E_{\mathit{n\kappa }}-c_s\right)\left(M-E_{\mathit{n\kappa }}\right)\right]}{{\alpha }^2},\\ \tilde{\gamma }=\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2},{\overline{\mathit{ϵ}}}^2={\mathit{ϵ}}^2+\tilde{\gamma },\\ {\eta }_{\kappa }=\left(\kappa +H+1\right).\end{array}$$

(37)

Comparing Equation (36) with Equation (4), we get

$$\begin{array}{l}{c}_1=1,{\xi }_1=\left({\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)+\frac{{D^{\prime }}^2{\overline{\mathit{ϵ}}}^2}{C^2}-\tilde{\gamma }\frac{B^2}{C^2}\right),\\ c_2=-\frac{D^{\prime }}{C},{\xi }_2=\left(2\frac{\mathit{AB}}{C^2}\tilde{\gamma }-\frac{2D^{\prime }{\overline{\mathit{ϵ}}}^2}{C}\right)\\ c_3=-\frac{D^{\prime }}{C},{\xi }_3=\left({\overline{\mathit{ϵ}}}^2-\tilde{\gamma }\frac{A^2}{C^2}\right)\end{array}$$

(38)

Equation (7) determines other coefficients as

$$\begin{array}{l}{c}_4=0,c_5=\frac{D^{\prime }}{2C},c_6=\frac{{D^{\prime }}^2}{C^2}\left({\overline{\mathit{ϵ}}}^2+\frac{1}{4}\right)+{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)-\tilde{\gamma }\frac{B^2}{C^2},\\ c_7=\frac{2D^{\prime }{\overline{\underset{\dot{}}{\mathit{ϵ}}}}^2}{C}-2\tilde{\gamma }\frac{\mathit{AB}}{C^2},c_8={\overline{\mathit{ϵ}}}^2-\tilde{\gamma }\frac{A^2}{C^2},\\ c_9=\frac{{D^{\prime }}^2}{C^2}\left[\frac{1}{4}-\tilde{\gamma }\frac{A^2}{C^2}\right]+\frac{D^{\prime }}{C}\left(2\frac{\mathit{AB}}{C^2}\tilde{\gamma }\right)+{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)-\tilde{\gamma }\frac{B^2}{C^2},\\ c_{10}=1+2\sqrt{{\overline{\mathit{ϵ}}}^2-\tilde{\gamma }\frac{A^2}{C^2}},\\ c_{11}=\frac{-2D^{\prime }}{C}+2\left[\sqrt{\frac{{D^{\prime }}^2}{C^2}\left[\frac{1}{4}-\tilde{\gamma }\frac{A^2}{C^2}\right]+\frac{D^{\prime }}{C}\left(2\frac{\mathit{AB}}{C^2}\tilde{\gamma }\right)+{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)-\tilde{\gamma }\frac{B^2}{C^2}}-\frac{D^{\prime }}{C}\sqrt{{\overline{\mathit{ϵ}}}^2-\tilde{\gamma }\frac{A^2}{C^2}},\right]\\ c_{12}=\sqrt{{\overline{\mathit{ϵ}}}^2-\tilde{\gamma }\frac{A^2}{C^2}},\\ c_{13}=\frac{D^{\prime }}{2C}-\left[\sqrt{\frac{{D^{\prime }}^2}{C^2}\left[\frac{1}{4}-\tilde{\gamma }\frac{A^2}{C^2}\right]+\frac{D^{\prime }}{C}\left(2\frac{\mathit{AB}}{C^2}\tilde{\gamma }\right)+{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)-\tilde{\gamma }\frac{B^2}{C^2}}-\frac{D^{\prime }}{C}\sqrt{{\overline{\mathit{ϵ}}}^2-\tilde{\gamma }\frac{A^2}{C^2}}\right].\end{array}$$

(39)

In order to obtain the bound state energy eigenvalues, we used Equation (12) and easily obtain the energy eigenvalue for the Dirac-Morse square problem including Coulomb-like tensor interaction as

$$\begin{array}{l}-\frac{D^{\prime }}{C}n-\left(2n+1\right)\left(\frac{D^{\prime }}{2C}\right)+\left(2n+1\right)\left(\begin{array}{l}\sqrt{\begin{array}{l}\frac{{D^{\prime }}^2}{C^2}\left[\frac{1}{4}-\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}\frac{A^2}{C^2}\right]+\frac{D^{\prime }}{C}\left(2\frac{\mathit{AB}}{C^2}\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}\right)\\ +{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)-\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}\frac{B^2}{C^2}\end{array}}\\ -\frac{D^{\prime }}{C}\sqrt{\begin{array}{l}\frac{\left(M+E_{\mathit{n\kappa }}-c_s\right)\left(M-E_{\mathit{n\kappa }}\right)}{{\alpha }^2}+\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}\\ -\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}\frac{A^2}{C^2}\end{array}}\end{array}\right)\\ -n\left(n-1\right)\frac{D^{\prime }}{C}+\frac{2D^{\prime }}{C}\left[\frac{\left(M+E_{\mathit{n\kappa }}-c_s\right)\left(M-E_{\mathit{n\kappa }}\right)}{{\alpha }^2}+\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}\right]-2\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}\frac{\mathit{AB}}{C^2}\\ -2\frac{D^{\prime }}{C}\left(\frac{\left(M+E_{\mathit{n\kappa }}-c_s\right)\left(M-E_{\mathit{n\kappa }}\right)}{{\alpha }^2}+\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}-\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}\frac{A^2}{C^2}\right)\\ +2\sqrt{\begin{array}{l}\left(\frac{\left(M+E_{\mathit{n\kappa }}-c_s\right)\left(M-E_{\mathit{n\kappa }}\right)}{{\alpha }^2}+\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}-\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}\frac{A^2}{C^2}\right)\left(\frac{{D^{\prime }}^2}{C^2}\left[\frac{1}{4}-\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}\frac{A^2}{C^2}\right]\right.\\ \left.+\frac{D^{\prime }}{C}\left(2\frac{\mathit{AB}}{C^2}\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}\right)+{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)-\frac{D_e\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}\frac{B^2}{C^2}\right)\end{array}}=0,\end{array}$$

(40)

or more explicitly, we get

$$\left(M+E_{\mathit{n\kappa }}-c_s\right)\left(M-E_{\mathit{n\kappa }}\right)=\frac{{\alpha }^2}{4}{\left[\frac{\beta }{\left(n+\sigma \right)}+\left(n+\sigma \right)\right]}^2+{\alpha }^2\left[\tilde{\gamma }\left(\frac{A^2}{C^2}-1\right)-{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)\right],$$

(41)

where

$$\sigma =n+\frac{1}{2}-\frac{C}{D^{\prime }}\sqrt{\frac{{D^{\prime }}^2}{C^2}\left[{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)+\frac{1}{4}-\tilde{\gamma }\frac{A^2}{C^2}\right]-\frac{D^{\prime }}{C}\left[2\underset{¨}{\gamma }\frac{\mathit{AB}}{C^2}\right]-\tilde{\gamma }\frac{B^2}{C^2}},$$

(42)

$$\beta =\left({\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)+\frac{\tilde{\gamma }}{C^2}\left(\frac{B^2{C}^2}{{D^{\prime }}^2}-A^2\right)\right).$$

(43)

The corresponding upper spinor wave function is obtained using Equation (16) as

$$\begin{array}{l}{F}_{\mathit{n\kappa }}\left(r\right)=N_{\mathit{n\kappa }}{\left(e^{-\mathit{\alpha r}}\right)}^{\sqrt{{\overline{\mathit{ϵ}}}^2-\tilde{\gamma }\frac{A^2}{C^2}}}{\left(1+\frac{D^{\prime }}{C}{e}^{-\mathit{\alpha r}}\right)}^{\frac{1}{2}-\frac{C}{D^{\prime }}\left[\sqrt{\frac{{D^{\prime }}^2}{C^2}\left[\frac{1}{4}-\tilde{\gamma }\frac{A^2}{C^2}\right]+\frac{D^{\prime }}{C}\left(2\frac{\mathit{AB}}{C^2}\tilde{\gamma }\right)+{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)-\tilde{\gamma }\frac{B^2}{C^2}}\right]}\\ P_n^{\left(2\sqrt{{\overline{\mathit{ϵ}}}^2-\tilde{\gamma }\frac{A^2}{C^2}},-2\frac{C}{D^{\prime }}\sqrt{\frac{{D^{\prime }}^2}{C^2}\left[\frac{1}{4}-\tilde{\gamma }\frac{A^2}{C^2}\right]+\frac{D^{\prime }}{C}\left(2\frac{\mathit{AB}}{C^2}\tilde{\gamma }\right)+{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)-\tilde{\gamma }\frac{B^2}{C^2}}\right)}\left(1+2\frac{D^{\prime }}{C}{e}^{-\mathit{\alpha r}}\right),\end{array}$$

(44)

where N _nκ is the normalization constant. The lower component of the wave function can be calculated from Equation (25) as

$$G_{\mathit{n\kappa }}\left(r\right)=\frac{1}{\left(M+E_{\mathit{n\kappa }}-\mathrm{\Delta }\left(r\right)\right)}\left(\frac{d}{\mathit{dr}}+\frac{\kappa }{r}-U\left(r\right)\right)F_{\mathit{n\kappa }}\left(r\right).$$

(45)

Figure 2

The centrifugal term (1/ r ² ) and its approximation for α = 0.01 fm ^-1 , D ′ = -1.

Special cases

Let us study two potential models of the generalized Morse potential.

Attractive radial potential

Zou et al. [37] and Eshghi and Hamzavi [38] proposed the attractive radial potential of the form

$$V\left(r\right)=\frac{V_1{e}^{-4\mathit{\alpha r}}+V_2{e}^{-2\mathit{\alpha r}}+V_3}{{\left(1-e^{-2\mathit{\alpha r}}\right)}^2},$$

(46)

where V₁,V₂,V₃ are constant. The NGMP model of Equation (2) can be rewritten as

$$V\left(r\right)=\frac{D_e\left(\left(1-A^2\right)-2\left(1+\mathit{AB}\right)e^{-\mathit{\alpha r}}+\left(1-B^2\right)e^{-2\mathit{\alpha r}}\right)}{{\left(1-e^{-\mathit{\alpha r}}\right)}^2},$$

(47)

for C = 1 and D′ = -1. If we set α → 2α, V₃ = D _e (1 - A²), V₂ = 2D _e (1 + AB), V₁ = D _e (1 - B²), we obtain the energy eigenvalues and the wave function for the attractive radial potential reported by Eshghi and Hamzavi [25] as

$$\begin{array}{ll}\left(M+E_{\mathit{n\kappa }}-c_s\right)& \left(M-E_{\mathit{n\kappa }}\right)={\alpha }^2{\left[\frac{{\beta }^{\prime }}{\left(n+{\sigma }^{\prime }\right)}+\left(n+{\sigma }^{\prime }\right)\right]}^2\\ +4{\alpha }^2\left[\frac{\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}{V}_3-{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)\right],\end{array}$$

(48)

$$\begin{array}{l}{F}_{\mathit{n\kappa }}\left(r\right)=N_{\mathit{n\kappa }}{\left(e^{-\mathit{\alpha r}}\right)}^{\sqrt{{\mathit{ϵ}}^2+\frac{\left(E_{\mathit{n\kappa }}+M-c_s\right)V_3}{{\alpha }^2}+{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)}}\\ {\left(1-e^{-\mathit{\alpha r}}\right)}^{2-\left[\sqrt{\left[\frac{V_0{A}^2\left(E_{\mathit{n\kappa }}+M-c_s\right)}{{\alpha }^2{C}^2}+{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)+\frac{1}{4}\right]+\left[\frac{2V_2\left(E_{\mathit{n\kappa }}+M-c_s\right)}{{\alpha }^2}\right]+\frac{V_1\left(E_{\mathit{n\kappa }}+M-c_s\right)}{{\alpha }^2}}+\sqrt{{\mathit{ϵ}}^2+\frac{V_3{A}^2\left(E_{\mathit{n\kappa }}+M-c_s\right)}{{\alpha }^2}+{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)}\right]}{P}_n^{\left(c_{10},c_{11}\right)}\left(1-2e^{-\mathit{\alpha r}}\right),\end{array}$$

(49)

where

$${\sigma }^{\prime }=\frac{1}{2}\left(1+\sqrt{\begin{array}{l}\left[4{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)+1-\frac{4\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}{V}_3\right]\\ +\frac{8\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}{V}_2-\frac{4\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}{V}_1\end{array}}\right)$$

(50)

$${\beta }^{\prime }=\left({\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)+\frac{\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}\left(V_3-V_1\right)\right).$$

(51)

Deng-Fan potential

Different attempt has been made by different authors to investigate Deng-Fan exponential potential proposed many years ago [39–43]

$$V\left(r\right)=D{\left(1-\frac{b}{\left(e^{\mathit{\alpha r}}-1\right)}\right)}^2,$$

(52)

with

$$b=e^{\alpha r_c}-1,r\in \left(0,\infty \right),$$

(53)

where D is dissociation energy, b and α are potential parameters, and r _c is the equilibrium distance. We can rewrite the Deng-Fan potential of Equation (52) in a simpler form as

$$V\left(r\right)=\frac{D\left(1-2\left(1+b\right)e^{-\mathit{\alpha r}}+{\left(1+b\right)}^2{e}^{-2\mathit{\alpha r}}\right)}{{\left(1-e^{-\mathit{\alpha r}}\right)}^2}.$$

(54)

By comparing Equation (47) and Equation (52), we have D _e (1 - A²) = D, D _e (1 + AB) = D(1 + b), D _e (1 - B²) = D(1 + b)². In the [41], the energy eigenvalues were obtained without tensor interaction. Then, we should write η _κ = (κ + 1).

$$\begin{array}{l}\left(M+E_{\mathit{n\kappa }}-c_s\right)\left(M-E_{\mathit{n\kappa }}\right)\\ =\frac{{\alpha }^2}{4}{\left[\frac{\mathit{Db}\left(b+2\right)\frac{\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}}{\left(n+{\sigma }^{\prime \prime }\right)}+\left(n+{\sigma }^{\prime \prime }\right)\right]}^2\\ +{\alpha }^2\left[\frac{D\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}-{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)\right],\end{array}$$

(55)

where

$${\sigma }^{\prime \prime }=\frac{1}{2}\left(1+\sqrt{{\left(1+2{\eta }_{\kappa }\right)}^2+4b^2\frac{D\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}}\right),$$

(56)

$$\begin{array}{ll}{F}_{\mathit{n\kappa }}\left(r\right)=& N_{\mathit{n\kappa }}{\left(e^{-\mathit{\alpha r}}\right)}^{\sqrt{{\mathit{ϵ}}^2+\frac{D\left(E_{\mathit{n\kappa }}+M-c_s\right)}{{\alpha }^2{C}^2}+{\eta }_{\kappa }\left({\eta }_{\kappa }-1\right)}}\\ \times {\left(1-e^{-\mathit{\alpha r}}\right)}^{\frac{1}{2}\left(1+\sqrt{{\left(1+2{\eta }_{\kappa }\right)}^2+4b^2\frac{D\left(M+E_{\mathit{n\kappa }}-c_s\right)}{{\alpha }^2}}\right)}\\ \times P_n^{\left(c_{10},c_{11}\right)}\left(1-2e^{-\mathit{\alpha r}}\right).\end{array}$$

(57)

Numerical results

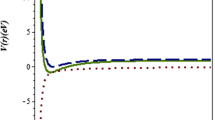
We obtain the energy eigenvalues in the absence (H = 0) and the presence (H =0.5 and 1) of the Coulomb-like tensor potential for various values of the quantum numbers n and κ. In Table 1, we have reported the numerical values of the energy for various values of H. We can clearly see that there is the degeneracy between the bound states and in the presence of the tensor interaction, these degeneracies are changed or removed. Also, we have reported the behavior of the energy in Figure 3, which represent energy vs. H which clearly see the degeneracy in the spin doublets for some values of H and the energy eigenvalue difference between the degenerate state increases as H increases. In Figure 4, we show the behavior of the energy vs. α for spin symmetry limits. It is seen that if the α-parameter increases, the bound states become more bounded both for the spin symmetry limit. Similarly, the energy has also been plotted vs. the potential coefficients D _e , A and B in Figures 5, 6, and 7. Finally, Figure 8 shows the plot of the energy for different values of C _s . It is seen in Figures 5, 6, 7, and 8 that although bound states obtained in view of spin symmetry become more bounded with increasing D _e , A and C _s , they become less bounded with increasing B.

Table 1 Energies in the spin symmetry limit for α = 0.01 fm ^-1 , M = 5 fm ^-1 , A = 1, B = -2, C = 1, D = -1, D _e = -0.8 fm ^-1 , C _s = 5

Figure 3

Energy vs. H for spin symmetry limit for first choice α = 0.01 fm ^-1 , M = 5 fm ^-1 , A = 1, B = -2, C = 1, D ′ = -1, D _e = -0.8 fm ^-1 , C _s = 5.

Figure 4

Energy vs. α for spin symmetry limit for H = 0.5, M = 5 fm ^-1 , A = 1, B = -2, C = 1, D ′ = -1, D _e = -0.8 fm ^-1 , C _s = 5.

Figure 5

Energy vs. D _e for spin symmetry limit for H = 0.5, α = 0.01 fm ^-1 , M = 5 fm ^-1 , A = 1, B = -2, C = 1, D ′ = -1, C _s = 5.

Figure 6

Energy vs. A for spin symmetry limit for H = 0.5, α = 0.01 fm ^-1 , M = 5 fm ^-1 , B = -2, C = 1, D ′ = -1, D _e = - 0.8 fm ^-1 , C =5.

Figure 7

Energy vs. B for spin symmetry limit for H = 0.5, α = 0.01 fm ^-1 , M = 5 fm ^-1 , A = 1, C = 1, D ′ = -1, D _e = -0.8 fm ^-1 , C _s = 5.

Figure 8

Energy vs. C _s for spin symmetry limit for H = 0.5, α = 0.04 fm ^-1 , M = 5 fm ^-1 , A = 1, B = -2, C = 1, D ′ = -0.8 fm ^-1 .

Conclusions

We have presented analytical expressions for the eigenvalues and wave function for the Dirac equation with a generalized Morse potential including Coulomb-like potential in view of the spin symmetry limit by using Nikiforov-Uvarov method. We have found the radial upper and lower wave functions in terms of the Jacobi polynomials. We have also discussed two special cases of this potential such as the attractive radial potential and Deng-Fan potential which is consistent with those found in the literature [37, 38, 40, 41]. These results we have obtained will be useful in many areas of physics such as theoretical, molecular, and nuclear physics.