Auto-Bäcklund transformation and new exact solutions of the (3+1)-dimensional KP equation with variable coefficients

Abstract

The (3+1)-dimensional variable coefficient Kadomtsev-Petviashvilli equation describes the dynamics of solitons and nonlinear waves in plasmas and superfluids. Based on computerized symbolic computation and extended variable coefficient homogeneous balance method, several families of exact soliton-like solutions, rational solutions, and auto-Bäcklund transformation are presented. With the use of the auto-BT and the ε-expansion method, we can obtain a soliton-like solution including N-solitary wave of the (3+1)-dimensional Kadomtsev-Petviashvilli equation with variable coefficients. Especially, we get a soliton-like solution including two-solitary waves as an illustrative example in detail.

Introduction

More and more physical structures of nonlinear dispersive equations have attracted a lot of interests due to their applications in many important scientific problems. With the help of symbolic computation[1–13], various methods have been developed for studying these physical structures, such as the inverse scattering method, Bäcklund transformation, Hirota bilinear forms, the tanh-sech method, the sine-cosine method, truncated Painlevé expansion method, similarity reduction method, and so on.

There has been considerable interest in the Kadomtsev-Petviashvili (KP) equation, which arises in many physical applications including shallow water waves and plasma physics. The KP equation describes the evolution of small amplitude surface waves, namely weak nonlinearity, weak dispersion, and propagation in one direction (the x-axis) with the waves weakly perturbed in the y direction[14]. In fact, the KP equation is a completely integrable soliton equation, which generally possesses almost all of the following remarkable properties: the existence of multisoliton solutions, an infinite number of independent conservation laws and symmetries, a bi-Hamiltonian representation, a prolongation structure, a Lax pair, Bäcklund transformations, the Hirota bilinear representation, and the Painlevé property, etc.[15].

Here, we consider the (3+1)-dimensional variable coefficient KP equation in the form[15]

$${(u_t+\lambda (t)u{u}_x+\mu (t)u_{\mathit{\text{xxx}}})}_x+\gamma (t)u_{\mathit{\text{yy}}}+\delta (t)u_{\mathit{\text{zz}}}=0,$$

(1)

where λ(t), μ(t), γ(t), and δ(t) are all functions of t only with λ(t) ≠0, μ(t) ≠ 0. If δ(t) = 0, Equation 1 becomes the (2+1)-dimensional KP equation. If γ(t) = δ(t) = 0, Equation 1 becomes the Korteweg-de Vries (KdV) equation. When λ(t), μ(t), γ(t), and δ(t) are arbitrary constants with λ(t) = 6, μ(t) = 1, Equation 1 becomes the (3+1)-dimensional KP equation, which describes the dynamics of solitons and nonlinear waves in plasmas and super fluids.

Zhang and coworkers[16] obtained an auto-Bäcklund transformation (BT) and the exact solution for the (3+1)-dimensional variable coefficient KP equation using the homogeneous balance principle. In virtue of the generalized variable coefficient algebraic method, Zhao[17] derived several new families of exact solutions of physical interest for the (3+1)-dimensional variable coefficient KP equation.

The structure of the present paper is as follows. The section ‘An extended variable coefficient homogeneous balance method’ presents the developing of the extended variable coefficient homogeneous balance (EvcHB) to solve the (3+1) dimensional equation. In section ‘Auto-Bäcklund transformation,’ an auto-BT of Equation 1 is obtained with the use of the EvcHB method. In section ‘Soliton-type solutions,’ using the auto-BT, we can derive the soliton-type solution of Equation 1. In section ‘ε-expansion method and two-solitary waves solutions,’ we discuss our method and results in detail.

An extended variable coefficient homogeneous balance method

An EvcHB has been proposed in[18]. In this paper, we will develop the EvcHB to solve the (3+1) dimensional equation and use Equation 1 as an illustration for the variable coefficient nonlinear evolution equations under investigation. Now, we describe what is the EvcHB method in solving the (3+1) dimensional equation and how to use it to look for the auto-BT and special exact solutions for the given (3+1) dimensional partial differential equation:

$$\begin{array}{l}P(u,u_x,u_y,u_z,u_t,u_{\mathit{\text{xy}}},u_{\mathit{\text{xz}}},u_{\mathit{\text{yz}}},u_{\mathit{\text{zt}}},u_{\mathit{\text{xt}}},u_{\mathit{\text{yt}}},\\ u_{\mathit{\text{xx}}},u_{\mathit{\text{zz}}},u_{\mathit{\text{tt}}},\dots )=0,\end{array}$$

(2)

where P is in general a polynomial function of its arguments, and the subscripts denote the partial derivatives.

First step: we assume a general transformation:

$$\begin{array}{ll}u(x,y,z,t)=& \psi (y,z,t){\partial }^{j}x{\partial }^{k}y{\partial }^{m}z{\partial }^{l}tf[\xi (x,y,z,t),\eta (x,y,z,t)]\\ +u_0(x,y,z,t),\end{array}$$

(3)

where ψ(y,z,t) is a differentiable function; j, k, m, and l are integers; u₀(x,y,z,t) is a special solution of Equation 2; f(ξ,η) is a function to be determined later.

Second step: by balancing the terms with the highest powers of the differential coefficients of ξ _x , we can obtain the values of j, k, m, and l. Substituting (3) into Equation 2, equating the coefficients of the highest powers of ξ _x to zero yields the value of f(ξ,η).

Third step: equating the coefficients of various partial derivatives of f(ξ,η) to zero, the corresponding auto-BT of Equation 2 can been derived.

Though the method is entirely algorithmic and it often has many tedious algebraic and auxiliary calculations which are virtually unmanageable manually, we can concisely and straightforwardly simplify them with the development of the symbolic computation systems[1–13].

Auto-Bäcklund transformation

In terms of the second step of the EvcHB method, we can obtain

$$\begin{array}{ll}u(x,y,z,t)=& \psi (y,z,t){\partial }^{2}xf[\xi (x,y,z,t),\eta (x,y,z,t)]\\ +u_0(x,y,z,t).\end{array}$$

(4)

In the following analysis, we will stay with the following conditions

$$\begin{array}{l}\psi (y,z,t)=1,\lambda (t)=6\mu (t),\\ {\eta }_x(x,y,z,t)=0\Rightarrow \eta (x,y,z,t)=\eta (y,z,t).\end{array}$$

(5)

Substituting (4) and (5) into Equation 1 we obtain

$$\begin{array}{l}+(6f_{\xi \xi \xi }^2+6f_{\xi \xi }{f}_{\xi \xi \xi \xi }+f_{\xi \xi \xi \xi \xi \xi })\mu {\xi }_x^6+[6\mu {\xi }_{\mathit{\text{xx}}}{u}_{0\mathit{\text{xx}}}\\ +\delta {\xi }_{\mathit{\text{xxzz}}}+\gamma {\xi }_{\mathit{\text{xxyy}}}+12\mu u_{0x}{\xi }_{\mathit{\text{xxx}}}+{\xi }_{\mathit{\text{xxxt}}}+6\mu u_0{\xi }_{\mathit{\text{xxxx}}}\\ +\mu {\xi }_{\mathit{\text{xxxxxx}}}]f_{\xi }+[6\mu u_{0\mathit{\text{xx}}}{\xi }_x^2+2\delta {\xi }_{\mathit{\text{xzz}}}{\xi }_x+2\gamma {\xi }_{\mathit{\text{xyy}}}{\xi }_x\\ +36\mu u_{0x}{\xi }_{\mathit{\text{xx}}}{\xi }_x+3{\xi }_{\mathit{\text{xxt}}}{\xi }_x+24\mu u_0{\xi }_{\mathit{\text{xxx}}}{\xi }_x\\ +6\mu {\xi }_{\mathit{\text{xxxxx}}}{\xi }_x+2\delta {\xi }_{\mathit{\text{xt}}}^2+2\gamma {\xi }_{\mathit{\text{xy}}}^2+18\mu u_0{\xi }_{\mathit{\text{xx}}}^2+10\mu {\xi }_{\mathit{\text{xxx}}}^2\\ +\delta {\xi }_{\mathit{\text{zz}}}{\xi }_{\mathit{\text{xx}}}+\gamma {\xi }_{\mathit{\text{yy}}}{\xi }_{\mathit{\text{xx}}}+3{\xi }_{\mathit{\text{xt}}}{\xi }_{\mathit{\text{xx}}}+2\delta {\xi }_z{\xi }_{\mathit{\text{xxz}}}+2\gamma {\xi }_y{\xi }_{\mathit{\text{xxy}}}\\ +{\xi }_t{\xi }_{\mathit{\text{xxx}}}+15\mu {\xi }_{\mathit{\text{xx}}}{\xi }_{\mathit{\text{xxxx}}}]f_{\xi \xi }+[12\mu u_{0x}{\xi }_x^3+\delta {\xi }_{\mathit{\text{zz}}}{\xi }_x^2\\ +\gamma {\xi }_{\mathit{\text{yy}}}{\xi }_x^2+3{\xi }_{\mathit{\text{xt}}}{\xi }_x^2+36\mu u_0{\xi }_{\mathit{\text{xx}}}{\xi }_x^2+15\mu {\xi }_{\mathit{\text{xxxx}}}{\xi }_x^2\\ +4\delta {\xi }_z{\xi }_{\mathit{\text{xz}}}{\xi }_x+4\gamma {\xi }_y{\xi }_{\mathit{\text{xy}}}{\xi }_x+3{\xi }_t{\xi }_{\mathit{\text{xx}}}{\xi }_x+60\mu {\xi }_{\mathit{\text{xx}}}{\xi }_{\mathit{\text{xxx}}}{\xi }_x\\ +15\mu {\xi }_{\mathit{\text{xx}}}^3+\delta {\xi }_z^2{\xi }_{\mathit{\text{xx}}}+\gamma {\xi }_y^2{\xi }_{\mathit{\text{xx}}}]f_{\xi \xi \xi }+[6\mu u_0{\xi }_x^4+{\xi }_t{\xi }_x^3\\ +20\mu {\xi }_{\mathit{\text{xxx}}}{\xi }_x^3+\delta {\xi }_z^2{\xi }_x^2+\gamma {\xi }_y^2{\xi }_x^2+45\mu {\xi }_{\mathit{\text{xx}}}^2{\xi }_x^2]f_{\xi \xi \xi \xi }\\ +15\mu {\xi }_x^4{\xi }_{\mathit{\text{xx}}}{f}_{\xi \xi \xi \xi \xi }+72\mu {\xi }_x^4{\xi }_{\mathit{\text{xx}}}{f}_{\xi \xi }{f}_{\xi \xi \xi }+6\mu {\xi }_x^4{\xi }_{\mathit{\text{xx}}}{f}_{\xi }{f}_{\xi \xi \xi \xi }\\ +[36\mu {\xi }_{\mathit{\text{xx}}}^2{\xi }_x^2+12\mu {\xi }_{\mathit{\text{xxx}}}{\xi }_x^3]f_{\xi }{f}_{\xi \xi \xi }+[72\mu {\xi }_{\mathit{\text{xx}}}^2{\xi }_x^2\\ +24\mu {\xi }_{\mathit{\text{xxx}}}{\xi }_x^3]f_{\xi \xi }^2+[6\mu (t){\xi }_{\mathit{\text{xxxx}}}{\xi }_x^2+36\mu {\xi }_{\mathit{\text{xx}}}{\xi }_{\mathit{\text{xxx}}}{\xi }_x\\ +6\mu {\xi }_{\mathit{\text{xx}}}\left(3{\xi }_{\mathit{\text{xx}}}^2+4{\xi }_x{\xi }_{\mathit{\text{xxx}}}\right)]f_{\xi }{f}_{\xi \xi }+[6\mu {\xi }_{\mathit{\text{xxx}}}^2\\ +6\mu {\xi }_{\mathit{\text{xx}}}{\xi }_{\mathit{\text{xxxx}}}]f_{\xi }^2+[\delta {\eta }_{\mathit{\text{zz}}}{\xi }_{\mathit{\text{xx}}}+\gamma {\eta }_{\mathit{\text{yy}}}{\xi }_{\mathit{\text{xx}}}+2\delta {\eta }_z{\xi }_{\mathit{\text{xxz}}}\\ +2\gamma {\eta }_y{\xi }_{\mathit{\text{xxy}}}+{\eta }_t{\xi }_{\mathit{\text{xxx}}}]f_{\xi \eta }+[\delta {\eta }_{\mathit{\text{zz}}}{\xi }_x^2+\gamma {\eta }_{\mathit{\text{yy}}}{\xi }_x^2+4\delta {\eta }_z{\xi }_{\mathit{\text{xz}}}{\xi }_x\\ +4\gamma {\eta }_y{\xi }_{\mathit{\text{xy}}}{\xi }_x+3{\eta }_t{\xi }_{\mathit{\text{xx}}}{\xi }_x+2\delta {\eta }_z{\xi }_z{\xi }_{\mathit{\text{xx}}}+2\gamma {\eta }_y{\xi }_y{\xi }_{\mathit{\text{xx}}}]f_{\xi \xi \eta }\\ +[{\eta }_t{\xi }_x^3+2\delta {\eta }_z{\xi }_z{\xi }_x^2+2\gamma {\eta }_y{\xi }_y{\xi }_x^2]f_{\xi \xi \xi \eta }+{\xi }_x^2[\delta {\eta }_z^2\\ +\gamma {\eta }_y^2]f_{\xi \xi \eta \eta }+{(u_{0t}+\lambda u_0{u}_{0x}+\mu u_{0\mathit{\text{xxx}}})}_x\\ +\gamma u_{0\mathit{\text{yy}}}+\delta u_{0\mathit{\text{zz}}}=0.\end{array}$$

(6)

Setting the coefficient of${\xi }_x^6$ in (6) to zero yields an ordinary differentiable equation (ODE) for f; namely

$$6f_{\xi \xi \xi }^2+6f_{\xi \xi }{f}_{\xi \xi \xi \xi }+f_{\xi \xi \xi \xi \xi \xi }=0,$$

(7)

which admits the solution

$$f=2ln(\xi )+\delta (\eta )+\xi \sigma (\eta ),$$

(8)

where δ(η) and σ(η) are differential functions. According to (8), we obtain

$$\begin{array}{l}{f}_{\xi }^2=\frac{-{[2+\xi \sigma (\eta )]}^2}{2}{f}_{\xi \xi },f_{\xi \xi }^2=-\frac{1}{3}{f}_{\xi \xi \xi \xi },\\ f_{\xi }{f}_{\xi \xi }=\frac{-2-\xi \sigma (\eta )}{2}{f}_{\xi \xi \xi },f_{\xi }{f}_{\xi \xi \xi }=\frac{-2-\xi \sigma (\eta )}{3}{f}_{\xi \xi \xi \xi },\\ f_{\xi \xi }{f}_{\xi \xi \xi }=-\frac{1}{6}{f}_{\xi \xi \xi \xi \xi },f_{\xi }{f}_{\xi \xi \xi \xi }=\frac{-2-\xi \sigma (\eta )}{4}{f}_{\xi \xi \xi \xi \xi }.\end{array}$$

(9)

According to the third step, substituting (7) and (9) into (6) yields a linear polynomial of f _ξ , f _{ξ ξ} ,…. Equating the coefficients of f _ξ , f _{ξ ξ} ,… to zero, holds

$$\mu \xi \sigma (\eta ){\xi }_x^4{\xi }_{\mathit{\text{xx}}}=0,$$

(10)

$$\begin{array}{ll}\delta {\xi }_z^2& +\gamma {\xi }_y^2+{\xi }_t{\xi }_x+\mu \{6u_0{\xi }_x^2-4[\xi \sigma (\eta )-1]\\ {\xi }_{\mathit{\text{xxx}}}{\xi }_x-3[4\xi \sigma (\eta )+1]{\xi }_{\mathit{\text{xx}}}^2\}=0,\end{array}$$

(11)

$$\begin{array}{ll}\delta [{\xi }_{\mathit{\text{zz}}}{\xi }_x^2& +{\xi }_z\left(4{\xi }_x{\xi }_{\mathit{\text{xz}}}+{\xi }_z{\xi }_{\mathit{\text{xx}}}\right)]+\gamma [{\xi }_{\mathit{\text{yy}}}{\xi }_x^2+{\xi }_y(4{\xi }_x{\xi }_{\mathit{\text{xy}}}\\ +{\xi }_y{\xi }_{\mathit{\text{xx}}})]+3{\xi }_x\left({\xi }_x{\xi }_{\mathit{\text{xt}}}+{\xi }_t{\xi }_{\mathit{\text{xx}}}\right)+12\mu u_{0x}{\xi }_x^3\\ +3\mu \{12u_0{\xi }_{\mathit{\text{xx}}}+[3-\xi \sigma (\eta )]{\xi }_{\mathit{\text{xxxx}}}\}{\xi }_x^2\\ -30\mu \xi \sigma (\eta ){\xi }_{\mathit{\text{xx}}}{\xi }_{\mathit{\text{xxx}}}{\xi }_x-3\mu [3\xi \sigma (\eta )+1]{\xi }_{\mathit{\text{xx}}}^3=0,\end{array}$$

(12)

$$\begin{array}{l}-3\mu {\xi }^2{\xi }_{\mathit{\text{xxx}}}^2\sigma {(\eta )}^2-3\mu {\xi }^2{\xi }_{\mathit{\text{xx}}}{\xi }_{\mathit{\text{xxxx}}}\sigma {(\eta )}^2\\ -12\mu \xi {\xi }_{\mathit{\text{xxx}}}^2\sigma (\eta )-12\mu \xi {\xi }_{\mathit{\text{xx}}}{\mathit{\text{xi}}}_{\mathit{\text{xxxx}}}\sigma (\eta )\\ +18\mu u_0{\xi }_{\mathit{\text{xx}}}^2-2\mu {\xi }_{\mathit{\text{xxx}}}^2+36\mu {\xi }_x{u}_{0x}{\xi }_{\mathit{\text{xx}}}\\ +3{\xi }_{\mathit{\text{xt}}}{\xi }_{\mathit{\text{xx}}}+6\mu {\xi }_x^2{u}_{0\mathit{\text{xx}}}+3{\xi }_x{\xi }_{\mathit{\text{xxt}}}\\ +\delta \left(2{\xi }_{\mathit{\text{xz}}}^2+2{\xi }_x{\xi }_{\mathit{\text{xzz}}}+{\xi }_{\mathit{\text{zz}}}{\xi }_{\mathit{\text{xx}}}+2{\xi }_z{\xi }_{\mathit{\text{xxz}}}\right)\\ +\gamma \left(2{\xi }_{\mathit{\text{xy}}}^2+2{\xi }_x{\xi }_{\mathit{\text{xyy}}}+{\xi }_{\mathit{\text{yy}}}{\xi }_{\mathit{\text{xx}}}+2{\xi }_y{\xi }_{\mathit{\text{xxy}}}\right)\\ +{\xi }_t{\xi }_{\mathit{\text{xxx}}}+24\mu u_0{\xi }_x{\xi }_{\mathit{\text{xxx}}}+3\mu {\xi }_{\mathit{\text{xx}}}{\xi }_{\mathit{\text{xxxx}}}\\ +6\mu {\xi }_x{\xi }_{\mathit{\text{xxxxx}}}=0,\end{array}$$

(13)

$$\begin{array}{ll}\delta {\xi }_{\mathit{\text{xxzz}}}& +\gamma {\xi }_{\mathit{\text{xxyy}}}+{\xi }_{\mathit{\text{xxxt}}}+\mu \left(6{\xi }_{\mathit{\text{xx}}}{u}_{0\mathit{\text{xx}}}+12u_{0x}{\xi }_{\mathit{\text{xxx}}}\right.\\ \left.+6u_0{\xi }_{\mathit{\text{xxxx}}}+{\xi }_{\mathit{\text{xxxxxx}}}\right)=0,\end{array}$$

(14)

$${(u_{0t}+\lambda u_0{u}_{0x}+\mu u_{0\mathit{\text{xxx}}})}_x+\gamma u_{0\mathit{\text{yy}}}+\delta u_{0\mathit{\text{zz}}}=0.$$

(15)

From (4) and (8), the new auto-BT for the (3+1)-dimensional variable coefficient KP equation can be written as follows

$$u(x,y,z,t)={\partial }^{2}x[2ln(\xi )+\delta (\eta )+\xi \sigma (\eta )]+u_0(x,y,z,t),$$

(16)

with σ(η), δ(η), and ξ satisfying Equations 10 to 15. The meaning of auto-BT consisted of 10 to 16 is that if u₀(x,y,z,t) be a special solution of Equation 1, then the expression (16) is another solution of Equation 1.

Soliton-type solutions

Now, we use the new auto-BT consisted of Equations 10 to 16 to obtain the exact solutions of Equation 1. Starting from Equation 10, we need to investigate different cases as follows

Case 1: ξ _xx  = 0

In this case, assume that

$$\xi (x,y,z,t)={\phi }_1(y,z,t)x+{\phi }_2(y,z,t),$$

(17)

where φ₁(y,z,t) and φ₂(y,z,t) are differentiable functions. Substituting (17) into (11) yields

$$u_0(x,y,z,t)=\frac{-\left(x{\phi }_{1t}+{\phi }_{2t}\right){\phi }_1-\delta {\left(x{\phi }_{1z}+{\phi }_{2z}\right)}^2-\gamma \left({\phi }_{2y}^2+x{\phi }_{1y}\right)}{6\mu {\phi }_1^2}.$$

(18)

Substituting (17) and (18) into (12), we get

$$\begin{array}{l}x:\delta {\phi }_{1\mathit{\text{zz}}}+\gamma {\phi }_{1\mathit{\text{yy}}}=0,\\ x^0:{\phi }_{1t}+\delta {\phi }_{2\mathit{\text{zz}}}+\gamma {\phi }_{2\mathit{\text{yy}}}=0.\end{array}$$

(19)

Equations 13 and 14 equate to zero naturally. So, we derive a family of rational solutions for Equation 1 as

$$\begin{array}{ll}u(x,y,z,t)=& -\frac{2{\phi }_1^2}{{\left(x{\phi }_1+{\phi }_2\right)}^2}\\ -\frac{\delta {\left(x{\phi }_{1z}+{\phi }_{2z}\right)}^2+\gamma {\left(x{\phi }_{1y}+{\phi }_{2y}\right)}^2+{\phi }_1\left(x{\phi }_{1t}+{\phi }_{2t}\right)}{6\mu {\phi }_1^2},\end{array}$$

(20)

with φ₁ = φ₁(y,z,t), φ₂ = φ₂(y,z,t) and u₀(x,y,z,t) satisfying constraint (19) and (15).

Case 2: σ(η) = 0.

Aiming at the exact solutions, we substitute a trial solution

$$\xi (x,y,z,t)=\lambda (y,z,t)+e^{\alpha (t)x+\beta (y,z,t)},$$

(21)

into Equations 11 to 15, where α(t), λ(y,z,t), and β(y,z,t) are differentiable functions. Substituting (21) into (11) yields

$$\begin{array}{ll}{u}_0(x,y,z,t)=& -\frac{{\alpha }^2}{6}-\frac{x{\alpha }^{\prime }}{6\mu \alpha }-\frac{{\beta }_t}{6\mu \alpha }-\frac{{\lambda }_t{e}^{-x\alpha -\beta }}{6\mu \alpha }\\ -\frac{\delta {\lambda }_z^2{e}^{-2x\alpha -2\beta }}{6\mu {\alpha }^2}-\frac{\gamma {\lambda }_y^2{e}^{-2x\alpha -2\beta }}{6\mu {\alpha }^2}\\ -\frac{\delta {\beta }_z^2}{6\mu {\alpha }^2}-\frac{\gamma {\beta }_y^2}{6\mu {\alpha }^2}-\frac{e^{-x\alpha -\beta }\gamma {\beta }_y{\lambda }_y}{3\mu {\alpha }^2}\\ -\frac{\delta {\beta }_z{\lambda }_z{e}^{-x\alpha -\beta }}{3\mu {\alpha }^2}.\end{array}$$

(22)

Substituting (21) and (22) into (12), we get

$$\begin{array}{l}{e}^{2(x\alpha +\beta )}:{\alpha }^{\prime }+\delta {\beta }_{\mathit{\text{zz}}}+\gamma {\beta }_{\mathit{\text{yy}}}=0,\\ e^{x\alpha +\beta }:\alpha {\lambda }_t+\delta \left(2{\beta }_z{\lambda }_z-{\lambda }_{\mathit{\text{zz}}}\right)+\gamma \left(2{\beta }_y{\lambda }_y-{\lambda }_{\mathit{\text{yy}}}\right)=0,\\ e^0:\delta {\lambda }_z^2+\gamma {\lambda }_y^2=0.\end{array}$$

(23)

Then, Equations 13 and 14 equate to zero naturally. Collecting all above terms, we can derive the general solutions of Equation 1 as follows

$$\begin{array}{ll}u(x,y,z,t)& =\frac{2\alpha {(t)}^2{e}^{x\alpha (t)+\beta }}{\lambda +e^{x\alpha (t)+\beta }}-\frac{2\alpha {(t)}^2{e}^{2x\alpha (t)+2\beta }}{{\left(\lambda +e^{x\alpha (t)+\beta }\right)}^2}\\ -\frac{\alpha {(t)}^2}{6}-\frac{x{\alpha }^{\prime }(t)+{\beta }_t+{\lambda }_t{e}^{-x\alpha (t)-\beta }}{6\mu (t)\alpha (t)}\\ -\frac{\delta (t){\beta }_z{\lambda }_z{e}^{-x\alpha (t)-\beta }+\gamma (t){\beta }_y{\lambda }_y{e}^{-x\alpha (t)-\beta }}{3\mu (t)\alpha {(t)}^2}\\ -\frac{\delta (t){\beta }_z^2+\delta (t){\lambda }_z^2{e}^{-2x\alpha (t)-2\beta }+\gamma (t){\beta }_y^2+\gamma (t){\lambda }_y^2{e}^{-2x\alpha (t)-2\beta }}{6\mu (t)\alpha {(t)}^2}.\end{array}$$

(24)

All parameters have been explained before. u₀(x,y,z,t), α(t), λ = λ(y,z,t), and β = β(y,z,t) satisfying constraint (15) and (23). Solution (24) contains more arbitrary parameters than the solution obtained before in[16] and[17].

ε-expansion method and two-solitary waves solutions

In order to obtain two-solitary waves solutions of Equation 1, we use the auto-BT consisted of Equations 10 to 15 to obtain a special single solitary wave solution of Equation 1. So, for simplicity, we take u₀(x,y,z,t) = 0, σ(η) = 0 and a direct assuming

$$\xi (x,y,z,t)=1+\mathit{\text{exp}}\theta ,\theta =cx+h(y,z,t),$$

(25)

where c is an arbitrary constant, h(y,z,t) are functions to be determined later. Substituting (25) into Equations 10 to 14, we hold

$$\begin{array}{l}\delta h_{\mathit{\text{zz}}}+\gamma h_{\mathit{\text{yy}}}=0,\\ c^4\mu (t)+c{h}_t+\delta h_z^2+\gamma h_y^2=0.\end{array}$$

(26)

Substituting (25) into Equation 16 yields a soliton-like solution containing single solitary wave of Equation 1

$$u(x,y,z,t)=\frac{1}{2}{c}^2\mathit{\text{sec}}{h}^2\frac{1}{2}\theta ,$$

(27)

where θ is expressed by (25), c and h = h(y,z,t) must satisfy Equation 26.

Next, we use the ε-expansion method[18–20] and assume that the solution of Equations 10 to 14 is of the form

$$\xi (x,y,z,t)=1+\sum _{i=1}^{\infty }{w}_i{\epsilon }^i,$$

(28)

where w _i  = w _i (x,y,z,t) (i = 1, 2, 3, …) to be determined later, ε be a small parameter. Substituting (28) into Equations 10 to 14. Equating the coefficient of ε^k (k = 1, 2, 3, …) to zero yields a set of PDEs for w _k (k = 1, 2, 3,…)

$$\epsilon :{[{(w_{1t}+\mu w_{1\mathit{\text{xxx}}})}_x+\gamma w_{1\mathit{\text{yy}}}+\delta w_{1\mathit{\text{zz}}}]}_{\mathit{\text{xx}}}=0,$$

(29)

$${\epsilon }^2:[{(w_{2t}+\mu w_{2\mathit{\text{xxx}}})}_x+\gamma w_{2\mathit{\text{yy}}}+\delta w_{2\mathit{\text{zz}}}=3w_1{w_1}_{\mathit{\text{xxxt}}}+\cdots ,$$

(30)

$${\epsilon }^3:[{(w_{3t}+\mu w_{3\mathit{\text{xxx}}})}_x+\gamma w_{3\mathit{\text{yy}}}+\delta w_{3\mathit{\text{zz}}}=3w_2{w_1}_{\mathit{\text{xxxt}}}+\cdots ,$$

(31)

and so on, to be solved.

For simplicity, we take a special solution of Equation 29 in the form

$$w_1=\sum _{i=1}^N{g}_i,g_i=\mathit{\text{exp}}{\theta }_i,{\theta }_i=c_{i}x+h_i(y,z,t),i=1,2,\dots ,N,$$

(32)

where c _i and h _i (y,z,t) satisfy Equation 26, N, a positive integer. Then, w₂ includes only all terms g _i g _j with i ≠ j; w₃ includes only all terms g _i g _j g _k with i ≠ j ≠ k; and so on. Thus the sequence w _k terminates at w _N  ∝ g₁g₂ ⋯ g _N , then the series (28) truncates. So, we have an exact solution (ε = 1) of Equations 10 to 15 in the form

$$\begin{array}{ll}\xi (x,y,z,t)& =1+w_1\\ =\sum _{i=1}^N{g}_i+\sum _{i\ne j}{h}_{\mathit{\text{ij}}}{g}_i{g}_j\\ +\sum _{i\ne j\ne k}{h}_{\mathit{\text{ijk}}}{g}_i{g}_j{g}_k+\cdots +h_{1,2,\dots ,N}{g}_1{g}_2{g}_N.\end{array}$$

(33)

Substituting (33) and u₀(x,y,z,t) = 0 into (16), we can obtain a soliton-like solution containing N-solitary wave of Equation 1; here, N-solitary wave means the interaction of N-solitary waves.

As an illustrative example, we look for a soliton-like solution containing two-solitary wave of Equation 1 in detail. Getting

$$w_1=g_1+g_2,g_i=\mathit{\text{exp}}{\theta }_i,{\theta }_i=c_{i}x+h_i(y,z,t),i=1,2,$$

(34)

for a solution of Equation 29. Substituting (34) into the right hand side of Equation 30, which admits a solution

$$w_2=h_{12}{g}_1{g}_2,h_{12}=\frac{{(c_1-c_2)}^2}{{(c_1+c_2)}^2}.$$

(35)

Substituting (34) and (35) into the right hand side of Equation 31 yields

$${(w_{3t}+\mu w_{3\mathit{\text{xxx}}})}_x+\gamma w_{3\mathit{\text{yy}}}+\delta w_{3\mathit{\text{zz}}}=0,$$

(36)

we may take w₃ = 0 for its solution, hence w _n  = 0 (n ≥ 3), therefore the series (28) truncates. Substituting (34), (35) and w _n  = 0 (n ≥ 3) into (28) (ε = 1) yields an exact solution of Equations 10 to 13

$$\xi (x,y,z,t)=1+g_1+g_2+h_{12}{g}_1{g}_2.$$

(37)

Substituting (37) and u₀(x,y,z,t) = 0 into (16), a soliton-like solution containing two-solitary wave of Equation 1 can be written as

$$\begin{array}{ll}u(x,y,t)& =2\frac{{c_1}^2{g}_1+{\left(c_1-c_2\right)}^2{g}_1{g}_2+{c_2}^2{g}_2}{1+g_1+g_2+h_{12}{g}_1{g}_2}\\ -2\frac{{[c_1{g}_1+c_2{g}_2+h_{12}\left(c_1+c_2\right)g_1{g}_2]}^2}{{\left(1+g_1+g_2+h_{12}{g}_1{g}_2\right)}^2},\end{array}$$

(38)

which represents the interaction of two-solitary waves.

In principle, families of the three-solitary wave, exact analytic solutions, and those for more solutions could be constructed similar to the above. However, the situations would become extremely complicated.

Discussions

In this letter, we have extended to Equation 1 an EvcHB method presented in[21–28], performed symbolic computation, and obtained a new auto-Bäcklund transformation and a families of the exact, analytic soliton-type solutions, two-solitary wave solution for Equation 1, which are Expression (24) and (38). The method can be implemented in the symbolic computation systems such as Mathematica or MatLab in Appendix A.

Of optical and physical interests, let us discuss the following special cases of our solutions which have appeared in the literature:

• (1) An interesting case of Expression (24), with λ = 1, $\alpha (t)=-2\int \gamma (t){\varphi }_5(t)\mathit{\text{dt}}$, β = ϕ ₅(t) y ² + ϕ ₆(t) y + [ϕ ₃(t) y + ϕ ₄(t)] z + ϕ ₇(t), is the set of the nebulonic solitons,

  $$\begin{array}{l}\gamma (t){\varphi }_5(t){\mu }^{\prime }(t)\int \gamma (t){\varphi }_5(t)\mathit{\text{dt}}-\mu (t)\left(\gamma (t)\delta (t){\varphi }_3{(t)}^2\right.\\ \left.+{\varphi }_5(t){\gamma }^{\prime }(t)\int \gamma (t){\varphi }_5(t)\mathit{\text{dt}}\right)=0,\end{array}$$
  $$\begin{array}{ll}u& =\frac{\alpha {(t)}^2}{cosh[-\alpha (t)x-\beta ]+1}-\frac{\alpha {(t)}^2}{6}\\ +\frac{2\{-2\mathrm{x\gamma }(t){\varphi }_5(t)+\mathit{\text{yz}}{\varphi }_3^{\prime }(t)+z{\varphi }_4^{\prime }(t)+y[y{\varphi }_5^{\prime }(t)+{\varphi }_6^{\prime }(t)]+{\varphi }_7^{\prime }(t)\}\alpha (t)}{\mu (t)}\\ -\frac{\delta (t){[y{\varphi }_3(t)+{\varphi }_4(t)]}^2+\gamma (t){[z{\varphi }_3(t)+2y{\varphi }_5(t)+{\varphi }_6(t)]}^2}{\mu (t)}\end{array}$$

  (39)

where u = u(x,y,z,t), ϕ _i (t)(i = 1,2,3,4,5,6,7)is the arbitrary function. We also find that

$$\alpha (t)=-2\int \gamma (t){\varphi }_5(t)\mathit{\text{dt}},$$

(40)

which has not been given in Refs.[16] and[17]. A family of exact analytic, nebulonic solutions (25) is shown in Figures1,2, and3.

Figure 1

The nebulonic solution (25), where μ ( t ) =  t², γ ( t ) =  ϕ ₅ ( t ) =  ϕ ₆ ( t ) =  t , ϕ ₇ ( t ) =  cost , ϕ ₃ ( t ) =  ϕ ₄ ( t ) = 0 , t  = −1.6.

Figure 2

The nebulonic solution (25), where t = −1.8.

Figure 3

The nebulonic solution (25), where t = −2.

• (2) Solution (3.3) in [16] is a special case of Expression (24).

• (3) The soliton-type solution for (2+1) dimensional KP equation,

  $${(u_t+\lambda (t)u{u}_x+\mu (t)u_{\mathit{\text{xxx}}})}_x+\gamma (t)u_{\mathit{\text{yy}}}=0,$$

in[16] is a special case of Expression (24), with α(t) = l, β = m y + ϕ₈(t) and δ(t) = 0, where l and m are arbitrary constants, ϕ₈(t) is arbitrary function. A soliton-type solution is shown in Figure4. which has been known in[29].

Figure 4

The soliton-type solution.

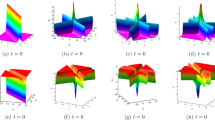
• (4) Figures 5, 6, 7, and 8 with the data of parameters illustrated in their captions, supply for us the propagating and interactions of the two-solitary wave in the different time.

Figure 5

The two-solitary wave solution (38), where c ₁  = 1, h ₁ ( y,z,t ) = − t  − 2 +  y  − 2 y², c ₂  = 2, h ₂ ( y,z,t ) = −  t  + 2 y  − 3 y², t  = −6.

Figure 6

The two-solitary wave solution (38), where t = 2 in Figure 5.

Figure 7

The two-solitary wave solution (38), where t = 6 in Figure 5.

Figure 8

The two-solitary wave solution (38). Where c₁ = 1, h₁(y,z,t) = −t − 2 + 2 y − 2 y², c₂ = 2, h₂(y,z,t) = t + 2 y − 3 y², t = −50.

Appendix A

The description of the symbolic code

The symbolic code of Equations 5 to 16 can be described as follows:

$$\begin{array}{ll}\mathit{\text{ln}}[1]:& =u[x,y,z,t]={\partial }_{x,x}f[\xi [x,y,z,t],\eta [y,z,t]]\\ +u_0[x,y,z,t]\\ \mathit{\text{ln}}[2]:& =J={\partial }_x({\partial }_{t}u[x,y,z,t]+6\mu [t]u[x,y,z,t]{\partial }_{x}u[x,y,z,t]\\ +\mu [t]{\partial }_{\mathit{\text{xxx}}}u[x,y,z,t])+\gamma [t]{\partial }_{\mathit{\text{yy}}}u[x,y,z,t]\\ +\delta [t]{\partial }_{\mathit{\text{zz}}}u[x,y,z,t]\\ \mathit{\text{ln}}[3]:& =\text{Coefficient}[J,{\xi }^{(1,0,0)}{[x,y,t]}^6]\\ \mathit{\text{ln}}[4]:& =M=\text{Expand}[J-\left(6{[f^{(3,0)}]}^2+6f^{(2,0)}{f}^{(4,0)}+f^{(6,0)}\right)\\ \ast {\xi }^{(1,0,0,0)}{(x,y,z,t)}^6]/.\{{[f^{(1,0)}]}^2\to \\ -{[2+\xi \sigma [\eta [y,z,t]]]}^2{f}^{(2,0)}/2\\ ,{[f^{(2,0)}]}^2\to -f^{(4,0)}/3,f^{(1,0)}{f}^{(2,0)}\to \\ --[2+\xi \sigma [\eta [y,z,t]]]f^{(3,0)}/2,\\ f^{(1,0)}{f}^{(2,0)}\to -[2+\xi \sigma [\eta [y,z,t]]]f^{(4,0)}/3\\ ,f^{(2,0)}{f}^{(3,0)}\to -f^{(5,0)}/6,\\ f^{(1,0)}{f}^{(4,0)}\to -[2+\xi \sigma [\eta [y,z,t]]]f^{(5,0)}/4\}\\ \mathit{\text{ln}}[5]:& =M_1=\text{Coefficient}[M,f^{(6,0)}[\xi [x,y,z,t],\eta [y,z,t]]]\\ \mathit{\text{ln}}[6]:& =M_2=\text{Coefficient}[M,f^{(5,0)}[\xi [x,y,z,t],\eta [y,z,t]]]\\ \mathit{\text{ln}}[7]:& =M_3=\text{Coefficient}[M,f^{(4,0)}[\xi [x,y,z,t],\eta [y,z,t]]]\\ \mathit{\text{ln}}[8]:& =M_4=\text{Coefficient}[M,f^{(3,0)}[\xi [x,y,z,t],\eta [y,z,t]]]\\ \mathit{\text{ln}}[8]:& =M_4=\text{Coefficient}[M,f^{(2,0)}[\xi [x,y,z,t],\eta [y,z,t]]]\\ \mathit{\text{ln}}[8]:& =M_4=\text{Coefficient}[M,f^{(1,0)}[\xi [x,y,z,t],\eta [y,z,t]]]\end{array}$$

(41)