Determination of the amplitude-frequency for strongly nonlinear oscillator by two approximate analytical techniques

Abstract

In this paper, we investigate two of the analytical approximate techniques, energy balance method and amplitude-frequency formulation, and these approximate techniques are applied to solve the strongly nonlinear differential equation of a mass attached to the center of a stretched elastic wire. We present a comparative study between the energy balance method and amplitude-frequency formulation with exact solution. The approximate results reveal that these methods are very effective and convenient for determining the frequencies of nonlinear dynamical systems.

Introduction

Nonlinear phenomena play important roles in applied mathematics, physics and also in engineering problems in which each parameter varies depending on different factors. Solving nonlinear equations may guide authors to know the described process deeply and sometimes leads them to know some facts which are not simply understood through common observations. Moreover, obtaining exact solutions for these problems is a great purpose which has been quite untouched.

With the rapid development of nonlinear science, many different methods were proposed to solve various nonlinear problems, such as perturbation method, homotopy perturbation method, energy balance method, amplitude-frequency formulation, variational iteration method, variational approach method, etc. [1–16].

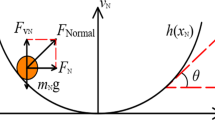
In this paper, we investigate two of the analytical approximate techniques, energy balance method and amplitude-frequency formulation, and these approximate techniques are applied to solve the strongly nonlinear differential equation of a mass attached to the center of a stretched elastic wire (Figure 1).

Figure 1

The oscillation of a mass attached to the center of a stretched elastic wire[1].

The differential equation of this dynamical system is in the following form [1]:

$$\frac{d^2}{d{t}^2}u\left(t\right)+u\left(t\right)-\frac{\lambda \cdot u\left(t\right)}{\sqrt{1+u{\left(t\right)}^2}}=0,0<\lambda \le 1,$$

(1)

with initial conditions [1]:

$$u\left(0\right)=A,\frac{d}{\mathit{dt}}u\left(0\right).$$

(2)

This system oscillates between symmetric bounds [−A, A], and its angular frequency and corresponding periodic solution are dependent on the amplitude A.

In this paper, our main purpose is to present a comparative study between the energy balance method and amplitude-frequency formulation with exact solution.

The description of energy balance method

In this section, we consider a general nonlinear oscillator in the following form [2]:

$$\frac{d^2}{d{t}^2}u\left(t\right)+f\left(u\left(t\right)\right)=0,$$

(3)

in which u and t are generalized dimensionless displacement and time variables, respectively. Its variational principle can be easily obtained:

$$J\left(u\left(t\right)\right)={\displaystyle {\int }_0^t\left[-\frac{1}{2}\cdot \frac{d}{\mathit{dt}}u{\left(t\right)}^2+F\left(u\left(t\right)\right)\right]\mathit{dt}},$$

(4)

where T = 2π/ω is the period of the nonlinear oscillator, F(u(t)) = ∫ f(u(t))du. Its Hamiltonian can be written in the following form:

$$\mathrm{\Delta }H=\frac{1}{2}\cdot \frac{d}{\mathit{dt}}u{\left(t\right)}^2+F\left(u\left(t\right)\right)=F\left(A\right)$$

(5)

or

$$R\left(t\right)=\frac{1}{2}\cdot \frac{d}{\mathit{dt}}u{\left(t\right)}^2+F\left(u\left(t\right)\right)-F\left(A\right)=0.$$

(6)

Oscillatory systems contain two important physical parameters, the frequency ω and the amplitude of oscillation, A. So let us consider such initial conditions:

$$u\left(0\right)=A,\frac{d}{\mathit{dt}}u\left(0\right)=0.$$

(7)

We use the following trial function to determine the angular frequency ω:

$$u\left(t\right)=Acos\left(\omega t\right).$$

(8)

Substituting Equation 8 into Equation 6, we obtain the following residual equation:

$$R\left(t\right)=\frac{1}{2}{A}^2{\omega }^2{sin}^2\left(\omega t\right)+F\left(Acos\left(\omega t\right)\right)-F\left(A\right)=0.$$

(9)

If by chance the exact solution had been chosen as the trial function, then it would be possible to make R zero for all values of t by appropriate choice of ω. Since Equation 8 is only an approximation to the exact solution, R cannot be made zero everywhere. Collocation at ωt = π/4 gives

$$\omega =\sqrt{\frac{2\left[F\left(A\right)-F\left(Acos\left(\omega \mathrm{t}\right)\right)\right]}{{\mathrm{A}}^2{sin}^2\left(\omega \mathrm{t}\right)}}.$$

(10)

Its period can be written in the following form:

$$T=\frac{2\pi }{\sqrt{\frac{2\left[F\left(A\right)-F\left(Acos\left(\omega \mathrm{t}\right)\right)\right]}{{\mathrm{A}}^2{sin}^2\left(\omega \mathrm{t}\right)}}}.$$

(11)

Therefore, we can obtain the following approximate solution:

$$u\left(t\right)=Acos\left(\sqrt{\frac{2\left[F\left(A\right)-F\left(Acos\left(\omega \mathrm{t}\right)\right)\right]}{{\mathrm{A}}^2{sin}^2\left(\omega \mathrm{t}\right)}}\cdot t\right).$$

(12)

The description of amplitude-frequency formulation

In this section, we consider a generalized nonlinear oscillator in the following form [3]:

$$\frac{d^2}{d{t}^2}u\left(t\right)+f\left(u\left(t\right)\right)=0,$$

(13)

with initial conditions:

$$u\left(0\right)=A,\frac{d}{\mathit{dt}}u\left(0\right)=0.$$

(14)

For solving nonlinear differential equation by means of amplitude-frequency formulations, we use two trial functions in the following form:

$$u_1\left(t\right)=Acos\left({\omega }_{1}t\right)$$

(15)

and

$$u_2\left(t\right)=Acos\left({\omega }_{2}t\right)$$

(16)

The residuals are

$$R_1\left(t\right)=-Acos\left({\omega }_{1}t\right)+f\left(cos\left({\omega }_{1}t\right)\right)$$

(17)

and

$$R_2\left(t\right)=-A{\omega }_2{2}^{}cos\left({\omega }_{2}t\right)+f\left(cos\left({\omega }_{2}t\right)\right).$$

(18)

The original frequency-amplitude formulation reads

$${\omega }^2=\frac{{\omega }_1{2}^{}{R}_2\left(t\right)-{\omega }_2{2}^{}{R}_1\left(t\right)}{R_2-R_1}.$$

(19)

He used the following formulation [3]; Geng and Cai improved the formulation by choosing another location point [4]. In other words, He solved the problem at the point zero, and they discussed at π/3, and by this work, they improved the method.

$${\omega }^2=\frac{{\omega }_1{2}^{}{R}_2\left({\omega }_{2}t=0\right)-{\omega }_2{2}^{}{R}_1\left({\omega }_{1}t=0\right)}{R_2-R_1}$$

(20)

This is the improved form by Geng and Cai:

$${\omega }^2=\frac{{\omega }_1{2}^{}{R}_2\left({\omega }_{2}t=\frac{\pi }{3}\right)-{\omega }_2{2}^{}{R}_1\left({\omega }_{1}t=\frac{\pi }{3}\right)}{R_2-R_1}.$$

(21)

By considering cos(ω₁t) = cos(ω₂t) = k and substituting the obtained ω into u(t) = cos(ωt), we can obtain the constant k in ω² equation in order to have the frequency without irrelevant parameter. To improve its accuracy, we can use the following trial function when they are required:

$$u_1\left(t\right)={\displaystyle \sum _{i=1}^m{A}_{i}cos({\omega }_i{\mathrm{t}),\mathrm{u}}_2\left(t\right)={\displaystyle \sum _{i=1}^m{A}_{i}cos\left({\mathrm{\Omega }}_i\mathrm{t}\right)}},$$

(22)

or we can use

$$\begin{array}{l}{u}_1\left(t\right)=\frac{{\displaystyle \sum _{i=1}^m{A}_{i}cos\left({\omega }_i\mathrm{t}\right)}}{{\displaystyle \sum _{j=1}^n{B}_{j}cos\left({\omega }_j\mathrm{t}\right)}},u_2\left(t\right)\\ =\frac{{\displaystyle \sum _{i=1}^m{A}_{i}cos\left({\mathrm{\Omega }}_i\mathrm{t}\right)}}{{\displaystyle \sum _{j=1}^n{B}_{j}cos\left({\mathrm{\Omega }}_j\mathrm{t}\right)}}\end{array}$$

(23)

However, in most cases because of the sufficient accuracy, trial functions are as follows and just the first term:

$$\begin{array}{l}{u}_1\left(t\right)=Acost,u_2\left(t\right)\\ =acos\left(\omega t\right)+\left(A-a\right)cos\left(3\omega t\right)\end{array}$$

(24)

and

$$u_1\left(t\right)=Acost,{\mathrm{u}}_2\left(t\right)=\frac{A\left(1+c\right)cos\left(\omega \mathrm{t}\right)}{1+\mathrm{c}\cos \left(2\omega \mathrm{t}\right)},$$

(25)

where a and c are unknown constants. In addition, we can set cos(t) = k in u₁(t) and cos(ωt) = k in u₂(t).

The application of energy balance method for the nonlinear oscillator

In this section, we consider the nonlinear equation in the following form [1]:

$$\frac{d^2}{d{t}^2}u\left(t\right)+u\left(t\right)-\frac{\lambda \cdot u\left(t\right)}{\sqrt{1+u{\left(t\right)}^2}}=0,0<\lambda \le 1,$$

(26)

with initial conditions [1]:

$$u\left(0\right)=A,\frac{d}{\mathit{dt}}u\left(0\right)=0.$$

(27)

For this problem,

$$f\left(u\left(t\right)\right)=u\left(t\right)-\frac{\lambda \cdot u\left(t\right)}{\sqrt{1+u{\left(t\right)}^2}}$$

(28)

and

$$F\left(u\left(t\right)\right)=\frac{1}{2}u{\left(t\right)}^2-\lambda \sqrt{1+u{\left(t\right)}^2}.$$

(29)

Its variational principle can be easily obtained:

$$J\left(u\left(t\right)\right)={\displaystyle {\int }_0^t\left(-\frac{1}{2}\cdot \frac{d}{\mathit{dt}}u{\left(t\right)}^2+\frac{1}{2}u{\left(t\right)}^2-\lambda \sqrt{1+u{\left(t\right)}^2}\right)}\mathit{dt}.$$

(30)

Its Hamiltonian, therefore, can be written in the following form:

$$\begin{array}{l}\mathrm{\Delta }\mathit{H}=\frac{1}{2}\cdot \frac{d}{\mathit{dt}}u{\left(t\right)}^2+\frac{1}{2}u{\left(t\right)}^2-\lambda \sqrt{1+u{\left(t\right)}^2}\\ =\frac{1}{2}{A}^2-\lambda \sqrt{1+A^2}\end{array}$$

(31)

or

$$\begin{array}{l}R\left(t\right)=\frac{1}{2}\cdot \frac{d}{\mathit{dt}}u{\left(t\right)}^2\\ +\frac{1}{2}u{\left(t\right)}^2-\lambda \sqrt{1+u{\left(t\right)}^2}-\frac{1}{2}{A}^2\\ +\lambda \sqrt{1+A^2}\\ =0.\end{array}$$

(32)

Substituting Equation 8 into Equation 32, we obtain

$$\begin{array}{l}R\left(t\right)=\frac{1}{2}{A}^2{\omega }^2{sin}^2\left(\omega \mathrm{t}\right)+\frac{1}{2}{A}^2{cos}^2\left(\omega \mathrm{t}\right)-.\\ \lambda \sqrt{1+A^2{cos}^2\left(\omega \mathrm{t}\right)}-\frac{1}{2}{A}^2+\lambda \sqrt{1+A^2}=0\end{array}$$

(33)

If we collocate at ωt = π/4, we obtain the following result:

$${\omega }_{\mathit{EBM}}=\sqrt{1+\frac{2\lambda \sqrt{4+2A^2}}{A^2}-\frac{4\lambda \sqrt{1+A^2}}{A^2}}.$$

(34)

Its period can be written in the following form:

$$T_{\mathit{EBM}}=\frac{2\pi }{\sqrt{1+\frac{2\lambda \sqrt{4+2A^2}}{A^2}-\frac{4\lambda \sqrt{1+A^2}}{A^2}}}.$$

(35)

The exact period is [1]

$$T_{\mathit{Exact}}=4{\displaystyle {\int }_0^{\frac{\pi }{2}}\left(1/\sqrt{1-\frac{2\lambda }{\sqrt{1+A^2{sin}^{2}t}+\sqrt{1+A^2}}}\right)}\mathit{dt}.$$

(36)

The application of amplitude-frequency formulation for the nonlinear oscillator

In this section, we consider the nonlinear equation in the following form [1]:

$$\frac{d^2}{d{t}^2}u\left(t\right)+u\left(t\right)-\frac{\lambda \cdot u\left(t\right)}{\sqrt{1+u{\left(t\right)}^2}}=0,0<\lambda \le 1,$$

(37)

with initial conditions [1]:

$$u\left(0\right)=A,\frac{d}{\mathit{dt}}u\left(0\right)=0.$$

(38)

For small values of A, we can write

$$\frac{1}{\sqrt{1+u{\left(t\right)}^2}}=1-\frac{1}{2}u{\left(t\right)}^2.$$

(39)

We can write nonlinear equation in the following form:

$$\frac{d^2}{d{t}^2}u\left(t\right)+\left(1-\lambda \right)u\left(t\right)+\frac{1}{2}\mathit{\lambda u}{\left(t\right)}^3=0$$

(40)

by using two trial functions in the following form:

$$u_1\left(t\right)=Acos\left(t\right)$$

(41)

and

$$u_2\left(t\right)=Acos\left(\omega t\right).$$

(42)

For Equation 40, we obtain the following residuals:

$$R_1\left(t\right)=-\mathit{\lambda Ak}+\frac{1}{2}\lambda A^3{k}^3.$$

(43)

By simple calculation, we obtain

$$R_2\left(t\right)=-3\mathit{Ak}-\mathit{\lambda Ak}+\frac{1}{2}\lambda A^3{k}^3.$$

(44)

With considering cos(ω₁t) = cos(ω₂t) = k, we have

$${\omega }^2=\frac{{\omega }_1{2}^{}{R}_2-{\omega }_2{2}^{}{R}_1}{R_2-R_1}$$

(45)

$${\omega }^2=\frac{-3\mathit{Ak}-\mathit{\lambda Ak}+\frac{1}{2}\lambda A^3{k}^3-{\omega }^2\left(-\mathit{\lambda Ak}+\frac{1}{2}\lambda A^3{k}^3\right)}{\left(-3\mathit{Ak}-\mathit{\lambda Ak}+\frac{1}{2}\lambda A^3{k}^3\right)-\left(-\mathit{\lambda Ak}+\frac{1}{2}\lambda A^3{k}^3\right)}.$$

(46)

Therefore, we have

$${\omega }_{\mathit{AFF}}=\sqrt{1-\lambda +\frac{1}{2}\lambda A^2{k}^2}.$$

(47)

We can rewrite u(t) = A cos(ωt) in the following form:

$$u\left(t\right)=Acos\left(\sqrt{1-\lambda +\frac{1}{2}\lambda A^2{k}^2}\cdot \mathrm{t}\right).$$

(48)

We can rewrite the main equation in the following form:

$$\begin{array}{l}\frac{d^2}{d{t}^2}u\left(t\right)+\left(\left(1-\lambda \right)+\frac{1}{2}\lambda A^2{k}^2\right)u\left(t\right)\\ =\frac{1}{2}\lambda A^2{k}^{2}u\left(t\right)-\frac{1}{2}\mathit{\lambda u}{\left(t\right)}^3.\end{array}$$

(49)

The right side of Equation 49 vanishes completely:

$$\begin{array}{l}B={\displaystyle {\int }_0^{\frac{T}{4}}\left(\frac{1}{2}\lambda A^2{k}^{2}u\left(t\right)-\frac{1}{2}\mathit{\lambda u}{\left(t\right)}^3\right)}\left(cos\left(\omega \mathrm{t}\right)\right)\mathrm{dt}\\ =0,\mathrm{T}=\frac{2\pi }{\omega }\end{array}$$

(50)

$$\begin{array}{l}{B}_1={\displaystyle {\int }_0^{\frac{T}{4}}\left(\frac{1}{2}\lambda A^2{k}^{2}Acos\left(\omega \mathrm{t}\right)\right)}\left(cos\left(\omega \mathrm{t}\right)\right)\mathrm{dt}\\ =\frac{1}{2}\lambda A^3{k}^2\frac{\pi }{4}\end{array}$$

(51)

$$B_2={\displaystyle {\int }_0^{\frac{T}{4}}\left(-\frac{1}{2}\lambda (A^3{cos}^3\left(\omega \mathrm{t}\right)\right)}\left(cos\left(\omega \mathrm{t}\right)\right)\mathrm{dt}=‒\frac{1}{2}\lambda A^3\frac{3\pi }{16}$$

(52)

So, we have

$$B=B_1+B_2\to \frac{1}{2}\lambda A^3{k}^2\frac{\pi }{4}-\frac{1}{2}\lambda A^3\frac{3\pi }{16}=0.$$

(53)

With solving and simplifying Equation 53, we have

$$k^2=\frac{3}{4}.$$

(54)

With substituting Equation 54 into Equation 47, we have approximate frequency in the following form:

$${\omega }_{\mathit{AFF}}=\sqrt{1-\lambda +\frac{3}{8}\lambda A^2}.$$

(55)

Its period can be written in the following form:

$$T_{\mathit{AFF}}=\frac{2\pi }{\sqrt{1-\lambda +\frac{3}{8}\lambda A^2}}.$$

(56)

The comparison of the approximate frequencies with exact frequencies

To illustrate the accuracy of the energy balance method and amplitude-frequency formulation, we present the comparison results of analytical approximate techniques with exact solution in Tables 1, 2, 3 and 4 and Figures 2, 3, 4 and 5 for different values of λ.

Table 1 Comparison of the approximate frequencies with the exact frequencies when λ = 0.1

Table 2 Comparison of the approximate frequencies with the exact frequencies when λ = 0.5

Table 3 Comparison of the approximate frequencies with the exact frequencies when λ = 0.75

Table 4 Comparison of the approximate frequencies with the exact frequencies when λ = 0.95

Figure 2

Comparison of energy balance method and amplitude-frequency formulation with exact solution when A = 1, λ = 0.1 .

Figure 3

Comparison of energy balance method and amplitude-frequency formulation with exact solution when A = 1, λ = 0.5 .

Figure 4

Comparison of energy balance method and amplitude-frequency formulation with exact solution when A = 1, λ = 0.75 .

Figure 5

Comparison of energy balance method and amplitude-frequency formulation with exact solution when A = 1, λ = 0.95 .

Conclusions

In this paper, we investigated and applied two of the analytical approximate techniques, energy balance method and amplitude-frequency formulation, for solving the strongly nonlinear differential equation of a mass attached to the center of a stretched elastic wire.

To illustrate the accuracy of the energy balance method and amplitude-frequency formulation, we presented a comparative study between the analytical approximate techniques with exact solution. The approximate results reveal that these methods are very effective and convenient for determining the frequencies of nonlinear dynamical systems.

Authors' information

AA received the B.S. degree in Civil Engineering from the University of Razi, Kermanshah, Iran, in 2002, and M.Sc. degree in Structure Engineering from Tarbiat Modares University, Tehran, Iran, in 2004, and Ph.D. degree in Civil Engineering from Tarbiat Modares University, Tehran, Iran, in 2011. He has been working as a consulting engineer in Design Structure in the private sector. Also, he is teaching in the fields of Earthquake Engineering and Steel Structure at the Islamic Azad University, Tehran, Iran. His research has been concentrated on numerical and experimental investigations on composite steel plate shear walls.

HEK was born in Tehran, Iran, on September 7, 1984. He received the B.S. degree in Civil Engineering-Building from the Shomal University, Amol, Iran, in 2006 and M.Sc. degree in Civil Engineering-Structure from the Shomal University, Amol, Iran, in 2008. At present, he is doing his researches toward Ph.D. degree in Friedrich Schiller University of Jena, Germany. He has published several technical manuscripts in refereed scientific journals. His research has been concentrated on numerical and approximate analytical solution of strongly nonlinear ODEs and PDEs, dynamical systems, and structural deformations.