Relativistic dynamics of electrons around impurities in high-density plasmas

Abstract

In this work, we focus our attention on the dynamic properties of relativistic electrons moving around an impurity in a plasma. This led us, in the first place, to compute the effective plasma potential (EPP) in which the electrons move. The EPP is built up as a sum of three contributions. These include the potential created by the impurity, the potential due to the ions assumed to form a uniform background of positive electric charges and the potential due to all the electrons. It turns out that the last potential depends on an integral of a function of the EPP in question. This then leads to a nonlinear integral equation where the EPP is the main quantity to compute. Thanks to the EPP, we derive the electron trajectories and compute their total electric field (microfield) at the impurity. According to different plasma conditions, two dynamical properties are then calculated: the time auto-correlation function of this microfield and the dielectric constant. These properties are calculated for both the relativistic case and non-relativistic (classical) case. The comparison between the relativistic and the classical results are also done for the different plasma conditions.

Introduction

The nonlinear behavior of electric charges around an impurity charge of the same sign is a problem that has been studied for a long time due to its great importance in many techniques [1–5]. Worth to mention that for fully ionized plasma composed of electrons and positive ions, the hypothesis of one-component plasma allows us to ignore the effects of ion movements to those of electrons because the ratio mass is about m _e /m _i  ≈ 1/2000. So, the system is only composed of one kind of mobile charge (electron), whereas the species of opposite charges (ions) are modeled by the continuous background which provides electrical neutrality. Coulomb forces between point charges are purely repulsive and do not get very close to each other almost always, irrespective of the plasma conditions. Concerning the ion-electron interaction, it is clear that it requires a quantum mechanical description. Indeed, if we make a classical estimation of the approach distance r _{i e} of an electron from the impurity (K _B T ∼ Z e²/r _{i e} ), we find that it is comparable to the thermal De Broglie wavelength λ _T which is equal to: λ _T  = h/(2π m _e K _B T)^1/2[6, 7]. If r _{i e}  > λ _T , the quantum effects do not exist, and if r _{i e}  < λ _T they exist and must be taken into account. Because the electrons are distributed over the velocities, some number of them reach distances less than λ _T and then require a quantal description. In this case, the Coulomb potential is replaced by the finite and regularized potential at the origin [8–10]$V_{\mathit{\text{ie}}}^{\mathit{\text{SD}}}\left(r\right)(\mathit{\text{Screened}}-\mathit{\text{Deutsch}})=-(Z{e}^2/r)\left(1-\mathit{\text{exp}}\right(-r/{\lambda }_T\left)\right)\text{exp}(-r/{\lambda }_D)$ or Kelbg interaction [11–14]$V_{\mathit{\text{ie}}}^K\left(r\right)=-\frac{Z{e}^2}{r}(1-\text{exp}(-r^2/{\left(\sqrt{\pi }{\lambda }_T\right)}^2)+\frac{r}{{\lambda }_T}(1-\text{erf}\left(\frac{r}{\sqrt{\pi }{\lambda }_T}\right)\left)\right)$ where λ _D  = (K _B T/(4π n _e e²))^1/2 is the Debye length and n _e is the density of the electrons. In this way, the quantum effects are approximately taken into account. The Kelbg potential is finite at zero distance and is an exact quantum potential in the case of weak coupling parameters Γ. It is also valid for the moderate coupling parameters taking into account the dominant quantum effects. The Kelbg potential is obtained by the first-order perturbation theory, its application is limited to the weak coupling parameter Γ < 1. We note that many recent works on the statistical properties of the electrons in plasmas exist in the literature. For example, we find in [6, 14] that the electrons are considered as classical particles moving according to the first Newton law ($d\vec{v}/\mathit{\text{dt}}=-m_e^{-1}\vec{\nabla }\mathrm{.V}\left(r\right)$, where m _e is the rest mass of the electron), and the interaction between the electron and the continuous background is taken as purely Coulomb potential as well as between the electrons themselves. In our work, we will consider these two potentials (screened Deutsch or Kelbg potential) for the interaction between the electron and the continuous positive background and we suppose that the electrons interact mutually via Debye potential. Furthermore, we consider the relativistic movement of the electron around the impurity to compute C _{E E} (t). This task passes through two steps: first, we compute the EPP V(r) in which the electron moves, and then in the second step, we solve the relativistic movement equation for the electron in the EPP ($d\vec{p}/\mathit{\text{dt}}=-\vec{\nabla }\mathrm{.V}\left(r\right)$ where $\vec{p}=m\vec{v}$ and m = m _e /(1-v²/c²)^1/2). In the ‘Integral equation for the effective energy potential’ section, we construct the integral equation governing the EPP on which all the subsequent results of this paper focus. We also solve this equation and make some discussions about its solutions. The dynamical properties, such as the trajectories of the electrons moving in the EPP as well as the time autocorrelation function of the electron microfield are presented in ‘The dynamical properties of the electrons’ section. The ‘Dielectric constant’ section applies the previous results to the dielectric constant of the plasma for different conditions. At the end, we close this paper with a conclusion.

Before starting the ‘Integral equation for the effective energy potential’ section, we mention the relevant parameters of our study: the charge number Z, the average distance between the electrons a = (3/4π n _e )^1/3, the electron coupling constant Γ = e²/(K _B T a), the degree of quanticity η = λ _T /a. The cases reviewed in this work are: the coupling parameter Γ = 0.1, the quanticity parameter η = 0.177, the dimensionless Debye length η^′ = λ _D /a = 1.826. These parameters correspond to the electron density n _e  = 2.×10²⁰cm^-3 and to the temperature T = 1.6×10⁵K. These parameters are found in a class of plasmas created by the laser or in some planets corresponding to the warm dense matter. It is worth to mention here that, at these conditions of temperatures and densities, the electron velocity is about v _{t h}  = 10⁸cm/s (m _e v²∼K _B T) whereas the Fermi velocity is about v _F  = 10⁷cm/s. This allows us to say that the electron gas is not degenerate (v _F  << v _{t h} ); therefore, it is sufficient to use the relativistic classical description of the electrons rather than the quantum one.

Integral equation for the effective energy potential

Construction of integral equation for the effective energy potential

Let us consider a medium consisting of electrons and a continuous background of neutralizing positive electrical charges. At first, the distribution of the electrons is that of Maxwell-Boltzmann governing the equilibrium state of the electron system. If we place a positive ion of charge Z e (called test charge or impurity) at the coordinate origin: the system is disturbed, and after a certain time t, it will reach a new equilibrium state described by a novel distribution of the electrons over the space around the charge Z e. This distribution is determined through the potential energy of an electron located at a distance r from the test charge Z e. The equilibrium potential energy is built up as a sum of three contributions:

$$V\left(r\right)=V_{\mathit{\text{ie}}}\left(r\right)+V_{\mathit{\text{ee}}}\left(r\right)+V_{\mathit{\text{ef}}}\left(r\right),$$

(1)

where V _{i e} (r) is the potential energy of ion-electron interaction (the ion is the test charge), V _{e e} (r) is the interaction energy of the electron with all the other electrons and V _{e f} (r) is the interaction energy of the electron with the continuous neutralizing background of ions. The ion-electron interaction is taken in a way that we can consider the quantum effects at short distances: we represent it here by the following pseudo-potential [8, 9]:

$$V_{\mathit{\text{ie}}}^{\text{SD}}\left(r\right)=-\frac{Z{e}^2}{r}\left(1-e^{-r/{\lambda }_T}\right)e^{-r/{\lambda }_D}$$

(2)

or Kelbg interaction [11–13]:

$$V_{\mathit{\text{ie}}}^{\mathrm{K}}\left(r\right)=-\frac{Z{e}^2}{r}(1-e^{-{(r/(\sqrt{\pi }{\lambda }_T\left)\right)}^2}+\frac{r}{{\lambda }_T}(1-\text{erf}\left(\frac{r}{\sqrt{\pi }{\lambda }_T}\right)\left)\right)$$

(3)

We will first investigate the case of screened Deutsch potential and the results for Kelbg potential are straightforward. The electron-electron interaction is that of the Debye potential energy $e^2{e}^{-r/{\lambda }_D}/r$ such as the potential energy V _{e e} (r), in the mean field approximation is equal to:

$$V_{\mathit{\text{ee}}}\left(r\right)=e^2\int f(\overrightarrow{r^{\prime }},\vec{p})\frac{e^{-\frac{1}{{\lambda }_D}\left|\vec{r}-\overrightarrow{r^{\prime }}\right|}}{\left|\vec{r}-\overrightarrow{r^{\prime }}\right|}d{\vec{p}}^{3}d{\overrightarrow{r^{\prime }}}^3,$$

(4)

where

$$f(\vec{r},\vec{p})=\frac{N}{\Omega }{\left(\frac{\mathrm{m\beta }}{2\pi }\right)}^{3/2}{e}^{-\beta (\frac{{\vec{p}}^2}{2m}+V(r\left)\right)}.$$

(5)

is the Maxwell-Boltzmann distribution, N is the total number of electrons and Ω is the volume of the system, whereas the potential energy of the electron with the positive background neutralizing charge is given by:

$$V_{\mathit{\text{ef}}}^{\text{SD}}\left(r\right)=-n_e{e}^2\int \frac{\left(1-e^{-\frac{\left|\vec{r}-\overrightarrow{r^{\prime }}\right|}{\mathrm{\lambda T}}}\right)e^{-\frac{\left|\vec{r}-\overrightarrow{r^{\prime }}\right|}{{\lambda }_D}}}{\left|\vec{r}-\overrightarrow{r^{\prime }}\right|}d{\overrightarrow{r^{\prime }}}^3$$

(6)

In this formula, we have introduced screened Deutsch interaction between the electron and the continuous background of positive charge. Then the potential interaction energy of the electron, with all the plasma components, satisfies the following nonlinear integral equation:

$$\begin{array}{c}{V}^{\text{SD}}\left(r\right)=V_{\mathit{\text{ie}}}^{\text{SD}}\left(r\right)+e^2\int \int f(\overrightarrow{r^{\prime }},\vec{p})\frac{e^{-\frac{\left|\vec{r}-\overrightarrow{r^{\prime }}\right|}{{\lambda }_D}}}{\left|\vec{r}-\overrightarrow{r^{\prime }}\right|}d{\vec{p}}^{3}d{\overrightarrow{r^{\prime }}}^3\hfill \\ -n_e{e}^2\int \frac{\left(1-e^{-\frac{\left|\vec{r}-\overrightarrow{r^{\prime }}\right|}{\mathrm{\lambda T}}}\right)e^{-\frac{\left|\vec{r}-\overrightarrow{r^{\prime }}\right|}{{\lambda }_D}}}{\left|\vec{r}-\overrightarrow{r^{\prime }}\right|}d{\overrightarrow{r^{\prime }}}^3\hfill \end{array}$$

(7)

Using spherical coordinates and some basic calculations, the last integral equation is transformed into the following:

$$\begin{array}{c}{V}^{\text{SD}}\left(r\right)=V_{\mathit{\text{ie}}}^{\text{SD}}\left(r\right)+2\pi n_e{e}^2\underset{0}{\overset{\infty }{\int }}\frac{r^{\prime }}{r}{\lambda }_D(e^{-(r+r^{\prime })/{\lambda }_D}\hfill \\ -e^{-|r-r^{\prime }|/{\lambda }_D}\left)\right(1-e^{-\beta V^{\text{SD}}\left(r^{\prime }\right)})d{r}^{\prime }\hfill \\ -2\pi n_e{e}^2\underset{0}{\overset{\infty }{\int }}\frac{r^{\prime }}{r}\lambda (e^{-(r+r^{\prime })/\lambda }\hfill \\ -e^{-|r-r^{\prime }|/\lambda })d{r}^{\prime },\hfill \end{array}$$

(8)

where λ=λ _D λ _T /(λ _T +λ _D ). In order to deal with an adimensional equation, put Y^SD(x) =- a V^SD(r)/(Z e²), a = (4π n _e /3)^-1/3, x = r/a, η = λ _T /a, η^′ = λ _D /a and ξ = η η^′/(η + η^′).

After that, we obtain the desired adimensional equation:

$$\begin{array}{c}{Y}^{\text{SD}}\left(x\right)=\frac{1}{x}(1-e^{-x/\eta })e^{-x/{\eta }^{\prime }}\hfill \\ -\frac{3}{2Z}\underset{0}{\overset{\infty }{\int }}\frac{x^{\prime }}{x}[{\eta }^{\prime }\left(e^{-\left(x+x^{\prime }\right)/{\eta }^{\prime }}{e}^{-\left|x-x^{\prime }\right|/{\eta }^{\prime }}\right)\hfill \\ \times \left(1-e^{\mathrm{Z\Gamma }{Y}^{\text{SD}}\left(x^{\prime }\right)}\right)\hfill \\ -\xi \left(e^{-\left(x+x^{\prime }\right)/\xi }-e^{-\left|x-x^{\prime }\right|/\xi }\right)]d{x}^{\prime }\hfill \end{array}$$

(9)

The same calculations for the case of Kelbg interaction give:

$$\begin{array}{c}{Y}^{\mathrm{K}}\left(x\right)=Y_{\mathit{\text{ie}}}^{\mathrm{K}}\left(x\right)+\frac{3}{2Z}\underset{0}{\overset{\infty }{\int }}\frac{x^{\prime }}{x}\left[{\eta }^{\prime }\right(e^{-\frac{x+x^{\prime }}{{\eta }^{\prime }}}-e^{-\frac{|x-x^{\prime }|}{{\eta }^{\prime }}})e^{\mathrm{Z\Gamma }{Y}^{\mathrm{K}}\left(x^{\prime }\right)}\hfill \\ -\frac{1}{\mathrm{\eta \surd \pi }}\left(F\right(x^{\prime }+x)-F(|x-x^{\prime }|\left)\right)]d{x}^{\prime },\hfill \end{array}$$

(10)

where

$$\begin{array}{c}{Y}_{\mathit{\text{ie}}}^{\mathrm{K}}\left(x\right)=\frac{1}{x}[1-e^{-{(x/(\sqrt{\pi }\eta \left)\right)}^2}+\frac{x}{\eta }(1-\text{erf}\left(\frac{x}{\sqrt{\pi }\eta }\right)\left)\right]\end{array}$$

and

$$\begin{array}{c}F\left(x\right)=x\frac{\sqrt{\pi }}{2}[-x(2\eta +x+\eta e^{-{(x/(\sqrt{\pi }\eta \left)\right)}^2})\hfill \\ +\pi {\eta }^2\mathit{\text{erf}}\left(\frac{x}{\sqrt{\pi }\eta }\right)(3/2+{\left(\frac{x}{\sqrt{\pi }\eta }\right)}^2)].\hfill \end{array}$$

Numerical solution of the integral equation for the potential energy

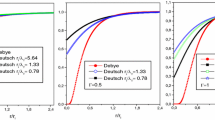
We can solve the nonlinear integral Equation 9 by the method of successive iterations (fixed-point method, FPM) starting with the initial function $Y_0\left(x\right)=Y_{\mathit{\text{ie}}}^{\text{SD}}\left(x\right)$. We can also solve this integral equation by transforming it into a second-order nonlinear differential equation that we have solved with the Runge-Kutta method. The numerical solution of the nonlinear integral Equations 9 and 10, in the case Γ = 0.1, η = 0.177, η^′ = 1.826 Z = 2 and Z = 8 by the iterative method gives the potential energy as shown in Figures 1 and 2.

Figure 1

Effective potential energy of the electron for Z = 2 in Deutsch and Kelbg cases.

Figure 2

Effective potential energy of the electron for Z = 8 in Deutsch and Kelbg cases.

In Figures 1 and 2, we notice that using the Kelbg interaction in the integral equation, between the electron and the impurity on the one hand and between the electron and the continuous background of positive charge on the other hand, gives a solution decreasing much slower than what is obtained when using the screened Deutsch potential. This means that the Deutsch solution is strongly screened, that is to say that its range is too inferior to that of Kelbg solution. The Runge-Kutta method (RKM) allows us to solve the nonlinear differential equation for the Deutsch case just equivalently to the integral equation:

$$\begin{array}{c}{Y}^{\mathrm{\prime \prime }}+\frac{2}{r}{Y}^{\prime }=\frac{3}{Z}(e^{\mathrm{Z\Gamma .Y}\left(r\right)}-1+{(\xi /{\eta }^{\prime })}^2)\hfill \\ +\frac{1}{{\eta }^{\prime 2}}Y\left(r\right)-\frac{1}{\mathrm{r\eta }}(2/{\eta }^{\prime }+1/\eta )e^{-r(1/{\eta }^{\prime }+1/\eta )}\hfill \end{array}$$

(11)

with initial conditions:

$$Y\left(0\right)\approx 1/\eta \mathit{\text{and}}{Y}^{\prime }\left(0\right)\approx -({\eta }^{\prime }/2\eta +1)/\eta {\eta }^{\prime }.$$

(12)

Figure 3 shows this equivalence, for Deutsch case, on the effective potential Y^SD(r) when Z = 8, Γ = 0.1, η = 0.177 and η^′ = 1.826.

Figure 3

Effective potential energy of electron for Z = 8 in Deutsch case. Computed with fixed-point method (line of stars) and Runge-Kutta method (solid line).

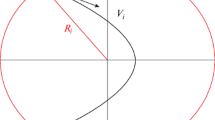
As expected we have also found that the RKM (differential equation) is faster than the fixed-point method (integral equation). The drawback of the RKM is that it is very sensitive to the initial conditions. Conversely, the FPM, despite that it requires much time for computation, it has more guarantees that the result converges towards an exact solution. Another drawback of the FPM is that it is adaptable only for the shielded initial potential. Mathematically, the integral Equation 9 admits finite solutions at short distance (when r has approximately the screening length as shown in Figure 4). This rapid convergence towards the solution is guaranteed by the screening effect. Physically, this may be interpreted by the following reasoning: a non-bounded electron interacts with a neighborhood of some mean inter-electron distance a. This neighborhood contains electrons that are distributed with a density n _e (r) around a single impurity of positive electric charge. This means that the impurities are distributed in plasma with a mean constant density such that the neighborhood of each electron contains only a single impurity (see schematic map in Figure 4). What has just been said suggests that numerical integration of the integral equation or the differential equation must be truncated to the size of this neighborhood. When the screening is weak (that is to say that λ _D is very large), the convergence towards the solution of the integral Equation 9 becomes slow, and the solution coincides at large distance with the Kelbg solution (see Figures 1 and 2).

Figure 4

Schematic map of electron distribution around the impurities in the plasma.

The dynamical properties of the electrons

Relativistic electron trajectories in plasma

The calculation of the real trajectories of relativistic electrons in a hot plasma, is a necessary step to calculate several dynamic properties such as the time autocorrelation function, the diffusion coefficient and the electric permittivity. So the purpose of this subsection is the calculation of relativistic trajectories of an electron in a plasma, and in the following subsection, we study the effect of those relativistic trajectories on the autocorrelation function.

The relativistic force acting on an electron in the plasma is equal to the derivative of the quantity of motion:

$$\vec{F}=\frac{d\vec{P}}{\mathit{\text{dt}}}=\frac{\mathit{\text{dm}}}{\mathit{\text{dt}}}\vec{v}+m\frac{d\vec{v}}{\mathit{\text{dt}}}$$

(13)

and the derivative of the mass is:

$$\frac{\mathit{\text{dm}}}{\mathit{\text{dt}}}=m_e\frac{d}{\mathit{\text{dt}}}\left(1/\sqrt{1-v^2/c^2}\right)=m_e\frac{1}{c^2}\vec{v}·\vec{g}\left(1-v^2/c^2\right){-3/2}^{}$$

(14)

where $\vec{g}$ is the relativistic acceleration and c the speed of light in vacuum; therefore, this force is equal to:

$$\vec{F}=\frac{m_e}{c^2}{\left(1-v^2/c^2\right)}^{-3/2}\left(\vec{v}·\vec{g}\right)\vec{v}+\frac{m_e}{\sqrt{1-v^2/c^2}}\vec{g}$$

(15)

and the force on the other hand equals:

$$\vec{F}=\frac{d\vec{P}}{\mathit{\text{dt}}}=-\vec{\nabla }V\left(r\right),$$

(16)

where V(r) represents the potential energy (Equation 8) of an electron plasma at position r of origin.

If we equate Equations 15 and 16 member to member, we find the equation:

$$\frac{m_e}{c^2}\left(1-v^2/c^2\right){-3/2}^{}\left(\vec{v}·\vec{g}\right)\vec{v}+\frac{m_e}{\sqrt{1-v^2/c^2}}\vec{g}=-\vec{\nabla }V\left(r\right).$$

(17)

To see the classical limit, we put (v²/c²) goes to zero in this equation, we obtain the classical form $m_e\vec{g}=-\vec{\nabla }V\left(r\right)$. Solving Equation 17 gives the relativistic trajectories of electrons around the impurity located at the coordinate origin. These trajectories permit us to compute the autocorrelation function of the electric field on the impurity and the constant dielectric.

The microfield autocorrelation function

The total electric microfield due to the electrons on the impurity centered at the coordinate origin is given by:

$$\vec{E}=\sum _{k=1}^{N_e}{\vec{e}}_{\mathit{\text{ie}}}\left(r_k\right),$$

(18)

where ${\vec{e}}_{\mathit{\text{ie}}}\left(r_k\right)$ is the individual electric field due to a plasma electron on the impurity. Then, the dimensionless electric field autocorrelation function is given by [7]:

$$\begin{array}{ll}{C}_{\mathit{\text{EE}}}\left(t\right)& =\frac{a^4}{e^2}〈\vec{E}\left(t\right)·\vec{E}〉\\ =\frac{a^4}{e^2}\int d{\vec{r}}_{1}d{\vec{v}}_1\mathrm{....d}{\vec{r}}_{N}d{\vec{v}}_N\vec{E}·\vec{E}(-t){\rho }_e\\ =\frac{a^4}{e^2}\int d{\vec{r}}_{1}d{\vec{v}}_1\vec{e}\left(r_1\right)N\\ \int d{\vec{r}}_{2}d{\vec{v}}_2\mathrm{....d}{\vec{r}}_{N}d{\vec{v}}_N\vec{E}(-t){\rho }_e\\ =\frac{a^4}{e^2}\int d{\vec{r}}_{1}d{\vec{v}}_1\vec{e}\left(r_1\right){\Psi }^{\left(1\right)}({\vec{r}}_1,{\vec{v}}_1,t)\end{array}$$

(19)

where ρ _e is the equilibrium canonical ensemble density matrix and e(r _α ) is the single particle field. The integrations over degrees of freedom 2,...,N in the second equality define a reduced function Ψ⁽¹⁾(r₁,v₁,t), which is the first member of a set of such functions,

$$\begin{array}{l}{\Psi }^{\left(s\right)}({\vec{r}}_1,{\vec{v}}_1\mathrm{....}{\vec{r}}_s,{\vec{v}}_s,t)\\ =N^s\int d{\vec{r}}_{s+1}d{\vec{v}}_{s+1}\mathrm{....d}{\vec{r}}_{N}d{\vec{v}}_N\vec{E}(-t){\rho }_e,\hfill \end{array}$$

(20)

it is straightforward to verify that these functions satisfy the BBGKY hierarchy [15].

$$\begin{array}{c}({\partial }_t+\vec{v}·{\vec{\nabla }}_r-\frac{{(1-\frac{v^2}{c^2})}^{1/2}}{m_e}\{{\vec{\nabla }}_r\left[V_{\mathit{\text{ie}}}\right(r)+V_{\mathit{\text{ef}}}(r\left)\right]\}\hfill \\ ·\{{\vec{\nabla }}_v-\frac{\vec{v}}{c}(\frac{\vec{v}.\overrightarrow{{\nabla }_v}}{c}\left)\right\}\left){\Psi }^{\left(1\right)}\right(\vec{r},\vec{v},t)\hfill \\ =\frac{1}{m_e\gamma }\int d{\vec{r}}_{1}d{\vec{v}}_1\left[{\vec{\nabla }}_r{V}_{\mathit{\text{ee}}}\right(\vec{r}-{\vec{r}}_1\left)\right]\hfill \\ ·\{{\vec{\nabla }}_v-\frac{\vec{v}}{c}(\frac{\vec{v}.\overrightarrow{{\nabla }_v}}{c}\left)\right\}{\Psi }^{\left(2\right)}(\vec{r},\vec{v};{\vec{r}}_1,{\vec{v}}_1,t),\hfill \end{array}$$

(21)

where γ = (1-(v/c)²)^-1/2, m _e is the electron mass at the rest and c is the light velocity. Recognizing this linear relationship, the basic approximation for weak coupling among the electrons is to neglect all of their correlations at all times.

$$\begin{array}{l}{\Psi }^{\left(2\right)}({\vec{r}}_1,{\vec{v}}_1,{\vec{r}}_2,{\vec{v}}_2,t)\to f({\vec{r}}_2,{\vec{v}}_2)\\ {\Psi }^{\left(1\right)}({\vec{r}}_1,{\vec{v}}_1,t),+f({\vec{r}}_1,{\vec{v}}_1)\\ {\Psi }^{\left(1\right)}({\vec{r}}_2,{\vec{v}}_2,t),\end{array}$$

(22)

where f(r,v) is the Maxwell-Juttner-Boltzmann distribution given by:

$$f(r,v)=\frac{\text{exp}(-(m{c}^2+V\left(r\right))/K_{B}T)}{m_e^3{c}^3{K}_2(m_e{c}^2/K_{B}T)}.$$

(23)

Here, m = m _e γ and K₂(x) is the modified Bessel function.

The use of Equation 22 in the first-hierarchy Equation 21 gives directly the kinetic equation:

$$\begin{array}{c}\left({\partial }_t+L\right)\Psi (\vec{r},\vec{v},t)=\frac{1}{m_e\gamma }[\overrightarrow{{\nabla }_v}-\frac{\vec{v}}{c^2}(\vec{v}.\overrightarrow{{\nabla }_v}\left)\right]f(\vec{r},\vec{v})·\hfill \\ {\vec{\nabla }}_r\int d{\vec{r}}_2{V}_{\mathit{\text{ee}}}\left(\vec{r}-{\vec{r}}_2\right)\int d{\vec{v}}_2{\Psi }^{\left(1\right)}({\vec{r}}_2,{\vec{v}}_2,t),\hfill \end{array}$$

(24)

where

$$L=\vec{v}.\vec{\nabla }-\frac{1}{m_e\gamma }\left[{\vec{\nabla }}_{r}V\left(r\right)\right].({\vec{\nabla }}_v-\frac{\vec{v}}{c^2}(\vec{v}.\overrightarrow{{\nabla }_v}).$$

(25)

We limit ourselves to the solution of the homogeneous equation (Equation 24) which is given by:

$${\Psi }^{\left(1\right)}(\vec{r},\vec{v},t)=f(\vec{r},\vec{v}){\vec{e}}_{\mathit{\text{mf}}}\left(\vec{r}\right(t\left)\right),$$

(26)

where

$${\vec{e}}_{\mathit{\text{mf}}}\left(\vec{r}\right)=\frac{1}{\mathit{\text{Ze}}}\vec{\nabla }V\left(r\right).$$

(27)

If we replace Equation 22 in Equation 19, we find:

$$C_{\mathit{\text{EE}}}\left(t\right)=\frac{a^4}{e^2}\int f\left(\vec{r},\vec{v}\right)\vec{e}\left(r\right)·{\vec{e}}_{\mathit{\text{mf}}}\left(r\right(t\left)\right)d\vec{r}d\vec{v},$$

(28)

where $\vec{r}\left(t\right)$ is the time-dependent position vector. We get it at all time t by solving numerically (using the Verlet algorithm) the movement equation $d\vec{P}/\mathit{\text{dt}}=-\mathrm{e.}{\vec{e}}_{\mathit{\text{mf}}}\left(r\right)$ with $\vec{P}=m_e\vec{v}/\surd (1-v^2/c^2)$ is the relativistic momentum of the electron. In the calculation of C _{E E} (t), the average on the velocities is done on the relativistic distribution f(r,v).

Regarding the function C _{E E} (t) (Figures 5 and 6), we find the following:

Figure 5

Classical and relativistic electric field autocorrelation function for Z =2 in Deutsch and Kelbg cases.

Figure 6

Classical and relativistic electric field autocorrelation function for Z =12 in Deutsch and Kelbg cases.

• When we move away from t = 0, the relativistic effect is manifested more clearly.

• When the charge number Z becomes large, the functions C _{E E} (t) according to the Deutsch solution become similar to those obtained from Kelbg solution, whether classical or relativistic (see Figure 6).

• In Figures 7 and 8, we note that when we increase the charge number Z, the covariance C(0) also increases, but all the relativistic curves in Kelbg and Deutsch cases decrease more quickly and have the same behavior at large time (vanish quickly and never become negative).

Figure 7

Relativistic electric field auto-correlation function for different Z in Deutsch case.

Figure 8

Relativistic electric field auto-correlation function for different Z in Kelbg case.

Dielectric constant

Another interesting property of plasma is the dielectric constant $\epsilon (\omega ,\vec{k})$ of the electron gas [16, 17]. This constant is, indeed, a function depending on the frequency Ω and the wave vector $\vec{k}$. This function has significant consequences for the physical properties of the plasma. In one limit, ε(ω,0) describes the collective excitations in the plasma. In another limit, $\epsilon (0,\vec{k})$ governs the screening of the electric charges in plasmas. The screening describes the interactions between electron-electron and electron-impurity in plasmas. We shall see how the impurity of the charge number Z and how the relativistic trajectories of the electrons around the impurity make the change on the dielectric constant. The latter is given by [18]:

$$\begin{array}{c}\tilde{\epsilon }(\vec{r},\vec{k};\omega )=\int d\overrightarrow{r^{\prime }}{e}^{i\vec{k}(\overrightarrow{r^{\prime }}-\vec{r})}\epsilon (\vec{r},\overrightarrow{r^{\prime }};\omega )\hfill \\ =1+\beta n_e\left(r\right){\tilde{V}}_{\mathit{\text{ee}}}\left(k\right)-\mathrm{\omega \beta }{n}_e\left(r\right){\tilde{V}}_{\mathit{\text{ee}}}\left(k\right)\hfill \\ \underset{-\infty }{\overset{0}{\int }}\mathrm{dt.}{e}^{\mathrm{i\omega t}}\int f\left(\vec{v}\right)d\vec{v}{e}^{i\vec{k}\left(\vec{r}\right(t)-\vec{r})},\hfill \end{array}$$

(29)

where

$${\tilde{V}}_{\mathit{\text{ee}}}\left(\vec{k}\right)=\frac{4\sqrt{2\pi }}{k^3}\underset{0}{\overset{\infty }{\int }}{e}^{-\mathrm{\beta V}\left(r^{\prime }\right)}{r}^{\prime }sin\left(k{r}^{\prime }\right)d{r}^{\prime }.$$

(30)

It is worth mentioning here, that we must recover the random-phase approximation (RPA) theory when we put the charge number of the impurity Z = 0. In this case, the density n _e (r) becomes constant (uniform plasma):

$$\begin{array}{c}\tilde{\epsilon }(\vec{k};\omega )\left(\mathit{\text{RPA}}\right)=\int d\overrightarrow{r^{\prime }}{e}^{i\vec{k}(\overrightarrow{r^{\prime }}-\vec{r})}\epsilon (\vec{r},\overrightarrow{r^{\prime }};\omega )\hfill \\ =1+\beta n_e{\tilde{V}}_{\mathit{\text{ee}}}\left(k\right)-\mathrm{\omega \beta }{n}_e{\tilde{V}}_{\mathit{\text{ee}}}\left(k\right)\hfill \end{array}$$

$$\begin{array}{c}\underset{-\infty }{\overset{0}{\int }}\mathrm{dt.}{e}^{\mathrm{i\omega t}}\int f\left(\vec{v}\right)d\vec{v}{e}^{i\vec{k}\vec{v}t}\hfill \\ =1+\beta n_e\left(r\right){\tilde{V}}_{\mathit{\text{ee}}}\left(k\right)-\mathrm{\omega \beta }{n}_e{\tilde{V}}_{\mathit{\text{ee}}}\left(k\right)\int \frac{f\left(\vec{v}\right)d\vec{v}}{\omega +i\vec{k}.\vec{v}+\mathrm{i\eta }}\hfill \end{array}$$

(31)

The excitation spectrum ω(k) can be obtained if we solve the equation $\tilde{\epsilon }(\vec{k};\omega )\left(\mathit{\text{RPA}}\right)=0$. Note here, in the RPA theory, that the relativistic effect participates only via the Maxwell-Juttner-Boltzmann distribution f(v) in Equation 31. Whereas in the general theory (see Equation 29), the relativistic effect participates further via the electron trajectories around the impurity. The limit behavior are also recovered: the short and long time (ω = ∞ and ω = 0, respectively); the first corresponds to the case where ε goes to delta function $\delta (\vec{r}-\overrightarrow{r^{\prime }})$ while the second corresponds to the static screening. We have calculated the dielectric constant from Equation 31. In Figures 9 and 10, we have presented the results for two fixed values of the wavelength k ($k=0.3\sqrt{3}$ and $k=0.4\sqrt{3}$) and at the same point $r=\sqrt{3}a)$. We have compared the curves with respect to the relativistic effect. The curves show the net difference between the classical and relativistic dielectric constant.

Figure 9

Real and imaginary parts of dielectric function for $k=\sqrt{3{\left(0.3\right)}^2}$ and $r=\sqrt{3}$ in Deutsch case.

Figure 10

Real and imaginary part of dielectric function for $k=\sqrt{3{\left(0.4\right)}^2})$ and $r=\sqrt{3}$ in Deutsch case.

Conclusion

The time autocorrelation function of the total electric microfield on positive charge impurity is considered when the relativistic dynamics of the electrons is taken into account. We have also calculated the dielectric constant as a response function of the plasma to the impurity. Concerning fixed coupling parameter Γ=0.1 and fixed density n _e and when the charge number Z of the impurity increases, we have found that the relativistic effect becomes important. The electron-impurity interaction is taken to be at the first time as screened Deutsch interaction and in the second time to be as of Kelbg’s. Comparisons of all interest quantities are made for these interactions as well as between classical and relativistic dynamics of electrons.