Evolutionary behavior of weak shocks in a non-ideal gas

Abstract

Except some empirical methods, which have been developed in the past, no analytical method exists to describe the evolutionary behavior of a shock wave without limiting its strength. In this paper, we have derived a system of transport equations for the shock strength and the induced continuity. We generate a completely intrinsic description of plane, cylindrical, and spherical shock waves of weak strength, propagating into a non-ideal gas. It is shown that for a weak shock, the disturbance evolves like an acceleration wave at the leading order. For a weak shock, we may assume that $\left[p\right]=O\left(\mathit{ϵ}\right),0<\mathit{ϵ}\ll 1.$_. We have considered a case when the effect of the first order-induced discontinuity or the disturbances that overtook the shock from behind are strong, i.e., [p _x ] = O(1). The evolutionary behavior of the weak shocks in a non-ideal gas is described using the truncation approximation.

Introduction

The study of the evolutionary behavior of non-linear waves in diverse branches of continuum mechanics has long been a subject of great interest from both mathematical and physical points of view. A rigorous mathematical approach to describe the kinematics of a shock has been proposed by Maslov [1] using the theory of generalized functions. Evolutionary behavior of shocks in fluids, using singular surface theory, has been discussed by Grinfeld [2], Anile [3], Straughan [4, 5], Jordan [6, 7], Radha et al. [8], and Pandey and Sharma [9]. Using a procedure based on the kinematics of one-dimensional motion, Sharma and Radha [10], Batt and Ravindran [11], and Sharma and Venkatraman [12] have studied the evolutionary behavior of shocks. In the present paper, we are concerned with planar, axially, and radially symmetric flows of a polytropic non-ideal gas behind a shock front which is propagating into a uniform region at rest; here, we employ the singular surface theory to derive asymptotic decay laws for shocks and the accompanying first-order discontinuity. Modulated simple wave theories have been developed by several authors; papers by Parker [13, 14] and an extensive review by Seymour and Mortell [15] are particularly illuminating.

The present paper is organized as follows: After setting up the basic equations and jump conditions across a shock of arbitrary strength, we devote ‘Transport equation for shock strength using singular surface theory’ and ‘Transport equation for the unknown term [p _x ]’ sections to the derivation of transport equations for the variation of jumps in pressure and their space derivatives; the equations are coupled with those involving jumps in higher order space derivatives of pressure. In section ‘Evolution laws for weak shocks’, we analyze the pair of coupled transport equations for the shock strength and accompanying first- and second-order discontinuities; the shock strength is assumed to be small, but the associated first-order jump discontinuity may be finite or small. Under these assumptions, the transport equations are solved exactly to the leading order once the strength of the accompanying second order discontinuity is neglected, and the evolutionary behavior of both the shock and the associated first-order discontinuity is completely analyzed.

Basic equations and jump conditions across shocks

The basic equations governing the one-dimensional unsteady flow in a non-ideal gas are as follows:

$$\begin{array}{l}{\rho }_t+\rho u_x+u{\rho }_x+\frac{\mathit{j\rho u}}{x}=0,\\ u_t+u{u}_x+\frac{1}{\rho }{p}_x=0,\\ p_t+u{p}_x+\frac{\mathit{\gamma p}}{\left(1-\mathit{b\rho }\right)}\left(u_x+\frac{\mathit{ju}}{x}\right)=0,\end{array}$$

(2.1)

where ρ is the density, u the gas velocity, p the pressure, and $a={\left(\frac{\mathit{\gamma p}}{\left(1-\mathit{b\rho }\right)\rho }\right)}^{1/2}$ the sound speed with γ as the specific heats ratio of the gas; here t stands for time and x the distance being either axial in flows with planar (j = 0) geometry, or radial in cylindrically symmetric (j = 1) and spherically symmetric (j = 2) flow configurations. As system (2.1) is quasilinear with each of these equations being a direct consequence of the corresponding conservation law, one expects shocks to appear in the flow after a finite running length or time. We consider the gas motion containing a shock wave propagating into a homogeneous quiescent equilibrium gas with intrinsic velocity U given by U^-1 = s^′(x) = dt/dx where t = s(x) denotes the location of the shock at position x.

The specific internal energy per unit mass of the non-ideal gas which may be given by [16] is

$$e=\frac{1}{\gamma -1}\frac{p\left(1-\mathit{b\rho }\right)}{\rho }.$$

(2.2)

The equation of state is taken to be of the form p(1 − bρ) = ρRT, where b is the internal volume of the gas molecules which is known in terms of the molecular interaction potential, R is the gas constant and T is the temperature. In addition, following the singular surface theory, we have the following compatibility condition

$$\frac{d\left[f\right]}{\mathit{dt}}=\left[f_t\right]+U\left[f_x\right],$$

(2.3)

where $\frac{d}{\mathit{dt}}$ denotes the time dervative following the shock front, [f] = f₋ − f₊ denotes the jump in a variable f with f₊ and f_- being the values of f immediately ahead of and immediately behind the shock, respectively. The medium ahead of the shock front is assumed to be uniform and at rest, i.e., ρ₊, ρ₊, and a₊ are constants, and u₊ = 0. The velocities u, a, and U appearing in (2.1) and (2.2) are non-dimensionalized by a₊, and the remaining variables ρ, p, x, and t are rendered dimensionless by ${\rho }_{+},{\rho }_{+}{a}_{+}^2,x_0$ and $\frac{x_0}{a_{+}},$ respectively; here, x₀ characterizes the reference length of the medium. Thus, the variables appearing in (2.1) and (2.2) will henceforth be regarded as dimensionless; indeed, in the medium ahead of the shock, we have a = a₊ = 1 and ρ = ρ₊ = 1. The following expressions follow readily from conditions (2.2), i.e.,:

$$\begin{array}{l}\left[u\right]=\frac{2}{\gamma +1}\frac{U^2-1}{U},\\ \left[\rho \right]=\frac{\left[u\right]}{U-\left[u\right]},\\ \left[p\right]=\left(1-b\right)\left[u\right]U.\end{array}$$

(2.4)

In view of (2.4), it follows that,

$$\begin{array}{ll}\frac{d\left[p\right]}{\mathit{dt}}& =\frac{2U^3\left(1-b\right)}{U^2+1}\frac{d\left[u\right]}{\mathit{dt}}\\ ={\left(\frac{\mu }{\gamma +1}\right)}^2\left(1-b\right)\frac{d\left[\rho \right]}{\mathit{dt}},\end{array}$$

(2.5)

where μ = 2 + (γ − 1)U².

Transport equation for shock strength using singular surface theory

In order to derive the equation for the shock strength, we take jumps in the Euler equations (2.1) and use the conditions (2.3) to (2.5) to obtain

$$\frac{d\left[V\right]}{\mathit{dt}}+A\left[V_x\right]+\Omega \left[u\right]B=0,$$

(3.1)

where,

$$\begin{array}{l}\left[V\right]={\left(\left[\rho \right]\left[u\right]\left[p\right]\right)}^{\mathit{tr}},\left[V_x\right]={\left(\left[{\rho }_x\right]\left[u_x\right]\left[p_x\right]\right)}^{\mathit{tr}}\text{,′}\\ A=\left(\begin{array}{ccc}\hfill \left[u\right]-U\hfill & \hfill 1+\left[\rho \right]\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \left[u\right]-U\hfill & \hfill \frac{1}{1+\left[\rho \right]}\hfill \\ \hfill 0\hfill & \hfill \frac{1-b+\gamma \left[p\right]}{1-b-b\left[\rho \right]}\hfill & \hfill \left[u\right]-U\hfill \end{array}\right),\\ B=\left(\begin{array}{c}\hfill 1+\left[\rho \right]\hfill \\ \hfill 0\hfill \\ \hfill \frac{1-b+\gamma \left[p\right]}{1-b-b\left[\rho \right]}\hfill \end{array}\right)\text{,′}\end{array}$$

(3.2)

and $\Omega =\frac{j}{x\left(t\right)}$. It may be noticed that the form (3.1) is not only convenient for algebraic manipulation but also is helpful in understanding the pattern of transport equations for higher order discontinuities.

We notice that (3.1) contains the unknown quantities [u _x ], [p _x ], and [ρ _x ]; eliminating the unknown discontinuities [ρ _x ] and [u _x ] between these equations by taking a suitable linear combination, we arrive at the first transport equation governing the shock strength:

$$\frac{d\left[p\right]}{\mathit{dx}}=k_{11}\left[p_x\right]+k_{12},$$

(3.3)

where the coefficients k₁₁ and k₁₂ are given by

$$k_{11}=\frac{2\mu \left(\left(1-b\right)\left(\mu -\nu \right)-2b\left(U^2-1\right)\right)}{\left(\gamma +1\right)\left(\left(2\mu \left(1-b\right)+\nu -4b\left(U^2-1\right)\right)U^2+\nu \right)},$$

$$k_{12}=-\frac{4\left(1-b\right)\mathit{\nu \mu }\left(U^2-1\right)\Omega }{{\left(\gamma +1\right)}^2\left(\left(2\mu \left(1-b\right)+\nu -4b\left(U^2-1\right)\right)U^2+\nu \right)},$$

with ν = 2γU² + 1 − γ. We note that an immediate consequence of (3.3) cannot reveal the complete history of the evolutionary behavior of the shocks under consideration because of the appearance of an unknown entity. It is clear from (3.3) that the evolutionary behavior of the shocks at any time t depends not only on the strength of the shock, its curvature, and the specific heat ratio γ, but also on the pressure gradient [p _x ] immediately behind the wave. In the following section, we determine a transport equation for the unknown [p _x ], which represents the effect of disturbances that overtake the shock from behind.

Transport equation for the unknown term [p _x ]

As the coupling term [p _x ] in (3.3) is unknown, we need to obtain a transport equation for it. Eliminating [u _x ] and [p _x ] from equations (3.1) along with (3.3), we get a relation between [ρ _x ] and [p _x ]. Similarly, eliminating the [ρ _x ] and [p _x ] from equations (3.1) along with (3.3), we obtain a relation between [u _x ] and [p _x ].

In this section, we determine the transport equation for the unknown pressure gradient jump as described in the preceding section. We first note that from equations (3.1),

$$\left(\begin{array}{c}\hfill \left[u_x\right]\hfill \\ \hfill \left[{\rho }_x\right]\hfill \end{array}\right)=T\left(\begin{array}{c}\hfill \left[p_x\right]\hfill \\ \hfill 1\hfill \end{array}\right),$$

(4.1)

where

$$T=\left(\begin{array}{cc}\hfill T_{11}\hfill & \hfill T_{12}\hfill \\ \hfill T_{21}\hfill & \hfill T_{22}\hfill \end{array}\right)$$

(4.2)

with

$$T_{11}=\frac{\mu }{U}\frac{\left(1+U^2\left(3-2b\right)\right)\left(\mu -b\left(\gamma +1\right)U^2\right)}{k_{13}},$$

$$T_{12}=-\frac{2\Omega \left(1-b\right)\mathit{\mu \nu }\left(U^4-1\right)}{\left(\gamma +1\right)U{k}_{13}},$$

$$T_{21}=\frac{{\left(\gamma +1\right)}^2{U}^2\left(U^2+3\right)}{\mu \left(U^2+1\right)}\frac{\left(1+U^2\left(3-2b\right)\right)\left(\mu -b\left(\gamma +1\right)U^2\right)}{k_{13}}-\frac{2{\left(\gamma +1\right)}^2{U}^2}{{\mu }^2\left(U^2+1\right)},$$

$$T_{22}=2\Omega \left(\gamma +1\right)U^2\left(U^2-1\right)\left(\frac{k_{13}-\mu v\left(U^2+3\right)}{{\mu }^2{k}_{13}}\right),$$

and

$$k_{13}=\left(2\mu +\nu \right)U^2+\nu -2b\left(\gamma +1\right)U^4.$$

Under this setting, we now differentiate equations (2.1), take jumps across the shock, and use the shock conditions (2.3) and (2.4) to obtain the following system of equations:

$$\frac{d\left[V_x\right]}{\mathit{dt}}+A\left[V_{\mathit{xx}}\right]+\mathit{\Omega D}\left[V_x\right]+{\Omega }^{\text{'}}\left[u\right]B+C=0,$$

(4.3)

where [V], [V _x ], A, and B have the same meaning as before and

$$\left[V_{\mathit{xx}}\right]={\left(\left[{\rho }_{\mathit{xx}}\right]\left[u_{\mathit{xx}}\right]\left[p_{\mathit{xx}}\right]\right)}^{\mathit{tr}},$$

$$D=\left(\begin{array}{ccc}\hfill \left[u\right]\hfill & \hfill 1+\left[\rho \right]\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{b\left(1-b+\gamma \left[p\right]\right)\left[u\right]}{1-b{\left(1+\left[\rho \right]\right)}^2}\hfill & \hfill \frac{1-b+\gamma \left[p\right]}{1-b\left(1+\left[\rho \right]\right)}\hfill & \hfill \frac{\gamma \left[u\right]}{1-b\left(1+\left[\rho \right]\right)}\hfill \end{array}\right)$$

$$C=\left(\begin{array}{c}\hfill 2\left[u_x\right]\left[{\rho }_x\right]\hfill \\ \hfill -\left(\frac{\left[p_x\right]\left[{\rho }_x\right]}{{\left(1+\left[\rho \right]\right)}^2}-{\left[u_x\right]}^2\right)\hfill \\ \hfill \frac{\gamma +1-b\left(1+\left[\rho \right]\right)}{1-b\left(1+\left[\rho \right]\right)}\left[u_x\right]\left[p_x\right]+b\frac{\left(1-b+\gamma \left[p\right]\right)}{{\left(1-b\left(1+\left[\rho \right]\right)\right)}^2}\left[{\rho }_x\right]\left[u_x\right]\hfill \end{array}\right).$$

Eliminating the unknown discontinuity terms [ρ _xx ] and [u _xx ] between equations (4.3) and using (2.2) and (4.1), we arrive at the second transport equation that governs the discontinuity [p _x ], i.e.,

$$\frac{d\left[p_x\right]}{\mathit{dx}}+k_{21}\left[p_{\mathit{xx}}\right]+k_{22}{\left[p_x\right]}^2+k_{23}\left[p_x\right]+k_{24}=0,$$

(4.4)

where

$$\begin{array}{l}{k}_{21}=\frac{\mathit{\mu \eta }}{\left(\gamma +1\right)U^2}\frac{\left(U^2-1\right)\left(1+\gamma +b\left(1-\gamma \right)\right)}{\mu -b\left(\gamma +1\right)U^2},\\ k_{22}=\frac{\eta }{U}\left(\begin{array}{l}\frac{\mathit{\nu U}\left(1-b\right)}{\mu -b\left(\gamma +1\right)U^2}\left(T_{11}^2-\frac{T_{21}{\mu }^2}{{\left(\gamma +1\right)}^2{U}^4}\right)+\frac{\left(\gamma +1\right)\left(\mu -b{U}^2\right)}{\mu -b\left(\gamma +1\right)U^2}{T}_{11}+\\ \frac{b\left(1-b\right)\nu {\mu }^2}{\mu -b\left(\gamma +1\right)U^2}\frac{1}{\gamma +1}{T}_{21}{T}_{11}-\frac{\left(1-b\right)\mathit{\nu U}}{\mu -b\left(\gamma +1\right)U^2}\frac{d{T}_{11}}{\mathit{du}}\frac{\left(\gamma +1\right)k_{11}}{4U\left(1-b\right)}\end{array}\right),\\ k_{23}=\frac{\eta }{U\left(\mu -b\left(\gamma +1\right)U^2\right)}\left(\begin{array}{l}\mathit{\nu U}\left(1-b\right)\left(2T_{11}{T}_{12}-\frac{{\mu }^2}{{\left(\gamma +1\right)}^2{U}^4}{T}_{22}\right)+\left(\gamma +1\right)\left(\mu -b{U}^2\right)T_{12}+\\ \frac{\Omega \left(1-b\right)\mathit{\nu \mu }{T}_{11}}{\gamma +1}+\frac{2\mathit{\Omega \gamma \mu }\left(U^2-1\right)}{\left(\gamma +1\right)U}+\frac{b\left(1-b\right)\nu {\mu }^2\left(T_{21}{T}_{12}+T_{11}{T}_{22}\right)}{\left(\gamma +1\right)\left(\mu -b\left(\gamma +1\right)U^2\right)}-\frac{\left(\gamma +1\right)\nu k_{12}}{4}\frac{d{T}_{11}}{\mathit{dU}}+\\ \frac{2\mathit{\Omega b}\left(1-b\right)\nu {\mu }^2\left(U^2-1\right)T_{21}}{U{\left(\gamma +1\right)}^2\left(\mu -b\left(\gamma +1\right)U^2\right)}-\frac{\left(\gamma +1\right)\nu k_{11}}{4}\frac{d{T}_{12}}{\mathit{dU}}\end{array}\right),\\ k_{24}=\frac{\eta }{U\left(\mu -b\left(\gamma +1\right)U^2\right)}\left(\begin{array}{l}\frac{2\mathit{\mu \nu }\left(1-b\right)\left(U^2-1\right){\Omega }^{\text{'}}}{U{\left(\gamma +1\right)}^2}+\frac{\Omega \left(1-b\right)\nu {\mu }^2{T}_{12}}{\gamma +1}-\frac{\left(\gamma +1\right)k_{12}\nu }{4}\frac{d{T}_{12}}{\mathit{dU}}+\\ \frac{b\left(1-b\right)\nu {\mu }^2{T}_{22}{T}_{12}}{\left(\gamma +1\right)\left(\mu -b\left(\gamma +1\right)U^2\right)}+\frac{2\mathit{\Omega b}\left(1-b\right)\nu {\mu }^2\left(U^2-1\right)T_{22}}{U{\left(\gamma +1\right)}^2\left(\mu -b\left(\gamma +1\right)U^2\right)}\end{array}\right).\end{array}$$

(4.5)

It may be noticed from (4.4) that an analytical description of [p _x ] is again obscured by the presence of higher order jump discontinuity [p _xx ] which is an unknown, the determination of which requires a repetition of the above procedure; proceeding in this manner, we arrive at an open system consisting an infinite set of transport equations for the coupling terms - the jumps in higher order derivatives of p. In order to provide a natural closure on the hierarchy of these equations, we consider the coupled system (3.3) and (4.4) and render it tractable by making assumptions on the higher order discontinuity [p _xx ] (see Sharma and Radha [10]).

Evolution laws for weak shocks

For a weak shock, we may assume that $\left[p\right]=O\left(\mathcal{ϵ}\right),0<\mathcal{ϵ}\ll 1.$ and consider the case, [p _x ] = O(1). In this case, direct perturbation ansatz yields a uniformly valid solution to the first-order approximation. We now present these details below:

For a weak shock, it follows from (2.4) that

$$\begin{array}{l}\left[u\right]=\frac{\left[p\right]}{1-b}+O\left({\mathcal{ϵ}}^2\right),\left[\rho \right]=\frac{\left[p\right]}{1-b}+O\left({\mathcal{ϵ}}^2\right),\\ U=1+\frac{\gamma +1}{4\left(1-b\right)}\left[p\right]+O\left({\mathcal{ϵ}}^2\right),\end{array}$$

(5.1)

and thus the equations (3.3) and (4.4) can be approximated to yield

$$\begin{array}{l}\frac{d\left[p\right]}{\mathit{dx}}+\frac{\gamma +1+b\left(1-\gamma \right)}{2\left(2-b\right)\left(1-b\right)}\left[p\right]\left[p_x\right]+\frac{j}{\left(2-b\right)x}\left[p\right]=0,\\ \frac{d\left[p_x\right]}{\mathit{dx}}+\frac{\gamma +1+b\left(1-\gamma \right)}{2\left(2-b\right)\left(1-b\right)}\left[p\right]\left[p_{\mathit{xx}}\right]+\frac{\gamma +1+b\left(1-\gamma \right)}{2\left(1-b\right)}{\left[p_x\right]}^2+\frac{j}{2x}\left[p_x\right]=0.\end{array}$$

(5.2)

We need to solve these equations assuming that the initial conditions are [p]_x = 1 = h and [p _x ]_x = 1 = k, where |h| is of the first-order of ϵ.

The second equation in (5.2) is the equation that governs the amplitude [p _x ] of an acceleration wave; a complete analysis of such an equation modifying and generalizing several known results in the literature has been reported in [17] and [18]. We thus conclude that the precursor disturbance that overtakes the shock from behind evolves like an acceleration wave at the first order. When the effect of the first-order-induced discontinuity or the disturbances that overtake the shock from behind are strong, i.e., [p _x ] = O(1) and $\left[p_{\mathit{xx}}\right]=O\left({\mathcal{ϵ}}^q\right)$, q > 0, system (5.2) can be directly integrated to yield

$$\begin{array}{l}\left[p\right]=h{\left(1+\frac{\gamma +1+b\left(1-\gamma \right)}{\left(1-b\right)}\frac{k}{j+2}\left(x^{\frac{2-j}{2}}-1\right)\right)}^{-\frac{1}{2-b}}{x}^{-\frac{j}{2-b}},\\ \left[p_x\right]=k{\left(1+\frac{\gamma +1+b\left(1-\gamma \right)}{\left(1-b\right)}\frac{k}{j+2}\left(x^{\left(2-j\right)/2}-1\right)\right)}^{-1}{x}^{-j/2},\end{array}$$

(5.3)

It may be noticed that if k > 0, equations (5.3) imply the following asymptotic decay laws for the shock and the associated first order discontinuity

$$\begin{array}{ll}\left[p\right]~h& \frac{{\left(2\left(1-b\right)\right)}^{1/\left(2-b\right)}}{{\left(\left(\gamma +1+b\left(1-\gamma \right)\right)k\right)}^{1/\left(2-b\right)}}\\ \times \left\{\begin{array}{ll}{x}^{-1/\left(2-b\right)},\hfill & \hfill \text{plane},\\ \frac{1}{2^{1/\left(2-b\right)}}{x}^{-3/2\left(2-b\right)},\hfill & \hfill \text{cylindrical},\\ x^{-2/\left(2-b\right)}{\left(logx\right)}^{-1/\left(2-b\right)},\hfill & \hfill \text{spherical},\end{array}\right.\end{array}$$

(5.4)

and

$$\left[p_x\right]~\frac{2\left(1-b\right)}{\gamma +1+b\left(1-\gamma \right)}\left\{\begin{array}{ll}{x}^{-1},\hfill & \hfill \text{plane},\\ \frac{1}{2}{x}^{-1},\hfill & \hfill \text{cylindrical},\\ {\left(\mathit{xlog}x\right)}^{-1},\hfill & \hfill \text{spherical},\end{array}\right.$$

(5.5)

as x → ∞; the asymptotic law for the shock is in full agreement with earlier results obtained using the simple wave theory (see, Whitham [19], page 330) in an ideal gas, i.e., for b = 0. The value of [p _x ] ~ (x log x)^− 1 which is in confirmation with Equation (9.62) at page 330 in Whitham [19] for the spherical symmetric case. It may be noticed that the decay of the induced discontinuity [p _x ] is much slower than that of the decay of the shock.

Conclusion

Using kinematics of one-dimensional motion, we have derived a system of transport equations for the variation of shock strength and induced discontinuities behind shocks of weak strength traveling into quiescent non-ideal gas. It is evident from the transport equation for the shock strength that the evolutionary behavior of the shock strength is described by the shock curvature, the internal volume (b) of the gas, and the first order-induced discontinuity behind the shock.

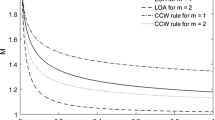
It is noticed that the transport equations for the shock strength [p] and the first-order jump discontinuity [p _x ] are non-linear in [p] and [p _x ], respectively; however, the transport equations for [p _xx ] are linear in [p _xx ], and this is true for all other higher-order jump discontinuities. The transport equation for the shock strength shows that the evolutionary behavior of the shock at any instant is influenced by the shock curvature and the first-order jump discontinuity, representing the effect of precursor disturbances that overtake the shock from behind. This transport equation, in some sense, generalizes the Chester-Chisnell-Whitham (CCW) approximation [19], although does not account for the effects of the disturbances that overtake the shock from behind, yet its success is unexpectedly remarkable for a particular class of problems. We show in the preceding section that the transport equation for the shock strength, in the limit of a weak shock and vanishing [p _x ], reduces exactly to the one obtained by the CCW approximation for the ideal gas.

Indeed, a pair of transport equations for [p] and [p _x ], subjected to a truncation approximation by neglecting the second-order jump discontinuity [p _xx ], yields a closed system consisting of only a pair of coupled ODEs, which can be regarded as a good approximation for the hierarchy of the system governing shock evolution. These equations are then solved for uniformly valid solutions using a singular perturbation technique [19–21] that eliminates secular terms in the perturbed solution; the shock strength is assumed small, but the accompanying first-order jump discontinuity may be finite (i.e., O(1)) or small. It is shown that the disturbances evolve to the leading order like an acceleration wave.

Authors’ information

RA is an assistant professor of the Applied Mathematics Department at the Indian Institute of Technology Roorkee. He received his Ph.D. in Applied Mathematics from the Indian Institute of Technology Bombay in 2005. His research interests include the propagation of shock waves in gas dynamics. MJS is a senior research fellow of the Applied Mathematics in the Department of Applied Science and Engineering at the Indian Institute of Technology Roorkee. His research interests include the hyperbolic conservation laws.