Calculation of state energy of (2n+ 1)-fold wells using the spectral properties of supersymmetry shape-invariant potential

Abstract

Shape invariance is an important factor of many exactly solvable quantum mechanics. Several examples of shape-invariant ‘discrete quantum mechanical systems’ are introduced and discussed in some detail. We present the spectral properties of supersymmetric shape-invariant potentials (SIP). Here we are interested in some time-independent integrable systems which are exactly solvable owing to the existence of supersymmetric shape-invariant symmetry. In 1981 Witten proposed (0+1)-dimensional limit of supersymmetry (SUSY) quantum field theory, where the supercharges of SUSY quantum mechanics generate transformation between two orthogonal eigenstates of a given Hamiltonian wit degenerate eigenvaluesfor the non-SIP as very few lower eigenvalues can be known analytically, which are small to calculate spectral fluctuation.

Introduction

Many exactly solvable quantum mechanical systems, for example, the harmonic oscillator without/with a centrifugal potential, the Coulomb problem, etc., are shape invariant [1]. Energy level statistics is one of the most important and well-studied characteristics of quantum systems. This problem has recently attracted new interest in different contexts because it indicates the type of motion in a quantum system. One of the main problems involved in many physical processes is the energy state difference between the ground state and first excited state for potential wells. This is generally solved using the approximation methods [1]. In this paper, we calculate these difference values for threefold, fivefold, and sevenfold potential wells using supersymmetry in quantum mechanics (SUSYQM). We finally generalize it to find a relation for (2n+ 1)-fold wells.

Factorization of SUSY Hamiltonian and shape invariance condition

Let us now explain precisely what one means by shape invariance. If the pair of SUSY partner potentials V_1,2(x) defined in Equation 1 is similar in shape and differs only in the parameters that appear in them, then they are said to be shape invariant [2–5]. The Hamiltonian of SUSYQM is given by

$$H=\left(\begin{array}{cc}\hfill H_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill H_2\hfill \end{array}\right)$$

(1)

where

$$H_{1,2}=-\frac{d_2}{d{x}^2}+V_{1,2}\left(x\right)$$

(2)

$$V_{1,2}=W^2\mp \dot{W}\left(x\right).$$

(3)

W(x) is called superpotential. Then the supercharges are as follows:

$$\begin{array}{cc}\hfill Q=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill A\hfill & \hfill 0\hfill \end{array}\right]\hfill & \hfill Q^{+}=\left[\begin{array}{cc}\hfill 0\hfill & \hfill A^{+}\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\hfill \end{array}$$

(4)

and

$$\begin{array}{cc}\hfill A=\frac{d}{\mathit{dx}}+W\left(x\right)\hfill & \hfill A^{+}=-\frac{d}{\mathit{dx}}+W\left(x\right).\hfill \end{array}$$

(5)

Then it is easy to present H_1,2 as the factorization

$$\begin{array}{cc}\hfill H_1=A^{+}A\hfill & \hfill H_2=A{A}^{+}\hfill \end{array}$$

(6)

$$W\left(x\right)=-\frac{{\dot{\psi }}_0^1}{{\psi }_0^1\left(x\right)}$$

(7)

and

$$\begin{array}{cc}\hfill \left\{Q^{+},Q^{+}\right\}=\left\{Q,Q\right\}=0\hfill & \hfill \left\{Q,Q^{+}\right\}=H.\hfill \end{array}$$

(8)

More precisely, if the partner potentials V_1,2 (x,a₁) satisfy the condition

$$V_2\left(x,a_1\right)=V_1\left(x,a_2\right)+R\left(a_1\right)$$

(9)

where a₁ is a set of parameters, a₂ is a function of a₁ (a₂ = f(a₁)), and the remainder R(a₁) is independent of x, then V₁(x,a₁) and V₂(x,a₁) are said to be shape invariant. The shape invariance condition is an integrability condition [6, 7].

Shape invariance and solvable potentials

We start from the SUSY partner Hamiltonians H₁ and H₂ whose eigenvalues and eigenfunctions are related by SUSY. Since SUSY is unbroken, we know that

$$\begin{array}{c}{E}_0^1\left(a_1\right)=0,{\psi }_0^1\left(x,a_1\right)\hfill \\ =N\exp \left[-\underset{0}{\overset{x}{{\displaystyle \int }}}{W}_1\left(y,a_1\right)\mathit{dy}\right].\hfill \end{array}$$

(10)

We now show that the entire spectrum of H₁ can be very easily obtained algebraically using the shape invariance condition (10). To that purpose we construct a series of Hamiltonians H _s , s = 1,2,3,…. On repeatedly using the shape invariance condition, it is then clear that

$$H_s=-\frac{d^2}{d{x}^2}+V_1\left(x,a_s\right)+{\Sigma }_{k=1}^{s-1}R\left(a_k\right)$$

(11)

where a _s = f^s-1(a _s ), i.e., the function f applied s - 1 times. Let us compare the spectrum of H _s and H_s+1. In view of Equations 9 and 10, we have

$$\begin{array}{c}{H}_{s+1}=-\frac{d}{d{x}^2}+V_1\left(x,a_{s+1}\right)+{\Sigma }_{k=1}^{s}R\left(a_k\right)\hfill \\ =-\frac{d}{d{x}^2}+V_2\left(x,a_s\right)+\Sigma -1_{k=1}^{s}R\left(a_k\right).\hfill \end{array}$$

(12)

Thus, H _s and H_{s+ 1} are SUSY partner Hamiltonians and hence have identical bound state spectra for the ground state of H _s whose energy is

$$E_0^s={\Sigma }_{k=1}^{s-1}R\left(a_k\right).$$

(13)

This follows from Equation 12 and the fact that E₀¹  =  0. On going back from H _s to H_s-1 etc., we would eventually reach H₂ and H₁ whose ground state energy is zero and whose n th level is coincident with the ground state of the Hamiltonian H _n [5, 6]. Hence, the complete eigenvalue spectrum of H₁ is given by

$$\begin{array}{cc}\hfill E_n^{-}\left(a_1\right)={\Sigma }_{k=1}^{n}R\left(a_k\right),\hfill & \hfill E_0^{-}\left(a_1\right)=0.\hfill \end{array}$$

(14)

In Table 1, we give expressions for the various shape-invariant potentials V₁(x), superpotentials W(x), parameters a₁and a₂, and the corresponding energy eigenvalues E _n ¹.

Table 1 Expressions for various shape-invariant potentials, superpotentials, parameters a ₁ and a ₂ , and the corresponding energy eigenvalues

Two remarks are in order at this time [8–12]:

• 1. In this section, we have used the convention of ℏ = 2 m = 1. It would naively appear that if we had not put ℏ = 1, then the shape-invariant potentials as given in Table 1 would all be ℏ - dependent. However, it is worth noting that in each and every case, the ℏ - dependence is only in the constant multiplying the x-dependent function so that in each case we can always redefine the constant multiplying the function and obtain an ℏ - independent potential.

• 2. It may be noted that the Coulomb and the harmonic oscillator potentials in n-dimensions are also shape-invariant potentials.

From 1987 until 1993, it was believed that the only shape-invariant potentials were those given in Table 1 and that there was no more shape-invariant potentials. Many of these potentials are reflectionless and have an infinite number of bound states. So far, none of these potentials have been obtained in a closed form, and they are obtained only in a series form [3, 13–15].

State energy of (2n+ 1)-fold wells using the spectral properties of supersymmetry shape-invariant potential

We see that spectral properties of supersymmetry shape-invariant potential are a necessary condition for unbroken SUSY, and when this condition is satisfied, then H_1,2 have identical spectra, including zero modes. In this case, using the known eigenfunctions ψ _n ¹(x) of V₁(x), one can immediately write down the corresponding (un-normalized) eigenfunctions ψ _n ²(x) of V₂(x).

Several comments are in order at this stage:

• a. State energy of threefold wells

At first we write the eigenfunction for one threefold well that oscillates between - x₀ and +x₀. This well is symmetric.

$${\psi }_0^1\left(x\right)=e^{-\left(x-x_0\right)}+e^{-x^2}+e^{-a{\left(x+x_0\right)}^2}$$

(15)

Superpotential W(x):

$$\begin{array}{c}W\left(x\right)=-\frac{{\psi }^{\text{'}}{0}_{}\left(x\right)}{{\psi }_0\left(x\right)}\hfill \\ =\frac{-2\left(x-x_0\right)e^{-{\left(x-x_0\right)}^2}-2x{e}^{-x^2}-2a\left(x+x_0\right)e^{-a{\left(x+x_0\right)}^2}}{e^{-{\left(x-x_0\right)}^2}+e^{-x^2}+e^{-a{\left(x+x_0\right)}^2}}\hfill \end{array}$$

(16)

Partner potential V₁(x) and V₂(x) show to this firm

$$V_{2,1}\left(x\right)=W^2\left(x\right)\pm W^{\text{'}}\left(x\right)$$

(17)

That

$$V_1\left(x\right)=\frac{\left(-2e^{-{\left(x-x_0\right)}^2}+{\left(-2x+2x_0\right)}^2{e}^{-{\left(x-x_0\right)}^2}-2a{e}^{-a{\left(x+x_0\right)}^2}+4a^2{\left(x+x_0\right)}^2{e}^{-a{\left(x+x_0\right)}^2}-2e^{-x^2}+4x^2{e}^{-x^2}\right)}{e^{-{\left(x-x_0\right)}^2}+e^{-{\left(x+x_0\right)}^2}+e^{-x^2}}$$

(18)

$$\begin{array}{c}{V}_2\left(x\right)=\frac{\left(2{\left(\left(-2x+2x_0\right)e^{-{\left(x-x_0\right)}^2}-2a\left(x+x_0\right)e^{-a{\left(x+x_0\right)}^2}-2x{e}^{-x^2}\right)}^2\right)}{{\left(e^{-{\left(x-x_0\right)}^2}+e^{-a{\left(x+x_0\right)}^2}+e^{-x^2}\right)}^2}\hfill \\ -\frac{(-2e^{-{\left(x-x_0\right)}^2}+{\left(-2x+2x_0\right)}^2{e}^{-{\left(x-x_0\right)}^2}-2a{e}^{-a{\left(x+x_0\right)}^2}+4a^2{\left(x+x_0\right)}^2{e}^{-a{\left(x+x_0\right)}^2}-2e^{-x^2}+4x^2{e}^{-x^2}}{e^{-{\left(x-x_0\right)}^2}+e^{-a{\left(x+x_0\right)}^2}+e^{-x^2}}\hfill \end{array}$$

(19)

and we calculate

$$\begin{array}{c}{H}_2\frac{1}{{\psi }_0^1}=H_2\frac{1}{e^{-{\displaystyle \int }W\left(x\right)\mathit{dx}}}=H_2{e}^{+{\displaystyle \int }W\left(x\right)\mathit{dx}}\hfill \\ =\left(-\frac{d^2}{d{x}^2}+V_2\right)e^{+{\displaystyle \int }W\left(x\right)\mathit{dx}}\hfill \\ =-\frac{d}{\mathit{dx}}\left(e^{{\displaystyle \int }W\left(x\right)\mathit{dx}}W\left(x\right)\right)\hfill \\ +V_2{e}^{{\displaystyle \int }W\left(x\right)\mathit{dx}}\hfill \\ =-\left\{W^{\text{'}}{e}^{{\displaystyle \int }W\left(x\right)\mathit{dx}}+W^2{e}^{{\displaystyle \int }W\left(x\right)\mathit{dx}}\right\}\hfill \\ +V_2{e}^{{\displaystyle \int }W\left(x\right)\mathit{dx}}\hfill \\ =-\left\{W^{\text{'}}+W^2\right\}{e}^{{\displaystyle \int }W\left(x\right)\mathit{dx}}\hfill \\ +\left\{W^2+W^{\text{'}}\right\}{e}^{{\displaystyle \int }W\left(x\right)\mathit{dx}}\hfill \\ =0=E\frac{1}{{\psi }_0^1}\Rightarrow E=0\hfill \end{array}$$

(20)

From the last equation, we have seen that if the excited state energy of a Hamiltonian H₂ is zero, then it can always be written in a factorizable form as a product of a pair of linear differential operators

$$\begin{array}{c}\phi \left(x\right)=\frac{{{\displaystyle \int }}_x^{\infty }{\left[{\psi }_0^1\left(y\right)\right]}^2\mathit{dy}}{2I_1{\psi }_0^1\left(x\right)}x>0\hfill \end{array}$$

(21)

$$\begin{array}{c}\phi \left(x\right)=\frac{1}{2{\psi }_0\left(x\right)}-x_0<x<x_0\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill \phi \left(x\right)=\frac{{{\displaystyle \int }}_{-\infty }^x{\left[{\psi }_0^1\left(y\right)\right]}^2\mathit{dy}}{2I_2{\psi }_0^1\left(x\right)}\hfill & \hfill x<x_0\hfill \end{array}$$

(23)

that

$$\begin{array}{c}\hfill I_1=\underset{x_0}{\overset{\infty }{{\displaystyle \int }}}{\left[{\psi }^1\left(y\right)\right]}^2\mathit{dy}\hfill \\ \hfill I_2=\underset{-\infty }{\overset{x_0}{{\displaystyle \int }}}{\left[{\psi }^1\left(y\right)\right]}^2\mathit{dy}.\hfill \end{array}$$

(24)

One of the main problems involved in many physical processes is the energy state difference between the ground state and first excited state for potential wells. The ground state wave energy is E¹ and the first excited state energy is E², as a result

$$\begin{array}{c}{H}_2=H_0+\mathit{\delta H}\hfill \\ =H_0+\frac{{\left[{\psi }_0^1\left(x_0\right)\right]}^2}{I_1}\delta \left(x-x_0\right)\hfill \\ +\frac{{\left[{\psi }_0^1\left(-x_0\right)\right]}^2}{I_1}\delta \left(x+x_0\right)\hfill \end{array}$$

(25)

In other words,

$$\begin{array}{c}{E}^1=\frac{{{\displaystyle \int }}_{-\infty }^{+\infty }\phi \left(x\right)\left(\mathit{\delta H}\right)\phi \left(x\right)\mathit{dx}}{{{\displaystyle \int }}_{-\infty }^{+\infty }{\phi }^2\left(x\right)\mathit{dx}}\hfill \\ =\frac{{{\displaystyle \int }}_{-\infty }^{+\infty }\phi \left(x\right)\left[\frac{{\left[{\psi }_0^1\left(x_0\right)\right]}^2}{I_1}\right]\delta \left(x-x_0\right)\phi \left(x\right)\mathit{dx}}{{{\displaystyle \int }}_{-\infty }^{+\infty }{\phi }^2\left(x\right)\mathit{dx}}\hfill \\ +\frac{{{\displaystyle \int }}_{-\infty }^{+\infty }\phi \left(x\right)\left[\frac{{\left[{\psi }_0^1\left(-x_0\right)\right]}^2}{I_1}\right]\delta \left(x+x_0\right)\phi \left(x\right)\mathit{dx}}{{{\displaystyle \int }}_{-\infty }^{+\infty }{\phi }^2\left(x\right)\mathit{dx}}\hfill \\ =\frac{1}{4}\left[\frac{1}{I_1}+\frac{1}{I_2}\right]\frac{1}{{{\displaystyle \int }}_{-\infty }^{+\infty }{\phi }^2\left(x\right)\mathit{dx}}\hfill \end{array}$$

(26)

$$\begin{array}{c}{E}^2=-\left\{\underset{-\infty }{\overset{-x_0}{{\displaystyle \int }}}\mathit{dx}{\left[\frac{E^1{{\displaystyle \int }}_{-\infty }^x{\phi }^2\left(x\right)\mathit{dx}}{\phi \left(x\right)}\right]}^2\right\}\hfill \\ +\underset{-x_0}{\overset{+x_0}{{\displaystyle \int }}}\mathit{dx}{\left[\frac{E^1{{\displaystyle \int }}_{-x_0}^x{\phi }^2\left(x\right)\mathit{dx}}{\phi \left(x\right)}\right]}^2\hfill \\ +\underset{x_0}{\overset{x}{{\displaystyle \int }}}\mathit{dx}{\left[\frac{E^1{{\displaystyle \int }}_x^{\infty }{\phi }^2\left(x\right)\mathit{dx}}{\phi \left(x\right)}\right]}^2\hfill \end{array}$$

(27)

Thus,

$$\mathit{\Delta E}=E^1+E^2.$$

(28)

In this relation, ΔE is the energy state difference between the ground state and first excited state for potential fivefold well.

• b. State energy of fivefold well

For calculation of the state energy of fivefold well, we start from eigenfunction, and then we have shown that E is an eigenvalue of the Hamiltonian H with eigenfunction ψ.

$$\begin{array}{c}{\psi }_0^1\left(x\right)=e^{-{\left(x-2x_0\right)}^2}+e^{-{\left(x-x_0\right)}^2}+e^{-x^2}\hfill \\ +e^{-a{\left(x+x_0\right)}^2}+e^{-a{\left(x+2x_0\right)}^2}.\hfill \end{array}$$

(29)

In this relation, a is the rate of antisymmetry (asymmetry) potential well, and if a = 1, potential well will be symmetric. Five potential wells for the oscillators that oscillate between -2x₀ and +2x₀ and eigenvalue for H are as follows:

$$\begin{array}{c}{E}^1=\frac{{{\displaystyle \int }}_{-\infty }^{+\infty }\phi \left(x\right)\frac{{\left({\psi }_0^1\left(2x_0\right)\right)}^2\delta \left(x-2x_0\right)\phi \left(x\right)\mathit{dx}}{I_{+}}}{{\displaystyle \int }{\phi }^2\left(x\right)\mathit{dx}}\hfill \\ +\frac{{{\displaystyle \int }}_{-\infty }^{+\infty }\phi \left(x\right)\frac{{\left({\psi }_0^1\left(-2x_0\right)\right)}^2\delta \left(x+2x_0\right)\phi \left(x\right)\mathit{dx}}{I_{+}}}{{\displaystyle \int }{\phi }^2\left(x\right)\mathit{dx}}\hfill \\ +\frac{{{\displaystyle \int }}_{-\infty }^{+\infty }\phi \left(x\right)\frac{{\left({\psi }_0^1\left(x_0\right)\right)}^2\delta \left(x-x_0\right)\phi \left(x\right)\mathit{dx}}{I_{+}}}{{\displaystyle \int }{\phi }^2\left(x\right)\mathit{dx}}\hfill \\ +\frac{{{\displaystyle \int }}_{-\infty }^{+\infty }\phi \left(x\right)\frac{{\left({\psi }_0^1\left(-x_0\right)\right)}^2\delta \left(x+x_0\right)\phi \left(x\right)\mathit{dx}}{I_{+}}}{{\displaystyle \int }{\phi }^2\left(x\right)\mathit{dx}}\hfill \end{array}$$

(30)

The equation E¹ can be interpreted in the following two different ways depending on the superpotential W(x) or the ground state wave function.

In this equation,

$$\begin{array}{cc}\hfill I_{+}=\underset{2x_0}{\overset{\infty }{{\displaystyle \int }}}{\left({\psi }_0^1\left(y\right)\right)}^2\mathit{dy}\hfill & \hfill I\_\hfill \end{array}=\underset{-\infty }{\overset{-2x_0}{{\displaystyle \int }}}{\left({\psi }_0^1\left(y\right)\right)}^2\mathit{dy},$$

(31)

then

$$E^1=\frac{2}{1}\left[\frac{1}{I_{+}}+\frac{1}{I\_}\right]\frac{1}{{{\displaystyle \int }}_{-\infty }^{+\infty }{\phi }^2\left(x\right)\mathit{dx}}.$$

(32)

From the last equation, we have seen that if the ground state energy of a Hamiltonian H₁ is zero, then it can always be written in a factorizable form as a product of a pair of linear differential operators.

$$\begin{array}{c}{E}^2=-\left\{\underset{-\infty }{\overset{-2x_0}{{\displaystyle \int }}}\mathit{dx}{\left[\frac{E^1{{\displaystyle \int }}_{-\infty }^{-2x}{\phi }^2\left(y\right)\mathit{dy}}{\phi \left(x\right)}\right]}^2\right\}\hfill \\ +\underset{-2x_0}{\overset{-x_0}{{\displaystyle \int }}}\mathit{dx}{\left[\frac{E^1{{\displaystyle \int }}_{-2x}^{-x}{\phi }^2\left(y\right)\mathit{dy}}{\phi \left(x\right)}\right]}^2\hfill \\ +\underset{-x_0}{\overset{x_0}{{\displaystyle \int }}}\mathit{dx}{\left[\frac{E^1{{\displaystyle \int }}_{-x}^x{\phi }^2\left(y\right)\mathit{dy}}{\phi \left(x\right)}\right]}^2\hfill \\ +\underset{x_0}{\overset{2x_0}{{\displaystyle \int }}}\mathit{dx}{\left[\frac{E^1{{\displaystyle \int }}_x^{2x}{\phi }^2\left(y\right)\mathit{dy}}{\phi \left(x\right)}\right]}^2\hfill \\ +\underset{2x_0}{\overset{\infty }{{\displaystyle \int }}}\mathit{dx}{\left[\frac{E^1{{\displaystyle \int }}_{2x}^{\infty }{\phi }^2\left(y\right)\mathit{dy}}{\phi \left(x\right)}\right]}^2\hfill \end{array}$$

(33)

It is then clear that if the ground state energy of a Hamiltonian H₁is E₀¹ with eigenfunction ψ₀¹, then in view of Equation 32, it can always be written in the form

$$\mathit{\Delta E}=E^1+E^2.$$

(34)

In this relation, ΔE is the energy state difference between the ground state and first excited state for potential fivefold well.

• c. State energy of sevenfold well

This case is similar to the state energy of fivefold well, but in this case, there are sevenfold wells oscillating between -3x₀, and + 3x₀.

$$\begin{array}{c}{\psi }_0^1\left(x\right)=e^{-{\left(x-3x_0\right)}^2}+e^{-{\left(x-2x_0\right)}^2}+e^{-{\left(x-x_0\right)}^2}\hfill \\ +e^{-x^2}+e^{-a{\left(x+x_0\right)}^2}+e^{-{\left(x-2x_0\right)}^2}\hfill \\ +e^{-a{\left(x+3x_0\right)}^2}\hfill \end{array}$$

(35)

• d. State energy of (2n+1)-fold wells

We shall now point out the key steps that go into the classification of SIPs in this case. Firstly, one notices the fact that the eigenvalue spectrum of the Schrodinger equation is always such that the n th eigenvalue E _n for large n obeys the constraint.

We calculate these difference values for a fivefold and sevenfold potential wells using SUSYQM. We finally generalize it to find a relation for (2n+1)-fold wells

$$E^1=\frac{n}{4}\left[\frac{1}{I_{+}}+\frac{1}{I\_}\right]\frac{1}{{{\displaystyle \int }}_{-\infty }^{+\infty }{\phi }^2\left(x\right)\mathit{dx}}$$

(36)

$$\begin{array}{c}{E}^2=-\left\{\underset{-\infty }{\overset{-n{x}_0}{{\displaystyle \int }}}\mathit{dx}{\left[\frac{E^1{{\displaystyle \int }}_{-\infty }^{-\mathit{nx}}{\phi }^2\left(y\right)\mathit{dy}}{\phi \left(x\right)}\right]}^2\right\}\hfill \\ +\underset{-n{x}_0}{\overset{n{x}_0}{{\displaystyle \int }}}\mathit{dx}{\left[\frac{E^1{{\displaystyle \int }}_{-\mathit{nx}}^{\mathit{nx}}{\phi }^2\left(y\right)\mathit{dy}}{\phi \left(x\right)}\right]}^2\hfill \\ +\underset{\mathit{nx}}{\overset{\infty }{{\displaystyle \int }}}\mathit{dx}{\left[\frac{E^1{{\displaystyle \int }}_{\mathit{nx}}^{\infty }{\phi }^2\left(y\right)\mathit{dy}}{\phi \left(x\right)}\right]}^2\hfill \end{array}$$

(37)

and

$$\begin{array}{cc}\hfill I_{+}=\underset{n{x}_0}{\overset{\infty }{{\displaystyle \int }}}{\left({\psi }_0^1\left(y\right)\right)}^2\mathit{dy},\hfill & \hfill I\_=\hfill \end{array}\underset{-\infty }{\overset{-n{x}_0}{{\displaystyle \int }}}{\left({\psi }_0^1\left(y\right)\right)}^2\mathit{dy}$$

(38)

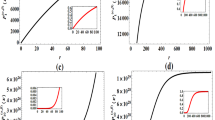
We show V₁(x) and V₂(x) in Figures 1, 2, 3, 4, 5, 6, 7, 8 for threefold well. It is immediately obvious that there are some quite significant differences between the two charts, for example, when a = 1, x₀ = 2, and a = 1.5, x₀ = 2. These figures have been drawn by the software Matlab.

Figure 8

V ₂ ( x ) when a = 1.5, x ₀ = 3 for threefold wells.

In these figures, one of the main problems involved in many physical processes is the energy state difference between the ground state and first excited state for potential wells. This is generally solved using the approximation methods. In these figures, we show these difference values for threefold potential wells using supersymmetry in quantum mechanics. We finally generalize it to find a relation for (2n+1)-fold wells. In these figures ‘a’ shows the symmetry of the potential wells. If a = 1, wells will be symmetric, and if a ≠ 1, wells will be antisymmetric. In these figures, x₀ is the oscillation range (amplitude). For example, x₀ = 2 means oscillator oscillation between +2 and -2.

Figure 1

V ₁ ( x ) when a = 1, x ₀ = 2 for threefold wells.

Figure 2

V ₁ ( x ) when a = 1.5, x ₀ = 2 for threefold wells.

Figure 3

V ₁ ( x ) when a = 1, x ₀ = 3 for threefold wells.

Figure 4

V ₁ ( x ) when a = 1.5, x ₀ = 3 for threefold wells.

Figure 5

V ₂ ( x ) when a = 1, x ₀ = 2 for threefold wells.

Figure 6

V ₂ ( x ) when a = 1.5, x ₀ = 2 for threefold wells.

Figure 7

V ₂ ( x ) when a = 1, x ₀ = 3 for threefold wells.

Conclusions

Shape invariance is an important factor of many exactly solvable quantum mechanics. In this paper, several examples of shape invariance are introduced and discussed in some detail. It is a well-established fact that systems with more than one degree of freedom have completely random energy level spacings. Lots of theoretical and numerical evidences are put forward in this context. One of the main problems involved in many physical processes is the energy state difference between the ground state and first excited state for potential wells. This is generally solved using the approximation methods. In this paper, we calculate these difference values for fivefold and sevenfold potential wells using supersymmetry in quantum mechanics. We finally generalize it to find a relation for (2n+1)-fold wells.