Surface wave excitations on magnetized over-dense plasma

Abstract

The dominant procedure for the transmission of electromagnetic waves on an over-dense plasma layer is the excitation of surface waves. The conditions for this wave excitation on the surface of over-dense plasma, hence, become important. Here, the dispersion relation for the surface wave excitation on an over-dense plasma medium which is exposed to a magnetic field is studied. These investigations lead to the condition required for producing the surface waves. By this dispersion condition, an analytical function for the wave vector in terms of the phase velocity and the cyclotron and collision frequencies is established. Specifically, the outgoings of these dependencies and also the condition for exciting more stable waves are discussed.

Background

The transmission of electromagnetic wave from normally opaque substances, such as left-handed materials (LHM) and over-dense plasmas, has attracted ever-increasing attentions. There exist a large number of both theoretical and experimental researches devoted to this subject[1–6]. The materials with negative index or LHM were theoretically predicted by Veselago[7], but their anomalous light transmission property has been proposed by Pendry[8]. After then, these materials have interested more attentions and opened a new avenue in physics and engineering.

In normal conditions, an over-dense plasma or LHM layer is completely opaque for electromagnetic waves. However, the plasma layer can appear highly transparent when the circumstances are organized for the incident electromagnetic wave to excite coupled surface modes on both sides of the layer. In this way, the energy of the surface wave was damped by the re-emission of the incoming electromagnetic wave from the backside and makes the slab transparent. Then, the anomalous light transmission is recognized to take place. This, in fact, is the main mechanism for total light transmission through an over-dense plasma layer.

In our previous work, we studied the high-transparency condition of an overcritical warm plasma layer due to the excitation of the electromagnetic surface waves[6]. Since surface waves can be excited on the interfaces within the stratified dielectric media[9], we have considered two dielectrics on both sides of the over-dense plasma. The electromagnetic waves then become evanescent within the dielectric layers, which leads to the excitation of the coupled plasmons on both sides of the over-dense plasma layer. The created coupled plasmons can then transfer the incident electromagnetic energy.

It is obvious that the main player for the phenomenon of electromagnetic wave transmission through an over-dense plasma slab is the excitation of the surface wave. The surface wave's footprints can also be followed in other areas[10, 12]. It is applicable in bounded plasmas and their distinct technical functions[13, 14]. The surface wave-produced plasmas can be used in plasma processing[15, 16]. Moreover, surface wave modes are applicable in astrophysics, specifically in the magnetosphere. It has important outcomes in the heating of the solar corona and the coupling of the ionosphere and the magnetosphere[17].

Plasmons have been theoretically investigated for magnetized plasma in the framework of fluid dynamics[18–21]. Furthermore, the dispersion relation of electrostatic surface wave propagation in a magnetized plasma slab has also been studied in the context of kinetic theory[10, 22].

In this paper, we study the dispersion relation for the surface wave excitations of a stratified plasma medium in the framework of fluid mechanics. It is supposed that the slab is made of an ordinary dielectric or under critical plasma layer and an overcritical plasma medium which is exposed to a magnetic field. We also consider the dispersion effects and specifically discuss and suggest the condition necessary for the surface wave's excitations. These conclusions are necessary to study the high-transparency situations of over-dense magnetized plasma. Let us postpone this latest issue to somewhere else.

Results and discussion

The model

Let us consider a plasma layer that is immersed in a steady, uniform, homogeneous magnetic field. In this case, the equivalent dielectric constant is not merely a scalar function of frequency. It would rather appear as a dielectric tensor with independent components, each one as a function of frequency and the plasma's characteristics. Here, the plane is to derive the wave equations in the case of infinite cold magnetized plasma and find the dielectric tensor. The solutions of these field equations would be used in the next section when the dispersion relation for the transmission of the electromagnetic waves from cold magnetized plasma is discussed.

In what follows, it is assumed that high-frequency oscillations will perturb the electrons and have neglecting effects on ions. Also, the plasma is considered to be uniform with electron densities n ₀ at rest in a uniform magnetic field$B=B_0\hat{k}$. The linearized set of cold fluid-Maxwell equations for collisional electrons can be written as

$$\nabla \times E=-\frac{1}{c}\frac{\partial B}{\partial t}\text{,}$$

(1)

$$\nabla \times B=-\frac{4\pi n_{0}e}{c}V+\frac{1}{c}\frac{\partial E}{\partial t}\text{,}$$

(2)

$$\frac{\partial V}{\partial t}=-\frac{e}{m}\left(E+V\times \frac{B_0}{c}\right)-\nu V\text{,}$$

(3)

$$\nabla .E=-4\pi en\text{,}$$

(4)

$$\nabla .B=0.$$

(5)

Here, the field quantities E, B, V and n denote perturbed quantities corresponding respectively to the electric and magnetic fields, electron's velocity, and electron's density. Also, e and m are the electron's electric charge and mass, respectively, and v is the collision frequency.

The physical quantities in Equations 1, 2, 3, 4, and 5 become dimensionless by applying the following transformations:

$$\left(\stackrel{\sim }{x},\stackrel{\sim }{y},\stackrel{\sim }{z},\stackrel{\sim }{t}\right)=\left(k_0\left(x,y,z\right),\omega t\right)\text{,}$$

(6)

$$\left(\stackrel{\sim }{E},\stackrel{\sim }{B}\right)=\frac{1}{E_0}\left(E,B\right)\text{,}$$

(7)

$$\stackrel{\sim }{n}=\frac{n}{n_0}\text{,}$$

(8)

$$\stackrel{\sim }{V}=\frac{V}{c}\text{,}$$

(9)

where$k_0=\frac{\omega }{c}$ and$E_0=\frac{m}{e}\omega c$. The dimensionless field equations then take the following forms:

$$\nabla \times E=-\frac{\partial B}{\partial t}\text{,}$$

(10)

$$\nabla \times B=-\frac{{{\omega }_p}^2}{{\omega }^2}V+\frac{\partial E}{\partial t}\text{,}$$

(11)

$$\frac{\partial V}{\partial t}=-E-\frac{{\omega }_c}{\omega B_0}V\times \frac{B_0}{c}-\stackrel{\prime }{\nu }V\text{,}$$

(12)

$$\nabla .E=-\frac{{{\omega }_p}^2}{{\omega }^2}n\text{,}$$

(13)

$$\nabla .B=0.$$

(14)

Here,${{\omega }_p}^2=\frac{4\pi e^2{n}_0}{m}$,${\omega }_c=\frac{e{B}_0}{m}$, and$\stackrel{\prime }{\nu }=\frac{v}{\omega }$ and the tile sign of the dimensional field quantities in Equations 10, 11, 12, 13, and 14 are ignored for simplicity.

Equations 10, 11, and 12 can be written in a compact elegant form as follows. Let us firstly take the time variation part of all field quantities as e^− it. Then, by finding the components of V from Equation 12 and inserting them into Equation 11, one obtains

$$\nabla \times B=-i\epsilon .E\text{,}$$

(15)

where ε is the equivalent dielectric tensor defined by

$$\epsilon =\left(\begin{array}{ccc}\hfill {\epsilon }_1\hfill & \hfill i{\epsilon }_2\hfill & \hfill 0\hfill \\ \hfill -i{\epsilon }_2\hfill & \hfill {\epsilon }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\epsilon }_3\hfill \end{array}\right)\text{.}$$

(16)

Here, ε ₁ , ε ₂ , and ε ₃ are assumed to take the following forms:

$${\epsilon }_1=1-\frac{s{{\omega }_p}^2}{{\omega }^2{s}^2-{{\omega }_c}^2}\text{,}$$

(17)

$${\epsilon }_2=\frac{{{\omega }_p}^2{\omega }_c}{\omega \left({\omega }^2{s}^2-{{\omega }_c}^2\right)}\text{,}$$

(18)

$${\epsilon }_3=1-\frac{{{\omega }_p}^2}{{\omega }^{2}s}\text{,}$$

(19)

where

$$s=1+i\stackrel{\prime }{\nu }.$$

(20)

Also, Equation 10 takes the form

$$\nabla \times E=i\omega B\text{.}$$

(21)

Finally, by eliminating B from Equations 15 and 21, the wave equation can be found as

$$\nabla \times \nabla \times E=\epsilon .E\text{,}$$

(22)

where the tensor of permittivity ε is given by Equation 16.

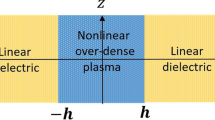
In order to study the transmission properties of electromagnetic waves through the plasma, one needs the solutions of the wave equation (Equation 22). To this aim, we consider a plasma layer with the geometry that is illustrated in Figure1. According to the figure,$B_0=B_0\hat{k}$ and the z axis is perpendicular to the plasma layer. In this case, the spatial part of all physical quantities varies as$\psi \left(z\right)e^{i{k}_{y}y}$, where z is the coordinate into the plasma and y runs along the interface. Let us not make any assumption about the direction of the electric and magnetic fields. By these considerations, Equation 22 can be expanded as follows:

$$\frac{d^2{E}_x\left(z\right)}{d{z}^2}-\left(k_y^2-{\epsilon }_1\right)E_x\left(z\right)+i{\epsilon }_2{E}_y\left(z\right)=0\text{,}$$

(23)

$$\frac{d^2{E}_y\left(z\right)}{d{z}^2}-i{k}_y\frac{d{E}_z\left(z\right)}{dz}-i{\epsilon }_2{E}_x\left(z\right)+{\epsilon }_1{E}_y\left(z\right)=0\text{,}$$

(24)

$$i{k}_y\frac{d{E}_y\left(z\right)}{dz}+\left(k_y^2-{\epsilon }_3\right)E_z\left(z\right)=0.$$

(25)

Figure 1

Orientation of the magnetized over-dense plasma slab. The z axis is perpendicular to the plasma layer, and the y and x axes run along the interface. A uniform magnetic field$B_0=B_0\hat{k}$, in the slab is considered.

These equations can explicitly be solved which lead to the following field components:

$$\begin{array}{l}{E}_x\left(z\right)=C_1{e}^{-k_{z1}z}+C_2{e}^{k_{z1}z}+C_3{e}^{-k_{z2}z}\\ +C_4{e}^{k_{z2}z}\text{,}\end{array}$$

(26)

$$\begin{array}{l}{E}_y\left(z\right)=a(C_1{e}^{-k_{z1}z}+C_2{e}^{k_{z1}z})\\ +b(C_3{e}^{-k_{z2}z}+C_4{e}^{k_{z2}z})\text{,}\end{array}$$

(27)

$$\begin{array}{l}{E}_z\left(z\right)=ca{k}_{z1}\left(-C_1{e}^{-k_{z1}z}+C_2{e}^{k_{z1}z}\right)\\ +cb{k}_{z2}\left(-C_3{e}^{-k_{z2}z}+C_4{e}^{k_{z2}z}\right)\text{.}\end{array}$$

(28)

Here, C ₁ , C ₂ , C ₃ , and C ₄ are integration constants. Also, k_{z 1}, k_{z 2}, a, b, and c are defined as

$$k_{z_2^1}={\left[\frac{\left({\epsilon }_1+{\epsilon }_3\right){k_y}^2-2{\epsilon }_1{\epsilon }_3\mp \alpha }{2{\epsilon }_3}\right]}^{1/2}\text{,}$$

(29)

$$ba=\frac{i}{2{\epsilon }_2{\epsilon }_3}\left[\left({\epsilon }_1-{\epsilon }_3\right){k_y}^2\mp \alpha \right]\text{,}$$

(30)

$$c=\frac{-i{k}_y}{{k_y}^2-{\epsilon }_3}\text{,}$$

(31)

with α being

$$\alpha ={\left[{\left({\epsilon }_1-{\epsilon }_3\right)}^2{k_y}^4-4{\epsilon }_3{{\epsilon }_2}^2{k_y}^2+4{{\epsilon }_2}^2{{\epsilon }_3}^2\right]}^{1/2}\text{.}$$

(32)

Dispersion relation for the surface waves

It has been shown that the electromagnetic waves are reflecting from the surface of a medium with negative permittivity and the surface of an over-dense plasma layer. However, there are some mechanisms why these materials become transparent. Among them is the mechanism that involved the excitation of the surface electromagnetic waves on the interface between a dielectric medium and the over-dense plasma layer. The ordinary dielectric medium adjacent to the over-dense plasma is needed to produce evanescent waves. In fact, the surface plasmons can be excited by the evanescent waves. Then, these excited plasmons carry the electromagnetic energy through the over-dense plasma and hence is responsible for the transmission of the electromagnetic waves.

Here, in order to investigate the dispersion relation on a magnetized over-dense plasma layer, let us consider an interface between the plasma and ordinary dielectric or cold unmagnetized plasma. Our strategy is in close correspondence to that of[6]. Let us assume that the interface is located at z = 0, and the dielectric and the over-dense plasma are located at z < 0 and z > 0, respectively. Taking into account Equations 17, 18, and 19, the permittivity of this simple dielectric region can be taken as ε₁ = ε₃ = ε and ε₂ = 0. Then, according to the solutions (Equations 26, 27, and 28), the surface waves in the z < 0 region would take the following forms:

$$z<0:\{\begin{array}{c}\hfill E_x\left(z\right)=A{e}^{\beta z}\hfill \\ \hfill E_y\left(z\right)=B{e}^{\beta z}\hfill \\ \hfill E_z\left(z\right)=\frac{-i{k}_y}{\beta }B{e}^{\beta z}\hfill \end{array}\text{,}$$

(33)

where β is defined as

$$\beta =\sqrt{\left(k_y^2-\epsilon \right)}\text{.}$$

(34)

The coefficients A and B are two integration constants. Also, since the wave must be damping away from the interface, only the positive exponential is considered in this region.

Equivalently, in the z > 0 region, the surface field can be written as

$$z>0:\{\begin{array}{c}\hfill E_x\left(z\right)=C_1{e}^{-k_{z1}z}+C_3{e}^{-k_{z2}z}\hfill \\ \hfill E_y\left(z\right)=a{C}_1{e}^{-k_{z1}z}+b{C}_3{e}^{-k_{z2}z}\hfill \\ \hfill E_z\left(z\right)=-ca{k}_{z1}{C}_1{e}^{-k_{z1}z}-cb{k}_{z2}{C}_3{e}^{-k_{z2}z}\hfill \end{array}\text{,}$$

(35)

where, for the same reasons, positive exponentials are omitted. The quantities k_{z 1}, k_{z 2}, a, b, and c are given in Equations 29, 30, and 31.

Using the standard boundary conditions on the interface which are concerned with the continuity of E _x and E _y and their perpendicular derivatives$\frac{d{E}_x}{dz}$ and$\frac{d{E}_y}{dz}$ on the z = 0 surface, one leads to the following solutions for the unknown coefficients in terms of the coefficient A:

$$C_1=\left(\frac{-k_{z2}-\beta }{k_{z1}-k_{z2}}\right)A\text{,}$$

(36)

$$C_3=\left(\frac{k_{z1}+\beta }{k_{z1}-k_{z2}}\right)A\text{,}$$

(37)

$$B=\left(\frac{-a\left(k_{z2}+\beta k_{z1}\right)+b\left(k_{z1}+\beta \right)}{k_{z1}-k_{z2}}\right)A\text{.}$$

(38)

Also, an extra relation has appeared which establishes a condition between the involved quantities. This relation is the dispersion relation of the surface wave excitation on the interface between dielectric and cold magnetized collisional plasma layer which can be written as follows:

$${\beta }^2+\beta \left(k_{z1}+k_{z2}\right)+k_{z1}{k}_{z2}=0.$$

(39)

This relation imposes a condition between β, k_{z 1} and k_{z 2}. However, according to Equations 29 and 34, these quantities are functions of ε, ε₁, ε₂, ε₃ and k _y . Hence, Equation 39 defines a condition for the allowed values of k _y . This means that acquiring specific values for ε, ε₁, ε₂ and ε₃ according to the physical characteristics of the plasma leads to a unique value of k _y .

We have found the explicit form of k _y in terms of ε, ε₁, ε₂, and ε₃ as follows:

$$k_y={\left\{\frac{{\epsilon }_3\left[{{\epsilon }_2}^2-{\left(\epsilon -{\epsilon }_1\right)}^2\right]}{\left(\epsilon -{\epsilon }_1\right)\left({\epsilon }_1-{\epsilon }_3\right)+{\epsilon }_2^2}\right\}}^{\frac{1}{2}}\text{.}$$

(40)

We should note that the quantities ε₁, ε_2, and ε₃, in according to Equations 17, 18, and 19 are functions of ω. Therefore, Equation 40, in fact, establishes a relation between k _y and ω. However, ω _c and$\stackrel{\prime }{\nu }$ also contribute to these relations. Hence, one may consider k _y as a function of ω, ω _c , and$\stackrel{\prime }{\nu }$ as$k_y\left(\omega ,{\omega }_c,\stackrel{\prime }{\nu }\right)$.

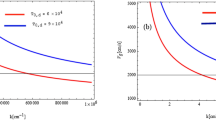
In Figures2,3,4, and5,$k_y\left(\omega ,{\omega }_c,\stackrel{\prime }{\nu }\right)$ is plotted as a function of the phase velocity ω. These figures include both imaginary and real parts of k _y which are respectively shown by dashed and solid lines. The cyclotron frequency ω _c is 0.5 ω _p , 0.9 ω _p , 2.5 ω _p , And 3.5 ω _p in Figures2,3,4, and5, respectively. In all figures,$\stackrel{\prime }{\nu }$ = 0.04 and ε = 0.297. As it is obvious from the figures, by increasing ω _c , the imaginary part of k _y grows up. For smaller values of ω _c , the imaginary part of k _y is so negligible, specifically for$\raisebox{1ex}{${\omega }_c$}\!\left/ \!\raisebox{-1ex}{${\omega }_p$}\right.<1$. In fact, in this region, the imaginary part of k _y is approximately zero. However, for larger values of$\raisebox{1ex}{${\omega }_c$}\!\left/ \!\raisebox{-1ex}{${\omega }_p$}\right.$, the imaginary part grows up and hence shows significant effects. The stability of the produced surface wave is recognized to be related to the imaginary part of k _y . Hence, it is expected to see more stable surface wave for ω _c slightly larger than ω _p , namely for$\raisebox{1ex}{${\omega }_c$}\!\left/ \!\raisebox{-1ex}{${\omega }_p$}\right.>1$.

Figure 2

${\mathit{k}}_{\mathit{y}}\left(\mathit{\omega },{\mathit{\omega }}_{\mathit{c}},\stackrel{\prime }{\mathit{\nu }}\right)$as a function of the phase velocity ω . The figure includes both imaginary and real parts of k _y which are respectively shown by dashed and solid lines. Also, it is considered that ω _c  = 0.5 ω _p , and$\stackrel{\prime }{\nu }$ = 0.04, and ε = 0.297.

Figure 3

${\mathit{k}}_{\mathit{y}}\left(\mathit{\omega },{\mathit{\omega }}_{\mathit{c}},\stackrel{\prime }{\mathit{\nu }}\right)$as a function of the phase velocity ω . The figure includes both imaginary and real parts of k _y which are respectively shown by dashed and solid lines. Also, it is considered that ω _c  = 0.9 ω _p , and$\stackrel{\prime }{\nu }$ = 0.04 and ε = 0.29.

Figure 4

${\mathit{k}}_{\mathit{y}}\left(\mathit{\omega },{\mathit{\omega }}_{\mathit{c}},\stackrel{\prime }{\mathit{\nu }}\right)$plotted as a function of the phase velocity ω . The figure includes of imaginary and real parts of k _y which are respectively shown by dashed and solid lines. It is considered that ω _c  = 2.5 ω _p ,$\stackrel{\prime }{\nu }$ = 0.04 and ε = 0.297.

Figure 5

${\mathit{k}}_{\mathit{y}}\left(\mathit{\omega },{\mathit{\omega }}_{\mathit{c}},\stackrel{\prime }{\mathit{\nu }}\right)$as a function of the phase velocity ω . The figure includes both imaginary and real parts of k _y which are respectively shown by dashed and solid lines. Also, it is considered that ω _c  = 3.5 ω _p , and$\stackrel{\prime }{\nu }$ = 0.04 and ε = 0.29.

In order to examine the dependence of the wave vector k _y on collisional effects, the real and imaginary parts of k _y are plotted distinctly in Figures6 and7 for three different values of$\stackrel{\prime }{\nu }$. In these figures, the solid, dashed, and dot dashed lines are corresponding to$\stackrel{\prime }{\nu }$ = 0.001,$\stackrel{\prime }{\nu }$ = 0.02, and$\stackrel{\prime }{\nu }$ = 0.09, respectively. As it is obvious in Figure4, the real part of k _y is not sensitive to the values of$\stackrel{\prime }{\nu }$. Indeed, all three lines, real parts of k _y for different values of$\stackrel{\prime }{\nu }$, have fallen on one another. However, the imaginary part of k _y are more sensitive in respect to the collisional effects. Figure5 shows that increasing$\stackrel{\prime }{\nu }$ leads to more separation of the figure branches and higher values of$\stackrel{\prime }{\nu }$ cause more effects on the imaginary part of k _y .

Figure 6

The real part of k _y is plotted for three different values of$\stackrel{\prime }{\mathit{\nu }}$. The solid, dashed, and dot dashed lines are corresponding to$\stackrel{\prime }{\nu }$ = 0.001,$\stackrel{\prime }{\nu }$ = 0.02 and$\stackrel{\prime }{\nu }$ = 0.09. All three curves corresponding to different values of$\stackrel{\prime }{\nu }$are placed on one another.

Figure 7

The imaginary part of k _y for three different values of$\stackrel{\prime }{\mathit{\nu }}$. The solid, dashed, and dot dashed lines are corresponding to$\stackrel{\prime }{\nu }$ = 0.001,$\stackrel{\prime }{\nu }$ = 0.02 and$\stackrel{\prime }{\nu }$ = 0.09, respectively.

In order to figure out the shape of the supposed surface wave on the interface, we plot the spatial distribution of the absolute value of the electric field, namely |E|, in Figure8. This figure is obtained from the field components (Equations 33, 34, and 35) by substituting Equations 36, 37, and 38 and considering ω = 0.35 ω _p , ω _c  = 2.5 ω _p , ε = 0.297, and$\stackrel{\prime }{\nu }$ = 0.01.

Figure 8

The shape of the supposed surface wave on the dielectric-plasma interface.

Conclusions

Here, the conditions for the electromagnetic wave transmission through an over-dense magnetized plasma with collision were studied. The study was mainly concentrated on the conditions required for the excitation of the surface waves on the interface between a dielectric medium and an over-dense magnetized plasma slab. It was supposed that the dominant procedure for the transmission of the electromagnetic waves through an over-dense plasma is the excitation of the surface waves. The required conditions were obtained by deriving the dispersion relation for the surface wave excitation on the interface. It was showed that the surface plasmons can be produced if the vector wave k _y acquires specific values. These values were recognized to depend on the phase velocity ω, the cyclotron velocity ω _c and also the collision frequency$\stackrel{\prime }{\nu }$. It was inferred that k _y acquires real values for$\raisebox{1ex}{${\omega }_c$}\!\left/ \!\raisebox{-1ex}{${\omega }_p$}\right.<1$ and its imaginary part is negligible in this regime. However, for slightly higher values of ω _c , the imaginary part of k _y grows up and hence leads to the excitation of more stable surface waves.

The sensitivity of k _y on the effects of collision was also investigated. It was showed that the real part of k _y doesis not affected by the collision effects, which, in our model, is handled by the frequency of collision$\stackrel{\prime }{\nu }$. Specifically, the real and imaginary parts of k _y for different values of$\stackrel{\prime }{\nu }$ were plotted. It was observed that on contrary to the real part of k _y , the collision effects have obvious influences on the imaginary part of k _y . By the increase of$\stackrel{\prime }{\nu }$, the imaginary part of k _y would be drawn to more negative values.

Authors’ information

The author did not provide this information.