Williamson-Hall analysis in estimation of lattice strain in nanometer-sized ZnO particles

Abstract

ZnO nanoparticles were prepared by coprecipitation method at 450C. X-ray diffraction result indicates that the sample is having a crystalline wurtzite phase. Transmission electron microscopy (TEM) result reveals that the ZnO sample is spherical in shape with an average grain size of about 50nm. X-ray peak broadening analysis was used to evaluate the crystalline sizes and lattice strain by the Williamson-Hall (W-H) analysis. All other relevant physical parameters such as strain, stress, and energy density values were also calculated using W-H analysis with different models, viz, uniform deformation model, uniform deformation stress model and uniform deformation energy density model. The root mean square strain was determined from the interplanar spacing and strain estimated from the three models. The three models yield different strain values; it may be due to the anisotropic nature of the material. The mean particle size of ZnO nanoparticles estimated from TEM analysis, Scherrers formula and W-H analysis is highly intercorrelated.

Background

Semiconductor research is a very important field in the ongoing research activity across the world. As the semiconductor particles exhibit size-dependant properties like scaling of the energy gap and corresponding change in the optical properties, they are considered as the front runners in the technologically important materials. Zinc oxide is a II-VI semiconductor with a large bandgap (E_g=3.37eV) and high exciton binding energy (60meV). It is widely used in a number of applications like photocatalysis, gas sensors, varistors, and low-voltage phosphor materials [1–4]. ZnO is the richest family of nanostructures among all semiconducting materials, both in structures and in properties due to its unique properties [5, 6].

A perfect crystal would extend in all directions to infinity, so no crystals are perfect due to their finite size. This deviation from perfect crystallinity leads to a broadening of the diffraction peaks. The two main properties extracted from peak width analysis are (a) crystallite size and (b) lattice strain. Crystallite size is a measure of the size of a coherently diffracting domain. The crystallite size of the particles is not generally the same as the particle size due to the presence of polycrystalline aggregates [7]. The most common techniques used for the measurement of particle size rather than the crystallite size are BET, light scattering, scanning electron microscopy, and transmission electron microscopy (TEM) analysis. Lattice strain is a measure of the distribution of lattice constants arising from crystal imperfections, such as lattice dislocation. The other sources of strain are the grain boundary triple junction, contact or sinter stresses, stacking faults, coherency stresses, etc. [8]. X-ray line broadening is used for the investigation of dislocation distribution.

Apart from crystallite size reduction and alloying, mechanical alloying induces a large amount of strain in the powders [9]. X-ray profile analysis is a simple and powerful tool to estimate the crystallite size and lattice strain [10]. Among the available methods to estimate the crystallite size and lattice strain are the pseudo-Voigt function, Rietveld refinement, and Warren-Averbach analysis [11–13]. Williamson-Hall (W-H) analysis is a simplified integral breadth method where both size-induced and strain-induced broadening are deconvoluted by considering the peak width as a function of 2[14]. In the present study, W-H analysis is employed for estimating crystallite size and lattice strain. Although X-ray profile analysis is an average method, they still hold an unavoidable position for grain size determination, apart from TEM micrographs.

In this present work, a comparative evaluation of the mean particle size of ZnO nanoparticles obtained from direct TEM measurements and from powder X-ray diffraction (XRD) peak broadening is reported. The strain associated with the as-prepared and annealed ZnO samples at 450C due to lattice deformation was estimated by a modified form of W-H, namely, uniform deformation model (UDM). The other modified models, such as uniform deformation stress model (UDSM) and uniform deformation energy density model (UDEDM), gave an idea of the stressstrain relation and the strain as a function of energy density u. In UDM, the isotropic nature of the crystal is considered, whereas UDSM and UDEDM assume that the crystals are of an anisotropic nature. The strain associated with the anisotropic nature of the hexagonal crystal is compared and plotted with the strain resulting from the interplanar spacing. We report such investigations on ZnO nanoparticles synthesized by coprecipitation method in this paper laconically and qualitatively.

Results and discussion

XRD analysis

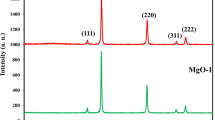
The XRD pattern of the ZnO powder as shown in Figure 1 is having a wurtzite structure. No extra diffraction peaks corresponding to Zn, Zn(OH₂), or other ZnO phases are detected, indicating that the pure ZnO nanoparticles are crystalline in nature. The peaks intensity is sharp and narrow, confirming that the sample is of high quality with good crystallinity and fine grain size. Using XRD data, lattice parameters were calculated (a=3.2491 and c=5.2063 ).

Figure 1

X-ray diffractogram of ZnO.

Crystalline size and strain

The significance of the broadening of peaks evidences grain refinement along with the large strain associated with the powder. The instrumental broadening (_hkl) was corrected, corresponding to each diffraction peak of ZnO material using the relation:

$${\beta }_{\text{hkl}}={\left[{\left({\beta }_{\text{hkl}}\right)}^2{}_{\text{Measured}}-{\left({\beta }_{\text{hkl}}\right)}^2{}_{\text{Instrumental}}\right]}^{1/2}\text{.}$$

(1)

The average nanocrystalline size was calculated using Debye-Scherrers formula:

$$D=\frac{K\lambda }{{\beta }_{\text{hkl}}\text{Cos}\theta }\text{,}$$

(2)

where D = crystalline size, K = shape factor (0.9), and = wavelength of Cuk radiation. From the calculations, the average crystalline size of the ZnO nanoparticles is 27nm.

The strain induced in powders due to crystal imperfection and distortion was calculated using the formula:

$$\epsilon =\frac{{\beta }_{\mathit{hkl}}}{4tan\theta }\text{.}$$

(3)

From Equations2 and 3, it was confirmed that the peak width from crystallite size varies as $\frac{1}{cos\theta }$ strain varies as tan.

Assuming that the particle size and strain contributions to line broadening are independent to each other and both have a Cauchy-like profile, the observed line breadth is simply the sum of Equations2 and 3.

$${\beta }_{\text{hkl}}=\frac{K\lambda }{Dcos\theta }+4\epsilon tan\theta$$

(4)

By rearranging the above equation, we get

$${\beta }_{\text{hkl}}cos\theta =\frac{K\lambda }{D}+4\epsilon sin\theta \text{.}$$

(5)

The above equations are W-H equations. A plot is drawn with 4sin along the x-axis and_hkl cos along the y-axis for as-prepared ZnO nanoparticles as shown in Figure 2. From the linear fit to the data, the crystalline size was estimated from the y-intercept, and the strain , from the slope of the fit. Equation5 represents the UDM, where the strain was assumed to be uniform in all crystallographic directions, thus considering the isotropic nature of the crystal, where the material properties are independent of the direction along which they are measured. The uniform deformation model for ZnO nanoparticles is shown in Figure 2.

Figure 2

Plot of _hkl cos vs 4sin of ZnO sample.

Uniform deformation stress and uniform deformation energy density were taken into account; the anisotropic nature of Youngs modulus of the crystal is more realistic [14–16]. The generalized Hooks law referred to the strain, keeping only the linear proportionality between the stress and strain, i.e., = E. Here, the stress is proportional to the strain , with the constant of proportionality being the modulus of elasticity or Youngs modulus, denoted by E. In this approach, the Williamson-Hall equation is modified by substituting the value of in Equation5; we get

$${\beta }_{\text{hkl}}cos\theta =\frac{K\lambda }{D}+4sin\theta \sigma /E_{\text{hkl}}\text{.}$$

(6)

E_hkl is Youngs modulus in the direction perpendicular to the set of the crystal lattice plane (hkl).

The uniform stress can be calculated from the slope line plotted between 4sin/E_hkl and_hkl cos, and the crystallite size D, from the intercept as shown in Figure 3. The strain can be measured if E_hkl of hexagonal ZnO nanoparticles is known. For samples with a hexagonal crystal phase, Youngs modulus E_hkl is related to their elastic compliances S_ij as [12, 13]

$$E_{\text{hkl}}=\frac{{[h^2+{(h+2k)}^2/3+{(al/c)}^2]}^2}{S_{11}(h^2+{(h+2k)}^2/3+S_{33}{(al/c)}^4+(2S_{13}+S_{44}\left)\right(h^2+{(h+2k)}^2/3{(al/c)}^2}\text{,}$$

(7)

where S₁₁S₁₃S₃₃, and S₄₄ are the elastic compliances of ZnO, and their values are 7.85810¹², 2.20610¹², 6.94010¹², and 23.5710¹²m²N¹, respectively [17]. Equation7 represents the UDSM. Plotting the values of_hkl cos as a function of 4sin/E_hkl, the uniform deformation stress can be calculated from the slope of the line and from lattice strain. UDSM for annealed ZnO nanoparticles is shown in Figure 3.

Figure 3

Plot of _hkl cos vs 4sin / E _hkl of ZnO sample.

In Equation5, we have considered the homogeneous isotropic nature of the crystal. However, in many cases, the assumption of homogeneity and isotropy is not fulfilled. Moreover, all the constants of proportionality associated with the stressstrain relation are no longer independent when the strain energy density u is considered. According to Hookes law, the energy density u (energy per unit volume) as a function of strain is u =²E_hkl/2. Therefore, Equation6 can be modified to the form, where u is the energy density (energy per unit volume):

$${\beta }_{\text{hkl}}cos\theta =\frac{K\lambda }{D}+\left(4\text{sin}\theta {(2u/E_{\text{hkl}})}^{1/2}\right)\text{.}$$

(8)

The uniform deformation energy density (UDEDM) can be calculated from the slope of the line plotted between_hkl cos and 4sin (2/E_hkl)^1/2. The lattice strain can be calculated by knowing the E_hkl values of the sample. W-H equations modified assuming UDEDM and the corresponding plot are shown in Figure 4. From Equations6 and 8, the energy density and the stress can be related with UDSM and UDEDM, but approaches are different, based on the assumption of uniform deformation stress, according to Equation6. The assumption of uniform deformation energy is as per Equation8, even though both models consider the anisotropic nature of the crystallites. From Equations6 and 8, the deformation stress and deformation energy density are related as u =²/E_hkl. It may be noted that though both Equations 6 and 8 are taken into account in the anisotropic nature of the elastic constant, they are essentially different. This is because in Equation 3, it is assumed that the deformation stress has the same value in all crystallographic directions allowing u to be anisotropic, while Equation 8 is developed assuming the deformation energy to be uniform in all crystallographic directions treating the deformation stress to be anisotropic. Thus, it is clear that from Williamson-Hall plots using Equations6 and 8, a given sample may result in different values for lattice strain and crystallite size. For a given sample, Williamson-Hall plots may be plotted using Equations1 to 8, and the most suitable model may be chosen as the one, which results in the best fit of the experimental data. A comparison of the three evaluation procedures for the nanocrystalline ZnO sample is possible from the analysis of Figure 4. The scattering of the points away from the linear expression is lesser for Figure 2 as compared with Figures 3 and 4. Further, the average crystallite sizes are estimated from the y-intercept of the graphs shown in Figures 23, and 4, i.e., 35, 36, and 36nm, respectively. It can be noted that the values of the average crystallite size obtained from the UDEDM, UDM, and UDSM are in good agreement with the results of the TEM analysis. Thus, it may be concluded that these models are more realistic in the present case. The values of crystallites obtained from the three models are in good agreement with the values obtained from Scherrers formula and TEM. Our results are more appropriate than the reported literature [18]. As far as authors are concerned, a detailed study using these models on the ZnO-synthesized sample annealed at 450C is not reported yet. This study throws some more light and reveals importance of models in the determination of particle size of ZnO nanomaterials. We suggest that these three models are the best models for the evaluation of the crystallite size of ZnO nanoparticles. This is in agreement with the results of Rosenberg et al. that for metallic samples with cubic structures, the uniform deformation energy model is suitable [19]. In our case, all three models are found suitable for the determination of crystallite size.

Figure 4

Plot of _hkl cos vs 4sin (2/ E _hkl ) ^1/2 of ZnO sample.

The root mean square (RMS) lattice strain, $<{\epsilon }_{\text{RMS}}>={(2/\pi )}^{1/2}(\Delta d/d_0)$, estimated [20] from the observed variation in the interplanar spacing values is plotted against those estimated using the uniform deformation energy density model, E_hkl as shown in Figure 5. Here, d and d₀ represent the observed and ideal interplanar spacing values, respectively. Figure 5 shows the plot of RMS strain against variation in the interplanar spacing for the uniform deformation energy density model. Theoretically, if the strain values agree, all the points should lie on a straight line with an angle of 45 to the x-axis. The RMS strain linearly varies with the strain calculated from the interplanar spacing, which attributed to no discrepancy on the (hkl) planes in the nanocrystalline nature [21]. Lattice strain in the nanocrystalline ZnO nanoparticles may arise from the excess volume of grain boundaries due to dislocations.

Figure 5

_RMS vs _hkl of ZnO sample.

In TEM, electron beams focused by electromagnetic lines are transmitted through a thin sample of ZnO nanopowders. Figures 6 and 7 display the TEM image and selected area electron diffraction (SAED) pattern of annealed ZnO nanoparticles. The mean size estimated from the TEM image is about 50nm and clearly indicates that the annealed ZnO nanoparticles are crystalline with a wurtzite structure, and no other impurities were observed. This is in close agreement with the results obtained from powder XRD data. In addition, the rings with a dotted pattern in SAED confirm the wide size distribution of ZnO nanoparticles.

Figure 6

TEM image of ZnO nanopowders.

Figure 7

SAED patterns of ZnO nanopowders.

Youngs modulus (E) is calculated using Equation7 for ZnO nanoparticles and is approximately 127GPa, which is in agreement with the bulk ZnO [22]. Table 1 summarizes the geometric parameters of ZnO nanoparticles obtained from Scherrers formula, various modified forms of W-H analysis, and TEM results. By comparing the values of average crystallite size obtained from UDM, UDSM, and UDEDM, it was found that the values are almost similar, implying that the inclusion of strain in various forms has a very small effect on the average crystallite size of ZnO nanoparticles. However, the average crystallite size obtained from Scherrers formula and W-H analysis shows a small variation; this is because of the difference in averaging the particle size distribution. The values of strain from each model are calculated by considering Youngs modulus E_hkl to be 127GPa. The average crystallite size and the strain values obtained from the graphs plotted for various forms of W-H analysis, i.e., UDM, UDSM, and UDEDM, were found to be accurate, comparable, and reasonable, as their entire preferred high intensity points lay close to the linear fit.

Table 1 Geometric parameters of the ZnO nanoparticles

Conclusions

ZnO nanoparticles were synthesized by coprecipitation process and characterized by powder XRD and TEM. The line broadening of ZnO nanoparticles due to the small crystallite size and strain was analyzed by Scherrers formula. The size and strain contributions to line broadening were analyzed by the method of Williamson and Hall using uniform deformation, uniform deformation stress, and uniform deformation energy density models. The uniform deformation energy density model models the strain most appropriately. A modified W-H plot has been worked out and accepted to determine the crystallite size and strain-induced broadening due to lattice deformation. With the assumption of a hexagonal anisotropic crystalline nature, the RMS lattice strain differs from the strain calculated from UDSM and UDEDM. TEM image of annealed ZnO nanoparticles reveals the nanocrystalline nature, and their particle size is found to be 50nm. The three modified forms of W-H analysis were helpful in determining the strain, stress, and energy density value with a certain approximation, and hence, these models are highly preferable to define the crystal perfection. The value of crystallite size calculated from the W-H analysis is in agreement with that of the average crystallite size measured from TEM.

Methods

Sample preparation

ZnO nanoparticles were prepared by the reaction of Zn²⁺ and OH in an alcoholic medium (methanol) at low temperature. Zinc acetate dehydrate Zn(CH₃COO)₂2H₂O, potassium hydroxide (KOH), and methanol are used as starting materials. In this procedure, pure ZnO and two solutions, one containing zinc acetate dehydrate dissolved in 100ml methanol and the other containing KOH in 100ml methanol, were prepared and aided by magnetic stirring while heating at 52C for 2 h. The KOH solution was added to the solution containing Zn(CH₃COO)₂2H₂O with constant stirring while heating at 52C for 2h; it was aged for 2days. The precipitate which formed was separated from the solution by filtration, washed several times with distilled water and absolute ethanol, and then dried in air at 127C to obtain ZnO nanocrystalline powders. The nanocrystalline sample was annealed at 450C in air for 8h.

Characterization

XRD and TEM were used to obtain the textural parameters like size, shape, and crystal structure in order to understand the enhanced properties of as-prepared and annealed ZnO nanoparticles. XRD was performed by powder X-ray diffraction (model: PW-3710; FEI Co., Hillsboro, OR, USA) using CuK radiation (=1.5406). For TEM analysis, it was used to examine the morphology of the annealed ZnO nanoparticles. Crystallite size and lattice strain were determined using Scherrers formula and W-H analysis.