Kaluza-Klein interacting cosmic fluid cosmological model

Abstract

In this paper, we have presented a power law scaling Kaluza-Klein cosmological model dominated by two interacting perfect fluid components during expansion. Barotropic equations of state for pressure and density are considered to get determinate solutions of the field equations. We have shown that the components are not conserved separately because of mutual interaction between the two fluids, and the energy densities are proportional to $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$t^2$}\right.$.

Background

It is supposed that the densities of two components, the dark matter and the dark energy, dominate the total energy density of the universe [1–4]. These universes are modeled with perfect fluids and with mixtures of non-interacting fluids [5–9] under the assumption that there is no energy transfer among the components. But no observational data confirms this. This inspires us to study general properties of cosmological models containing more than one fluid which interact with each other.

The interaction between dust-like matter and radiation was first considered by Tolman [10] and Davidson [11]. The late time acceleration of the universe [12–14] and the coincidence problem [15–17] were explained by the energy transfer among the fluids. Gromov et al. [18] studied cosmological models with decay of massive particles into radiation or with matter creation. Cataldo et al. [19] considered the simplest non-trivial cosmological scenarios for an interacting mixture of two cosmic fluids described by power law scale factors, i.e., the expansion (contraction) as a power law in time. An interacting and non-interacting two-fluid scenario for dark energy in an FRW universe with constant deceleration parameter had been recently described by Pradhan et al. [20].

The Kaluza-Klein theory was introduced to unify Maxwell’s theory of electromagnetism and Einstein's gravity theory by adding the fifth dimension. Kaluza-Klein theory has been regarded as a candidate of fundamental theory due to its potential function to unite the fundamental interactions. Kaluza-Klein cosmological models have been studied with different matters [21–25]. In Kaluza-Klein theory, the inflation was considered [26], the cosmological constant problem was studied, [27] and the Schwarzschild solution for three space and n dimensions were formed [28]. String cloud and domain walls with quark matter in N-dimensional Kaluza-Klein cosmological model have also been studied [29].

Generally, the power law cosmologies are defined by the growth of the cosmological scale factor as a(t) = t^α. For α > 0, the universe is expanding, whereas for α < 0, the universe is contracting (t > 0). The Hubble parameter $H=\raisebox{1ex}{$\dot{a}$}\!\left/ \!\raisebox{-1ex}{$a$}\right.$ and the deceleration parameter $q\left(t\right)=-\frac{a\stackrel{}{a}}{{\dot{a}}^2}$ completely describe the behavior of the universe in power law cosmologies. For a(t) = t^α, it reduces to the form $q\left(t\right)=-\frac{\left(\alpha -1\right)}{\alpha }$ which implies that the universe expands with a constant velocity for α = 1. The universe expands with an accelerated expansion for α > 1, since, if the expansion is speeding up, the deceleration parameter must be negative.

A simple inflationary model characterized by a period in which the scale factor is a power law in time with α > 1 was considered by [30, 31]. There is a class of cosmological models which dynamically solve the cosmological constant problem where the scale factor grows as a power law in time regardless of the matter content.

The aim of this paper is to investigate the simplest non-trivial cosmological scenario for an interacting mixture of two cosmic fluids described by power law scale factors. Here, we have shown that the mutual exchange of energy between two perfect fluids can be described by energy densities which are proportional to $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$t^2$}\right.$ and the interacting term proportional to $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$t^3$}\right.$. Due to consideration of interacting fluids, we get the energy densities evolve at the same rate and their ratio is constant. This satisfies the so-called cosmological coincidence problem.

Field equations

We consider the Kaluza-Klein type metric as

$$d{s}^2=d{t}^2-a^2\left(d{x}^2+d{y}^2+d{z}^2\right)-b^{2}d{\varphi }^2$$

(1)

where a and b are scale factors and are functions of cosmic time t.

The Einstein field equations are

$$R_{\mathit{ij}}-\frac{1}{2}{g}_{\mathit{ij}}R=-T_{\mathit{ij}}$$

(2)

where R _ij is the Ricci tensor, R is the Ricci scalar, and T _ij is energy momentum tensor.

The energy momentum tensor for two fluids is given by

$$T_i^{\mathit{j}}=\left[\left({\rho }_1+{\rho }_2\right)+\left(p_1+p_2\right)\right]u_i{u}^j-\left(p_1+p_2\right){\delta }_i^{\mathit{j}}$$

with components

$$T_1^1=T_2^2=T_3^3=T_4^4=-p_1-p_2,T_0^0={\rho }_1+{\rho }_2$$

(3)

where p₁, p₂, and ρ₁ , ρ₂ are pressures and densities of two fluids satisfying barotropic equations of state

$$p_1={\omega }_1{\rho }_1$$

$$p_2={\omega }_2{\rho }_2\text{,}$$

(4)

with ω₁ and ω₂ are constant state parameters, where 0 ≤ ω₁, ω₂ ≤ 1, and ω₁ ≠ ω₂.

The field Equation 2 with Equations 1 and 3 reduce to

$$2\frac{\stackrel{‥}{a}}{a}+\frac{\stackrel{‥}{b}}{b}+\frac{{\dot{a}}^2}{a^2}+2\frac{\dot{a}\dot{b}}{ab}=-\left(p_1+p_2\right)$$

(5)

$$3\frac{\stackrel{‥}{a}}{a}+3\frac{{\dot{a}}^2}{a^2}=-\left(p_1+p_2\right)$$

(6)

$$3\frac{{\dot{a}}^2}{a^2}+3\frac{\dot{a}\dot{b}}{ab}={\rho }_1+{\rho }_2$$

(7)

where overhead dot represents derivative with respect to cosmic time t.

The conservation law T _j ^ij = 0 implies that the two components ρ₁ and ρ₂ interact through the interacting term Q as follows:

$${\dot{\rho }}_1+4H\left({\rho }_1+p_1\right)=Q$$

(8)

$${\dot{\rho }}_2+4H\left({\rho }_2+p_2\right)=-Q\text{.}$$

(9)

The nature of the interacting term Q is not clear at all.

If Q > 0, then there exist an energy transfer from the fluid ρ₂ to the fluid ρ₁. If Q < 0, then there exist an energy transfer from the fluid ρ₁ to the fluid ρ₂. If Q = 0, then we have two non-interacting fluids, each satisfying the standard conservation equation separately. We consider different forms of the interacting term Q for solving these equations. By putting Q = 0 in Equations 8 and 9, we get ${\rho }_1=c_1{\left(a^{3}b\right)}^{-\left(1+w_1\right)}$ and ${\rho }_2=c_2{\left(a^{3}b\right)}^{-\left(1+w_2\right)}$, where c₁ and c₂ are constants of integration.

Solutions of the field equations

In order to get determinate solution, we consider the relation between expansion (θ) and shear tensor (σ). This condition leads to a = b^k which implies

$$H_{\varphi }=k{H}_x\text{,}$$

(10)

where k is arbitrary constant usually assumed to take positive values only and it takes care of anisotropic nature of the model.

Here, $H_x=\frac{\dot{a}}{a}$ and $H_{\varphi }=\frac{\dot{b}}{b}$ are the directional Hubble parameters.

So, the mean Hubble parameter is defined as $H=\frac{\left(3H_x+H_{\varphi }\right)}{4}$.

Using Equation 10, the field Equations 5 to 7 reduce to

$$\left(k+2\right){\dot{H}}_x+\left(k^2+2k+3\right)H_x^2=-\left(p_1+p_2\right)$$

(11)

$$3{\dot{H}}_x+6H_x^2=-\left(p_1+p_2\right)$$

(12)

$$3\left(k+1\right)H_x^2={\rho }_1+{\rho }_2$$

(13)

Now, we define spatial volume as

$$V{=}^{3}b=t^{4/\alpha }\text{,}$$

(14)

where α is a constant parameter which gives $H=\frac{1}{3}\frac{\alpha }{t}$.

If α = 1, then q = 2, .i.e., there is decelerating universe. Whereas, for α = 3, we get q = 0, which means universe is undergoing accelerated expansion.

From Equations 9 and 10, we obtain

$${\rho }_1=\frac{24\left(k+1\right)\left[\alpha -2\left(1+w_2\right)\right]}{{\left(k+3\right)}^2\left(w_1-w_2\right){\alpha }^2{t}^2}$$

(15)

$${\rho }_2=\frac{24\left(k+1\right)\left[2\left(1+w_1\right)-\alpha \right]}{{\left(k+3\right)}^2\left(w_1-w_2\right){\alpha }^2{t}^2}$$

(16)

The interacting term is given by

$$Q=\frac{48\left(k+1\right)\left[\alpha -2\left(1+w_2\right)\right]\left[2\left(1+w_1\right)-\alpha \right]}{{\left(k+3\right)}^2\left(w_1-w_2\right){\alpha }^3{t}^3}$$

(17)

Using Equations 15 and 16 in Equation 4, we get

$$p_1=\frac{24\left(k+1\right)\left[\alpha -2\left(1+w_2\right)\right]w_1}{{\left(k+3\right)}^2\left(w_1-w_2\right){\alpha }^2{t}^2}$$

(18)

$$p_2=\frac{24\left(k+1\right)\left[2\left(1+w_1\right)-\alpha \right]w_2}{{\left(k+3\right)}^2\left(w_1-w_2\right){\alpha }^2{t}^2}$$

(19)

If we require simultaneously ρ₁ ≥ 0 and ρ₂ ≥ 0, we obtain the following possible conditions:

$$2\left(1+w_2\right)<\alpha <2\left(1+w_1\right),w_2<w_1$$

and

$$2\left(1+w_1\right)<\alpha <2\left(1+w_2\right),w_1<w_2$$

(20)

The constraints (20) on the state parameter using Equation 17 give Q < 0 (for w₁ < w₂). Therefore, the energy is transferred from a dark fluid or a phantom fluid to another matter component.

Also, we consider the behavior of the constant ratio r of energy densities which is a function of the model parameters w₁ and w₂ given as $r=\frac{{\rho }_2}{{\rho }_1}=-\frac{1+2w_1}{1+2w_2}$.

As the energy densities ρ₁ and ρ₂ are proportional to ($\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$t^2$}\right.$), the ratio is always constant. Now, we consider specific two fluid interactions.

Dust-perfect fluid interaction (w₁= 0, w₂≠ 0)

Here, we consider the interaction of dust with any other perfect fluid. So, we have w₁ = 0, and w₂ is a free parameter.

The Equations 15 and 16 give the dust (d) and a perfect fluid (pf) interacting configurations with the equations of state p_d = 0 and p_pf = ω₂ρ_pf.

$${\rho }_d=\frac{24\left(k+1\right)\left[2\left(1+w_2\right)-\alpha \right]}{{\left(k+3\right)}^2{w}_2{\alpha }^2{t}^2}$$

(21)

$${\rho }_{\mathit{pf}}=\frac{24\left(k+1\right)\left[\alpha -2\right]}{{\left(k+3\right)}^2{w}_2{\alpha }^2{t}^2}$$

(22)

Equations 17, 18, and 19 reduce to

$$p_d=0$$

(23)

$$p_{\mathit{pf}}=\frac{24\left(k+1\right)\left[\alpha -2\right]}{{\left(k+3\right)}^2{\alpha }^2{t}^2}$$

(24)

$$Q=\frac{48\left(k+1\right)\left[\alpha -2\left(1+w_2\right)\right]\left[\alpha -2\right]}{{\left(k+3\right)}^2{w}_2{\alpha }^2{t}^3}\text{.}$$

(25)

For simultaneous fulfillment of the conditions ρ₁ ≥ 0 and ρ₂ ≥ 0, we must have

$$2<\alpha <2\left(1+w_2\right),\left(w_2>0and{w}_2\ne -1\right)$$

$$2>\alpha >2\left(1+w_2\right),\left(-1<w_2<0\right)\text{.}$$

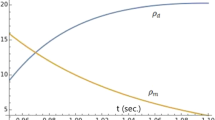
As a specific example, we consider the dust-radiation interaction then put $\left(w_1=0,w_2=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\right)$ and we get

$${\rho }_d=\frac{24\left(k+1\right)\left[8-3\alpha \right]}{{\left(k+3\right)}^2{\alpha }^2{t}^2};p_d=0$$

(26)

$${\rho }_{\mathit{pf}}=\frac{72\left(k+1\right)\left(\alpha -2\right)}{{\left(k+3\right)}^2{\alpha }^2{t}^2};p_{\mathit{pf}}=\frac{1}{3}{\rho }_{\mathit{pf}}$$

(27)

Also, we get

$$p_d=0$$

(28)

$$p_{\mathit{pf}}=\frac{24\left(k+1\right)\left[\alpha -2\right]}{{\left(k+3\right)}^2{\alpha }^2{t}^2}$$

(29)

$$Q=\frac{48\alpha \left(k+1\right)\left[3\alpha -8\right]\left[\alpha -2\right]}{{\left(k+3\right)}^2{\alpha }^2{t}^3}$$

(30)

We get positive energy densities if $2<\alpha <\raisebox{1ex}{$8$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$.

Here, we have transfer of energy from dust to radiation as the interaction term Q is negative for the same interval.

Phantom fluid-perfect fluid interaction $\left(w_1=\raisebox{1ex}{$-4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.,w_2\ne 0\right)$

Now, we consider the interaction of a phantom field with any other perfect fluid. We choose as a representative cosmic fluid of phantom matter the perfect fluid given by the equation of state $p=-\frac{4}{3}\rho$.

So, we put $w_1=\raisebox{1ex}{$-4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$, and ω₂ is a free parameter.

Therefore, Equations 15 to 17 reduce to

$${\rho }_{\mathit{ph}}=\frac{72\left(k+1\right)\left[2\left(1+w_2\right)-\alpha \right]}{{\left(k+3\right)}^2\left(3w_2+4\right){\alpha }^2{t}^2}$$

(31)

$${\rho }_{\mathit{pf}}=\frac{24\left(k+1\right)\left[2+3\alpha \right]}{{\left(k+3\right)}^2\left(3w_2+4\right){\alpha }^2{t}^2}$$

(32)

$$Q=\frac{48\left(k+1\right)\left[\alpha -2\left(1+w_2\right)\right]\left[2+3\alpha \right]}{{\left(k+3\right)}^2\left(3w_2+4\right){\alpha }^2{t}^3}\text{.}$$

(33)

If the following constraints are satisfied, then we get the positive energy density for phantom fluid and perfect fluid.

$$\frac{-2}{3}<\alpha <2\left(1+w_2\right)\left(w_2>0\right)$$

$$2\left(1+w_2\right)<\alpha <\frac{-2}{3}\left(\raisebox{1ex}{$-4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.<w_2<-1\right)\text{,}$$

i.e., when phantom fluid interacts with perfect fluid, the universe expands if w₂ > −1. The transfer of energy from dust to phantom matter takes place as the interacting term Q is positive.

As a specific example, we consider the interaction of this kind of phantom matter with a dust distribution. So now, we have $w_1=\raisebox{1ex}{$-4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.,w_2=0$ then

$${\rho }_{\mathit{ph}}=\frac{18\left(k+1\right)\left[2-\alpha \right]}{{\left(k+3\right)}^2{\alpha }^2{t}^2}$$

$${\rho }_2=\frac{6\left(k+1\right)\left[2+3\alpha \right]}{{\left(k+3\right)}^2{\alpha }^2{t}^2}$$

and

$$Q=\frac{24\left(k+1\right)\left[\alpha -2\right]\left[2+3\alpha \right]}{{\left(k+3\right)}^2{\alpha }^2{t}^3}\text{.}$$

To get simultaneous positive densities, we must have 0 < α < 2. The interacting term Q is positive for α < 2 which means that there is transfer of energy from dust to phantom matter.

The effective fluid interpretation

The effective fluid interpretation and the interaction of the two-fluid mixture are associated here. This is done by equating the sum of pressures p₁ and p₂ with an effective pressure p. We get

$$p=p_1+p_2$$

(34)

$$.p=w_1{\rho }_1+w_2{\rho }_2\text{.}$$

We have the equation of state

$$p=\gamma \rho =\gamma \left({\rho }_1+{\rho }_2\right)\text{,}$$

(35)

where γ is a constant effective state parameter.

It should be noted that the equation of the state of the associated effective fluid is not produced by physical particles and their interactions [9].

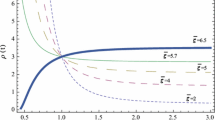
The effective state parameter γ is related to the parameter α by

$$\gamma =\frac{\left(k^2+2k+9\right)-4\alpha \left(k^2-k+6\right)}{12\alpha \left(k+1\right)}\text{.}$$

(36)

Hence, the effective state parameter γ → −1 as α → ± ∞ for all positive values of k.

Conclusions

In this paper, we have provided a detailed description for Kaluza-Klein power law scaling cosmological model dominated by two interacting perfect fluid components during the expansion. In this mathematical description, we have shown that for $2<\alpha <\raisebox{1ex}{$8$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ dust-radiation interacting cosmological model is dominated by dust or radiation throughout all evolution. When α < 2, energy transfer takes place from dust to the phantom fluid.

The energy densities of the two interacting perfect fluid components are proportional to ($\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$t^2$}\right.$), and the interaction term is proportional to ($\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$t^3$}\right.$) in all cases. We have also shown that the effective state parameter γ is a function of α by investigating the effective fluid interaction in the model.

Authors’ information

KSA is working as a professor and the head of the Department of Mathematics, SGB Amravati University, Amravati, India. MVD is working as an associate professor and the head of the Department of Mathematics, Bharatiya Mahavidyalaya, Amravati, India. SMB is working as an assistant professor in the Department of Mathematics, Sipna College of Engineering and Technology, Amravati, India.