Oblique propagating whistler mode wave with parallel AC electric field at magnetosphere of Uranus

Abstract

Oblique propagating electromagnetic whistler mode instability has been studied having a k vector at angle to ambient magnetic field for bi-Maxwellian distribution function with parallel AC electric field in the magnetosphere of Uranus. The dispersion relation and growth rate have been calculated for plasma parameters suited to the magnetosphere of Uranus by using the method of characteristic solutions and kinetic approach. The effect of AC electric field and temperature anisotropy for oblique propagating electromagnetic whistler mode instability has been reported and discussed in the ‘results and discussion section. The comparisons have been made with observations made by Voyager 2. It is found that whistler mode emissions observed at lower radial distances cannot reproduce in our calculations. The present studies should be helpful in making estimates on the scattering properties of whistler mode waves and, thus, contribute to a better understanding of auroral activity in the planetary atmosphere.

Introduction

The Voyager 2 encounter of Uranus in January 1986 provided the opportunity to observe yet another planetary magnetosphere and compare the plasma physical processes taking place there to those occurring in the magnetosphere of the Earth, Jupiter, and Saturn. In particular, in this paper, we survey the electromagnetic emissions observed at Uranus and apply our knowledge of similar emissions at the Earth to establish similarities and differences in the signatures. In this way, we can begin to understand how variations in the configuration of the Uranian magnetosphere might affect changes in the emissions. We can also use the known behavior of the electromagnetic waves as diagnostic tools to lend insight into such questions as the variation of electron density within the magnetosphere and possibly some information about the configuration of the magnetic field itself.

Voyager 2 carried a plasma wave receiver designed to measure the amplitude of the electric fields associated with waves in the frequency range of 10 to 56 Hz [1]. The instrument utilizes a single electric dipole antenna for a sensor. Since no wave magnetic field measurements were made, information concerning the mode of propagation of the detected waves must be deduced from the spectral and temporal characteristics of the emissions, the relationship of the frequency of the emission to characteristic frequencies of the plasma, and comparisons with similar emissions studied at the Earth. Fortunately, most of the waves observed in the magnetospheres of the outer planets thus far are easily associated with terrestrial analogs; hence, much progress can be made even without more sophisticated instrumental and additional sensors. Whistler mode emissions are also triggered by lightning-generated whistler Plasma waves such as lightning-generated whistler provide also important diagnostics tools, from which fundamental plasma parameters such as the electron density can be computed. As is well known, whistler mode waves are electromagnetic waves in a magnetized plasma that propagate through the magnetosphere at frequencies below the electron-cyclotron frequency and electron plasma frequency. Because magnetic field introduces anisotropy in the plasma, whistler waves tend to be guided along the ambient magnetic field [2, 3]. Recently, up-to-date views of plasma waves at each outer planets have been reviewed by Zarka [4].

An initial overview of plasma waves observed in the Uranian magnetoshere was given by Gurnett et al. [5, 6] and a general comparison with plasma waves observed at Jupiter and Saturn is included [7]. The observations of electromagnetic waves in the magnetosphere of Uranus have been studied, focusing primarily on the Bernstein or (n + 1/2) f_c emissions, where f_c is the electron cyclotron frequency f_c (Hz) = 28 |B| (nT). Bernstein waves were first observed at the Earth by Kennel et al. [8] and have been studied extensively both experimentally and theoretically by a large number of investigators [9–11] Survey of electrostatic waves at Jupiter and Saturn were given by Kurth et al. [12, 13]. In recent past, Kurth [14, 15] and Kurth and Gurnett [16] have provided for the first time, overviews of comparative study of plasma wave spectra at the outer planetary magnetosphere. They have also reported various modes of wave. Gurnett et al. [17] and Kurth [15] have reported that significant whistler mode emissions could exist near the magnetic equator in the intermediate radial distance ranges say 3 < R < 8 R_N as in the other planetary magnetospheres. The intensity of these emissions is quite weak from 10 to 30 μV/m. The variation of field intensity, magnetic field strength, and electron cyclotron frequency with radial distance has similar characteristics as occurred in Uranus.

An analysis of the Voyager 2 plasma science experiment electron measurements made during the Uranus encounter of a thermal (cold) plasma (K_BT is approximately 10 eV) and non-Maxwellian suprathermal (hot) plasma (K_BT is approximately 1 KeV) component [18] could not be explained in terms of an internal source provided by the Uranian satellites. The source of the thermal ion component could be either the Uranian ionosphere or the ‘Uranus’ hydrogen corona observed by the ultraviolet spectrometer on Voyager 2 [19] if some acceleration mechanism which heats the newly picked up ions from 1 to 10 eV is present. It has also been suggested by Brice and Lucas [20] that cold plasma plays an important role in controlling the wave particle interactions in the radiation belts within the plasma sphere because of the possibility of excitation of whistler mode instability by injection of cold plasma in the magnetosphere. The modifications in the whistler mode instability produced by cold plasma injection to an infinite uniform anisotropic distribution function plasma in the presence of a perpendicular AC electric field have been studied by [21] in the Uranus.

Pandey et al. [22] have studied oblique whistler mode instabilities for a generalized drifted distribution function in the presence of perpendicular AC electric field by the method of characteristic solution. The growth rate was evaluated for the plasma parameters suited to the magnetosphere of Uranus. It was found that only AC frequencies significantly affect the growth characteristic of the whistler waves, in addition to the external triggering AC field [23, 24] studied, by taking into account the finite size of the cold plasma enhancement region, the temporal evolution of whistler growth in a time-dependent cold plasma injection experiment and made semi-quantitative estimates of the magnitude and duration of enhancement of very low frequency (VLF) noise and electron precipitation effects. The results of these studies have shown that the injected cold plasma modifies the propagation characteristics of whistlers, and there is a possibility to have stabilization through finite electron density.

A theoretical study of relativistic whistler mode with perpendicular AC electric field has been studied for the generalized distribution function at the Uranian bow shock by Pandey et al. [25]. The effect of cold plasma injection and temporal evolution of whistler mode instability have been studied in the presence of perpendicular AC electric field for the generalized distribution function in the magnetosphere of Uranus [21, 24, 25].

In this paper, oblique propagating electromagnetic whistler mode wave has been studied having a k vector at an angle to ambient magnetic field for bi-Maxwellian distribution function with parallel AC electric field. The dispersion relation and growth rate have been calculated for plasma parameters suited to the magnetosphere of Uranus.

Dispersion relation

The plasma under consideration is of infinite extent embedded with a uniform magnetic field ${\mathbf{B}}_0{\widehat{e}}_z$ and an electric field $E_{0}sin\nu t{\widehat{e}}_z$ and whose distribution function f(r,v,t) is governed by the Boltzmann equation. In the collisionless case, the self-consistent Vlasov-Maxwell equations to be used are

$$\frac{\partial f_s}{\partial t}+v.\frac{\partial f_s}{\partial r}+\frac{e_s}{m_s}\left[E+\frac{v\times \mathbf{B}}{c}\right]\frac{\partial f_s}{\partial v}=0$$

(1)

and

$$\begin{array}{l}\nabla .\mathbf{E}={\displaystyle \sum _{s}4\pi e_s{\displaystyle \int d^{3}v{f}_s}}\hfill \\ \nabla \times \mathbf{B}={\displaystyle \sum _s\frac{4\text{π}{e}_s}{c}}{\displaystyle \int d^{3}vv{f}_s+\frac{1\partial \mathbf{E}}{c\partial t}}\hfill \\ \nabla .\mathbf{B}=0\hfill \\ \nabla \times \mathbf{E}=-\frac{1}{c}\frac{\partial B}{\partial t}\hfill \end{array}$$

(2)

Here, the subscript s denotes the particle species, and i, e, for ions and electrons, respectively. The electric field E₀ and the magnetic field B₀ represent the resultants of the external AC field and magnetic field together with the self-consistent characteristic oscillations of E and B, and all other symbols have their usual meanings.

In this analysis, AC frequency has been assumed much smaller than the plasma and gyrofrequency and the collision frequency negligibly small and independent of particle velocity, where as the thermal velocity of the background electrons are much larger than the induced velocity due to AC field. The directed motion of the electrons due to AC field along the magnetic field may lead to the appearance of an electromagnetic field whose effect is neglected.

In order to find the dispersion relation, first, the motion of the particles (trajectories) in the given fields are computed, and the perturbed distribution function, which depends on the integrals of motion, is then determined following a method similar to that adopted by Harris [26]. Following the methods and techniques of Misra and Pandey [27] and Misra and Haile [28], the unperturbed particle trajectories are obtained as

$$x_0=x+\frac{v_y}{{\omega }_{\text{cs}}}-\frac{1}{{\omega }_{\text{cs}}}\left(v_{x}sin{\omega }_{\text{cs}}t\text{'}+v_{y}cos{\omega }_{\text{cs}}t\text{'}\right)$$

$$y_0=y+\frac{v_x}{{\omega }_{\text{cs}}}-\frac{1}{{\omega }_{\text{cs}}}\left(v_{x}cos{\omega }_{\text{cs}}t\text{'}+v_{y}sin{\omega }_{\text{cs}}t\text{'}\right)$$

$$z_0=z-v_{z}t\text{'}+\frac{{\Gamma }_z}{{\upsilon }^2}sin\upsilon t\text{'}-\frac{{\Gamma }_z}{\upsilon }t\text{'}$$

(3)

and the velocities as

$$v_{x_0}=v_{x}cos{\omega }_{\text{cs}}t\text{'}-v_{y}sin{\omega }_{\text{cs}}t\text{'}$$

$$v_{y_0}=v_{x}sin{\omega }_{\text{cs}}t\text{'}-v_{y}cos{\omega }_{\text{cs}}t\text{'}$$

$$v_{z_0}=v_z+\frac{{\Gamma }_z}{\upsilon }\left(cos\upsilon t^{\prime }-1\right)$$

(4)

where ω_cs = e _s B₀/m _s is the cyclotron frequency and Γ _z  = e _s E₀/m _s . From Maxwell's curl E equation, for the perturbed quantities, one gets the following:

$${\mathbf{B}}_1=\frac{c}{\omega }\left(\mathbf{k}\times {\mathbf{E}}_1\right)$$

$$S\left(\mathbf{r},\mathbf{v},t\right)=\frac{-e_s}{m_s\omega }{e}^{i\left(k.r-\omega t\right)}\left[\left(\omega -\mathbf{k}.\mathbf{v}\right){\mathbf{E}}_{\mathbf{1}}+\left(v.{\mathbf{E}}_{\mathbf{1}}\right)\mathbf{k}\right].\frac{\partial f_0}{\partial v}\text{,}$$

(5)

where E₁ = E₁e^{i(k. r − ωt ')} has been used.

Inverting Equation 5, one can get the following:

$$S\left({\mathbf{r}}_{\mathbf{0}},{\mathbf{v}}_{\mathbf{0}},t-t\text{'}\right)=\frac{e_s}{m_s\omega }{e}^{i\left(\mathbf{k}.\mathbf{r}(\mathbf{r},\mathbf{v},t\text{'}\right)-\omega \left(t-t\text{'}\right)}\times \left[\left(\omega -\mathbf{k}.{\mathbf{v}}_{\mathbf{0}}\right){\mathbf{E}}_{\mathbf{1}}+\left({\mathbf{v}}_{\mathbf{0}}.{\mathbf{E}}_{\mathbf{1}}\right)\mathbf{k}\right].\frac{\partial f_0}{\partial v}\text{,}$$

(6)

where Bessel identity $e^{i\lambda sin\alpha }={\displaystyle \sum _{k=-\infty }^{\infty }{j}_k\left(\lambda \right)e^{\mathit{ik\alpha }}}$ has been used.

The result of Equation 6 is used to obtain the first order perturbed distribution function f₁(r,v,t).

$$f_1\left(r,\mathbf{v},t\right)=\frac{-ie}{m\omega }{\displaystyle \sum _{m,n,p}\frac{J_m\left({\lambda }_1\right)J_p\left({\lambda }_2\right)e^{i\left(m-n\right)\alpha }}{\left(\omega -k_{\left|\right|}{v}_{\left|\right|}-\frac{k_{\left|\right|}{\Gamma }_{\text{z}}}{\upsilon }-n{\omega }_c+p\upsilon \right)}}$$

$$\left[U^{*}{\mathbf{E}}_{1x}\frac{\text{n}}{{\text{λ}}_1}{\text{J}}_n\left({\text{λ}}_1\right)-i{U}^{*}{\mathbf{E}}_{1y}J{\text{'}}_n\left({\text{λ}}_1\right)+W^{*}{\mathbf{E}}_{1z}{J}_n\left({\lambda }_1\right)\right]\text{,}$$

(7)

where α is the angle between the vectors k and B_0.

$$\begin{array}{l}{U}^{*}=\frac{1}{v_{\perp }}\frac{\partial f_0}{\partial v_{\perp }}\left[\left(\omega -k_{||}{v}_{||}\right)v_{\perp }+\frac{k_{||}{\Gamma }_z}{\upsilon }{v}_{||}\left(1-\frac{p}{{\lambda }_2}\right)\right]\hfill \\ +k_{||}{v}_{\perp }\frac{\partial f_0}{\partial v_{||}}{W}^{*}=\frac{1}{v_{\perp }}\frac{\partial f_0}{\partial v_{\perp }}\left[v_{||}n{\omega }_{\text{c}}-\frac{{\Gamma }_z}{\upsilon }n{\omega }_{\text{c}}\left(1-\frac{p}{{\lambda }_2}\right)\right]\end{array}$$

$${\lambda }_1=\frac{k_{\perp }{v}_{\perp }}{\omega },{\lambda }_2=\frac{k_{||}{\Gamma }_z}{{\upsilon }^2}\text{and}J{\text{'}}_n\left({\lambda }_1\right)=\frac{d{J}_n\left({\lambda }_1\right)}{d{\lambda }_1}\text{.}$$

(8)

The current density is calculated using the relation

$$J={\displaystyle \sum _s{e}_s{\displaystyle \int d^{3}v{f}_1\left(v\right)v}}$$

(9)

or in terms of the conductivity ||σ(k,ω)|| by

$$J=‖\sigma \left(\mathbf{k},\omega \right)‖.{\mathbf{E}}_1\text{.}$$

(10)

Using Equations 7, 9, and 10, the conductivity is written in matrix form as

$$\sigma \left(k,\omega \right)=-i{\displaystyle \sum _{np}\frac{e^2}{m\omega }{J}_p\left({\lambda }_2\right)\frac{S_{\mathit{ij}}}{\omega -k_{\left|\right|}{v}_{\left|\right|}-\frac{k_{\left|\right|}{\Gamma }_z}{\upsilon }+p\upsilon -n{\omega }_{\text{c}}}}\text{,}$$

(11)

where

$$S_{\mathit{ij}}=\left[\begin{array}{ccc}\hfill v_{\perp }{U}^{*}{\left(\frac{n}{{\lambda }_1}{J}_n\right)}^2\hfill & \hfill i{v}_{\perp }{U}^{*}\frac{n}{{\lambda }_1}{J}_{n}J{\text{'}}_n\hfill & \hfill v_{\perp }{W}^{*}\frac{n}{{\lambda }_1}{J}_n^2\hfill \\ \hfill i{v}_{\perp }{U}^{*}\frac{n}{{\lambda }_1}{J}_{n}J{\text{'}}_n\hfill & \hfill v_{\perp }{U}^{*}J{\text{'}}_n^2\hfill & \hfill i{v}_{\perp }{W}^{*}{J}_{n}J{\text{'}}_n\hfill \\ \hfill v_{\left|\right|}{U}^{*}\frac{n}{{\lambda }_1}{J}_n^2\hfill & \hfill -i{v}_{\left|\right|}{U}^{*}{J}_{n}J{\text{'}}_n\hfill & \hfill v_{\left|\right|}{W}^{*}{J}_n^2\hfill \end{array}\right]\text{.}$$

Now, from Maxwell's curl equations, the dielectric tensor is given as

$${\epsilon }_{\mathit{ij}}=1+{\displaystyle \sum _{np}\frac{4\text{π}{e}^2}{m{\omega }^2}{J}_p\left({\lambda }_2\right)\frac{S_{\mathit{ij}}{d}^{3}v}{\left(\omega -k_{||}{v}_{||}-\frac{k_{||}{\Gamma }_z}{\upsilon }+p\upsilon -n{\omega }_{\text{c}}\right)}}\text{.}$$

(12)

The generalized dielectric tensor may be written as

$$\left[\begin{array}{ccc}{N}^2{cos}^2{\theta }_1+{\epsilon }_{11}\hfill & {\epsilon }_{12}& N^{2}cos{\theta }_{1}sin{\theta }_1+{\epsilon }_{13}\\ \hfill {\epsilon }_{21}\hfill & N^2{\epsilon }_{22}& {\epsilon }_{23}\\ \hfill N^{2}cos{\theta }_{1}sin{\theta }_1+{\epsilon }_{31}\hfill & {\epsilon }_{33}& N^2{sin}^2{\theta }_1+{\epsilon }_{33}\end{array}\right]\text{.}$$

If we remove the contribution of AC electric field above, the dielectric tensor is similar to Sazhin [29]. After using the limits k_⊥ = ksinθ₁ → 0 and k_‖ = kcosθ₁, the generalized dielectric tensor becomes a simplified tensor and the dispersion relation is reduced as

$$\left[\begin{array}{ccc}\hfill -N^2+{\epsilon }_{11}\hfill & {\epsilon }_{12}& 0\\ \hfill -{\epsilon }_{21}\hfill & -N^2+{\epsilon }_{22}& 0\\ \hfill 0\hfill & 0& {\epsilon }_{33}\end{array}\right]\text{.}$$

This is rewritten in a more convenient form. Now, for whistler wave

$$-N^4-2{\epsilon }_{11}{N}^2+{\epsilon }_{11}^2+{\epsilon }_{12}^2=0$$

(13)

for electrostatic wave, ε₃₃ = 0.

Neglecting the higher power of N, the resulting relation becomes as follows:

$${\epsilon }_{11}\pm {\epsilon }_{12}=N^2$$

(14)

$$f_0=\frac{n_0}{{\text{π}}^{\frac{3}{2}}{\alpha }_{\perp }^2{\alpha }_{||}}\text{exp}\left[-{\left(\frac{v_{\perp }}{{\alpha }_{\perp }}\right)}^2-{\left(\frac{v_{||}}{{\alpha }_{||}}\right)}^2\right]\text{,}$$

(15)

where the parallel and perpendicular thermal velocities are

$${\alpha }_{\perp }={\left(\frac{K_{\text{B}}{T}_{\perp }}{m}\right)}^{\frac{1}{2}},{\alpha }_{\left|\right|}={\left(\frac{K_B{T}_{\left|\right|}}{m}\right)}^{\frac{1}{2}},A_{\text{T}}=\frac{{\alpha }_{\perp }^2}{{\alpha }_{||}^2}-1\text{.}$$

Using Equations 14 and 15 and doing lengthy velocity integrations, now the dispersion relation of oblique whistler wave is obtained from above for n = 1, p = 1 and J_p = 1, J_q = 1:

$$\begin{array}{l}D\left(k,\omega \right)=1\\ +\frac{{\omega }_p^2}{{\omega }^2}\left\{\frac{\omega +{\omega }^{*}}{k_{\left|\right|}{\alpha }_{\left|\right|}}Z\left(\xi \right)+A_T\left(1+\xi Z\left(\xi \right)\right)\right\}\text{,}\end{array}$$

(16)

where Z(ξ) is the plasma dispersion function

$$Z\left(\xi \right)=i\sqrt{\text{π}}\text{exp}{\left(\xi \right)}^2-\frac{1}{\xi }\left(1+\frac{1}{2{\xi }^2}\right)$$

(17)

$$\xi =\frac{\omega -n{\omega }_{\text{c}}+p\upsilon -\frac{k_{\left|\right|}{\Gamma }_z}{\upsilon }}{k_{\left|\right|}{\alpha }_{||}}\text{.}$$

Now, using the asymptotic expansion of plasma dispersion function, the dispersion relation may be separated in real and imaginary form of dispersion relation for limit k²c² / ω² > > 1:

$$D_I=\left[\frac{\omega +{\omega }^{*}}{k_{\left|\right|}{\alpha }_{\left|\right|}}\xi +A_T\xi \right]\sqrt{\pi }exp\left(-{\left(\xi \right)}^2\right)$$

(18)

$$D_R=-\frac{k^2{c}^2}{{\omega }^2}+\left\{\frac{\omega +{\omega }^{*}}{k_{\left|\right|}{\alpha }_{\left|\right|}}\left(-\frac{1}{\xi }\left(1+\frac{1}{2{\xi }^2}\right)+A_T\left(-\left(1+\frac{1}{2{\xi }^2}\right)\right)\right)\right\}\text{.}$$

(19)

Using the standard definition of growth rate

$${\gamma /{\omega }_{\text{c}}=\frac{-\text{Im}D\left(k,\omega \right)}{{\omega }_{\text{c}}\frac{\partial \text{R}D\left(k,\omega \right)}{\partial \omega }}|}_{\omega ={\omega }_{\text{r}}}$$

(20)

after using Equations 17 to 20, the required growth rate and real frequency dimensionless form is written as follows:

$$\gamma /{\omega }_c=\frac{\frac{\sqrt{\pi }}{K_1}\left(A_T-\frac{X_3+X_4}{K_3}\right)K_3^3{\left(-\left(\frac{K_3}{K_1}\right)\right)}^2}{1+\frac{K_1^2}{2K_3^2}-\frac{K_1^2}{K_3}\left(A_T-\frac{X_3+X_4}{K_3}\right)}\text{,}$$

(21)

where

$$\begin{array}{l}{X}_3=\frac{{\omega }_r}{{\omega }_c}=\frac{K_1^2}{\beta }\left[1+X_4+\frac{A_T\beta }{1+X_4}\right]-X_4\hfill \\ X_4=\frac{{\omega }^{*}}{{\omega }_{\text{c}}},{\omega }^{*}=p\upsilon -\frac{k_{||}{\Gamma }_z-k_{||}{v}_{\text{d}}}{\upsilon }\hfill \\ \bar{k}=\frac{k_{\left|\right|}{\alpha }_{||}}{{\omega }_{\text{c}}},K_3=1-X_3+X_4\hfill \end{array}$$

(22)

$$\beta =\frac{K_{\text{B}}{T}_{||}{\mu }_0{n}_0}{B_0^2},K_1=\bar{k}cos{\theta }_1\text{.}$$

Results and discussion

Numerical calculations for the growth rate of the whistler instabilities with plasma parameters suited to the Uranian magnetosphere [21, 24, 30]B₀ = 5 × 10⁻¹⁰ T, K_BT_|| = 1 KeV, n₀ = 5 × 10⁴ m⁻³, A_T = .25 and external field parameters E₀ from 10 MV/m to 30 mV/m with frequency υ from 400 to 800 Hz have been carried out. The growth rate of whistler waves in the presence of a parallel AC electric field have been displayed in a series of curves from (Figures 12345).

Figure 1

Variation of growth rate with respect to$\bar{\mathbf{k}}$for various values of AC field frequency. At other fixed plasma parameters.

Figure 2

Variation of growth rate with respect to$\bar{\mathbf{k}}$for various values of temperature anisotropy. At other fixed plasma parameters.

Figure 3

Variation of growth rate with respect to$\bar{\mathbf{k}}$for various values of magnitude of AC field. At other fixed plasma parameters.

Figure 4

Variation of growth rate with respect to$\bar{\mathbf{k}}$for various values of the magnitude of AC field. At other fixed plasma parameters.

Figure 5

Variation of growth rate with respect to$\bar{\mathbf{k}}$for various values of angle of propagation. At other fixed plasma parameters.

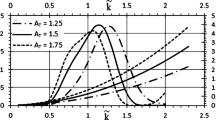
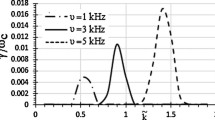
Figure 1 shows the dependence of growth rate of whistler waves with respect to a dimensionless parameter ($\stackrel{}{k}=k_{\left|\right|}{\alpha }_{\left|\right|}/{\omega }_{\text{c}}$) for various values of AC field frequency υ. The introduction of the AC signal for fixed values of other plasma parameters increases the magnitude of the growth rate while increasing the possible range of wave propagation. The contribution of AC frequency reduces the upper limit of wave number $\bar{k}$ and normalized real frequency X₃ = ω_r / ω_ci and increases the growth rate. The AC frequency appears only through modification of resonant instability. This shows that the presence of a minimum value of parallel AC field frequency is enough to trigger the whistler emission [27, 28]. This result is different from the magnetosphere; it is only due to the low values of the Earth's magnetic field. In Figure 2, the dependence of growth rate on various values of thermal anisotropy has been plotted. It is seen that for other fixed plasma parameters, an increase in thermal anisotropy increases the growth rate. For a fixed value of temperature anisotropy increases the growth rate initially increases rapidly, reaches a maxima and then levels off with a small decrease from the maxima. Temperature anisotropy is the prime source of instability. Thermal electrons in bi-Maxwellian distribution are supposed to modify the intensity and frequency of electron plasma [3]. Figure 3 shows the variation of growth rate with $\bar{k}$ for different values of the number density n₀. The increase in the number density for other fixed plasma parameters increases the growth, and the maxima shifted toward the higher values of $\bar{k}$. The effect of the number density is an important role because it changes the plasma frequency, and modification has been made in the value of β. It means that the value of β is lower in comparison with the magnetosphere.

Figure 4 shows the dependence of growth rate with $\bar{k}$ on various values of external electric field. Increase of the magnitude of AC field increases the growth rate and widens the bandwidth significantly. Figure 5 shows the variation of growth rate with $\bar{k}$ for various values of angle of propagation θ₁ at other fixed plasma parameters. In this case, increasing the angle of propagation increases the growth rate. After 40°, the electrostatic conditions start dominating and non-resonant instability starts contributing or even change in polarization may take place making it as a right-handed mode.

Conclusion

The results are compared with the magnetospheric study which has been done by Misra and Pandey [27] and Misra and Haile [28]. The perpendicular electric field is modifying the perpendicular velocity and contributing to the energy exchange significantly to the emission of VLF signals and can explain the low frequency side of the spectrum. In this case, only AC frequency is effective for growth rate, but in the case of parallel AC electric field, the Doppler shift in frequency is affected by both magnitude and AC frequency. In the case of Uranus, the growth rate is affected by AC frequency as well as the magnitude of parallel AC electric field. However, in the case of Uranus, low value of AC frequency is enough to trigger the whistler mode instability. The growth rate is also affected by the magnitude of AC electric field due to the low value of gyrofrequency in Uranus with respect to the magnetosphere. In Uranus, the density of plasma particle is less than the magnetosphere. Hence, the low value of β is enough to the generation and propagation of whistler mode emission. The effect of temperature anisotropy is the same for Uranus and the magnetosphere. From all figures, it is clear that our results are very much in order of the observed normalized frequency range of whistler emission at Uranus as reported by Coroniti et al. [31]. It is clear that whistler mode propagates even at the low magnitude of magnetic field and other Uranus condition. In the case of Misra and Haile [28], the propagation of wave along the direction of magnetic field is considered, but in this paper, oblique incidence. The magnitude of growth rate has been changed, and band increases with respect to wave number.