Abstract
Nowadays, customer expectations are increasing and organizations are prone to operate in an uncertain environment. Under this uncertain environment, the ultimate success of the firm depends on its ability to integrate business processes among supply chain partners. Supply chain management emphasizes cross-functional links to improve the competitive strategy of organizations. Now, companies are moving from decoupled decision processes towards more integrated design and control of their components to achieve the strategic fit. In this paper, a new approach is developed to design a multi-echelon, multi-facility, and multi-product supply chain in fuzzy environment. In fuzzy environment, mixed integer programming problem is formulated through fuzzy goal programming in strategic level with supply chain cost and volume flexibility as fuzzy goals. These fuzzy goals are aggregated using minimum operator. In tactical level, continuous review policy for controlling raw material inventories in supplier echelon and controlling finished product inventories in plant as well as distribution center echelon is considered as fuzzy goals. A non-linear programming model is formulated through fuzzy goal programming using minimum operator in the tactical level. The proposed approach is illustrated with a numerical example.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
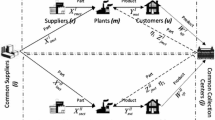
Globalization itself is a great change in business environment which causes great trend towards global trade and competition. It became important for enterprises to develop long-term strategic relations between suppliers and customers. Also, due to the introduction of new products with shorter life cycles and the heightened expectations of customers, it became a must for business organizations to focus on their supply chains. The supply chain, which is also referred to as the network of suppliers, manufacturing centers, warehouses, distribution centers, and customers as well as logistic information systems connected by an organization's suppliers and customers of its customers. Basing on the organization's competitive strategy, efficient or responsive supply chains are modeled by integrating business plans at strategic and tactical levels.
Cohen and Lee (1988) developed a model of material requirement policy for every shop in a production system using cost-based stochastic sub-models, namely material control sub-model, production sub-model, and distribution sub-model, to predict the performance of alternative manufacturing strategies. Robinson et al. (1993) designed an integrated distribution system for a two-echelon, uncapacitated distribution location problem as a mixed integer programming problem and illustrated with a case study. Pyke and Cohen (1994) developed a supply chain model by considering multiple products, with independent demand and expedited batches, and optimized the total cost of supply chain subjected to the service levels for all products. Petrovic and Roy (1998) developed a simulation model of supply chain in an uncertain environment, with customer demand and supply of raw materials as vague, which are represented with fuzzy sets. Beamon (1998) presented an overview and evaluation of the performance measures used in supply chain models.
Sabri and Beamon (2000) developed a supply chain model that facilitates simultaneous strategic and operational planning using an interactive method. Vorst (2000) formulated supply chains for agriculture products through linear programming approach. Chen and Tzeng (2000) adopted fuzzy multi-objective approach in order to reduce the computational complexity of the integrated supply chain model. Tsiakis et al. (2001) developed a mixed integer linear programming model for the design of multi-product, multi-echelon supply chain networks consisting of manufacturing sites, warehouses, distribution centers, and customer zones. Yu et al. (2003) proposed a strategic production-distribution mixed integer programming model for supply chain design by incorporating logical constraints to represent the BOM. Lee et al. (2002) presented a hybrid methodology that combines the analytic and simulation models for an integrated production-distribution model in supply chain. Li (2002) proposed a method of building a supply chain management system that determines production plan purchasing plan, inventory plan, and distribution plan by minimizing the total cost. Chen et al. (2003) formulated a multi-objective mixed integer non-linear programming problem and adopted a two-phase fuzzy decision-making method to solve the supply chain model involving manufacturing plants, distribution centers, and retailers. Eskigun et al. (2005) modeled a supply chain network design and proposed Lagrangian heuristic method to obtain strategic decision of the model. Amiri (2006) developed a mixed integer programming model and proposed a heuristic procedure for a supply chain network design. The paper addresses network design problem in a supply chain system that involves locating production plants and distribution warehouses and determining the best strategy for distributing the product from plants to warehouses and from the warehouses to the customers. Liang (2008) developed a fuzzy multi-objective linear programming model with piecewise linear membership function to solve integrated multi-product and multi-time-period production-distribution planning decision problems with fuzzy objectives.
Farahani and Elahipanah (2008) developed a mixed integer linear programming model with two objective functions, namely minimizing costs and minimizing the sum of backorders and surpluses of products. Peidro et al. (2009) proposed a fuzzy mixed integer linear programming model where data are ill known and modeled by triangular fuzzy numbers for supply chain planning under supply, process, and demand uncertainties. Troncoso et al. (2011) adopted a mixed integer programming method for integrated strategy and compared this strategy with decoupling strategy. Narayana Rao and Venkatasubbaiah (2011) developed an integrated procurement, production, and distribution supply chain model in fuzzy environment. Bouzembrak et al. (2011) developed a green supply chain network design problem with environmental concerns. In the study, the authors considered warehouse and distribution center locations, building technology selection, and processing-distribution planning as the strategic decisions in the model.
Supply chain models developed, except for a few ones, ignored vagueness, but in the real world, supply chains operate in a vague or uncertain environment. In this context, uncertainty may be related to the specification of objectives, constraints, or variables. In this paper, a supply chain model is developed through simultaneous strategic and tactical planning in fuzzy environment.
In fuzzy environment, a fuzzy goal programming method is adopted to incorporate the inherent vagueness in supply chain cost and volume flexibility at strategic level. In tactical level also, a fuzzy goal programming method is developed to incorporate vagueness present in three objectives, viz. cost of controlling raw material inventory at the supplier echelon and cost of controlling products at plant and distribution center echelons.
A numerical illustration with four echelons, to produce and distribute four types of products using four types of raw materials from five suppliers, is presented. The mixed integer programming problem is formulated at strategic level and non-liner programming problem is formulated at tactical level, and both are solved using LINGO 8.0 optimization solver.
Strategic level
The strategic level considers the design of an integrated procurement, production, and distribution supply chain network. The objective functions (supply chain cost and volume flexibility) and the constraints considered in the model are discussed below.
Supply chain cost
The supply chain cost (SCC) is a mixed integer linear function. This linear objective function contains various components. These components are raw material purchase price, transportation cost of raw materials shipped from suppliers to plants, fixed cost associated plant and distribution center operations, transportation cost of products shipped from plants to distribution centers, and transportation cost of products from distribution centers to customer zones:
Volume flexibility
It is the linear objective function that comprises plant volume flexibility VF and distribution volume flexibility. Plant volume flexibility is measured as the difference between plant capacity and capacity utilization. Distribution volume flexibility is measured as the difference between the available throughput and demand requirements. The following function represents volume flexibility of the supply chain:
The various constraints governing the supply chain model are shown below.
-
Raw material availability
-
Raw material requirement at the plants should be within the limits of raw material availability at the supplier.
(2.3)
-
Plant production capacity
-
Total production quantities at each plant should not exceed the plant capacity.
(2.4)
-
Raw material supply
-
Shipping of raw materials from the ranked suppliers to the plants should be sufficient to meet the production requirement of the products at the plants.
(2.5)
-
Minimum and maximum bounds on production quantity
(2.6)
-
Minimum and maximum bounds on throughput capacities of distribution centers
(2.7)
-
Assignment of each customer zone to exactly one distribution center
(2.8)
-
Production requirement
-
Quantity of the products available at the plant ensures the shipping quantity from the plant.
(2.9)
-
Shipping quantity of products
-
Total shipments to customer zones should be equal to the demand at the customer zones.
(2.10)
-
Demand requirement at each distribution center
-
Shipping quantity of the product should satisfy the demand of the product at the distribution center.
(2.11)
-
Non-negativity constraints
-
Ensure the following variables to be non-negative.
(2.12)
-
Binary variable restriction
-
Ensure the following variables to be binary.
(2.13)
Tactical level
In the tactical level, a non-linear programming model is formulated at supplier, plant and distribution center echelons to minimize the cost of controlling raw materials and finished products at plant and distribution center echelons. Continuous review inventory policy is assumed at the echelons. The models at these echelons are discussed below.
Supplier echelon model
In the supplier echelon, the total cost of controlling raw material n required at plant k under continuous review policy is given by the following equation:
where TCS nk total cost of controlling raw material n required at plant k, MDI nk mean demand of raw material n required at plant k, ML1 nk expected demand of raw material n during lead time at plant k, LI1 nk = I N ((u s ) nk ), loss integral representing the expected number of units out of stock during an order cycle of raw material n at plant k, and (u s ) nk standardized variable at the supplier echelon.
The reorder point of raw material n required at plant k can be determined from the following relationship:
The expected demand over lead time is determined from the following relationship:
The average total lead time of raw material n at plant k is calculated as the sum of the raw material lead time and delay time considering all the suppliers, as shown below (Sabri and Beamon 2000):
where N is the number of vendors.
The following relation gives the lead-time demand variance and standard deviation since production demand (X ij ) is fixed:
The following relation gives variance of total lead time of raw material n at plant k:
Customer service level of raw material n at plant k is given by the following relation (Ballou 2004):
Determine the optimal lot size by minimizing the total cost of controlling raw material n required at plant k subjected to the given customer service level of raw material n at plant k.
Plant echelon model
In the plant echelon, the cost function to be minimized consists of setup costs, processing costs, and work-in-process carrying costs and cost related to the finished product stockpile. The finished product stockpile cost comprises stockpile holding cost, transportation holding cost, and backorder cost. The optimum order quantity, reorder point, and service level of product i at plant k are obtained by optimizing the cost function. The following equations represent the total cost of production and cost of controlling finished product stockpile, respectively:
where TC ik total cost of controlling finished product i at plant k, TCP ik cost of production of product i at plant k, TCF ik total cost of controlling finished product stockpile, MD2 ik mean demand of product i at plant k,ML2 ik expected demand of product i during leadtime at plant k,LI2 ik = I N (u p ) ik , loss integral representing the expected number of units out of stock during an order cycle of product i at plant k, and (u p ) ik standardized variable of product i at plant echelon.
Reorder point is determined from the following relationship:
Expected demand of product i over production lead time at plant k is determined from the following relationship:
Determination of various parameters is given by the following relations (Sabri and Beamon 2000):
The total production lead time of product i at plant k is given as the sum of setup time and waiting time at the work stations, processing times, and material delay times:
The material delay time can be determined from the following relationship:
The following relation gives variance of the production lead time:
Variance of the material delay time is determined from the following relation:
Variance and standard deviation of demand during lead time are determined from the following equations:
Customer service level of product i at plant k is given by the following relation (Ballou 2004):
The expected replenishment lead time for product i from plant k to distribution center l is given by the following relation:
Variance of lead time for product i from plant k to distribution center l is calculated from the following relation:
Determine the optimal lot size (Q 2 ik ) by minimizing total cost of production and cost of controlling finished product stockpile subjected to customer service level of product.
Distribution center echelon model
In the distribution echelon, the total cost of distribution of product i at the distribution center (DC)l under dynamic continuous review policy is given by the following equation:
where TCD il total cost of controlling finished product i at distribution center l,MD3 il mean demand of product i at distribution center l,ML3 il expected demand of product i during lead time at distribution center l, LI3 il = I N ((u d ) il ) loss integral representing the expected number of units out of stock during an order cycle of product i at distribution center l, and (u d ) il standardized variable at distribution center echelon.
The reorder point of product i at distribution center l is determined from the following relationship:
Find out the expected and variance of transportation lead time for product i to distribution center l from the following relation (Sabri and Beamon 2000):
Determine lead time demand variance and standard deviation of product i at distribution center l from the following relation:
Customer service level of product i at distribution center l is calculated from the following relation (Ballou 2004):
Determine the optimum order quantity (Q 3 il ) by minimizing total cost of controlling finished product i at distribution center l subjected to the given customer service level of product i at distribution center l.
Problem formulation in fuzzy environment
In this section, formulation of fuzzy goal programming with minimum operator in strategic and tactical level planning is presented.
Fuzzy goal programming
Fuzzy set theory in goal programming (GP) was first considered by Narasimhan (1982). Ramik (2000), Mohamed (2000), and Abd El-Wahed and Abo-Sinna (2001) have investigated various aspects of decision-making problems using FGP theoretically. In fuzzy goal programming, membership functions are formulated for the objectives. After considering the aspiration levels of the objectives and the nature of the objectives, ‘approximately less than or equal to,’ and ‘approximately greater than or equal to,’ the membership functions can be developed for each objective as follows:
-
For approximately less than or equal to:
(4.1)
-
For approximately greater than or equal to:
(4.2)
Fuzzy goal programming with minimum operator
Using the approach of Bellman and Zadeh (1970), the feasible fuzzy solution set is obtained by the intersection of all membership functions representing the fuzzy goals. This solution set is then characterized by its membership μ F (x) which is,
Then, the optimum decision can be determined to be the maximum degree of membership for the fuzzy decision:
By introducing the auxiliary variable λ, which is the overall satisfactory level of compromise, the following conventional mathematical programming problem can be formulated:
Strategic level
These objective functions (supply chain cost and volume flexibility) and constraints are discussed in the ‘Methodology’ section. The supply chain model that is developed at strategic level with uncertainty in the objectives is taken care by specifying aspiration levels for the objectives. The decision-maker is able to specify the aspiration levels for each objective. Linear membership functions are defined for each objective depending on their nature. The nature may be approximately less than or equal or greater than or equal to the specified value. Considering the nature of the fuzzy parameters, linear membership functions of either non-increasing or non-decreasing are formulated. Membership function of total supply chain cost is assumed as non-increasing, and membership function of volume flexibility is assumed as non-decreasing.
Formulation of the membership functions of the fuzzy variables are shown below:where C 1min and C 2min are the minimum aspiration levels of SCC and VF and C 1max and C 2max are the maximum aspiration levels of SCC and VF.
-
1.
Membership function for supply chain cost (μ SCC)
(4.6)
-
2.
Membership function for volume flexibility (μ VF)
(4.7)
According to Zimmermann (1978), Zadeh's minimum operator is used in aggregating the objectives to determine the optimal solution at the strategic level. The following are the equations in a fuzzy goal programming approach at the strategic level with minimum operator:
and also subject to the crisp constraints shown in (2.3) to (2.13), where
Tactical level
In tactical level, the total cost of controlling raw materials, cost of controlling finished products at the plant echelon, and cost of controlling finished products at the distribution center echelon are assumed as fuzzy goals. Service levels at the respective echelons are assumed as constraints. Formulation of the membership functions of the fuzzy goals are shown below:where C 3min, C 4min, and C 5min are the minimum aspiration levels of TCS, TCP, and TCD and C 3max, C 4max, and C 5max are the maximum aspiration levels of TCS, TCP, and TCD.
-
1.
Membership function of the fuzzy goal (cost of controlling raw materials)
(4.9)
-
2.
Membership function of the fuzzy goal (cost of controlling products at plant echelon)
(4.10)
-
3.
Membership function of the fuzzy goal (cost of controlling products at distribution center echelon)
(4.11)
The following equations are obtained in fuzzy goal programming approach at tactical level with minimum operator:
and the following service level constraints:
Methodology
A supply chain model in fuzzy environment is formulated, and the decision variables at strategic and tactical levels are determined by combining strategic level and tactical level models through the following iterative procedure:
-
1.
Stage 1: Solve the supply chain modeling problem in crisp environment and obtain a payoff table.
-
(a)
Step 1: Formulate the mixed integer linear programming problem at strategic level with total supply chain cost as objective function and equations given in (2.3), (2.4), (2.5),… (2.13) as constraints and solve to determine supply chain cost and the volume flexibility.
-
(a)
Step 2: Formulate tactical level models discussed in the ‘Tactical level’ section and solve to determine total cost of controlling raw material at the supplier echelon, total cost of production and cost of controlling finished product stockpile at the plant echelon, and total cost of controlling products at the distribution center echelon.
-
(a)
Step 3: Formulate the mixed integer linear programming problem with volume flexibility as objective function and constraints given in Equations 2.3, 2.4, 2.5,… 2.13.
-
(a)
Step 4: Repeat step 2.
-
(a)
Step 5: Prepare the payoff table which contains extreme values of the objectives in strategic and tactical levels.
-
2.
Stage 2: Formulate the strategic level model in fuzzy environment and solve.
-
(a)
Step 1: Formulate membership functions of the fuzzy goals (supply chain cost and volume flexibility) using the aspiration levels of supply chain cost and volume flexibility from the payoff table obtained in the crisp environment.
-
(a)
Step 2: Formulate tactical level models (strategic, plant, and distribution center echelon models) as discussed in the ‘Tactical level’ section and solve to determine total cost of controlling raw material at the supplier echelon, total cost of production and cost of controlling finished product stockpile at the plant echelon, and total cost of controlling products at the distribution center echelon.
Numerical illustration
As a numerical illustration, a supply chain with four echelons, namely supplier, plant, distribution center, and customer zone, is considered. In the supply chain, it is assumed that four types of raw materials flow between five suppliers and four plants. In addition, it is assumed that four types of products flow from plants to four customer zones through four distribution centers.
The input variables required for developing and analyzing the supply chain model under study are shown in the Appendix. The procedure discussed in the methodology is used to determine the extreme solutions. These extreme solutions are useful to formulate membership functions of the fuzzy objectives in strategic and tactical levels.
Model formulation in strategic level
A fuzzy goal programming problem is formulated in strategic level as discussed in the ‘Strategic level’ subsection and is given below.
and also subjected to the constraints given in Equations 2.3 to 2.13.
Model formulation in tactical level
A fuzzy goal programming problem in tactical level is formulated as discussed in the ‘Tactical level’ subsection and is given below.
and also the service level constraints.
Results and discussions
The supply chain model is solved in crisp environment by implementing the methodology for the numerical example given in the ‘Numerical illustration’ section. LINGO code is developed to solve the mixed integerprogramming problem formulated at the strategic level and the non-linear programming problems at the three echelons. The extreme solutions are obtained by implementing step 1 to step 11 of stage 1 of the ‘Methodology’ section.
The extreme solutions shown in Table 1 indicate that the performance measures have two strategies, namely efficient strategy and responsive strategy. The supply chain cost at strategic level in efficient strategy is 0.28% less than the supply chain cost in responsive strategy. The cost of controlling raw materials at the supplier echelon in perspective 2 is 4.22% less than that of the responsive strategy. The cost of controlling products at the plant echelon in perspective 1 is 12.66% less than that of the responsive strategy. The cost of controlling products at the distribution center echelon in both perspectives is almost the same. In the case of volume flexibility, the responsive strategy is 2.94% more than that obtained in efficient strategy. Further, the total supply chain cost in the efficient strategy is 0.4% less than that of the responsive strategy.
The models developed in strategic and tactical levels in fuzzy environment are solved using LINGO 9.0. Table 2 shows the values of supply chain cost, volume flexibility, total cost of controlling raw materials at the supplier echelon, total cost of controlling products at the plant echelon, and total cost of controlling products at the distribution center echelon in tactical level.
The minimum operator assures minimum satisfaction of all the goals: supply chain cost (175,758.2), volume flexibility (10,627.1), total cost of controlling raw materials (5,184.1) at the supplier echelon, total cost of controlling products at the plant echelon (3,767.8), and total cost of controlling products (1,024.7) at the distribution center echelon obtained with the minimum operator lying between the extreme solutions. The above performance measures obtained in fuzzy environment indicate the compensation strategy. Comparison of the performance measures (normalized values) of the three strategies, namely efficient (EF), responsive (RS), and compensation (CS), is shown in Figure 1.
In the case of heavy industries like integrated steel plants, they can choose perspective 1 as they adopt efficient (cost-effective) supply chain strategy. On the other hand, companies involved in the manufacture of electronic goods like computers, cell phones, etc. can choose responsive supply chain strategy. Today, companies involving manufacturing of volatile and unforeseeable products like apparel and automotive must pioneer in compensation strategy.
Conclusions
In this paper, a multi-objective-oriented approach is adopted for supply chain modeling in fuzzy environment. Aspiration levels of the fuzzy objectives are derived from extreme solutions obtained by modeling in crisp environment. The results revealed that supply chain cost is low with low volume flexibility in the case of efficient supply chain strategy. In responsive strategy, volume flexibility is high with high total supply chain cost. In fuzzy environment, the total supply chain cost and volume flexibility which lie between the values obtained with the two perspectives indicate the compensation strategy. Implementing the proposed methodology may generate more satisfactory solutions, and the developed model is robust to evaluate different supply chain strategies. Further, fuzzy goal programming techniques provide feasible solutions with flexible model formulation in decision-making problems, which involve human judgments in decision-making.
This paper focuses on how supply chain is designed by implementing a structured methodology which integrates strategic planning and tactical planning. This study can be extended to develop interactive user-friendly application software for supply chain planning in an organization. Also, investigation of integrating, operational level planning is an interesting research area.
Appendix
Input data
i, product index; j, vendor index; k, plant index; l, distribution center index; m, customer zone index; n, raw material index
f 1 k , fixed charges for plant k (Rs/period) (4,750, 4,450, 4,550, 5,000)
f 2 l , fixed charges for distribution center l (Rs/period) (120, 150, 120, 150)
P k , production capacity of plant k (unit/period) (3,750, 2,600, 2,500, 3,000)
(T 3 l ) L , minimum throughput of DC l (unit/period) (100, 100, 50, 50)
(T 3 l ) H , maximum throughput of DC l (unit/period) (300,500,300,300)
R nj , raw material n availability at vendor j (2,500, 2,500, 2,500, 2,500, 2,500, 2,500, 2,500, 3,000, 3,500, 3,500, 2,000, 2,500, 2,000, 2,000, 2,500, 2,000, 2,500, 2,500, 2,000, 2,000)
C 1 nj , unit cost of raw material n at vendor j (Rs/unit) (5, 4, 5, 6, 6, 4, 5, 5, 6, 3, 4, 5, 4, 6, 5, 5, 4, 3, 4, 5)
u ni , utilization rate of each raw material n per unit of product i(1.3, 1.2, 1.2, 1.3, 1.2, 1.2, 1.3, 1.2, 1.2, 1.2, 1.1, 1.2, 1.2, 1.2, 1.2, 1.3)
E 2 ik , equivalent units at plant k per unit of product i (2, 2, 5, 5, 2, 2, 5, 4, 5, 2, 2, 2, 5, 2, 5, 2)
E 3 il , equivalent units at DC l per unit of product i (3, 2, 2, 3, 2, 2, 3, 2, 3, 2, 2, 3, 2, 2, 3, 3)
D im , average demand for product i at customer zone m (unit/period) (20, 30, 20, 20, 40, 50, 40, 30, 40, 30, 40, 20, 20, 30, 40, 40)
(P 2 ik ) L , minimum production volume of product i at plant k (unit/period) (5, 10, 5, 10, 5, 5, 12, 5, 5, 12, 15, 5, 15, 15, 15, 15)
(P 2 ik ) H , maximum production volume of product i at plant k (unit/period) (50, 50, 100, 50, 50, 50, 50, 50, 50, 100, 100, 50, 50, 50, 100, 50)
a njk , unit transportation cost from vendor j to plant k of raw material n (Rs/unit) (1, 1.25, 1.45, 1.4, 1.85, 1.6, 1.5, 1.9, 1, 1, 1.4, 1.4, 1.65, 1.15, 1.5, 1.5, 1, 1.25, 1, 1.4, 1.5, 1.6, 1.7, 1.8, 1, 1.25, 1.4, 1, 1.15, 1.5, 1.5, 1.5, 1.6, 1.6, 1.6, 1.6, 1.5, 1.65, 1.65, 1.65, 1.5, 1, 1, 1, 1.15, 1.5, 1.5, 1.5, 1.4, 1.4, 1.25, 1.25, 1.5, 1.5, 1.5, 1.15, 1.25, 1.4, 1.3, 1.4, 1.5, 1.6, 1.5, 1.5)
T 2 nj (×10-3), expected delay time of raw material n at vendor j (period) (13, 17, 14, 14, 11, 12, 14, 14, 16, 15, 16, 12, 14, 13, 14, 15)
V 2 nj (×10-4), variance of lead time for raw material n from vendor j to plant k (period2) (41, 28, 35, 33, 39, 34, 41, 39, 38, 40, 48, 48, 36, 32, 42, 35)
d ilm , unit transportation cost of product i from DC l to customer zone m (Rs/unit) (1.66, 1.3, 1.86, 1.62, 1.94, 1.38, 1.96, 1.74, 1.72, 1.38, 1.54, 1.16, 1.3, 1.24, 1.64, 1.68, 1.02, 1.7, 1.56, 1.1, 1.9, 1.32, 1.18, 1.88, 1.14, 1.14, 1.28, 1.72, 1.02, 1.58, 1.82, 1.08, 1.26, 1.66, 1.72, 1.86, 1.44, 1.98, 1.48, 1.1, 1.16, 1.75, 1.46, 1.56, 1.2, 1.3, 1.38, 1.14, 1.74, 1.46, 1.92, 1.88, 1.62, 1.38, 1.72, 1.72, 1.72, 1.84, 1.04, 1.24, 1.36, 1.62, 1.02, 1.82)
T 1 njk (×10-3), expected lead time for raw material n from vendor j to plant k (period) (27, 27.8, 27.2, 27.6, 27.6, 27.6, 27.6, 27.2, 27.1, 27.6, 27.3, 27.5, 27.2, 27.1, 27.6, 27.3, 27.5, 27.2, 28.1, 27.8, 27.4, 27.8, 28.1, 27.4, 27.4, 26.8, 27.7, 27.5, 28.1, 27.4, 28.3, 27.4, 27.6, 27.9, 26.3, 27.4, 27.3, 27.5, 28.4, 26.7, 26.9, 26.8, 27.7, 28.1, 26.8, 28.3, 27.1, 27.4, 27.4, 27.7, 27.1, 27.2, 27.3, 26.9, 28.1, 27.8, 27.8, 26.5, 26.7, 27.7, 27, 26.7, 27.3, 27.3, 27.3, 27.2, 27.1, 27.5, 26.9)
V 1 njk (×10-4), variance of lead time for raw material n from vendor j to plant k (period2) (26, 23, 14, 13, 25, 33, 36, 22, 16, 31, 26, 45, 26, 25, 26, 26, 23, 26, 25, 29, 13, 20, 257, 19, 25, 28, 23, 25, 30, 30, 35, 18, 36, 26, 26, 25, 41, 12, 20, 22, 26, 41, 26, 27, 13, 28, 26, 23, 30, 20, 19, 22, 25, 20, 17, 15, 27, 31, 21, 26, 24, 19, 39, 21)
K 1 nk , order setup cost of replenishing raw material n required at plant k (Rs) (35, 38, 33, 38, 38, 37, 33, 35, 32, 35, 35, 39, 33, 37, 32, 32)
H 1 nk , holding cost of raw material n required at plant k (Rs/period/unit) (1, 2, 5, 2, 5, 2, 1, 2, 5, 3, 4, 1, 4, 5, 2, 2)
P 1 nk , backorder cost for shortage of raw material n required at plant k (Rs/unit) (17, 15, 20, 17, 25, 19, 18, 16, 28, 19, 21, 26, 25, 25, 14, 18)
K 2 ik , production setup cost of product i at plant k (Rs) (54, 50, 53, 55, 50, 55, 56, 57, 55, 51, 52, 53, 53, 55, 54, 56)
H 2 ik , holding cost of product i at plant k (Rs/period/unit) (1.6, 1.2, 1.5, 1.1, 1.3, 1.1, 1.3, 1.7, 1.2, 1.3, 1.5, 1.3, 1.6, 1.4, 1.1, 1.5)
P 2 ik , backorder cost for shortage of product i required at plant k (Rs/unit) (24, 30, 32, 45, 30, 32, 38, 39, 38, 36, 34, 44, 37, 38, 33, 39)
K 3 il , order setup cost of product i at DC l (Rs) (44, 40, 43, 44, 40, 45, 45, 46, 45, 41, 42, 43, 43, 45, 43, 44)
H 3 il , holding cost of product i at DC l (Rs/period/unit) (1.5, 1.6, 1.11, 1.5, 1.3, 1.3, 1.6, 1.2, 1.6, 1.2, 1.2, 1.4, 1.4, 1.3, 1.5, 1.6)
P 3 il , backorder penalty cost for shortage of product i at DC l (Rs/unit) (30, 32, 31, 30, 31, 29, 28, 23, 29, 30, 27, 28, 27, 26, 25, 29)
PC ik , processing cost of product i at plant k (Rs/unit) (1, 1.2, 1, 0.8, 1.2, 0.9, 1.1, 1.2, 0.9, 1, 1.3, 1.3, 0.85, 0.75, 1.2, 1)
HP ik , work-in-process holding cost of product i at plant k (Rs/period/unit) (5, 2, 9, 6, 2, 5, 2, 8, 1, 9, 5, 9, 9, 1, 3, 7)
S ik (×10-3), production setup time for product i at plant k (period) (10, 20, 30, 40, 20, 10, 20, 10, 30, 30, 10, 20, 10, 20, 10, 10)
P ik (×10-3), production processing time for product i at plant k (period) (40, 30, 20, 10, 30, 20, 50, 40, 60, 50, 70, 50, 30, 40, 30)
A 1 nj (%), availability of raw material n at vendor j (90, 85, 95, 90, 90, 95, 95, 90, 90, 85, 95, 90, 90, 85, 95, 90, 90, 85, 95, 90)
BN ikl (×10-3), normal transportation lead time for product i from plant k to DC l (period) (6, 3, 7, 6, 2, 3, 7, 7, 2, 7, 5, 8, 5, 6, 4, 5, 4, 5, 5, 4, 4, 7, 5, 5, 7, 6, 5, 5, 4, 4, 4, 3, 76, 5, 7, 6, 8, 5, 5, 5, 1, 5, 8, 8, 6, 1, 7, 8, 6, 7, 7, 9, 4, 5, 10, 3, 9, 6, 6, 6, 9, 3, 5)
BE ikl (×10-3), expedited transportation lead time of product i from plant k to DC l (period) (5, 2, 6, 5, 1, 2, 6, 6, 1, 6, 4, 7, 4, 5, 3, 4, 3, 4, 4, 3, 3, 6, 4, 4, 6, 5, 4, 4, 3, 3, 3, 2, 6, 5, 4, 6, 5, 7, 4, 4, 4, 1, 4, 7, 5, 6, 6, 7, 5, 6, 6, 8, 3, 4, 9, 2, 8, 5, 5, 5, 8, 2, 4)
w ik (×10-3), waiting time of the product i at plant k (period) (5, 2, 2, 2, 0.3, 4, 2, 3, 2, 2, 4, 2, 3, 5, 4, 2)
Var w ik (×10-3), 1, 4, 8, 7, 2, 7, 7, 6, 3, 3, 8, 7, 5, 6, 9, 5
s ikl , unit transportation cost from plant k to DC l of product i (Rs/unit), from tactical model (2, 3, 1, 1, 5, 3, 3, 1, 3, 5, 1, 1, 3, 1, 3, 3, 3, 2, 2, 1, 2, 3, 2, 1, 4, 3, 2, 1, 3, 4, 2, 2, 1, 4, 4, 1, 3, 4, 3, 1, 4, 1, 3, 1, 1, 4, 1, 2, 4, 4, 1, 2, 4, 3, 2, 2, 4, 3, 4, 2, 3, 4, 3, 1)
CH ikl , holding for i product from plant k to DC l (Rs/period/unit) (0.5, 0.7, 0.8, 0.8, 0.6, 0.11, 0.2, 0.3, 0.3, 0.13, 0.1, 0.19, 0.6, 0.12, 0.13, 0.17, 0.9, 0.1, 0.11, 0.1, 0.14, 0.18, 0.14, 0.18, 0.5, 0.14, 0.18, 0.5, 0.14, 0.17, 0.16, 0.11, 0.1, 0.12, 0.11, 0.1, 0.15, 0.11, 0.02, 0.2, 0.12, 0.12, 0.11, 0.1, 0.1, 0.11, 0.1, 0.1, 0.11, 0.1, 0.13, 0.16, 0.14, 0.12, 0.17, 0.1, 0.11, 0.19, 0.16, 0.11, 0.13, 0.14, 0.18, 0.12, 0.11, 0.1.17, 0.13, 0.14, 0.10)
References
Abd El-Wahed WF, Abo-Sinna MA: A hybrid fuzzy goal programming approach to multiple objective decision making problems. Fuzzy Set Syst 2001,119(1):71–85. 10.1016/S0165-0114(99)00050-0
Amiri A: Design a distribution network in a supply chain system formulation and efficient solution procedure. Eur J Oper Res 2006, 171: 567–576. 10.1016/j.ejor.2004.09.018
Ballou RH: Business logistics/supply chain management. New Delhi: Pearson Education; 2004.
Beamon BM: Supply chain design and analysis: models and methods. Int J Prod Econ 1998, 55: 281–294. 10.1016/S0925-5273(98)00079-6
Bellman RE, Zadeh LA: Decision-making in a fuzzy environment. Manag Sci 1970, 17: 141–164.
Bouzembrak Y, Allaoui H, Goncalves G, Bouchriha H: A multi-objective green supply chain network design. In 2011 4th International conference on logistics (LOGISTIQUA). Hammamet; 2011. 31 May 3 June2011, pp 357–361
Chen YW, Tzeng GH: Fuzzy multi-objective approach to the supply chain model. Int J Fuzzy Syst 2000,1(3):220–227.
Chen CL, Wang BW, Lee WC: Multi-objective optimization for a multi-enterprise supply chain network. Ind Eng Chem Res 2003, 42: 1879–1889. 10.1021/ie0206148
Cohen MA, Lee HL: Strategic analysis of integrated production-distribution systems. Model Meth Oper Res 1988,36(2):216–228.
Eskigun E, Uzsoy R, Preckel PV, Beaujon G, Krishnan S, Tew JD: Outbound supply chain network design with mode selection, leadtimes and capacitated vehicle distribution centers. Eur J Oper Res 2005,165(1):182–206. 10.1016/j.ejor.2003.11.029
Farahani RZ, Elahipanah M: A genetic algorithm to optimize the total cost and service level for just-in-time distribution in a supply chain. Int J Prod Econ 2008, 111: 229–243. 10.1016/j.ijpe.2006.11.028
Lee HL, Kim SH, Moon C: Production-distribution planning in supply chain using a hybrid approach. Prod Plann Contr 2002,13(1):46–75.
Li H-L: SCM system in Taiwan electronic industry. Productivity 2002,42(4):574–581.
Liang TF: Fuzzy multi-objective production/distribution planning decisions with multi-product and multi-time period in supply chain. Comput Ind Eng 2008, 55: 676–694. 10.1016/j.cie.2008.02.008
Mohamed W: Chance constrained fuzzy goal programming and right-hand side uniform random variable coefficients. Fuzzy Set Syst 2000, 109: 107–110. 10.1016/S0165-0114(98)00151-1
Narasimhan R: Geometric averaging procedure for constructing super transitive approximation to binary comparison matrix. Fuzzy Set Syst 1982, 8: 53. 10.1016/0165-0114(82)90029-X
Narayana Rao K, Venkatasubbaiah K: Electronic supply network coordination in intelligent and dynamic environments. Hershey: IGI Global; 2011:146–167.
Peidro D, Mula J, Poler R, Verdegay JL: Fuzzy optimization for supply chain planning under supply, demand and process uncertainties. Fuzzy Set Syst 2009,160(18):2640–2657. 10.1016/j.fss.2009.02.021
Petrovic D, Roy R: Modeling and simulation of a supply chain in an uncertain environment. Eur J Oper Res 1998, 109: 299–309. 10.1016/S0377-2217(98)00058-7
Pyke DF, Cohen MA: Multiproduct integrated production–distribution systems. Eur J Oper Res 1994, 74: 18–49. 10.1016/0377-2217(94)90201-1
Ramik J: Fuzzy alternatives in goal programming problems. Fuzzy Set Syst 2000, 111: 81–86. 10.1016/S0165-0114(98)00454-0
Robinson PE, Goa LL, Muggenborg ST: Designing an integrated distribution system at Dowbrands, Inc. Interfaces 1993,23(3):107–117. 10.1287/inte.23.3.107
Sabri EH, Beamon BM: A multi-objective approach to simultaneous strategic and operational planning in supply chain design. Omega 2000,28(5):581–595. 10.1016/S0305-0483(99)00080-8
Troncoso J, D’Amours S, Flisberg P, Ronnqvist M, Weintraub A: A mixed integer programming model to evaluate integrating strategies in the forest value chain – a case study in the Chilean forest industry. CIRRELT 2011, 28: 1–29.
Tsiakis P, Shah N, Pantelidas CC: Design of multi-echelon supply chain networks under demand uncertainty. Ind Eng Chem Res 2001, 40: 3585–3604. 10.1021/ie0100030
van der Vorst JGAJ: Effective food supply chains:generating modeling and evaluating supply chain scenarios. Wageningen: Wageningen University; 2000.
Yu Y, Zu H, Cheng TCE: A strategic model for supply chain design with logical constraints: formulation and solution. Comput Oper Res 2003, 30: 2135–2155. 10.1016/S0305-0548(02)00127-2
Zimmermann HJ: Fuzzy programming and linear programming with several objective functions. Fuzzy Set Syst 1978, 1: 45–55. 10.1016/0165-0114(78)90031-3
Acknowledgement
The authors are very much thankful to the anonymous reviewers for their constructive comments and useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
NR coined the problem and its formulation. VS helped in the manuscript preparation. PS helped in problem solving. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rao, K.N., Subbaiah, K.V. & Singh, G.V.P. Design of supply chain in fuzzy environment. J Ind Eng Int 9, 9 (2013). https://doi.org/10.1186/2251-712X-9-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2251-712X-9-9