Behavioral study of piston manufacturing plant through stochastic models

Abstract

Piston plays a vital role in almost all types of vehicles. The present study discusses the behavioral study of a piston manufacturing plant. Manufacturing plants are complex repairable systems and therefore, it is difficult to evaluate the performance of a piston manufacturing plant using stochastic models. The stochastic model is an efficient performance evaluator for repairable systems. In this paper, two stochastic models and computation algorithm of the piston manufacturing plant are illustrated using the state-space transition diagram and availability parameter is used for its behavioral study. Finally, the conclusion is discussed based on the resulting computations.

Introduction

Piston is a cylindrical shaped component tightly fitted within another cylinder. Piston plays an important role in all vehicles and thus, the performance of the piston manufacturing process is equally important as that of piston quality and needs to be evaluated. The present study discusses the behavioral study of a piston manufacturing plant.

Manufacturing plants are complex repairable systems, and therefore, it is difficult to evaluate their performance metric including reliability and availability. The stochastic process is an efficient performance evaluator model for repairable systems. Several authors have considered such models to analyze the reliability and availability of manufacturing plants such as plastic manufacturing plant (Gupta et al. [2007]), cement industries (Gupta et al. [2005b]), butter oil manufacturing plant (Gupta et al. [2005c]), and thermal power plant (Gupta and Tiwari [2009]) for performance evaluation. Gupta et al. ([2005a]) discussed the performance of the polymer powder production process using the supplementary variable method.

In some of above studies, analytical approaches like Laplace transforms (Gupta [2003]), matrix method (Gupta et al. [2007]), and Lagrange’s method (Mahajan and Singh [1999]) are used to discuss transient state of the resulting mathematical expression in order to study the performance metrics including reliability and time-dependent availability. However, the computational part and analysis have not been effectively performed using these analytic methods and thus these were not used in the analysis of steady state behavior of the process in these studies. Further, various other techniques such as genetic algorithm (Kumar et al. [2010]), GABLT (Sharma and Kumar [2010]), and stochastic reward petri nets (Sachdeva et al. [2009]) have also been used to analyze the steady state behavior of the systems. However, these analytic methods are not useful to obtain the solution of the transient state of complex manufacturing system. Therefore, we have used a numerical method to solve such a complex mathematical problem relating to the piston manufacturing plant.

In this paper, two stochastic models and computation algorithm of the piston manufacturing plant are illustrated using the state transition diagram. The objective of this study is to help the industry management by developing a mathematical model for piston manufacturing plant to evaluate its performance results based on availability. In the subsequent section, we will discuss the piston manufacturing process and its further division into subsystems in order to develop the stochastic models.

The process and its systems and subsystems

In the piston manufacturing plant, a gravity die casting process is carried out in the foundry to make the piston with the help of semiautomatic die machines without external pressures. The resultant pistons are sent for cleaning up the surface of the piston from the risers and runners and later, the strength, hardness, and other foundry defects are evaluated. Then a bunch of pistons is placed in the piston blank for its machining operations after which a fixture seat machine is used. Then, two rough grooves are made on the piston by using a carbide tool tip to fit a pin in them. Subsequently, another hole is drilled on the piston for oil passage and then finishing is given to the rough grooves using a diamond tool. Later, the piston is shaped into an oval to ensure its smooth movement within the cylinder using the carbide tool. In the next process, finish crown and cavity machines are used to put a rough cavity first and then a finish cavity on the piston. Further, valves are made on the piston using the diamond tool followed by a rounding-off operation on the corners of piston. Then, circlip grooves are made on the piston in the absence of any coolant and air pressure. After that, deburring, cleaning, and surface treatment operations are performed. Final inspections are carried out on the manufactured piston under some operational tests before packing.

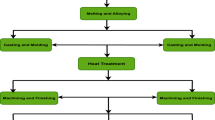
In order to reduce the complexity for the effective behavioral (or performance) analysis, the piston manufacturing process is categorized into two systems namely, S1 and S2. The system which formed the piston into oval shape is denoted by S1 and the system which produces the final product as piston is denoted by S2. The flow chart of the piston manufacturing process is given in Figure 1.

Figure 1

Flow chart of piston manufacturing plant.

Further, system S1 is divided into six subsystems, namely, A, B, C, D, E, and F. The brief description of these subsystems is as follows:

• 1. Subsystem A is a fixture seat machining operation which is performed for clamping of pistons.

• 2. Subsystem B is a machining operation of rough grooving and turning operation.

• 3. Subsystem C is rough pin hole boring machine used to make pin holes on the piston to give proper size to the holes, which are used to fit the pin by which a rod is connected to crankshaft.

• 4. An oil hole is drilled on the piston for oil passage and the operating machine; oil hole drilling is considered as sub-system D.

• 5. Subsystem E is the finishing grooving machine used to give finishing to the rough grooves.

• 6. Subsystem F is the finish profile turning operation in which the piston is formed into oval shape in order to overcome expansion problems during working of the piston at high temperatures.

Similarly, system S2 is divided into nine subsystems namely G, H, I, J, K, L, M, N, and O which are described as follows:

• 1. Subsystem G is a finish pin hole boring machine.

• 2. Finish crown and cavity is subsystem H, which is operated to give finishing to the crown of piston, i.e., the upper part of the piston.

• 3. Subsystem I is a valve milling machine to make the valve recession of the piston.

• 4. Subsystem J is the chamfering or radiusing machine used to round off the corners of the piston to ensure smooth run in the cylinder.

• 5. Circlip grooves are made on the piston through subsystem K, a circlip grooving machine.

• 6. Subsystem L is the deburring machine. The deburring or brushing operation is performed on the piston using this machine.

• 7. Subsystem M is the cleaning machine which helps to clean the inside and outside of the piston.

• 8. Subsystem N is the surface treatment operation to coat the piston with some mixture.

• 9. Subsystem O is the final inspection of the manufactured product though operational tests before being packed.

In addition to above discussion, we have considered two kinds of failures for each subsystem, which are major and minor. Major failures are those in which the system shows complete breakdown while the minor failures are those which can be repaired during working conditions (reduced state). Now, we proceed with each system description and its subsystem. The subsystems A, B, C, D, F, F, I, J, and M are subject to major failure while C, E, G, and K are subject to both major and minor failures. Subsystems L, N, and O are considered to have no failure. Next, the state space of stochastic process for both systems is described in a diagrammatic form, known as transition diagram.

Transition diagrams

Transition diagrams for system S1 and S2 are shown in Figures 1 and 2, respectively. In the transition diagrams, we consider system S1 or system S2 in good state when all of its subsystems show good conditions, in reduced state when any of its subsystem is in reduced state, and in failed state when any of its subsystem fails. The corresponding subsystem state notations are described in the Section ‘Notations’.

Figure 2

State transition diagram for systemS ₁ . The constant failure rates of subsystems A, B, D, F, $\overline{\mathrm{C}}$, $\overline{\mathrm{E}}$, C, and E are represented by α _i (i = 1 to 8), respectively. The parameter β _i represents the respective constant repair rates of subsystems A, B, D, F, $\overline{\mathrm{C}}$, $\overline{\mathrm{E}}$, C, and E, for i = 1 to 8. Lowercase letters, including a, b, c, d, e, and f represent the failed state of subsystems A, B, C, D, E, and F respectively.

Notations

In this section, the notations are presented as follows:

• 1. The good condition of each subsystem is represented by capital letters, as A, B, C, D, E, and F for subsystems in S1 and G, H, I, J, K, and M for subsystems in S2, respectively.

• 2. Lowercase letters, including a, b, c, d, e, and f and g, h, i, j, k, and m, represent the failed state of subsystems A, B, C, D, E, and F, and G, H, I, J, K, and M, respectively.

• 3. The reduced working state of subsystems C, E, and G is indicated by $\overline{\mathrm{C}}$, $\overline{\mathrm{E}}$, and $\overline{\mathrm{G}}$, respectively.

• 4. The constant failure rates of subsystems A, B, D, F, $\overline{\mathrm{C}}$, $\overline{\mathrm{E}}$, C, and E are represented by α _i (i = 1 to 8), respectively, in Figure 2. This parameter α _i (i = 1 to 7) also represents the respective constant failure rates of subsystems H, I, J, K, M, $\overline{\mathrm{G}}$, and G in Figure 3.

Figure 3

State transition diagram for systemS ₂ . Parameter α _i (i = 1 to 7) represents the respective constant failure rates of subsystems H, I, J, K, M, $\overline{\mathrm{G}}$, and G. Parameter β _i represents the respective constant repair rates of subsystems H, I, J, K, M, $\overline{\mathrm{G}}$, and G for i = 1 to 7. Lowercase letters, including g, h, i, j, k, and m, represent the failed state of subsystems G, H, I, J, K, and M, respectively.

• 5. The parameter β _i represents the respective constant repair rates of subsystems A, B, D, F, $\overline{\mathrm{C}},\overline{\mathrm{E}}$, C, and E, for i = 1 to 8 in Figure 2. In Figure 3, it represents respective constant repair rates of subsystems H, I, J, K, M, $\overline{\mathrm{G}}$, and G for i = 1 to 7.

• 6. Symbol P _j (t) represents the probability that the system is in j th state at time t (j = 1 to 24 for system S1 and j = 1 to 13 for system S2). Symbol P _j '(t) represent the rate of change of probability of j th state with respect to time t. (j = 1 to 24 for system S1 and j = 1 to 13 for system S2).

Assumptions

The following assumptions are used to model the performance analysis of the process for both systems S1 and S2:

• 1. Failure and repair rates are independent with each other and their unit is per hour.

• 2. There are no simultaneous failures among the subsystems.

• 3. Subsystems C, E, and G fail only through reduced states.

• 4. Repair of C, E, and G in the reduced state does not make these subsystems completely functional.

• 5. Switching to standby components is perfect.

• 6. Subsystems L, N, and O are considered as subsystems that never failed.

Stochastic models and computation algorithm of piston manufacturing plant

Systems S1 and S2 have been formulated by following the mnemonic rule discussed in the work of (Gupta et al. [2005a], [b]) using transition diagrams. The resulting Chapman-Kolmogorov first-order differential-difference equations for both systems under probabilistic considerations of each state discussed in state transition diagrams (Figures 2 and 3) are obtained as shown in the succeeding sections.

Mathematical formulation of system S₁

In this section, the mathematical formulation of system S1 is performed, with the help of transition diagram shown in Figure 2, as follows:

$$\begin{array}{ll}\hfill P_1^{\text{'}}\left(t\right)+{\lambda }_1{P}_1\left(t\right)=& {\displaystyle \sum _{i=1}^4{\beta }_i{P}_{4+i}\left(t\right)}+{\displaystyle \sum _{i=2}^3{\beta }_{3+i}{P}_i\left(t\right)}\\ +{\displaystyle \sum _{i=7}^8{\beta }_i{P}_{10+i}\left(t\right)},\end{array}$$

(1)

$$P_2^{\text{'}}\left(t\right)+{\lambda }_2{P}_2\left(t\right)={\displaystyle \sum _{i=1}^4{\beta }_i{P}_{8+i}\left(t\right)}+{\beta }_8{P}_{20}\left(t\right)+{\alpha }_5{P}_1\left(t\right),$$

(2)

$$P_3^{\text{'}}\left(t\right)+{\lambda }_3{P}_3\left(t\right)={\displaystyle \sum _{i=1}^4{\beta }_i{P}_{12+i}\left(t\right)}+{\beta }_7{P}_{19}\left(t\right)+{\alpha }_6{P}_1\left(t\right),$$

(3)

$$P_4^{\text{'}}\left(t\right)+{\lambda }_4{P}_4\left(t\right)={\displaystyle \sum _{i=1}^4{\beta }_i{P}_{20+i}\left(t\right)}+{\alpha }_5{P}_3\left(t\right)+{\alpha }_6{P}_2\left(t\right),$$

(4)

$$P_{4+i}^{\text{'}}\left(t\right)+{\beta }_i{P}_{4+i}\left(t\right)={\alpha }_i{P}_1\left(t\right),i=1,2,3,4$$

(5)

$$P_{8+i}^{\text{'}}\left(t\right)+{\beta }_i{P}_{8+i}\left(t\right)={\alpha }_i{P}_2\left(t\right)$$

(6)

$$P_{12+i}^{\text{'}}\left(t\right)+{\beta }_i{P}_{12+i}\left(t\right)={\alpha }_i{P}_3\left(t\right)$$

(7)

$$P_{16+i}^{\text{'}}\left(t\right)+{\beta }_7{P}_{16+i}\left(t\right)={\alpha }_7{P}_j\left(t\right),i=1,2;j=2,4$$

(8)

$$P_{18+i}^{\text{'}}\left(t\right)+{\beta }_8{P}_{18+i}\left(t\right)={\alpha }_8{P}_j\left(t\right),i=1,2j=3,4$$

(9)

$$P_{20+i}^{\text{'}}\left(t\right)+{\beta }_i{P}_{20+i}\left(t\right)={\alpha }_i{P}_4\left(t\right),i=1,23,4,$$

(10)

where

$${\lambda }_1={\alpha }_1+{\alpha }_2+{\alpha }_3+{\alpha }_4+{\alpha }_5+{\alpha }_6$$

(11)

$${\lambda }_2={\alpha }_1+{\alpha }_2+{\alpha }_3+{\alpha }_4+{\alpha }_6+{\alpha }_7+{\beta }_5$$

(12)

$${\lambda }_3={\alpha }_1+{\alpha }_2+{\alpha }_3+{\alpha }_4+{\alpha }_5+{\alpha }_8+{\beta }_6$$

(13)

$${\lambda }_4={\alpha }_1+{\alpha }_2+{\alpha }_3+{\alpha }_4+{\alpha }_7+{\alpha }_8$$

(14)

with initial conditions P₁(0) = 1 and 0, otherwise.

The time-dependent availability A₁(t) of the system (S1) is

$$A_1\left(t\right)={\displaystyle \sum _{i=1}^4{P}_i\left(t\right)}.$$

(15)

Mathematical formulation of system S2

In this section, the mathematical formulation of system S2 is performed, with the help of transition diagram shown in Figure 3, as follows:

$$\begin{array}{ll}\hfill P_1^{\text{'}}\left(t\right)+{\lambda }_1{P}_1\left(t\right)=& {\displaystyle \sum _{i=1}^5{\beta }_i{P}_{2+i}\left(t\right)}+{\beta }_6{P}_2\left(t\right)\\ +{\beta }_7{P}_{13}\left(t\right)\end{array}$$

(16)

$$P_2^{\text{'}}\left(t\right)+{\lambda }_2{P}_2\left(t\right)={\displaystyle \sum _{i=1}^5{\beta }_i{P}_{7+i}\left(t\right)}+{\alpha }_6{P}_1\left(t\right)$$

(17)

$$P_{2+i}^{\text{'}}\left(t\right)+{\beta }_i{P}_{2+i}\left(t\right)={\alpha }_i{P}_j\left(t\right),$$

(18)

where

$$j=\left\{\begin{array}{c}\hfill 1\mathrm{for}i=1,2,\dots ,5\hfill \\ \hfill 2\mathrm{for}i=6,7,\dots ,13\hfill \end{array}\right.,{\lambda }_1={\alpha }_1+{\alpha }_2+{\alpha }_3+{\alpha }_4+{\alpha }_5+{\alpha }_6$$

(19)

$${\lambda }_2={\alpha }_1+{\alpha }_2+{\alpha }_3+{\alpha }_4+{\alpha }_5+{\alpha }_7+{\beta }_6$$

(20)

with initial conditions

$$P_1\left(0\right)=1\mathrm{and}{P}_i\left(0\right)=0,i=2-15.$$

(21)

The time-dependent availability A₂(t) of the system (S2) is

$$A_2\left(t\right)={\displaystyle \sum _{i=1}^2{P}_i\left(t\right)}.$$

(22)

System S1 completes its target only when system S2 starts, with the output of the previous system for further operation. Thus, S1 and S2 are in series which helps us to compute the time-dependent availability of the process industry as

$$A_{\mathrm{P}}\left(t\right)=A_1\left(t\right)\times A_2\left(t\right).$$

(23)

As the system of differential Equations (1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 and 16, 17, and 18) is very complex, it is difficult to find its analytical solution, particularly using Laplace transformation method. Therefore, a numerical procedure is used to obtain the computation for the availability of the process, which is discussed next.

Computational algorithm

In order to obtain the availability parameter of the process industry, the results are approximated for the following transient probabilities:

$$p_{1i}\left(t\right)=P\left[X\left(t\right)=i|X\left(0\right)=1\right]$$

(24)

using initial distribution

$$P_1\left(0\right)=1,P_j\left(0\right)=0,\mathrm{for}j=2,\dots ,24$$

(25)

to study the effect of failure and repair rate variations on the plant performance. Also, as the transition matrix changes with respect to the change in transition rates, the complete transition matrix data for this case study was, thus, not evaluated for both the systems under different failure and repair rate variations. The algorithm for solving the system of equations (1, 2, 3, 4, 5, 6, 7, 8, 9, and 10) that corresponds to system S1 is as follows:

• 1. Input initial time, step size, transition rates (i.e., failure and repair rates) of each state.

• 2. Set initial distribution P₁(0) = 1, P _j (0) = 0, for j = 2, …, 24.

• 3. Apply Runge–Kutta fourth-order method on differential equations (1, 2, 3, 4, 5, 6, 7, 8, 9, and 10) to obtain probabilities p_1i(t), p₁₂(t), …, p_1n(t), n = 24.

• 4. Compute time-dependent availability using Equation 15.

Further, in order to compute the second row of transition matrix, replace step 2 with initial distribution, P₂(0) = 1, P _j (0) = 0, for j = 1, 3, …, 24 for computing the following transition probabilities:

$$p_{2i}\left(t\right)=P\left[X\left(t\right)=i|X\left(0\right)=2\right]$$

(26)

and proceed this way to analyze the results to compute each row of transition matrix. Similarly, results for S2 systems were computed.

We have performed 72,000 iterations on the system of differential-difference equations (1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 and 16, 17, and 18) together with conditions (Equations 14 and 21) to solve them using the above algorithm, taking step size t = 0.005 with the assumption that it equals to 1 h, considering the fact discussed (Gupta et al. [2007]). This leads us to computations of time-dependent availability from 30 to 360 h. The resulting computations are shown in Table 1. The availability results are also simulated for various fluctuations of repair as well as failure rates of each subsystem (Tables 2,3,4,5,6,7,8,9,10,11,12,13). The simulated data for various fluctuating environment of failure and repair rates can be referred from Tables 2,3,4,5,6,7 for system S1 and from Tables 8,9,10,11,12,13 for system S2. Based on these results, the behavior study of both the system is discussed next.

Table 1 Time-dependent availability of the systems S ₁ and S ₂ and process industry

Behavior study of both systems

Results are obtained for the overall time-dependent availability of the process, using Equation 23, with empirical data collected from industry. The data has been taken from industry in the form of operating hours, number of failures, number of repairs, and corresponding time for each repair for all the subsystems of the process industry. This data is composed into parameterized form of exponentially distributed failure rate and repair rates and given as α₁ = 0.0014, α₂ = 0.0006, α₃ = 0.0009, α₄ = 0.0009, α₅ = 0.0208, α₆ = 0.0208, α₇ = 0.0009, and α₈ = 0.0039 and β₁ = 1.08, β₂ = 0.043, β₃ = 0.5, β₄ = 0.286, β₅ = 0.154, β₆ = 0.25, β₇ = 0.059 and β₈ = 0.087 for system S1, respectively; and α₁ = 0.0014, α₂ = 0.0003, α₃ = 0.0001, α₄ = 0.0003, α₅ = 0.0001, α₆ = 0.0208, and α₇ = 0.004 and β₁ = 0.33, β₂ = 0.5, β₃ = 0.67, β₄ = 0.035, β₅ = 3.03, β₆ = 0.222, and β₇ = 0.125 for system S2, respectively.

The computations of overall time-dependent availability of the process industry are shown in Table 1. The tabular form of computations helps us to conclude that the process is 96% reliable for operation at 30 h.

Further, we found that the time-dependent availability of system S1 is more affected by fixture seat machining (A) in comparison to the effect of other systems as observed from the simulated results shown in Tables 2,3,4,5,6,7. The time-dependent availability of the system S1 decreases by 1.02% from the empirical results (shown in Table 1), while it decreases by approximately 0.4% with the increase in time from 30 to 360 h. However, other subsystems’ failure rate affects the system availability by 0.2% (for rough grooving cum turning and oil hole drilling), 0.06% (rough pin hole boring), 0.01% (for finish grooving), and 0.03% (finish profile turning) in comparison to fixture seat machining when compared to empirical results of system S1 availability, A₁ (Table 1).

Table 2 Fixture seat machining’s failure ( α ₁ ) and repair rate ( β ₁ ) effect on time-dependent availability of S ₁

Table 3 Rough grooving and turning’s failure ( α ₂ ) and repair rate ( β ₂ ) effect on time-dependent availability of S1

Table 4 Rough pin hole boring failure rate ( α ₇ ) and repair rate ( β ₇ ) effect on time-dependent availability of S1

Table 5 Oil hole drilling’s failure ( α ₃ ) and repair ( β ₃ ) rate on time-dependent availability of S1

Table 6 Finish grooving’s failure ( α ₈ ) and repair rate ( β ₈ ) effect on time-dependent availability of S1

Table 7 Finish profile turning’s failure ( α ₄ ) and repair ( β ₄ ) rate effect on time-dependent availability of S1

Similarly, repair rate fluctuations have been studied for the effect of maintenance on time-dependent availability of the system. We found that the time-dependent availability of system S1 shows 0.001% increase for fixture seat machining and rough pin hole boring, and for other subsystems, time-dependent availability shows 0.01% (for rough grooving cum tuning and finish profile turning), 0.02% (for rough oil drilling), and 0.025% increase (for finish grooving) with corresponding increase in repair rates as observed from Tables 2,3,4,5,6,7. So the weak subsystem was found to be the fixture seat machining which is due to the effect maintenance practice as well.

Likewise, the results were simulated for systems in S2 and can be referred from Tables 8,9,10,11,12,13. We observed that the time-dependent availability of this system is more affected by circlip grooving (K), in comparison to other subsystems. It is observed that the availability of system S2 decreases by 0.18% when compared with the empirical values of A₂; the availability of system S2 is presented in Table 1. This decreases by 0.34% with the increase in time from 30 to 360 h. However, the decrease in percentage effect of the other subsystem’s failure rate on system time-dependent availability is observed as 0.06% for finish pin hole boring, 0.02% for chamfering, 0.01% for finish crown and cavity, 0.003% for cleaning machine, and 0.002% decrease for valve milling in comparison to circlip grooving, as compared to empirical results of system S2 time-dependent availability (Table 1) which can be referred from Tables 8,9,10,11,12,13.

Table 8 Effect of failure rate ( α ₁ ) and repair rate ( β ₁ ) of finish crown and cavity on time-dependent availability of S2

Table 9 Effect of failure rate of valve milling ( α ₂ ) on time-dependent availability of the system S2

Table 10 Effect of failure rate ( α ₃ ) and repair rate ( β ₃ ) of chamfering or radiusing on time-dependent availability of S2

Table 11 Effect of failure rate ( α ₄ ) and repair rate ( β ₄ ) of circlip grooving on time-dependent availability of the system S2

Table 12 Effect of failure rate ( α ₅ ) and repair rate ( β ₅ ) of cleaning machine on time-dependent availability of the system S ₂

Table 13 Effect of failure rate ( α ₇ ) and repair rate ( β ₇ ) of finish pin hole boring on time-dependent availability of the system S2

Similarly, the repair rate fluctuations have been studied for the effect of maintenance on time-dependent availability in the case of system S2 as well. We found that time-dependent availability of the system S2 shows 0.5% increase for circlip grooving with decrease in value of its repair rate parameter. In case of finish pin hole boring, the time-dependent availability of the system improved by 0.2% when its repair rates decrease. The effect on time-dependent availability was found to be negligible in case of other subsystems and can be referred from Tables 8,9,10,11,12,13.

Conclusion

From the comparative study of this paper, we have observed that the time-dependent availability of the system S1 and system S2 is affected by fixture seat machining (A) and circlip grooving (K), respectively. Therefore, it is recommended that management should pay more attention to fixture seat machining (A) and circlip grooving (K) in order to increase the time-dependent availability of the piston manufacturing plant. The conclusion drawn from the analysis is consistent with the actual performance of the manufacturing plant and will help the industry to improve its performance. The main advantage of this work is that we can examine the time-dependent analysis.

Authors’ information

AKL, Associate Professor in the School of Mathematics and Computer Application, Thapar University Patiala. His research fields are computational Astrophysics and Reliability Engineering.

MK is a Ph.D student in the School of Mathematics and Computer Applications, Thapar University, Patiala. She worked as JRF and SRF in UGC sponsored major research project entitled “Reliability, Availability and Maintainability of industrial process” under the supervision of AKL and Prof. S.S. Bhatia. Her research interests are in the field of Reliability Engineering and Stochastic Models.

SL was a Ph.D student in School of Mathematics and Computer Applications, Thapar University. She, presently, works as an assistant professor of University institute of Engineering, Chandigarh University. Her research interests are in the field of Reliability Engineering and Fuzzy Theory.