Bi-product inventory planning in a three-echelon supply chain with backordering, Poisson demand, and limited warehouse space

Abstract

In this paper, we apply continuous review (S-1, S) policy for inventory control in a three-echelon supply chain (SC) including r identical retailers, a central warehouse with limited storage space, and two independent manufacturing plants which offer two kinds of product to the customer. The warehouse of the model follows (M/M/1) queue model where customer demands follow a Poisson probability distribution function, and customer serving time is exponential random variable. To evaluate the effect of considering bi-product developed model, solution of the developed model is compared with that of the two (M/M/1) queue models which are separately developed for each product. Moreover, and in order to cope with the computational complexity of the developed model, a particle swarm optimization algorithm is adopted. Through the conducted numerical experiments, it is shown that total profit of the SC is significantly enhanced using the developed model.

Background

Today, increasing competitive pressure and market globalization directly results in an environment in which supply chains (SCs) are organized in such a way to be able to respond to the customer needs (Gumus and Guneri 2007). In this regard, diverse competitive metrics are elicited as cost, quality, delivery, and flexibility; while some are noted with respect to the production process and planning, such as technology, capacity, facilities, and workforce planning (Sana 2011). To do so, integrated multi-echelon inventory management is employed in SCs in order to obtain inventory cost reduction as well as customer service improvement of the total SC (Gumus and Guneri 2007). Upon the principles of integrated inventory management, two main concerns are considered: coordination of different SC elements and arranging their inventory levels according to the interrelationship among the elements.

Most of today’s manufacturing firms are organized as a network of manufacturing plants and distribution centers, which consists of a value chain including providing raw material, processing them into end-products, and distributing/delivering the finished goods to the customers. In this regard, the term ‘multi-echelon’ or ‘multi-level’ production/distribution network is adopted in order to refer to a network during which a good is delivered to the end customer after more than one step. In multi-echelon supply networks, there might be various forms of inventories: raw material, work in process, and/or finished products. Procured raw materials from suppliers are processed to finished products in manufacturing plants. Then, the finished products are sold to distributors, retailers, and/or end customers. As mentioned above, a multi-echelon SC is a network when an item moves towards the final customer after passing more than one stage (Ganeshan 1999). The echelon stock of a stockpoint comprises all stock at this stockpoint, plus in-transit to or on-hand at any of its downstream stockpoints, minus the backorders at its downstream stockpoints (Diks and de Kok 1998).

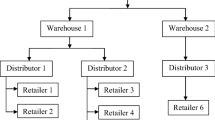
Upon multi-echelon inventory systems, distribution of products to customers is widely conducted over extensive geographical areas. Given the importance of these systems, many studies have been presented based upon the various conditions and assumptions (Moinzadeh and Aggarwal 1997). On the other hand, numerous studies have been devoted to the inventory control policy of multi-echelon systems with stochastic demands (Gumus and Guneri 2007). In this paper, a bi-product, three-echelon SC is considered which comprises r identical retailers, a central warehouse with limited storage space, and two independent manufacturing plants. The assumed network presents two types of product to the customers who arrived into the retailer nodes. Customer demands for each product j enter retailer i upon Poisson probability distribution function with rate λ _ij . Also, central warehouse responds the needs upon exponential probability distribution function with respect to the on-hand inventory. When a retailer places an order and faces inventory shortage in the warehouse, she/he waits up until product availability (backordering). The warehouse holds inventory and applies a continuous review (S-1, S) inventory policy; that is, a replenishment order is forwarded to the manufacturer after each order enters the warehouse. Therefore, the purpose of this study is to seek an optimal S^* for inventory control in order to minimize both inventory holding cost and backordering cost. The detailed descriptions of the problem are elaborated in ‘Single-product model’ and ‘Bi-product model’ sections.

The aim of the paper is the improvement of the total network costs in a stochastic environment. On the other hand, increasing the profit of the SC is the purpose of this study. In this regard, we suppose a bi-product three-echelon SC which is modeled as an (M/M/1) queue model for each type of product offered through the developed network. In addition, to show the performance of the proposed bi-product SC, a network including two Markov models (M/M/1) for each type of product is also considered. The procedure of the comparison of both proposed SCs is executed applying a particle swarm optimization (PSO) algorithm.

Sherbrooke’s (1968) paper can be introduced as one of the oldest researches conducted in the field of continuous review multi-echelon inventory systems, leading to several instances of the papers which addressed continuous review models of multi-echelon inventory systems during 1980s, such as Graves (1985), Moinzadeh and Lee (1986), Lee and Moinzadeh (1987), Deuermeyer and Schwarz (1981), and Svoronos and Zipkin (1988). In addition, other authors have studied the continuous review (S-1, S) policy in multi-echelon inventory systems with the assumption of stochastic environments (Axsäter 1990; Axsäter 1993; Andersson and Melchiors 2001). Besides, other inventory control policies such as continuous review (R, Q) and (s, Q) policies and one-for-one have been investigated in this era under different assumptions on echelon number, product number, demand probability distribution function, transportation times, and backlogging assumptions (Kevin Chiang and Monahan 2005; Thangam and Uthayakumar 2008; Haji et al. 2009; Teimoury et al. 2010).

Kevin Chiang and Monahan (2005) developed a two-echelon dual-channel inventory model which was controlled upon a one-for-one policy. They supposed stochastic demands of two customer segments. Thangam and Uthayakumar (2008) studied a two-level supply chain consisting of a single supplier and several identical retailers. In their considered problem, retailers received Poisson demands while partial backordering was permitted. The finished goods were delivered to the customers in a network with constant transportation times. In another paper, a modified one-for-one policy was extended to inventory control of one central warehouse in a two-echelon inventory system with a number of non-identical retailers. The authors considered that the central warehouse was facing uniformly distributed demands from each retailer (Haji et al. 2009).

Since problems of stochastic inventory systems have a significant level of complexity, queueing approach has been applied to obtain a simple performance result. In this regard, Chao (1987) developed a Markov decision process model to describe the optimal control policy for an inventory system with zero lead time and market interruptions. Gupta (1996) presented an exact cost function for a lost-sale (s, Q) inventory system with Poisson demand, constant lead time, and exponentially distributed supplier’s on/off periods, while a similar paper was presented by Mohebbi (2003) in this context. He developed an analytical model for computing the stationary distribution of the on-hand inventory in a continuous review inventory system with lost sales in which demands and lead times were stochastic. In the study, demand process was performed upon Poisson probability distribution function and replenishment lead time based on Erlang (E _k ). Under a continuous-time Markov chain, the author assumed two available and unavailable states at any points of time. Moreover, a modified (s, Q) policy was applied for the inventory system.

Some authors have developed queuing models which are related to production authorization strategy for supply chain inventory analysis and optimization (Dong 2003; Teimoury et al. 2011a2011b). Teimoury et al. (2011a) modeled an inventory system of a three-echelon multi-product supply chain including a manufacturing plant, several warehouses, and several retailers as queue model GI/G/1. In their network, after manufacturing products in batches, each type of products which are demanded by several retailers is held in separate warehouses with different holding and backorder costs. Moreover, they studied a multi-product multi-echelon manufacturing supply chain network with batch ordering in which performance evaluation had been analyzed upon the developed queuing models. The purpose of their study was to determine the optimal inventory level at the warehouse of each product so as to minimize total expected cost (Teimoury et al. 2011b). Some other papers have been published towards another aspect of the integrated inventory systems of SCs and disruption effects. One of the notable instances is the paper by Bozorgi Atoei et al. (2013). The authors designed a reliable capacitated supply chain network considering random disruptions in both distribution centers and suppliers.

To the best of our knowledge, there is no attention to extend equilibrium equations in multi-item multi-echelon supply chain in order to achieve one-stage transition probabilities in the related literature. To do so, we developed a bi-product three-echelon SC with full backordering. The considered SC comprises one central warehouse with limited storage space, several identical retailers, and two independent manufacturing plants. We modeled the central warehouse which is investigated upon a continuous review (S-1, S) inventory policy as a (M/M/1) queue model. Besides, a network including two Markov models (M/M/1) for each type of product is also considered.

The remaining of the paper is organized as follows. The proposed three-echelon supply chain structure is elaborated in the ‘Bi-product model’ section. Steps of the proposed structure including proposed assumptions and equilibrium equations are described thoroughly as well. ‘Single-product model’ section describes single-product inventory model in order to compare its performance with that of the developed bi-product model. Proposed PSO algorithm is stated in details in ‘Solution methodology’ section, while experimental results are reported in the ‘Results and discussion’ section. Eventually, remarkable conclusions and future research directions are provided in the ‘Conclusion’ section.

Bi-product model

The notations used in two coming sections are as follows:

● r Number of retailers.

●  λ _ij Demand rate at retailer i for product j, i = 1, 2,…, r; j = 1,2.

● λ _j Demand rate for product j, j = 1,2 (λ _j = ∑ λ _ij ).

● h _j Holding cost rate at central warehouse for product j.

● b _j Backordering cost rate at central warehouse for product j.

● Ch Holding cost at central warehouse in steady state for each product.

● Cb Backordering cost at central warehouse in steady state for each product.

● TC Total cost at central warehouse in steady.

Problem assumptions

In order to describe the developed model further in subsequent sections of the paper, the following assumptions are made:

● Two kinds of products are offered to the customer in the supposed SC.

● Customer demands enter the retailers upon Poisson distributions with rates λ_{i 1} and λ_{i 2} for the two product kinds.

● The accumulation of retailer demands enters the central warehouse with rate λ₁ and λ₂ for the products.

● The corresponding service time and the on-hand inventory at the warehouse are random exponential variables with means 1/μ _j and 1/μ _j ^’, respectively.

● The central warehouse has limited storage space.

● Continuous review (S-1, S) inventory policy controls the warehouse inventory system.

Model description and assumptions

In this study, a bi-product three-echelon supply chain network which consists of r identical retailers, a central warehouse with limited storage space, and two independent manufacturing plants are supposed. The system receives stochastic demands from retailers. Two types of products are offered to the customer who arrived into the retailer nodes. The whole accumulation of customer needs which arrived into the retailers depletes the on-hand inventory at warehouse, if any. Otherwise, stockout situation occurred in the warehouse, and the backlogged orders have to wait to be fulfilled. Moreover, it is assumed that the retailer orders are filled using FIFO policy by the single server. The demand for each product j, j = 1, 2, at each retailer i; i = 1, 2, …, r, which is independent, and distributed upon Poisson distribution with rates λ_{i 1} and λ_{i 2} enter to the central warehouse. The demand rate arrived to the warehouse equals λ₁ and λ₂ for each product j, j = 1, 2, respectively, and the warehouse places orders of products 1 and 2 with rates λ₁ and λ₂, respectively, to the corresponding manufacturing plant, where, λ₁ = ∑ λ_{i 1} and λ₂ = ∑ λ_{i 2}(i = 1,, …, r). Whenever the retailers face available on-hand inventory at the warehouse, the service time (including transportation time from the warehouse to each retailer and warehouse service time) for each product is considered as random exponential variables with means 1/μ _j (j = 1, 2). Otherwise, when a retailer places an order and faces inventory shortage at the warehouse (backordering conditions), the service time (including transportation time from the warehouse to each retailer, warehouse service time, transportation time from the manufacturer to the central warehouse, and manufacturing time) is considered a random exponential variable with mean 1/μ _j ^’(j = 1, 2). With respect to the above described network, the space Markov system is as the one depicted in Figure 1. Figure 1a shows the demand rate of the described network, while the corresponding response rates are depicted in Figure 1b.

Figure 1

The demand rate (a) and the response rate (b) of the supposed system.

The central warehouse holds inventory and applies a continuous review (S-1, S) inventory policy; that is, a replenishment order is forwarded to the manufacturer after each order enters the warehouse. The supposed model seeks a S^* in order to minimize a cost function which captures two different operational cost factors including inventory holding and backordering costs. We modeled the central warehouse as a (M/M/1) queue model with the state space (N ₁ , N ₂ ), where, n ₁ and n ₂ represent stocks on hand of product 1 and product 2 at central warehouse, respectively. Moreover, − S ≤ ∑ _j = 1,2n _j  ≤ S is satisfied. Figure 2 demonstrates the transition diagram of the system. As mentioned earlier, the objective function seeks to minimize the total cost including holding cost of on-hand inventory at the central warehouse and backordering cost of unsatisfied demands based upon the inventory controlling policy (S-1, S) by Equation 1.

Figure 2

Transition diagram of the described system in this paper.

Objective function:

$$\mathrm{Min}z:\mathit{TC}=\mathit{Ch}+\mathit{Cb}.$$

(1)

Subject to:

$$\mathit{Ch}=I.\Pi \left(p,q\right);$$

(2)

$$\mathit{Cb}=b.\Pi \left(p,q\right);$$

(3)

$$\mathit{I}=p^{+}+q^{+};$$

(4)

$$\mathit{b}=p^{-}+q^{-};$$

(5)

$$n_1+n_2\le {\mathit{S}}_{\mathit{max}}$$

(6)

$$n_1+n_2=S*$$

(7)

In the above model, inventory holding costs and backordering costs are estimated by Equations 2 and 3, respectively. Equation 4 calculates on-hand inventory of both products at the warehouse as well as Equation 5 for the unsatisfied demands. The limited storage space of the central warehouse is considered using Equation 6. Finally, Equation 7 shows that the sum of the two kinds of products equals to the optimal on-hand inventory at the supposed warehouse to respond the customers’ needs.

Determining one-stage transition probabilities

The state of the system is defined by (N₁, N₂), where n ₁ and n ₂ denote the number of on-hand stock of product 1 and product 2 at central warehouse, respectively. (N₁, N₂) can be depicted as a matrix. In this regard, we introduce the states matrix that is a ((2 × n₁+ 1) × (2 × n₂+ 1)) matrix as in Figure 3. The states matrix has one-stage transitions among states of the system. In states matrix, the states of the system are divided into four different sections: A, B, C, and D. The central warehouse on-hand stock of both types of products are not available in section A. In section B, on-hand inventory of product 1 is not available while it is sufficient for product 2. In section C, on-hand inventory of product 2 is not available while it is sufficient for product 1. Finally, and in section D, on-hand stock of both types of products are available at the central warehouse.

Figure 3

States matrix.

Equilibrium equations

In order to denote the equilibrium equation in a given state (p, q), all the departure states with state (p, q) as their corresponding destination state are specified. To do so, the system states are divided into nine categories according to their similarities among departure states. States in one category are the ones which have similar departure states. The nine mentioned categories are illustrated in Figure 4. All states which are classified in a category have a similar form of equilibrium equations. The equilibrium equations for the states located in each of the nine categories presented in Figure 3 are computed upon the one-stage transition probabilities. These equations are presented through (8 to 16) for regions 1 to 9, respectively.

$$\left({\lambda }_1+{\lambda }_2\right){\mathrm{\Pi }}_{\mathit{n}1,n2}={\mu }_{\mathit{1}}{\mathrm{\Pi }}_{n1-1,n2}+{\mu }_2{\mathrm{\Pi }}_{n1,n2-1}$$

(8)

$$\left({\lambda }_2+{\mu }_1^{\prime }\right){\mathrm{\Pi }}_{-n1,n2}={\lambda }_1{\mathrm{\Pi }}_{-n1+1,n2}+{\mu }_2{\mathrm{\Pi }}_{-n1,n2-1}$$

(9)

$$\left({\lambda }_1+{\mu }_2^{\prime }\right){\mathrm{\Pi }}_{n1,-n2}={\lambda }_2{\mathrm{\Pi }}_{n1,-n2+1}+{\mu }_1{\mathrm{\Pi }}_{n1-1,-n2}$$

(10)

$$\begin{array}{ll}\left({\mu }_1\prime +{\mu }_2\prime \right){\mathrm{\Pi }}_{-n1,-n2}=& {\lambda }_1{\mathrm{\Pi }}_{-n1+1,-n2}\\ +{\lambda }_2{\mathrm{\Pi }}_{-n1,-n2+1}\end{array}$$

(11)

$$\begin{array}{l}\left({\lambda }_1+{\lambda }_2+{\alpha }_1{\mu }_{1+}{\beta }_1{\mu }_1\prime \right){\mathrm{\Pi }}_{n1-k1,n2}\\ ={\lambda }_1{\mathrm{\Pi }}_{n1-k1+1,n2}+\left({\alpha }_1{\mu }_{1+}{\beta }_1{\mu }_1\prime \right){\mathrm{\Pi }}_{n1-k1-1,n2}\\ +{\mu }_2{\Pi }_{n1-k1,n2-1}\end{array}$$

(12)

$$\begin{array}{l}\left({\lambda }_1+{\lambda }_2+{\alpha }_2{\mu }_{2+}{\beta }_2{\mu }_2\prime \right){\mathrm{\Pi }}_{n1,n2-k2}\\ ={\lambda }_2{\mathrm{\Pi }}_{n1,n2-k2+1}+\left({\alpha }_2{\mu }_{2+}{\beta }_2{\mu }_2\prime \right){\mathrm{\Pi }}_{n1,n2-k2-1}\\ +{\mu }_1{\mathrm{\Pi }}_{n1-1,n2-k2}\end{array}$$

(13)

$$\begin{array}{l}\left({\lambda }_2+{\mu }_1\prime +{\alpha }_2{\mu }_{2+}{\beta }_2{\mu }_2\prime \right){\mathrm{\Pi }}_{-n1,n2-k2}\\ ={\lambda }_2{\Pi }_{-n1,n2-k2+1}+\left({\alpha }_2{\mu }_{2+}{\beta }_2{\mu }_2\prime \right){\mathrm{\Pi }}_{-n1,n2-k2-1}\\ +{\lambda }_1{\Pi }_{-n1+1,n2-k2}\end{array}$$

(14)

$$\begin{array}{l}\left({\lambda }_1+{\mu }_2\prime +{\alpha }_1{\mu }_{1+}{\beta }_1{\mu }_1\prime \right){\mathrm{\Pi }}_{n1-k1,-n2}\\ ={\lambda }_2{\mathrm{\Pi }}_{n1-k1,-n2+1}+\left({\alpha }_1{\mu }_{1+}{\beta }_1{\mu }_1\prime \right){\mathrm{\Pi }}_{n1-k1-1,-n2}\\ +{\lambda }_1{\mathrm{\Pi }}_{-n1-k1+1,-n2}\end{array}$$

(15)

$$\begin{array}{l}\left({\lambda }_1+{\lambda }_2+{\alpha }_1{\mu }_{1+}{\beta }_1{\mu }_1\prime +{\alpha }_2{\mu }_{2+}{\beta }_2{\mu }_2\prime \right){\mathrm{\Pi }}_{n1-k1,n2-k2}\\ ={\lambda }_2{\mathrm{\Pi }}_{n1-k1,n2-k2+1}\\ +\left({\alpha }_1{\mu }_{1+}{\beta }_1{\mu }_1\prime \right){\mathrm{\Pi }}_{n1-k1-1,n2-k2}\\ +\left({\alpha }_2{\mu }_{2+}{\beta }_2{\mu }_2\prime \right){\mathrm{\Pi }}_{n1-k1,n2-k2-1}\\ +{\lambda }_1{\mathrm{\Pi }}_{n1-k1+1,n2-k2}\end{array}$$

(16)

where:

$$k_j=1,2,\dots ,2n_j-1;j=1,2.$$

Figure 4

Different regions of various equilibrium equations.

If p ≤ n ₁ α ₁ = 1 , β ₁ = 0; Otherwise α ₁ = 0, β ₁ = 1 .

If q ≤ n ₂ α ₂ = 1, β ₂ = 0; Otherwise α ₂ = 0, β ₂ = 1 .

In order to solve the above formulated problem with regard to the various numbers of the equilibrium equations as well as their complexity, all equilibrium equations are coded in the form of a matrix in MATLAB software for the first time in this context. In the proposed program, all equation components are transferred to the left side, and then, the equation coefficients, the one-stage transition probability, and the quantities of right-hand side appeared as matrices A, X, and b (i.e., AX = b), respectively. In addition, the constraints of the storage space at the warehouse are added as a violation coefficient to the objective function. It is noted that initial solution is generated randomly in the proposed solution methodology, while one-stage transition probabilities are computed exactly. Problem solution includes a twofold string that represents optimal on-hand inventory of each product at the warehouse.

Single-product models

In order to compare SC performance of the proposed bi-product multi-echelon SC with the single product SC, a network including two Markov models (M/M/1) for each type of product is considered in this section. Note that in this network, the common warehouse holds inventory and applies a continuous review (S _j-1 , S _j ) inventory policy for each type of product; that is, a replenishment order is forwarded to the manufacturer after each order enters the warehouse. The supposed model seeks a S^* _j in order to minimize a cost function which captures two different operational cost factors including inventory holding and backordering costs. Here, the corresponding Markov model (M/M/1) for product j has the state space (N _j ) in which n _j represents on-hand stock of product j at the common warehouse (−S_max≤ S^* _j ≤ S_max). The transition diagram of this system is obtained as shown in Figure 5.

Figure 5

Transition diagram of the single-product SC.

In order to denote the equilibrium equation in a given state (p _j ), all the departure states with state (p _j ) as their corresponding destination state are specified. To do so, system states are divided into three categories according to their similarity among departure states. All states which are classified in a category have a similar form of equilibrium equations. The equilibrium equations for the states located in each of the three categories are computed upon the one-stage transition probabilities. These equations are as the ones in (17 to 19) for regions 1 to 3, respectively.

$${\lambda }_j\mathit{П}\left(n_j\right)={\mu }_j\mathit{П}\left(n_{j-1}\right)$$

(17)

$$\begin{array}{l}\left({\lambda }_j+\alpha {\mu }_j+\mathit{\beta \mu }{\text{'}}_j\right)\mathit{П}\left(n_{j-h}\right)\\ ={\lambda }_j\mathit{П}\left(n_{j-h+1}\right)+\left(\alpha {\mu }_j+\mathit{\beta \mu }{\text{'}}_j\right)\mathit{П}\left(n_{j-h-1}\right);h\\ =1,2,\dots ,2n_j-1\end{array}$$

(18)

$$\left(\alpha {\mu }_j+\mathit{\beta \mu }{\text{'}}_j\right)\mathit{П}\left(-n_j\right)={\lambda }_j\mathit{П}\left(-n_j+1\right)$$

(19)

while:

$$\mathit{If}{p}_j\le {\mathit{n}}_j\alpha =1,\beta =0;\mathit{Otherwise}\alpha =0,\beta =1.$$

The objective function and constraints of the second condition are constructed as the bi-product model. Here, Ch _j , Cb _j , I _j , and b _j denote holding cost, backorder cost, on-hand inventory, and unsatisfied demand of product j, respectively. Optimal solution of the developed model represents optimal on-hand inventory of each product at the warehouse.

Objective function:

$$\mathrm{Min}\mathrm{z}:\mathrm{TC}={\displaystyle {\sum }_j{\mathrm{Ch}}_j}+{\mathrm{Cb}}_j$$

(20)

Subject to:

$${\mathrm{Ch}}_j={\mathrm{I}}_j.\Pi \left(p_j\right);$$

(21)

$${\mathrm{Cb}}_j={\mathrm{b}}_j.\Pi \left(p_j\right);$$

(22)

$${\mathrm{I}}_j=p^{+}{j}_{;}$$

(23)

$${\mathrm{b}}_j=p^{-}{j}_{;}$$

(24)

$$n_j\le S\max$$

(25)

The developed bi-product and single-product models are non-linear integer programming models. In the next section, a solution algorithm is proposed to cope with complexity of the models.

Solution methodology

Having the problem defined, solution methodology is developed to tackle computational complexity of the problem. To do so, a metaheuristic algorithm (i.e., particle swarm optimization) is developed because of two major reasons: numerous numbers of the equilibrium equations as well as their levels of complexity. Moreover, there is no compact mathematical formulation available for the index of the system steady state.

The introduced PSO by Kennedy and Eberhart (1995) and Eberhart and Kennedy (1995) is an evolutionary calculations technique. Particle swarm concept has been driven from the simulation of social behavior. The PSO algorithm works as the behavior of flying birds which exchange their information to solve optimization problems. This algorithm is an optimization technique in real-world spaces, while many of these problems are set in discrete space (Xia and Wu 2005). The PSO solutions are as particles in the position of search space. In order to achieve the best point in the solution space, they collect both information of their experiences and the others’ (Equations 26 and 27). In this regard, they investigate the solution space through exchanging their position and velocity. The velocity is updated by Equation 26. The first part refers to the inertia of previous velocity, while the private particle thinking is denoted by the second part, the ‘cognition’ part. The third part, the ‘social’ part, represents the cooperation among the particles.

$$\begin{array}{l}{V}_i\left(t+1\right)=w\times V_i\left(t\right)+\\ c_1\times r_1\times \left(x_{i-\mathrm{best}}\left(t\right)-x_i\left(t\right)\right)\\ +c_2\times r_2\times \left(x_{\mathrm{gbest}}\left(t\right)-x_i\left(t\right)\right)\end{array}$$

(26)

$$x_i\left(t+1\right)=x_i\left(t\right)+V_i\left(t+1\right)$$

(27)

V _i (t) is called the velocity of particle i in iteration t. In this study, the initial velocity is considered zero. x _i (t) is called the i th particle position, x_{i- best}(t) is called local best solution that shows the best previous position of each particle, x_gbest(t) represents the best position among all particles in the swarm. W as inertial weight balances the global exploration and the local exploitation abilities of the swarm. c₁ and c₂ represent the weight of the stochastic acceleration terms which is assumed to be equal to 2. r₁ and r₂ are random functions to seek better the space in the range [0,1]. The inertial weight is considered 1 in the first iteration and then, slowly reduces in each other iteration by following Equation 28. wdam p is assumed as 0.9:

$$w=w\times \mathit{wdamp}$$

(28)

The V_max equation with search space width that has been presented by Shi and Eberhart (1999) is applied to converge more the search space. As a result of using this approach, particle’s velocity and position must be limited through a defined space width.

An initial solution is generated randomly regarding the constraint of the limited storage space at the central warehouse in order to be a feasible solution. Based on the obtained initial solution, we calculate one-stage transition probabilities certainly by Equations 8 to 19. After computing the transition probabilities, the on-hand inventory of each product as problem solution and objective function values are entered to the PSO algorithm to seek neighbor space of the present solution in order to achieve better one. The above procedure will be repeated up to given number of maximum iterations of the algorithm. The PSO algorithm is implemented by considering population size 20, maximum iteration 100, c₁ = c₂ = 2. Algorithm 1 shows the structure of the proposed solution methodology as pseudocode.

Results and discussion

This section is developed to evaluate the tractability of the proposed programming model in terms of the solution quality and the required computational time. In this regard, some numerical experiments of the considered supply chain network on a set of randomly generated problem instances are performed. The developed models and the proposed algorithm are coded in MATLAB 7.11.0 (R2010b) software on a PC with 2 GHz processor. The holding cost rate and backordering cost rate at central warehouse for each product are generated from a uniform distribution of [5,10], the demand rate for products is uniformly generated in the interval [1,5], the corresponding service rate with the on-hand inventory at the central warehouse is generated from a uniform distribution of [1,10]. Table 1 shows the values of the parameters of the generated instances. The threshold of the optimal on-hand inventory at the warehouse is considered 100 for all cases.

Table 1 Network’s data

It is well known that the quality of an algorithm is significantly influenced by the values of its parameters. In this section, for optimizing the behavior of the proposed algorithm, appropriate tuning of the parameters has been realized using response surface methodology (RSM). RSM is defined as a collection of mathematical and statistical method-based experiential, which can be used to optimize processes. Regression equation analysis is employed to evaluate the response surface model. First, the parameters of the supposed algorithm that statistically have significant impact on the algorithm should be recognized. Each factor is measured at two levels, which can be coded as −1 when the factor is at its low level (L) and +1 when the factor is at its high level (H). The coded variable can be defined as follows:

$$x_i=\frac{r_i-\left(\frac{H+L}{2}\right)}{\left(\frac{H-L}{2}\right)}$$

(29)

where x _i and r _i are coded variable and natural variable, respectively. H and L represent high level and low level of the factor, respectively. Factors and their levels are indicated in Table 2.

Table 2 Parameters and their levels

After developing regression models for each problem size separately, tuned parameters of the proposed PSO are obtained as in Table 3.

Table 3 Tuned parameters of the proposed PSO

Tables 4 and 5 show the solutions and the objective function values of the single and the bi-product models solved by the developed PSO algorithm. Also, the required computational times of the algorithm are reported.

Table 4 Computational results of the single-product model

Table 5 Computational results of the bi-product

As shown, using bi-product model leads to lower total cost of the network. Also, the solutions of the two single-product models violate the capacity of the common warehouse. This result confirms the necessity of considering multi-product models in the real situation where we have many common sources with limited capacity for products. In these experiments, we also evaluate the convergence rate of the PSO algorithm to obtain a solution for all five considered bi-product problems. Figures 6, 7, 8, 9, 10, 11, 12, 13, 14, and 15 illustrate the convergence trend of the solution for each problems 1 to 10, respectively. These figures show that the PSO algorithm is capable to reach a good solution in its early iterations.

Figure 6

Cost diagram of problem 1.

Figure 7

Cost diagram of problem 2.

Figure 8

Cost diagram of problem 3.

Figure 9

Cost diagram of problem 4.

Figure 10

Cost diagram of problem 5.

Figure 11

Cost diagram of problem 6.

Figure 12

Cost diagram of problem 7.

Figure 13

Cost diagram of problem 8.

Figure 14

Cost diagram of problem 9.

Figure 15

Cost diagram of problem 10.

Conclusions

In this paper, a bi-product inventory planning problem is proposed. The problem is developed in a three-echelon SC consisting of r identical retailers, a central warehouse with limited storage space, and two independent manufacturing plants. In this study, demanding process and lead time are stochastic. Customer demands arrived to each retailer following Poisson distribution function with rates λ_{i 1} and λ_{i 2} for products 1 and 2, and the accumulation of demands with rate λ₁ = ∑ λ_{i 1} and λ₂ = ∑ λ_{i 2} which enter the central warehouse responded the demand of each product j by the on-hand inventory at warehouse based upon exponential distribution function with mean 1/μ _j , if any. Otherwise, unsatisfied demands are backlogged. In these circumstances, customer demands are satisfied with mean 1/μ _j ^’. Hence, an (M/M/1) queue model has been developed at the warehouse. Then, the problem with two Markov models (M/M/1) has been developed at the warehouse to evaluate the performance of the first problem. Finally, as depicted in the ‘Results and discussion’ section, the single-product model cannot satisfy the constraint on the warehouse storage space. Moreover, the developed bi-product three-echelon inventory model decreases total network costs significantly, indicating outperformance of the developed bi-product model over the single-product one.

As further research direction, first, it is suggested to consider other assumptions in the considered supply chain to make it more practical, such as more echelons or more products. Second, considering other probability distribution functions for demanding process and service times such as Erlang is recommended. Finally, developing proper exact and inexact algorithm might be of great contribution to the theory of the problem.