Analysis of unreliable bulk queue with statedependent arrivals

Abstract

In this paper, we investigate a single-server Poisson input queueing model, wherein arrivals of units are in bulk. The arrival rate of the units is state dependent, and service time is arbitrary distributed. It is also assumed that the system is subject to breakdown, and the failed server immediately joins the repair facility which takes constant duration to repair the server. By using supplementary variable technique, we obtain the probability generating function of the number of units in the system which is further used to establish some performance indices such as the mean number of units in the system, mean waiting time, etc. Special cases are also discussed. In order to obtain approximate values of system state probabilities, the principle of maximum entropy is employed. Numerical results are also presented to validate the analytical formulae.

Introduction

In many congestion problems of the queueing systems, it is a common phenomenon that the server is always available in the service station without any interruption and the service system never fails. But in some real life examples, these assumptions are not realistic. In many practical activities, we face the situation where service stations may fail and can be repaired by the repairman available in the system. For example, in manufacturing systems, the machine may break down due to some physical problems. Similarly, many other examples are available in the area of computer communication networks and flexible manufacturing systems where the performance of such systems may be affected by service station breakdown.

There is extensive literature on the M/G/1 queue which has been studied in various forms by numerous researchers; some of them are mentioned by Levy and Yechiali (1976), Keilson and Servi (1986), Madan (1999), and many others. The unreliable service systems with repair facility of the server or some other type of service interruptions can be experienced in manufacturing and production process. Among some earlier papers on service interruptions, we refer the papers by Avi-ltzhak and Naor (1963) and Mitrany and Avi-Itzhak (1968) for some fundamental works. Madan (1989), Sengupta (1990), Tang (1997), and Takine and Sengupta (1998) have studied some queueing systems with interruptions, wherein one of the underlying assumptions is that the server immediately joins repair facility as soon as it fails. Li et al. (1997) obtained the reliability analysis of M/G/1 queueing system with server breakdowns and vacations. The concept of essential service and optional service in M/G/1 queue with server breakdowns and repairs was discussed by Wang (2004). Ke and Pearn (2004) described the management policy for single-server model of queueing system wherein the server is unreliable and the arrival of the units depends on server's current status. The cost analysis is also considered to obtain the optimal results of service quality. The homogeneous finite source queue with server subject to breakdowns and repairs was explored by Almasi et al. (2005). Ke (2007) discussed the operating characteristics of single server non-Markovian queueing model with server breakdowns. It is assumed that the arrival of units is in batches and server may breakdowns.

M^x/G/1 queue with random set-up time with a Bernoulli vacation schedule under a restricted admissibility policy to obtain queue size distribution was generalized by Choudhury (2008). Falin (2010) investigated a retrial queueing system, wherein the customer may leave the system on server breakdowns and may join the retrial group for getting service. In his investigation, he studied the steady-state behavior of the generally distributed system. Choudhury and Tadj (2011) considered an unreliable bulk queue vacation model with two phase service, wherein it is assumed that server may breakdowns during any phase of service. It is also considered that server can start the service when he finds at least N customers in the system and wait for getting the service.

Recently, Choudhury and Ke (2012) analysed an unreliable M^x/G/1 queueing system under Bernoulli schedule vacation policy, wherein it is assumed that customer may join the system as retrial customer if his service is not completed on first time service due to any reason and it is also assumed that server may suffer from unpredictable breakdown and delay repair.

The main objective of the maximum entropy principle is to provide a method of estimating an unknown probability distribution which has been widely applied in the field of queueing theory and computer performance analysis. The complex queueing systems by using maximum entropy principle were analysed by several researchers such as Ferdinand (1970), Shore (1982), El-Affendi and Kouvatsos (1983), Kouvatsos (1986), Wu and Chan (1989), Arizono et al. (1991), and the references cited therein. Wang et al. (2007) utilized the MEP technique to analyse a queueing system with multiple vacations and server breakdowns to obtained the approximate values of performance indices. Single server non-Markovian model with removable and unreliable server under (p, N) -policy was discussed by Wang and Huang (2009). In this investigation, they have obtained the expressions for approximate values of queue length distribution for the number of customers in the system and the expected waiting time. By using improved maximum entropy principle, randomized queueing situation with N - policy was considered by Wang et al. (2011) and carried out comparative analysis between the exact and approximate result obtained and showed that it can provide enough accurate result for practical purpose.

Madan (2003) studied the steady-state behavior of M/G/1 queueing system, wherein the units arrive at the system one by one according to Poisson process with uniform arrival rate and the service system is subject to random breakdowns. In many congestion situations, the arrival of units may be in bulk. Due to sudden breakdowns of the server, the arrivals of units may also be affected. For example, if a public telephone system breaks down, some of the customers in the queue depart from the telephone booth without getting the service. Such type of models has also applications in call centers and other computer centers where different types of facilities for arrived customers are available. In fact, the server may be subject to lengthy and unpredictable breakdowns while serving a customer because there may be sudden major fault in the system and the arrival rate of the jobs that arrive during the breakdown period may be different from the arrival rate in the operating state.

The facts discussed above have motivated us to extend the model presented by Madan (2003) to single-server model, wherein the arrival of units is in bulk and follows Poisson process with varying arrival rates depending upon server status which may be in idle state, operating state, and repair state. The layout of the investigation is as follows: The mathematical description of the model is presented in the ‘Model description’ section. The set of steady state equations governing the model is constructed in ‘Governing equations’ section. In the ‘Analysis’ section, we analyse the model to obtain various performance measures. Special cases are deduced in the ‘Special cases’ section by taking appropriate parameter values. In the ‘Maximum entropy results’ section, maximum entropy principle is discussed to find the queue size distribution. Next, the ‘Numerical illustration’ section is devoted to numerical results and sensitivity analysis. Finally, the conclusion is drawn in the ‘Conclusions’ section.

Model description

We consider an M^x/G/1 queueing system wherein the customers arrive according to a Poisson process with state-dependent rates. The service system is subject to random breakdowns in working or idle state. As soon as the server fails, it immediately joins the repair facility, which performs repair work in constant duration. The service times of the units follow arbitrary distribution. The life time of the server is exponentially distributed. The notations used in the formulation of the model are as follows:

• λ₁, λ₂, λ₃: Mean arrival rate of the units when the server is in idle state, busy state, and under repair server, respectively.

• B(v), b(v): Distribution and density functions of the service time, respectively.

• μ(x)dx: The conditional probability of completion of service during the interval (x, x + dx) with elapsed time x of the unit which is in service.

• α dt: The probability at which the system may fail during time interval (t, t + dt).

• d: The duration of the repair time of the failed system.

• ρ: Traffic intensity

• N: Number of units in the queue, excluding the unit which one is in service (≥0) with elapsed service time x.

• W _n (t, x): The probability of n units in the queue excluding one being served with elapsed time x when server is busy at time t.

• R _n (t): The probability of n units in the queue at time t when the broken down server is under repair.

• Q(t): The probability that there are no units in the system and the server is in idle state at time t.

• K _r : The probability of r arrivals during a repair time period.

• C _i : Probability mass function of batch size X.

• C _r ^(k): The probability that there are r units during k batches arrives.

• P _q (z): The probability generating function of the queue length, whether the server is in operating state or in breakdown state.

• P(z), C(z): The probability generating functions of the number of units in the system and for bulk size, respectively.

• X, E(X), E(X⁽²⁾): The random variable of batch size of the arriving units, the first and second factorial moments of batch size of the arrived units, respectively.

• E(B), E(B²): First and second moments, respectively, of the service time distribution.

Denote

$$\begin{array}{c}{W}_n\left(x\right)=\underset{t\to \infty }{{\displaystyle \lim }}{W}_n\left(t,x\right);W_n=\underset{t\to \infty }{{\displaystyle \lim }}{W}_n\left(t\right);\\ R_n=\underset{t\to \infty }{{\displaystyle \lim }}{R}_n\left(t\right);Q=\underset{t\to \infty }{{\displaystyle \lim }}Q\left(t\right).\end{array}$$

Also,

$$\mu \left(x\right)=\frac{b\left(x\right)}{1-B\left(x\right)};$$

(1)

$$b\left(v\right)=\mu \left(v\right)exp.\left[-{\displaystyle \underset{0}{\overset{v}{\int }}\mu \left(x\right)\mathit{dx}}\right];$$

(2)

$$W_n\left(t\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}{W}_n\left(x,t\right)\mathit{dx}};$$

(3)

$$K_r={\displaystyle \sum _{k=0}^r\frac{e^{-{\lambda }_{3}d}{\left({\lambda }_{3}d\right)}^k}{k!}{C}_r^{\left(k\right)}},r=0,1,2...$$

(4)

The steady-state equations

In this section, we formulate the steady state equations of the system by using the probability reasoning as follows:

$$\frac{d}{\mathit{dx}}{W}_n\left(x\right)+\left({\lambda }_2+\alpha +\mu \left(x\right)\right)W_n\left(x\right)={\lambda }_2{\displaystyle \sum _{k=1}^n{C}_k{W}_{n-k}\left(x\right)};n\ge 1$$

(5a)

$$\frac{d}{\mathit{dx}}{W}_0\left(x\right)+\left({\lambda }_2+\alpha +\mu \left(x\right)\right)W_0\left(x\right)=0;$$

(5b)

$$\left({\lambda }_1+\alpha \right)Q={\displaystyle \underset{0}{\overset{\infty }{\int }}{W}_0\left(x\right)\mu \left(x\right)\mathit{dx}+R_0{K}_0};$$

(5c)

$$R_n=\alpha W_{n-1};n\ge 1;$$

(5d)

$$R_0=\mathit{\alpha Q}.$$

(5e)

For the solution of above set of equations, the following boundary conditions are

$$\begin{array}{c}{W}_n\left(0\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}{W}_{n+1}\left(x\right)\mu \left(x\right)\mathit{dx}+R_0{K}_{n+1}}+R_1{K}_n\\ +\dots +R_{n+1}{K}_0+{\lambda }_1{C}_{n+1}Q;n\ge 0.\end{array}$$

(6)

We define the following probability generating functions

$$\begin{array}{l}W\left(x,z\right)={\displaystyle \sum _{n=0}^{\infty }{W}_n}\left(x\right)z^n;W\left(z\right)\\ ={\displaystyle \sum _{n=0}^{\infty }{W}_n}{z}^n;R\left(z\right)={\displaystyle \sum _{n=0}^{\infty }{R}_n}{z}^n;\end{array}$$

(7a)

$$C\left(z\right)={\displaystyle \sum _{k=1}^{\infty }{C}_k{z}^k}.$$

(7b)

Analysis

In this section, we obtain the probability generating functions of the number of units in the system. By using Equations (5a) and (5b), we have

$$\frac{d}{\mathit{dx}}W\left(x,z\right)+\left(p_{\alpha }+\mu \left(x\right)\right)W\left(x,z\right)=0.$$

(8)

Similarly, Equations (5d) and (5e) give

$$R\left(z\right)=\alpha \left(Q+\mathit{zW}\left(z\right)\right).$$

(9)

Also, from Equation (6), we have

$$\begin{array}{c}\mathit{zW}\left(0,z\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}W\left(x,z\right)\mu \left(x\right)\mathit{dx}+R\left(z\right)e^{-r_{\alpha }}}-K_0{R}_0\\ +{\lambda }_{1}C\left(z\right)Q-{\displaystyle \underset{0}{\overset{\infty }{\int }}{W}_0}\left(x\right)\mu \left(x\right)\mathit{dx},\end{array}$$

(10)

where ${\displaystyle \sum _{n=0}^{\infty }{K}_n}{z}^n=e^{-r_{\alpha }}$.

By using Equation (5c), Equation (10) can be written as

$$\mathit{zW}\left(0,z\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}W\left(x,z\right)\mu \left(x\right)\mathit{dx}+R\left(z\right)e^{-r_{\alpha }}}-q_{\alpha }Q.$$

(11)

On integration between the limits 0 and x, Equation (8) gives

$$W\left(x,z\right)=W\left(0,z\right)exp.\left(-p_{\alpha }x\right)exp.\left\{-{\displaystyle \underset{0}{\overset{x}{\int }}\mu \left(t\right)\mathit{dt}}\right\},$$

(12)

where W(0, z) can be obtained from Equation (11).

On multiplying Equation (12) by μ(x) and integrating with respect to x and by taking limit 0 to ∞ and using Equation (2), we get

$$\begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}W\left(x,z\right)\mu \left(x\right)\mathit{dx}=W\left(0,z\right){\displaystyle \underset{0}{\overset{\infty }{\int }}exp.\left(-p_{\alpha }x\right)b\left(x\right)\mathit{dx}}}\hfill \\ =W\left(0,z\right)\overline{b}\left(p_{\alpha }\right),\hfill \end{array}$$

(13)

where $\overline{b}\left(p_{\alpha }\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}exp\left(-p_{\alpha }x\right)b\left(x\right)\mathit{dx}}$

is the Laplace transform of the service time density function b(x).

Here,

$$\begin{array}{l}{p}_{\alpha }=\left({\lambda }_2-{\lambda }_{2}C\left(z\right)+\alpha \right),q_{\alpha }=\left({\lambda }_1-{\lambda }_{1}C\left(z\right)+\alpha \right),\\ r_{\alpha }={\lambda }_{3}d\left(1-C\left(z\right)\right).\end{array}$$

Theorem 1

The probability generating function of the queue length, whether the server is in operating state or in broken down state is

$$P_q\left(z\right)=\frac{\left[\left[1-\overline{b}\left(p_{\alpha }\right)]\left[\alpha e^{-r_{\alpha }}-q_{\alpha }\right]+\alpha \{z\left(p_{\alpha }-q_{\alpha }\right)+\left(z{q}_{\alpha }-p_{\alpha }\right)\overline{b}\left(p_{\alpha }\right)\right\}\right]Q}{p_{\alpha }\left\{z-\overline{b}\left(p_{\alpha }\right)\right\}-\left\{1-\overline{b}\left(p_{\alpha }\right)\right\}\mathit{\alpha z}{e}^{-r_{\alpha }}}$$

where Q is given by Equation (32).

Proof

By using the above mentioned steady-state equations and boundary conditions, we obtain the probability generating function of the queue length.

[For proof, see Appendix 1].

Theorem 2

The probability generating function of the number of units in the system is

$$P\left(z\right)=\left(1+\mathit{\alpha z}\right)\left[\frac{z\left(p_{\alpha }-q_{\alpha }\right)+\left(z{q}_{\alpha }-p_{\alpha }\right)\overline{b}\left(p_{\alpha }\right)}{p_{\alpha }\left\{z-\overline{b}\left(p_{\alpha }\right)\right\}-\left\{1-\overline{b}\left(p_{\alpha }\right)\right\}\mathit{\alpha z}{e}^{-r_{\alpha }}}\right]Q.$$

Proof

[For proof, see Appendix 2].

The expected number of units in the queue can be obtained as

$$L_q=\underset{z\to 1}{\lim }\frac{d}{\mathit{dz}}{P}_q\left(z\right)=\frac{D\text{'}\left(1\right)N"\left(1\right)-N\text{'}\left(1\right)D"\left(1\right)}{2{\left[D\text{'}\left(1\right)\right]}^2},$$

(14)

where

$$N\text{'}\left(1\right)=\left[\begin{array}{l}\left\{\alpha {\lambda }_3\mathit{dE}\left(X\right)+{\lambda }_{1}E\left(X\right)-\alpha \left({\lambda }_2-{\lambda }_1\right)E\left(X\right)\right\}\\ +\left\{\mathit{\alpha E}\left(X\right)\left({\lambda }_2-{\lambda }_1\right)+{\alpha }^2-\alpha {\lambda }_3\mathit{dE}\left(X\right)-{\lambda }_{1}E\left(X\right)\right\}\overline{b}\left(\alpha \right)\end{array}\right]Q;$$

$$\begin{array}{ll}N"\left(1\right)=\hfill & \left[\left\{\begin{array}{l}\alpha {\lambda }_3^2{d}^2{\left(E\left(X\right)\right)}^2+\alpha {\lambda }_3\mathit{dE}\left(X^{\left(2\right)}\right)+{\lambda }_{1}E\left(X^{\left(2\right)}\right)\\ -\alpha \left({\lambda }_2-{\lambda }_1\right)\left(2E(X\right)+E\left(X^{\left(2\right)}\right)\end{array}\right\}\right.\hfill \\ +2{\lambda }_{2}E\left(X\right)\left\{\alpha {\lambda }_3\mathit{dE}\left(X\right)+{\lambda }_{1}E\left(X\right)-{\alpha }^2+\mathit{\alpha E}\left(X\right)\left({\lambda }_1-{\lambda }_2\right)\right\}\overline{b}\text{'}\left(\alpha \right)\hfill \\ \left.-\left\{\begin{array}{l}\mathit{\alpha E}\left(X^{\left(2\right)}\right)\left({\lambda }_1-{\lambda }_2\right)+2\alpha {\lambda }_{1}E\left(X\right)+\alpha {\left({\lambda }_3\mathit{dE}\left(X\right)\right)}^2\\ +\alpha {\lambda }_3\mathit{dE}\left(X^{\left(2\right)}\right)+{\lambda }_{1}E\left(X^{\left(2\right)}\right)\end{array}\right\}\overline{b}\left(\alpha \right)\right]Q\hfill \end{array}$$

$$D\text{'}\left(1\right)=\left[\overline{b}\left(\alpha \right)\left(\alpha +{\lambda }_{2}E\left(X\right)+{\lambda }_3\mathit{\alpha dE}\left(X\right)\right)-\left({\lambda }_2+{\lambda }_3\mathit{\alpha d}\right)E\left(X\right)\right];$$

$$\begin{array}{l}D"\left(1\right)=\left[-\left\{2{\lambda }_{2}E\left(X\right)+{\lambda }_{2}E\left(X^{\left(2\right)}\right)+2\alpha {\lambda }_3\mathit{dE}\left(X\right)+\alpha {\left({\lambda }_3\mathit{dE}\left(X\right)\right)}^2+\alpha {\lambda }_3\mathit{dE}\left(X^{\left(2\right)}\right)\right\}\right.\\ -2\left\{\alpha +{\lambda }_{2}E\left(X\right)+\alpha {\lambda }_3\mathit{dE}\left(X\right)\right\}{\lambda }_{2}E\left(X\right)\overline{b\text{'}}\left(\alpha \right)\\ \left.+\left\{{\lambda }_{2}E\left(X^{\left(2\right)}\right)+2\alpha {\lambda }_3\mathit{dE}\left(X\right)+\alpha {\lambda }_3^2{d}^2{\left(E\left(X\right)\right)}^2+\alpha {\lambda }_3\mathit{dE}\left(X^{\left(2\right)}\right)\right\}\overline{b}\left(\alpha \right)\right]\end{array}$$

with

$$\begin{array}{l}Q=\frac{\left\{\alpha \overline{b}\left(\alpha \right)-\left(1-\overline{b}\left(\alpha \right)\right)\left({\lambda }_2+{\lambda }_3\mathit{d\alpha }\right)E\left(X\right)\right\}}{\left(1+\alpha \right)\left\{\left(1-\overline{b}\left(\alpha \right)\right)\left({\lambda }_1-{\lambda }_2\right)E\left(X\right)+\alpha \overline{b}\left(\alpha \right)\right\}};\\ \rho =1-Q.\end{array}$$

• The average waiting time in the queue can be obtained by using Little’s formula as

  $$\begin{array}{l}{W}_q=\frac{L_q}{{\lambda }_{\mathit{eff}}E\left(X\right)};\\ {\lambda }_{\mathit{eff}}=\left\{{\lambda }_{1}Q+{\lambda }_{2}W\left(1\right)+{\lambda }_{3}R\left(1\right)\right\}.\end{array}$$

  (15a)

• The units in the system can be obtained as

  $$L_s=L_q+\rho .$$

  (15b)

Special cases

In this section, we establish key performance measures of some models as special cases of our model.

Unreliable M^x/M/1 queue with state-dependent arrival rates

In this case, the queue length is obtained by using

$$L_q=\underset{z\to 1}{\lim }\frac{d}{\mathit{dz}}{P}_q\left(z\right)=\frac{D\text{'}\left(1\right)N"\left(1\right)-N\text{'}\left(1\right)D"\left(1\right)}{2{\left[D\text{'}\left(1\right)\right]}^2},$$

(16)

where

$$\begin{array}{l}N\text{'}\left(1\right)=\left[\begin{array}{l}\left\{\alpha {\lambda }_3\mathit{dE}\left(X\right)+{\lambda }_{1}E\left(X\right)-\alpha \left({\lambda }_2-{\lambda }_1\right)E\left(X\right)\right\}\\ +\left\{\mathit{\alpha E}\left(X\right)\left({\lambda }_2-{\lambda }_1\right)+{\alpha }^2-\alpha {\lambda }_3\mathit{dE}\left(X\right)-{\lambda }_{1}E\left(X\right)\right\}\left(\frac{\mu }{\alpha +\mu }\right)\end{array}\right]Q;\end{array}$$

$$\begin{array}{ll}N"\left(1\right)=\hfill & \left[\left\{\alpha {\lambda }_3^2{d}^2{\left(E\left(X\right)\right)}^2+\alpha {\lambda }_3\mathit{dE}\left(X^{\left(2\right)}\right)+{\lambda }_{1}E\left(X^{\left(2\right)}\right)-\alpha \left({\lambda }_2-{\lambda }_1\right)(2E\left(X\right)+E\left(X^{\left(2\right)}\right)\right\}\right.\hfill \\ +2{\lambda }_{2}E\left(X\right)\left\{\alpha {\lambda }_3\mathit{dE}\left(X\right)+{\lambda }_{1}E\left(X\right)-{\alpha }^2+\mathit{\alpha E}\left(X\right)\left({\lambda }_1-{\lambda }_2\right)\right\}\left(\frac{-\mu }{{\left(\alpha +\mu \right)}^2}\right)\hfill \\ \left.-\left\{\mathit{\alpha E}\left(X^{\left(2\right)}\right)\left({\lambda }_1-{\lambda }_2\right)+2\alpha {\lambda }_{1}E\left(X\right)+\alpha {\left({\lambda }_3\mathit{dE}\left(X\right)\right)}^2+\alpha {\lambda }_3\mathit{dE}\left(X^{\left(2\right)}\right)+{\lambda }_{1}E\left(X^{\left(2\right)}\right)\right\}\left(\frac{\mu }{\alpha +\mu }\right)\right]Q\hfill \end{array};$$

$$D\text{'}\left(1\right)=\left[\left(\alpha +{\lambda }_{2}E\left(X\right)+{\lambda }_3\mathit{\alpha dE}\left(X\right)\right)\left(\frac{\mu }{\alpha +\mu }\right)-\left({\lambda }_2+{\lambda }_3\mathit{\alpha d}\right)E\left(X\right)\right];$$

$$\begin{array}{ll}D"\left(1\right)=\hfill & \left[-\left\{2{\lambda }_{2}E\left(X\right)+{\lambda }_{2}E\left(X^{\left(2\right)}\right)+2\alpha {\lambda }_3\mathit{dE}\left(X\right)+\alpha {\left({\lambda }_3\mathit{dE}\left(X\right)\right)}^2+\alpha {\lambda }_3\mathit{dE}\left(X^{\left(2\right)}\right)\right\}\right.\hfill \\ -2\left\{\alpha +{\lambda }_{2}E\left(X\right)+\alpha {\lambda }_3\mathit{dE}\left(X\right)\right\}{\lambda }_{2}E\left(X\right)\left(\frac{-\mu }{{\left(\alpha +\mu \right)}^2}\right)\hfill \\ \left.+\left\{{\lambda }_{2}E\left(X^{\left(2\right)}\right)+2\alpha {\lambda }_3\mathit{dE}\left(X\right)+\alpha {\lambda }_3^2{d}^2{\left(E\left(X\right)\right)}^2+\alpha {\lambda }_3\mathit{dE}\left(X^{\left(2\right)}\right)\right\}\left(\frac{\mu }{\alpha +\mu }\right)\right]\hfill \end{array};$$

$$Q=\frac{\left\{\mu -\left({\lambda }_2+{\lambda }_3\mathit{d\alpha }\right)E\left(X\right)\right\}}{\left(1+\alpha \right)\left\{\left({\lambda }_1-{\lambda }_2\right)E\left(X\right)+\mu \right\}}.$$

Reliable M^x/G/1 queue with state-dependent arrival rates

For this model, the queue length becomes

$$L_q=\frac{{\lambda }_1\left\{{\lambda }_2{\left(E\left(X\right)\right)}^{2}E\left(B^2\right)+E\left(X^{\left(2\right)}\right)E\left(B\right)\right\}}{2\left(1-{\lambda }_{2}E\left(X\right)E\left(B\right)\right)\left(1+\left({\lambda }_1-{\lambda }_2\right)E\left(X\right)E\left(B\right)\right)}.$$

(17)

Reliable M^x/G/1 queue with homogeneous arrival rates

In this case, the queue length is given by

$$L_q=\frac{\left\{{\lambda }^2{\left(E\left(X\right)\right)}^{2}E\left(B^2\right)+\mathit{\lambda E}\left(X^{\left(2\right)}\right)E\left(B\right)\right\}}{2\left(1-\mathit{\lambda E}\left(X\right)E\left(B\right)\right)}.$$

(18)

Reliable M/G/1 queue with state-dependent arrival rates

The queue length can be obtained by setting

$$L_q=\frac{{\lambda }_1{\lambda }_{2}E\left(B^2\right)}{2\left(1-{\lambda }_{2}E\left(B\right)\right)\left(1+\left({\lambda }_1-{\lambda }_2\right)E\left(B\right)\right)}.$$

(19)

Unreliable M/G/1 queue with homogeneous arrival rates

In this case, queue length can be determined as

$$L_q=\underset{z\to 1}{\lim }\frac{d}{\mathit{dz}}{P}_q\left(z\right)=\frac{D\text{'}\left(1\right)N"\left(1\right)-N\text{'}\left(1\right)D"\left(1\right)}{2{\left[D\text{'}\left(1\right)\right]}^2},$$

(20)

where

$$\begin{array}{l}N\text{'}\left(1\right)=\left[\left\{\mathit{\alpha \lambda d}+\lambda \right\}+\left\{{\alpha }^2-\alpha {\lambda }_{3}d-{\lambda }_1\right\}\overline{b}\left(\alpha \right)\right]Q\hfill \\ N"\left(1\right)=\left[\alpha {\lambda }^2{d}^2\right.+2\lambda \{\mathit{\alpha \lambda d}+\lambda -{\alpha }^2\}\overline{b}\text{'}\left(\alpha \right)\left.-\left\{2\mathit{\alpha \lambda }+\alpha {\lambda }^2\right\}\overline{b}\left(\alpha \right)\right]Q\hfill \\ D\text{'}\left(1\right)=\left[\overline{b}\left(\alpha \right)\left(\alpha +\lambda +\mathit{\lambda \alpha d}\right)-\left(\lambda +\mathit{\lambda \alpha d}\right)\right]\hfill \\ D"\left(1\right)=\left[-\left\{2\lambda +2\mathit{\alpha \lambda d}+\alpha {\left(\mathit{\lambda d}\right)}^2\right\}\right.-2\{\alpha +\lambda +\mathit{\alpha \lambda d}\}\lambda \overline{b\text{'}}\left(\alpha \right)\\ \left.+\left\{2\mathit{\text{αλd}}+\alpha {\lambda }_3^2{d}^2\right\}\overline{b}\left(\alpha \right)\right]\\ Q=\frac{\left\{\alpha \overline{b}\left(\alpha \right)-\left(1-\overline{b}\left(\alpha \right)\right)\left(\lambda +\mathit{\lambda d\alpha }\right)\right\}}{\alpha \left(1+\alpha \right)\overline{b}\left(\alpha \right)}\end{array}$$

In this case, our model reduces to M/G/1 queue with uniform arrival rates with time-homogeneous breakdowns and deterministic repair times [see Madan (2003)].

Reliable M/G/1 queue with homogeneous arrival rates

The queue length is

$$L_q=\frac{{\lambda }^{2}E\left(B^2\right)}{2\left(1-\mathit{\lambda E}\left(B\right)\right)}.$$

(21)

Equation (21) is a well-known Pollaczec-Khinchine formula for M/G/1 queue [see Kashyap and Chaudhary (1988) and Medhi (1982)].

Maximum entropy results

In this section, we describe the maximum entropy principle to obtain the estimate of the probability distributions of the queue size and determine the steady-state probabilities for complex queuing systems where the exact probability distribution cannot be found. We formulate the maximum entropy model as follows:

Consider entropy function Z of the bulk arrival queue with unreliable server of the form

$$Z=-QlogQ-{\displaystyle \sum _{n=0}^{\infty }{W}_{n}log{W}_n-}{\displaystyle \sum _{n=0}^{\infty }{R}_{n}log{R}_n}.$$

(22)

The maximum entropy solutions for the model are obtained by maximizing Equation (22) subject to the following constraints:

$$Q+{\displaystyle \sum _{n=0}^{\infty }{W}_n+}{\displaystyle \sum _{n=0}^{\infty }{R}_n}=1;\mathrm{Q}={\eta }_0=1-\rho ;$$

(23a)

$${\displaystyle \sum _{n=0}^{\infty }{W}_n}={\eta }_1=W\left(1\right);$$

(23b)

$${\displaystyle \sum _{n=0}^{\infty }{R}_n}={\eta }_2=R\left(1\right);$$

(23c)

$${\displaystyle \sum _{n=1}^{\infty }n{W}_n+}{\displaystyle \sum _{n=1}^{\infty }n{R}_n}=L_q.$$

(23d)

Theorem 3: The steady-state probabilities of the state-dependent bulk arrival queue with unreliable server for different states are given as

$$W_n={\eta }_1\left(\frac{{\eta }_1+{\eta }_2}{{\eta }_1+{\eta }_2+L_q}\right){\left(\frac{L_q}{{\eta }_1+{\eta }_2+L_q}\right)}^n;$$

(24a)

$$R_n={\eta }_2\left(\frac{{\eta }_1+{\eta }_2}{{\eta }_1+{\eta }_2+L_q}\right){\left(\frac{L_q}{{\eta }_1+{\eta }_2+L_q}\right)}^n.$$

(24b)

Proof: [For proof, see Appendix 3].

Numerical illustration

In this section, we present the numerical illustration to evaluate the queue size distribution for unreliable bulk queueing model by using analytical results derived in previous section. It is assumed that the batch size of the units follows a geometrical distribution with $E\left(X\right)=\frac{q}{p}$, $E\left(X^2\right)=\frac{q\left(1+q\right)}{p^2}$ ; q = 1 − p. The service time is generally distributed with deterministic repair time $\left(\frac{1}{d}>\alpha \right)$. To be more specific, we assume that the service time is Erlangian (E _k ) queuing model with $E\left(B\right)=\frac{1}{\mu }$, $E\left(B^2\right)=\frac{k+1}{k{\mu }^2}$, $\overline{b}\left(\alpha \right)={\left(\frac{\mathit{k\mu }}{\alpha +\mathit{k\mu }}\right)}^k$, $\overline{b}\text{'}\left(\alpha \right)=\frac{-k{\left(\mathit{k\mu }\right)}^k}{{\left(\alpha +\mathit{k\mu }\right)}^{k+1}}$. For computation purpose, we set default parameters as α =. 21, d = 1.5, λ₁ = 1.2λ, λ₂ = λ, λ₃=.8λ. In Tables 1 and 2, we observe that queue length (L _q ) and waiting time (W _q ) decrease with the increase in service time but increase with the increase in the arrival rate of the units. It is also noticed that the queue length (L _q ) and waiting time (W _q ) increase significantly with the increase in the number of service phases (k). The approximate values of steady-state probabilities W _n and R _n by using maximum entropy principle are summarized in Table 3. The value of Q is obtained as .4,468 by using the formula given by Equation (32).

Figure 1

L _q on λ vs. E ( X ) for M / E 4/1 model.

Figure 2

L _q on μ vs. E ( X ) for M / E 4/1 model.

Table 1 L _q ( L _s ) by varying μ and λ for α = .21, d = 1.5, E ( X ) = 3, λ ₁ = 1.2 λ , λ ₂ = λ , λ ₃ = .8 λ

Table 2 W _q ( W _s ) by varying μ and λ for α = .21, d = 1.5, E ( X ) = 3, λ ₁ = 1.2 λ , λ ₂ = λ , λ ₃ = .8 λ

Table 3 Steady-state probabilities W _n and R _n ( α =.21, d = 1.5, Q = .4,468, E ( X ) = 2, λ ₁ = 1.2, λ ₂ = 1, λ ₃ =. 8, k = 4, μ = 6)

Figure 3

L _q on d vs. E ( X ) for M / E 4/1 model.

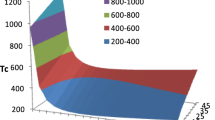
Figure 1 exhibits the queue length (L _q ) by varying homogenous arrival rates (λ₁ = λ₂ = λ₃ = λ) and heterogeneous arrival rates (λ₁ = 1.2λ, λ₂ = λ, λ₃=.8λ) with mean batch size 1(2) for default parameters α =.21, d = 1.5, μ = 6, k = 4. This figure reveals that the queue length (L _q ) increases with the increase in arrival rate (λ) as well as mean batch size E(X). Figure 2 exhibits the queue length (L _q ) by varying service time (μ) and mean batch size E(X) for default parameters α =.21, d = 1.5, λ₁ = 1.5, λ₂ = 1.25, λ₃ = 1, k = 4. It is observed that the queue length (L _q ) decreases with the increase in service time (μ) but it increases with the increase in mean batch size E(X). Figure 3 exhibits the queue length (L _q ) by varying repair time (d) and mean batch size E(X) for default parameters fixed as α =.21, λ₁ = 1.5, λ₂ = 1.25 λ₃ = 1, k = 4, μ = 6. It is noticed that the queue length (L _q ) increases with the increase in repair time (d) and batch size mean E(X).

Finally, we conclude that

• When arrival rate (service rate) increases, the queue length and waiting time increase (decrease); this situation matches with our expectation in various real life congestion problems.

• The queue length increases with the increase in repair time as well as in batch size of the arriving units.

• As many situations can be observed in production/manufacturing systems where the server is unreliable and arrival of units are in bulk, the queue length increases with the increase in the number of service phases.

Conclusions

In this investigation, we have studied the single server queueing model with vacation, wherein arrivals of units are in bulk. By incorporating the state-dependent arrival rate of units and server breakdowns, our model deals with more versatile and realistic scenario of congestion problems. The suggested method determines the queue length and other performance indices in explicit form. For the real life situations, where the arrival of units depends on the server status, such performance indices established may be very helpful in the designing and development of many systems in the field of computer system, manufacturing system, telecommunication networks, etc. The model studied can be further extended for retrial queue and N - policy queue.

Appendices

Appendix 1 Proof of Theorem 1

From Equations (11) and (13), we have

$$W\left(0,z\right)=\frac{R\left(z\right)e^{-r_{\alpha }}-q_{\alpha }Q}{z-\overline{b}\left(p_{\alpha }\right)}.$$

(25)

On integrating Equation (12) with respect to x, we have

$$W\left(z\right)=W\left(0,z\right)\left[\frac{1-\overline{b}\left(p_{\alpha }\right)}{p_{\alpha }}\right].$$

(26)

By using Equation (25), Equation (26) becomes

$$W\left(z\right)=\left[\frac{1-\overline{b}\left(p_{\alpha }\right)}{p_{\alpha }}\right]\left[\frac{R\left(z\right)e^{-r_{\alpha }}-q_{\alpha }Q}{z-\overline{b}\left(p_{\alpha }\right)}\right].$$

(27)

On using Equation (9), Equation (27) becomes

$$W\left(z\right)=\left[\frac{1-\overline{b}\left(p_{\alpha }\right)}{p_{\alpha }}\right]\left[\frac{\alpha \left(Q+\mathit{zW}\left(z\right)\right)e^{-r_{\alpha }}-q_{\alpha }Q}{z-\overline{b}\left(p_{\alpha }\right)}\right].$$

(28)

On simplification, Equation (28) gives

$$W\left(z\right)=\frac{\left[1-\overline{b}\left(p_{\alpha }\right)\right]\left[\alpha e^{-r_{\alpha }}-q_{\alpha }\right]Q}{p_{\alpha }\left[z-\overline{b}\left(p_{\alpha }\right)\right]-\left[1-\overline{b}\left(p_{\alpha }\right)\right]\mathit{\alpha z}{e}^{-r_{\alpha }}}.$$

(29)

To obtain the value of Q, we use the normalizing condition

$$W\left(1\right)+R\left(1\right)+Q=1.$$

(30)

From Equation (29), we have

$$\begin{array}{l}W\left(1\right)=\underset{z\to 1}{\lim }W\left(z\right)\\ =\frac{\left(1-\overline{b}\left(\alpha \right)\right)\left({\lambda }_3\mathit{\alpha d}+{\lambda }_1\right)E\left(X\right)Q}{\alpha \overline{b}\left(\alpha \right)-\left(1-\overline{b}\left(\alpha \right)\right)\left({\lambda }_2+{\lambda }_3\mathit{d\alpha }\right)E\left(X\right)},\end{array}$$

where $\overline{b}\left(\alpha \right)=E\left(e^{-\mathit{\alpha x}}\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-\mathit{\alpha x}}b\left(x\right)\mathit{dx}.}$ From Equation (9), we have

$$R\left(1\right)=\frac{\mathit{\alpha Q}\left\{\alpha \overline{b}\left(\alpha \right)+\left(1-\overline{b}\left(\alpha \right)\right)\left({\lambda }_1-{\lambda }_2\right)E\left(X\right)\right\}}{\left[\alpha \overline{b}\left(\alpha \right)-\left(1-\overline{b}\left(\alpha \right)\right)\left({\lambda }_2+{\lambda }_3\mathit{d\alpha }\right)E\left(X\right)\right]}.$$

(31)

From Equation (30), we get

$$Q=\frac{\left\{\alpha \overline{b}\left(\alpha \right)-\left(1-\overline{b}\left(\alpha \right)\right)\left({\lambda }_2+{\lambda }_3\mathit{d\alpha }\right)E\left(X\right)\right\}}{\left(1+\alpha \right)\left\{\left(1-\overline{b}\left(\alpha \right)\right)\left({\lambda }_1-{\lambda }_2\right)E\left(X\right)+\alpha \overline{b}\left(\alpha \right)\right\}}.$$

(32)

On putting the value of Q in Equation (29), we have

$$\begin{array}{l}W\left(z\right)=\\ \left[\frac{\left\{1-\overline{b}\left(p_{\alpha }\right)\left\}\right\{\alpha e^{-r_{\alpha }}-q_{\alpha }\right\}}{p_{\alpha }\left\{z-\overline{b}\left(p_{\alpha }\right)\right\}-\left\{1-\overline{b}\left(p_{\alpha }\right)\right\}\mathit{\alpha z}{e}^{-r_{\alpha }}}\right].\left[\frac{\left\{\alpha \overline{b}\left(\alpha \right)-\left(1-\overline{b}\left(\alpha \right)\right)\left({\lambda }_2+{\lambda }_3\mathit{d\alpha }\right)E\left(X\right)\right\}}{\left(1+\alpha \right)\left\{\left(1-\overline{b}\left(\alpha \right)\right)\left({\lambda }_1-{\lambda }_2\right)E\left(X\right)+\alpha \overline{b}\left(\alpha \right)\right\}}\right].\end{array}$$

(33)

On using Equations (32) and (33) in Equation (9), we obtain

$$\begin{array}{l}R\left(z\right)=\left[\frac{\alpha \left\{z\left(p_{\alpha }-q_{\alpha }\right)+\left(z{q}_{\alpha }-p_{\alpha }\right)\overline{b}\left(p_{\alpha }\right)\right\}}{p_{\alpha }\left\{z-\overline{b}\left(p_{\alpha }\right)\right\}-\left\{1-\overline{b}\left(p_{\alpha }\right)\right\}\mathit{\alpha z}{e}^{-r_{\alpha }}}\right]\\ \times \left[\frac{\left\{\alpha \overline{b}\left(\alpha \right)-\left(1-\overline{b}\left(\alpha \right)\right)\left({\lambda }_2+{\lambda }_3\mathit{d\alpha }\right)E\left(X\right)\right\}}{\left(1+\alpha \right)\left\{\left(1-\overline{b}\left(\alpha \right)\right)\left({\lambda }_1-{\lambda }_2\right)E\left(X\right)+\alpha \overline{b}\left(\alpha \right)\right\}}\right].\end{array}$$

(34)

On adding Equations (33) and (34), we have

$$P_q\left(z\right)=W\left(z\right)+R\left(z\right);$$

$$\frac{\left[\left[1-\overline{b}\left(p_{\alpha }\right)]\left[\alpha e^{-r_{\alpha }}-q_{\alpha }\right]+\alpha \{z\left(p_{\alpha }-q_{\alpha }\right)+\left(z{q}_{\alpha }-p_{\alpha }\right)\overline{b}\left(p_{\alpha }\right)\right\}\right]Q}{p_{\alpha }\left\{z-\overline{b}\left(p_{\alpha }\right)\right\}-\left\{1-\overline{b}\left(p_{\alpha }\right)\right\}\mathit{\alpha z}{e}^{-r_{\alpha }}},$$

(35)

where Q is given by Equation (32).

Appendix 2 Proof of Theorem 2

By using Equations (32) and (35), we get

$$P\left(z\right)=Q+z{P}_q\left(z\right);$$

(36)

$$\left(1+\mathit{\alpha z}\right)\left[\frac{z\left(p_{\alpha }-q_{\alpha }\right)+\left(z{q}_{\alpha }-p_{\alpha }\right)\overline{b}\left(p_{\alpha }\right)}{p_{\alpha }\left\{z-\overline{b}\left(p_{\alpha }\right)\right\}-\left\{1-\overline{b}\left(p_{\alpha }\right)\right\}\mathit{\alpha z}{e}^{-r_{\alpha }}}\right]Q,$$

(37)

where Q is given by Equation (32).

Appendix 3 Proof of Theorem 3

By using Lagrange’s multipliers method, the entropy function (22) and set of constraints (23a) to (23d) give

$$\begin{array}{l}Z=-QlogQ-{\displaystyle \sum _{n=0}^{\infty }{W}_{n}log{W}_n-}{\displaystyle \sum _{n=0}^{\infty }{R}_{n}log{R}_n}-{\alpha }_1\hfill \\ \times \left(Q+{\displaystyle \sum _{n=0}^{\infty }{W}_n+}{\displaystyle \sum _{n=0}^{\infty }{R}_n}-1\right)-{\alpha }_2\left({\displaystyle \sum _{n=0}^{\infty }{W}_n-{\eta }_1}\right)\hfill \\ -{\alpha }_3\left({\displaystyle \sum _{n=0}^{\infty }{R}_n-{\eta }_2}\right)-{\alpha }_4\left({\displaystyle \sum _{n=1}^{\infty }n{W}_n+}{\displaystyle \sum _{n=1}^{\infty }n{R}_n-L_q}\right)\hfill \end{array},$$

(38)

where α₁, α₂, α₃, and α₄ are the Lagrangian multipliers corresponding to constraints (23a) to (23d), respectively.

By taking the partial derivatives of Z with respect to Q, W _n , and R _n and setting the results equal to zero, we have

$$\frac{\partial Z}{\partial Q}=-1-logQ-{\alpha }_1=0;$$

(39)

$$\frac{\partial Z}{\partial W_n}=-\left(1+log{W}_n\right)-{\alpha }_1-{\alpha }_2-{\alpha }_{4}n=0;n\ge 0;$$

(40)

$$\frac{\partial Z}{\partial R_n}=-\left(1+log{R}_n\right)-{\alpha }_1-{\alpha }_3-{\alpha }_{4}n=0;n\ge 0.$$

(41)

On simplifying, we have

$$\begin{array}{l}Q=e^{-\left(1+{\alpha }_1\right)};W_n=e^{-\left(1+{\alpha }_1\right)}{e}^{-{\alpha }_2}{e}^{-{\alpha }_{4}n};R_n\\ =e^{-\left(1+{\alpha }_1\right)}{e}^{-{\alpha }_3}{e}^{-{\alpha }_{4}n}.\end{array}$$

(42)

Let ${\xi }_1=e^{-\left(1+{\alpha }_1\right)},{\xi }_2=e^{-{\alpha }_2},{\xi }_3=e^{-{\alpha }_3},{\xi }_4=e^{-{\alpha }_4}$. From Equation (42), we have

Equations (23b) and (23c) give

$$Q={\xi }_1,W_n={\xi }_1{\xi }_2{\xi }_4^n,R_n={\xi }_1{\xi }_3{\xi }_4^n.$$

(43)

$${\xi }_1{\xi }_2={\eta }_1\left(1-{\xi }_4\right);$$

$${\xi }_1{\xi }_3={\eta }_2\left(1-{\xi }_4\right).$$

From Equation (23d), we have

$${\xi }_4=\frac{L_q}{{\eta }_1+{\eta }_2+L_q}.$$

(44)

Also,

$$\begin{array}{c}{\xi }_2=\frac{{\eta }_1}{Q}\left(\frac{{\eta }_1+{\eta }_2}{{\eta }_1+{\eta }_2+L_q}\right);{\xi }_3\\ =\frac{{\eta }_2}{Q}\left(\frac{{\eta }_1+{\eta }_2}{{\eta }_1+{\eta }_2+L_q}\right)\end{array}$$

(45)

Using Equations (44) and (45) in Equation (43), we get the required results.