Background

Nowadays, rapid economic changes and competitive pressure in the global market make companies pay more attention on supply chain topics. The company whose supply chain network structure is more appropriate has higher competitive advantage. This structure helps to overcome environmental disturbances (Dullaert et al. 2007). Analyzing location issues and decision making about facility location is considered as one of the important issues of decision making in companies. Certainly, appropriate facility location has high effects on economic benefits, appropriate service, and customer's satisfaction. Propounding the supply chain because of its effect on factors of operational efficiency, such as inventory, response, and lead time, specific attention is focused on how to create a distribution network. Facility location and how to relate them with customers are an important factor in designing a distribution network (Francis et al. 1992; Gong et al. 1997).

As nowadays living conditions have changed due to increasing world changes, mutually, situations have changed where supply chains are confronted with and influenced by them. The manager is confronted with more unknown conditions and new risks. Customers' demands have been more uncertain and various, and the lead time on their services is very effective. The demand variety can be recognized as one of the important sources of uncertainty in a supply chain (Gupta et al. 2000). Hence, inventory and product holding in a distribution center are an important issue in the supply chain (Liao et al. 2010). The inventory existence in these centers can lead to a great success in reaching the risk-pooling advantage in order to overcome the variability of customer demands. The proposed risk-pooling strategy and centralizing the inventory at distribution centers are considered as one of the effective ways to manage such a demand uncertainty to achieve appropriate service levels to customers. The lead time is one of the effective factors in safety stock levels due to customer demand uncertainty (Park et al. 2010). For sure, whether the amount of the level is low for the product, it is considered an additional value that one can gain a long-term or short-term competitive advantage in the market.

The lead time is dependent on different factors, such as transportation mode. Different modes of transportation include a reverse relation between cost and time. It contains different routes for any type of vehicles (Cardona-Valdés et al. 2011). The implicit assumption is that a faster transportation mode is also the more expensive one, creating a trade-off between cost and time affecting the distribution network configuration. In the recent decades, the topic of multi-depot heterogeneous vehicle routing problem is presented in order to increase the productivity and efficiency of transportation systems, in which this model leads to the least cost function by minimizing the number of vehicles (Bettinelli et al. 2011).

Literature review

One of the important factors of the total productivity and profitability of a supply chain is to consider its distribution network, which can be used to achieve variety of the supply chain objectives. Designing a distribution network consists of three subproblems, namely, location allocation, vehicle routing, and inventory control. In the literature, there are some research studies amalgamating two of the above subproblems, such as location-routing problems, inventory-routing problems, and location-inventory problems. These three subproblems of a distribution network design are considered in few papers simultaneously. Location-routing problems are surveyed and classified by Min et al. (1998) and Nagy and Salhi (2007). Inventory-routing problems are studied in several studies (Zhao et al. 2008; Yu et al. 2008; Oppen and Loketangen 2008; Day et al. 2009). In addition, a number of studies have considered location-inventory problems (Daskin et al. 2002; Shen 2005). Finally, Ahmadi Javid and Azad (2010) presented a new model for a location-routing-inventory problem. They considered one objective for their model and did not consider transportation time and risk-pooling. However, in this paper, we present a multi-objective model to concurrently optimize location, allocation, capacity, inventory, selection of vehicles, and routing decisions with risk-pooling in a stochastic supply chain system for the first time. These decisions are made in a way that the total system cost and the total transportation time are minimized.

Problem formulation

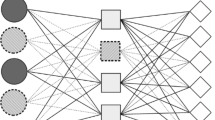
Problem description

The trade-off between cost and time creates a bi-objective problem. One criterion tries to minimize the fixed cost of locating the opened distribution centers, the safety stock costs of distribution center by considering uncertainty in customer's demand, inventory ordering and holding costs, the transportation costs from a plant to its allocated distribution centers, and also vehicle routing costs beginning from a distribution center (DC) with the aim of replying to and covering the devoted customer's demands to the DC by considering risk-pooling. The other criterion looks for the reduction of the time to transport the product along the supply chain. It is desired to minimize the transportation time from a plant to customers. The important assumptions in this paper are as follows:

  1. 1.

    One kind of product is involved (Paksoy and Chang 2010).

  2. 2.

    Each distribution center j is assumed to follow the (Q i , R j ) inventory policy (Ahmadi Javid and Azad 2010).

  3. 3.

    The inventory control is to be conducted only at DCs in this paper (Park et al. 2010; Ahmadi Javid and Azad 2010).

  4. 4.

    A single-sourcing strategy is considered in the whole supply chain (Park et al. 2010).

  5. 5.

    It is considered that the customers' demands after reaching the retailer are independent and follows a normal distribution (Park et al. 2010; Ahmadi Javid and Azad 2010).

  6. 6.

    Each plant has a limited capacity (Cardona-Valdés et al. 2011).

  7. 7.

    We consider different capacity levels for each distribution center, and finally, one capacity for each of them is selected (Ahmadi Javid and Azad 2010).

  8. 8.

    Each DC with the limited capacity carries on-hand inventory to satisfy demands from customer demand zones as well as safety stock to deal with the mutability of the customer demands at customer demand zones to attain risk-pooling profits (Park et al. 2010).

  9. 9.

    All customers should be served.

  10. 10.

     The number of available vehicles for each type and the number of allowed routes for each DC are limited (Bettinelli et al. 2011).

  11. 11.

    There are several modes of transportation between two consecutive levels.

  12. 12.

    Between two nodes on an echelon, only one type of vehicle is used.

  13. 13.

    A faster transportation mode is the more expensive one (Cardona-Valdés et al. 2011).

  14. 14.

    The amount of products is transported from each plant to each distribution center that is associated with it, and an equal amount of products has been ordered from the desired distribution center to that plant.

  15. 15.

    To determine all feasible routes, the following factors are taken into account:

  • Each customer should be visited by only one vehicle.

  • Each route begins at a DC and ends at the same DC.

  • The sum of the demands of the customers served in each route must not exceed the capacity of the associated vehicle.

  • Each of the distribution center and the vehicle have various limited, and determined capacity (Bettinelli et al. 2011; Marinakis and Marinaki 2010).

Model formulation

Following are the notations introduced for the mathematical description of the proposed model.

  1. 1.

    Indices

  2. (a)

    I, set of plants indexed by i

  3. (b)

    J, set of candidate DC locations indexed by j

  4. (c)

    K, set of customer demand zones indexed by k

  5. (d)

    N j , set of capacity levels available to DC j (j ∈ J)

  6. (e)
    Ω j l 2

    , set of all feasible routes using a vehicle of type l2 from DC j (j∈J)

  7. (f)

    LP ij , set of vehicles l1 between nodes i and j

  8. (g)

    LW jk , set of vehicles l2 between nodes j and k

  9. 2.

    Parameters

  10. (a)

    F j n, yearly fixed cost for opening and operating distribution center j with capacity level n (∀ n ∈ N j , ∀ j ∈ J)

  11. (b)
    CP i j l 1

    , cost of transporting one unit of product from plant i to distribution center j using vehicle l1

  12. (c)
    CW r l 2

    , cost of sending one unit of product in route r using vehicle l2 (These costs include the fixed cost of vehicle plus the transportation cost of each demand unit in route r. The mentioned transportation cost for each demand unit is not related to customer demand zone, and it is considered fixed for all locations in each route r.)

  13. (d)
    TP ij l 1

    , time for transporting any quantity of a product from plant i to DC j using vehicle l1

  14. (e)
    TW j l 2 r

    , time for transporting any quantity of a product from DC j on route r using vehicle l2

  15. (f)

    λ j , safety stock factor of DC j (j ∈ J)

  16. (g)

    h j , unit inventory holding cast at DC j (j ∈ J), (annually)

  17. (h)

    μ k , mean demand at customer demand zone k

  18. (i)

    δ2 k , variance of demand at customer demand zone k

  19. (j)

    E j , fixed inventory ordering cost at DC j

  20. (k)

    b j n, capacity with level n for DC j

  21. (l)

    MP i , capacity of plant i

  22. (m)
    ω l 2

    , number of available vehicles of each type l2

  23. (n)

    g j , number of routes associated with each distribution center j

  24. 3.

    Binary coefficients

  25. (a)

    P kr , 1 if and only if customer k is visited by route r, and 0 otherwise

  26. 4.

    Decision variables

  27. (a)

    Un j , 1 if distribution center j is opened with capacity level n, and 0 otherwise

  28. (b)
    A i j l 1

    , binary variable equal to 1 if vehicle l1 connecting plant i and DC j is used, and equal to 0 otherwise

  29. (c)
    B j k l 2

    , binary variable equal to 1 if vehicle l2 connecting DC j and customer k is used, and equal to 0 otherwise

  30. (d)

    X r , 1 if and only if route r is selected, and 0 otherwise

  31. (e)
    X i j l 1

    , quantity transported from plant i to DC j using vehicle l1

  32. 5.

    Mathematical model

  33. (a)

    The problem formulation is as follows:

    min f 1 = ∑ n ∈ N j ∑ j ∈ J F j n U j n + ∑ i ∈ I ∑ j ∈ J ∑ l 1 ∈ LP ij CP ij l 1 A ij l 1 X ij l 1 + ∑ j ∈ J ∑ k ∈ K ∑ l 2 ∈ LW jk ∑ r ∈ Ω j l 2 CW r l 2 μ k P kr X r + ∑ i ∈ I ∑ j ∈ J ∑ k ∈ K ∑ l 1 ∈ LP ij ∑ l 2 ∈ LW jk E j B jk l 2 μ k X ij l 1 A ij l 1 + ∑ i ∈ I ∑ j ∈ J ∑ l 1 ∈ LP ij A ij l 1 X ij l 1 h j 2 + ∑ j ∈ J λ j h j ∑ i ∈ I ∑ k ∈ K ∑ l 1 ∈ LP ij ∑ l 2 ∈ LW jk δ k 2 B jk l 2 L ji l 1 A ij l 1
    min f 2 = max j max i , l 1 TP ij l 1 A ij l 1 + max r , l 2 TW j l 2 r X r

s.t.

∑ n ∈ N j U j n ≤ 1 ∀ j ∈ J
(1)
∑ k ∈ K ∑ l 2 ∈ LW jk μ k B jk l 2 ≤ ∑ n ∈ N j b j n U j n ∀ j ∈ J
(2)
∑ i ∈ I ∑ l 1 ∈ LP ij X ij l 1 + λ j ∑ i ∈ I ∑ k ∈ K ∑ l 1 ∈ LP ij ∑ l 2 ∈ LW jk δ k 2 B ik l 2 L ji l 1 A ij l 1 ≤ ∑ n ∈ N j b j n U j n ∀ j ∈ J
(3)
∑ j ∈ J ∑ l 1 ∈ LP ij X ij l 1 ≤ MP i ∀ i ∈ I
(4)
∑ i ∈ I ∑ l 1 ∈ LP ij A ij l 1 ≥ ∑ n ∈ N j U j n ∀ j ∈ J
(5)
∑ j ∈ J ∑ l 2 ∈ LW jk B jk l 2 = 1 ∀ k ∈ K
(6)
∑ l 2 ∈ LW jk B jk l 2 ≤ 1 ∀ j ∈ J , ∀ k ∈ K
(7)
∑ l 1 ∈ LP ij A ij l 1 ≤ 1 ∀ i ∈ I , ∀ j ∈ J
(8)
∑ l 1 ∈ LP ij ∑ i ∈ I A ij l 1 ≥ ∑ l 2 ∈ LW jk B jk l 2 ∀ j ∈ J , ∀ k ∈ K
(9)
∑ n ∈ N j U j n ≥ ∑ l 2 ∈ LW jk B jk l 2 ∀ j ∈ J , ∀ k ∈ K
(10)
∑ j ∈ J ∑ l 2 ∈ LW jk ∑ r ∈ Ω j l 2 P kr X r ≥ 1 ∀ k ∈ K
(11)
∑ j ∈ J ∑ r ∈ Ω j l 2 X r ≤ W l 2 ∀ l 2 ∈ LW jk
(12)
∑ l 2 ∈ LW jk ∑ r ∈ Ω j l 2 X r ≤ g j ∀ j ∈ J
(13)
X ij l 1 − A ij l 1 ≥ 0 ∀ i ∈ I , ∀ j ∈ J , ∀ l 1 ∈ LP ij
(14)
μ k ≥ ∑ l 2 ∈ LW jk ∑ n ∈ N j ∑ j ∈ J B jk l 2 U j n ∀ k ∈ K
(15)
MP i − A ij l 1 X ij l 1 ≥ 0 ∀ i ∈ I , ∀ j ∈ J , ∀ l 1 ∈ LP ij
(16)
U j n ∈ 0 , 1 ∀ j ∈ J , ∀ n ∈ N j
(17)
X r ∈ 0 , 1 ∀ r ∈ ∪ j ∈ J , l 2 ∈ LW jk Ω j l 2
(18)
A ij l 1 ∈ 0 , 1 ∀ i ∈ I , ∀ j ∈ J , ∀ l 1 ∈ LP ij
(19)
B jk l 2 ∈ 0 , 1 ∀ j ∈ J , ∀ k ∈ K , ∀ l 2 ∈ LW jk
(20)
X ij l 1 ≻ 0 ∀ i ∈ I , ∀ j ∈ J , ∀ l 1 ∈ LP ij
(21)

In this model, the first objective function minimizes the total expected costs consisting of the fixed cost for opening distribution centers with a certain capacity level, transportation costs from plants to distribution centers, annual routing costs between distribution centers and customer demand zones, and expected annual inventory costs. The second objective function looks for the minimum time to transport the product along any path from the plants to the customers.

Constraint (1) ensures that each distribution center can be assigned to only one capacity level. Constraints (2) and (3) are the capacity constraints associated with the distribution centers, and also, constraint (4) is the capacity constraints associated with the plants. Constraint (5) states that if distribution center j with n capacity is opened, it is serviced by a plant. Constraint (6) represents the single-sourcing constraints for each customer demand zone. Constraints (7) and (8) ensure that if two nodes on an echelon are related to each other, one type of vehicle transports products between them. Constraint (9) makes sure that if the distribution center j gives the service to the customer k, that center must get services at least from a plant. Constraint (10) ensures that if the distribution center j is allocated to customer k by vehicle l 2 , that center should certainly be established with a determined capacity level. Constraint (11) is the standard set covering constraints, modeling assumption 9. Constraints (12) and (13) impose limits on the maximum number of available vehicles of each type and the maximum number of allowed routes for each DC, modeling assumption 10. Constraint (14) makes sure that if plant i gives the service to the DC j , the amount of transported products from that plant to the desired distribution center would be more than one. Constraint (15) implies that customers' demands of zone k are more than 1. Constraint (16) is the capacity constraint associated with plant i. Constraints (17) to (20) enforce the integrality restrictions on the binary variables. Finally, constraint (21) enforces the non-negativity restrictions on the other decision variables.

Solution method

Optimization is a mathematical procedure to determine devoting the optimal allocation to scarce resources, and it helps to get the best result from the model solution. In this paper, we consider five examples, and then they are solved by the Lingo 9.0 software to show that this model works well. This software is a comprehensive tool designed to make building and solving linear, nonlinear, and integer optimization models faster, easier, and more efficient. It provides a completely integrated package that includes a powerful language for expressing optimization models, a full featured environment for building and editing problems, and a set of fast built-in solvers. Objective functions (f i ) have been normalized between zero and one. In other words, they have been without any dimension (i.e., scaleless). By using the following formula, these objectives are converted to a single objective function, where f1′ and f2′ are the normalized forms of f1 and f2 objective functions.

min f = α f 1 ' + 1 − α f 2 '

To minimize deviations from the ideal, this function is reduced. As the first objective function (f1) is more important than the second objective function (f2) in the given problem, the coefficients of the above formula are considered in the form of α = 0.7 and 1 − α = 0.3.

This problem is implemented by this software, and a global optimal solution is obtained. The computational results are shown in Tables 1, 2, 3, 4, and 5.

Table 1 U j n is 1 if distribution center j is opened with capacity level n . and 0 otherwise
Full size table
Table 2 X r is 1 if and only if route r is selected, and 0 otherwise
Full size table
Table 3 A i j l 1 binary variable, where it is 1 if vehicle l 1 connecting plant i and DC j is used
Full size table
Table 4 B j k l 2 binary variable, where it is 1 if vehicle l 2 connecting DC j and customer k is used
Full size table
Table 5 X i j l 1 quantity transported from plant i to DC j using vehicle l 1
Full size table

Conclusions

In this paper, a new mathematical model to design a three-level supply chain has been presented by considering the inventory under uncertain demands, risk-pooling, vehicle routing, transportation time, and cost. The decision related to the transportation options has an impact on the transportation time from plants to customers. The trade-off between cost and time is considered in the formulation of a mathematical model that minimizes both criteria. Therefore, this model holding two objectives has been formulated for the first time as a location-inventory-routing problem with a risk-pooling strategy in a three-level supply chain. The Lingo software has been used to solve the given problem. Some future studies are as follows: considering each parameter as a fuzzy, multi-period planning and solving the presented model by using heuristic or meta-heuristic algorithms.