Abstract
This investigation presents a heuristic method for consumable resource allocation problem in multi-class dynamic Project Evaluation and Review Technique (PERT) networks, where new projects from different classes (types) arrive to system according to independent Poisson processes with different arrival rates. Each activity of any project is operated at a devoted service station located in a node of the network with exponential distribution according to its class. Indeed, each project arrives to the first service station and continues its routing according to precedence network of its class. Such system can be represented as a queuing network, while the discipline of queues is first come, first served. On the basis of presented method, a multi-class system is decomposed into several single-class dynamic PERT networks, whereas each class is considered separately as a minisystem. In modeling of single-class dynamic PERT network, we use Markov process and a multi-objective model investigated by Azaron and Tavakkoli-Moghaddam in 2007. Then, after obtaining the resources allocated to service stations in every minisystem, the final resources allocated to activities are calculated by the proposed method.
Similar content being viewed by others

Avoid common mistakes on your manuscript.
Introduction
Today, multi-project scheduling which considers all projects of organization as one system and therefore sharing limited resources among multiple projects is mostly noticed, whereas up to 90% of organizations handle the projects in a multi-project environment (Payne 1995). On the other hand, for better management, in some organizations, the project-zoriented approach is primarily adopted and the operations of the organization are dependently executed on projects.
In the literature of multi-project scheduling, multi-project resource constrained scheduling problem (MPRCSP) in static and deterministic conditions is a major topic of most researches. Generally, two approaches for analyzing MPRCSP exist. One approach by linking all projects of organization synthetically together into a large single project, analyzes MPRCSP, while the other approach by considering the projects as independent component and also resources constraints, proposes an objective function that contains all projects (possibly appropriately weighted) for analyzing MPRCSP.
Wiest (1967) and Pritsker et al. (1969) were the first pioneering researchers in studying MPRCSP who presented, respectively, a zero–one programming approach and a heuristic model for analyzing this problem. Then Kurtulus and Davis (1982) and Kurtulus and Narula (1985), by employing the priority rules and describing measures, studied the MPRCSP. Moreover, some investigations have been concentrated on MPRCSP by applying multi-objective and multi-criteria approaches; for example, Chen (1994) proposed the zero–one goal programming model in MPRCSP for the maintenance of mineral processing, and Lova et al. (2000) analyzed MPRCSP with applying a lexicographically two criteria. Also recently, Kanagasabapathi et al. (2009) by defining performance measures and considering maximum tardiness and mean tardiness of projects studied the MPRCSP in a static environment.
On the other hand, some researchers such as Tsubakitani and Deckro (1990), Lova and Tormos (2001), Kumanan et al. (2006), Goncalves et al. (2008), Ying et al. (2009), and Chen and Shahandashti (2009) proposed heuristic and metaheuristic algorithms for solving MPRCSP. Kruger and Scholl (2008) extended the MPRCSP by considering transfer times and its cost.
In all of the mentioned investigations, MPRCSP has been analyzed in static and deterministic environment, while a few studies have been concentrated on multi-project scheduling under uncertainty conditions. Fatemi-Ghomi and Ashjari (2002) by considering a multi-channel queuing introduced a simulation model for multi-project resource allocation with stochastic activity durations. Nozick et al. (2004) also presented a nonlinear mixed-integer programming model to optimally allocate the resources, while the probability distribution of activity duration and allocated resources depend on together. Moreover, event-driven approach and Critical Chain Project Management (CCPM) approach were proposed for overcoming uncertainty in multi-project system by Kao et al. (2006) and Byali and Kannan (2008), respectively.
Normally, greater resource allocation will incur a greater expense; therefore, we have a trade-off between the time to complete an activity and its cost (a function of the assigned resource). When the task duration is a linear function of the allocated resource, we have the linear time–cost trade-off problem which was analyzed by Fulkerson (1961). The nonlinear case of the time–cost trade-off problem was studied by Elmaghraby and Salem (1982, 1984) and Elmaghraby (1993, 1996). Moreover, Elmaghraby and Morgan (2007) presented a fast method for optimizing resource allocation in a single-stage stochastic activity network.
Clearly, multi-project scheduling is more elaborate than single-project scheduling. On the other hand, in some organizations, not only the task durations are uncertain, but also new projects dynamically enter to the organization over the time horizon. In such conditions, the organization is faced with a multi-project system in which the scheduling procedure would be more elaborate than before. Adler et al. (1995) studied such multi-project system by considering the organization as a ‘stochastic processing network’ and using simulation. They assumed that the organization is comprised of a collection of ‘service stations’ (work stations) or ‘resources’, where several types (classes) of projects exist in a system and one or more identical parallel servers can be settled in each service station. Therefore, such multi-project system, denominated as Dynamic PERT Network, can be considered as a queuing network and is attractive for organizations having the same projects, for example, maintenance projects.
Anavi-Isakow and Golany (2003) by applying simulation study used the concept of CONWIP (constant work-in-process) in multi-class dynamic Project Evaluation and Review Technique (PERT) networks. They described two control mechanisms, constant number of projects in process (CONPIP) and constant time of projects in process (CONTIP), namely, CONPIP mechanism restricts the number of projects, while CONTIP mechanism limits the total processing time by all the projects that are active in the system.
In addition, Cohen et al. (2005, 2007) by using cross entropy, based on simulation, investigated the resource allocation problem in multi-class dynamic PERT networks, where the resources can work in parallel. Indeed, the number of resources allocated and servers in each service station are equal (e.g., mechanical work station with mechanics, electrical work station with electricians), and the total number of resources in the system also is constant.
On the other hand, Azaron and Tavakkoli-Moghaddam (2007) proposed an analytical multi-objective model to optimally control consumable resources allocated to the activities in a dynamic PERT network, where only one type of project exists in the system and the number of servers in every service station is either 1 or infinity. They assumed that the activity durations are exponentially distributed random variables, resources allocated affect the mean of service times, and the new projects are generated according to a Poisson process. A risk element was considered in a dynamic PERT network by Li and Wang (2009) who, by using general project risk element transmission theory, proposed a multi-objective risk-time–cost trade-off problem. Recently, Azaron et al. (2011) introduced an algorithm in computing optimal constant lead time for each particular project in a repetitive (dynamic) PERT network by minimizing the average aggregate cost per project.
In practice, due to various projects' requirements, most organizations execute the projects from several classes, where new projects from different classes arrive to the system dynamically over the time horizon and service stations that stochastically serve to projects. In such conditions, organization is encountered with multi-class dynamic PERT networks, while projects from different classes differ in their precedence networks, the mean of their service time in every service station, and also their arrival rates.
Reviewing the above-mentioned investigations indicated that the multi-class dynamic PERT network has been studied only using simulation. As the main contribution of this paper, we present a heuristic method for the consumable resource allocation problem (or time–cost trade-off problem) in multi-class dynamic PERT networks. Note that the resource allocation problem in multi-class dynamic PERT networks is a generalization of the resource allocation problem in dynamic PERT network, investigated by Azaron and Tavakkoli-Moghaddam (2007) by considering only one type (class) of projects in multi-project system.
In this paper, it is assumed that the new projects from different classes, including all their activities, are entered to the system according to independent Poisson processes with different arrival rates and each activity of any project is executed at a devoted service station settled in a node of the network based on first come, first served (FCFS) discipline. Moreover, the number of servers in every service station is either 1 or infinity, while the service times (activity durations) are independent random variables with exponential distributions. Indeed, each project arrives to the first service station and continues its routing according to precedence network of its class.
For determining the resources allocated to the service stations, the multi-class system is decomposed into several single-class dynamic PERT networks, whereas each class is considered separately as a minisystem. For modeling of a single-class dynamic PERT network, we use Markov process and a multi-objective model, investigated by Azaron and Tavakkoli-Moghaddam (2007), namely, we first convert the network of queues into a stochastic network. Then, by constructing a proper finite-state absorbing continuous-time Markov model, a system of differential equations is created. Moreover, we apply a multi-objective model containing four conflicted objectives to optimally control the consumable resources allocated to service stations in the single-class dynamic PERT network and further employ the goal attainment method to solve a discrete-time approximation of the primary multi-objective problem. Finally, after obtaining the resources allocated to service stations in every minisystem, the final resources allocated to servers are calculated by the proposed method.
This paper is composed of five sections. The remainder is organized as follows. In ‘Single class dynamic PERT networks,’ we model the single-class dynamic PERT network by employing a finite-state continuous-time Markov process and apply a multi-objective model to optimally control the consumable resources allocated to service stations in a single-class dynamic PERT network. In ‘Consumable resource allocation in multi-class dynamic PERT networks,’ a heuristic model is proposed for consumable resources allocated in the multi-class dynamic PERT networks. We solve an example in ‘An illustrative case’ section and conclusion is given in ‘Conclusions.’
Single-class dynamic PERT networks
In this section, we represent a multi-objective model to optimally control the consumable resources allocated to the service stations investigated by Azaron and Tavakkoli-Moghaddam (2007). For this purpose, we first explain an analytical method to compute the distribution function of project completion time and then we describe a multi-objective model in single-class dynamic PERT network.
It is assumed that a project is represented as an activity-on-node (AoN) graph, and also the new projects, including all their activities, are arrived to the system according to a Poisson process with the rate of λ. Moreover, each activity of a project is executed in a devoted service station settled in a node of the network based on FCFS discipline.
Such system can be considered as a network of queues, where the service times represent the durations of the corresponding activities. It is also assumed that the number of servers in each service station to be either one or infinity, while the service times (activity durations) are independent random variables with exponential distributions.
Project completion time distribution
For presenting an analytical method to compute the distribution function for single-class dynamic PERT network, the method of Kulkarni and Adlakha (1986) will be used because this method presents an analytical, simple, and easy approach to implement on a computer and a computationally stable algorithm to evaluate the distribution function of the project completion time. This method models PERT network with independent and exponentially distributed activity durations by continuous-time Markov chains with upper triangular generator matrices. The special structure of the chain allows us to develop very simple algorithms for the exact analysis of the network.
It is assumed that the service time in service station a is exponentially distributed with the rate of μ a , where the arrival stream of projects to each service station is according to a Poisson process with the rate of λ. Moreover, the number of server in node a is either one or infinity and therefore the node a treats as an M/M/1 or M/M/∞ model. The main steps of method to determine a finite-state absorbing continuous-time Markov process to computing the distribution function in single-class dynamic PERT network are as follows:
Step 1. Compute the density function of the sojourn time (waiting time plus activity duration) in each service station.
Step 1.1. If there is one server in service station a, then the queuing system would be M/M/1, and the density function of time spent in the service station a would be exponentially expressed with parameter μ a − λ a (μ a ≻ λ) a ; therefore, w a (t) is calculated as follows:
Step 1.2. If there are infinite servers in service station a, then the queuing system would be M/M/∞, and the density function of time spent in the service station a would be exponentially expressed with parameter μ a ; therefore, w a (t) is calculated as follows:
Step 2. Transform the single-class dynamic PERT network, represented as an AoN graph, to a classic PERT network represented as an activity-on-arc (AoA) graph.
When considering AoN graph, substitute each node with a stochastic arc (activity) whose length is equal to the sojourn time in the corresponding queuing system. For this purpose, node a in the AoN graph is replaced with a stochastic activity. Assume that b1,b2,…,b n are the incoming arcs to node a and d1,d2,…,d m are the outgoing arcs from it in the queuing network. Then, node a is substituted by activity (v,w), whose length is equal to the activity duration a. Furthermore, all arcs b1,b2,…,b n terminate to node v while all arcs d1,d2,…,d m originate from node w [for more details, see Azaron and Modarres (2005 )].
Step 3. Calculate the distribution function of the project completion time (longest path time) in the AoA obtained in step 2, while activity durations are distributed exponentially. For the computation of longest path time distribution in AoA, the method of Kulkarni and Adlakha (1986) is applied.
Let G = (V, A) be the PERT network, obtained in step 2, with a single source and a single sink, in which V represents the set of nodes and A represents the set of arcs of the stochastic network (AoA). Let s and t be the source and sink nodes, respectively, and length of arc a ϵ A be a random variable that exponentially distributed with parameter γ a . For a ϵ A, the starting node and the ending node of arc a are denoted as α(a) and β(a), respectively.
Definition 1. Let I(v) be the set of arcs ending at node v and O(v) be the set of arcs starting at node v, which are defined as follows:
Definition 2. For X ⊂ V such that s ∊ X and t ∊ X— = V − X, an (s,t) cut is defined as follows:
An (s,t) cut is denominated a uniformly directed cut (UDC), if , i.e., there are no two arcs in the cut belonging to the same path in the project network. Each UDC is clearly a set of arcs, in which the starting node of each arc belongs to X and the ending node of that arc belongs to .
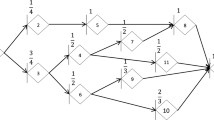
Example 1. Consider the stochastic network shown in Figure 1 taken from Azaron and Tavakkoli-Moghaddam (2007). According to the definition, the UDCs of this network are (1,2); (2,3); (1,4,6); (3,4,6); and (5,6).
Definition 3. (E,F), subsets of A, is defined as admissible 2-partition of a UDC D if D = E ∪ F and E ∩ F = φ, and also I(β(a)) ⊄ F for any a ∈ F.
Again consider Example 1 that (1,4,6) is one of the UDCs. For example, this cut can be decomposed into E = {1, 6} and F = {4}. In this case, the cut is an admissible 2-partition because I(β(4)) = {3, 4} ⊄ F. Furthermore, if E = {6} and F = {1, 4}, then the cut is not an admissible 2-partition because I(β(1)) = {1} ⊂ F = {1, 4}
Definition 4. Along the projects execution at time t, each activity can be in one and only one of the active, dormant or idle states, which are defined as follows:
-
(i)
Active. An activity a is active at time t, if it is being performed at time t.
-
(ii)
Dormant. An activity a is called dormant at time t, if it has completed but there is at least one unfinished activity in I(β(a)) at time t.
-
(iii)
Idle. An activity a is denominated idle at time t, if it is neither active nor dormant at time t.
In addition, Y(t) and Z(t) are defined as follows:
and X(t) = (Y(t), Z(t)).
A UDC is divided into E and F that contain active and dormant activities, respectively. All admissible 2-partition cuts of network of Figure 1 are presented in Table 1.
The set of all admissible 2-partition cuts of the network is defined as S and also . Note that X(t) = (ø,ø) presents that the all activities are idle at time t and therefore the project is finished by time t. It is demonstrated that {X(t), t ≥ 0} is a finite-state absorbing continuous-time Markov process (for more details, see Kulkarni and Adlakha (1986)).
If activity a terminates with the rate of γ a , and I(β(a)) ⊄ F ∪ {a}, namely, there is at least one unfinished activity in I(β(a)), then E′ = E − {a}, F′ = F ∪ {a}. Furthermore, if by terminating activity a, all activities in I(β(a)) become idle (I(β(a)) ⊂ F ∪ {a}), then E′ = (E − {a}) ∪ O(β(a)), F′ = F − I(β(a)). Namely, all activities in I(β(a)) will become idle and also the successor activities of this activity, O(β(a)), will become active. Therefore, the components of the infinitesimal generator matrix denoted by Q = [q{(E, F), (E′, F′)}], where (E,F) and are obtained as follows:
A continuous-time Markov process, {X(t), t ≥ 0}, is with finite-state space and since q{(ø,ø),(ø,ø)} = 0, the project is completed. In this Markov process, all of states except X(t) = (ø,ø) that is the absorbing state are transient. Furthermore, the states in should be numbered such that this Q matrix be an upper triangular one. It is assumed that the states are numbered as such that X(t) = (O(s), ø) and X(t) = (ø,ø) are state 1 (initial state) and state N (absorbing state), respectively.
Let T be the length of the longest path or the project completion time in the PERT network, obtained in step 2. Obviously, T = min{t ≥ 0 : X(t) = N|X(0) = 1 }.
Chapman-Kolmogorov backward equations can be used to calculate F(t) = P(T ≤ t). If it is defined
then F(t) = P1(t).
The system of linear differential equations for the vector is presented by
where P′(t) and Q represent the derivation of the state vector P(t) and the infinitesimal generator matrix of the stochastic process {X(t), t ≥ 0}, respectively.
Multi-objective consumable resource allocation
In this section, we apply a multi-objective model to optimally control the consumable resources allocated to the service stations in a single-class dynamic PERT network, representing as a network of queues, where we allocate more resources to service station and where the mean service time will be decreased and the direct cost of service station per period will be increased. This means the mean service time in each service station is a non-increasing function and the direct cost of each service station per period is a non-decreasing function of the amount of resource allocated to it, i.e., the total direct costs of service station per period and the mean project completion time are dependent together and an appropriate trade-off between them is required. Also, the variance of the project completion time should be accounted in the model because the mean and the variance are two complementary concepts. The last objective that should be considered is the probability that the project completion time does not exceed a certain threshold for on-time delivery performance.
Let x a be the resource allocated in service station a (a ∈ A); also, d a (x a ) represents the direct cost of service station a (a ∈ A) per period in the PERT network, obtained in ‘Project completion time distribution’ section step 2, while it is assumed to be a non-decreasing function of amount of resources x a allocated to it. Thus, the project direct cost (PDC) would be PDC = ∑ a ∈ Ad a (x a ). Also, the mean service time in the service station a, g a (x a ), is assumed to be a non-increasing function of the amount of resource x a allocated to it that would be equal to
Let U a be the maximum amount of resource available to be allocated to the activity a (a ∈ A), L a be the minimum amount of resource needed to execute the activity a, x = [x a : a ∈ A]T, and J be the amount that represents the resource available to be allocated to all of activities. Moreover, we define u as a threshold time that project completion time does not exceed it. In practice, d a (x a ) and g a (x a ) can be obtained by employing linear regression based on the previous similar activities or applying the judgments of experts in this area.
Therefore, the objective functions are given by the following:
-
1.
Minimizing the project direct cost per period
(12) -
2.
Minimizing the mean of project completion time (P ′ 1(t) is the density function of project completion time)
(13) -
3.
Minimizing the variance of project completion time
(14) -
4.
Maximizing the probability that the project completion time does not exceed a certain threshold
(15)
The infinitesimal generator matrix Q would be a function of the control vector μ = [μ a :a ∊ A]T (x = [x a :a ∊ A]T). Therefore, the nonlinear dynamic model is
Let B and C be the set of arcs in the PERT network, obtained in ‘Project completion time distribution’ section step 2 that there are, respectively, one server and infinite servers settled on the corresponding service stations (A = B ∪ C). The next constraint should be satisfied to show the response in the steady-state:
In the mathematical programming, we do not use such constraints. Hence, ∃ε, following the establishment of constraint
Consequently, the appropriate multi-objective optimal control problem is
This stochastic programming is impossible to solve, therefore, based on the definition of integral thinking, we divide time interval into R equal portions with the length of ∆t. Indeed, we transform the differential equations into difference equations. Thus, the corresponding discrete state model can be given as follows (for more details see Azaron and Tavakkoli-Moghaddam, 2007):
Goal attainment method
We now need to use a multi-objective method to solve (20), and we actually use goal attainment technique for this purpose. The goal attainment method needs to determine a goal, b j , and a weight, c j , for every objective, namely, the total project direct cost per period, the mean project completion time, the variance of project completion time, and the probability that the project completion time does not exceed a certain threshold. c j s represent the importance of objectives, whereas, if an objective has the smallest c j , then it will be the most important objective. c j s (j = 1,2,3) are commonly normalized such that . Goal attainment method is actually a variation of goal programming method intending to minimize the maximum weighted deviation from the goals.
Since goal attainment method has a fewer variables to work with, compared to other simple and interactive multi-objective methods, it will be computationally faster and more suitable to solve our complex optimization problem. Therefore, the appropriate goal attainment formulation of the resource allocation problem is given by
Consumable resource allocation in multi-class dynamic PERT networks
In practice, due to various projects' requirements, most organizations execute the projects from several classes, where new projects from different classes arrive to the system dynamically over the time horizon and service stations that stochastically serve to projects. In such conditions, organization is encountered with multi-class dynamic PERT networks, while projects from different classes differ in their precedence networks, the mean of their service time in every service station, and also their arrival rates.
In this section, we present a heuristic algorithm for consumable resource allocation problem in multi-class dynamic PERT networks, while this problem is a generalization of the resource allocation problem in dynamic PERT network, as investigated by Azaron and Tavakkoli-Moghaddam (2007) by considering only one type (class) of projects in multi-project system. For this purpose, it is assumed that we have K different classes from projects, where the new projects of class i (i = 1, …, K) arrive to system according to Poisson process with the rate of λ i , and the service times in service station a for the projects of class i are exponentially distributed with the rate of . On the basis of this algorithm, multi-class dynamic PERT networks problem is decomposed into K single-class dynamic PERT network problem, while each class is considered separately as a minisystem. In every minisystem i (i = 1, …, K), all projects from different classes are considered as class i with the arrival rate of . Then every minisystem is solved by using the steps found in the sections of ‘Single class dynamic PERT networks’ as a single-class dynamic PERT network problem.
Let G i = (V i ,A i ) be a directed stochastic network of class i (i = 1, …, K), in which V i represents the set of nodes and A i represents the set of arcs of the network in class i. Let s i and t i be the source and sink nodes in the AoA graph of class i, respectively. Let represent the amount of resource to be allocated to the service station a (a ∈ A i ) in minisystem i, while all projects from different classes are considered as class i with the arrival rate of and , where . Then the resources allocated to service station a in minisystem i should be computed by the model represented in ‘Multi-objective consumable resource allocation’ section. Therefore, the resources allocated to service station a would be
Let x = [x a : a ∈ A]T; therefore, the resources allocated to service stations are calculated as follows:
Moreover, Let zi represent the objective function of minisystem i using goal attainment formulation. Therefore, the objective function of multi-class system would be
Consequently, the proposed algorithm is as follows.
Proposed Algorithm:
Step 1. Convert the multi-class dynamic PERT networks problem into K single-class dynamic PERT network problem (minisystem). For this purpose, in every minisystem i, consider the all projects from different classes as class i with the arrival rate of .
Step 2. For every minisystem i, compute the resources allocated to service stations, xi = [x a i:a ∊ A]T, and objective function, zi, by the model represented in ‘Multi-objective consumable resource allocation’ section.
Step 3. Calculate the resources allocated to service stations, x = [x a :a ∊ A]T, by and also obtain the objective function of multi-class system by .
An illustrative case
In this section, to illustrate the proposed heuristic algorithm, we consider the three classes of projects depicted in Figure 2. The assumptions are as follows:
-
The system has three different classes of projects.
-
The new projects from different classes, including all their activities, are generated according to Poisson processes with the rates of λ1 = 2.5, λ2 = 1.5, λ3 = 1 per year.
-
The activity durations in service station a for the projects of class i (i = 1, 2, 3) are exponentially distributed. Table 2 shows the characteristics of the activities in different classes, where the time unit and the cost unit are, respectively, in year and in thousand dollars.
-
There are infinite servers in service station 3 and other stations have only one server settled in the nodes.
-
The capacity of the system is infinite.
-
The threshold time that the project completion time does not exceed it for every minisystem is 3.
-
The maximum amount of consumable resource available to be allocated to all service stations is J = 15.
-
In all experiments, the value of ε is equal 0.01.
-
The goals and the weights of objectives for goal attainment method in every class, are b1 = 25, b2 = 1, b3 = 0.25, b4 = 0.95 and c1 = 0.3, c2 = 0.1, c3 = 0.3, c4 = 0.3, respectively. Note that the goals and the weights of objectives for different classes can be different.
In this example, three-class dynamic PERT networks problem is decomposed into three single-class dynamic PERT network problem, while each class is considered separately as a minisystem. In every minisystem i(i = 1,2,3), all projects from different classes are considered as class i with the arrival rate of λ = 5(=2.5 + 1.5 + 1). Then, every minisystem is solved as single-class dynamic PERT network problem by using the steps found in the sections of ‘Single class dynamic PERT networks.’
The objective is to obtain the resources allocated to the different activities by using proposed algorithm in ‘Consumable resource allocation in multi-class dynamic PERT networks’. For this purpose, the system states and transition rates for every minisystem are determined (depicted in Figure 3), where the states are showed in nodes and the rate diagrams are represented on arcs.
We obtain the infinitesimal generator matrix Q(μ) for forming the corresponding discrete state model in every class. We consider the mentioned goals and weights and also the various combinations of R and ∆t. To do so, we employ LINGO 8 on a PC Pentium 4, CPU 3 GHz. The optimal allocated resources in every minisystem, the computational times, CT (mm/ss), and also the values of all objectives for the different combinations of R and ∆t, are shown in Table 3 for every minisystem. So based on proposed algorithm in ‘Consumable resource allocation in multi-class dynamic PERT networks’ section the allocated consumable resources are , x2 = 3.9797, x3 = 1.6626, x4 = 1.1976, x5 = 1.9224, and x6 = 4.3017 (z = 5.7993).
To illustrate the performance of proposed algorithm, we evaluate its results with a simulation method that randomly allocate the resources to service stations and simulate the multi-class dynamic PERT network through Mont Carlo simulation. Note that Fatemi Ghomi and Hashemin (1999) proposed conditional Monte Carlo simulation and crude Monte Carlo simulation to compute the network completion time distribution function. However, the simulation method will be as follows:
Simulation method:
Step 1. n=1
Step 2. Generate one initial solution x = [x a : a ∈ A]T, randomly, where x a ∈ [L a , U a ] and
Step 3. Simulate the multi-class dynamic PERT network (Figure 2) according to the initial solution
Step 4. Calculate the objective function, z, for the initial solution
Step 5. Repeat
-
Generate a new solution, , randomly, where and
-
Simulate the multi-class dynamic PERT network according to the new solution
-
Calculate the objective function, znew, for the new solution
-
Calculate Δz = znew − z
-
If ∆z≺0 then x = xnew, z = znew
-
Until n ≥ N, where N is number of simulation run
Step 6. Present x and z
We set the number of simulation run to be N = 8,000. According to simulation method, the simulation results are , , , , , (zsim = 5.051). In Figure 4, a comparative analysis of our proposed model in ‘Consumable resource allocation in multi-class dynamic PERT networks,’ and simulation results for this example is presented. Based on this example, the objective function values obtained through both algorithms are close.
Conclusions
In this article, we proposed a heuristic method for the consumable resource allocation problem (or time–cost trade off problem) in multi-class dynamic PERT networks. It was assumed that the new projects of different classes, including all their activities, are entered to the system according to an independent Poisson processes, and each activity of any project is executed at a devoted service station settled in a node of the network according to its class. The number of servers in every service station is either 1 or infinity, while the service times (activity durations) are independent random variables with exponential distributions. Indeed, each project arrives to the first service station and continues its routing according to its precedence network of corresponding class. Such system was considered as a queuing network, while the discipline of queues is first come, first served.
For determining the resources allocated to the service stations, the multi-class system was decomposed into several single-class dynamic PERT networks, whereas each class was considered separately as a minisystem. For modeling of single-class dynamic PERT network, we used Markov process and a multi-objective model, investigated by Azaron and Tavakkoli-Moghaddam (2007), namely, we first converted the network of queues into a stochastic network. Then, by constructing a proper finite-state absorbing continuous-time Markov model, a system of differential equations was created. Next, we applied a multi-objective model containing four conflicted objectives to optimally control the resources allocated to service stations in single-class dynamic PERT network and further used the goal attainment method to solve a discrete-time approximation of the primary multi-objective problem. Finally, after obtaining the resources allocated to service stations in every minisystem, the final resources allocated to servers were calculated by proposed algorithm.
In multi-objective model, the total project direct cost was considered as an objective to be minimized and the mean project completion time, as another effective objective, should also be accounted that to be minimized. The variance of the project completion time was another effective objective in the model because the mean and the variance are two complementary concepts. The probability that the project completion time does not exceed a certain threshold was considered as the last objective.
For obtaining the best optimal allocated consumable resource in single-class dynamic PERT network, we considered the various combinations of portions for specific time interval. Based on the presented example, If the length of every portion is decreased, the accuracy of solution is increased, i.e., the value of objective is decreased and the computational time, CT, is also increased.
Authors' information
SY is an Assistant Professor of Industrial Engineering at Iran University of Science and Technology (IUST), Tehran, Iran. His current research interests include stochastic processes and their applications, project scheduling and supply chains. He has contributed articles to different international journals, such as European Journal of Operational Research, International Journal of System Science, Iranian Journal of Science & Technology, and International Journal of Advanced Manufacturing Technology. SN is the Associate Professor of Industrial Engineering Department in IUST since October 1990. The teaching experiences are mainly in project management, human resource management, and engineering economics. MMM also is the Assistant Professor of Industrial Engineering Department in IUST. His research interests include performance measurement systems, inventory planning, and control and strategic planning.
References
Adler PS, Mandelbaum A, Nguyen V, Schwerer E: From project to process management: an empirically-based framework for analyzing product development time. Manag Sci 1995,41(3):458–484. 10.1287/mnsc.41.3.458
Anavi-Isakow S, Golany B: Managing multi-project environments through constant work-in-process. Int J Proj Manag 2003,21(1):9–18. 10.1016/S0263-7863(01)00058-8
Azaron A, Modarres M: Distribution function of the shortest path in networks of queues. OR Spectr 2005, 27: 123–144. 10.1007/s00291-004-0169-3
Azaron A, Tavakkoli-Moghaddam R: Multi-objective time–cost trade-off in dynamic PERT networks using an interactive approach. Eur J Oper Res 2007, 180: 1186–1200. 10.1016/j.ejor.2006.05.014
Azaron A, Fynes B, Modarres M: Due date assignment in repetitive projects. Int J Prod Econ 2011, 129: 79–85. 10.1016/j.ijpe.2010.09.004
Byali RP, Kannan MV: Critical Chain Project Management - a new project management philosophy for multi project environment. J Spacecraft Technol 2008, 18: 30–36.
Chen V: A 0–1 goal programming-model for scheduling multiple maintenance projects at a copper mine. Eur J Oper Res 1994, 6: 176–191.
Chen PH, Shahandashti SM: Hybrid of genetic algorithm and simulated annealing for multiple project scheduling with multiple resource constraints. Autom Constr 2009, 18: 434–443. 10.1016/j.autcon.2008.10.007
Cohen I, Golany B, Shtub A: Managing stochastic, finite capacity, multi-project systems through the cross entropy methodology. Ann Oper Res 2005, 134: 183–199. 10.1007/s10479-005-5730-1
Cohen I, Golany B, Shtub A: Resource allocation in stochastic, finite-capacity, multi-project systems through the cross entropy methodology. J Sched 2007, 10: 181–193. 10.1007/s10951-007-0013-0
Elmaghraby SE: Resource allocation via dynamic programming in activity networks. Eur J Oper Res 1993, 64: 199–215. 10.1016/0377-2217(93)90177-O
Elmaghraby SE: Optimal procedures for the discrete time/cost trade-off problem in project networks. Eur J Oper Res 1996, 88: 50–68. 10.1016/0377-2217(94)00181-2
Elmaghraby SE, Morgan CD: A sample-path optimization approach for optimal resource allocation in stochastic projects. J Econ Manag 2007, 3: 367–389.
Elmaghraby SE, Salem AM: Optimal project compression under convex functions, I and II. Appl Manag Sci 1982, 2: 1–39.
Elmaghraby SE, Salem AM: Optimal linear approximation in project compression. IIE Trans 1984, 16: 339–347. 10.1080/07408178408975253
Fatemi Ghomi SMT, Ashjari B: A simulation model for multi-project resource allocation. Int J Proj Manag 2002, 20: 127–130. 10.1016/S0263-7863(00)00038-7
Fatemi Ghomi SMT, Hashemin SS: A new analytical algorithm and generation of Gaussian quadrature formula for stochastic network. Eur J Oper Res 1999, 114: 610–625. 10.1016/S0377-2217(98)00197-0
Fulkerson DR: A network flow computation for project curves. Manag Sci 1961, 7: 167–178. 10.1287/mnsc.7.2.167
Goncalves JF, Mendes JJM, Resende MGC: A genetic algorithm for the resource constrained multi-project scheduling problem. Eur J Oper Res 2008, 189: 1171–1190. 10.1016/j.ejor.2006.06.074
Kanagasabapathi B, Rajendran C, Ananthanarayanan K: Performance analysis of scheduling rules in resource-constrained multiple projects. Int J Ind Syst Eng 2009, 4: 502–535.
Kao H-P, Hsieh B, Yeh Y: A petri-net based approach for scheduling and rescheduling resource-constrained multiple projects. J Chinese Inst Ind Eng 2006,23(6):468–477.
Kruger D, Scholl A: Managing and modelling general resource transfers in (multi-) project scheduling. OR Spectr 2008, 32: 369–394.
Kulkarni V, Adlakha V: Markov and Markov-regenerative PERT networks. Oper Res 1986, 34: 769–781. 10.1287/opre.34.5.769
Kumanan S, Jegan JG, Raja K: Multi-project scheduling using an heuristic and a genetic algorithm. Int J Adv Manuf Technol 2006, 31: 360–366. 10.1007/s00170-005-0199-2
Kurtulus IS, Davis EW: Scheduling: categorization of heuristic rules performance. Manag Sci 1982, 28: 161–172. 10.1287/mnsc.28.2.161
Kurtulus IS, Narula SC: Multi-project scheduling: analysis of project performance. IIE Trans 1985, 17: 58–66. 10.1080/07408178508975272
Li C, Wang K: The risk element transmission theory research of multi-objective risk-time–cost trade-off. Compute Math with Appl 2009, 57: 1792–1799. 10.1016/j.camwa.2008.10.051
Lova A, Tormos P: Analysis of scheduling schemes and heuristic rules performance in resource-constrained multiproject scheduling. Ann Oper Res 2001, 102: 263–286. 10.1023/A:1010966401888
Lova A, Maroto C, Tormos P: A multicriteria heuristic method to improve resource allocation in multiproject scheduling. Eur J Oper Res 2000, 127: 408–424. 10.1016/S0377-2217(99)00490-7
Nozick LK, Turnquist MA, Xu N: Managing portfolios of projects under uncertainty. Ann Operation Res 2004, 132: 243–256.
Payne JH: Management of multiple simultaneous projects: a state-of-the-art review. Int J Proj Manag 1995, 13: 163–168. 10.1016/0263-7863(94)00019-9
Pritsker AAB, Watters LJ, Wolfe PM: Multiproject scheduling with limited resources: a zero–one programming approach. Manag Sci 1969,16(1):93–108. 10.1287/mnsc.16.1.93
Tsubakitani S, Deckro RF: A heuristic for multi-project scheduling with limited resources in the housing industry. Eur J Oper Res 1990, 49: 80–91. 10.1016/0377-2217(90)90122-R
Wiest JD: A heuristic model for scheduling large projects with limited resources. Manag Sci 1967,13(6):359–377.
Ying Y, Shou Y, Li M: Hybrid genetic algorithm for resource constrained multi-project scheduling problem. J Zhejiang University (Eng Sci) 2009, 43: 23–27.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
SY studied the associated literature review and presented the mathematical model and simulation algorithm. He was also responsible for revising the manuscript. SN managed the study and participated in the problem solving approaches. MMM approved the model and analyzed the required data and conducted the experimental analysis. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yaghoubi, S., Noori, S. & Mazdeh, M.M. A heuristic method for consumable resource allocation in multi-class dynamic PERT networks. J Ind Eng Int 9, 17 (2013). https://doi.org/10.1186/2251-712X-9-17
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2251-712X-9-17