Abstract
In many circumstances, the quality of a process or product is best characterized by a given mathematical function between a response variable and one or more explanatory variables that is typically referred to as profile. There are some investigations to monitor auto-correlated linear and nonlinear profiles in recent years. In the present paper, we use the linear mixed models to account autocorrelation within observations which is gathered on phase II of the monitoring process. We undertake that the structure of correlated linear profiles simultaneously has both random and fixed effects. The work enhanced a Hotelling’s T2 statistic, a multivariate exponential weighted moving average (MEWMA), and a multivariate cumulative sum (MCUSUM) control charts to monitor process. We also compared their performances, in terms of average run length criterion, and designated that the proposed control charts schemes could effectively act in detecting shifts in process parameters. Finally, the results are applied on a real case study in an agricultural field.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Control charts are used to detect anomalies in the processes. They are most often used to monitor production-related processes. In many business-related processes, the quality of a process or product can be characterized by a relationship between a response variable and one or more explanatory variables which is referred to as profile. The purpose of the analyzing of profile in phase I is to determine the stability of the process and estimate parameters, however, in phase II, analyzers are interested in rapidly detecting the significant shifts in the process parameters. Phase I analysis of simple linear profiles has been investigated by a number of authors such as Stover and Brill (1998), Kang and Albin (2000), Kim et al. (2003) and Mahmoud et al. (Mahmoud and Woodall 20042007). Many authors including Kang and Albin (2000), Kim et al. (2003), Noorossana et al. (2004), Gupta et al. (2006), Zou et al. (2006), Saghaei et al. (2009), and Mahmoud et al. (2009) have investigated phase II monitoring of simple linear profiles. Noorossana et al. (2010a, b) investigated monitoring of multivariate simple linear profiles on phase II. Zou et al. (2007) and Kazemzadeh et al. (2009a, b) considered cases when the profiles can be characterized by multiple and polynomial regression models respectively. Mahmoud (2008) considered phase I monitoring of multiple linear profiles, and Kazemzadeh et al. (2008) proposed three methods for monitoring the k th-order polynomial profile in phase I. Ding et al. (2006), Moguerza et al. (2007), Williams et al. (2007), and Vaghefi et al. (2009) investigated nonlinear profiles. In these studies, it is implicitly assumed that the error terms within or between profiles is independently and identically normally distributed; however in some cases, these assumptions can be violated. Noorossana et al. (2010a, b) analyzed the effects of non-normality on the monitoring of simple linear profiles. Noorossana et al. (2008) and Kazemzadeh et al. (2009a, b) investigated autocorrelation between successive simple linear and polynomial profiles respectively. Soleimani et al. (2009) proposed a transformation to eliminate the autocorrelation between observations within a simple linear profile in phase II. Jensen et al. (2008) proposed two T2 control charts based on linear mixed model (LMM) to account for the autocorrelation within linear profiles in phase I. They concluded that the linear mixed model is superior to the least square approach for unbalanced or missing data, especially when the number of observation within a profile is small and the correlation is weak. Jensen and Birch (2009) used nonlinear mixed model to account correlation within nonlinear profiles. Qie et al. (2010) investigated nonparametric profile monitoring with arbitrary design using mixed models. They proposed a control chart that combines the exponentially weighted moving average control chart based on local linear kernel smoothing and a nonparametric regression test under the assumption that observations within and between individual profiles are independent of each other.
The present study acts as an extension of the work of Jensen et al. (2008) in applying a linear mixed model on the presence of autocorrelation within linear profiles on phase I control chart applications; conversely, our focus is on phase II of profile monitoring in which one could use the proposed control charts to detect any departures from the given profile parameters.
The remainder of the paper is organized as follows. In ‘Linear mixed model’ Section, the LMM is mathematically presented. In the ‘Proposed methods’ Section, our methods including three modified multivariate control charts namely Hotelling T2, multivariate exponential weighted moving average (MEWMA) and a multivariate cumulative sum control charts (MCUSUM) are illustrated. In ‘Simulation studies’ Section, the results of simulation study to evaluate the performance of the methods are presented. In addition, a case study from an agriculture field is investigated on the Section ‘Case study’. The final section closes with concluding remarks.
Linear mixed model
Linear mixed models (Laird and Ware 1982) are popular for analysis of longitudinal data. A linear mixed model contains fixed and random effects and is linear in these effects. This model allows us to account autocorrelation within profiles. In matrix notation, a mixed model can be represented as
where y is a vector of observations, with mean E(y) = Xβ, β is a vector of fixed effects, b is a vector of independent and identically distributed (IID) random effects with mean E(b) = 0 and variance-covariance matrix Var(b) = D,ϵ is a vector of IID random error terms with mean and variance , and X and Z are matrices of regressors relating the observations y to β and b.
In the 1950s, Charles Roy Henderson provided the best linear unbiased estimate ( BLUE) of fixed effects and best linear unbiased predictions (BLUP) of random effects. Subsequently, mixed modeling has become a major area of statistical research, including work on the computation of maximum likelihood estimates, nonlinear mixed effect models, missing data in mixed effects models, and Bayesian estimation of mixed effects models (West et al. 2007).
Henderson’s ‘mixed model equations’ (MME) are (Robinson 1991) as follows:
The solutions to the MME, , and are BLUEs and BLUPs for β and b, respectively.
Mixed models require somewhat sophisticated computing algorithms to fit. Solutions to the MME are obtained by methods similar to those used for linear least squares. For complicated models and large datasets, iterative methods may be needed.
In profile monitoring, one could suppose that the j th response follows a LMM; therefore,
where X i is a (n j × p) matrix of regressors, and Z j is a (n j × q) matrix associated with random effects. β is a (p × 1) vector of fixed effects, and y j is the (n j × 1) response vector for the j th profile. The coefficient vector of the random effect terms is b j ~ MN (0,D), and D is assumed to be a diagonal matrix; thus, the random effects are assumed not to be correlated with each other. In addition, it is assumed that Cov(ϵ j , b j ) = 0 and ϵ j is (n j × 1) vector of errors where ϵj ~ MN (0,R j ). If the errors are assumed to be independent, R j = σ2I, but correlated, the functional structure for the error terms may be used.
As noted before, it is considered that is an estimator of β, and is a predictor of b j , then is the population average, and is the profile specific prediction; so if D and R j are known, then it can be shown as follows:
and the BLUP of b is
where is the overall estimated variance covariance matrix (Schabenberger and Pierce 2002).
Proposed methods
In this paper, we propose a linear mixed model approach for accounting the correlation within linear profiles in phase II. It is assumed that profiles are correlated based on first-order autoregressive (AR(1)) structure.
If the errors follow an auto-correlated structure such as an AR(1) structure, then R j by Schabenberger and Pierce (2002) is given as Equation 6. More details on the types of correlated errors structures could be acquired in this reference as
It is assumed that for the j th sample collected over time, our observations are (X i ,y ij ), i = 1,2,…,n and j = 1,2,…,m. We considered the case that all the fixed effects have a corresponding random effect, (X j = Z j ). If the process is in control, the problem can be formulated as follows:
and
where ϵ ij are the correlated error terms and a ij are white noises as a ij ~ N(0,σ2). The β0, β1,…,βp − 1 are fixed effects that are the same for all profiles. The b0j,b1j,…,bp − 1j are random effects for the j th profile and they are normal random variables with zero mean and variance of , respectively, which are not to be correlated with each other and also not to be correlated with the errors. The x values are fixed and constant from profile to profile. In this article we especially focused on phase II of the monitoring process, so all profile’s parameters, process variance, and correlation coefficient are known in phase I. Accordingly, we utilized the modified Jensen et al. (2008) approach to monitor autocorrelation on phase II.
The Hotelling’s T2statistic control chart
As a first proposed control chart, we use T2 statistic to monitor the fixed effects for each sample. This statistic is given by
where and β0 denote the in-control value of β.
In Equation 9 the variance covariance matrix of fixed effects is .
The upper control limit, UCL, is chosen to achieve a specified in control average run length (ARL).
The MEWMA control chart
Our second proposed control chart is based on MEWMA proposed by Lowry et al. (1992) for monitoring the vector of . Here the MEWMA statistics is as follows:
where z0 = 0 and θ(0 < θ < 1) is the smoothing parameter. Therefore, the chart statistic denotes by MEWMA j is given by
where .
This control chart gives a signal when EWMA j > UCL, where (UCL > 0) is chosen to achieve a specified in control ARL.
The MCUSUM control chart
The third suggested method is based on the MCUSUM control chart which is proposed by Crosier (1988). In this method, the statistic is given by
where
and s0 = 0 and k is a selected constant.
The estimator of variance covariance matrix is
The chart gives a signal if where (UCL > 0) is chosen to achieve the desired in-control ARL.
Simulation studies
To show the performance of the proposed methods, we considered the underlying linear profile as Equation 14:
where
and a ij ~ N(0,1),b0j ~ N(0,.1),b1j ~ N(0,.1). In our simulation investigation, we considered three significant different autocorrelation coefficients: a ρ = 0. 1 to designate a weak type auto-correlated process, intermediate autocorrelation by ρ = 0. 5, and strong autocorrelation by ρ = 0.9. The in-control ARL is roughly set equal to 200 and the ARL values were evaluated through 10,000 simulation replications under different shifts in intercept, slope, and errors (standard deviation). For MEWMA control chart, the smoothing parameter θ is chosen to be 0.2. As a general rule, to design MCUSUM control chart with the k approach, one chooses k to be half of the delta shift which is the amount of shift in the process that we wish to detect, expressed as a multiple of the standard deviation of the data points. Accordingly, we set k equal to 0.5 (for more detail see Montgomery 2005). UCLs of control charts are designed to achieve a specified in control ARL of 200. The simulated UCLs for each proposed control chart are shown in Table 1.
The three proposed control charts are compared on different scenarios of the example in terms of ARL, and the calculated amounts for the different changes in the intercept is shown in Table 2.
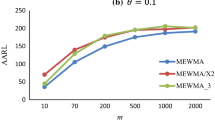
According to the Table 2, under σ shift in the intercept, when autocorrelation is weak (ρ = 0.1), the MEWMA method performs relatively similar to MCUSUM control chart, and they also have better performance for detecting the small, moderate, and large shifts than the T2 control chart. In the intermediate and strong autocorrelation circumstance (ρ = 0.5) and (ρ = 0.9), MCUSUM performs uniformly better than the other two methods. Moreover, MEWMA uniformly performs better than T2 control chart. Figure 1 presented the derivative ARL under different shifts in intercept when autocorrelation is different in three levels. Table 3 shows the simulation results under different shifts in slope.
From Table 3, under βσ shift in slope, while the autocorrelation is weak (ρ = 0.1), the proposed MCUSUM method uniformly performs better than MEWMA method. Also, MEWMA performs consistently better than T2 method. In addition, similar results are obtained when the autocorrelation is intermediate (ρ = 0.5). Once the amount of autocorrelation coefficient is high, MCUSUM and MEWMA methods perform uniformly better than the T2 method and also, MCUSUM method performs relatively similar to MEWMA method. Figure 2 illustrates ARL under different shifts in slope once autocorrelation be changed in the aforementioned levels.
Next comparisons of the proposed three control charts in terms of ARL under δσ shift in the standard deviation followed. Table 4 shows that the proposed T2 chart performs significantly better than MEWMA and MCUSUM charts in different amount of correlation coefficients. In addition for strong and intermediate autocorrelation condition, MEWMA and MCUSUM have similar manners and when the autocorrelation is weak, MEWMA relatively achieves better performance. Derivative ARL under different shifts of standard deviation is presented in Figure 3 when autocorrelation is different.
Based on the simulation results, it is evident that the proposed MEWMA and MCUSUM methods act relatively better than the T2 chart in detecting shift in the parameters of profile; conversely, the proposed T2 chart performs better than the MEWMA and MCUSUM in detecting shift in the variation.
Case study
Consider the case study carried out by Schabenberger and Pierce (2002). It was a real data set from ten apple trees which 25 apples are randomly chosen on each tree. Their focus was on the analysis of the apples in the largest size, with initial diameters exceeded 2.75 in. Totally there were 80 apples in aspiration size. Diameters of the apples were recorded in every 2 weeks during 12 weeks. Figure 4 shows 16 diameters out of 80 apples in the time domain. In their investigation, functional profile between time and diameter considered as quality characteristic that needs to be monitored over time. Schabenberger and Pierce (2002) and also later Soleimani et al. (2009) modeled such correlation between observations by a first-order autoregressive model of AR(1). Based on the preceding analysis, the following statements hold a linear mixed model equation for the declared case study:
where b0j ~ N(0,0.008653), b1j ~ N(0,0.00005), and a0j ~ N(0,0.000365).
Measured diameters of apples during a period of 12 weeks. (Schabenberger and Pierce 2002).
The estimator of variance-covariance matrix of fixed effects gives by
Consequences of simulation run in the previous section leads us to use MEWMA and MCUSUM which have relatively similar performance on detecting shift in the profile parameters rather than the T2 method. Hence, the proposed MEWMA control chart was applied in monitoring the linear profile. The smoothing constant (θ) is set equal to 0.2. In order to achieve an in control ARL of 200, the upper control limit is set equal to 7 based on 10,000 simulation runs. In order to examine performance of the control chart, six random samples from the in control simple linear profile are initially generated. Formerly, three random samples are generated to show an out-of-control condition under the intercept shift coefficient of 0.6. Figure 5 illustrates sensitivity of the MEWMA control chart based on our proposed method which temperately depicts quick signal.
Concluding remarks
We have studied the sensitivity of three multivariate control charts to detect one-step permanent shift in any parameters of a mixed model linear profile. Our specially designed MCUSUM, MEWMA, and T2 control charts were also studied as competitors of each other to depict shifts in intercept and slope parameters and also process variation while first-order autoregressive model describes correlations within observations.
The performances of the methods were compared in terms of average run length criteria. Table 5 shows the summarized results.
The following summary recommendations are made:
-
1
The proposed approach has good performance across the range of possible shifts and it can be used in phase II of linear profile monitoring on the presence of autocorrelation within observations.
-
2
The anticipated MEWMA and MCUSUM methods almost uniformly perform better efficiency than the T 2 Hotelling control chart under different step shifts in the intercept and slope parameters of linear profile.
-
3
The Hotelling T 2 control chart has better performance in comparison with the MEWMA and MCUSUM methods under shifts in the process standard deviation.
-
4
The process circumstance in terms of correlation coefficient has no significant effects on selecting the best choice for monitoring method.
Authors’ information
SR (IRAN, Male, 1962). Ph.D., Associate Professor, worked at School of Industrial Engineering in Islamic Azad University, Tehran South Branch (IAU-STB). He obtained his Ph.D., Master and Bachelor degrees in Industrial Engineering. He was engaged in the industrial system engineering technology development and the technical consultant from 1988 up to year. He worked in different management positions both in private sector and university. The last one was deputy of research and planning in Islamic Azad University-Tehran South Branch. During his management period more than 10 scientific journals initiated and research activities facilitated. Currently, Dr. Raissi act as Editor-in-Chief of Journal of Industrial Engineering, International (JIEI) a Springer open journal and also has major responsibility on Ph.D. department of Industrial Engineering in IAU-STB. His main research fields are statistical quality control, quality engineering, system simulation and statistical methods in engineering. PS is an assistant professor of Industrial Engineering at IAU-STB. She especially focused on multivariate profile monitoring techniques under correlated process in her MS and PhD thesis. Her research interests are in the areas of Statistical Quality Control, Time Series, Multivariate Analysis and Metaheuristic algorithms. AN received his Master's of Science degrees in Industrial Engineering from IAU-STB. He especially focused on developing profile monitoring techniques as his academicals task under supervision of PS and SR. His research interests are in the areas of Time Series Analysis and Statistical Quality Control.
References
Crosier RB: Multivariate Generalizations of Cumulative Sum Quality Control Schemes. Technometrics 1988, 30: 291–303. 10.1080/00401706.1988.10488402
Ding Y, Zeng L, Zhou S: Phase I analysis for monitoring nonlinear profiles in manufacturing processes. J QualTechnol 2006,38(3):199–216.
Gupta S, Montgomery DC, Woodall WH: Performance evaluation of two methods for online monitoring of linear calibration profiles. Int J Prod Res 2006, 44: 1927–1942. 10.1080/00207540500409855
Hotelling H: Multivariable Quality Control—Illustrated By The Air Testing Of Sample Bombsights. In Techniques of Statistical Analysis. Edited by: Eisenhart C, Hastay MW, Wallis WA. New York: McGraw Hill; 1947:111–184.
Jensen WA, Birch JB: Profile monitoring via nonlinear mixed model. J QualTechnol 2009, 41: 18–34.
Jensen WA, Birch JB, Woodall WH: Monitoring correlation within linear profiles using mixed models. J QualTechnol 2008,40(2):167–183.
Kang L, Albin SL: On-line monitoring when the process yields a linear profile. J QualTechnol 2000,32(4):418–426.
Kazemzadeh RB, Noorossana R, Amiri A: Phase I monitoring of polynomial profiles. Commun Stat-Theor M 2008,37(10):1671–1686. 10.1080/03610920701691714
Kazemzadeh RB, Noorossana R, Amiri A: Phase II monitoring of autocorrelated polynomial profiles in AR(1) processes. Int J SciTechnol, Sci Iran 2009,17(1):12–24.
Kazemzadeh RB, Noorossana R, Amiri A: Monitoring polynomial profiles in quality control applications. Int J Adv Manuf Technol 2009,42(7):703–712.
Kim K, Mahmoud MA, Woodall WH: On the monitoring of linear profiles. J QualTechnol 2003,35(3):317–328.
Laird NM, Ware JH: Random affects models for longitudinal data. Biometrics 1982, 38: 963–974. 10.2307/2529876
Lowry CA, Woodal WH, Champ CH, Rigdon SE: A Multivariate Exponentially Weighted Moving Average Control Chart. Technometrics 1992, 34: 46–53. 10.2307/1269551
Mahmoud MA: Phase I analysis of multiple regression linear profiles. Commun Stat Simul C 2008,37(10):2106–2130. 10.1080/03610910802305017
Mahmoud MA, Woodall WH: Phase Ianalysis of linear profiles with applications. Technometrics 2004, 46: 380–391. 10.1198/004017004000000455
Mahmoud MA, Parker PA, Woodall WH, Hawkins DM: A change point method for linear profile data. Qual Reliab Eng Int 2007, 23: 247–268. 10.1002/qre.788
Mahmoud MA, Morgan JP, Woodall WH: The monitoring of simple linear regression profiles with two observations per sample. J Appl Stat 2009, 37: 1249–1263.
Moguerza JM, Muñoz A, Psarakis S: Monitoring nonlinear profiles using support vector machines. Lect Notes Comput Sc 2007, 4789: 574–583.
Montgomery DC: Introduction to statistical quality control. 5th edition. New Jersey, NJ: John Wiley & Sons; 2005.
Noorossana R, Amiri A, Vaghefi A, Roghanian E: Monitoring Quality Characteristics Using Linear Profile. In Proceedings of the 3rd InternationalIndustrial Engineering Conference. Tehran, Iran; 2004.
Noorossana R, Amiri A, Soleimani P: On the monitoring of autocorrelated linear profiles. Commun Stat-Theor M 2008,37(3):425–442. 10.1080/03610920701653136
Noorossana R, Eyvazian M, Vaghefi A: Phase II monitoring of multivariate simple linear profiles. Comput Ind Eng 2010, 58: 563–570. 10.1016/j.cie.2009.12.003
Noorossana R, Vaghefi A, Dorri M: Effect of non-normality on the monitoring of simple linear profiles. Qual Reliab Eng Int 2010, 27: 1015–1021.
Qie P, Zhang Y, Wang Z: Nonparametric profile monitoring by mixed effects modeling. Technometrics 2010,52(3):283–285. 10.1198/TECH.2010.09174
Robinson GK: That BLUP is a good thing: the estimation of random effects. Stat Sci 1991,6(1):15–32. 10.1214/ss/1177011926
Saghaei A, Mehrjoo M, Amiri A: A CUSUM-based method for monitoring simple linear profiles. Int J Adv Manuf Technol 2009. 10.1007/s00170-009-2063-2
Schabenberger O, Pierce FJ: Contemporary statistical models for the plant and soil sciences. Boca Raton: CRCPress; 2002.
Soleimani P, Noorossana R, Amiri A: Monitoring simple linear profiles in the presence of autocorrelation within profiles. Comput Ind Eng Int 2009,57(3):1015–1021. 10.1016/j.cie.2009.04.005
Stover FS, Brill RV: Statistical quality control applied to ion chromatography calibration. J Chromatogr A 1998, 804: 37–43. 10.1016/S0021-9673(98)00094-6
Vaghefi A, Tajbakhsh SD, Noorossana R: Phase II monitoring ofnonlinear profiles. Commun Stat-Theor M 2009, 38: 1834–1851. 10.1080/03610920802468707
West BT, Welch KB, Galecki AT: Linear mixed models: a practical guide to using statistical software. New York: Chapman & Hall/CRC; 2007.
Williams JD, Woodall WH, Birch JB: Statistical monitoring of nonlinear product and process quality profiles. Qual Reliab Eng Int 2007, 23: 925–941. 10.1002/qre.858
Zou C, Zhang Y, Wang Z: Control chart based on change-point model for monitoring linear profiles. IIE Transactions 2006,38(12):1093–1103. 10.1080/07408170600728913
Zou C, Tsung F, Wang Z: Monitoring general linear profiles using multivariate exponentially weighted moving average schemes. Technometrics 2007,49(4):395–408. 10.1198/004017007000000164
Acknowledgments
The authors thank the referee and the grateful editor in chief of JIEI for their valuable comments and suggestions. This research was supported by deputy of research in the Modeling and Optimization Research Center of Industrial Engineering Faculty on Islamic Azad University, South Tehran Branch.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
AN and PS studied the associated literature review and presented the mathematical models. SR managed the study and participated in the problem solving approaches. PS and SR approved and validate the model and SR was responsible for revising the manuscript. SR as corresponding author read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Narvand, A., Soleimani, P. & Raissi, S. Phase II monitoring of auto-correlated linear profiles using linear mixed model. J Ind Eng Int 9, 12 (2013). https://doi.org/10.1186/2251-712X-9-12
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2251-712X-9-12