Strategy-aligned fuzzy approach for market segment evaluation and selection: a modular decision support system by dynamic network process (DNP)

Abstract

In competitive markets, market segmentation is a critical point of business, and it can be used as a generic strategy. In each segment, strategies lead companies to their targets; thus, segment selection and the application of the appropriate strategies over time are very important to achieve successful business. This paper aims to model a strategy-aligned fuzzy approach to market segment evaluation and selection. A modular decision support system (DSS) is developed to select an optimum segment with its appropriate strategies. The suggested DSS has two main modules. The first one is SPACE matrix which indicates the risk of each segment. Also, it determines the long-term strategies. The second module finds the most preferred segment-strategies over time. Dynamic network process is applied to prioritize segment-strategies according to five competitive force factors. There is vagueness in pairwise comparisons, and this vagueness has been modeled using fuzzy concepts. To clarify, an example is illustrated by a case study in Iran's coffee market. The results show that success possibility of segments could be different, and choosing the best ones could help companies to be sure in developing their business. Moreover, changing the priority of strategies over time indicates the importance of long-term planning. This fact has been supported by a case study on strategic priority difference in short- and long-term consideration.

Background

Porter 1980) described a category scheme including three general types of strategies: Cost leadership, differentiation, and market segmentation which are commonly used by various businesses to achieve and maintain competitive advantages. These three generic strategies are defined along two dimensions: strategic scope and strategic strength. Strategic scope is a demand-side dimension and looks at the size and composition of the market you intend to target. Strategic strength is a supply-side dimension and looks at the strength or core competency of the firm. Market segmentation is narrow in scope when both cost leadership and differentiation are relatively broad in market scope. Market segmentation divides the market into homogeneous groups of individual markets with similar purchasing response as a number of smaller markets have differences based on geography, demographics, firm graphics, behavior, decision-making processes, purchasing approaches, situation factors, personality, lifestyle, psychographics, and product usage (Aaker 1995; Bonoma and Shapiro 1983; Dickson 1993; Kotler 1997; Bock and Uncles 2002; Nakip 1999; File and Prince 1996). The results of segmentation could be improved considerably if information on competitors is considered in the process of market segmentation (Söllner and Rese 2001). Market segmentation allows the marketing program to focus on a special part of the market to increase its competitiveness by applying various strategies. These strategies can be new products development, differentiated marketing communications, advertisements creation, different customer services development, prospects targeting with the greatest potential profits, and multi-channel distribution development. Many researchers developed the evaluation and selection of market segmentation methods to achieve more customer satisfaction by focusing on marketing programs designed to satisfy customer requirements efficiently. The vast majority of decision-making methods have focused on evaluating the different segmentation methods and techniques (Kuo et al. 2002; Lu 2003; Coughlan and Soberman 2005; Liu and Serfes 2007; Ou et al. 2009; Phillips et al. 2010; Tsai et al. 2011a, 2011b). In the market segment evaluation and selection, there are four stages or procedures that were introduced by Montoya-Weiss and Calentone (2001): problem structuring, segment formation, segment evaluation and selection, and description of segment strategy.

Distinction of segmentation at a strategic or at an operational level has been made by several authors such as Goller et al. (2002) and Sausen et al. (2005). The general assumption behind the dimension is that there is a fundamental difference in how the firm is affected by the segmentation (Clarke and Freytag 2008). At a strategic level, the consideration is on the top management level and concerns the creation of missions and strategic intent, and can become closely linked to the capabilities and nature of the organization (Jenkins and McDonald 1997). At the operational level, there is a concern for planning and operational schemes for reaching target segments with an effectively adjusted offering as well as monitoring the performance (Albert 2003). In a competitive market, strategies are critical points of business, which lead the companies towards their vision as their final destination. Strategy description and selection is an important part of strategic management process. Many approaches, techniques, and tools can be used to analyze strategic cases in this process (Dincer 2004). Ray (2000) applied strategic segmentation where, prior to price competition, each firm targets the information to specific consumers who are informed by a firm that they can buy from it.

Among the strategic tools, SPACE matrix (Rowe et al. 1982) is a common method. It is used as a strategy description and success evaluation technique that includes two dimensions: internal perspectives (financial strength (FS) and competitive advantage (CA)) and external perspectives (environmental stability (ES) and industry strength (IS)).

All marketing strategies include a search for competitive advantages (Bharadwaj and Varadarajan 1993; Day and Wensley 1988; Varadarajan and Cunningham 1995; Hunt and Arnett 2004). According to Söllner and Rese (2001), ‘The consideration of competitive structure provides additional basic information on segment formation’ and ‘The consideration of competitive structure facilitates the selection of promising segments’. SPACE matrix is a support tool for decision-making process, and it is very useful when the market competitiveness is a critical point of decision-making process. In this method, internal and external perspectives are evaluated according to the overall situation of the company in the market to build strategies basing on the factors in the four main groups (FS, CA, ES, and IS). These generic strategies are termed as ‘defensive’, ‘aggressive’, ‘conservation’, and ‘competitive’ which can be broken from the main strategies. Moreover, the SPACE matrix can indicate success possibility through the algebraic summation of the evaluated factor scores within its two dimensions (Figure 1).

Figure 1

Space graph and generic strategies.

In a dynamic and ever-changing world, the time frame is important for a segmentation process (Nakip 1999; Freytag and Clarke 2001). Market segments and strategies can be selected based on a set of factors and sub-factors which vary over time. In competitive markets, the effects of time are more sensible on prioritization. It means that their priorities could be changed particularly when the factors are time-dependent. Saaty (2007) extended the analytic hierarchy process (AHP)/analytic network process (ANP) to deal with time-dependent priorities and referred them as dynamic hierarchy process (DHP)/dynamic network process (DNP). In his method, prioritization is done by considering the changes in the market over time, which affect the importance of factors. Moreover, the fuzzy concept has been applied to solve the problem due to the vagueness of the importance and the priorities of these factors. Below, Table 1 shows the recent works on this subject and summarizes their main considerable issues. As presented in the table, this work ‘considers risk’ and ‘factors interdependency’ in studying and in ‘selecting the segment-strategies over time’.

Table 1 Market segment evaluation and selection of literatures

As it is observed in the above table, recent researches have considered the important factors of this problem, but none of them provides a comprehensive model. Also, time-dependent decision making is an affective item that is provided in this paper, which was not considered in previous works.

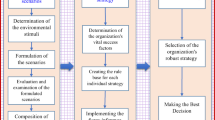
In this paper, a strategy-aligned fuzzy approach is developed to select the best segment-strategy in market segment evaluation and selection problem. A modular decision-making process is implemented in two stages:

The first one selects the segments with more chance of success which has an acceptable risk in a competitive market according to their situation in the SPACE matrix. As the first contribution, by applying the SPACE matrix method, competition is taken into account by defining the distance of segments from the best situation of competitive advantage. On the other hand, this method can give an overall view of the competitive advantage of all segments with a risk evaluation of choosing the segments in a simple graph. The second stage is segment-strategy selection, considering that priorities change over time, by dynamic network process. As the second contribution, segments are selected by considering the effect of time on the decision-making criteria. Moreover, the effects of strategies on changing the priorities are considered over time, and the trend of segment-strategy priorities can be determined in various time horizons. Porter's (1980) five force factors and sub-factors have been applied as well known decision-making criteria in dealing with competitive advantage. This approach defines the risk level of the segments; thus, decision makers (DMs) could select the appropriate segments according to their acceptable risk levels. Furthermore, they could select more exact strategies by focusing on selected segment. In addition, the proposed DNP method enables them to analyze segment-strategies over time, and this ability could affect their decision. The steps of the proposed DSS are shown in Figure 2.

Figure 2

The steps of the proposed DSS.

The rest of this paper is organized as follows: In the ‘Methods’ section, the dynamic network process is shown including the explanation of its applications in the next section. The ‘Fuzzy fundamental’ section presents a brief overview of the fuzzy concepts. In section ‘Fuzzy dynamic network process’, the fuzzy DNP calculation method is presented. In the ‘Results and discussion’ section, a procedure for segment-strategy selection is introduced, including how to select an optimum solution. A case study with its computational results is also presented for the proposed model. The final section gives the conclusions and future works.

Methods

Time-dependent analytic network process

Market segment evaluation and selection can be classified as a multi-criteria decision-making (MCDM) problem. AHP is the well known and the most widely used method among several MCDM approaches such as SAW, MEW, TOPSIS, and ELECTRE. AHP was introduced by Saaty (1980) for decision-making as a theory of relative measurement based on paired comparisons used to derive normalized absolute scales of numbers, the elements of which are then used as priorities. The ANP was developed and implemented by Saaty (1996) as an AHP with feedback. The ANP feedback approach replaces hierarchies with networks in which the relationships among the levels are not easily represented as higher or lower, dominant or subordinate, and direct or indirect (Meade and Sarkis 1999). In AHP and ANP, static and derived numbers are used to represent priorities. When the priorities vary across the time, AHP and ANP need to be dynamic through the use of numbers or functions and then derive either numbers that represent functions like expected values, or derive functions directly to represent priorities. Saaty (2007) extended the AHP/ANP to deal with time-dependent priorities and referred them as DHP/DNP. In this way, Saaty (2007) presented two methods: the (1) numerical solution of the principal eigenvalue problem by raising the matrix to powers and the (2) analytical solution of the principal eigenvalue problem by solving algebraic equations of degree n. In ANP, the problem is to obtain the limiting result of powers of the super-matrix with dynamic priorities. Because its size will increase in the near future, the super-matrix would have to be solved numerically (Saaty 2007). In the numerical solution, the best fitting curves for the components of the eigenvector were obtained by plotting the principal eigenvector for the indicated values of t. In the analytical solution for the pairwise comparison judgments in dynamic conditions, Saaty (2007) purposed some functions for the dynamic judgments, which are given in Table 2.

Table 2 Mathematician's formulation of a dynamic judgment scale

To solve the problem and to obtain the time-dependent principal eigenvector, Saaty (2007) introduced the numerical approach by simulation, in which at first, the judgments express functionally but then derives the eigenvector from the judgments for a fixed instant of time, substitutes the numerical values of the eigenvectors obtained for that instant in a super-matrix, solves the super-matrix problem, and derives the priorities for the alternatives. This process is repeated for different values of time, which generates a curve for the priorities of the alternatives and then approximates these values by curves with a functional form for each component of the eigenvector. This procedure is used in this paper to obtain the priorities of the alternatives in fuzzy dynamic network process (FDNP).

Why dynamic network process?

In a decision-making process of selecting market segments, priorities are calculated based on competitive factors with respect to some important criteria such as the effects of the interdependency among the factors and the trend of segment-strategy priorities in various time horizons. Dynamic network process as a powerful decision-making method can cover these important criteria by considering interdependency in networks in a dynamic decision-making process. Thus, DNP is a more useful method that can be applied to prioritize the alternatives in comparison with other decision-making processes.

Fuzzy fundamental

Fuzzy set theory was introduced by Zadeh (1965) to deal with the uncertainty caused by imprecision and vagueness in real world conditions. A fuzzy set is a class of objects with a continuum of grades of membership, which assigns to each object a grade of membership ranging between zero and one (Kahraman et al. 2003).

A triangular fuzzy number (TFN; $\tilde{\xi }$) with its membership function is shown in Figure 3. TFN can be denoted by (l, m, u), where the triplet (l, m, u) are crisp numbers and l ≤ m ≤ u. These parameters l, m and u denote the smallest possible value, the most promising value, and the largest possible value, respectively. The triplet (l, m, u) as a TFN has a membership function with following form:

$$\mu \left(x\right)=\left\{\begin{array}{c}\begin{array}{cc}\frac{x-l}{m-l}& \mathit{if}l\le x\le m\\ 1& \mathit{if}x=m\end{array}\\ \begin{array}{cc}\frac{u-x}{u-m}& \mathit{if}\mathit{m}\le \mathit{x}\le \mathit{u}\\ 0& \mathrm{Otherwise}.\end{array}\end{array}\right.$$

Figure 3

A triangular fuzzy number$\tilde{\mathbf{\xi }}\mathbf{=}\left(\mathbf{l}\mathbf{,}\mathbf{m}\mathbf{,}\mathbf{u}\right)$. The broken line is a guide to present the position of the most promising value of a TFN (m), while the solid line denotes the membership values of a TFN.

Fuzzy operations for TFNs

Let $\tilde{A}=\left(l_{\mathrm{A}},m_{\mathrm{A}},u_{\mathrm{A}}\right)$ and $\tilde{B}=\left(l_{\mathrm{B}},m_{\mathrm{B}},u_{\mathrm{B}}\right)$ be two TFNs; there are some primary fuzzy operations as bellow (Keufmann and Gupta 1991; Kahraman et al. 2002):

• 1) Addition of two fuzzy numbers:

  $$\tilde{A}\oplus \tilde{B}=\left(l_{\mathrm{A}}+l_{\mathrm{B}},m_{\mathrm{A}}+m_{\mathrm{B}},u_{\mathrm{A}}+u_{\mathrm{B}}\right)$$

• 2) Multiplication of two fuzzy numbers:

  $$\tilde{A}\otimes \tilde{B}=\left(l_{\mathrm{A}}{l}_{\mathrm{B}},m_{\mathrm{A}}{m}_{\mathrm{B}},u_{\mathrm{A}}{u}_{\mathrm{B}}\right),\mathrm{where}{l}_{\mathrm{A}}\mathrm{and}{l}_{\mathrm{B}}\ge 0$$

• 3) Multiplication of a crisp number k and a fuzzy number:

  $$k.\tilde{A}=\left(k{l}_{\mathrm{A}},k{m}_{\mathrm{A}},k{u}_{\mathrm{A}}\right),\mathrm{where}{l}_{\mathrm{A}}\mathrm{and}{l}_{\mathrm{B}}\ge 0$$

• 4) Division of two fuzzy numbers:

  $$\tilde{A}\mathrm{\Delta }\tilde{B}=\left(l_{\mathrm{A}}/u_{\mathrm{B}},m_{\mathrm{A}}/m_{\mathrm{B}},u_{\mathrm{A}}/l_{\mathrm{B}}\right),\mathrm{where}{l}_{\mathrm{A}}\mathrm{and}{l}_{\mathrm{B}}\ge 0$$

• 5) Addition of two fuzzy numbers:

  $$\tilde{A}\oplus \tilde{B}=\left(l_{\mathrm{A}}+l_{\mathrm{B}},m_{\mathrm{A}}+m_{\mathrm{B}},u_{\mathrm{A}}+u_{\mathrm{B}}\right)$$

• 6) Multiplication of two fuzzy numbers:

  $$\tilde{A}\otimes \tilde{B}=\left(l_{\mathrm{A}}{l}_{\mathrm{B}},m_{\mathrm{A}}{m}_{\mathrm{B}},u_{\mathrm{A}}{u}_{\mathrm{B}}\right),\mathrm{where}{l}_{\mathrm{A}}\mathrm{and}{l}_{\mathrm{B}}\ge 0$$

• 7) Multiplication of a crisp number k and a fuzzy number:

  $$k.\tilde{A}=\left(k{l}_{\mathrm{A}},k{m}_{\mathrm{A}},k{u}_{\mathrm{A}}\right),\mathrm{where}{l}_{\mathrm{A}}\mathrm{and}{l}_{\mathrm{B}}\ge 0$$

• 8) Division of two fuzzy numbers:

  $$\tilde{A}\mathrm{\Delta }\tilde{B}=\left(l_{\mathrm{A}}/u_{\mathrm{B}},m_{\mathrm{A}}/m_{\mathrm{B}},u_{\mathrm{A}}/l_{\mathrm{B}}\right),\mathrm{where}{l}_{\mathrm{A}}\mathrm{and}{l}_{\mathrm{B}}\ge 0$$

Linguistic variables and fuzzy numbers

Linguistic variables represent an opinion independent of measuring system. While variables in mathematics usually take numerical values, in fuzzy logic applications, the non-numeric linguistic variables are often used to facilitate the expression of rules and facts (Zadeh et al. 1996). The fuzzy scale regarding the relative importance to measure the relative weights is proposed by Kahraman et al. (2006). This scale was used to solve fuzzy decision-making problems (Kahraman et al. 2006; Tolga et al. 2005; Dağdeviren and Yüksel 2010) in the literature of strategic management. This scale was later used by Mikhailov (2000, 2003) in fuzzy prioritization approach. Linguistic scales for difficulty and importance are shown in Table 3 and Figure 4, and the linguistic values and the mean of fuzzy numbers are shown in Table 4 and Figure 5.

Table 3 Linguistic scales for difficulty and importance

Figure 4

The membership functions of linguistic variables for importance weights. EI, equally important; WMI, weakly more important; SMI, strongly more important; VSMI, very strongly more important; AMI, absolutely more important. The broken line is a guide to present the position of the most promising value of a TFN (m), while the solid line denotes the membership values of a TFN.

Table 4 Linguistic values and mean of fuzzy numbers

Figure 5

The membership functions of linguistic variables for ratings. VH, very high; VL, very low; H, high; L, low; M, medium. The broken line is a guide to present the position of the most promising value of a TFN (m), while the solid line denotes the membership values of a TFN.

Why fuzzy logic?

In most of cases, pairwise comparisons are vague because every decision has its special specifications. Using fuzzy numbers is a powerful tool to overcome the uncertainty and vagueness of data. On the other hand, pairwise comparisons with linguistic variables are easier for experts. Fuzzy set theory was introduced by Zadeh (1965) to deal with uncertainty due to imprecision and vagueness; since then, many applications have been developed in fuzzy decision-making processes. For computational efficiency, trapezoidal or triangular fuzzy numbers are usually used to represent fuzzy numbers (Klir and Yuan 1995). In this paper, TFNs are used to make the mathematics manageable and easy to understand, and to facilitate presentation of the case.

Fuzzy dynamic network process

Mikhailov (2000, 2003) developed a fuzzy prioritization approach with the advantage of the measurement of consistency indexes for the fuzzy pairwise comparison matrices. In other methods (Buckley 1985; Chang 1996; Cheng 1997; Deng 1999; Leung and Cao 2000), it is not possible to determine the consistency ratios of fuzzy pairwise comparison matrices without conducting an additional study. Mikhailov (2000, 2003) introduced three stages:

• 1) Statement of the problem

• 2) Assumptions of the fuzzy prioritization method

• 3) Solving the fuzzy prioritization problem that has survived as follows:

In a decision making problem with n elements, decision maker provides a set of $F=\left\{{\tilde{a}}_{\mathit{ij}}\right\}$ of m ≤ n (n - 1) / 2 pairwise comparison judgments, where i = 1, 2, …, n - 1, j = 2, 3, …, n, j > i, represented as triangular fuzzy numbers ${\tilde{a}}_{\mathit{ij}}=\left(l_{\mathit{ij}},m_{\mathit{ij}},u_{\mathit{ij}}\right)$. A crisp priority vector w = (w₁, w₂, …, w _n ) could reach from the problem with the fuzzy condition as follows:

$$l_{\mathit{ij}}\tilde{\le }\frac{w_i}{w_j}\tilde{\le }{\mathit{u}}_{\mathit{ij}},$$

(1)

where the symbol $\tilde{\le }$ denotes ‘fuzzy equal or less than’ and with a membership function of inequality shown as follows:

$${\mu }_{\mathit{ij}}\left(\frac{w_i}{w_j}\right)=\left\{\begin{array}{c}\begin{array}{cc}\frac{\left(w_i/w_j\right)-l_{\mathit{ij}}}{m_{\mathit{ij}}-l_{\mathit{ij}}}& \frac{w_i}{w_j}\le {\mathit{m}}_{\mathit{ij}}\end{array}\\ \begin{array}{cc}\frac{u_{\mathit{ij}}-\left(w_i/w_j\right)}{u_{\mathit{ij}}-m_{\mathit{ij}}}& \frac{w_i}{w_j}\ge {\mathit{m}}_{\mathit{ij}}\end{array}\end{array}\right..$$

(2)

There are two main assumptions that the solution of prioritization is based on. The first one is the existence of non-empty fuzzy feasible area P on the (n - 1) dimensional simplex Q^{n - 1}:

$$Q^{n-1}=\left\{\left(w_1,w_2,\dots ,w_n\right)|w_i>0,{\displaystyle \sum }_{i=1}^n{w}_i=1\right\},$$

(3)

where the membership function of the fuzzy feasible area is given by:

$${\mu }_p\left(w\right)=\underset{\mathit{ij}}{\text{min}}\left\{{\mu }_{\mathit{ij}}\left(w\right)|\begin{array}{c}i=1,2,\dots ,n-1;\\ j=2,3,\dots ,n;j>i\end{array}\right\}.$$

(4)

The second one is a priority vector that is selected with having the highest degree of membership in the aggregated membership function (4).

$${\lambda }^{*}={\mu }_p\left(w^{*}\right)=\underset{w\in Q^{n-1}}{\text{max}}\underset{\mathit{ij}}{min}\left\{{\mu }_{\mathit{ij}}\left(w\right)\right\}$$

(5)

The maximum decision rule from the Game Theory is used to solve the fuzzy prioritization problem. The maximum prioritization problem (5) is extended as follows:

$$\mathrm{Maximize}\lambda$$

(6)

subject to:

$$\lambda \le {\mu }_{\mathit{ij}}\left(w\right),i=1,2,..,n-1,j=2,3,\dots ,n,i<j$$

$${\displaystyle \sum }_{i=1}^n{w}_i=1$$

$$w_i>0,i=1,2,\dots ,n_{.}$$

With regard to the membership function (2), problem (6) can be transferred into another form that is shown as follows:

$$\mathrm{Maximize}\lambda$$

(7)

$$\begin{array}{l}\left(m_{\mathit{ij}}-l_{\mathit{ij}}\right)\mathrm{\lambda }{w}_j-w_i+l_{\mathit{ij}}{w}_j\le 0\hfill \\ \left(u_{\mathit{ij}}-m_{\mathit{ij}}\right)\mathrm{\lambda }{w}_j+w_i-u_{\mathit{ij}}{w}_j\le 0\hfill \\ {\displaystyle \sum }_{k=1}^n{w}_k=1,w_k>0,k=1,2,\dots ,n.\hfill \\ i=1,2,\dots ,n-1j=2,3,\dots ,nj>i\hfill \end{array}.$$

The non-linear problem (7) will be optimized where λ = λ^* and W = W^*, and the fuzzy judgment will be satisfied if the λ^* is positive. Also, it can be applied as the consistency measure of the initial set of fuzzy judgments. When the value of λ^* is negative, the solution ratios approximately satisfy all double-side inequalities (1), that means, the fuzzy judgments are inconsistent. To obtain the time-dependent principal eigenvector, W^* should be calculated for different values of time N_t. These eigenvectors (W^*) are used to generate a curve that shows the alternative priority in each period. The alternative curves are gathered in a graph that could help DMs to select the best option.

Results and discussion

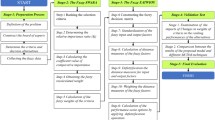
Procedure of segment-strategy selection

In this section, a procedure for segment-strategy selection is developed in ten steps to select the best potential segment with its strategies by considering an acceptable risk and in five competitive forces factors which have been developed by Porter (1980). According to this procedure, the market segments and strategies are selected in two main modules of a decision support system. In the first step, the risk amount is assigned by SPACE matrix method, and the segments are filtered based on special acceptable risk level which has been defined by DMs. In the second step, there are some segments which come from the first step. For every segment, some strategies are defined according to their position on SPACE matrix. DNP method in fuzzy environment has been applied to rank the segment-strategies.

Regarding this model, DM will be able to select the segments that have more chance of success according to their risk amount and to select proper strategies in each segment with competitive conditions. These steps are defined as follows:

Step 1. Segment filtering based on risk amount

• 1 Develop appropriate factors based on SPACE dimensions including internal perspectives (FS and CA) and external perspectives (ES and IS)

• 2 Assign relevant scores for each factor of segments and compute the total score in each dimension (internal and external); then, trace the position of each segment on SPACE graph

• 3 Assign a proper risk level for each segment and omit the segments which are out of the acceptable risk level (ARL)

• 4 Define feasible strategies for each segment and make a list of segment-strategy

Step 2. Select the best segment-strategy

• 1 Develop proper factors to choose the best segment-strategy, considering the vision statement

• 2 Compare factors for each alternative by considering the time variation and determine the effect of factors on each other

• 3 Calculate the score by FDNP for each segment-strategy according to the five competitive force factors

• 4 Make a discussion based on the score and choose the best segment-strategy

A case study is illustrated to select an optimum segment-strategy for a special coffee product in Iran market with regard to the procedure that was introduced before. While coffee is not technically a commodity, coffee is bought and sold by roasters, investors, and price speculators as a tradable commodity insofar as coffee has been described by many, including historian Pendergrast (1999), as the world's ‘second most legally traded commodity’. Decaffeination is the act of removing caffeine from coffee beans. As of 2009, progress towards growing coffee beans that do not contain caffeine is still continuing (Mazzafera et al. 2009). Consumption of decaffeinated coffee appears to be as beneficial as caffeine-containing coffee in regard to all-cause mortality, according to a large prospective cohort study (Brown et al. 1993). Decaffeinated products are produced in a coffee firm in Iran as a special product that can be put into the narrow markets from a demand perspective, particularly in the Middle East area. In Middle East, tea is a more popular beverage than coffee. This decreases the demand of coffee as a substitute product (especially decaffeinated coffee which has not existed before) in comparison with tea.

To focus on a special part of the market to increase competitiveness, a committee defines five segments (Table 5) to develop decaffeinated coffee around the Middle East. This committee includes business and market experts which have more than eight years of experience in sales or marketing in the Middle East. This committee consists of six managers within the company, who are professional in market with high experience in strategy development. All data have been collected by a team of market research experts to present to the committee to evaluate and segment the market, define and select factors and sub-factors, develop strategies, and execute pairwise comparisons in the decision-making process.

Table 5 Segments in the coffee market

Segment filtering based on risk amount

Definition of segment positions

After developing the appropriate factors based on SPACE dimensions, DMs assign a relevant score to each sub-factor for each segment (Table 6).

Table 6 Factors and sub-factors of the risk definition model

The scores should be between 0 to 6, where 6 indicates the best condition and 0 indicates the worst for positive factors (financial strength and industry strength) and vice versa for negative factors (environmental stability and competitive advantage). For example, the amount of product distribution power (CA₅) which is a sub-factor of competitive advantage as a negative factor is 1 in S₅, which means there are suitable conditions to distribute the products in S₅ in comparison with the competitors. On the other hand, the amount of Profitability (IS₃) as a positive factor of industry strength is 6 in S₁, which means there are suitable conditions to produce the product with high profitability in S₁ in comparison with other products in the other segments. According to these scores, total scores are calculated in each dimension of SPACE matrix using (8) and (9). The position of each segment is traced on SPACE graph according to the obtained pairs. It could assign a proper risk amount to each segment. Segment filtering will be done according to the assigned risk amounts and by a certain acceptable risk level.

( _x ^j, y^j) shows the position of segment j, where x and y are horizontal and vertical dimensions of the SPACE matrix, respectively. These pairs are calculated based on the sub-factor scores in two dimensions, where x is calculated by (8) and y by (9).

$$\begin{array}{l}{x}^j={\mathrm{IS}}^j-{\mathrm{CA}}^j={\displaystyle \sum }_{i=1}^N\left({\mathrm{IS}}_i^j-{\mathrm{CA}}_i^j\right)\\ i=1,2,\dots ,N\left(\mathrm{number}\mathrm{of}\mathrm{sub-factors}\right)\\ j=1,2,\dots ,5\end{array}$$

(8)

$$\begin{array}{l}{y}^j={\mathrm{FS}}^j-{\mathrm{ES}}^j={\displaystyle \sum }_{i=1}^N\left({\mathrm{FS}}_i^j-{\mathrm{ES}}_i^j\right)\\ i=1,2,\dots ,N\left(N=\mathrm{number}\mathrm{of}\mathrm{sub-factors}\right)\\ j=1,2,\dots ,5.\end{array}$$

(9)

The position of each segment has been calculated based on the sub-factor scores:

$$\begin{array}{ll}{x}^1& ={\mathrm{IS}}^1-{\mathrm{CA}}^1={\displaystyle \sum }_{i=1}^5\left({\mathrm{IS}}_i^1-{\mathrm{CA}}_i^1\right)\\ =\left(2+3+6+4+3\right)-\left(3+4+3+2+4\right)=2\end{array}$$

$$\begin{array}{ll}{y}^1& ={\mathrm{FS}}^1-{\mathrm{ES}}^1={\displaystyle \sum }_{i=1}^5\left({\mathrm{FS}}_i^1-{\mathrm{ES}}_i^1\right)\\ =\left(2+6+5+5+3\right)-\left(5+3+5+3+4\right)=1\text{.}\end{array}$$

The position of S₁ is (2,1), and in this way, other positions are calculated as follows:

$$S_2=\left(3,0\right),S_3=\left(4,-2\right),S_4=\left(-1,1\right)\mathrm{and}{S}_5=\left(6,-5\right)$$

Definition of risk levels

Different points on SPACE matrix show the success possibility of each segment that is considered as risk amount of segments. The most possibility occurs when financial strength and industry strength get the most score as positive factors, and environmental stability and competitive advantage get the lowest score as negative factors. So, the pair (6, 6) has the most success possibility with lowest risk amount in the SPACE matrix, and the pair (-6,-6) has the most risk amount. Risk of other points is defined based on their distance from (6, 6). The surface of the SPACE matrix is separated into five areas according to the distance from the best point. These areas are defined by radiuses which have been calculated based on fuzzy approach. It means that the Euclidean distance from the worst and the best points has been separated into five sections according to the linguistic values and the mean of fuzzy numbers (Table 3 and Figure 5). Thus, the Euclidean distance of each segment from the best point towards the worst point can show a level of risk.

Let (x^j, y^j) show the position of segment j. Let (X, Y) show the best position, and (X′, Y′) show the worst position in a SPACE graph. The risk amount of (x^j, y^j) is defined based on its Euclidean distance proportion that is showed as follows:

$$\mathrm{Risk}\left(x^j,y^j\right)~\frac{\sqrt{{\left(X-x^j\right)}^2+{\left(Y-y^j\right)}^2}}{\sqrt{{\left(X-X^{\text{'}}\right)}^2+{\left(Y-Y^{\text{'}}\right)}^2}}.$$

(10)

Euclidean distance proportions of all positions are calculated by (10). It helps assign linguistic variables to each position according to Table 7.

Table 7 Risk levels based on Euclidean distance proportion

Euclidean distances and proper risk of each segment was calculated as shown in Table 8 and Figure 6. ARL is defined to filter segments according to ability of risk acceptance of DMs. In this case, low risk level is considered as maximum ARL; it means that segments with risk level higher than low are rejected. Thus, S₁ and S₂ are selected to define proper strategies, and S₃, S₄, and S₅ are rejected because of their high risk levels.

Table 8 Proper risks for each segment with regard to Euclidean distance

Figure 6

Fuzzy risk definition model by SPACE graph. The success possibility shown by the spectrum (the best situation is shown as green, and the worst situation as red). VH, very high; H, high; M, medium; L, low; VL, very low.

Strategy definition

Strategy definition is done by SPACE matrix. Generic strategies of SPACE matrix are defensive, aggressive, conservative, and competitive which could be broken into the main strategies. In this case, aggressive and conservative strategies are suitable for S₂, and aggressive strategies for S₁. The two main strategies were defined for S₂ from two different views: the first one is ‘putting decaffeinated coffee in old basket’ as conservative strategy, and the second one is ‘A new basket of decaffeinated coffee products with decaffeinated coffee stores development’ as aggressive strategy. The aggressive strategy that was defined for S₁ is ‘A new basket of decaffeinated coffee and decaffeinated coffee stores development’.

Select the best segment-strategy

The five competitive forces model is a common tool used in analyzing and supporting the competitive strategic management in competitive markets. Porter (1980) developed these forces that model every single industry and market, and help DMs analyze industry competition for profitability and attractiveness. The five force factors and sub-factors in Porter's model, which are determined by the committee, are shown in Table 9.

Table 9 Factors and sub-factors of the five forces model

Factors and sub-factors of Porter's (1980) five forces model are applied as decision criteria to select the best segment-strategy. FDNP is implemented to rank the segment-strategies. This method can consider all inner dependency effects among factors and sub-factors over time. Using the factors and sub-factors, a decision tree is made to rank the segment-strategies (Figure 7). The decision tree includes four levels. The first level is the decision making (choosing the best segment-strategy). The second comprise the factors and sub-factors; the third level includes the problem criteria. The fourth level consists of the alternatives.

Figure 7

The proposed ANP model for measuring segment-strategy level.

The local weights of the factors are calculated by a useful method that Saaty and Takizawa (1986) and Saaty (1996) presented and developed in fuzzy prioritization approach. These are the fuzzy comparison values presented in Table 10.

Table 10 Pair-wise comparison matrix of factors with local weights

The non-linear programming presented as follows resulted from pairwise comparisons and was solved using the LINGO 11 (2008) software (Lindo Systems Inc., Chicago). The other weights were calculated using the same approach for each pairwise comparison matrix.

Maximize = λ

Subject to:

$$\begin{array}{l}1/6\times \lambda \times w_2-w_1+1/2\times w_2\le 0\hfill \\ 1/3\times \lambda \times w_2+w_1-w_2\le 0\hfill \\ 1/6\times \lambda \times w_3-w_1+1/2\times w_3\le 0\hfill \\ 1/3\times \lambda \times w_3+w_1-w_3\le 0\hfill \\ 1/10\times \lambda \times w_4-w_1+2/5\times w_4\le 0\hfill \\ 1/6\times \lambda \times w_4+w_1-2/3\times w_4\le 0\hfill \\ 1/2\times \lambda \times w_5-w_1+w_5\le 0\hfill \\ 1/2\times \lambda \times w_5+w_1-2\times w_5\le 0\hfill \\ 1/2\times \lambda \times w_3-w_2+1/2\times w_3\le 0\hfill \\ 1/2\times \lambda \times w_3+w_2-3/2\times w_3\le 0\hfill \\ 1/6\times \lambda \times w_4-w_2+1/2\times w_4\le 0\hfill \\ 1/3\times \lambda \times w_4+w_2-w_4\le 0\hfill \\ 1/2\times \lambda \times w_5-w_2+3/2\times w_5\le 0\hfill \\ 1/2\times \lambda \times w_5+w_2-5/2\times w_5\le 0\hfill \\ 1/6\times \lambda \times w_4-w_3+1/2\times w_4\le 0\hfill \\ 1/3\times \lambda \times w_4+w_3-w_4\le 0\hfill \\ 1/2\times \lambda \times w_5-w_3+3/2\times w_5\le 0\hfill \\ 1/2\times \lambda \times w_5+w_3-5/2\times w_5\le 0\hfill \\ 1/2\times \lambda \times w_5-w_4+2\times w_5\le 0\hfill \\ 1/2\times \lambda \times w_5+w_4-3\times w_5\le 0\hfill \\ w_1+w_2+w_3+w_4+w_5=1\hfill \\ w_i>0i=1,2,\dots ,5\hfill \end{array}.$$

The effects of the interdependency among the five force factors are shown in Figure 8. The inner dependency matrix is presented in Tables 11, 12, and 13, which was defined by the expert committee to obtain the local weights of the factors.

Figure 8

Network framework of the five forces.

Table 11 The inner dependence matrix of the factors with respect to ‘F ₄ ’

Table 12 The inner dependence matrix of the factors with respect to ‘F ₁ ’

Table 13 The inner dependence matrix of the factors with respect to ‘F ₂ ’

The vectors of the inner dependency weight of the factors (Tables 11, 12, and 13) are normalized to find the degree of relative impact matrix (Table 14). The final weights of the factors (w_Factors) are calculated by multiplying the normalized degree matrix (Table 14) with the local weight of the factors that had been calculated before in Table 10.

$$\begin{array}{ll}{W}_{\mathrm{Factrs}}& =\left[\begin{array}{c}{F}_1\\ F_2\\ \begin{array}{c}{F}_3\\ F_4\\ F_5\end{array}\end{array}\right]=\left[\begin{array}{ccc}0.50& 0.00& \begin{array}{ccc}0.00& 0.09& 0.00\end{array}\\ 0.00& 0.50& \begin{array}{ccc}0.00& 0.14& 0.00\end{array}\\ \begin{array}{c}0.17\\ 0.00\\ 0.33\end{array}& \begin{array}{c}0.33\\ 0.00\\ 0.17\end{array}& \begin{array}{ccc}\begin{array}{c}1.00\\ 0.00\\ 0.00\end{array}& \begin{array}{c}0.15\\ 0.50\\ 0.12\end{array}& \begin{array}{c}0.00\\ 0.00\\ 1.00\end{array}\end{array}\end{array}\right]\\ \times \left[\begin{array}{c}0.16\\ 0.22\\ \begin{array}{c}0.22\\ 0.29\\ 0.11\end{array}\end{array}\right]=\left[\begin{array}{c}0.106\\ 0.149\\ \begin{array}{c}0.362\\ 0.147\\ 0.236\end{array}\end{array}\right].\end{array}$$

Table 14 Degree of relative impact for the factors

In the next step, the pairwise comparisons of the sub-factors should be done with respect to each factor to calculate the local weights and global weights. Tables 15, 16, 17, 18, and 19 show the pairwise comparisons of the sub-factors and their calculated weight for each sub-factor. To calculate the global weights of each sub-factor, their calculated local weights should be multiplied with the weight of each factor directly (Table 20).

Table 15 Pair-wise comparison matrix of F ₁ sub-factors with local weight

Table 16 Pair-wise comparison matrix of F ₂ sub-factors with local weight

Table 17 Pair-wise comparison matrix of F ₃ sub-factors with local weight

Table 18 Pair-wise comparison matrix of F ₄ sub-factors with local weight

Table 19 Pair-wise comparison matrix of F ₅ sub-factors with local weight

Table 20 Global weights for sub-factors and computed total weight of each

To obtain the priority of the alternatives, the alternatives are compared with respect to each sub-factor. These comparisons should be done for each time period of the planning horizon. To make a better decision, considering the facts like ‘changing future conditions’ ‘more preferred business in each time period’ and ‘changing the priority of each factor or its sub-factors’ are very important. The certain planning horizon is dependent on the strategies that the company applied to launch a product in the market. It could be considered as the product life cycle that is planned for a certain time in a certain area. In this case, 5 years of planning horizon are considered to compare the alternatives considering the sub-factors and future changes of alternative priorities. Table 21 shows the final priorities of the alternatives regarding the importance of each strategy that is planned for each segment on the specific periods. As shown in Figure 9, it is clear that the priority of segment₁-startegy₁ is preferred over the others at first, although its priority is decreased during the planning horizon. In the end, segment₂-startegy₂ becomes more interesting than the others. On the other hand, results show that the priority of segment₂-startegy₂ is preferred almost after 1 year; thus, it could be selected for a long-term strategic planning.

Figure 9

The numerical estimate for weight of each segment-strategy. Broken line, dotted line, and the solid line denote the weights of ‘segment₂-strategy₂’, ‘segment₁-strategy₁’, and ‘segment₂-strategy₁’ over time, respectively.

Table 21 Global weights for each segment-strategy and computed total weight in each year

Conclusion

The purpose of the current study is to provide a modular decision support system to determine the best marketing strategy with an acceptable risk. This DSS helps companies to select appropriate segments to develop their business while they can care about their risk. Also, they can consider the effects of the strategies in their success based on priorities which may be changed over time. Two modules have been developed in this study: the first one used the SPACE matrix to allocate the risk to each segment, and the second one used FDNP method to monitor the segment-strategies over time and select the best one accordingly.

In the first module, segments have been evaluated based on the four main factors (and their sub-factors) of the SPACE matrix, and their risk have been calculated according to their success possibility. Then, the segments have been filtered with regard to their risk level which had been defined using the fuzzy approach. This method helps managers to take their acceptance risk level into consideration and leads DMs to select segments with their reasonable risk levels. Moreover, the SPACE matrix helps managers define proper strategies, too. Filtered segments help them have more suitable alternatives in the decision-making process.

In the second module, the five forces model of Porter (1980) has been developed in a decision-making process to select the best segment-strategy. Because of the changing conditions in the market and the decreasing or increasing attractiveness of the alternatives, the alternative priorities are changed over time, so the FDNP is developed to consider the variation of segment priorities. As it is clear in the numerical results, time variation could affect the DMs' decision. The priority of segment₁-startegy₁ is more preferred over the others at first, although its priority decreased during the planning horizon. In the end, segment₂-startegy₂ becomes more interesting than the others. On the other hand, results show that the priority of segment₂-startegy₂ is more preferred almost after 1 year; thus, it could be selected for a long-term strategic plan.

Market segmentation is one of the most important issues in marketing process of industries such as food, dairy, beverage, home care, etc. In this process, risk consideration is very essential because it may have big effects on the expected results. The proposed method in this paper could mitigate this risk by bringing the risk into calculation, and it could be applied to mitigate risk consequences. Using this method, DM could filter its alternative and will not count on segments which are in high risk space. As a result, DM will not select strategies based on high risk segments, and the company could lead its investment to the most secure space. As shown in the results, segment 5 (S₅) has the maximum risk of selection because in this segment, environment stability is weaker than the other potential segments. Hence, disregarding risk factors and selecting S₅ as a potential segment, the company will enter an unstable market. In this way, the other steps of strategy definition such as distribution channels, pricing, and long-term and short-term strategies will undergo selected market instability. So, disregarding the risk effects could lead a business to the spaces which can decrease the possibility of success.

On the other hand, for each segment, a special strategy could be developed while the importance of each segment-strategy has its special trend over time. Practically, when a company is going to invest on segment-strategy, it should have a serious attention on the long-term results of its decision. In this condition, having a good view on the trend of segment-strategy importance could help DMs make effective decisions over time. In considering this issue, the developed FDNP method of this paper could be applied. The application of this method in industries will be more significant when they have marketing strategies such as pricing, distribution channels, and promotion in their appropriate segment.

Considering the risk amount and competitive factors with their effects on each other will drive the company to be more successful. Analysis effects of these strategies to decrease risk amount could be helpful in making a better and more complete decision merits future research.

Authors’ information

AMN received his MSc from the Industrial Engineering Department of K. N. Toosi University of Technology of Iran. He has work experience in automotive and food production companies. Now, he is working in the PSIG Co. as Business Development Manager. His research interests are project portfolio selection, strategic management, market segmentation and multi-attribute decision making, supply chain management, and risk management. MHH received his MSc from the Industrial Engineering Department of Islamic Azad University of Qazvin. He has work experience in automotive, food and FMCG production companies. Now, he is working in Unilever Company as a demand planner. His research interests are project portfolio selection, strategic management, market segmentation, and multi-attribute decision making. SE is an assistant professor of operation research in the Islamic Azad University, Karaj Branch. He received his PhD in Operation Research and Operation Management from Science and Research Branch of the Islamic Azad University (SRBIAU), MSc from Amirkabir University of Technology (Tehran Polytechnic), and BS from Iran University of Science and Technology. His research interests include risk management, construction projects selection, fuzzy MADM, scheduling, mathematical programming, shortest path networks, and supply chain management.