Abstract
The production planning problem of flexible manufacturing system (FMS) concerns with decisions that have to be made before an FMS begins to produce parts according to a given production plan during an upcoming planning horizon. The main aspect of production planning deals with machine loading problem in which selection of a subset of jobs to be manufactured and assignment of their operations to the relevant machines are made. Such problems are not only combinatorial optimization problems, but also happen to be non-deterministic polynomial-time-hard, making it difficult to obtain satisfactory solutions using traditional optimization techniques. In this paper, an attempt has been made to address the machine loading problem with objectives of minimization of system unbalance and maximization of throughput simultaneously while satisfying the system constraints related to available machining time and tool slot designing and using a meta-hybrid heuristic technique based on genetic algorithm and particle swarm optimization. The results reported in this paper demonstrate the model efficiency and examine the performance of the system with respect to measures such as throughput and system utilization.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Background
In recent years, competitive market conditions coerce manufacturing firms to enhance response times and flexibility in all operations. Flexible manufacturing systems (FMSs) have been proved to respond this challenge positively because of their ability to produce a variety of parts using the same system in the shortest possible lead time. According to [Stecke (1983)], FMS is characterized as an integrated, computer-controlled, complex arrangement of automated material handling devices and computer numerically controlled (CNC) machine tools that can simultaneously process medium-sized volumes of a variety of part types. The highly integrated FMS offers the opportunity to combine the efficiency of transfer line and the flexibility of a job shop to best suit the batch production of mid-volume and mid-variety of products. However, flexibility has a cost, and the capital investment sustained by firms to acquire such systems is generally very high. Therefore, adequate planning of FMS during its development phase is pivotal so as to evaluate the performance of the system and justify the investment incurred. Prior to production, careful operational planning is essential to establish how well the system interacts with the operations over time. Hence, successful operation of FMS requires more intense planning as compared to any conventional production system. The decisions related to FMS operations can be broadly divided into pre-release and post-release decisions. Pre-release decisions include the FMS operational planning problem that deals with the pre-arrangement of jobs and tools before the processing begins, whereas post-release decisions deal with the scheduling problems. Pre-release decisions, viz machine grouping, part type selection, production ratio determination, resource allocation, and loading problems, must be solved while setting up an FMS. Amongst pre-release decisions, machine loading is considered as one of the most vital production planning problems since operational effectiveness of FMS largely depends on it. Loading problem, in particular, deals with allocation of jobs to various machines under technological constraints with the objective of meeting certain performance measures. Therefore, the problem is combinatorial in nature and happens to be non-deterministic polynomial-time (NP)-hard.
Researchers recognized early on that not all problems can be solved this quickly, and they had a hard time figuring out exactly which ones could and which ones could not. There are several so-called NP-hard problems, which cannot be solved in polynomial time, even though nobody can prove a super-polynomial lower bound.
A decision problem is a problem whose output is a single Boolean value: YES or NO. There are three classes of decision problems:
• P is the set of decision problems that can be solved in polynomial time. Intuitively, P is the set of problems that can be solved quickly.
• NP is the set of decision problems with the following property: If the answer is YES, then there is a proof of this fact that can be checked in polynomial time. Intuitively, NP is the set of decision problems where it can verify a YES answer quickly if we have the solution for it.
• Co-NP is the opposite of NP. If the answer to a problem in co-NP is NO, then there is a proof of this fact that can be checked in polynomial time.
The induction of the model is NP. There is a set of m input values that produces a TRUE output as a proof of this fact; the proof can be checked by evaluating the model in polynomial time.
Literature review
Formulations of loading problems in FMS and solution techniques have drawn the attention of researchers for quite some time. FMS planning problem was formulated as nonlinear 0–1 mixed integer programming by [Stecke (1983)], and subsequently, a branch-and-bound algorithm was developed by Berrada and [Stecke (1986)]. Although analytical and mathematical programming-based methods are robust in applications, yet they tend to become impractical when the problem size increases. This motivated the researchers to develop fast and effective heuristics for solving loading problems in large-sized FMSs. One of the important heuristics based on the concept of essentiality ratio for maximization of throughput and minimization of system unbalance simultaneously was proposed by [Mukhopadhyay et al. (1992)]. Later on, [Tiwari et al. (1997)] developed heuristics using fixed, predetermined job ordering rules as an input while solving loading problems. [Moreno and Ding (1993)] solved the loading problem using standard sequencing rules such as the shortest processing time (SPT), longest processing time (LPT), first in, first out (FIFO), and last in, first·out (LIFO) and established that the SPT rule works well in comparison to other rules. The major limitation of heuristics lies in the fact that their inability to estimate the results in a new or completely changed environment as they are generally rule-based and mostly rely on empirical data. Therefore, numerous researchers have used meta-heuristic approaches for solving the machine loading problem. Usually, FMS loading problem seeks a solution that optimizes multiple objectives simultaneously. In this regard, [Kumar and Shanker (2000), Tiwari and Vidyarthi (2000)], and [Swamkar and Tiwari (2004)] have addressed a machine loading problem having the bi-criterion objectives of minimizing system unbalance and maximizing the throughput using a hybrid algorithm based on Tabu search and simulated annealing (SA). Genetic algorithm (GA)-based approaches for loading problems is found to ensure an optimal solution with less computational effort ([Tiwari et al. 2007]).
Since the objective of this paper is to propose an efficient evolutionary search heuristic to solve problems pertaining to job selection and machine loading in random FMS to optimize the system imbalance and throughput simultaneously, only the relevant literature are reviewed in this section. [Tiwari and Vidyarthi (2000)] proposed a GA-based heuristic to solve the machine loading problem of a random-type FMS. The proposed GA-based heuristic determines the part-type sequence and the operation-machine allocation that guarantee the optimal solution to the problem, rather than using fixed, predetermined part sequencing rules. Swarnkar and Tiwari ([Swamkar and Tiwari 2004]) proposed a generic 0–1 integer programming formulation and a hybrid algorithm based on Tabu search, and SA is employed to solve the problem. Prakash et al. ([Prakash et al. 2008]) proposed a special immune algorithm (IA) named ‘modified immune algorithm.’ This method is capable of learning and memory acquisition, improves some issues inherent in existing IAs, and proposes a more effective IA with reduced memory requirements and reduced computational complexity. [Chan et al. (2005)] proposed a fuzzy goal programming approach to model the machine tool selection and operation allocation problem of FMSs. The model is optimized using an approach based on artificial immune systems, and the results of the computational experiments are reported. [Tripathi et al. (2005)] proposed a multi-agent-based approach for solving the part allocation problems in FMSs that can easily cope with the dynamic environment. [Kumar et al. (2006)] extended the simple GA and proposed a new methodology, a constraint-based GA to handle a complex variety of variables and constraints in a typical FMS loading problem. [Yogeswaran et al. (2008, in press)] proposed a hybrid algorithm using genetic algorithm and simulated annealing algorithm for their problem. They also proposed efficient machine loading heuristics. The machine loading problem of an FMS is well known for its complexity. This problem encompasses various types of flexibility aspects pertaining to part selection and operation assignments along with constraints ranging from simple algebraic to potentially very complex conditional constraints. In this paper, a hybrid optimization algorithm involving GA and particle swarm optimization (PSO) is proposed to solve this problem. The literature survey clearly supports the proposal of an efficient heuristic to this problem. Besides that, the justification to adopt PSO is mainly due to its performance in solving scheduling problems.
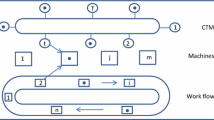
The FMS under consideration in this paper consists of a number of multifunctional CNC machines, tools with the potential to execute several operations. The jobs are available in batches and arrive in random sequences with different requirements for processing. The batch size, number of operations, processing time, and number of tool slots needed for each job are known initially. There are two types of operations accessible for a job, namely essential operation - the job can be performed only in a particular machine - and optional operation - the job can be performed in a number of machines available, which gives the flexibility in the routing of the jobs. The FMS considered has a maximum of six multifunctional machines with each having 960 min of available processing time (8 h = one shift) and six tool slots.
Numerous methods based on mathematics, heuristics, and meta-heuristics have been suggested by the researchers in the pursuit of obtaining quality solutions to loading problems and reducing computational burden. However, these approaches are hardly capable of producing optimal/near optimal solutions or require excessive computational efforts to arrive at quality solutions. In order to alleviate these difficulties, an attempt has been made in this paper to propose a multi-objective meta-heuristic technique based on a hybrid algorithm using genetic and particle swarm optimization (HAO) to solve the machine loading problem of a random FMS with the objective of minimization of system unbalance and maximization of throughput while satisfying the constraints related to available machining time and tool slots. However, GA has an inherent drawback of trapping at local optimum due to appreciable reduction in velocity values as iteration proceeds and hence reduces solution variety. This drawback has been addressed effectively by incorporating mutation, a commonly used operator in GA, to improve the solution quality.
The remainder of this paper is organized as follows: the ‘Problem description’ section formally defines the problem studied in this paper along with the objectives and assumptions made to solve the problem. In the ‘Results and discussion’ section, results of benchmark problems from the open literature are compared with those from the proposed method to illustrate its advantage over other methods. Conclusions drawn from this study are summarized and direction for future research is outlined in the ‘Conclusions’ section. Finally, the proposed hybrid algorithm based on genetic algorithm optimization (GAO) and PSO is presented in the ‘Methods’ section.
Problem description
The loading problem in manufacturing deals with selecting a subset of jobs from a set of all the jobs to be manufactured and assigning their operations to the relevant machines in a given planning horizon with the technological constraints in order to meet certain performance measures such as minimization of system unbalance and maximization of throughput. System unbalance can be defined as the sum of unutilized or over-utilized times on all the machines available in the system, whereas throughput refers to the summation of the batch size of the jobs that are to be produced during a planning horizon. Minimization of system unbalance is equivalent to maximization of machine utilization. The processing time and tool slots required for each operation of the job and its batch size are known beforehand. There are two types of operations associated with the part types: essential and optional. Essential operations can be carried out on a particular machine using a certain number of tool slots, while the optional operation can be performed on a number of machines with the same or different processing time and tool slots. The FMS under consideration derives its flexibility in the selection of a machine for optional operation of the job. Generally, the complexity of these problems depends on whether the FMS is of a dedicated type or a random type. A dedicated FMS is designed to produce a rather small family of similar parts with a known and limited variety of processing requirements, while in a random-type system, a large family of parts having a wide range of characteristics with random elements is produced and the product mix is not completely defined at the time of installing the system. This paper addresses the loading problem in a random FMS. The proposed approach has been tested on problems pertaining to three sizes of FMSs (the details are given in Table 1). The details of data related to problem l of FMS type l (jobs, batch size, unit processing time, machine options, number of tool slots, etc.) having four machines are given in Table 2.
In order to minimize the complexities in analyzing the problem for a practical FMS as depicted in Figure 1, the mathematical model is based on the following assumptions:
• Initially, all the jobs and machines are simultaneously available.
• Processing time required to complete an entire job order is known a priori.
• Job undertaken for processing is to be completed for all its operation before considering a new job. This is called non-splitting of the job.
• Operation of a job, once started on a machine, is continued until it is completed.
• Transportation time required to move a job between machines is negligible.
• Sharing and duplication of tool slots is not allowed.
Objectives
The overall objective function is represented as: Maximize
where F1 indicates minimization of system imbalance which is equivalent to maximizing the system utilization, and F2 indicates the maximization of throughput which is equivalent to maximizing the system efficiency.
Constraints
where ensures that overloading of machines is not permitted.
where and ensure that a particular operation of a job is done only on one machine, and ensures that the jobs will be loaded only when there is availability of tool slots on each machine.
where ensures that the job cannot be split.
Results and discussion
The proposed HAO algorithm for the FMS loading problem is coded in Visual C++ and implemented in a Pentium IV PC. The performance of the HAO algorithms is evaluated using ten benchmark problems available in the open literature representing three different FMS scenarios. In solving the problems, parameters are set as population size = 50, w = 0.85, α = 0.9, and c 1 = c 2 = 2 after a thorough examination of the results.
One of the drawbacks of HAO is its premature convergence. In order to alleviate such difficulties and improve solution quality, the mutation operator is adopted from the genetic algorithm. The results of the proposed HAO with mutation (HAOM) are compared with those of the standard HAO, and four standard sequencing rules such as LPT, SPT, FIFO, and LIFO are shown in Table 3. The results are also tabulated for exact solutions using LINDO software for the same data sets. The results indicate that HAOM improves the solution quality and outperforms other techniques in most of the instances. The combined objective of both HAO and HAOM is summarized in Table 4. The last column of Table 4 shows the percentage improvement of HAOM over HAO. The result indicates that the maximum improvement of 4.83 can be made using HAOM.
Figure 2 illustrates the convergence behavior of the HAOM. It can be observed from the figure that the algorithm can achieve the optimal solution after 33 iterations for problem number 7 because no further improvement is observed beyond 33 iterations.
Conclusions
This paper presents an efficient and reliable meta-heuristic-based approach to solve the FMS loading problem. The designed and proposed algorithm based on HAO defined the trade-off regions between the two objectives. Extensive computational experiments have been conducted on different benchmark problems to show the effectiveness of the proposed approach. A comparative study has been carried out for the same problem with similar objective functions and constraints, and the computational experience manifests that the proposed meta-heuristic approach based on HAO outperforms the existing methodologies as far as the solution quality is concerned with reasonable computational efforts. To avoid premature convergence, HAO algorithm is modified in this paper with the introduction of mutation operation. The performance of this algorithm is compared with that of the standard HAO, and the percentage improvement of up to 4.83 is possible using HAOM over HAO.
It is clear from this research that the machine loading problem can be solved using a hybrid algorithm-based heuristic that can tackle the problem in a synergistic way. By combining effective GAO and PSO, resource allocation can be done efficiently. This research had also highlighted the efficiency of the HAOM in the optimization process. The HAOM reduced the time to reach the best fitness value by a considerate amount in most cases. The results presented in Table 5 clearly show that the HAOM algorithm is comparable to the better performing algorithms reported in the literature and it obtains the best results obtained so far at a faster rate. The future work is to fine-tune the parameters of GAO and PSO. In the future, the study can be extended to solve the loading problem by considering more realistic variables and constraints such as availability of pallets, jigs, fixtures, AGVs, etc. in addition to tool slots and machining time.
Methods
Genetic algorithms
GAs are evolutionary programs and adaptive search and optimization algorithms based on the mechanics of natural selection and natural genetics. These are robust in complex search spaces and are versatile in their application. GA is a search and optimization technique operated on Darwin's principle of the ‘survival of the fittest,’ where weak individuals die before reproducing, while stronger ones survive, bear many offspring, and breed children, which often inherit qualities that are, in many cases, superior to their parents' qualities. GA evolves with a population of strings created randomly. Each string is evaluated in the population. There are three main GA operators: reproduction, crossover, and mutation. The reproduction is an operator in which the individual strings are copied according to their objective values which results in more highly fit individuals and less weak individuals in the intermediate mating pool. The reproduction operator is followed by the crossover operator which is done in two steps: First, the members of the mating pool are mated at random. Second, each pair of mating individuals undergoes crossover with respect to one or more crossing sites in which portions of the strings are interchanged between pairs. The mechanics of reproduction and crossover, though, seem to be simple; the combined action provides the GA with much of its searching power. Mutation plays a secondary role in the GA and tries to ensure potential solutions (individuals). The other operator's reproduction and crossover provide solution convergence, avoiding local optima. The resulting new population is then further evaluated and tested for termination. The termination criteria are designed based on the available response time within which the solution is to be obtained or based on an expected performance level. If the termination criteria are not met, the new population is again produced by the above three genetic operators and evaluated. This procedure is continued and repeated until the termination criteria are met.
Coding
If the binary coding system is considered for making up chromosomes directly, then the digit of the chromosome chain will reach n × m, and the genes will not be independent of each other. This coding system sets the line number of the element valued 1 in each row of matrix X as genes. A natural number is adopted to code the genes since they are independent with each other. The gene code , where k j Є [1;m], is a repeatable positive integer. The gene code is also the number of the machine on which every job is processed; hence, the method is named as genetic algorithm based on the machine code.
Select initial population
Firstly, generate N positive integer-coded n-digit chromosome chains randomly, and set them as the initial population.
Calculate x(i,j)
Reproduce
The fitness function is obtained by means of transforming the objective function, i.e.,
where α and β are positive real numbers, and the selection tactics is roulette wheel selection. Assume that P(i) is the selection probability of individual i, then
Let S(0)=0, then
Generate N random real numbers ζs which are uniformly distributed between 0 and 1, that is,
If , therefore, individual i is sent to the . The objective function is as follows:
Crossover
The crossover is carried with the combination of two genes in proper order. The coding method used in this paper makes the crossover completely independent of the genes between each other; if k j (1,m), the crossover method could adopt a common two-point crossover whose advantages include making message exchange between genes more abundant and obtaining the best solution quickly. Consider a crossover between individuals A and B, randomly select two positions from the chromosome chain, and exchange the chromosome between two positions, thereby generating two child chromosome chains.
The crossover is as follows:
where the symbol | represents the position of the crossover point selected randomly, and signal X represents the crossover operation.
Mutation
First, generate a one-digit positive integer, k j Є [1; m], randomly, then replace the old one when mutating. If k j is equal to the old one, then select a new positive integer again until they are different; the efficiency of the mutation could be greatly improved using the method. The optimization procedure is explained in Figure 3.
Particle swarm optimization
PSO is a population-based, bio-inspired optimization method. It was originally inspired in the way crowds of individuals move towards predefined objectives, but it is better viewed using a social metaphor. Individuals in the population try to move towards the fittest position known to them and to their informants, that is, the set of individuals of their social circle. The objective is to maximize a fitness function. The structure of the proposed PSO algorithm is as follows:
t → 0;
for (k = 1, N)
Generate Pkt ;
Evaluate Z Pkt;
e Pkt → Pkt
Gt → P having max {Z (e Pkt), k 1, N}
for (k = 1,N)
Initialize vkt
//iterative improvement process
do {
for (k = 1,N)
update Position Pkt+1
update velocity vkt+1
Apply local search on all particle positions;
Evaluate all particles;
update e Pkt and Gt+1 , (k = 1,N);
t → t +1 ;
}( ) while t < tmax
Output Gt
Solution representation
One of the most important issues when designing the HAO lies on its solution representation. In order to construct a direct relationship between the problem domain and the HAO chromosomes for the FMS loading problem, a number of dimensions for n number of jobs are considered. In other words, each dimension represents a typical job. In addition, the chromosome corresponds to the continuous position values for n number of jobs in the loading problem. The particle itself does not present a permutation. Instead, we use the smallest position value (SPV) rule to determine the sequence implied by the position values of particle .Table 6 illustrates the solution representation of particle for the FMS loading problem together with its corresponding velocity and sequence. According to the SPV rule, the SPV is , so the dimension is assigned to the first job in the sequence; the second SPV is , so the dimension is assigned to be the second job in the sequence; and so on. In other words, dimensions are sorted according to the SPV rule, i.e., according to the position values to construct the initial sequence.
Lack of diversity and mutation operator
HAO schemes described above typically converge relatively rapidly in the first part of the search and then slows down or stops. This behavior has been attributed to the loss of diversity in the population, and a number of researchers have suggested methods to overcome this drawback with varying degrees of success.
As mutation is capable of introducing diversity in the search procedure, two types of mutation have attracted the researchers - mutation of global best and mutation based on sharing information from neighbors. Because the global best individual attracts all members of the swarm, it is possible to lead the swarm away from a current location by mutating a single individual if the mutated individual becomes the new global best. This mechanism potentially provides a means of both escaping local optima and speeding up the search. Looking at the individual components of solution vectors corresponding to the global best function values revealed that it was often only a few components which had not converged to their global optimum values. This suggested the possibility of mutating a single component only of a solution vector. The latter approach introduces diversity by mutating few individuals in the swarm.
In this work, a mutation operator is introduced which mutates position vectors of few particles selected randomly. The mutation operation is not executed in every iteration. HAO algorithm with mutation operation is as follows:
// t: time // // P: populations // n A // DELTA: the elapsed time of no further progress //
// MAXT: maximum time of no further progress // "
t = 0
Initialize P (t)
Evaluate P (t)
While (not—termination—conditi0n) do
t = t + 1
Update swarm according to formulae (ll) and (l2)
If (DELTA > Randi (0, MAXT)
Do mutation
End if
Evaluate the swarm
End
Proposed algorithm
The following are the steps of the proposed algorithm:
Step 1. Input the total number of available machines, jobs, batch size, tool slots on each machine operation of all the jobs (both essential and optional), and processing time of every operation of each job.
Step 2. Initialize the parameters. Generate initial population randomly. Construct the initial position values of the particle uniformly: , where , , and U(0, 1) is a uniform random number between 0 and l. Generate initial velocities of the particle , where , , and U(0, l) is a uniform random number between 0 and l.
Step 3. Get the initial sequence by using the SPV rule. Then, select the first job from that sequence, and do the following:
-
a.
First, load the essential operation on the machine if and only if the available machining time is greater than the time required by the essential operation; otherwise, reject the job.
-
b.
Similarly load the optional operation if and only if the available machining time and tool slot is greater than the time and tool slot required by the optional operation on the basis of the machine having the maximum available time; otherwise, reject the job.
Step 4. Evaluate each particle fitness value, i.e., the objective function.
Step 5. Find out the personal best (pbest) and global best (gbest).
Step 6. If no progress in the pbest value is observed for an elapsed period of DELTA, carry out the mutation of a particle using the mutation strategy as outlined in the ‘Particle swarm optimization’ section provided that DELTA is greater at random number between zero and maximum time of no progress (MAXT).
Step 7. Update velocity, position, and inertia weight.
Step 8. Compute particle fitness similar to step 3, and find a new pbest and gbest.
Step 9. Terminate if the maximum number of iterations is reached, and store the gbest value; otherwise, go to step 2.
Abbreviations
Notations used for defining the objective function
J, job index, j = l, 2,…,J; M, machine index, m = 1, 2,…,M; Sm, tool slot capacity of machine m; O, number of operations for job j, o = l, 2,…,O j; Bj, batch size of job j; Tm, length of scheduling period for the m th machine; Pjom, processing time of operation o of job j on machine m; Sjom, number of tool slots required for processing operation 0 of job i on machine m; B(j,o), set of machines on which operation o of job j can be performed.
Variables used for defining the objective function
SU, system unbalance V; TH, throughput ({l, if operation 0 of job j is assigned on machine m).
Parameters used for defining the objective function
Xjom = {0, otherwise; Xj = {1, if job is selected; {0, otherwise.
References
Berrada M, Stecke KE: A branch and bound approach for machine load balancing in flexible manufacturing systems. Management Science 1986,32(10):1316–1335.
Chan FTS, Swamkar R, Tiwari MK: Fuzzy goal programming model with an artificial immune system (AIS) approach for a machine tool selection and operation allocation problem in a flexible manufacturing system. International Journal of Production Research 2005,43(19):4147–4163.
Chandrasekaran S, Ponnambalam SG, Suresh RK: (2007) Multi-objective particle swarm optimization algorithm for scheduling in flow shops to minimize make span, total flow time and completion time variance. In: Proceedings of the IEEE international congress on evolutionary computation 2007, 2007: 25–28.
Kennedy J, Eberhart R, Shi Y: Swarm intelligence. Morgan Kaufmann, San Mateo; 2001.
Kumar N, Shanker K: A genetic algorithm for FMS part type selection and machine loading. International Journal of Production Research 2000, 38: 3861–3887.
Kumar RR, Singh AK, Tiwari MK: A fuzzy based algorithm to solve the machine-loading problems of a FMS and its neuro fuzzy Petri net model. International Journal of Advanced Manufacturing Technology 2004,23(5–6):318–341.
Kumar A, Prakash TMK, Shankar R, Baveja A: Solving machine-loading problem of a flexible manufacturing system with constrained-based genetic algorithm. European Journal of Operational Research 2006,175(2):1043–1069.
Moreno AA, Ding FY: Heuristics for the FMS loading and part type selection problems. International Journal of Flexible Manufacturing System 1993,5(4):287–300.
Mukhopadhyay SK, Midha S, Muralikrishna V: A heuristic procedure for loading problems in flexible manufacturing systems. International Journal of Production Research 1992,30(9):2213–2228.
Nagarjuna N, Mahesh RK: A heuristic based on multistage programming approach for machine loading problem in a flexible manufacturing system. Robotics and Computer Integrated Manufacturing 2006,22(4):342–352.
Prakash A, Khilwani N, Tiwari MK, Cohen Y: Modified immune algorithm for job selection and operation allocation problem in flexible manufacturing systems. Advances in Engineering Software 2008,39(3):219–232.
Shankar K, Srinivasulu A: Some solution methodologies for loading problems in flexible manufacturing system. International Journal of Production Research 1989,27(6):1019–1034.
Srinivas TMK, Allada V: Solving the machine loading problem in a flexible manufacturing system using a combinatorial auction-based approach. International Journal of Production Research 2004,42(9):1879–1893.
Stecke KE: Formulation and solution of non-linear integer production planning problem for flexible manufacturing system. International Journal of Management Science 1983,29(3):273–288.
Swamkar R, Tiwari MK: Modeling machine loading problem of FMSs and its solution methodology is using a hybrid tabu search and simulated annealing-based heuristic approach. Robotics and Computer Integrated Manufacturing 2004, 20: 199–209.
Tiwari MK, Vidyarthi NK: Solving machine loading problems in a flexible manufacturing system using a genetic algorithm based heuristic approach. International Journal of Production Research 2000, 38: 3357–3384.
Tiwari MK, Hazarika B, Vidyarthi NK, Jaggi P, Mukhopadhyay SK: A heuristic solution approach to the machine loading problem of an FMS and its Petri net model. International Journal of Production Research 1997,35(8):2269–2284.
Tiwari MK, Saha J, Mukhopadhyay SK: Heuristic solution approaches for combined job sequencing and machine loading problem in flexible manufacturing systems. International Journal of Advanced Manufacturing Technology 2007,31(7–8):716–730.
Tripathi AK, Tiwari MK, Chan FTS: Multi-agent-based approach to solve part section and task allocation problem in flexible manufacturing systems. International Journal of Production Research 2005,43(7):1313–1335.
Varadharajan TK, Rajendran C: A multi-objective simulated annealing algorithm for scheduling in flowshops to minimize the makespan and total flowtime of jobs. European Journal of Operational Research 2005,167(3):772–795.
Vidyarthi NK, Tiwari MK: Machine loading problem of FMS: a fuzzy-based heuristic approach. International Journal of Production Research 2001,39(5):953–979.
Yogeswaran M, Ponnambalam SG, Tiwari MK: An hybrid evolutionary heuristic using genetic algorithm and simulated annealing algorithm to solve machine loading problem in FMS. Taylor & Francis, Oxford; 2008. (in press)
Author information
Authors and Affiliations
Corresponding author
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kumar, V.M., Murthy, A. & Chandrashekara, K. A hybrid algorithm optimization approach for machine loading problem in flexible manufacturing system. J Ind Eng Int 8, 3 (2012). https://doi.org/10.1186/2251-712X-8-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2251-712X-8-3