Abstract
We consider an open shop scheduling problem with setup and processing times separately such that not only the setup times are dependent on the machines, but also they are dependent on the sequence of jobs that should be processed on a machine. A novel bi-objective mathematical programming is designed in order to minimize the total tardiness and the makespan. Among several multi-objective decision making (MODM) methods, an interactive one, called the TH method is applied for solving small-sized instances optimally and obtaining Pareto-optimal solutions by the Lingo software. To achieve Pareto-optimal sets for medium to large-sized problems, an improved non-dominated sorting genetic algorithm II (NSGA-II) is presented that consists of a heuristic method for obtaining a good initial population. In addition, by using the design of experiments (DOE), the efficiency of the proposed improved NSGA-II is compared with the efficiency of a well-known multi-objective genetic algorithm, namely SPEA-II. Finally, the performance of the improved NSGA-II is examined in a comparison with the performance of the traditional NSGA-II.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Background
An open shop scheduling problem (OSSP) is a kind of shop scheduling such that the operations can be executed in any order. The open shop allows much flexibility in scheduling, but it is difficult to develop rules that give an optimum sequence for every problem (Sule1997). This problem is a class of NP-hard ones (Gonzalez and Sahni1976). In this paper, we consider a special feature in OSSPs, called sequence-dependent setup time. The process of preparing machines between jobs is considered as a setup. In fact, setup times affect on the completion time of each job. As a result, they also affect on tardiness, earliness and other important criteria. Allahverdi et al. (2008) surveyed the literature of setup times or costs in scheduling problems. They classified scheduling problems into those with batching and non-batching considerations as well as sequence-independent and sequence-dependent setup times. According to the technology and the kind of machines used in a work environment and variety of products, setup times can be dependent on both machines and the sequence of jobs that should be processed on a machine.
In many practical production systems (e.g., chemical, printing, pharmaceutical and automobile manufacturing), the setup tasks (i.e., cleaning up and changing tools) are sequence-dependent (Zandieh et al.,2006 and Roshanaei et al.,2009). Low and Yeh (2008) addressed an open shop scheduling problem as a 0–1 integer programming model with the objective of minimizing the total job tardiness along with some assumptions, such as sequence-independent setup and sequence-dependent removal times. They proposed some hybrid genetic-based heuristics to solve the problem in an acceptable computing time. Mosheiov and Oron (2008) addressed batch scheduling problems on an open-shop with m machines and n jobs. Identical processing time jobs, machine-independent and sequence-independent setup times are the main assumptions of their problems. The objectives are to minimize the makespan and minimize flow time. They proposed an O(n) time algorithm for the flow time minimization problem.
To achieve Pareto-optimal sets for medium to large-sized open shop problems using efficient meta-heuristic methods can be necessary and helpful. Naderi et al. (2011) considered an open shop with a set of parallel machines at each stage to minimize the total completion times. They proposed a mixed-integer linear programming (MILP) model for this problem. Moreover, they applied a memetic algorithm to solve the problem. Ahmadizar et al. (2010) addressed a stochastic group shop scheduling problem with known distributions for random release dates and random processing times. They formulated a stochastic programming problem and solved it by the use of an approach being a hybrid of an ant colony optimization (ACO) algorithm and a heuristic algorithm to minimize the expected makespan. Zhang and van de Velde (2010) considered an on-line two-machine open shop scheduling problem with time lags between the completion time and the start time of two consecutive operations of any job. They developed and analyzed the performance of a greedy algorithm to minimize the makespan. Mastrolilli et al. (2010) dealt with a concurrent open shop and proposed a primal–dual 2-approximation algorithm to minimize the total weighted completion times. They also considered several natural linear programming relaxations for the problem.
Fei et al. (2010) considered a weekly surgery schedule in an operating theatre. The objectives are to maximize the utilization of the operating rooms, minimize the overtime cost in the operating theatre, and minimize the unexpected idle time between surgical cases. They proposed a column-generation-based heuristic (CGBH) procedure and a hybrid genetic algorithm (HGA) for solving the planning problem as a set-partitioning integer-programming model and the daily scheduling problem as a 2-stage hybrid flow-shop problem, respectively. Matta (2009) developed two original mixed-integer programming (MIP) models (i.e., time-based model and sequence-based model) for the proportionate multiprocessor open shop scheduling problem and proposed a genetic algorithm (GA) to schedule the shop with the objective of the makespan minimization. Seraj and Tavakkoli-Moghaddam (2009) proposed a TS method to solve a new bi-objective mixed-integer mathematical programming model for an OSSP. This model seeks to minimize the mean tardiness and the mean completion time. Panahi and Tavakkoli-Moghaddam (2011) proposed a hybrid method based on multi-objective simulated annealing (SA) and ant colony optimization (ACO) to solve an open shop scheduling problem that minimizes bi-objectives, namely makespan and total tardiness. They compared their computational results with a well-known multi-objective genetic algorithm, namely NSGA II.
By considering the previous studies, we can conclude that there is only one paper considered the sequence-dependent setup time as an assumption for a single-objective OSSP without any mathematical model and written by Roshanaei et al. (2009). Therefore, in this paper, a bi-objective mixed-integer linear programming (MILP) model is designed with the sequence-dependent setup time as a constraint for the OSSP. To solve medium to large-sized problems, the well-known NSGA-II proposed by Deb et al. (2002) is improved by using a heuristic method in order to achieve good approximate Pareto-optimal frontiers.
The rest of this paper is organized as follows. The mathematical programming is presented in Section 2. The interactive multi-objective decision making approach is presented in Section 3. Section 4 elaborates the proposed improved NSGA-II. The numerical examples, computational results and performance analysis are given in Section 5. Finally, Section 6 includes the conclusion remark.
Mathematical Programming
The OSSP considered in this study includes n jobs to be processed on at most m machines. We extend the mathematical model proposed by Low and Yeh (2008) by changing it to a bi-objective model with sequence-dependent setup times.
Problem assumptions
The main assumptions of the presented model are as follows.
-
Each job is to be processed on at most m machines.
-
The processing sequence of each job is immaterial.
-
A job is not processed by more than one machine simultaneously.
-
Each machine processes at most one operation at a time.
-
All jobs are available at time 0.
-
No preemption is allowed.
-
Machine-dependent and sequence-dependent setup times are considered for each operation.
Notations
The indices, parameters and decision variables used to formulate the mathematical model are introduced below.
Indices
N Set of jobs to be processed, N=
L Set of machines,.
i,k,g Job indices, (i,k,g= 0,1,…,n),where job 0 is a dummy job.
j,h Machine indices, (j,h=1,2,…,m).
Parameters
M A large positive number.
O ij Operation of job i on machine j ;.
S kij Setup time of job i on machine j immediately after job k.
p ij Processing time of job i on machine j.
d i Due date of job i.
H j Dependent set up time matrix of machine j.
Decision variables
Starting time of a setup task for operation O ij .
T i Tardiness of job i.
C max Makespan.
Mathematical model
As mentioned at the beginning of Section 2, the model designed in this paper is developed by extending and modifying the mathematical model proposed by Low and Yeh (2008). In this new model, the sequence-dependent setup time is used instead of the sequence-independent setup time considered in the traditional model. The makespan is added to the model as another criterion along with the total tardiness for the minimization purpose. According to these changes and for the validity of the extended model, all of the existing constraints are changed and four new constraints are added to the model. Thus, the bi-objective MILP (BOMILP) model is formulated. It should be noted that S0ij is the setup time of job i on machine j when i is the first job on machine j. Moreover, if job i is the first job on machine j, then Z0ij = 1. The proposed model is as follows:
s.t.
Two objective functions (i.e., total tardiness and makespan) are shown by Eqs. (1) and (2).Constraint (3) describes the makespan. Constraints (4) and (5) express the relationship between two operations of job i that do not require being consecutive. The starting time for setup task of operation O ih is greater than or equal to the completion time of operation O ij . Constraints (6) and (7) state the operational sequence of the operations which are processed on the same machine and do not require to be consecutive. The setup task of operation O gj cannot be started until machine j has finished the processing task of operation O ij . Constraint (8) describes the tardiness for job i. Constraint (9) expresses the order of any two operations of a job; if Y ijh = 1 then Y ihj = 0; otherwise, Y ijh = 0 and Y ihj = 1. Constraint (10)expresses the order of any operation pairs (O ij ,O gj ) on the same machine j; if X igj = 1 then X gij = 0, otherwise, X igj = 0 and X gij = 1. Constraints (11) and (12) describe the relationship between X kij and Z kij ; if X kij = 1, then Z kij = 1 or 0; otherwise, X kij = 0 and Z kij = 0, by considering the dummy job 0. If X kij = 1 then Z ikj = 0; otherwise, X kij = 0 and Z ikj = 1 or 0; in this case, the dummy job 0 is not considered. Because the dummy job cannot be located after any job, it is only used for characterizing the first job on each machine to apply the corresponding relative setup time. Constraint (13) indicates that there is at most one job which can be processed immediately after job k on machine j. if job k is the last job on machine j, then Z kij = 0. Constraint (14) indicates that there is only one job that can be processed immediately before job i on machine j by considering the dummy job 0. Constraint (15) expresses that all jobs should be available for scheduling at time 0.Constraints (16) to (18) define the continuous and binary decision variables, respectively.
Interactive MODM Approach
To solve the original bi-objective decision making (BODM) problem, an interactive fuzzy programming solution method, called the TH method proposed by Torabi and Hassini (2008), is used. This method is applied to achieve the Pareto-optimal solutions of the presented bi-objective crisp model. Torabi and Hassini (2008) proved that the TH method obtains efficient solutions for the original multi-objective model. According to the characteristics of the given problems, the steps of the TH method are as follows.
Algorithm1: TH method
Step 1
Calculate the positive ideal solution (PIS) and the negative ideal solution (NIS) for each objective function by solving the corresponding MILP model given below.
where X is a feasible solution vector consists of all of the continuous and binary variables in the original model and F(x)denotes the feasible area consists of Constraints (3) to (18).
Obtainment of the above ideal solutions requires solving four mixed-integer linear programs. In order to reduce the computational time and complexity, we can calculate the PIS for each objective function by solving the corresponding MILP models given in Eqs. (19) and (21). Then, the negative ideal solutions can be determined by the use of the following heuristic rule:
It is noted that anddenote the decision vector associated with the PIS of the h- th objective function and the corresponding value of the h- th objective function, respectively (Torabi and Hassini,2008). The related results are shown in Table1.
Step 2
For each objective function, determine a linear membership function by:
Figure1 illustrates the graph of these membership functions.
Step 3
Transform the BOMILP model into an equivalent single-objective MILP using the following auxiliary formulation.
s.t.
According to the two objective functions considered in the problem, Constraint (27) can be written by:
whereis the satisfaction degree of the h- th objective function andis the minimum satisfaction degree of objectives. Also, θ h denotes the importance level of the h- th objective function such that. The θ h parameters are determined linguistically by the decision maker based on her preference. Moreover, γ is the coefficient of compensation. By changing the values of this parameter in the interval [0,1], the TH method can obtain both unbalanced and balanced compromised solutions. It means that for higher values of γ, the solution method results bigger lower bound for the satisfaction degrees of objectives (λ0) for a given sample example. These solutions are balanced compromised solutions. These kinds of solution can be more appropriate when the importance levels of all objective functions are equal. On the other hand, for lower values of γ, the solution method resulting solutions with bigger satisfaction degrees for some objectives with higher importance levels than others. These solutions are unbalanced compromised solutions. These kinds of solutions can be more appropriate when the importance levels of the objective functions are different.
Step 4: Solve equivalent single-objective MILP model using the given coefficients (θ h ,γ). If the decision maker is satisfied with obtained efficient compromised solution, then stop; otherwise, change the value of some controllable parameters and then go to Step 2.
A set of non-dominated solutions as the Pareto-optimal solutions can be obtained for the BOMILP model by changing the values of controllable parameters of the MILP model given in Eqs. (26) to (31). As mentioned at the beginning of Section 3, it is proved that the TH method achieves efficient solutions for multi-objective optimization problems. It means that each optimal solution of the single-objective model given in Eqs. (26) to (31) is a Pareto-optimal solution of the original BOMILP model.
Proposed Method
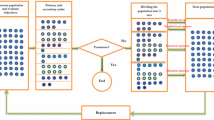
The OSSP studied in this paper is the NP-hard problem. Thus, to solve medium to large-sized problems considered in this paper, an improved non-dominated sorting genetic algorithm II (NSGA-II) is proposed. Noori-Darvish and Tavakkoli-Moghaddam (2011) used the original NSGA-II for an OSSP. NSGA-II belongs to a class of multi-objective evolutionary algorithms (MOEAs). In most problems, it is able to find much better spread of solutions and better convergence near the true Pareto-optimal front compared to two other elitist MOEAs, namely Pareto-archived evolution strategy (PAES) and strength-Pareto evolutionary algorithm (SPEA), which pay special attention to creating a diverse Pareto-optimal front (Deb et al.,2002).
Solution Representation
In our proposed method, a chromosome is an operation-based array or permutation list that has been a typical solution representation studied in OSSPs. As illustrated in Figure2, the permutation list is a single-row array consisting of n×m operations. By using this encoding scheme, the basic assumptions of OSSPs are satisfied, in which the processing sequence of each job is immaterial and a job is not processed more than once by one machine. In this representation, operations are listed in the relative order by which they are scheduled. p denotes the position of an operation in the list.
To decode the list presented in Figure2 and obtain its equivalent solution in the solution space, we start from the beginning of the list and schedule the first operation. Then, according to the corresponding order of operations in the list, we schedule other operations one by one. It means, job 5 is first scheduled on machine 3. Then, job 2 is scheduled on machine 4 and so on. According to the rule that each operation is scheduled at the earliest time, there are two variables, namely 1) Max {C ij } for all i as the maximum completion time of jobs on machine j and 2) Max {C ij } for all j as the maximum completion time of job i. The starting time and completion time of each operation are computed by:
Initialization
A good initial population can help an evolutionary algorithm to start multi-objective optimization from good solutions in the solution space and have a better performance that will be discussed in the next section. In our algorithm, a heuristic method is applied to generate the initial set of solutions or population. It first constructs a set of random sequences of operations as chromosomes (as many as the population size). By using the swapping of two adjacent or non-adjacent operations (see Figures3 and4), it generates all the feasible sequences in the neighborhood of each permutation list. For each chromosome, the best feasible solution obtained by these neighborhood searches is a member of the initial population. According to the dominance concept, the best solution is an efficient solution of the Pareto-optimal frontier. The set of Pareto-optimal solutions dominate any other solutions in the feasible area and improve all the objective functions simultaneously. It should be noted that k,k' = 1,2,…, n×m, as shown in Figures3 and4.
Crossover
A procedure proposed by Low and Yeh (2008) is used for the crossover operator.
Algorithm 2: Crossover operator
Step 1 Select two cut points randomly along the positions of the strings for each pair of parent strings (A and B). So, each permutation list is divided into three sections, called substring 1, substring 2 and substring 3.
Step 2 Exchange substring 1 of parent string A and substring 3 of parent string B. Similarly, exchange substring 3 of parent string A and substring 1 of parent string B. Do not change the elements of substring 2 of each parent string. Therefore, two proto-children are generated which are named A0 and B0.
Step 3 Legalize two generated offsprings A0 and B0. In order to do this, remove the elements of substring 1 and substring 3 of offspring string A0, which are the same as substring 2, and then replace them with corresponding elements of substring 2 of offspring string B0. Also, do the same procedure for offspring string B0. Thus, two offspring strings (i.e., A0 and B0) are produced.
Mutation
As depicted in Figure5, the insertion operator is applied for the mutation operator. In the permutation shown in this figure, k,k’ = 1,2,….,n×m.
Elitism and selection operator
Deb et al. (2002) designed an elitist NSGA including “Fast non-dominated sorting approach” and “Diversity Preservation” for solving multi-objective problems. In order to rank solutions (individuals) and sort them into different non-dominated frontiers, an approach called “Fast non-dominated sorting” is applied. By the use of this approach, a domination count (n p ) is calculated for each solution to specify its non-dominated frontier. The domination count of all solutions in the first non-dominated frontier (irank=1) is equal to zero. At the end of the multi-objective optimization process, solutions with n p =0, dominate all other solutions in the solution space. It means they are the best global solutions. This approach results better convergence near the true Pareto-optimal frontier.
Along with the convergence to the Pareto-optimal set, it is also desired that an EA maintains a good spread of solutions in the obtained set of solutions (Deb et al.,2002). An operator called crowded-comparison operator is proposed for “Diversity Preservation”. By considering the value of crowding distance of each solution (idistance) in its frontier, this operator guides the selection process at the various stages of the algorithm toward a uniformly spread-out Pareto-optimal frontier. When the improved NSGA-II is iterated as many as the pre-specified iterations (i.e., maximum number of generations), the multi-objective optimization process is terminated (Noori-Darvish and Tavakkoli-Moghaddam,2011).
Results and discussion
Several numerical examples in small to large sizes are generated randomly by the use of a classic approach of the literature in order to examine and analyze the validity and efficiency of the mathematical model presented in Section 2, the TH method presented in Section 3, and the performance of the improved NSGA-II presented in Section 4. The small-sized problems are solved exactly by the use of the Lingo 9 software and the results of the TH method are analyzed. If the number of jobs and the number of machines are more than 4, the sizes of the problems are medium to large. In these conditions, even after several hours of running, Lingo cannot yield an optimal solution in a reasonable time. Thus, the improved NSGA-II is applied to solve these kinds of problems. Finally, the efficiency of this algorithm is first compared with the efficiency of a well-known multi-objective genetic algorithm, namely SPEA-II, by using the design of experiments (DOE). Then, the proposed algorithm is compared with the traditional NSGA-II. These algorithms are coded in Turbo C++4.5 on a PC (Main board P4, CPU E5200 2.5GHz, 6M Cache, RAM 2GB BUS 800).
SPEA-II
The strength Pareto evolutionary algorithm II (SPEA-II) proposed by Zitzler, et al. (2001) is specially designed for multi-objective optimization problems. This algorithm includes some special features (i.e., fitness assignment strategy) considering a number of solutions that dominate each individual and a number of solutions that each individual dominates the “nearest neighbor density estimation technique” that yields a density value for each solution, and the “archive truncation method” that preserves a specified number of solutions in the external non-dominated archive.
In our SPEAII, the solution representation is the permutation list and the initial population is generated randomly. Moreover, the binary tournament selection procedure is applied. When the SPEA-II is iterated as many as the pre-specified number of iterations (i.e., maximum number of generations), the multi-objective optimization process is terminated.
Generating numerical examples
In this section, we use a classical approach in the literature proposed by Loukil et al. (2005) to generate several numerical examples of small to large sizes randomly. The processing times and due dates are uniformly distributed in the intervals [0,100] and, respectively.
where and which is the mean values of the processing times. Parameters R and T take their values in the sets {0.2,0.6,1},{0.4,0.6,0.8},respectively. Also, the setup times are random variables between 10 and 50.
Parameter setting
Various sets of controllable parameters and different sizes of problems are considered. Then, many experiments are designed and run by using them. The effective values in terms of solution quality are determined. The parameter of the TH method are as follows. Parameter γ takes its values in the set {0,0.1,…,1}. Also, it is assumed that the preference information corresponding to the importance levels of the objective functions are specified linguistically by the decision maker as: θ1= θ2 and θ1> θ2. So, the values of these parameters in the first condition are θ1=θ2=0.5, and in the second condition are θ1=0.8 and θ2=0.2. It should be mentioned that the values of controllable parameters (i.e., R and T) of the generating instances approach are given in the following subsections. Tables2 and3 depict the values are set for the parameters of the NSGA-II and SPEA-II, respectively. Moreover, each example is solved 10 times independently.
Solving small-sized problems
Two kinds of sample examples in small sizes with 4 jobs and 3 machines (i.e., 4×3), and 4 jobs and 4 machines (i.e., 4×4) are considered. For each type of these examples, three numerical instances are generated randomly. Tables4 and5 represent the values of controllable parameters and the values of positive ideal solutions () and negative ideal solutions () for each numerical instances, respectively. Using the obtained values of the PIS and the NIS of each objective function, the final MILP model is exactly solved for each numerical instances by the Lingo 9 software. Table6 illustrates the results of example 4×4-b.
The obtained resuts are analyzed as follows.
In more cases with different importance levels of objective functions, the TH method performs correctly and efficiently. It means according to the importance levels , the solutions found by this method are unbalanced compromised solutions. However, in some cases, the TH method does not perform well and the satisfaction degree of the objective function with lower importance is more than that of the objective function with higher importance.
When the importance levels are equal, the satisfaction degrees of objective functions are very close to each other, in some cases. Thus, the method approximately finds balanced compromised solutions.
According to the discussion in Section 3, each optimal solution of the final MILP model is an efficient solution to the BOMILP model. Thus, in all cases, by changing the values of controllable parameters (i.e. γ and θ) two Pareto-optimal solutions are found by the TH method. Figure6 indicates the Pareto-optimal frontier of example 4×4-b.
Solving medium to large-sized problems
In this section, three types of sample examples in medium to large sizes with different combinations of jobs and machines are designed. For each kind of these examples, three numerical instances are generated randomly. The values of controllable parameters for each instance are considered as shown in Table4 and the characteristic of sample examples are presented in Table7. All of these instances are solved independently by the proposed improved NSGA-II with the features described in Section 4 and SPEA-II. The performance of the improved NSGA-II is compared with the performance of the SPEA-II by using the design of experiments (DOE) based on three comparison metrics. Meanwhile, the instance 20×9-c is solved by traditional NSGA-II in order to compare the efficiency of the improved NSGA-II with the efficiency of the traditional NSGA-II.
Performance evaluation metrics
There are various metrics in the literature for evaluating the performance of multi-objective metaheuristics. Here we use three common and valid metrics to evaluate the performance of the improved NSGA-II, traditional NSGA-II and SPEA-II. These comparison metrics are defined as follows:
Quality Metric (QM): This kind of the metric was applied by Schaffer (1985). According to this metric, each algorithm that finds more Pareto solutions is considered to have a higher quality. However, some Pareto solutions of an algorithm may dominate those of another algorithm. Thus, a number of the final non-dominated solutions found by each algorithm are counted.
Diversity Metric (DM): This metric was applied by Zitzler (1999). To calculate the spread of the solutions in the final Pareto frontier found by each algorithm, the diversity metric is used and computed by:
where, F is the set of obtained Pareto solutions, and are two solution vectors of Pareto frontier, and n denotes the dimension of the solution space that is equal to the number of objective functions. In this paper, n is equal to 2.
Spacing Metric (SM): This kind of the metric was applied by Srinivas and Deb (1994). This metric is used for estimating the uniformity of the spread of the points in the final Pareto solution frontier found by each algorithm and is calculated by:
where, d i represents the Euclidean distance between the consecutive solutions of the obtained Pareto solution set, is the mean value of all Euclidean distances, and N denotes the number of the final obtained Pareto solutions. For this metric, a higher quality value is a lower value and, of course, the best value is equal to 0.
Comparative results of the improved NSGAII and SPEAII by DOE
All of the medium to large-sized problems defined in Tables4 and7 are solved by the improved NSGA-II and the SPEA-II. In order to analyze the results, two-factor factorial experiments are designed to examine the effect of the two solution methods and nine test problems on each of three comparison metrics with 10 times executions of each algorithm for each test problem. This approach is similar to the approach given in, (Noori-Darvish et al.2011). The computational results of three comparison metrics, which are calculated for the sets of Pareto solutions obtained by the improved NSGA-II and the SPEA-II in each time of running, are illustrated in Tables8,9 to10. The following statistical linear model (Montgomery and Design and analysis of experiments,2001) can represent the results of these tables.
where μ is a common effect for the whole experiment, τ i is the effect of the i- th test problem, β j is the effect of the j- th solution method, (τβ) ij is the interaction effect of the i- th test problem and the j- th solution method, and ε ijk is the random error.
It should be noted that the adequacy of factorial designs is checked formerly. The hypothesis tests are considered as follows. The row treatment (i.e., test problems) effects are equal to 0. The column treatment (i.e., solution methods) effects are equal to 0. The interactions are equal to 0. In addition, the significance level (α) is set as 0.05.
Table11 depicts the ANOVA result for the QM. Considering the results, the p- value for the solution method and the test problem main effects are less than α=0.05. Thus, the effects of the solution method and the test problem are significant. It means that there is a significant difference between the mean values for the two solution methods and there is a significant difference between the mean values for the nine test problems. However, the interaction is not significant. Figure7 indicates that more Pareto solutions are found by the improved NSGA-II, and this method performs better than the SPEA-II.
Table12 shows the ANOVA result for the DM. Considering the results, the p- value for the main effects of the solution method and the test problem are less than α=0.05. Therefore, the method effects of the solution method and the test problem are significant. However, the interaction is not significant. The diversity of solutions found by the improved NSGA-II is more than the SPEAII. Thus, the improved NSGA-II method performs better than the SPEA-II, as shown in Figure8.
The ANOVA result for the SM, which are illustrated in Table13, shows that the p- value for the main effect of the solution method is less than α=0.05. Therefore, the effects of the solution method is significant. Moreover, the main effect of the test problem and the interaction are not significant. The spacing metric value for solutions found by the improved NSGA-II is less than the SPEA-II, as shown in Figure9. Thus, the performance of the improved NSGA-II is better than the SPEA-II.
Considering the above descriptions, all of the three hypothesis tests indicate the significant effect and better performance of the improved NSGA-II than the SPEA-II based on three performance metrics.
Comparative results of the improved and the traditional NSGAII
As discussed in Subsection 5.5, in order to examine if our improved NSGA-II performs better than the original NSGA-II, one of the large-sized instances (i.e., 20×9-c) is solved for 10 times independently by using the original NSGA-II. Then, three-mentioned comparison metrics (i.e., QM, DM and SM) are calculated based on the set of Pareto solutions achieved by this algorithm in each time of running. These results are compared with the results of solving the instance 20×9-c by the improved NSGA-II, as shown in Tables8 to10. The computational results and the mean values of these three performance metrics are illustrated in Tables14 and15.
According to the obtained results, the mean values of the quality and diversity metrics calculated for the sets of Pareto solutions, which are found by the improved NSGA-II, are more than those of the original NSGA-II. In addition, the mean value of the spacing metric calculated for the sets of Pareto solutions obtained by improved NSGA-II are less than those of the traditional NSGA-II. Therefore, considering the above descriptions, all results indicate the better performance of the improved NSGA-II than the traditional NSGAII based on three performance metrics.
Conclusion
In this paper, an open shop scheduling problem with sequence-dependent setup times was examined. A novel bi-objective mathematical programming was designed in order to minimize the total tardiness and the makespan. An interactive multi-objective decision making (MODM) approach proposed by Torabi and Hassini (2008) was applied for solving small-sized instances optimally and obtaining Pareto-optimal solutions. Considering the results in more cases, the TH method has performed well according to the importance levels of the objective functions, and two Pareto-optimal solutions have been found. In order to achieve Pareto-optimal sets for medium to large-sized problems, an improved non-dominated sorting genetic algorithm II (NSGA-II) was presented by embedding a heuristic method for obtaining the good initial population. Finally, by using the design of experiments (DOE), the efficiency of the proposed improved NSGA-II was compared with the efficiency of the SPEA-II. Moreover, the performance of the improved NSGA-II was compared with the performance of the traditional NSGA-II. The results have indicated the better performance of the improved NSGA-II based on three performance metrics.
References
Ahmadizar F, Ghazanfari M, Fatemi Ghomi SMT: Group shops scheduling with makespan criterion subject to random release dates and processing times. Comput Oper Res 2010, 37: 152–162. 10.1016/j.cor.2009.04.002
Allahverdi A, Ng CT, Cheng TCE, Kovalyov MY: A survey of scheduling problems with setup times or costs. European Journal Of Operational Research 2008, 187: 985–1032. 10.1016/j.ejor.2006.06.060
Deb K, Pratap A, Agarwal S, Meyarivan T: A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 2002, 6: 182–197. 10.1109/4235.996017
Fei H, Meskens N, Chu C: A planning and scheduling problem for an operating theatre using an open scheduling strategy. Comput Ind Eng 2010, 58: 221–230. 10.1016/j.cie.2009.02.012
Gonzalez T, Sahni S: Open shop scheduling to minimize finish time. J ACM 1976,23(4):665–679. 10.1145/321978.321985
Loukil T, Teghem J, Tuyttens D: Solving multi-objective production scheduling problems using metaheuristics. Eur J Oper Res 2005, 161: 42–61. 10.1016/j.ejor.2003.08.029
Low C, Yeh Y: Genetic algorithm-based heuristics for an open shop scheduling problem with setup, processing, and removal times separated. Robotics and Computer-Integrated Manufacturing 2008, 25: 314–322.
Mastrolilli M, Queyranne M, Schulz AS, Svensson O, Uhan NA: Minimizing the sum of weighted completion times in a concurrent open shop. Oper Res Lett 2010,38(5):390–395. 10.1016/j.orl.2010.04.011
Matta ME: A genetic algorithm for the proportionate multiprocessor open shop. Comput Oper Res 2009, 36: 2601–2618. 10.1016/j.cor.2008.11.009
Montgomery DC: Design and analysis of experiments. 5th edition. John Wiley & Sons, INC, New York; 2001.
Mosheiov G, Oron D: Open-shop batch scheduling with identical jobs. Eur J Oper Res 2008, 187: 1282–1292. 10.1016/j.ejor.2006.03.068
Naderi B, FatemiGhomi SMT, Aminnayeri M, Zandieh M: Scheduling open shops with parallel machines to minimize total completion time. J Comput Appl Math 2011, 235: 1275–1287. 10.1016/j.cam.2010.08.013
Noori-Darvish S, Tavakkoli-Moghaddam R: Solving a bi-objective open shop scheduling problem with fuzzy parameters. Journal of Applied Operational Research 2011,3(2):59–74.
Noori-Darvish S, Tavakkoli-Moghaddam R, Javadian N: A multi-objective particle swarm optimization algorithm for possibilistic open shop problems with weighted mean tardiness and weighted mean completion times criterions. Iranian Journal of Operations Research (IJOR) 2011. Accepted for publication Accepted for publication
Panahi H, Tavakkoli-Moghaddam R: Solving a multi objective open shop scheduling problem by a novel hybrid ant colony optimization. Expert Syst Appl 2011,38(3):2817–2822. 10.1016/j.eswa.2010.08.073
Roshanaei V, SeyyedEsfehani MM, Zandieh M: Integrating non-preemptive open shops scheduling with sequence-dependent setup times using advanced metaheuristic. Expert Syst Appl 2009, 37: 259–266.
Schaffer JD: Multiple objective optimizations with vector evaluated genetic algorithms. In Genetic algorithms and their applications: Proceedings of the first international conference on genetic algorithms. Edited by: Schaffer JD. Lawrence Erlbaum, Hillsdale, New Jersey; 1985:93–100.
Seraj O, Tavakkoli-Moghaddam R: A tabu search method for a new bi-objective open shop scheduling problem by a fuzzy multi-objective decision making approach. Int J of Engineering, Transaction B: Application 2009, 22: 269–282.
Srinivas N, Deb K: Multi-objective optimization using non-dominated sorting in genetic algorithms. Evol Comput 1994, 2: 221–248. 10.1162/evco.1994.2.3.221
Sule DR: Industrial scheduling. PWS Publishing Company, Boston, MA ; 1997.
Torabi SA, Hassini E: An interactive possibilistic programming approach for multiple objective supply chain master planning. Fuzzy Set Syst 2008, 159: 193–214. 10.1016/j.fss.2007.08.010
Zandieh M, Fatemi Ghomi SMT, Moattar Husseini SM: An immune algorithm approach to hybrid flowshops scheduling with sequence-dependent setup times. Appl Math Comput 2006, 180: 111–127. 10.1016/j.amc.2005.11.136
Zhang X, van de Velde S: On-line two machine open shop scheduling with time lags. European Journal Of Operational Research 2010, 204: 14–19. 10.1016/j.ejor.2009.09.023
Zitzler E: Evolutionary algorithm for multi-objective optimization: methods and applications. Ph.D. Dissertation, Swiss Federal Institute of Technology (ETH), Zurich, Switzerland; 1999.
Zitzler E, Laumanns M, Thiele L: Improving the Strength Pareto Evolutionary Algorithm. In EUROGEN 2001, Evolutionary Methods for Design, Optimization and Control with Applications to Industrial Problems. Edited by: Giannakoglou K, Tsahalis D, Periaux J, Papailou P, Fogarty T. Athens, Greece; 2001:95–100.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
SND studied the literature review and proposed the problem solving methods. She analyzed the computational results and drafted the manuscript. RTM presented the mathematical model and was responsible for revising the whole manuscript. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Noori-Darvish, S., Tavakkoli-Moghaddam, R. Minimizing the total tardiness and makespan in an open shop scheduling problem with sequence-dependent setup times. J Ind Eng Int 8, 25 (2012). https://doi.org/10.1186/2251-712X-8-25
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2251-712X-8-25