Constrained consumable resource allocation in alternative stochastic networks via multi-objective decision making

Abstract

Many real projects complete through the realization of one and only one path of various possible network paths. Here, these networks are called alternative stochastic networks (ASNs). It is supposed that the nodes of considered network are probabilistic with exclusive-or receiver and exclusive-or emitter. First, an analytical approach is proposed to simplify the structure of the network. This approach transforms the network into a simpler equivalent one. This paper discusses the constrained consumable resource allocation problem in an ASN. Many recent researchers apply heuristic and simulation methods to solve the constrained resource allocation in these problems. In this paper, we propose an analytical approach based on multi-objective modeling. The objective functions of this model are the cumulative distribution function of the completion time of ASN paths. These functions must be maximized within the desired network completion time. Lexicographic method is used to solve the proposed multi-objective model. The proposed method is illustrated by an example.

Introduction

In many real world projects, the occurrence of activities and their durations are stochastic. This is why these projects are formulated as a stochastic network ([Pritsker and Happ 1966]). On the other hand, the completion of projects on time has a significant effect on its cost, revenue, and usefulness. Therefore, the main objective of project managers is to avoid any delay. To achieve this goal, consuming extra resources can shorten the duration of each individual activity.

To the best of our knowledge, many recent researchers apply heuristic and simulation methods to solve the constrained resource allocation in ASNs. Constrained resource allocation in ASNs is dependent on the estimation of completion time of networks. Analytical methods for this subject have been introduced in ([Pritsker and Happ 1966]; [Pritsker and Whitehouse 1966, 1969]; []Pritsker 1966; [Whitehouse 1973]). Furthermore, simulation methods have also been introduced in [Whitehouse (1973)]. Efficient Monte Carlo simulation methods to estimate ASN characteristics such as project time, and project cost have been proposed in [Kurihara and Nishiuchi (2002]). An algorithm to fulfill the equivalent simplifying transformations of the structure of ASN has been described in ([Shibanov 2003]). A two-level decision-making model to control stochastic projects has been proposed in [Golenko-Ginzburg (1993]). [Golenko-Ginzburg et al. (1996]) have developed a hierarchical three-level decision-making model. These levels are upper level (company level), medium level (project level), and subnetwork level. The main goal has been to develop a unified three-level decision-making model and to indicate planning and control action and optimization problems for all levels. When the constrained resources are nonconsumable, [Golenko-Ginzburg and Gonik (1997]), using a zero–one integer programming, have maximized the total contribution of accepted activities to the expected project duration. The contribution of each activity is the product of the average duration of the activity and its probability of being on the critical path. A new heuristic control algorithm for stochastic network projects has been presented in [Golenko-Ginzburg and Gonik (1998a]). The developed control algorithm is essentially more efficient than the step-by-step control procedures. This algorithm has reduced computational time and has provided better solutions than the ones which would be attained using online sequential statistical analysis. [Golenko-Ginzburg and Gonik (1998b]) have developed a look over heuristic algorithm for allocation of resource-constrained in program evaluation and review technique type networks. Each activity is of random duration, depending on the resource amounts assigned to that activity. The aim has been to minimize the expected project duration. An optimization procedure to maximize the probability confidence for project due dates under budget constraints or to minimize the project budget under due dates chance constraints has been developed in [Golenko-Ginzburg et al. (2000]). The study of [Golenko-Ginzburg et al. (2003]) has presented a resource-constrained scheduling simulation model for alternative stochastic network projects when several renewable activity-related resources, such as machines and manpower, are imbedded in the model. Each type of resources is limited. The activity duration is a random variable with given density function. The aim of the problem is to minimize the expected project duration.

Up to now, because of the complexity of computations, only simulation and heuristic methods have been used to allocate the resources to ASN. Among our investigations, we have not found an analytical approach to the problem.

However, this paper proposes an analytical stochastic model based on multi-objective decision-making (MODM) model. This model has some advantages. First, this model, unlike previous researches, has no limitations related to the type of random variables of activity durations. Second, in the studied problem, the number of feasible allocations can be very great, especially in large scale networks. Evaluation of all allocations requires tedious computations. The proposed method prevents us from evaluating all of feasible solutions because of solving the problem in several stages (using MODM model). Furthermore, for solving the proposed model, simulation is combined with analytical method (conditional Monte Carlo simulation method). Also, one of the most accurate numerical methods (generalization of Gaussian quadrature formula) is applied for solving the model.

The paper has the following structure. The ‘Problem description’ section describes the problem. The ‘Analytical approach’ section introduces MODM model. Solving the MODM model is described in ‘Solving the MODM model’ section. ‘Example’ section gives a numerical example to demonstrate how the proposed method works. ‘Conclusion’ section is devoted to conclusions and recommendations for future studies.

The problem description

Suppose that a project is formulated as an ASN and has the following characteristics:

• 1. The network has a single source node and it can have one or more sink nodes.

• 2. The network contains only exclusive-or probabilistic nodes (nodes with exclusive-or receiver and exclusive-or emitter).

• 3. The network does not contain any loop.

• 4. Activity implementation requires only one kind of consumable (non-renewable) resource.

• 5. The amount of available resource is limited and deterministic.

• 6. The resource allocation for activities is performed discretely. In other words, the amount of resource allocated for each activity is limited to some specific levels.

• 7. The duration of network activities is arbitrary continuous random variable or they can have constant values.

• 8. Probability density function of activity durations is dependent on the amount of resource allocated to the activity and varies as this amount changes. By increasing the allocated resource to each activity, completion time will be shorter.

• 9. The due date of the project is constant and known value. We want the project completion time be smaller than or equal with the due date.

• 10. The objective is to allocate the total constrained resource among the activities such that the cumulative distribution function (CDF) of the project completion time is being maximized for the due date. Since by maximizing the CDF of the project completion time, we also maximize the probability of project completion on time.

Analytical approach

In this section we develop an analytical approach to allocate the resource among the activities of the projects. This analytical approach uses a multi-objective decision-making model. The following symbols introduce the necessary notations before MODM model is explained.

Notations

_N  : Number of activities (arcs)

_M  : Number of sink nodes

n_i : Number of paths which start from source node and terminate in i-th sink node

$F_{\mathit{ij}}\left(t\right)$ : CDF of j-th path which terminates in i-th sink node

P _ij  : Occurrence probability of j-th path which terminates in i-th sink node

$F_i\left(t\right)$ : CDF of occurrence time of i-th sink node, given that this node has occurred

p _i  : Occurrence probability of i-th sink node when $t\to +\infty$

${\overline{\mathit{P}}}_k$ : Accomplishment probability of k-th activity, given that start node of this activity has occurred

$P_i\left(t\right)$ : Occurrence probability of i-th sink node in t

S _ij  : Activity set of j-th path which terminates in i-th sink node

t _k  : Duration time random variable of k-th activity

$S_{\left[\gamma \right]}$ : The set of activities of a path with preference γ

$F_{\left[\gamma \right]}\left(t\right)$ : CDF of a path with preference γ

Z : Number of network paths

$s_{l_K}$ : The amount of resource allocated to k-th activity

T : Due date of project network

RS : The available amount of limited resource

v _k  : Number of discrete values which indicates the amount of resource allocated to k-th activity

$s_{l_K}^{\ast }$ : The optimal amount of resource allocated to k-th activity

$F_{{}_{\left[\gamma \right]}}^{\ast }\left(T\right)$ : The optimal value of CDF of a path with preference γ in T

Q : The set of activities which the optimal amount of resource allocated to them is determined

$f_{t_r}^{}\left(s_{l_r},t_r\right)$ : Probability density function of r-th activity completion time, when the allocated resource is $s_{l_r}$

$t_{K,S_{l_k}}$ : Duration time random variable of k-th activity when allocated resource is $s_{l_k}$

$F\left(t\right)$ : CDF of network completion time

$T_{\left[\gamma \right]}$: Completion time of a path with preference γ

$F_{t_r}^{}\left(s_{l_r},t_r\right)$ : CDF of r-th activity when allocated resource is $s_{l_r}$

$t_{{}_{K,S_{l_k}}}^{\left(q\right)}$ : Duration time of k-th activity in q-th simulation run when the allocated resource is $s_{l_k}$

$\overline{\mathit{Q}}$ : Number of simulation runs

A multi-objective decision-making model

Based on conditional probability, we can transform the above-mentioned ASN to the graphical evaluation and review technique networks with $\sum _{\mathit{i}=1}^{\mathit{M}}\sum _{j=1}^{{}_{\mathit{n}\mathit{i}}}1$ parallel paths. This transformation has been described in [Hashemin and Fatemi Ghomi (2005]). Based on the study, we can write:

$$F_i\left(t\right)=\frac{\sum _{j=1}^{n_i}{P}_{\mathit{ij}}{F}_{\mathit{ij}}\left(t\right)}{\sum _{j=1}^{n_i}{P}_{\mathit{ij}}}i=1,2,\dots ,M$$

(1)

Where $P_{\mathit{ij}}=\prod _{\mathit{k}\in {\mathit{S}}_{\mathit{ij}}}{\overline{\mathit{P}}}_k$

For shorter times (when t is remarkably smaller than $+\infty$), we have

$$P_i\left(t\right)=\sum _{j=1}^{n_i}{P}_{\mathit{ij}}{F}_{\mathit{ij}}\left(t\right)i=1,2,\dots ,M$$

(2)

and $\underset{t\to +\infty }{Lim}{P}_i\left(t\right)=P_i$ is evident.

After the above transformation, we order the paths and their CDF on the basis of priority. The most probable path is the path with the highest priority.

This ordering is performed by a simple algorithm described in Appendix B. Ordered CDF of ASN paths are shown by $F_{\left[1\right]}\left(t\right),\dots ,F_{\left[Z\right]}\left(T\right)\text{.}$

The proposed MODM model with Z objective function is as follows:

$$\begin{array}{c}\hfill \text{Max}\left\{F_{\left[1\right]}\left(T\right),F_{\left[2\right]}\left(T\right),\dots ,F_{\left[Z\right]}\left(T\right)\right\}\hfill \\ \hfill s.t.\sum _{K\in S_{\mathit{ij}}}{s}_{l_k}\le \mathit{R}\mathit{S}i=1,\dots ,M,j=1,\dots n_i\hfill \\ \hfill s_{l_K}=s_1,\dots ,s_{v_K}k=1,\dots ,N\hfill \end{array}$$

(3)

The decision variables of this model are$s_{l_K}\text{,}k=1,\dots ,N\text{.}$ One of the discrete values $s_1,\dots s_{v_K}$ can be the value of these variables. Each objective function is the sum of some continuous random variables. Hence, the proposed model is a stochastic multi-objective model with discrete decision variables. Lexicographic method ([Hwang and Masud 1979]) is used to solve the model because the CDF of completion time of the path with the highest occurrence probability has the highest effectiveness in network completion time CDF. Furthermore, execution of lexicographic method is simple in practice because as each activity is realized, it becomes evident that some paths are unlikely to occur. Then, some paths will be eliminated and the network can be smaller. Consequently, the remaining resources will be allocated to this reduced network. This trend continues until the problem is solved. This process is introduced in the succeeding section.

Solving the MODM model

Let’s suppose that, before project implementation, the allocated resource to each activity should be predetermined. To determine each one of the objective functions of the model, it is required to determine the CDF of the sum of some random variables. [Fatemi Ghomi and Hashemin (1999]) have generalized the numerical integration with Gaussian quadrature formula to determine the CDF of completion time of stochastic networks.

The conditional Monte Carlo simulation to determine CDF of completion time of stochastic networks is presented in [Burt and Garman (1971]). Here, these two methods are converted and introduced in such a way that they would be compatible with requisitions and aims of the paper (see Appendix A). To solve the MODM model using lexicographic method, the following algorithm is devised.

Algorithm 1

Step1. Obtain the optimal solution of the following problem for γ = 1.

$$\begin{array}{l}Max{F}_{\left[\gamma \right]}\left(T\right)\hfill \\ s.t.\hfill \\ \sum _{k\in S_{\left[\gamma \right]}}{s}_{l_K}\le RS\hfill \\ \sum _{k\in S_{\left[\gamma \right]}\cap S_{\left[W\right]}}{s}_{l_K}\le RS-\sum _{k\in S_{\left[w\right]}-S_{\left[\gamma \right]}}min{s}_{l_K}W=\gamma +1,\dots ,Z\hfill \\ \forall k\in S_{\left[\gamma \right]}{s}_{l_K}=s_1,\dots ,s_{v_K}\hfill \end{array}$$

(4)

Suppose the optimal values of $s_{l_K}$ for $k\in S_{\left[\gamma \right]}$ are denoted by $s_{l_K}^{\ast }$. These values are obtained with computing $F_{\left[\gamma \right]}\left(T\right)$ for all feasible values $s_{l_K}\text{,}k\in S_{\left[\gamma \right]}$ and determining optimal value of $F_{\left[\gamma \right]}\left(T\right)\text{,}$ namely, $F_{{}_{\left[\gamma \right]}}^{\ast }\left(T\right)\text{.}$ If for each k = 1, …, N, $s_{l_K}^{\ast }$ has been determined, stop. Otherwise, set $Q=S_{\left[\gamma \right]}$ and go to step 2.

Step 2. Set $\gamma \leftarrow \gamma +1$ and obtain the optimal solution of the following problem.

$$\begin{array}{l}Max{F}_{\left[\gamma \right]}\left(T\right)\hfill \\ s.t.s_{l_K}=s_{l_K}^{\ast }\forall k\in Q\hfill \\ \sum _{k\in S_{\left[\gamma \right]}-Q}{S}_{l_K}\le RS-\sum _{k\in S_{\left[\gamma \right]}\cap Q}{s}_{l_K}^{\ast }\hfill \\ \sum _{k\in S_{\left[\gamma \right]}\cap S_{\left[W\right]}-Q}{s}_{l_K}\le RS-\sum _{k\in S_{\left[W\right]}-S_{\left[\gamma \right]}-Q}min{s}_{l_K}-\sum _{k\in S_{\left[W\right]}\cap Q}{s}_{l_K}^{\ast }\hfill \\ W=\gamma +1,\dots ,Z\hfill \\ \forall k\in S_{\left[\gamma \right]}{s}_{l_K}=s_1,\dots ,s_{v_K}\hfill \end{array}$$

(5)

If for each $k=1,\dots ,N\text{,}{s}_{l_K}^{\ast }$, has been determined, stop. Otherwise, set $Q\leftarrow Q\cup S_{\left[\gamma \right]}$ and repeat step 2.

Note that in step 2, if the amount of resource allocated to one activity is unknown, then this amount would be the greatest feasible number that satisfies the inequality$\underset{k\in S_{\left[\gamma \right]}-Q}{s_{l_K}}\le RS-\sum _{k\in S_{\left[\gamma \right]}\cap Q}{s}_{l_K}^{\ast }\text{.}$ In other words, the optimal value can be found without the solution procedure being performed.

In all steps of the above algorithm, to find the optimal solution of problem, the objective function of problem is computed for all feasible values $s_{l_K}$ using one of the introduced methods in Appendix A. Feasible values of $s_{l_K}$ which maximize the objective function would be the optimal solution of the problem.

In some practical situations, it may not be necessary to determine the amount of resource allocated to each activity before the project is started. In other words, the constrained resource allocation and project implementation can be done simultaneously. In such situations, the gathered information resulting from the previous activities can be helpful in the resource allocation to the succeeding activities. The following algorithm is devised for such situations.

Algorithm 2

Step1.Since the network under study has a single source node and all network nodes are exclusive-or and probabilistic type, only one activity can be implemented in the beginning of project. Determine the amount of resource allocated to this activity using step 1 of algorithm described in ‘Analytical approach’ section. Start the implementation of this activity. When the end node of the activity occurs and if this node is one of the sink nodes of the network, stop. Otherwise, go to step 2.

Step 2.Set T ← T—implemented activity duration time and RS ← RS—the amount of consumed resource for implemented activity.

Among all activities emanating from the last realized node, determine the activity which must be realized and omit the other activities, and hence, the paths of network which have no possibility of occurrence. If T > 0, return to step 1. Otherwise, if (T ≤ 0), conclude that the project has not been completed in T.

Example

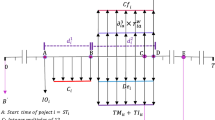
Consider the network in Figure 1. The amount of limited resource is 14 units (RS = 14) and the due date of project network is 9 units of time (T = 9).

Figure 1

Network of example.

First, we suppose that before project implementation, the allocated resource to each activity should be predetermined.

Results and discussion

The duration times of activities 4, 5, and 7 are not random variables. They are constant values but dependent on the amount of resource allocated to the corresponding activities.

The duration times of remaining activities are continuous random variables and their probability density functions are dependent on the amount of resource allocated to them. Table 1 contains the information of the activities duration times.

Table 1 Information of activity durations for the example

Paths and their occurrence probabilities are

$$\begin{array}{c}\hfill t_1+t_3+t_7+t_9\hfill \\ \hfill P_{21}={\overline{P}}_1{\overline{P}}_3{\overline{P}}_7{\overline{P}}_9=\left(1\right)\left(.75\right)\left(1\right)\left(.95\right)=.7125\hfill \\ \hfill t_1+t_2+t_4+t_5+t_7+t_9\hfill \\ \hfill P_{22}={\overline{P}}_1{\overline{P}}_2{\overline{P}}_4{\overline{P}}_5{\overline{P}}_7{\overline{P}}_9=\left(1\right)\left(.25\right)\left(1\right)\left(.7\right)\left(1\right)\left(.95\right)=.16625\hfill \\ \hfill t_1+t_2+t_4+t_6\hfill \\ \hfill P_{11}={\overline{P}}_1{\overline{P}}_2{\overline{P}}_4{\overline{P}}_6=\left(1\right)\left(.25\right)\left(1\right)\left(.3\right)=.075\hfill \\ \hfill t_1+t_3+t_7+t_8\hfill \\ \hfill P_{12}={\overline{P}}_1{\overline{P}}_3{\overline{P}}_7{\overline{P}}_8=\left(1\right)\left(.75\right)\left(1\right)\left(.05\right)=.0375\hfill \\ \hfill t_1+t_2+t_4+t_5+t_7+t_8\hfill \\ \hfill P_{13}={\overline{P}}_1{\overline{P}}_2{\overline{P}}_4{\overline{P}}_5{\overline{P}}_7{\overline{P}}_8=\left(1\right)\left(.25\right)\left(1\right)\left(.7\right)\left(1\right)\left(.05\right)=.00875\text{.}\hfill \end{array}$$

(6)

According to the preferences introduced in Appendix B, we have

$$\begin{array}{c}\hfill S_{\left[1\right]}=S_{21}=\left\{1,3,7,9\right\}\hfill \\ \hfill S_{\left[2\right]}=S_{22}=\left\{1,2,4,5,7,9\right\}\hfill \\ \hfill S_{\left[3\right]}=S_{11}=\left\{1,2,4,6\right\}\hfill \\ \hfill S_{\left[4\right]}=S_{12}=\left\{1,3,7,8\right\}\hfill \\ \hfill S_{\left[5\right]}=S_{13}=\left\{1,2,4,5,7,8\right\}\text{.}\hfill \end{array}$$

(7)

So, the transformed network can be illustrated as Figure 2.

Figure 2

Transformed network of example.

The MODM model of problem would be as follows:

$$\begin{array}{l}Max\left\{F_{\left[1\right]}\left(9\right),F_{\left[2\right]}\left(9\right),F_{\left[3\right]}\left(9\right),F_{\left[4\right]}\left(9\right),F_{\left[5\right]}\left(9\right)\right\}\hfill \\ \begin{array}{l}s.t.\sum _{k\in S_{\left[1\right]}}{s}_{l_K}\le 14s_{l_1}=4,5\\ s_{l_2}=1,2\\ \sum _{k\in S_{\left[2\right]}}{s}_{l_K}\le =14S_{l_3}=5,6\\ S_{l_4}=1,2\\ \sum _{k\in S_{\left[3\right]}}{S}_{l_K}\le =14\\ S_{l_5}=1,2\\ \sum _{k\in S_{\left[4\right]}}{S}_{l_K}\le 14\\ S_{l_6}=5,6\\ S_{l_7}=3,4\\ \sum _{k\in S_{\left[5\right]}}{S}_{l_K}\le 14S_{l_8}=1,2\\ S_{l_9}=1,2\end{array}\hfill \end{array}$$

(8)

In step 1, the problem should be solved in the following way:

$$\begin{array}{c}\hfill Max{F}_{\left[1\right]}\left(9\right)\hfill \\ \hfill s.t.s_{l_1}+s_{l_3}+s_{l_7}+s_{l_9}\le 14s_{l_1}=4,5\hfill \\ \hfill s_{l_1}+s_{l_7}+s_{l_9}\le 11s_{l_3}=5,6\hfill \\ \hfill s_{l_1}\le 7s_{l_7}=3,4\hfill \\ \hfill s_{l_1}+s_{l_3}+s_{l_7}\le 13s_{l_9}=1,2\hfill \\ \hfill s_{l_1}+s_{l_7}\le 10\hfill \end{array}$$

(9)

The optimal solution of problem, using the generalized Gaussian quadrature formula introduced in Appendix A, is found as below:

Table 2

In step 2, γ = 2 and $Q=S_{\left[1\right]}=\left\{1,3,7,9\right\}$, and the following problem should be solved.

$$\begin{array}{c}\hfill Max{F}_{\left[2\right]}\left(9\right)\hfill \\ \hfill s.t.s_{l_1}=4\text{,}{s}_{l_3}=6\text{,}{s}_{l_7}=3\text{,}{s}_{l_9}=1\hfill \\ \hfill s_{l_2}+s_{l_4}+s_{l_5}\le 6s_{l_2}=1,2\hfill \\ \hfill s_{l_2}+s_{l_4}\le 5s_{l_4}=1,2\hfill \\ \hfill s_{l_5}=1,2\hfill \end{array}$$

(10)

The optimal solution, using generalized Gaussian quadrature formula, is as follows:

Table 3

On path $S_{\left[3\right]}$, only the amount of allocable resource to activity 6 has not been determined. Its optimal value will be $s_{l_6}^{\ast }=6$ and $F_{\left[3\right]}^{\ast }\left(9\right)=.9823442$. On path $S_{\left[4\right]}$, only the amount of allocable resource to activity 8 has not been determined. Its optimal value will be $s_{l_8}^{\ast }=1$ and $F_{\left[4\right]}^{\ast }\left(9\right)=.9882507\text{.}$

Now, the amount of allocated resource to all activities $S_{\left[5\right]}$ has been determined and $F_{\left[5\right]}^{*}\left(9\right)=.7584068\text{.}$

Utilizing the formula 1 in the ‘A multi-objective decision-making model’ section, F₁(9) and F₂(9) would be:

$$\begin{array}{c}\hfill F_1\left(9\right)=.96801\hfill \\ \hfill F_2\left(9\right)=.76454\hfill \end{array}$$

(11)

Utilizing the formula 2 in ‘A multi-objective decisionmaking model’ section, P₁(9) and P₂(9) would be:

$$\begin{array}{c}\hfill P_1\left(9\right)=.11737\hfill \\ \hfill P_2\left(9\right)=.67184\hfill \end{array}$$

(12)

Finally, the network completion time distribution function for T = 9 can be computed as follows:

$$F\left(9\right)=P_1{F}_1\left(9\right)+P_2{F}_2\left(9\right)=P_1\left(9\right)+P_2\left(9\right)=.78921$$

(13)

Now, suppose that, it may not be necessary to determine the amount of resource allocated to each activity before the project is started.

The algorithm 2 is described in one of the cases, which can happen for the example in the ‘Example’ section. In step 1, the amount of resource allocated to activity 1, as explained before, is 4 units.

Assume that activity 1 is implemented using 4 units of limited resource ($s_{l_1}^{\ast }=4$) and this activity is completed in 0.7 units of time and the end node of activity is realized. Since this latter node is not the sink node of network, we go to step 2.

In step 2, we set T = 9–0.7 = 8.3 and RS = 14–4 = 10. Assume that, among the activities emanating from the end node of activity 1, activity 2 has been realized. So, the activity 3 will never occur and the remaining network is as Figure 3.

Figure 3

Remaining network in the first iteration of step 2 of algorithm 2 (first subnetwork).

Above results are as follows.

Table 4

With T = 8.3 and RS = 10, steps 1 and 2 of algorithm are repeated for subnetwork of Figure 3. Results are shown below.

Table 5

By omitting the implemented activity, the remaining network would be as Figure 4.

Figure 4

Remaining network in the second iteration of step 2 of algorithm 2 (second subnetwork).

With T = 7 and RS = 9, steps 1 and 2 of algorithm are applied for the second subnetwork, results are shown as follows.

Table 6

Assume that, among the activities emanating from the end node of activity 4, activity 5 is realized. So, the activity 6 is not realized and the remaining network is as seen in Figure 5.

Figure 5

Remaining network in the third iteration of step 2 of algorithm 2 (third subnetwork).

With T = 5 and RS = 7, the steps 1 and 2 of algorithm are repeated. For the third subnetwork, results are shown below.

Table 7

By omitting the implemented activity, the remaining network would be as Figure 6.

Figure 6

Remaining network in the fourth iteration of step 2 of algorithm 2 (fourth subnetwork).

With T = 4 and RS = 5, the steps 1 and 2 of algorithm are repeated. For the fourth subnetwork, results are shown in the following way.

Table 8

One unit of limited resource remains for one of the realized activity which will be emanated from the end node of activity 7. If activity 8 is realized, the allocated resource will be $s_{l_8}^{\ast }=1$. Otherwise, the allocated resource will be $s_{l_9}^{\ast }=1$. In this approach, the allocation of limited resource is performed simultaneously with the project implementation, based on the last available information. In the given example, the allocation of resource was explained for the special cases that the path {1,2,4,5,7,8} or {1,2,4,5,7,9} was realized. For the other cases of path occurrences, the similar limited resource allocation can be performed.

Conclusions

The following conclusions can be made:

• 1. The proposed model, unlike previous researches, has no limitations related to the type of random variables of activity durations.

• 2. In the problem under study, the number of feasible allocations can be very great, especially in large scale networks. Evaluation of all of these allocations requires tedious computations. The proposed method of this paper prevents us from evaluating all of feasible solutions because of solving the problem in several stages (using MODM model).

• 3. In solving the example of paper, generalized Gaussian quadrature formula and conditional Monte Carlo simulation have been used, respectively. Both methods have desirable accuracy. But in comparison, generalized Gaussian quadrature formula is more accurate.

Recommendations

• 1. This paper utilizes the path occurrence probability as a criterion to determine path preference. If, in some networks, the sink nodes have some preferences to each other, this matter can be considered as a new criterion to determine path preference. This new criterion can be combined with the current criterion of this paper. This combination of criteria is recommended for future studies.

• 2. Other methods concerning the optimization of multi-objective problems can be studied to solve the current problem of this paper.

• 3. In this paper, proposed methods were designed to be applicable for alternative stochastic networks with exclusive-or, probabilistic nodes. Constrained resource allocation in ASN with other types of nodes is recommended as an area for future studies. In these networks, using a critical chain is suggested.

• 4. The solution procedure of this paper can be extended for the case where several types of limited resources are concerned.

• 5. Optimal resource allocation can be a very interesting subject to study, when some resources are of renewable types and some others are of non-renewable types.

• 6. In some networks, the allocation of limited resource to activities might be performed continuously. In this case, development of a method for optimal allocation of resource to the activities would be valuable.

• 7. It is evident that each combination of recommendations 1–6 can be utilized for future studies.

Appendix A

To compute the CDF completion time of path $S_{\left[\gamma \right]}=S_{\mathit{ij}}$ we can write

$$T_{\left[\gamma \right]}=\sum _{k\in S_{\left[\gamma \right]}}{t}_{k,s_{l_K}}$$

(14)

$$P(T_{\left[\gamma \right]}\le T)=P(\sum _{k\in S_{\left[\gamma \right]}}{t}_{k,s_{l_K}}\le T)$$

(15)

If $r\in S_{\left[\gamma \right]}$, then $P(T_{\left[\gamma \right]}\le T|t_{k,s_{l_k}},k\in S_{\left[\gamma \right]},k\ne r)$

$$=P(t_{r,s_{l_r}}\le T-\sum _{\begin{array}{l}k\in S_{\left[\gamma \right]}\\ k\ne r\end{array}}{t}_{k,s_{l_K}})$$

(16)

So, we can write $F_{\left[\gamma \right]}\left(T|t_{k,s_{l_K}},k\in S_{\left[\gamma \right]},k\ne r\right)$

$$=F_{t_r}(s_{l_r},T-\sum _{\begin{array}{l}k\in S_{\left[\gamma \right]}\\ k\ne r\end{array}}{t}_{k,s_{l_K}})$$

(17)

Based on the above equality, two algorithms, A and B, are developed to apply conditional Monte Carlo simulation and generalized Gaussian quadrature formula, respectively.

Algorithm A

Compute $F_{\left[\gamma \right]}\left(T\right)$ by using the following steps for all sets of feasible values $\left\{s_{l_K}|k\in S_{\left[\gamma \right]}\right\}$. The set $\left\{s_{l_K}|k\in S_{\left[\gamma \right]}\right\}$is feasible, if it satisfies the constraints of mathematical model of step1 or step 2 of algorithm 1. That set which provides the greatest value for $F_{\left[\gamma \right]}\left(T\right)$, indicates the optimal allocation of limited resource to activities of path $S_{\left[\gamma \right]}$.

Step 1. Set q=1.

Step 2. Set $L_{\left[\gamma \right]}=$0.

Step 3. For each $k\in S_{\left[\gamma \right]}$, $k\ne r$, generate random variables $t_{k,s_{l_k}}^{\left(q\right)}$.

Step 4. $L_{\left[\gamma \right]}\leftarrow L_{\left[\gamma \right]}+F_{t_r}(s_{l_r},T-\sum _{\begin{array}{l}k\in S_{\left[\gamma \right]}\\ k\ne r\end{array}}{t}_{k,s_{l_K}}^{\left(q\right)})$

Step 5. Set $q\leftarrow q+$1. If $q\le \overline{Q}$, go to step 3. Otherwise, go to step 6.

Step 6. $F_{\left[\gamma \right]}\left(T\right)=\frac{L_{\left[\gamma \right]}}{\overline{Q}}$

Algorithm B

Compute$F_{\left[\gamma \right]}\left(T\right)$ by using the following equality for all sets of feasible values $\left\{s_{l_K}|k\in S_{\left[\gamma \right]}\right\}$. Here, the feasible set is defined the same as defined in algorithm A. That set which provides the greatest value for $F_{\left[\gamma \right]}\left(T\right)$, indicates the optimal allocation of limited resource to the activities of path $S_{\left[\gamma \right]}$.

$$F_{\left[\gamma \right]}\left(T\right)=\underset{\sum _{k\in S_{\left[\gamma \right]}}{t}_k\le T}{\iint }\dots \int F_{t_r}(s_{l_r},T-\sum _{\begin{array}{l}k\in S_{\left[\gamma \right]}\\ k\ne r\end{array}}{t}_k)\prod _{\begin{array}{l}k\in S_{\left[\gamma \right]}\\ k\ne r\end{array}}{f}_{t_k}(s_{l_K},t_k)d{t}_k$$

(18)

Except for special cases, the above analytical computation is not so much easy job. So, now application of Gaussian quandrature formula generalized for stochastic networks is being proposed by [Fatemi Ghomi and Hashemin (1999]).

Appendix B

The sets $S_{\left[1\right]}$ to $S_{\left[Z\right]}$ and functions $F_{\left[1\right]}\left(t\right)$to $F_{\left[Z\right]}\left(t\right)$ are determined using the following steps.

Step 1. Set $\gamma$=1 and $A=\phi$

Step 2. If $P_{\mathit{\alpha \beta }}=max\left\{\left\{P_{\mathit{ij}}|i=1,\dots ,M,j=1,\dots ,n_i\right\}-A\right\}$,then $S_{\left[\gamma \right]}=S_{\mathit{\alpha \beta }}$ and $F_{\left[\gamma \right]}\left(t\right)=F_{\mathit{\alpha \beta }}\left(t\right)$.

Step 3. If $\gamma =Z$, stop. Otherwise set $\gamma \leftarrow \gamma +1$and $A\leftarrow A\cup \left\{P_{\mathit{\alpha \beta }}\right\}$ and return to step 2.

The aim of implementing the above steps is ordering the paths based on their criticality indices in descending manner.