Abstract
Supply chain is an accepted way of remaining in the competition in today's rapidly changing market. This paper presents a coordinated seller-buyer supply chain model in two stages, which is called Joint Economic Lot Sizing (JELS) in literature. The delivery activities in the supply chain consist of a single raw material. We assume that the delivery lead time is stochastic and follows an exponential distribution. Also, the shortage during the lead time is permitted and completely back-ordered for the buyer. With these assumptions, the annual cost function of JELS is minimized. At the end, a numerical example is presented to show that the integrated approach considerably improves the costs in comparison with the independent decisions by seller and buyer.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Background
Supply chain takes on an importance because of the rapid market changes which is the result of the explosion of product varieties with short life cycles in today’s global market ([Ben-Daya et al. 2008]). The effective collaboration of partners and coordination of all activities within the supply chain are prerequisites in such competitive and dynamic market conditions ([Soroor et al. 2009b];[Tarantilis 2008]). So in the recent years, supply chain was dealt with from many points of view such as pricing problem in[Hu et al. (2010]),[Chen and Kang (2010)], and[Huang et al. (2010)], or the fuzzy conditions in supply chain elements in[Xu and Zhai (2010)] and many others.
One major subject in this topic is managing the inventory across the whole supply chain to reduce the costs for customers ([Soroor et al. 2009a]). To deal with this problem, some researchers follow real-time data processing such as radio frequency identification, global positioning system, flow control sensors, cellular telephones, navigation systems, and satellite positioning systems ([Tarantilis 2008];[Soroor et al. 2009c)]. There are some other parallel researches that try to elicit a mathematical model from the integrated supply chain. In order to construct such a model, it is necessary to use some simplifying assumptions. The first integrated supply chain model which was introduced by[Goyal (1977)] and contained only one seller and one buyer was called Joint Economic Lot Sizing (JELS) problem. It was under the most simplifying and deterministic conditions.[Goyal (1977)] presented a solution to the problem under the assumption of the seller’s infinite production rate and lot-for-lot policy for the shipments from the seller to the buyer. In this policy, before shipment, the entire production lot should be ready and each production lot is sent to the buyer as a single shipment.[Banerjee (1986)] eliminated the infinite production rate assumption, but retained lot-for-lot policy. Then the lot-for-lot policy was relaxed by[Goyal (1988)] in an effort to generalize the problem. By constructing a model which allowed shipments to take place during production,[Lu (1995)] decreased the assumption of completing a batch before starting shipments.[Banerjee and Kim (1995)],[Ha and Kim (1997)], and[Kim and Ha (2003)] also considered JELS model with equal-shipment policies.[Viswanathan (1998)] proposed an optimal policy for a particular model relating to problem parameters.[Hill (1997)] further took the geometric growth factor as a decision variable and so generalized the model of[Goyal (1995)].[Goyal and Nebebe (2000)] suggested another simple geometric policy to produce acceptable results. This was a model in which a small shipment is followed by a series of larger and equal-sized shipments. Another generalization made by[Hill (1999)] found the optimal solution and proposed an exact iterative algorithm for solving the problem. The structure of the optimal policy presented on the basis of geometric series was followed by equal-sized shipments.[Hill and Omar (2006)] and[Zhou and Wang (2007)] relaxed the assumption of holding costs. The resultant assumption is that the successive shipment sizes are increased by a fixed factor when the vendor’s holding cost is larger than the buyer’s. The unreliability of the process on JELS is considered by[Ben-Daya and Zamin (2002a)] and[Huang (2004)]. Other extensions of this problem are considered as stochastic parameters.[Ben-Daya and Zamin (2002b)] considered a JELS problem under equal-shipment policy with stochastic demand.
[Ouyang et al. (2004)] assumed the lead time to be stochastic and controllable. He also permitted a shortage during the lead time. In this paper we relax the assumption of deterministic lead time of transporting products from the seller to the buyer and assume lead time as a stochastic variable with exponential distribution. This paper is organized in the following form. In Section Definition of the problem, we define the problem, and also introduce notations and assumptions. The Model formulation Section gives a discussion on independent and integrated policies for seller and buyer. Solution for separate and joint models Section deals with the optimal solution of the independent and integrated model. Numerical results Section presents some numerical examples to compare two models. The conclusion of the paper is given in the Conclusions Section.
Definition of the problem
Model notation
The model is a supply chain which represented a seller with a constant produce rate of ‘p’, and his product is sent to a buyer by shipment equal size of ‘ Q’. The demand for the buyer inventory is constant value of ‘ D’, when the inventory drops to r; buyer makes a new order in the size of ‘ Q’. The notations below are used in the model:
D demand rate for buyer inventory
p production rate of the seller
Q shipment size
r buyer’s reorder point
Av seller’s setup cost
Ab buyer’s ordering cost
hv holding cost for the seller
hb holding cost for the buyer
π shortage cost for the buyer per unit per unit time
n number of shipments
T buyer’s cycle time (time between two successive orders)
L lead time to replenish the buyer’s order
TCb(r, Q) buyer’s expected total cost per unit time
tcb(r, Q, L) buyer total cost of one time cycle in term of L
tcb(r, Q) expected total cost in one cycle for given r and Q
TIv seller’s total inventory
TCv seller’s expected total cost
STC(r, Q, n) separate total cost for buyer and seller
JTC(r, Q, n) joint total cost for buyer and seller
Model assumptions
The assumptions made in the paper are as follow:
-
(1)
Product is manufactured with a finite product rate p.
-
(2)
The final demand for product is deterministic and constant D, where p > D.
-
(3)
The lots delivered to buyer by seller in equal size batches, Q.
-
(4)
The buyer makes an order of Q-size as soon as the inventory drops to r.
-
(5)
In each setup, seller manufactures nQ product to reduce the average setup cost.
-
(6)
Shortage is acceptable and completely back ordered for the buyer.
-
(7)
The policy of shipment is non-delayed i.e., as soon as receiving an order, the seller delivers it, if available; otherwise, it manufactures product of nQ-size and delivers orders during manufacturing phase and after that.
-
(8)
The lead time to deliver the shipment from seller to buyer follows an exponential distribution with parameter λ, i.e., L approximately exp(λ).
-
(9)
Time horizon is infinite.
Model formulation
To obtain the buyer’s expected total cost per unit time, TCb(r, Q), it is considered that the orders are received in a sequence which are not necessarily the same as they have been made. Some extra simplifying assumptions are introduced here to avoid facing intractable problem.
-
(1)
The orders do not cross in time ( [Hadly and Whitin 1963]).
-
(2)
At the start of each time cycle, the net stock is considered to be r.
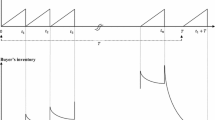
Figure1 presents different possible cases in each cycle for the buyer. Considering the demand rate as D, from the time of ordering in which the inventory position is r until the time r/D current cycle inventory vanishes and after this time if a new lot reaches, shortage cost should be paid because the shipment size is Q. If the lot is delivered to the buyer after time of Q/D, the ordering of new lot is given before reaching the previous lot.
Figure1, case 1 shows the condition in which ordered lot ships the buyer before consuming the recent stock (L ≤ r/ D). In this condition shortage cost does not exist. In case 2, the lead time is more than r/D, but in order that the outstanding order would be delivered before the time of Q/D, it is possible to send next order at the time in which the inventory position decrease to r. But in case 3 in which the lead time exceeds Q/D, the next order is released before receiving the outstanding order.
The buyer total cost of single cycle in terms of L, tcb(r, Q, L), can be written as follows:
and the expected total cost in one cycle for given r and Q, tcb(r, Q) is as follows:
Substituting into the above expression and by dividing the length of the buyer order cycle, Q/D, we obtain the buyer's expected total cost per unit time as the following expression,
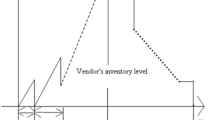
The way of obtaining the seller’s total inventory is presented in such literatures as[Lee (2005)],[Wee and Chung (2007)],[Lin (2008)],[Ouyang et al. (2007)],[Chang et al. (2006)], and[Ouyang et al. (2004)]. We present a simple manner in Figure2 for calculating the seller's total inventory.
By using S as area of a surface, we can write:
and since orders are received by the seller at known intervals, the seller’s expected total cost (TCv) is as follows:
We have proved (see Appendix 2) that TCv(n) is convex in n, and optimal solution ( n*), satisfies the condition:
Solution for separate and joint models
First, we consider solution for the case in which the seller and buyer optimize their total cost functions separately. The optimal solution will be denoted by (rs*, Qs*, ns*) in this case, and we show sum of costs of seller and buyer with
In the other case, joint total cost (JTC) function is optimized as a whole. In this case we sum the costs together to obtain joint total cost
and show its optimal solution with (rj*,Qj*,nj*). Because of convexity of TCb (see Appendix 1) and TCv, the obtained separate solution is general. On the other hand, it can be shown that in spite of convexity of JTC on each of r, Q, or n alone, it is not a convex function generally. It can be observed thatand hence, the optimality condition on n (Equation 6) is valid here. Thus in the procedure of solving JTC, we set n = i, with start of i = 1, and calculate the optimal values of r and Q, and increase i one unit in each step until the optimality in condition (Equation 6) is satisfied. It is not necessary to focus on the method of finding optimal solution of JTC (when n is fixed), TCb and TCv because general methods like derivative-free method in many types of software such as MATLAB (MathWorks, Natick, MA, USA) can solve this problem easily.
Results and discussion
Numerical results
In this part an example with the following data will be presented as follows: D = 1,000/years, Ab = $25/order, hv = $4/unit/year, hb = $5/unit/year, π = $30/unit/year; and we change p by the values 5,000, 7,000, and 9,000, and 1/λ by the values 10, 15, 20, 25, 30, 35, 40, 45, and 50 to explore variation effects of lead time to the percentage of saving in individually optimized total cost over integrated inventory policy. As mentioned by[Goyal (1977)] and[Ouyang et al. (2004)], the total benefit under integrated optimization should be shared by both parties to encourage them to cooperate together. It can be done as follows:
Referring to the existing literature, we consider percentage saving ‘ps’ as (STC-JTC)/STC*100. Figure3 shows ps increases for more variable lead time, which is the characteristic of many cases in unpredictable real environment. It also shows that the percentage of improvement increases when there is a rise in the production rate. For instance, the percentage of improvement is 3.7 % for p = 5,000 (increase from 1.6 for 1/λ = 5 days to 5.3 for 1/λ = 50 days) and where it is 6.2 % for p = 9,000 (increase from 2.4 for 1/λ = 5 days to 8.6 for 1/λ = 50 days). By joining and coordinating, both seller and buyer can control the variability effect of lead time by decreasing the number of shipments and increasing batch sizes for higher level of production rate. However, this does not happen when they work separately and cannot react to the variation of shipment lead time (Table1).
Conclusions
An integrated model for JELS in which lead time of delivering the shipment is not deterministic, which follows an exponential distribution, was presented in this article. We showed that integrated inventory policy increases profit of both buyer and seller, if they can compromise to divide the gained benefit of coordination. This policy is completely executable in a unit system containing two parts, but may not be suitable for separate systems when percentage of improvement is low. A numerical example showed that the cooperation between two supply chain partners in the integrated situation is more useful in unreliable purchasing environments in terms of lead times of shipments. Stochastic lead time with an exponential distribution is the difference of the current research with the previous ones. Authors are in the process of decreasing. simplifying or adding assumptions of this model ((1) the orders don not cross in time and (2) at the start of cycle time, the net stock is considered to be r) to conform it more to the real system. The model also can be extended to situations, such as general distributions for lead times, multi vendor case, stochastic demand, and stochastic price. We hope that this extension will be helpful to researchers who are interested in integrating decisions on supply chain.
Methods
The used method in this article is mathematical modeling. This model is an expansion of previous version with a change in delivery lead time assumption. Like all such models, to confirm the performance of model, a computer simulation experiment was conducted.
Appendix 1
Here we survey convexity of TCb. By calculating the second partial derivations of TCb, we get
Since h11 > 0, to prove H is positive definite and therefore TCb is convex, it should be only shown that Hessian determinant i.e., is positive. To avoid the complexity of calculation in general cases for all values of parameters, we construct some conditions that stated problems in literature that were satisfied, and so they are logically acceptable for the application purpose. These conditions are. Also, we define.
The first sentence is positive. The sum of next two sentences is also positive since r < Q, thus, and with substitution, it will be to gain
In the last expression, all elements including second parenthesis are positive, since
On the other hand, the sum of the last two sentences of |H| is also positive, because
Consequently TCb is strictly convex.
Appendix 2
In equating the first derivation of TCv with zero, we obtain
On the other hand, derivation of the second order of TCv is, and hence, TCv is strictly convex on n.
Author’s information
Mehrab Bahri is a PhD student from the Department of Industrial Engineering, Science and Research Branch in the Islamic Azad University in Tehran.
References
Banerjee A: A joint economic-lot-size model for purchaser and vendor. Decis Sci 1986, 17: 292–311. 10.1111/j.1540-5915.1986.tb00228.x
Banerjee A, Kim SL: An integrated JIT inventory model. Intern J Oper & Production Management 1995,15(9):237–244. 10.1108/01443579510099760
Ben-Daya M, Zamin SA: Effect of preventive maintenance on the joint economic lot sizing problem with imperfect processes. Systems Engineering Department, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia, Technical Report; 2002.
Ben-Daya M, Zamin SA: Joint economic lot sizing problem with stochastic demand. Systems Engineering Department, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia, Technical Report; 2002.
Ben-Daya M, Darwish M, Ertogral K: The joint economic lot sizing problem: review and extensions. Eur J Oper Res 2008, 185: 726–742. 10.1016/j.ejor.2006.12.026
Chang HC, Ouyang LY, Wu KS, Ho CH: Integrated vendor-buyer cooperative inventory models with controllable lead time and ordering cost reduction. Eur J Oper Res 2006, 170: 481–495. 10.1016/j.ejor.2004.06.029
Chen LH, Kang FS: Integrated inventory models considering permissible delay in payment and variant pricing strategy. Appl Math Model 2010,34(1):36–46. 10.1016/j.apm.2009.03.023
Goyal SK: An integrated inventory model for a single supplier-singl e customer problem. Int J Prod Res 1977,15(1):107–111. 10.1080/00207547708943107
Goyal SK: A joint economic-lot-size model for purchaser and vendor: a comment. Decis Sci 1988, 19: 236–241. 10.1111/j.1540-5915.1988.tb00264.x
Goyal SK: A one-vendor multi-buyer integrated inventory model: a comment. Eur J Oper Res 1995, 82: 209–210. 10.1016/0377-2217(93)E0357-4
Goyal SK, Nebebe F: Determination of economic production-shipment policy for a single-vendor single-buyer system. Eur J Oper Res 2000, 121: 175–178. 10.1016/S0377-2217(99)00013-2
Ha D, Kim SL: Implementation of JIT purchasing: an integrated approach. Production Planning & Control 1997, 8: 152–157. 10.1080/095372897235415
Hadley G, Whitin TM: Analysis of inventory systems. Wiley, New York; 1963.
Hill RM: The single-vendor single-buyer integrated production-inventory model with a generalized policy. Eur J Oper Res 1997, 97: 493–499. 10.1016/S0377-2217(96)00267-6
Hill RM: The optimal production and shipment policy for the single-vendor single-buyer integrated production-inventory model. Int J Prod Res 1999, 37: 2463–2475. 10.1080/002075499190617
Hill R, Omar M: Another look at the single-vendor single-buyer integrated production-inventory problem. Int J Prod Res 2006,44(4):791–800. 10.1080/00207540500334285
Hu O, Wei Y, Xia Y: Revenue management for a supply chain with two streams of customers. Eur J Oper Res 2010,200(2):582–598. 10.1016/j.ejor.2009.01.006
Huang CK: An optimal policy for a single-vendor single-buyer integrated production inventory problem with process unreliability consideration. Int J Prod Econ 2004, 91: 91–98. 10.1016/S0925-5273(03)00220-2
Huang CK, Tsai DM, Wu JC, Chung KJ: An integrated vendor-buyer inventory model with order-processing cost reduction and permissible delay in payments. Eur J Oper Res 2010,202(2):473–478. 10.1016/j.ejor.2009.05.035
Kim SL, Ha D: A JIT lot-splitting model for supply chain management: enhancing buyer–supplier linkage. Int J Prod Econ 2003, 86: 1–10. 10.1016/S0925-5273(03)00006-9
Lee W: A joint economic lot size model for raw material ordering, manufacturing setup, and finished goods delivering. Omega 2005, 33: 163–174. 10.1016/j.omega.2004.03.013
Lin YJ: An integrated vendor-buyer inventory model with backorder price discount. Computers &Industrial Engineering 2008. 10.1016/j.cie.2008.10.009
Lu L: A one-vendor multi-buyer integrated inventory model. Eur J Oper Res 1995, 81: 312–323. 10.1016/0377-2217(93)E0253-T
Ouyang LY, Wu KS, Hu CH: Integrated vendor-buyer cooperative models with stochastic demand in controllable lead time. Int J Prod Econ 2004,92(3):255–266. 10.1016/j.ijpe.2003.10.016
Ouyang LY, Wu KS, Ho CH: An integrated vendor-buyer inventory model with quality improvement and lead time reduction. Int J Production Economics 2007, 108: 349–358. 10.1016/j.ijpe.2006.12.019
Soroor J, Tarokh MJ, Keshtgary M: Preventing failure in IT-enabled systems for supply chain management. Int J Prod Res 2009,47(23):6543–6557. 10.1080/00207540802314837
Soroor J, Tarokh MJ, Shemshadi A: Theoretical and practical study of supply chain coordination. J Bus Ind Mark 2009,24(2):131–142. 10.1108/08858620910931749
Soroor J, Tarokh MJ, Shemshadi A: Initiating an state of the art system for real time supply chain coordination. Eur J Oper Res, Elsevier BV 2009,196(2):635–650.
Tarantilis CD: Topics in real-time supply chain management. Comput Oper Res 2008, 35: 3393–3396. 10.1016/j.cor.2007.01.028
Viswanathan S: Optimal strategy for the integrated vendor-buyer inventory model. Eur J Oper Res 1998, 105: 38–42. 10.1016/S0377-2217(97)00032-5
Wee HM, Chung CJ: A note on the economic lot size of the integrated vendor-buyer inventory system derived without derivatives. Eur J Oper Res 2007, 177: 1289–1293. 10.1016/j.ejor.2005.11.035
Xu R, Zhai X: Analysis of supply chain coordination under fuzzy demand in a two-stage supply chain. Appl Math Model 2010,34(1):129–139. 10.1016/j.apm.2009.03.032
Zhou Y, Wang S: Optimal production and shipment models for a single-vendor-single-buyer integrated system. Eur J Oper Res 2007,180(1):309–328. 10.1016/j.ejor.2006.04.013
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
MB carried out the literature review and constructed the proposal model and drafted the manuscript. MJT supervised the research and guided him to do correction. He also revised and improved the model, then designed the simulation for validation of the model. Both authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bahri, M., Tarokh, M.J. A seller-buyer supply chain model with exponential distribution lead time. J Ind Eng Int 8, 13 (2012). https://doi.org/10.1186/2251-712X-8-13
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2251-712X-8-13